Abstract
Philippou and Kouzapas have proposed a privacy-related framework, consisting of (i) a variant of the \(\pi \)-calculus, called Privacy Calculus, that describes the interactions of processes, (ii) a privacy policy language, (iii) a type system that serves to check whether Privacy Calculus processes respect privacy policies. We present an executable implementation of (a version of) it in the programming/specification language Maude: we give an overview of the framework, outline the key aspects of its implementation, and offer a simple example of how the implementation can be used.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
1.1 Related Work
In recent years, the advancement of technology has posed a great threat to privacy. As a result, privacy enforcement needs relevant tools that protect user privacy and detect potential or actual breaches. A long-term goal that follows from these concerns and has attracted some interest recently is to have sound and efficient formal systems that can be used in practice to reason about privacy-related properties of information systems and enforce privacy requirements.
[6] defines a framework which uses type checking and a custom variant of the \(\pi \)-calculus, in order to reason about data on the Web, particularly the data expressed with standards such as RDF. [13] defines a rather expressive formal system based on epistemic logic, tailored to reasoning about the privacy policies of social networks. Another formal framework for privacy, which is the basis of the present paper, is described in [8] and its extensions [7, 9, 15]; it consists of privacy policies and processes/systems of a variant of \(\pi \)-calculus, bridged with a type checker. Moreover, since privacy policies share some common properties with access control policies, there have been attempts to extend access control policies, in order to be usefully applicable for privacy purposes; such an extension, which has influenced our work, is P-RBAC [1, 11, 12].
Maude is a powerful tool with many uses. We opted for it due to its firm mathematical foundations (equational and rewriting logic), its executable semantics, and its reflective character, which simplifies proving properties of specifications in the same framework they are defined; it is also claimed to be rather efficient [10]. We believe that having executable implementations of the frameworks defined can aid in applying them at greater scale and, thus, in spotting difficulties in their widespread use. In addition, one could use automatic theorem proving on such implementations to mechanically prove useful properties of their specifications.
1.2 Overview
The work we present here has mostly been carried out as part of a diploma thesis [16] in the School of Applied Mathematical and Physical Science of the National Technical University of Athens, supervised by Prof. Petros Stefaneas. The main contributions of the thesis were (i) the extension of the framework of [7] (privacy policy language, processes/systems of \(\pi \)-calculus, type checker), mostly by the incorporation of the concept of conditions and (ii) the implementation of the (extended) framework in Core Maude. The first part has been presented in [15], but the essential parts of it will be summed up here (in some cases, there have been improvements; we indicate them and compare them with [15]).
The code of the specification is not included in this paper (for lack of space), but can be found in http://users.ntua.gr/gpitsiladis/isola2018/privacy.maude. It is split into several modules in order to facilitate its reading and its future examination with Maude tools, such as the Church-Rosser Checker and the Sufficient Completeness Checker [4, Sect. 1.3]. The code of the running Example (Examples 1, 2, and 3 below) is in http://users.ntua.gr/gpitsiladis/isola2018/example-sales.maude.
As depicted in Fig. 1, the framework (and, hence, the tool) is split into three parts: Privacy Calculus, privacy policy language, and type system. The Privacy Calculus, using the construct of Systems, models the code of the application whose privacy properties are under scrutiny. The privacy policy language models rules and policies regarding privacy as Privacy Policies. The type system, using the construct of \(\varGamma \)-Environments to model information about the environment the code is running in, checks (using the function \(\vdash \)) syntactic well-formedness of Systems and, more importantly, with the help of the internal construct of \(\varTheta \)-Interfaces (which are the types of Systems), checks (using the relation \(\models \)) compliance of Systems (hence application code) to Privacy Policies.
The structure of the framework. It is comprised of three parts: the Privacy Calculus, a privacy policy language, and a type system. Each contains a construct to model application code, privacy policies, and execution environment respectively. The framework can check for the syntactic well-formedness of code and for its compliance to a privacy policy.
The structure of the paper closely follows the structure of the framework: Sect. 2 describes the privacy policy language, Sect. 3 describes the Privacy Calculus, and Sect. 4 describes the type checker that can be used to test systems of the Privacy Calculus for policy compliance; each of these sections is split into a subsection describing the mathematical specification of the respective part of the framework and a subsection describing its implementation in Maude (design choices, sort and operator declarations, and example of usage). Finally, Sect. 5 contains concluding remarks and possible directions for future work.
2 The Privacy Policy Language
The privacy policy language of our tool is a slightly more mature version of the one in [15, Sect. 2], which itself extends the language of [7, Sect. 3] with conditions and splits the notion of groups into users and roles, in the spirit of [11].
2.1 Mathematical Specification
Policies are specified on top of some basic notions: (i) groups (split in users and roles), (ii) purposes, and (iii) data types (or basic types). Groups are characterisations of entities that can act upon private data. The concept of purposes is vital when dealing with privacy issues [2, Sect. 1]. Data types are types (such as \(\mathtt {Age}\), \(\mathtt {Time}\)) of private or not private data. Each data type X can be granted with a finite data value set \(\mathrm {D}_X\) that serves for the formation of conditions; a condition is either a statement that a data type has (or has not) a specific value or a conjunction of such statements; for example, \(\mathtt {AgeRange}\ne \mathtt {under18}\wedge \mathtt {Consent}=\mathtt {Yes}\).
A policy maps each of the (private) basic types in its domain to a hierarchy of purpose-endowed groups and a permission function, which grants permissions to group-purpose pairs; the available permissions in our tool (which can easily be adapted to the needs of different applications) are \(\mathtt {read}\), \(\mathtt {write}\), \(\mathtt {access}\), \(\mathtt {disc}\,G\) where G can be any group. All (unconditional) permissions can become conditional, by appending to them the keyword \(\mathtt {if}\) and a condition.
Conditions can be partially ordered by the “strictness” relation \(\le \), that is \(c_1\le c_2\) iff for each data type X appearing in \(c_2\), X also appears in \(c_1\) and the values of X satisfying \(c_1\) also satisfy \(c_2\). This induces a partial order \(\le \) on (conditional) permissions, where \(p_1\le p_2\) iff \(p_1=p_2\) or \(p_1\) is \(p_2\) with some extra condition(s). This, in turn, induces a preorder \(\lesssim \) on permission sets, where \(P_1\lesssim P_2\) iff \(P_2\) contains an upper bound for each element of \(P_1\).
2.2 Implementation and Usage
All the above are easily (if carefully) implemented in membership equational logic. For the sets of purposes, hierarchies, permissions, data types, and data type values (and, later, names, types, and groups), we include the parametric
 module available in Maude, instantiated with the corresponding sort. The sets of data types and data type values get all their operators renamed, so as to avoid clashes with further importations of sets of their supersorts. Also, the sets of permissions and purposes get their constructing operator
module available in Maude, instantiated with the corresponding sort. The sets of data types and data type values get all their operators renamed, so as to avoid clashes with further importations of sets of their supersorts. Also, the sets of permissions and purposes get their constructing operator
 renamed to
renamed to
 .
.
Example 1
Suppose we are modelling a company whose privacy policy with regard to marketing contains the clause “Personal information of customers may be disclosed to third parties if the customer gives their consent. Personal information of customers under thirteen years old will never be disclosed to third parties.” and we consider the private data of a single user named Alice. The entities that interest us in this case are of course Alice and the marketing department, but also the server and database of the company. Alice and the server act for the purpose of purchasing a product, the database acts for the purpose of storage, and the marketing department acts for the purpose of marketing.
First, we have to start a new module (or several modules) that includes those components of the tool that we wish to use. The main modules of interest are:
-
 , a functional module that provides everything needed for type checking Privacy Calculus systems against policies,
, a functional module that provides everything needed for type checking Privacy Calculus systems against policies, -
 , a functional module that defines the sorts containing application-specific information (
, a functional module that defines the sorts containing application-specific information (
 ,
,
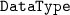 ,
,
 , etc.), so we have to extend it when using the tool.
, etc.), so we have to extend it when using the tool.
Inside our module, we have to define the groups, purposes, and data types we are going to use. In our example, the groups are: a user \(\mathtt {Alice}\), the roles of the company (\(\mathtt {Company}\), \(\mathtt {Server}\), \(\mathtt {DB}\), \(\mathtt {MarketingDpt}\)), and the roles \(\mathtt {Clients}\), \(\mathtt {ThirdParty}\); since hierarchies need to have a single root, we employ the role \( \mathtt {Comp \& Clients}\). So, we declare

The declaration of purposes is simple:

As for data types, we have Alice’s private data: \(\mathtt {Age}\) and \(\mathtt {Consent}\), with specific value sets, and \(\mathtt {OrderData}\), with no specific value set. \(\mathtt {OrderData}\) is declared as
 , \(\mathtt {Age}\) is declared as
, \(\mathtt {Age}\) is declared as

and \(\mathtt {Consent}\) (with values \(\mathtt {yes}\) and \(\mathtt {no}\)) is similar. If we had a non-private data type (such as \(\mathtt {Time}\)), we would follow the same procedure, using
 instead of
instead of
 and
and
 instead of
instead of
 .
.
We can now model the policy at hand. For ease of presentation, we will use the same hierarchy for all private data types. Hierarchies are built with the operator
 , but shorthands are provided for cases where there is no purpose or no subhierarchy. Thus, the hierarchy of our example can be defined as follows:
, but shorthands are provided for cases where there is no purpose or no subhierarchy. Thus, the hierarchy of our example can be defined as follows:

Note that hierarchies can have cycles, but a group is not permitted to appear in its subhierarchy. The privacy policy of the company can be defined as follows:

Note that conditions bind to the nearest permission; for example,
 states that the marketing department can access order data (for marketing purposes) unconditionally, but can only disclose it to third parties (for the same purpose) if two conditions hold. Note also that any permission not given explicitly is not allowed by the policy.
states that the marketing department can access order data (for marketing purposes) unconditionally, but can only disclose it to third parties (for the same purpose) if two conditions hold. Note also that any permission not given explicitly is not allowed by the policy.
3 The Privacy Calculus
Privacy Calculus is a version of (typed) \(\pi \)-calculus with the group construct of [3]. In our tool, we use it as presented in [15, Sect. 3], with the addition of CINNI [18] and some alterations in its semantics described below.
3.1 Mathematical Specification and Implementation in Maude
Syntax. For names of channels, hereafter ranged over by x, y, z, in order to tackle the usual issues with name binding, we employ CINNI: consider an (infinitely countable) set of name IDs (ranged over by a, b); each name ID can be turned into an (indexed) name by subscripting it with a non negative integer, referring to the bindings for the same ID we have to skip. In the Maude implementation, we use
 as the source of name IDs (by specifying
as the source of name IDs (by specifying
 ) and add an operator
) and add an operator
 to signify subscripting. We also include all data values as names in our calculus, thinking of them as constants:
to signify subscripting. We also include all data values as names in our calculus, thinking of them as constants:
 .
.
One of the principal goals of CINNI is to define name substitution (declared as
 and
and
 ) elegantly; it also defines the
) elegantly; it also defines the
 ,
,
 and
and
 operators, behaving is as described in Table 1, all of which are constructors of the sort
operators, behaving is as described in Table 1, all of which are constructors of the sort
 .
.
 ,
,
 and
and
 .
.
 and
and
 are different name labels.
are different name labels.
 is some term of sort
is some term of sort
 . It is defined in [18, p. 6] and also described in [19, Table 1].
. It is defined in [18, p. 6] and also described in [19, Table 1].Types, hereafter denoted by T, are defined recursively: data types are types and for each group G and type T, G[T] is a type; intuitively, G[T] means a channel belonging to group G carries data of type T. For example, the term
 is a channel (to be used by members of group
is a channel (to be used by members of group
 ) that carries names of channels (to be used by members of group
) that carries names of channels (to be used by members of group
 ) carrying data of type
) carrying data of type
 .
.
Programmes of privacy calculus are defined in two levels: processes (denoted by P) and systems (denoted by S):
-
1.
The processes \(\mathbf {0}\), \(P_1 \mathbin {\mid }P_2\), !P, \((\mathrm {\nu } \, a \mathrel {:} T) P\), \(x(a \mathrel {:} T). P\), \(\overline{x}\mathord {\langle }y\mathord {\rangle }. P\) and \(\left[ x \mathbin {=} y\right] \left( P_1\mathbin {;}P_2\right) \) are standard constructs of \(\pi \)-calculus: the empty process (does nothing), the parallel composition of two processes, the (unbounded) replication of a process, the binding of a name (thought of as creation of a channel), the input process (a is a placeholder for a name to be received by P through x), the output process (output y through x and then continue as P), and the conditional (if the names x and y are equal, then proceed as \(P_1\), else proceed as \(P_2\)).
-
2.
The system \(G : u\left[ P\right] \) declares that a process P is running on behalf of group G for the purpose u (the group G is bound). The system \(R\left[ S\right] \) declares that the system S is running on behalf of role R (the group R is bound). Finally, the systems \(\mathbf {0}\), \((\mathrm {\nu } \, a \mathrel {:} T)S\), \(S_1 \mathbin {\parallel }S_2\) act like the respective processes (we use \(\mathbin {\parallel }\) instead of \(\mathbin {\mid }\) for the parallel composition of systems).
The declaration of the above definitions in Maude is mostly straightforward. As explained in [4, Sect. 14.2.6], \(\mathbf {0}\) being the identity element of parallel composition could (and would) lead to non termination, so we use sorts
 and
and
 of non empty processes/systems to avoid this issue. We then have to declare how operators behave with respect to these subsorts; for example:
of non empty processes/systems to avoid this issue. We then have to declare how operators behave with respect to these subsorts; for example:

Notice the usage of
 in all the declarations of operators that form processes and systems. As seen later, in the operational semantics of \(\pi \)-calculus, the next step of a process/system happens at the root of its syntactic tree (of course, it may then propagate to subterms). Without the
in all the declarations of operators that form processes and systems. As seen later, in the operational semantics of \(\pi \)-calculus, the next step of a process/system happens at the root of its syntactic tree (of course, it may then propagate to subterms). Without the
 attribute, rewriting (that is, operational steps) could be triggered in subterms of a process/system.
attribute, rewriting (that is, operational steps) could be triggered in subterms of a process/system.
In the declaration of parallel composition, we also use the equational attributes
 , which specify properties that normally are part of the structural congruence of \(\pi \)-calculus. These attributes allow Maude to identify processes/systems with the same behaviour; since they are built-in, using them is more computationally efficient than specifying explicitly the corresponding rules of structural congruence.
, which specify properties that normally are part of the structural congruence of \(\pi \)-calculus. These attributes allow Maude to identify processes/systems with the same behaviour; since they are built-in, using them is more computationally efficient than specifying explicitly the corresponding rules of structural congruence.
For ease of usage, when defining processes/systems, we sometime want to write a instead of \(a_0\); since
 is not a subsort of
is not a subsort of
 and we do not wish to introduce an extra operator, we add special cases of constructor operators; for example:
and we do not wish to introduce an extra operator, we add special cases of constructor operators; for example:

For ease of reading, some operators are written differently in Maude: \(\mathbf {0}\) become
 and
and
 , \(x(a \mathrel {:} T).P\) becomes
, \(x(a \mathrel {:} T).P\) becomes
 , and \(\overline{x}\mathord {\langle }y\mathord {\rangle }.P\) becomes
, and \(\overline{x}\mathord {\langle }y\mathord {\rangle }.P\) becomes
 . For the conditional, we declare shorthands for cases where one of the branches is the empty process. Finally, we define a normal form for condition checking: if a name is compared to a constant, the constant is written after the name.
. For the conditional, we declare shorthands for cases where one of the branches is the empty process. Finally, we define a normal form for condition checking: if a name is compared to a constant, the constant is written after the name.
As usual, we define the operator  that collects the names free in a process/system. Its declaration is simple, except for name binders, where we have to use shifting; for example:
that collects the names free in a process/system. Its declaration is simple, except for name binders, where we have to use shifting; for example:

Moreover, we define the operators  and
and  for free and bound groups.
for free and bound groups.
For name substitution and other CINNI operations, we have an operator
 (similarly for systems) that carries CINNI operations to free names. As specified by CINNI, name binders need lifting; for example:
(similarly for systems) that carries CINNI operations to free names. As specified by CINNI, name binders need lifting; for example:
 .
.
Semantics. As is usual, our discussion of \(\pi \)-calculus semantics commences with structural congruence, i.e. a relation that identifies syntactically different processes/systems with identical intended behaviour. The structural congruence of our calculus is simple: it states that (i) \(\alpha \)-equivalent constructs are congruent, (ii) parallel composition is associative commutative, with the empty process/system as identity element, (iii) binding a name or group in the empty process/system leaves us with the empty process/system, and (iv) replicating the empty process leaves us with the empty process. As explained above, we included part (ii) in the declaration of some operators; since CINNI takes care of name bindings, \(\alpha \)-equivalence can be silently ignored with no problems; the rest can be dealt with by adding some equalities, such as
 and
and
 .
.
Note that the structural congruence of [3] includes rules regarding group binding; as explained in [8, pp. 3–4], since we give extra privacy-related meaning to the binding of a group, we have to omit the one stating that the binding of a group in a (non-empty) system can be omitted when the group is not used in the system. Due to this peculiarity of our structural congruence, the operational semantics of privacy calculus is better defined as a labelled transition semantics.
In all its other versions, privacy calculus is presented with early semantics, but its implementation would either lead to a state explosion (since the possible messages that can be received by a process are infinite) or require some workaround, as in [19, pp. 7–8]. As a consequence, we employ late semantics, which avoids this issue; incidentally, [14, p. 35] states “experimental evidence indicates that proof systems and decision procedures using the late semantics are slightly more efficient”.
Labels for labelled transition semantics are built as follows: \(\tau \) is the silent/internal action, \(x(a)\) is input, \(\overline{x}\mathord {\langle }y\mathord {\rangle }\) is output and \((\mathrm {\nu } \, y \mathrel {:} T)\overline{x}\left\langle y\right\rangle \) is bound output; all names are free, except for y in \((\mathrm {\nu } \, y \mathrel {:} T)\overline{x}\left\langle y\right\rangle \). The rules of our semantics are presented in Fig. 2.
The primary aim of our tool is to statically check whether a system adheres to a policy; as a consequence, we need not have implemented the semantics of Privacy Calculus in Maude. However, we did implement it, aiming for a more complete tool and for the ability to study the behaviour of a Privacy Calculus system using Maude’s
 command [4, Sect. 5.4.3], something that might turn out to be useful in applications. The semantics can be found in a rewrite module called
command [4, Sect. 5.4.3], something that might turn out to be useful in applications. The semantics can be found in a rewrite module called
 . For its implementation, we use some ideas from [19, Sect. 3–4]:
. For its implementation, we use some ideas from [19, Sect. 3–4]:
-
1.
A one-step transition \(F\mathrel {\xrightarrow {l}}F^\prime \) is encoded as a rewrite
 ; in order for this kind of expressions to be well-defined, we have to define a sort
; in order for this kind of expressions to be well-defined, we have to define a sort
 , as follows (and similarly for systems):
, as follows (and similarly for systems): 
The interesting cases of (Congr) are taken care of by CINNI (which reduces \(\alpha \)-equivalence to bound name selection) and Maude (via the equations and equational attributes defining structural congruence). The other rules of Fig. 2 are just transcribed in the chosen form; for example:

-
2.
The operator that builds objects of
 is declared using the
is declared using the
 attribute, so as to control rewrites (as described above on page 7). Consequently, a mechanism must be provided explicitly for multi-step transitions; for processes, it suffices to provide the following code, with
attribute, so as to control rewrites (as described above on page 7). Consequently, a mechanism must be provided explicitly for multi-step transitions; for processes, it suffices to provide the following code, with
 a variable of
a variable of
 (transitions of systems are similar):
(transitions of systems are similar): 
Objects of sort
 trigger rules
trigger rules
 and
and
 . Operator
. Operator
 prevents infinite regressions where rules are used as conditions to themselves, a situation that would result if we just defined
prevents infinite regressions where rules are used as conditions to themselves, a situation that would result if we just defined
 to be a subsort of
to be a subsort of
 .
.
3.2 Usage
In applications, Privacy Calculus will most probably be used as an intermediate language between the code in need of privacy analysis and the modules that will check adherence to policies. However, at this stage, one has to model the situation directly in \(\pi \)-calculus and provide the resulting system to the framework. This is achieved by defining (as in Example 1) the groups, purposes, data types, and data values in use and then synthesising the system that describes the behaviour to be analysed.
As discussed above, one can use Maude’s
 (or
(or
 ) command to find possible transitions of a system, although searching can take a lot of time for large system. Of course, this requires that the module specifying the system includes the rewrite module
) command to find possible transitions of a system, although searching can take a lot of time for large system. Of course, this requires that the module specifying the system includes the rewrite module
 .
.
Example 2
In the context of Example 1, the system
 below contains (among other subsystems that have been replaced with ellipses for ease or presentation) a subsystem for the marketing department that reads the consumer’s age and consent, checks their values, and (if the conditions hold) gets the order data and forwards it through an unknown channel.
below contains (among other subsystems that have been replaced with ellipses for ease or presentation) a subsystem for the marketing department that reads the consumer’s age and consent, checks their values, and (if the conditions hold) gets the order data and forwards it through an unknown channel.

The
 command may be used as follows (after loading the tool and the module(s) defining
command may be used as follows (after loading the tool and the module(s) defining
 ):
):

gives all the possible single-step transitions of
 , while
, while

gives 10 possible multi-step transitions of
 with a silent transition as their last step. Due to the rule of transitivity in our specification of multi-step transitions, the second numerical argument to
with a silent transition as their last step. Due to the rule of transitivity in our specification of multi-step transitions, the second numerical argument to
 is irrelevant, since the search tree always has depth 1; for the same reason, using
is irrelevant, since the search tree always has depth 1; for the same reason, using
 may lead to non-terminating computation (since there are non-terminating systems), so one has to use
may lead to non-terminating computation (since there are non-terminating systems), so one has to use
 for searching multi-step transitions.
for searching multi-step transitions.
4 The Type Checker
The type checker enforces the well-formedness of processes/systems and statically extracts their types, which describe the permissions needed in a structured form that also logs the relevant groups and purposes. The extracted information can then be compared to a privacy policy to check the adherence of a system to it. In [7], it is proved that the type checker is safe, in the sense that it does not flag non-adherent systems as adherent; as argued in [15], this property is not violated by the addition of conditions in the manner presented here.
4.1 Mathematical Specification
Type checking is based on \(\varGamma \)-Environments, \(\varDelta \)-Environments, and \(\varTheta \)-Interfaces.
\(\varGamma \)-Environments map (free) channel names to types and store the groups and conditions in scope; they serve to check the syntactic well-formedness of processes/systems and extract their type. \(\varGamma \)-Environments can be appended (if they contain different names and groups) with the operator \(\mathbin {\cdot }\).
\(\varDelta \)-Environments are the types of processes; they map private data types to permission sets. \(\varDelta \)-Environments can be appended (if the types in their domain are different) with  and combined with
and combined with  . A condition can be added to a \(\varDelta \)-Environment with
. A condition can be added to a \(\varDelta \)-Environment with  . Functions
. Functions  and
and  create default \(\varDelta \)-Environments, according to the type T given as argument; these should probably be tailored for specific applications, depending mainly on the basic permissions included; in our tool, where the basic permissions are
create default \(\varDelta \)-Environments, according to the type T given as argument; these should probably be tailored for specific applications, depending mainly on the basic permissions included; in our tool, where the basic permissions are  ,
,  ,
,  , and
, and  , we have opted for the following definitions, where t signifies some private data type:
, we have opted for the following definitions, where t signifies some private data type:

\(\varTheta \)-Interfaces are the types of systems; they map private data types to pairs of a linear single-purpose group hierarchy and a permission set. They can be appended with  . We can add a group to their hierarchies with
. We can add a group to their hierarchies with  . Given a group G, a purpose u, and a \(\varDelta \)-Environment \(\varDelta \), we can form the \(\varTheta \)-Interface \(G\left[ u\right] \oplus \varDelta \).
. Given a group G, a purpose u, and a \(\varDelta \)-Environment \(\varDelta \), we can form the \(\varTheta \)-Interface \(G\left[ u\right] \oplus \varDelta \).
The rules of the type system, presented in Fig. 3, are mostly as in [15, Fig. 3]. Rules (Out), (ParP), (ParS), (Nil), (Rep), (ResGP), and (ResGS) remain as before. CINNI affects (In), (ResNP), and (ResNS). Rules (CondC) and (GCond) have replaced the equivalent (CondA), (CondB). Comparison of two arbitrary names (note that this does not provide any information about the condition holding) is handled by (CondV). Finally, (Name) is split to (VName), (CName), since types of constants are known a priori.
Once extracted, a \(\varTheta \)-Interface can be tested for conformance to a policy with the operator \(\models \) of [15, Sect. 4]. In effect, given a policy \(\mathcal {P}\) and a \(\varTheta \)-Interface \(\varTheta \), \(\mathcal {P}\models \varTheta \) iff for each private data type in \(\varTheta \) used by a set of groups for a purpose, the set of permissions exercised is bounded above (according to \(\lesssim \)) by the permissions granted by the policy to the game groups for the same purpose and data type.
As proved in [15, Sect. 5], the operators \(\models \) and \(\vdash \) can be jointly used to test a process for errors, in a suitable sense of the terms “error” and “test”. In particular, define a system S to be an error with respect to policy \(\mathcal {P}\) and \(\varGamma \)-Environment \(\varGamma \) (notation \(\mathrm {error}_{\mathcal {P}, \varGamma }(S)\)) iff it does not type-check or it is going to violate the policy in its next operation (this can be decided statically, by inspecting the outermost input/output subterms of S; see [15, Definition. 4] for a formal definition). Then, by the definitions of error, \(\models \), and \(\vdash \), it follows that \(\models \) and \(\vdash \) offer a semi-decision procedure that ensures error-free behaviour (with respect to \(\varGamma \) and \(\mathcal {P}\)).
Theorem 1
Let S be a system and \(\mathcal {P}\) a policy. If there is a \(\varGamma \)-Environment \(\varGamma \) such that \(\varGamma \mathrel {\vdash }S \mathrel {\triangleright } \varTheta \) and \(\mathcal {P}\models \varTheta \), then \(\lnot \mathrm {error}_{\mathcal {P}, \varGamma }(S)\).
Moreover, the above property survives transitions, as demonstrated by the following theorem.
Theorem 2
Let S be a system and \(\mathcal {P}\) a policy. Suppose that, after an arbitrary number of transitions, S becomes \(S^\prime \). If there is some \(\varGamma \)-Environment \(\varGamma \) such that \(\varGamma \mathrel {\vdash }S \mathrel {\triangleright } \varTheta \) and \(\mathcal {P}\models \varTheta \), then there is an extension \(\varGamma ^\prime \) of \(\varGamma \) such that \(\lnot \mathrm {error}_{\mathcal {P}, \varGamma ^\prime }(S^\prime )\).
Proof sketch
The ordering \(\lesssim \) of permission sets induces an ordering \(\lesssim \) of \(\varDelta \)-Environments and \(\varTheta \)-Interfaces, with the property that if a \(\varTheta \)-Interface respects a policy, then all “smaller” \(\varTheta \)-Interfaces respect the same policy. Moreover, if \(\varGamma \mathrel {\vdash }S \mathrel {\triangleright } \varTheta \) and \(S \mathrel {\xrightarrow {l}} S^\prime \), then there exists some extension \(\varGamma ^\prime \) of \(\varGamma \) such that \(\varGamma ^\prime \mathrel {\vdash }S^\prime \mathrel {\triangleright } \varTheta ^\prime \) and \(\varTheta ^\prime \lesssim \varTheta \).
4.2 Implementation and Usage
For the implementation of the above, one mostly has to translate the specification to Maude. For the operators \(\mathbin {\uplus }\), \(\mathbin {\oplus }\), and \(\mathbin {\odot }\) we use the plain symbol
 . The empty \(\varGamma \)-Environment, \(\varDelta \)-Environment, and \(\varTheta \)-Interface are identity elements of their respective appending –and, moreover, the empty \(\varDelta \)-Environment is also the identity element of \(\mathbin {\uplus }\)–, so we use sorts of non empty environments, for the reasons explained in [4, Sect. 14.2.6]. Type checking is implemented as a partial function that given a \(\varGamma \)-Environment and a name (resp. process; system) returns its resulting type (resp. \(\varDelta \)-Environment; \(\varTheta \)-Interface); for example, (ParP) becomes:
. The empty \(\varGamma \)-Environment, \(\varDelta \)-Environment, and \(\varTheta \)-Interface are identity elements of their respective appending –and, moreover, the empty \(\varDelta \)-Environment is also the identity element of \(\mathbin {\uplus }\)–, so we use sorts of non empty environments, for the reasons explained in [4, Sect. 14.2.6]. Type checking is implemented as a partial function that given a \(\varGamma \)-Environment and a name (resp. process; system) returns its resulting type (resp. \(\varDelta \)-Environment; \(\varTheta \)-Interface); for example, (ParP) becomes:

and (CondC), stating that the type of a condition check is the combination of the types that result from its branches if we add to the \(\varGamma \)-Environment the (positive or negative, according to the branch) condition holding, but only in case
 is a data value and the type of
is a data value and the type of
 is the data type of
is the data type of
 , becomes:
, becomes:

We can then specify an operator
 that tries to extract the type of the given system and, if successful, checks its satisfaction against the given policy using the operator \(\models \).
that tries to extract the type of the given system and, if successful, checks its satisfaction against the given policy using the operator \(\models \).
Example 3
Suppose we want to know whether the system of Example 2 abides to the privacy policy of Example 1.
First, we have to specify a proper \(\varGamma \)-Environment, giving a type to all names free in the system and containing all groups and conditions within the scope of which we are implicitly working; in our case, we use
 , since
, since
 is free in
is free in
 . We then load the tool and our module(s) and write
. We then load the tool and our module(s) and write

to the Maude prompt, which in our case returns

and, thus, we are confident that our system respects the policy. If we remove the condition checks of
 above (making it violate the policy), we observe that
above (making it violate the policy), we observe that
 returns
returns
 .
.
Several factors can cause the outcome of
 to be
to be
 :
:
-
The policy, the \(\varGamma \)-Environment, or the system may be syntactically invalid; in this case, either (probably) our module will not be accepted by Maude or the problematic term will have a kind but not a sort.
-
The policy may be ill-formed (i.e. containing multiple subpolicies for the same data type or a subpolicy for a non-private data type or an ill-formed hierarchy); in this case, it will have a kind but not a sort.
-
The system may be ill-formed; in this case, the outcome of
 , where
, where
 is our \(\varGamma \)-Environment will have a kind but not a sort; in particular, it will be a
is our \(\varGamma \)-Environment will have a kind but not a sort; in particular, it will be a
 term pointing to the problematic subterm of
term pointing to the problematic subterm of
 .
. -
The system may not respect the policy.
-
The system may respect the policy (semantically), but its syntax may falsely indicate otherwise (for example, it may contain a branch that violates the policy but will never be reached).
5 Conclusion
5.1 Successes and Limitations
As (hopefully) is demonstrated by the running example, the framework we present can be used to check conformance of privacy-related applications with a wide range of (conditional) policies. The type checker can assure the user that a system is safe to use (in the context given, modelled by a \(\varGamma \)-Environment), a property that has been proved as a (meta)theorem of our type system. The specification in Maude is fully executable and closely follows the mathematical one, making it easier to reason about.
However, the privacy policy language is still less expressive and realistic than might be needed in practice. The language we described is not well-suited for multi-user environments, although this can probably be alleviated by introducing variables in policies and hierarchical data. [9] has already extended the framework to better accommodate anonymised data, identification, and storage of private data in databases.
Powerful as they may be, verification techniques, such as type checking, require non-trivial effort from the user, who has to model the real-world scenario in a way that fits the language of the formal framework in use. This severely restricts their application outside critical systems and calls for solutions bridging theory with practice.
Admittedly, the Privacy Calculus is too abstract for use in actual applications. In order for our framework to be useful, one must find some solution to bridge actual code-writing with this level of abstraction. One possibility would be to provide a compiler that transforms programmes in widely used languages, such as Java, to Privacy Calculus. In environments where it can be enforced that all private data will be handled by a specific (software) entity, it might be possible to include Privacy Calculus in the design of the libraries that manage private data handling. Certainly, some aspects, such as the particular groups, purposes, and data types, but also the specific permissions that can be reasoned about, will always have to be adapted to each case (or kind of cases) separately.
Of course, static verification has limits. An issue that has been mentioned in [8, p. 15] is that, in principle, group membership may change over time in ways that can interfere with static analysis. In addition, complex cases may render type checking impractical. Also, it is possible that a system may be safe for reasons having to do with its semantics, but static analysis alone may flag it unsafe. For such reasons, static and runtime approaches to verification should be combined.
5.2 Future Work
The work we presented here can be extended in many directions.
Maude is a very powerful tool, whose capabilities are far wider that what we have used so far. Its reflective character (that is, the fact that specifications can themselves be handled as data in other Maude modules) has been used to create a number of useful tools for the examination of the properties of modules [5, Sect. 21.1]. We could use these tools to mechanically prove that our specification has some desirable properties (for example, termination of type checking, validity of equational properties corresponding to soundness of type checking), even while it gets extended with more features.
Besides the features added in [9] we mentioned above, the framework can be extended in many ways. For example, Universal P-RBAC [12] uses the construct of obligation (that is, an action that must precede or follow the usage of private data) and gives hierarchical structure to purposes and data; both ideas are certainly useful in real-world situations regarding privacy. [17] provides a taxonomy of kinds of privacy violations; it can be (and has been) used as a source of inspiration for the creation of policies.
Eventually, that is when the framework and the tool have reached a certain maturity, it will be valuable to empirically evaluate their expressibility and their efficiency in a real-world scenario.
References
Byun, J.W., Bertino, E., Li, N.: Purpose based access control of complex data for privacy protection. In: Proceedings of the Tenth ACM Symposium on Access Control Models and Technologies, SACMAT 2005, pp. 102–110. ACM, New York (2005). https://doi.org/10.1145/1063979.1063998
Byun, J.W., Li, N.: Purpose based access control for privacy protection in relational database systems. VLDB J. 17(4), 603–619 (2008). https://doi.org/10.1007/s00778-006-0023-0
Cardelli, L., Ghelli, G., Gordon, A.D.: Secrecy and group creation. Inf. Comput. 196(2), 127–155 (2005). https://doi.org/10.1016/j.ic.2004.08.003
Clavel, M., et al.: Maude Manual (Version 2.7). Technical report, SRI International Computer Science Laboratory (2015). http://maude.cs.uiuc.edu/maude2-manual
Clavel, M., et al.: All About Maude - A High-Performance Logical Framework: How to Specify, Program, and Verify Systems in Rewriting Logic. Programming and Software Engineering. Springer, Heidelberg (2007). https://www.springer.com/la/book/9783540719403
Jakšić, S., Pantović, J., Ghilezan, S.: Linked data privacy. Math. Struct. Comput. Sci. 27(1), 33–53 (2017). https://doi.org/10.1017/S096012951500002X
Kokkinofta, E., Philippou, A.: Type checking purpose-based privacy policies in the \(\pi \)-Calculus. In: Hildebrandt, T., Ravara, A., van der Werf, J.M., Weidlich, M. (eds.) WS-FM 2014-2015. LNCS, vol. 9421, pp. 122–142. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-33612-1_8
Kouzapas, D., Philippou, A.: Type checking privacy policies in the \(\pi \)-calculus. In: Graf, S., Viswanathan, M. (eds.) FORTE 2015. LNCS, vol. 9039, pp. 181–195. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-19195-9_12
Kouzapas, D., Philippou, A.: Privacy by typing in the \(\pi \)-calculus. Logical Methods Comput. Sci. 13(4) (2017). https://doi.org/10.23638/LMCS-13(4:27)2017
Meseguer, J.: Twenty years of rewriting logic. J. Log. Algebr. Program. 81(7), 721–781 (2012). https://doi.org/10.1016/j.jlap.2012.06.003
Ni, Q., et al.: Privacy-aware Role-based access control. ACM Trans. Inf. Syst. Secur. 13(3), 24:1–24:31 (2010). https://doi.org/10.1145/1805974.1805980
Ni, Q., Lin, D., Bertino, E., Lobo, J.: Conditional privacy-aware role based access control. In: Biskup, J., López, J. (eds.) ESORICS 2007. LNCS, vol. 4734, pp. 72–89. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74835-9_6
Pardo, R., Schneider, G.: A formal privacy policy framework for social networks. In: Giannakopoulou, D., Salaün, G. (eds.) SEFM 2014. LNCS, vol. 8702, pp. 378–392. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10431-7_30
Parrow, J.: An introduction to the \(\pi \)-calculus. In: Bergstra, J.A., Ponse, A., Smolka, S.A. (eds.) Handbook of Process Algebra, pp. 479–543. Elsevier Science, Amsterdam (2001). https://doi.org/10.1016/B978-044482830-9/50026-6
Pitsiladis, G.V.: Type checking conditional purpose-based privacy policies in the \(\pi \)-calculus. Limassol, Cyprus (2016). http://users.ntua.gr/gpitsiladis/files/documents/2016-11-fmpriv-conditions.pdf
Pitsiladis, G.V.: Type Checking Privacy Policies in the \(\pi \)-calculus and its Executable Implementation in Maude (in Greek). Diploma thesis, National Technical University of Athens, Greece (2016). http://dspace.lib.ntua.gr/handle/123456789/44439
Solove, D.J.: A Taxonomy of Privacy. SSRN Scholarly Paper ID 667622, Social Science Research Network, Rochester, NY, February 2005. https://papers.ssrn.com/abstract=667622
Stehr, M.O.: CINNI - A generic calculus of explicit substitutions and its application to \(\lambda \)- \(\varsigma \)- and \(\pi \)-calculi. Electron. Notes Theor. Comput. Sci. 36, 70–92 (2000). https://doi.org/10.1016/S1571-0661(05)80125-2
Thati, P., Sen, K., Martí-Oliet, N.: An executable specification of asynchronous \(\pi \)-calculus semantics and may testing in Maude 2.0. Electron. Notes Theor. Comput. Sci. 71, 261–281 (2004). https://doi.org/10.1016/S1571-0661(05)82539-3
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Pitsiladis, G.V., Stefaneas, P. (2018). Implementation of Privacy Calculus and Its Type Checking in Maude. In: Margaria, T., Steffen, B. (eds) Leveraging Applications of Formal Methods, Verification and Validation. Verification. ISoLA 2018. Lecture Notes in Computer Science(), vol 11245. Springer, Cham. https://doi.org/10.1007/978-3-030-03421-4_30
Download citation
DOI: https://doi.org/10.1007/978-3-030-03421-4_30
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03420-7
Online ISBN: 978-3-030-03421-4
eBook Packages: Computer ScienceComputer Science (R0)






 , a functional module that provides everything needed for type checking Privacy Calculus systems against policies,
, a functional module that provides everything needed for type checking Privacy Calculus systems against policies, , a functional module that defines the sorts containing application-specific information (
, a functional module that defines the sorts containing application-specific information (
 ,
,
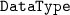 ,
,
 , etc.), so we have to extend it when using the tool.
, etc.), so we have to extend it when using the tool.
 ; in order for this kind of expressions to be well-defined, we have to define a sort
; in order for this kind of expressions to be well-defined, we have to define a sort
 , as follows (and similarly for systems):
, as follows (and similarly for systems): 

 is declared using the
is declared using the
 attribute, so as to control rewrites (as described above on page 7). Consequently, a mechanism must be provided explicitly for multi-step transitions; for processes, it suffices to provide the following code, with
attribute, so as to control rewrites (as described above on page 7). Consequently, a mechanism must be provided explicitly for multi-step transitions; for processes, it suffices to provide the following code, with
 a variable of
a variable of
 (transitions of systems are similar):
(transitions of systems are similar): 
 trigger rules
trigger rules
 and
and
 . Operator
. Operator
 prevents infinite regressions where rules are used as conditions to themselves, a situation that would result if we just defined
prevents infinite regressions where rules are used as conditions to themselves, a situation that would result if we just defined
 to be a subsort of
to be a subsort of
 .
.
 , where
, where
 is our
is our  term pointing to the problematic subterm of
term pointing to the problematic subterm of
 .
.