Abstract
Object-oriented (OO) programs, which use subtyping and dynamic dispatch, make specification and verification difficult because the code executed by a method call may dynamically be dispatched to an overriding method in any subtype, even ones that did not exist at the time the program was specified. Modular reasoning for such programs means allowing one to add new subtypes to a program without re-specifying and re-verifying it. In a 2015 ACM TOPLAS paper we presented a model-theoretic characterization of a Hoare-style modular verification technique for sequential OO programs called “supertype abstraction,” defined behavioral subtyping, and proved that behavioral subtyping is both necessary and sufficient for the validity of supertype abstraction. The present paper is aimed at graduate students and other researchers interested in formal methods and gives a comprehensive overview of our prior work, along with the motivation and intuition for that work, with examples.
Leavens’s work was supported in part by the US National Science Foundation under grants CNS 08-08913 and CCF 1518789 and Naumann’s work was supported in part by the US NSF under grant CNS 1718713.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
- Object-oriented programming
- Hoare-style verification
- JML specification language
- Behavioral subtyping
- Supertype abstraction
- Specification inheritance
1 Introduction
The goal of our prior work [17] and the 2017 SETSS lectures, was to explain how to modularly reason about sequential object-oriented (OO) programs that use subtyping and dynamic dispatch. The key modular verification technique is “supertype abstraction” [16, 20, 21]. In supertype abstraction, one verifies a call to a method by using the specification of the receiver’s static type. The validity of this reasoning technique depends on two conditions:
-
1.
in each method call, E.m(), the dynamic type of the actual receiver object (the value of E) must be a subtype of the static type of the receiver expression, E, and
-
2.
every override of the method named m must correctly implement each of the specifications (given in its supertypes) for that method.
Together, these two conditions allow the specification of the method m in E’s static type to be used in verification of the call E.m(), since any subtype of that static type will correctly implement that specification. The first condition can be enforced by a static type system, such as the one in Java, in which the static type of an expression is an upper bound on the dynamic types of all objects it may denote (in the sense that the expression’s static type must be a supertype of the runtime classes of those objects). The second condition is the essence of behavioral subtyping [1,2,3, 17, 20,21,22,23]. To a first approximation, behavioral subtyping is necessary for valid use of supertype abstraction, because the supertype’s specification is used in reasoning, so the subtypes must all correctly implement that specification.
1.1 JML
This paper illustrates (with examples, not pictures) the idea of supertype abstraction using sequential Java, with specifications written in the Java Modeling Language (JML) [16, 19]. As a behavioral interface specification language, JML specifies the functional behavior of Java methods, classes, and interfaces. Functional behavior involves the values of data; thus a JML method specification describes the allowed values of variables (e.g., method formals) and object fields before the method starts running (its precondition) and the relationship between such values and the method’s result after the method finishes (its postcondition and frame condition).
JML and the work reported here only deal with sequential Java programs, so we henceforth assume that there is no multi-threading or parallelism in the programs discussed.
1.2 OO Programs and Dynamic Dispatch
As the start of a JML example that illustrates how OO programs use dynamic dispatch, consider the type IntSet, which is shown in Fig. 1 on the next page.
JML specifications are written as comments that start with an at-sign ( ); these are processed by the JML compiler (but would be ignored by a standard Java compiler). Figure 1 on the next page shows the specification of an interface, which specifies five methods. The contains method is only specified as being pure, which means that it has no write effects (i.e.,
); these are processed by the JML compiler (but would be ignored by a standard Java compiler). Figure 1 on the next page shows the specification of an interface, which specifies five methods. The contains method is only specified as being pure, which means that it has no write effects (i.e.,  ). It has no precondition (the default in JML is
). It has no precondition (the default in JML is  ), which means it can be called in any state. It also has no postcondition; the default (
), which means it can be called in any state. It also has no postcondition; the default ( ) imposes no obligations on an implementation. The last method, size, is also specified as being pure. However, size has a specified postcondition, which is that the result of the method is always non-negative. (As can be seen in this example, the specification for each method is written before the method’s header.) The contains and size methods are used to specify the behavior of the other methods. This specification technique is similar to that used in equational algebraic specifications [10] and in Meyer’s Eiffel examples [24].
) imposes no obligations on an implementation. The last method, size, is also specified as being pure. However, size has a specified postcondition, which is that the result of the method is always non-negative. (As can be seen in this example, the specification for each method is written before the method’s header.) The contains and size methods are used to specify the behavior of the other methods. This specification technique is similar to that used in equational algebraic specifications [10] and in Meyer’s Eiffel examples [24].
The other methods in Fig. 1 have more extensive specifications. The pick method exhibits the three standard clauses used in a JML method specification. The pick method’s precondition, given by its  clause, is that the result of calling size() must be strictly greater than zero; that is, the method should only be called when the object contains some elements. The frame condition for pick is given by its
clause, is that the result of calling size() must be strictly greater than zero; that is, the method should only be called when the object contains some elements. The frame condition for pick is given by its  clause, which says that it may assign to the locations in the data group named state; this datagroup is declared in the interface. The state datagroup will be populated with fields in the types that implement the IntSet interface (as we will see below). The postcondition, given in the
clause, which says that it may assign to the locations in the data group named state; this datagroup is declared in the interface. The state datagroup will be populated with fields in the types that implement the IntSet interface (as we will see below). The postcondition, given in the  clause, says that the result will be an element of the set, since the value returned will satisfy the assertion
clause, says that the result will be an element of the set, since the value returned will satisfy the assertion  . The add method has a default precondition of
. The add method has a default precondition of  , can assign to the locations in the datagroup state, and has a postcondition that says that its argument (i) will be in the set at the end of the operation, and that the size of the set will not decrease. The notation
, can assign to the locations in the datagroup state, and has a postcondition that says that its argument (i) will be in the set at the end of the operation, and that the size of the set will not decrease. The notation  , which is borrowed from Eiffel [24], denotes the value of the expression E in the method’s pre-state. (The pre-state of a method m is the state of the program after passing parameters to m, but before running any of its code.) Similarly, the remove method’s postcondition says that after the method executes, its argument (i) will no longer be in the set and the size will not increase.Footnote 1
, which is borrowed from Eiffel [24], denotes the value of the expression E in the method’s pre-state. (The pre-state of a method m is the state of the program after passing parameters to m, but before running any of its code.) Similarly, the remove method’s postcondition says that after the method executes, its argument (i) will no longer be in the set and the size will not increase.Footnote 1
1.3 Verifying Method Calls with Supertype Abstraction
The basic technique for verifying a method call is to:
-
1.
check (assert) the method’s precondition before the call,
-
2.
“havoc” all locations that are assignable by the method, and
-
3.
assume that the method’s postcondition holds after the call.
Locations that are assignable by the called method are imagined to be set by the method to an arbitrary, unknown value; this is what “havoc” does. However, such locations will usually be constrained by the method’s postcondition to values that satisfy that postcondition. On the other hand, locations that are not assignable in the method are preserved by the method’s execution. Thus the frame in the method’s specification can be used to prove that properties that hold before the call (in the call’s pre-state) also hold after the call (in the call’s post-state). Properties are automatically preserved by the call if they do not depend on locations that may be assigned by the method called (i.e., if they are independent of the method’s frame).
This technique for method call verification is modular because it avoids checking the correctness of the method’s implementation each time the method is called. The verification technique is independent of the method’s implementation, as verification relies only on its specification (its precondition, frame, and postcondition). Therefore a method’s specification plays the key role in verifying calls to that method.
With supertype abstraction, once we know the specification of IntSet, we can verify client code written for it, even though we do not know any of the details of the classes that implement IntSet. Two simple examples of some client code are shown in Fig. 2.
We demonstrate the above technique by verifying the testPick method; the verification is recorded with intermediate assertions in Fig. 3 on the next page. At the beginning of the method testPick, its precondition is assumed. To verify the call to pick, following supertype abstraction we use the specification of pick from the static type of the call’s receiver (iset), which is IntSet. So the method’s specification is taken from Fig. 1. Its precondition is the same as the assumption (with the receiver substituted for the implicit receiver ( ) in the specificationFootnote 2). Since we are assuming that
) in the specificationFootnote 2). Since we are assuming that  , that follows, and so we can assume the postcondition of the pick method. Again, in the assumed postcondition the actual receiver (iset) is substituted for the implicit receiver (
, that follows, and so we can assume the postcondition of the pick method. Again, in the assumed postcondition the actual receiver (iset) is substituted for the implicit receiver ( ) in the specification. With this assumption, the assertion to prove at the end of the method follows immediately.
) in the specification. With this assumption, the assertion to prove at the end of the method follows immediately.
For the testAddRemove method, the assertions can also be verified using just the specifications given for IntSet’s methods (see Fig. 4 on the next page). Again this is independent of the implementation of the argument iv. Note that only the specifications given in IntSet can be used, so one cannot conclude that the value of s, the size of iv after adding 1 to iv, will be 4, only that s will be no less than the original size (3).
These examples illustrate the modularity properties of supertype abstraction. There are two important points to make. First, the specification is modular in the sense that it is given independently of any subtypes of IntSet, and does not need to be changed if new subtypes implementing IntSet are added to the program. Second, the verification of the client code is similarly modular in the sense that it does not depend on the possible subtypes of IntSet, and thus does not need to be redone when new subtypes are added to the program.
1.4 Subtypes for the IntSet Example
To make some of these ideas more concrete, we will consider several subtypes of IntSet.
One family of simple implementations for IntSet are closed intervals of integers, represented by objects that track a lower and upper bound in the fields lb and ub. The  declaration adds these fields to the datagroup state. This design’s common parts are described in the abstract class AbsInterval (see Fig. 5 on the next page). The objects of subtypes of this class represent closed intervals of integers, which we can think of as containing all integers between the instance field values lb and ub, inclusive, i.e., \([\texttt {lb},\texttt {ub}]\). An interval such as [3, 2] represents the empty set.
declaration adds these fields to the datagroup state. This design’s common parts are described in the abstract class AbsInterval (see Fig. 5 on the next page). The objects of subtypes of this class represent closed intervals of integers, which we can think of as containing all integers between the instance field values lb and ub, inclusive, i.e., \([\texttt {lb},\texttt {ub}]\). An interval such as [3, 2] represents the empty set.
The abstract class AbsInterval represents lb and ub as  (64-bit) integers. These fields have
(64-bit) integers. These fields have  visibility in Java, but are also declared to be
visibility in Java, but are also declared to be  in the first JML annotation. One can think of
in the first JML annotation. One can think of  fields as being declared to be public for purposes of specification, but having the declared visibility (protected in this case) for use in Java code. Declaring the fields to be public for specification purposes allows them to be used in specifications intended to be seen by all clients. There is a public invariant; invariants state properties that must hold whenever a method call is not in progress [19, Sect. 8.2]. The invariant states that lb must be in the range of
fields as being declared to be public for purposes of specification, but having the declared visibility (protected in this case) for use in Java code. Declaring the fields to be public for specification purposes allows them to be used in specifications intended to be seen by all clients. There is a public invariant; invariants state properties that must hold whenever a method call is not in progress [19, Sect. 8.2]. The invariant states that lb must be in the range of  values (between
values (between  and
and  ). It also says that ub cannot be greater than the largest
). It also says that ub cannot be greater than the largest  value and that it can only be one smaller than the smallest int value. The type
value and that it can only be one smaller than the smallest int value. The type  is used for the fields lb and ub in order to (a) avoid integer overflow, and (b) to allow representation of extreme cases of empty intervals. An empty interval is one in which the value of ub is less than the value of lb; indeed the invariant
is used for the fields lb and ub in order to (a) avoid integer overflow, and (b) to allow representation of extreme cases of empty intervals. An empty interval is one in which the value of ub is less than the value of lb; indeed the invariant  implies that this only happens when
implies that this only happens when  . (Note that conjunct of the invariant would not make sense if both these fields had type
. (Note that conjunct of the invariant would not make sense if both these fields had type  and if lb held the smallest
and if lb held the smallest  value.)
value.)
The constructor for AbsInterval has a requirement that its arguments, l and u, must be such that l is not greater than  , so that the invariant will hold when l is assigned to lb and u is assigned to ub. The constructor of AbsInterval has a “heavyweight” specification [19, Sect. 2.3], which says that when called in a state that satisfies its precondition, it must terminate normally (without throwing an exception), as it is a
, so that the invariant will hold when l is assigned to lb and u is assigned to ub. The constructor of AbsInterval has a “heavyweight” specification [19, Sect. 2.3], which says that when called in a state that satisfies its precondition, it must terminate normally (without throwing an exception), as it is a  specification.
specification.
The specification of the contains method starts with the keyword  , to indicate that the specification adds to the specification inherited from the supertype IntSet. Since both specifications have the same precondition (
, to indicate that the specification adds to the specification inherited from the supertype IntSet. Since both specifications have the same precondition ( ), effectively this adds an additional postcondition to the method’s specification for all subtypes of AbsInterval. This specification thus allows a verifier to equate contains(i) with
), effectively this adds an additional postcondition to the method’s specification for all subtypes of AbsInterval. This specification thus allows a verifier to equate contains(i) with  in proofs, as
in proofs, as  means “if and only if” in JML.
means “if and only if” in JML.
The specification of the method size (at the end of the figure) is similar. It says that the size of the set is the value of the expression  . The reader can check that this expression is the number of integers i such that contains(i) is true.
. The reader can check that this expression is the number of integers i such that contains(i) is true.
The add method in AbsInterval inherits the specification from IntSet unchanged. Thus, if iv is an object of type AbsInterval, then when iv.add(i) returns, it must be that iv.contains(i) holds. The implementation may add more elements to the set, in addition to the argument (i), as the implementation can only represent closed intervals. Indeed the implementation will set either the lower bound (lb) or the upper bound (ub) to i. This may not seem like the expected behavior for sets, but it satisfies the specification given in IntSet.
The remove method similarly inherits its specification from IntSet. The implementation will set either the lower or the upper bound to just past the element to be removed. The assert statements used in the method are designed to help the prover in the JML tools conclude that the method is implemented correctly. In each case the method must ensure that the argument is no longer in the set and that the second invariant ( ) holds. The reader is urged to verify these assertions, recalling that both the lower and upper bound fields are of type
) holds. The reader is urged to verify these assertions, recalling that both the lower and upper bound fields are of type  .
.
As an example of supertype abstraction, the verification of the client code in figure Fig. 4 still holds, even if the argument is a subtype of AbsInterval.
To understand these modularity properties better, it will be useful to consider some concrete subtypes of IntSet, which implement the pick method.
The first of these concrete subtypes of AbsInterval is the class Interval shown in Fig. 6. This class’s implementation of pick always returns the lower bound of the interval. The specification of pick in Fig. 6 says that, in addition to the inherited specification, it returns the value of lb, when  , i.e., when the interval is not empty. Since that precondition is equivalent (by the specification of contains) to the precondition of pick given in IntSet (see Fig. 1), this added specification case effectively adds an additional postcondition to pick, when the receiver’s type is a subtype of Interval. The implementation satisfies both the inherited postcondition and the postconditions in this additional specification when the interval is not empty.
, i.e., when the interval is not empty. Since that precondition is equivalent (by the specification of contains) to the precondition of pick given in IntSet (see Fig. 1), this added specification case effectively adds an additional postcondition to pick, when the receiver’s type is a subtype of Interval. The implementation satisfies both the inherited postcondition and the postconditions in this additional specification when the interval is not empty.
The second of these concrete subtypes of AbsInterval is the class Interval2 shown in Fig. 7 on the next page. This class’s implementation of pick returns the value of the field  , which is constrained by its invariants to be an element of the interval and to have a value that can be represented by an
, which is constrained by its invariants to be an element of the interval and to have a value that can be represented by an  . The added specification for pick in Fig. 7 describes this behavior. Again, the implementation is correct if the interval is not empty.
. The added specification for pick in Fig. 7 describes this behavior. Again, the implementation is correct if the interval is not empty.
Consider now the code in Fig. 8 on page 10. The final assertion in that figure verifies because iv has type Interval, and the added specification case for pick in Interval’s specification (see Fig. 6) says it returns the lower bound of the interval. In JML, a method that is specified with several specification cases (some of which may be inherited) must obey all of them, so a client can either pick one specification case and use that to verify a call to the method, as is done in Fig. 8, or use the combined meaning of the specification cases.
However, suppose that the type of iv in Fig. 8 were changed to IntSet, and the initialization for that variable called the constructor of Interval2. In that case, the value of iv would be an object of the class Interval2. And in that case the last assertion in Fig. 8 would not always be valid, since Interval2’s method pick need not always return the lower bound of the interval. Supertype abstraction safely avoids drawing such invalid conclusions, because it only allows using the specification of the supertype (e.g., IntSet) in such cases.
2 Background and Motivation
Ideally, one could characterize supertype abstraction in a way that does not depend on the details of a specification language and the details of a particular verification logic. This is what was done in our earlier TOPLAS paper [17]. Instead of repeating that formal development, in what follows we will try to adapt those more general results (from the TOPLAS paper [17]) to Java and JML. In the process we will skim over some of the formal details, which may not match Java and JML exactly.
2.1 Background: Denotational and Axiomatic Semantics
A verification logic that is sound must, by definition, only draw conclusions that are valid in all possible executions. This requires a model of both the meaning of a specification and of how a program executes: the semantics of the specification language and the semantics of the programming language.
There are three broad families of programming language semantics, developed in the 1960s:
-
Denotational semantics, developed by Strachey and Scott [28,29,30,31]. A standard summary is found in Schmidt’s book [27]. A denotational semantics describes the meaning of a program as a mathematical function.
-
Operational semantics, developed by Landin [14, 15]. A modern treatment is given in Hennessy’s book [11]. An operational semantics describes the meaning of a program as a rewrite machine.
-
Axiomatic semantics, developed by Floyd and (Tony) Hoare [9, 12]. An axiomatic semantics describes the meaning of a program as a proof system. A modern treatment is given in Apt and Olderog’s book [4].
For example, in the denotational semantics of a simple imperative language, one may use states, \(\sigma \), that are finite functions from variable names to values. Thus the denotational semantics of an assignment statement such as  would be given by a meaning function, such as \(\mathcal{C}\), that maps commands (statements) and states to states; for example
would be given by a meaning function, such as \(\mathcal{C}\), that maps commands (statements) and states to states; for example

where the notation \([\sigma \mid \texttt {k}:(\sigma (\texttt {k})+1)]\) means a mapping that is the same as \(\sigma \) except that for the argument k the result is the value \(\sigma (\texttt {k})+1\):

An axiomatic semantics describes states using predicates; one can think of a predicate as representing the set of all states that satisfy it. For example, the predicate  describes all states in which the value of the variable k (presumably an integer) is strictly greater than zero. A Hoare logic for a programming language gives axioms and rules for drawing conclusions about program states. Hoare logic uses “Hoare triples” of the form \(\{P\}~C~\{Q\}\) which mean that if the command C is executed starting in a state satisfying the predicate P (the precondition), and if C terminates normally, then the predicate Q (the postcondition) will hold. For example, the following is a valid Hoare triple (ignoring integer overflow):
describes all states in which the value of the variable k (presumably an integer) is strictly greater than zero. A Hoare logic for a programming language gives axioms and rules for drawing conclusions about program states. Hoare logic uses “Hoare triples” of the form \(\{P\}~C~\{Q\}\) which mean that if the command C is executed starting in a state satisfying the predicate P (the precondition), and if C terminates normally, then the predicate Q (the postcondition) will hold. For example, the following is a valid Hoare triple (ignoring integer overflow):

We will sometimes write Hoare triples using assume and assert in JML; thus the example above would be written in JML as follows.

To define a programming language’s meaning, one must generalize from specific examples, such as those above. In a Hoare Logic, this is done by giving axiom schemes for simple statements and proof rules for compound statements. Some simple axioms and inference rules in a Hoare Logic are presented in Fig. 9. The “turnstile”, \(\vdash \), can be read as “one can prove that.” The rules Seq, Conseq, While, and If are inference rules, with hypotheses above the horizontal line and a conclusion below it. The Conseq rule has a side condition, starting with if, which tells when the rule can be used.
Example 1
A proof in Hoare logic can be written as a tree. For example to prove the Hoare triple in the conclusion below, one uses the Seq rule, with two sub-derivations (sub-trees, growing upwards), named (A1) and (I1), corresponding to the two hypotheses of the Seq rule. So overall the tree looks as follows, where the subderivations (A1) and (I1) will be explained below.

Derivation (A1) uses the Conseq rule and has a hypothesis that is an instance of the Assign axiom scheme. The conclusion of (A1) is the first hypothesis needed by the Seq rule above.

The derivation (I1) uses the If rule. Since the If rule has two hypotheses, there are two more sub-derivations, named (C1), and (C2) as required by the If rule.

The derivation (C1) is as follows. Note that the conclusion is the formula needed for the first hypothesis of the If rule. The implications can be proven using the theory of integer arithmetic.

The derivation (C2) is similar. Its conclusion is the formula needed for the second hypothesis of the If rule.

\(\blacksquare \)
Another way to display this proof is to use intermediate assertions, as shown in Fig. 10 below. In the figure preconditions of Hoare triples follow the keyword  and postconditions follow
and postconditions follow  . Two such conditions written next to each other indicate a use of the Conseq rule. Overall the first assume and the last assert are the formulas in the main derivation given above, with the assertion
. Two such conditions written next to each other indicate a use of the Conseq rule. Overall the first assume and the last assert are the formulas in the main derivation given above, with the assertion  being the assertion that is between the two statements as demanded by the Seq rule. The proof of the first statement (lines 1–5) corresponds to the derivation (A1) above. The proof of the if-statement is given in the rest of the lines, with the five lines around each assignment statement corresponding to derivations (C1) and (C2) above. Comments to the right of each assume or assert indicate which rule these preconditions and postconditions correspond to.
being the assertion that is between the two statements as demanded by the Seq rule. The proof of the first statement (lines 1–5) corresponds to the derivation (A1) above. The proof of the if-statement is given in the rest of the lines, with the five lines around each assignment statement corresponding to derivations (C1) and (C2) above. Comments to the right of each assume or assert indicate which rule these preconditions and postconditions correspond to.
In sum, Hoare Logic uses predicates to represent sets of states. Statements transform preconditions into postconditions. And intermediate assertions can stand for a Hoare Logic proof.
The challenge is to extend this verification technique in a modular way to the verification of method calls in Java.
2.2 Specification Language Semantics
A fundamental step towards modular verification of method calls is to specify the state transformation that a method call achieves. Declaring method specifications avoids having to inline method bodies to verify method calls. It also allows the verification of recursive and mutually-recursive methods.
In JML method specifications are written with  and
and  clauses (and possibly with
clauses (and possibly with  clauses). For example, a specification for a max method on two
clauses). For example, a specification for a max method on two  arguments is shown in Fig. 11.
arguments is shown in Fig. 11.
To deal with Java’s  statement, some extension to Hoare Logic is needed, as this statement does not terminate normally, but abruptly stops execution of the surrounding method [13]. Instead of investigating such extensions here, we will content ourselves with proving that the value returned satisfies the appropriate condition, just before the return statement.
statement, some extension to Hoare Logic is needed, as this statement does not terminate normally, but abruptly stops execution of the surrounding method [13]. Instead of investigating such extensions here, we will content ourselves with proving that the value returned satisfies the appropriate condition, just before the return statement.
In this way one can show that the code given in Example 1, when put in sequence with  correctly implements the specification of Fig. 11.Footnote 3
correctly implements the specification of Fig. 11.Footnote 3
To abstract a bit from the syntax of specifications we define some terms, following the TOPLAS paper [17]. (A table of notations appears in Fig. 18 on page 42 at the end of this paper.)
A pair of a precondition and a postcondition, (P, Q), is called a simple specification [17].
Validity of specifications is defined with respect to the denotational semantics of the language. If \(\mathcal{C}\) is the meaning function for commands, then a Hoare formula \(\{P\}~C~\{Q\}\) is valid in state \(\sigma \), written  if and only if: whenever P holds in state \(\sigma \) and the meaning of C starting in state \(\sigma \) is a state \(\sigma '\), then Q holds in state \(\sigma '\). As a mathematical formula, we write this as follows
if and only if: whenever P holds in state \(\sigma \) and the meaning of C starting in state \(\sigma \) is a state \(\sigma '\), then Q holds in state \(\sigma '\). As a mathematical formula, we write this as follows

thinking of predicates as sets of states, so that \(\sigma \in P\) means that P holds in state \(\sigma \) and using \(\mathcal{C}[\![{C}]\!](\sigma ) = \sigma '\) to mean that the meaning of command C started in state \(\sigma \) is state \(\sigma '\). This is partial correctness; since if the command C does not terminate normally (does not produce a state \(\sigma '\)), then the implication holds trivially.
A Hoare triple \(\{P\}~C~\{Q\}\) is valid, written  , if and only if it is valid for all states.
, if and only if it is valid for all states.
Definition 1
(Validity of Simple Specifications). A command C correctly implements a simple specification (P, Q) if and only if  .
.
The concept of refinement of specifications is of great importance in what follows. To define refinement, it is useful to define the set of commands that correctly implement a specification. We notate this  .
.
Definition 2
(Refinement). Let (P, Q) and \((P',Q')\) be simple specifications. Then \((P',Q')\) refines (P, Q), written \((P',Q') \sqsupseteq (P,Q)\), if and only if \( Impls(P',Q') \subseteq Impls(P,Q)\).
It is an easy corollary that if \((P',Q') \sqsupseteq (P,Q)\), then for all commands C, if  , then
, then  .
.
2.3 Programming Language Semantics
An object in an OO language is data with an identity (its address on the heap) and several named fields (also called instance variables). In most OO languages objects have infinite lifetimes and live on the heap. Objects are referred to indirectly by their addresses and their fields are mutable (can hold different values over time). In addition, in a class-based OO language, like Java, objects refer to their class, so it is possible to determine their class dynamically.
A class is a code module that describes objects. Classes are a built-in feature of Java and other OO languages, such as Smalltalk-80, C++, and C#. Classes contain declarations for the fields of objects of that class, methods, which are procedures that operate on objects, and constructors, which initialize objects. Examples of classes in Java are given in Figs. 6 and 7. A method declaration in a class may be abstract if it does not have an implementation. In Java an abstract method is either declared with a semicolon ( ) instead of a method body or is inherited from a supertype but not implemented.
) instead of a method body or is inherited from a supertype but not implemented.
An interface is like a class, but with no method implementations; that is, all the methods it declares are abstract. Interfaces can be used as types in Java.
In Java, subtype relationships are declared. A class may declare that it implements one or more interfaces, making it a subtype of all of those interfaces, and those interfaces are its supertypes. For example, the examples in the introduction directly declare the following subtype relationships.
In addition, subtyping is reflexively and transitively closed, so Interval \(\le \) IntSet.
Types are upper bounds in an OO language. Thus, if S is a subtype of T, which we write as \(S \le T\), then one can assign an object of type S to a variable declared to have type T and one can pass an actual parameter of type S to a formal parameter of type T.
To have indefinite lifetimes, objects are stored in the heap, as shown in Fig. 12. Local variables, such as ivl, are stored in the runtime stack. When a variable’s type is a reference type its contents consist of a reference (i.e., a pointer) to an object, in this case an object of class Interval. Objects are typically represented as records that can be mathematically modeled as mappings from field names to values. There is a distinguished field named class that contains a reference to the class object, which is a run-time representation of the class declaration.
Class objects themselves contain their name, a reference to their superclass object, and a method table that maps method names to the a closure for that method. The closure contains the code for the method’s body as well as the names of its formal parameters.
To explain how the dynamic dispatch mechanism for method calls works in Java and other OO languages, consider the call  . To evaluate this expression, Java:
. To evaluate this expression, Java:
-
1.
Evaluates ivl, producing a reference to an object, o (a pointer).
-
2.
Finds the class of o (o.class), say this is the class whose class object is Iv.
-
3.
Looks up the method code for the method named size (with no arguments) in the method table found via Iv.
-
4.
Allocates space for the result of the call.
-
5.
Creates a stack frame for the call, binding
 to o (and in general also binding formals to actuals).
to o (and in general also binding formals to actuals). -
6.
Runs the code in the new stack frame.
-
7.
Executing a
 statement evaluates the expression E, copies the value of E to the space allocated for it, and then pops the call’s stack frame off the runtime stack.
statement evaluates the expression E, copies the value of E to the space allocated for it, and then pops the call’s stack frame off the runtime stack.
Calling methods indirectly via the method table found at runtime from the receiver object is what makes this calling mechanism dynamic. Consider the call to pick in Fig. 3. The argument iset could be any subtype of IntSet, including Interval, Interval2, and even subtypes of IntSet that have not yet been programmed.
As another example, consider the call to pick shown in Fig. 13. In this figure, the argument has type AbsInterval, and thus the actual argument could have a dynamic type that is Interval, Interval2, or any other subtype of AbsInterval. The integer returned by the call must be in the interval, but although Interval’s method will return 5, there is no guarantee that if iv denotes an object of dynamic type Interval2 (or some other subtype) that the result will be 5, so the last assertion may fail. Thus the verification technique must take dynamic dispatch into account.
The essence of the problem is that specification and verification are done statically, before runtime, but the dynamic types of objects are only known (in general) at runtime. Furthermore, OO programs are “open” in the sense that new types may be added after the program is specified and verified, so even an exhaustive case analysis of the program’s existing types will not be sound. Finally, not only is the code of the method that is run by a call determined dynamically, but the different subtypes may have different specifications for what the method should do. (However, for modular verification to be possible, we will always assume that methods correctly implement their specifications.)
To explain this problem in verification, imagine a verification technique that relies on a table of specifications for each method, indexed by dynamic types, and that verifies code involving method calls exhaustively, with a verification for each possible dynamic type of each call’s receiver, using the dynamic type’s specification. When new types are added to a program, all proofs must be examined and new cases must be added where needed to account for the new types. An advantage of this verification technique is that it would be very precise, as it could consider the exact effects of each method call. However, such a technique would not be scalable, since adding a new type to a program would require finding and reproving an unbounded number of assertions. The number of cases that would need to be considered would explode with the number of combinations of different dynamic types that are possible in a program fragment that is to be verified. In essence, such a technique would not be modular.
We would like a reasoning technique that is both static (so that specification and verification are done before runtime) and modular (so that adding new types to a program does not cause re-specification or re-verification). In addition, a suitable reasoning technique should be not much more difficult than reasoning about non-OO programs.
2.4 Supertype Abstraction
A reasoning technique for OO programs that is both static and modular is supertype abstraction [16, 17, 20, 21]. Supertype abstraction relies on static type information to give upper bounds on the types of expressions; in a language without a built-in static type system, a separate static analysis could provide this information. Verification of a method call uses the specification of the method being called found in the receiver’s static type. For validity, an overriding method in a subtype must obey all specifications for that method in all its supertypes, since these supertype specifications could be used in reasoning; that is, all subtypes must be behavioral subtypes [1,2,3, 17, 20,21,22,23]. In addition, if other properties of supertypes, such as invariants, can be used in reasoning, then subtype objects must also obey those properties.
An example of reasoning using supertype abstraction is shown in Fig. 2, which uses the specifications found in the supertype IntSet to verify the call to pick.
Behavioral subtyping, which is necessary for the validity of supertype abstraction [17], must be checked when new types are added to a program. These new types must each be behavioral subtypes of all of their supertypes (in particular of those that are already present in the program).
Even though supertypes generally have more abstract (less precise) specifications than subtypes, one can recover the precision of reasoning by using dynamic type information, while still using supertype abstraction. The way to do this is to use type tests ( in Java) and downcasting to align the static types of receiver objects with dynamic type information. Figure 14 shows an example in which there is a supertype Staff of types Doctor and Nurse, and type tests and downcasting are used to specialize the static types of receivers. Then supertype abstraction can be used to verify the calls to methods on these subtypes. Thus by using supertype abstraction, one does not lose any ability to verify OO programs, compared to an exhaustive case analysis, since by using type tests and downcasts, one can add explicit case analysis on dynamic types.
in Java) and downcasting to align the static types of receiver objects with dynamic type information. Figure 14 shows an example in which there is a supertype Staff of types Doctor and Nurse, and type tests and downcasting are used to specialize the static types of receivers. Then supertype abstraction can be used to verify the calls to methods on these subtypes. Thus by using supertype abstraction, one does not lose any ability to verify OO programs, compared to an exhaustive case analysis, since by using type tests and downcasts, one can add explicit case analysis on dynamic types.
3 Semantics
In order to investigate the connection between supertype abstraction and behavioral subtyping, our TOPLAS paper [17] used a small “core” programming language that is similar to Java. To avoid repeating that formal development here, we will simply outline the main ideas and results.
3.1 A-Normal Form
A small problem with verification in a language such as Java is that expressions may, in general, have side effects. These side effects make it unsound to use substitution (of such expressions) in verification rules. To avoid these problems the core language used in the TOPLAS paper has a syntax that is in “A-normal form” [26]. In A-normal form, variables are used for certain expressions, such as the tests in while loops and if-statements, so that effects in such sub-expressions do not complicate the semantics. Although Java and JML do not require A-normal form syntax, we assumed it in presenting Hoare Logic rules for Java previously (in Fig. 9). Some verification tools (such as OpenJML) transform a complex expression in Java into A-normal form by rewriting the program; for example, if the condition  were used as the test in an if-statement, it would first declare a boolean variable, such as
were used as the test in an if-statement, it would first declare a boolean variable, such as  , and assign
, and assign  the value of that expression, as was done in Fig. 10. This transformation would be applied recursively to eliminate complex subexpressions within expressions. For example the code
the value of that expression, as was done in Fig. 10. This transformation would be applied recursively to eliminate complex subexpressions within expressions. For example the code

would be transformed into A-normal form in a way similar to the following.Footnote 4

Such a program transformation would be carried out mechanically and would need to respect the semantics of Java expressions. The idea would be to allow Java expressions that involve at most one operation in an assignment statement, so that the semantics of that operator can be isolated from any side effects (or exceptions) caused by other operators.
Since method calls are expressions in Java, using A-normal form requires each actual argument be evaluated and its value stored in a variable, if it is not already a variable. Thus a call such as

would be transformed to something like the following (depending on the types of i and j, which the following assumes to be  ).
).

Henceforth let us assume that all programs have been converted to A-normal form.
3.2 Semantic Domains and Meaning Functions
In order to prove the soundness of a verification technique (i.e., that all conclusions reached are valid), one needs a semantics of the programming language and the specification language. To that end, the following development will discuss (but not precisely define all the details of) a denotational semantics for the programming and specification languages Java and JML. This subsection is adapted from our TOPLAS paper [17].
Java is a statically typed language, and our specification and verification approach requires that the static types of expressions are upper bounds of the types of values they may denote. We write typing judgments using a context (type environment), \(\varGamma \), which is a finite mapping from names to types. Such finite maps are often treated as sets of pairs; for example, suppose  . Then the value of \(\varGamma _0\) applied to x, \(\varGamma _0(x)\), is K and \(\varGamma _0(y)\) is
. Then the value of \(\varGamma _0\) applied to x, \(\varGamma _0(x)\), is K and \(\varGamma _0(y)\) is  . We extend such finite mappings using a comma, thus
. We extend such finite mappings using a comma, thus  is the finite map
is the finite map  . This extension notation (with the comma) is only used when the variable is not in the domain of the finite function; if it may be in the domain, then we use an override notation, such as \([\varGamma _0\mid x:L]\), which is the finite map
. This extension notation (with the comma) is only used when the variable is not in the domain of the finite function; if it may be in the domain, then we use an override notation, such as \([\varGamma _0\mid x:L]\), which is the finite map  .
.
Types in Java can be either primitive (value) types, such as  and
and  or reference types, which are class or interface names (instantiated with type parameters if necessary). The notation \( RefType\) denotes the set of all reference types.
or reference types, which are class or interface names (instantiated with type parameters if necessary). The notation \( RefType\) denotes the set of all reference types.
Our denotational semantics for a language like Java [17, 18] assumes that the class and interface declarations of a program are available in a class table, CT, that maps reference types to their declarations. From now on the class table, CT, of the program being considered is assumed to be fixed.Footnote 5
Types are partially ordered by the subtype relation \(\le \), which is derived from the reflexive-transitive closure of the declarations in classes and interfaces in the same way as in Java. Primitive types such as  are only subtypes of themselves. Subtyping for method types follows the usual contravariant ordering [6], although the formal parameter names must be identical. That is,
are only subtypes of themselves. Subtyping for method types follows the usual contravariant ordering [6], although the formal parameter names must be identical. That is,
if and only if \(\overline{U}\le \overline{T}\), \(T_1\le U_1\), and \(\overline{x}\) is identical to \(\overline{y}\) [17].
Example 2
Consider the interface and classes declared in Fig. 15 on the next page. This figure would produce a class table, call it \(CT_1\), that maps AbsCounter to its declaration, Counter to its declaration, and Gauge to its declaration.
In this example Counter \(\le \) AbsCounter and Gauge \(\le \) AbsCounter, and each of these types is also a subtype of itself. \(\blacksquare \)
As in Java, both expressions and commands (i.e., statements) can have effects. To model exceptions, our earlier work used a distinguished variable,  in the post-state of a command; when no exception is thrown,
in the post-state of a command; when no exception is thrown,  is null, otherwise it contains the exception object thrown [17].
is null, otherwise it contains the exception object thrown [17].
We formalize semantics uses the domains shown in Fig. 16 below.

adapted from our earlier work [17].
A guide to the domains used in the semantics,
We assume that there is a set, \(\textit{Ref}\), of references; these are the abstract addresses of objects.
To model the “class” field in an object’s runtime representation that was shown in Fig. 12 we use a ref context, which is a finite partial function, r, that maps references to class names (and not interface names). The idea is that if \(o\in \textit{dom}(r)\) then o is allocated and moreover o points to an object of dynamic type r(o). We define the set of reference contexts:
where \(\mathbin {\rightharpoonup }\) denotes finite partial functions. For r and \(r'\) in \(\textit{RefCtx}\), \(r\subseteq r'\) means that \(\textit{dom}(r) \subseteq \textit{dom}(r')\) and, for objects allocated in r, the dynamic types are the same in \(r'\) [17].
For data type T its domain of values in a reference context r is defined by cases on T, where K is a class name and I is an interface name [17]:

A store, s, for a context \(\varGamma \) is a dependent function from variables in scope to type-correct and allocated values. Thus for each \(x\in \textit{dom}(\varGamma )\), s(x) is an element of \(Val(\varGamma (x),r)\). In a store,  cannot be \({\textit{null}}\).
cannot be \({\textit{null}}\).

A heap h maps each allocated reference o to an object record, where the auxiliary function fields returns a context for all the fields of the given class (taking inheritance into account) [17].

Given a type environment, \(\varGamma \), a state for \(\varGamma \) is a tuple consisting of a ref context, r, together with an appropriate heap and store for r:

Example 3
An example of a state for the class table \(CT_1\) (in Example 2) is as follows. Let the type environment \(\varGamma _2\) be \([\texttt {c}:\texttt {AbsCounter}, \texttt {g}:\texttt {AbsCounter}]\). Let the store \(s_2\) be \([\texttt {c}: o_1, \texttt {g}:o_2]\). Let a reference context, \(r_2\) be \([o_1: \texttt {Counter},o_2:\texttt {Gauge}]\). Let a heap for \(r_2\) be defined by \(h_2(o_1) = [\texttt {count}:0]\) and \(h_2(o_2) = [\texttt {count}:2]\). Then \((r_2,h_2,s_2)\) is an element of \(State(\varGamma _2)\). \(\blacksquare \)
A state transformer, which is an element of  is a function \(\varphi \) that maps each state \(\sigma \) in \(State(\varGamma )\) to either \(\bot \) or a state \(\varphi (\sigma )\) in \(State(\varGamma ')\), with a possibly extended heap, subject to some additional conditions.
is a function \(\varphi \) that maps each state \(\sigma \) in \(State(\varGamma )\) to either \(\bot \) or a state \(\varphi (\sigma )\) in \(State(\varGamma ')\), with a possibly extended heap, subject to some additional conditions.

The predicate \(extState(\sigma ,\sigma ')\) says that the ref context of \(\sigma \) is extended by the ref context of \(\sigma '\). The predicate \(imuThis(\sigma ,\sigma ')\) says that  is not changed (if present in both states).
is not changed (if present in both states).
Example 4
Let \(\varDelta _3\) be  and \(\varDelta _3'\) be
and \(\varDelta _3'\) be  . A state transformer that is an element of
. A state transformer that is an element of  is \(\varphi _3\) defined by
is \(\varphi _3\) defined by
where for some \(o \in \textit{Ref}\) and integer n, if  and \((h(o))(\texttt {count}) = n\), then the resulting heap is defined by \(h' = [h\mid o:[h(o)\mid \texttt {count}:n+1]]\), and the resulting store is defined by
and \((h(o))(\texttt {count}) = n\), then the resulting heap is defined by \(h' = [h\mid o:[h(o)\mid \texttt {count}:n+1]]\), and the resulting store is defined by  . (This state transformer would be appropriate for a call to Counter’s method inc; see Fig. 15. This transformer uses
. (This state transformer would be appropriate for a call to Counter’s method inc; see Fig. 15. This transformer uses  to hold the method’s normal result. It also uses \({\textit{it}}\) as a value of type
to hold the method’s normal result. It also uses \({\textit{it}}\) as a value of type  , which avoids a special case for
, which avoids a special case for  state transformers.) \(\blacksquare \)
state transformers.) \(\blacksquare \)
State transformers are used for the meanings of expressions, commands, and methods as follows (where mtype returns the declared type of a method from the class table):

Note that the meanings for expressions and method bodies are similar and neither contains  (or the formals in the case of methods). This means that expressions and method calls cannot change the store. Thus the conversion to A-normal form must make any expressions that have effects on the store that occur in a command or expression become commands that store the expression’s value in a fresh variable, with this fresh variable replacing the expression with the effect. For example to convert a command such as the following
(or the formals in the case of methods). This means that expressions and method calls cannot change the store. Thus the conversion to A-normal form must make any expressions that have effects on the store that occur in a command or expression become commands that store the expression’s value in a fresh variable, with this fresh variable replacing the expression with the effect. For example to convert a command such as the following

into A-normal form, one would add extra commands to evaluate the expression  first, such as the following.
first, such as the following.

In Java, arguments are passed by value,Footnote 6 so a method itself cannot change the formal parameters (or  ).
).
Example 5
Let \(\varGamma _{xy}\) be  . A state transformer in
. A state transformer in  is the following. \(\varphi _{xy}(r,h,s) {\mathop {=}\limits ^{\mathrm{def}}}(r,h,s')\), where
is the following. \(\varphi _{xy}(r,h,s) {\mathop {=}\limits ^{\mathrm{def}}}(r,h,s')\), where  . The state transformer \(\varphi _{xy}\) would be the denotation of the expression
. The state transformer \(\varphi _{xy}\) would be the denotation of the expression  in the context \(\varGamma _{xy}\). \(\blacksquare \)
in the context \(\varGamma _{xy}\). \(\blacksquare \)
Example 6
Exceptions in expressions and commands are handled by examining the special variable  in the post-state. For example, the semantics of the Java assignment statement \(x{\texttt {=}}E{\texttt {;}}\) would be as follows.
in the post-state. For example, the semantics of the Java assignment statement \(x{\texttt {=}}E{\texttt {;}}\) would be as follows.

If the expression goes into an infinite loop, then the meaning of the command is an infinite loop (\(\bot \)) also, since \(\mathbf{lets}\) is a strict let expression in the notation. If the expression completes normally, then the state is updated with the variable being assigned bound to the result of the expression. Otherwise, if the expression threw an exception, then the command throws the same exception (and the store does not undergo any changes). (The meaning functions \([\![{\cdot }]\!]\) are curried functions that take a typing judgment and a method environment and then a state and produce a state of the appropriate type. Typing judgments for commands have no result type, but typing judgments for expressions do include a result type.)
\(\blacksquare \)
Example 7
The state transformer \(\varphi _3\) in Example 4 is an element of \(SemMeth(\texttt {Counter},\texttt {inc})\), where Counter is defined in Fig. 15. The transformer \(\varphi _3\) would be the denotation of Counter’s inc method. \(\blacksquare \)
A normal method environment is a table of denotations for all methods in all classes:
A normal method environment \(\eta \) is defined on pairs (K, m) where K is a class with method m; and \(\eta (K,m)\) is a state transformer suitable to be the meaning of a method of type \(\textit{mtype}(K,m)\). In case m is inherited in K from class L, \(\eta (K,m)\) will be the restriction of \(\eta (L,m)\) to receiver objects of type K.
In our formulation of modular reasoning based on static types, we need to associate method meanings to interfaces as well as to classes, even though the receiver of an invocation is always an object of some class. So we define the set of extended method environments by
The metavariable \(\dot{\eta }\) is used to range over extended method environments; think of the dot as a reminder that interfaces are included.
3.3 Dynamic vs Static Semantics
Mathematically modeling supertype abstraction is essentially about modeling a reasoning process that uses static type information for method calls and comparing that to the actual (dynamic) semantics of the programming language. In our prior work [17] we avoided committing to a particular verification technique by using an imaginary semantics for the language that runs method calls using a state transformer for a called method that is based on a specification table, given statically, and the static types of receivers. Thus, following this prior work, we will work with two different semantics for Java:
-
\(\mathcal {D}[\![{\cdot }]\!]\), the dynamic dispatch semantics, which is the operationally accurate and models dynamic dispatch for method calls, and
-
\(\mathcal {S}[\![{\cdot }]\!]\), the static dispatch semantics, which models static reasoning by using a static dispatch semantics based on method specifications as the semantics for method calls.
These semantics differ primarily in the way they treat method calls.
The dynamic dispatch semantics of method call expressions is as follows [17]:

This semantic function’s definition makes use of a helping function except, that returns a state that has the reference context and heap passed to it along with  bound to \({\textit{null}}\) and
bound to \({\textit{null}}\) and  bound to a new object of type \(\texttt {NullPointerException}\) [17]. The auxiliary function \(\textit{formals}\) returns the list of formal parameter names for a method. Note that in this semantics, K is the dynamic type of the receiver x and \(\eta (K,m)\) is the meaning of the method m in the method environment, \(\eta \). That method meaning is applied to a state, \((r,h,s_1)\), which has bindings for
bound to a new object of type \(\texttt {NullPointerException}\) [17]. The auxiliary function \(\textit{formals}\) returns the list of formal parameter names for a method. Note that in this semantics, K is the dynamic type of the receiver x and \(\eta (K,m)\) is the meaning of the method m in the method environment, \(\eta \). That method meaning is applied to a state, \((r,h,s_1)\), which has bindings for  and the formal parameters (\(\overline{z}\)).
and the formal parameters (\(\overline{z}\)).
The static dispatch semantics of a method call uses the receiver’s static type (T below) and a method meaning taken from an extended method environment, \(\dot{\eta }\), which is ultimately determined by specifications [17]:

Note that in the static dispatch semantics, not only is the method meaning taken from an extended method environment, but the type used to look up the method is based on the context (type environment) \(\varGamma \), so the meaning can be determined statically.
There are both dynamic and static semantics for other expressions and statements, \(\mathcal {D}[\![{\cdot }]\!]\) and \(\mathcal {S}[\![{\cdot }]\!]\), which are constructed with identical definitions, except for their treatment of method call expressions.
The method environment for a program is constructed, using the dynamic disptach semantics \(\mathcal {D}\), from the program’s declarations (i.e., from the program’s class table). Since methods may be mutually recursive, a chain of approximations is used to reach a fixed point [17, 27]. We write \(\mathcal {D}[\![{CT}]\!]\) for the method environment that is the least upper bound of this fixed point.
4 Specification Semantics
In order to formalize behavioral subtyping and supertype abstraction, we need to formalize specifications and refinement of specifications.
Recall that we think of the meaning of predicates as sets of states. For example, the meaning of the predicate  is \(\{ (r,h,s) \mid s(\texttt {x}) > s(\texttt {y}) \}\). As another example, the meaning of the predicate
is \(\{ (r,h,s) \mid s(\texttt {x}) > s(\texttt {y}) \}\). As another example, the meaning of the predicate  would be
would be  .
.
To consider the relationship between specifications in supertypes and subtypes, we need a notion of subtyping for contexts and state transformers.
Subtyping for type contexts, \(\varGamma \le \varDelta \), holds when the domains of \(\varGamma \) and \(\varDelta \) are equal and for each x in their domain, \(\varGamma (x)\le \varDelta (x)\). Since a subtype relation between types, \(S\le T\), implies that for each ref context r, \(Val(S,r)\subseteq Val(T,r)\), states for \(\varGamma \) are a subset of the states for \(\varDelta \) when \(\varGamma \le \varDelta \):
Subtyping for state transformer types follows the usual contravariant rule [6]:

4.1 Formalizing JML Specifications
In JML, postconditions specify a relationship between two states, by using the notation  to refer to the pre-state. We formalize such specifications as a pair of a predicate and a relation.
to refer to the pre-state. We formalize such specifications as a pair of a predicate and a relation.
Definition 3
(Specification in two-state form). Let \(\varGamma \) and \(\varGamma '\) be contexts, Then (P, R) is a specification in two-state form of type  if and only if P is a predicate on \(State(\varGamma )\) and R is a relation between \(State(\varGamma )\) and \(State(\varGamma ')\).
if and only if P is a predicate on \(State(\varGamma )\) and R is a relation between \(State(\varGamma )\) and \(State(\varGamma ')\).
However, Hoare logic typically uses one-state specifications, where each assertion only refers to a single state, as in our semantics for predicates above. JML does have a way to turn two-state postconditions into one-state postconditions, by using universal quantification over a specification.
Example 8
For example, the specification of AbsCounter’s method inc in Fig. 15,

can be written with JML’s forall clause in an equivalent way as follows.

The idea is that this specification applies for all values of oldCount that happen to equal the pre-state value of count.
One must also remember that references to field names such as count mean  in Java. Furthermore, since
in Java. Furthermore, since  is not available in the denotational semantics of the post-state, one also needs to use a
is not available in the denotational semantics of the post-state, one also needs to use a  to save the value of
to save the value of  and thereby allow the postcondition to access its fields. (This works because
and thereby allow the postcondition to access its fields. (This works because  cannot be changed by commands.) Thus the above should be rewritten as follows.
cannot be changed by commands.) Thus the above should be rewritten as follows.

To approach Hoare logic even more closely, the formalization in the TOPLAS paper [17] assumed that the meaning of JML’s assignable clauses could be written into the method’s postcondition; these added postconditions would state that all locations that are not assignable are unchanged. For example, if the only other location in the program is the field size, then the above specification would be translated as follows into an equivalent specification.

(As can be seen from this example, this translation to eliminate assignable clauses is not modular, as it depends on the locations in the rest of the program.)
\(\blacksquare \)
Such specifications as last the one above, which have universally quantified variables, a precondition, and a postcondition, are termed “general specifications” in our TOPLAS paper [17].
Definition 4
(General Specification). A general specification of type  is a triple of form (J, pre, post) such that:
is a triple of form (J, pre, post) such that:
-
1.
J is a non-empty set,
-
2.
pre is a J-indexed family of predicates over \(\varGamma \)-states, i.e., a function from J to the powerset of \(State(\varGamma )\), and
-
3.
post is a J-indexed family of predicates over \(\varGamma '\)-states, i.e., a function from J to the powerset of \(State(\varGamma ')\).
Example 9
Let \(\varGamma _3\) be  and \(\varGamma _3'\) be
and \(\varGamma _3'\) be  . Let \(J_{cst}\) be the set of triples of two integers and an AbsCounter reference. Let \(pre_{cst}\) and \(post_{cst}\) be the functions defined by:
. Let \(J_{cst}\) be the set of triples of two integers and an AbsCounter reference. Let \(pre_{cst}\) and \(post_{cst}\) be the functions defined by:

(We assume that  denotes MaxInt.) Then \((J_{cst},pre_{cst},post_{cst})\) is a general specification of type
denotes MaxInt.) Then \((J_{cst},pre_{cst},post_{cst})\) is a general specification of type  that would be an appropriate meaning for the specification of AbsCounter’s method inc (from Fig. 15) with the rewrites shown in Example 8. \(\blacksquare \)
that would be an appropriate meaning for the specification of AbsCounter’s method inc (from Fig. 15) with the rewrites shown in Example 8. \(\blacksquare \)
As a general technique, one can use the entire pre-state as the index set J, which allows one to access any features of the pre-state in postconditions [17]. This idea allows us to define an operator for converting specifications in two-state form into general specifications.
Definition 5
(Translation from two-state to general specifications). Let (P, R) be a specification in two-state form of type  . Then the translation of (P, R) into a general specification of type
. Then the translation of (P, R) into a general specification of type  is as follows.
is as follows.
4.2 Satisfaction and Refinement
With the above semantics of Java and JML in hand, we can resume the study of their relationship.
4.2.1 Satisfaction
The key relation is satisfaction of a method specification by its implementation; in the formal model this boils down to satisfaction of the meaning of a specification by the meaning of a method implementation, which is a state transformer. For simple (pre/post) specifications (P, Q) of type  , a state transformer
, a state transformer  , whose type is a subtype of the specification’s,
, whose type is a subtype of the specification’s,  , we say that \(\varphi \) satisfies (P, Q), written
, we say that \(\varphi \) satisfies (P, Q), written  , if and only if for all \(\sigma \in State(\varGamma )\), \(\sigma \in P \Rightarrow \varphi (\sigma ) \in Q\). The definition for general specifications is analogous [17].
, if and only if for all \(\sigma \in State(\varGamma )\), \(\sigma \in P \Rightarrow \varphi (\sigma ) \in Q\). The definition for general specifications is analogous [17].
Definition 6
(Satisfaction). Let (J, pre, post) be a general specification of type  . Let
. Let  be a state transformer, where
be a state transformer, where  . Then \(\varphi \) satisfies (J, pre, post), written
. Then \(\varphi \) satisfies (J, pre, post), written  , if and only if for all \(j \in J\), and for all \(\sigma \in State(\varGamma )\),
, if and only if for all \(j \in J\), and for all \(\sigma \in State(\varGamma )\),
This definition of satisfaction is a total correctness one, since the resulting state of a state transformer, \(\varphi (\sigma )\), must be defined.
Example 10
Consider the general specification \((J_{cst}, pre_{cst}, post_{cst})\) from Example 9, which has the type:

This is a formalization of the specification in AbsCounter for the method inc (from Fig. 15). Consider also the state transformer \(\varphi _3\) from Example 4. This state transformer has type:

However, the type of \(\varphi _3\) is not a subtype of the type of the specification, since Counter is a subtype of AbsCounter, but for subtyping of transformer types the argument contexts should be in a supertype relationship (as subtyping is contravariant on arguments) and the opposite is true. Thus \(\varphi _3\) does not satisfy \((J_{cst}, pre_{cst}, post_{cst})\). \(\blacksquare \)
4.2.2 Restrictions of Specifications
The above example shows that the type of the receiver argument ( ) requires a careful treatment in an OO language like Java. The problem is that the dynamic dispatch mechanism will guarantee that the receiver for a method m in class K has a dynamic type that is a subtype of K, but the receiver’s type is part of the context that is used to define the state spaces in the semantics, which leads to the subtyping problem in the above example.
) requires a careful treatment in an OO language like Java. The problem is that the dynamic dispatch mechanism will guarantee that the receiver for a method m in class K has a dynamic type that is a subtype of K, but the receiver’s type is part of the context that is used to define the state spaces in the semantics, which leads to the subtyping problem in the above example.
In what follows, we use the auxiliary function \( selftype\), which is defined as:

Using \( selftype\) we can define two restrictions on predicates.
Definition 7
(Exact Restriction). Let T be a reference type and let \(\varGamma \) be a context which is defined on  . If pre is a predicate on \(State(\varGamma )\), then the exact restriction of pre to T, written \(pre\mathord {\downharpoonright }T\), is the predicate on
. If pre is a predicate on \(State(\varGamma )\), then the exact restriction of pre to T, written \(pre\mathord {\downharpoonright }T\), is the predicate on  defined by
defined by
If (J, pre, post) is a general specification of type,  , where
, where  is in the domain of \(\varDelta \), then the exact restriction of (J, pre, post) to T, written \((J,pre,post)\mathord {\downharpoonright }T\), is the general specification \((J,pre',post)\) of type
is in the domain of \(\varDelta \), then the exact restriction of (J, pre, post) to T, written \((J,pre,post)\mathord {\downharpoonright }T\), is the general specification \((J,pre',post)\) of type  , where \(pre'(j) {\mathop {=}\limits ^{\mathrm{def}}}pre(j)\mathord {\downharpoonright }T\).
, where \(pre'(j) {\mathop {=}\limits ^{\mathrm{def}}}pre(j)\mathord {\downharpoonright }T\).
For simple specifications, \((P,Q)\mathord {\downharpoonright }T\) is \((P\mathord {\downharpoonright }T, Q)\).
As methods may be inherited in subtypes in Java, they may be applied to receivers that do not have the exact type of the class in which they are defined. Thus it is useful to have a similar notion that permits the type of  to be a subtype of a given type.
to be a subtype of a given type.
Definition 8
(Downward Restriction). Let T be a reference type and let \(\varGamma \) be a context that is defined on  . If pre is a predicate on \(State(\varGamma )\), then the downward restriction of pre to T, written \(pre\mathord {\downharpoonright ^{\!*}}T\), is the predicate on
. If pre is a predicate on \(State(\varGamma )\), then the downward restriction of pre to T, written \(pre\mathord {\downharpoonright ^{\!*}}T\), is the predicate on  defined by
defined by
If (J, pre, post) is a general specification of type  where
where  , then the downward restriction of (J, pre, post) to T, written \((J,pre,post)\mathord {\downharpoonright ^{\!*}}T\), is the general specification \((J,pre',post)\) of type
, then the downward restriction of (J, pre, post) to T, written \((J,pre,post)\mathord {\downharpoonright ^{\!*}}T\), is the general specification \((J,pre',post)\) of type  , where \(pre'(j) {\mathop {=}\limits ^{\mathrm{def}}}pre(j)\mathord {\downharpoonright ^{\!*}}T\).
, where \(pre'(j) {\mathop {=}\limits ^{\mathrm{def}}}pre(j)\mathord {\downharpoonright ^{\!*}}T\).
Example 11
Consider the precondition specification \((J_{cst}, pre_{cst}, post_{cst})\) from Example 9, which has the type:

The exact restriction \((J_{cst}, pre_{cst}, post_{cst})\mathord {\downharpoonright }\texttt {Counter}\), is \((J_{cst}, pre_{cst}', post_{cst})\), where

Note that \((J_{cst}, pre_{cst}, post_{cst})\mathord {\downharpoonright }\texttt {Counter}\), has the type

Since the type of this exact restriction is the same as the type of \(\varphi _3\) from Example 4, the reader can check that  .
.
The downward restriction \((J_{cst}, pre_{cst}, post_{cst})\mathord {\downharpoonright ^{\!*}}\texttt {Counter}\) is \((J_{cst}, pre_{cst}'', post_{cst})\), where

The reader can check that the type of this downward restriction is the same as the type of the state transformer \(\varphi _3\) from Example 4, so that  . \(\blacksquare \)
. \(\blacksquare \)
4.2.3 Refinement of Specifications
In general, a specification \(S_2\) refines a specification \(S_1\) if \(S_2\) restricts the set of correct implementations such that every correct implementation of \(S_2\) is a correct implementation of \(S_1\). The importance of this is that if a verifier uses \(S_1\), then any conclusions it draws are valid for implementations that satisfy \(S_2\). This is exactly the property that supertype abstraction should have to permit modular reasoning about OO programs, hence refinement is key to the results reported in our TOPLAS paper [17].
Definition 9
Let \(spec_1\) be a specification of type  and let \(spec_2\) be a specification of type
and let \(spec_2\) be a specification of type  where
where  . Then \(spec_2\) refines \(spec_1\), written \(spec_2 \sqsupseteq spec_1\), if and only if for all
. Then \(spec_2\) refines \(spec_1\), written \(spec_2 \sqsupseteq spec_1\), if and only if for all  ,
,

In terms of specifications, refinement can be characterized as follows [17].
Theorem 1
Let (I, pre, post) be a specification of type  and let \((J,pre',post')\) be a specification of type
and let \((J,pre',post')\) be a specification of type  where
where  . Then the following are equivalent:
. Then the following are equivalent:
-
1.
\((J,pre',post') \sqsupseteq (I,pre,post)\),
-
2.

\(\blacksquare \)
Example 12
Imagine that in the abstract class AbsInterval the method pick was specified as follows:

This JML specification corresponds to the general specification \((J_{pai},pre_{pai},post_{pai})\) of the type  , where
, where

Consider the following JML specification for pick in the subtype Interval.

This JML specification corresponds to the general specification \((J_{pi},pre_{pi},post_{pi})\), which has type  , where
, where

Then \((J_{pi},pre_{pi},post_{pi}) \sqsupseteq ((J_{pai},pre_{pai},post_{pai})\mathord {\downharpoonright }\texttt {Interval})\), since

To see this, let \(\varphi \) be such that  and consider an arbitrary pre-state
and consider an arbitrary pre-state  such that
such that
The above means that \((r,h,s) \in pre_{pai}(r,h,s) \wedge selftype(r,h,s) = \texttt {Interval}\). It follows that  and \((r,h,s) \in pre_{pi}(r,h,s)\). Let reference ot be such that
and \((r,h,s) \in pre_{pi}(r,h,s)\). Let reference ot be such that  . By assumption \(\varphi (r,h,s) \in post_{pi}(r,h,s)\). Let \((r',h',s')\) be \(\varphi (r,h,s)\). Then by definition of \(post_{pi}(r,h,s)\): \(r \subseteq r'\), \(h \subseteq h'\),
. By assumption \(\varphi (r,h,s) \in post_{pi}(r,h,s)\). Let \((r',h',s')\) be \(\varphi (r,h,s)\). Then by definition of \(post_{pi}(r,h,s)\): \(r \subseteq r'\), \(h \subseteq h'\),  , and
, and  . It follows that
. It follows that  and
and  , so \(\varphi (r,h,s) = (r',h',s') \in post_{pai}(r,h,s)\). \(\blacksquare \)
, so \(\varphi (r,h,s) = (r',h',s') \in post_{pai}(r,h,s)\). \(\blacksquare \)
As in the above example, due to subtyping and inheritance, it is useful to consider combinations of refinement with exact or downward restrictions of specifications (from supertypes). So we make the following definitions [17].
Definition 10
(Refinement at a subtype). Let \(spec_1\) be a specification of type  , where
, where  . Let \(spec_2\) be a specification of type
. Let \(spec_2\) be a specification of type  , which is such that
, which is such that  .
.
Then \(spec_2\) refines \(spec_1\) at exact subtype T, written \(spec_2 \sqsupseteq ^T spec_1\), iff  .
.
Further, \(spec_2\) refines \(spec_1\) at downward subtype T, written \(spec_2 \sqsupseteq ^{*T} spec_1\), if and only if \(spec_2 \sqsupseteq (spec_1\mathord {\downharpoonright ^{\!*}}T)\).
Example 13
Consider the specifications \((J_{pai},pre_{pai},post_{pai})\) and \((J_{pi},pre_{pi},post_{pi})\) from Example 12. Since that example showed that
it follows that \((J_{pi},pre_{pi},post_{pi}) \sqsupseteq ^{\texttt {Interval}} (J_{pai},pre_{pai},post_{pai})\). The reader can check that it is also the case that \((J_{pi},pre_{pi},post_{pi}) \sqsupseteq ^{*\texttt {Interval}} (J_{pai},pre_{pai},post_{pai})\). \(\blacksquare \)
It happens that the downward restriction of a specification refines the exact restriction of that specification (at the same type), and so downward refinement implies exact refinement [17]. Thus downward refinement is a stronger notion than exact refinement.
Corollary 1
Let \(spec_1\) be a specification of type  , where
, where  . Let \(spec_2\) be a specification of type
. Let \(spec_2\) be a specification of type  , which is such that
, which is such that  . Then \(spec_2 \sqsupseteq ^{*T} spec_1\) implies \(spec_2 \sqsupseteq ^{T} spec_1\). \(\blacksquare \)
. Then \(spec_2 \sqsupseteq ^{*T} spec_1\) implies \(spec_2 \sqsupseteq ^{T} spec_1\). \(\blacksquare \)
5 Supertype Abstraction
Armed with the understanding of the semantics of specifications and programs discussed above, we can return to the topic of supertype abstraction and its soundness and completeness.
Recall that we want verification to be modular, so that one can verify OO programs in a way that will remain valid when new subtypes are added to the program. In addition, for the verification technique to be practical, it should be able to verify one method at a time, using the specifications of all other methods (to allow for mutually-recursive methods).
5.1 Specification Tables
The method specifications available in a program are modeled [17] in a specification table, ST, which is a function from pairs of reference types and method names to general specifications. That is, for all reference types T and method names m such that \(mtype(T,m) = \overline{x:U} \rightarrow V\):

An element of ST, ST(T, m) is a general specification, and thus models the meaning of specification of m in type T, taking into account all of the specification language’s semantics.
Each method in a program should satisfy its specification; this can be summarized by saying that the method environment satisfies the specification table.
Definition 11
(Satisfaction of ST by a method environment). Let ST be a specification table.
An extended method environment \(\dot{\eta }\) satisfies ST, written  , if and only if for all reference types T and method names \(m \in Meths(T)\),
, if and only if for all reference types T and method names \(m \in Meths(T)\),  .
.
A normal method environment \(\eta \) satisfies ST, written  , if and only if for all class types K and methods \(m \in Meths(K)\),
, if and only if for all class types K and methods \(m \in Meths(K)\),  .
.
5.2 Modular Verification
Verification is modular with respect to methods if it relies on the specifications of called methods, from the specification table for a program, not on the code of those methods (from the class table). The main advantage of modular verification is that it is scalable, since verification can proceed one method at a time and does not depend on how many other methods are called in a method (or how deep the call graph is in a program). Another advantage is that modular verification does not need to be changed when the code changes. For example, code in a method may be changed in any way (e.g., to make it more efficient), and as long as it correctly implements the method’s specification (and that specification is unchanged), then verification of method calls that uses that method does not need to change. Another important example is that one should be able to add new subtypes to a program without re-verifying it. The main disadvantage of modular verification is that when the specifications used (to make it modular) are too weak, then one will not be able to draw all the conclusions that might be valid operationally.
In Java all code is part of a method. If every method has a (JML) specification, then satisfaction of the specification table means that the program is correct. That is, a program with class table CT and specification table ST is correct if and only if  , i.e., when the method environment constructed by the dynamic semantics satisfies the specification table, so that every method correctly implements its specification. This models the way a verification logic would prove the implementation of each method separately, using the specifications of all methods as assumptions.
, i.e., when the method environment constructed by the dynamic semantics satisfies the specification table, so that every method correctly implements its specification. This models the way a verification logic would prove the implementation of each method separately, using the specifications of all methods as assumptions.
To formalize that reasoning is not dependent on method implementations, but only relies on the specifications of methods, one can quantify over all correct method implementations, as in the following.
Definition 12
Let ST be a specification table, let \(\varGamma \) be a context, and let C be a command that type checks in the context \(\varGamma \), i.e., \(\varGamma \vdash C\). Then C modularly satisfies spec with respect to ST, written  , if and only if for all \(\eta \in MethEnv\),
, if and only if for all \(\eta \in MethEnv\),

We will use a similar notation for any phrase-in-context (i.e., typing judgment), \(\mathcal{P}\), so that  if and only if in every correct method environment for ST,
if and only if in every correct method environment for ST,  . The idea is that modular satisfaction can only depend on the specifications in ST, since all correct method environments must satisfy the specification.
. The idea is that modular satisfaction can only depend on the specifications in ST, since all correct method environments must satisfy the specification.
Example 14
Let ST be such that \(ST(\texttt {AbsCounter},\texttt {inc})\) is the general specification from Example 9: \((J_{cst},pre_{cst},post_{cst})\). Let \(\varGamma _3\) and \(\varGamma _3'\) be as in Example 9. Let the command \(C_{inc}\) be as follows.

Then \(\varGamma _3 \vdash C\) is a valid typing judgment. Let \(\eta \) be a method environment that satisfies ST and in particular \(\eta (\texttt {AbsCounter},\texttt {inc})\) is the state transformer \(\varphi _3\). Since \(C_{inc}\) does not involve any method calls, the following is independent of the type environment \(\eta \).

Then  follows (ignoring overflow and the field size, which is mentioned in the specification). \(\blacksquare \)
follows (ignoring overflow and the field size, which is mentioned in the specification). \(\blacksquare \)
More interesting examples involve method calls. For example, the verification shown in Fig. 4 is modular, as it only uses the specifications from IntSet to verify several commands in sequence. We formalize such modular reasoning using the specifications associated with static types as follows [17].
Definition 13
Let ST be a specification table. Let \(\mathcal{P}\) be a phrase-in-context. Let spec be a specification. Then \(\mathcal{P}\) modularly satisfies spec with respect to ST under static dispatch, written  , if and only if for all extended method environments \(\dot{\eta }\in XMethEnv\),
, if and only if for all extended method environments \(\dot{\eta }\in XMethEnv\),

5.3 Supertype Abstraction
Supertype abstraction allows one to prove modular correctness using the static dispatch semantics. What we call strong supertype abstraction is formalized as modular satisfaction under static dispatch implying modular satisfaction [17].
Definition 14
(strong supertype abstraction). Let ST be a specification table. Then ST allows strong supertype abstraction if and only if for all phrases-in-context \(\mathcal{P}\) and specifications spec,

Specification tables that allow strong supertype abstraction thus have the property that one can reason in a modular way using just specifications based on static type information, and yet can draw conclusions that are dynamically valid, in spite of subtyping and dynamic dispatch.
Of course, we would like to reason in a way that is more economical than considering all possible extended method environments. The approach for doing this is to use specifications in reasoning, as in JML.
5.4 Supertype Abstraction and Behavioral Subtyping
Leaving aside many technical details, we can point to the main theoretical result of our TOPLAS paper [17].
One approach to more economical reasoning is to treat calls of the form \(x.m(\overline{y})\), where x has static type T as indicated in the introduction as predicate transformers. If ST(T, m) is the simple specification (pre, post), then the call can be treated as a specification statement that asserts pre and then assumes post, which in JML can be written as follows.

Following the TOPLAS paper [17], we can give semantics to such specification statements as weakest precondition (wp) predicate transformers, which map postconditions to the weakest preconditions that guarantee the postcondition will be reached. Recall that one can think of predicates as set of states, so a predicate transformer can also be thought of as mapping sets of states to sets of states. We write \(\{\![{(pre, post)}]\!\}\) for the weakest precondition predicate transformer above that maps the predicate post to the predicate pre. One can also think of this as mapping the set of all states that satisfy post to the set of all states that satisfy pre.
The weakest precondition transformer for a general specification [17] (J, pre, post) of type  , written \(\{\![{(J,pre,post)}]\!\}\), is defined such that for any state \(\sigma \) and predicate Q:
, written \(\{\![{(J,pre,post)}]\!\}\), is defined such that for any state \(\sigma \) and predicate Q:

The TOPLAS paper used such wp predicate transformers to define an environment of predicate transformers derived from the specifications of each method. That is, the method environment, \(\{\![{ST}]\!\}\), is such that for all types T and method names m, the transformer for the method m in type T is the weakest precondition predicate transformer that corresponds to the specification of that method:

This extended method environment is called the least refined specification table [17].
The least refined specification table and predicate transformers provide another characterization of modular verification [17]. This notion of modular verification uses a static dispatch predicate transformer semantics (\(\mathcal {S}\{\![{\cdot }]\!\}\)) and the least refined specification table that satisfies ST (\(\{\![{ST}]\!\}\)), to avoid quantifying over all extended method environments.
Definition 15
(Modular Verification). Let ST be a specification table. Let \(\varGamma \) be a type context that type checks a command C, i.e., \(\varGamma \vdash C\). Let spec be a specification of type  . Then C is modularly verified for spec with respect to ST if and only if
. Then C is modularly verified for spec with respect to ST if and only if

Supertype abstraction means that one can establish modular correctness using supertype specifications and static type information. Our TOPLAS paper [17] formalized this in two ways. Weak supertype abstraction uses the idea of modular verification above.
Definition 16
(Weak supertype abstraction). Let ST be a specification table. Then STallows weak supertype abstraction if and only if for every phrase-in-context \(\mathcal{P}\) and every specification spec:

We explained the notion of strong supertype abstraction above (Definition 14). Strong supertype abstraction says that any conclusions drawn using the static dispatch semantics are valid using the dynamic dispatch semantics. Thus strong supertype abstraction generalizes from any particular reasoning technique.
Behavioral subtyping is a property of a specification table, as it relates the specifications of subtypes to their supertypes. There are two notions of behavioral subtyping, corresponding to exact refinement and downward refinement of specifications.
Behavioral subtyping means that each overriding method in a class K refines the specification of that method at exact type K (i.e., assuming that the type of  is equal to K).
is equal to K).
Definition 17
(Behavioral Subtyping). Let ST be a specification table. Then ST has behavioral subtyping if and only if for all reference types U, method names \(m \in Meths(U)\) and classes K:
Robust Behavioral subtyping means that each overriding method in a class K downward refines the specification of that method at type K (i.e., assuming that K is an upper bound on the type of  ).
).
Definition 18
(Robust Behavioral Subtyping). Let ST be a specification table. Then ST has robust behavioral subtyping if and only if for all reference types U, method names \(m \in Meths(U)\) and classes K:
Note that in neither case is there any necessary relationship between specifications in interfaces. Although JML insists that overriding methods in interfaces (downward) refine the specifications in the interfaces that they override, this is not needed for such specifications that appear in interfaces. What is needed is that overriding methods in classes refine all specifications in their supertypes (including interfaces).
Practical examples seem to have robust behavioral subtyping, which corresponds to what JML enforces. Even Parkinson and Bierman’s Cell and DCell examples [25], which make liberal use of a  primitive in specifications, exhibit robust behavioral subtyping [17, Example 8.5].
primitive in specifications, exhibit robust behavioral subtyping [17, Example 8.5].
Since downward refinement is stronger than exact refinement, robust behavioral subtyping implies behavioral subtyping [17].
The main result in our TOPLAS paper is the following theorem [17, Theorem 8.15].
Theorem 2
Let ST be a specification table that is satisfiable. Then the following are equivalent:
-
1.
ST has behavioral subtyping,
-
2.
ST allows strong supertype abstraction, and
-
3.
ST allows weak supertype abstraction.
6 Specification Inheritance
Because supertype abstraction is desirable for modular reasoning about OO programs, and because the validity of supertype abstraction is equivalent to specifications having behavioral subtyping, it is desirable to have a way to either: (a) check that specifications have behavioral subtyping, or (b) construct specifications with behavioral subtyping. Some authors (e.g., Findler and Felleisen [8]) take the view that it is the responsibility of the specifier to ensure behavioral subtyping, and thus that tools should check that what has been specified satisfies some definition of behavioral subtyping. An advantage of this approach is that specifiers will know exactly what specifications are being used for each type. A disadvantage is that writing such specifications may be more work than with the other approach.
JML uses specification inheritance to force all subtypes to be behavioral subtypes [7, 16], which implicitly constructs specifications with behavioral subtyping. An advantage of this approach is that behavioral subtyping is automatic. A disadvantage is that specifiers need to be aware of how specifications are automatically constructed.
In this section we will explain the formal model of specification inheritance developed in our prior work [17] and how it forces behavioral subtyping.
6.1 Joining Specifications
The idea of specification inheritance is that the obligations for a method should be inherited from supertypes in a way that is similar to the way code is inherited. This makes the construction of new subtypes easier, approaching the ease of constructing new subclasses in code.
The approach that is adopted in JML is due to Alan Wills, whose mechanism for Smalltalk [32] combines method specifications from supertypes. The basic idea is simple: all the specifications from all supertypes are combined so that an implementation that satisfies the combined specification also satisfies each inherited specification (considered separately). In JML a method specification may have several “specification cases,” each of which can be formally modeled with a general specification. Methods must correctly implement each of these specification cases [33]. Conversely, a client, when calling a method, may choose any of a method’s specification cases to use when verifying a call to the method (by checking the precondition of that case and assuming its postcondition).
Example 15
Consider the method pick, specified in both the interface IntSet and the subtype Interval. The specifications of this method from IntSet (see Fig. 1) and from Interval (see Fig. 6) are combined by JML into the specification shown in Fig. 17. This combined specification has two specification cases, separated by  . The first specification case is the specification inherited from IntSet. The second specification case is the one added for the type Interval.
. The first specification case is the specification inherited from IntSet. The second specification case is the one added for the type Interval.
This textual combination form is the source of the  that must precede added specifications in overriding methods in JML [19]. \(\blacksquare \)
that must precede added specifications in overriding methods in JML [19]. \(\blacksquare \)
To connect the idea of specification inheritance to the formal model developed so far, we need a way to combine several method specifications into one specification. This will also serve to explain the meaning of how method specifications are combined. As with behavioral subtyping, however, one must be careful about typing. However, unlike the typing of specification refinement related to behavioral subtyping, for specification inheritance the problem is not the type of  , which can be handled by a (downward) restriction, but the type of the result.
, which can be handled by a (downward) restriction, but the type of the result.
Example 16
Imagine a method in a supertype T has a general specification \((J,pre',post')\) of type  . A subtype K can also write a specification for the same method, (I, pre, post) of type
. A subtype K can also write a specification for the same method, (I, pre, post) of type  . The type system ensures that
. The type system ensures that  , (i.e.,
, (i.e.,  and \(\varDelta ' \le \varGamma '\)).
and \(\varDelta ' \le \varGamma '\)).
Suppose \(I \cap J = \emptyset \) and we combined these disjoint partial specifications to form the general specification \((I \cup J, pre \cup pre'\mathord {\downharpoonright ^{\!*}}K, post \cup post')\) for the subtype’s method. This nearly formalizes the idea of combining specification cases [7, 32], since a call can satisfy the precondition by choosing either \(i \in I\) or \(j \in J\) such that pre(i) or \(pre'(j)\mathord {\downharpoonright ^{\!*}}K\) holds, and then, given the choice for i or j, the corresponding postcondition can be assumed. Conversely, an implementation must satisfy all these partial specifications, due to the definition of satisfaction of a general specification by a predicate transformer (Definition 6), which requires the transformer to satisfy the specification for each index.
However, this specification should have a type appropriate for the subtype, i.e.,  . For the arguments,
. For the arguments,  , so for any \(j\in J\), \(pre'(j)\mathord {\downharpoonright ^{\!*}}K \in State(\varDelta )\), which works. However, for the result \(\varDelta ' \not \le \varGamma '\), since for some \(j \in J\), \(post'(j)\) may not be contained in \(State(\varDelta ')\), so the postcondition cannot be inherited in this way. \(\blacksquare \)
, so for any \(j\in J\), \(pre'(j)\mathord {\downharpoonright ^{\!*}}K \in State(\varDelta )\), which works. However, for the result \(\varDelta ' \not \le \varGamma '\), since for some \(j \in J\), \(post'(j)\) may not be contained in \(State(\varDelta ')\), so the postcondition cannot be inherited in this way. \(\blacksquare \)
The problem shown in the above example is the type of the method’s result. In a method specification, the domain of the result context always contains just  and
and  . The type of
. The type of  is always \(\texttt {Throwable}\), so that does not cause any difficulties. The problem is that in a supertype’s method, the type of
is always \(\texttt {Throwable}\), so that does not cause any difficulties. The problem is that in a supertype’s method, the type of  may be a supertype of the type of the result type in the subtype’s method, so \(post'\) needs to be strengthened to make the result have the type needed (
may be a supertype of the type of the result type in the subtype’s method, so \(post'\) needs to be strengthened to make the result have the type needed ( ). (Note that if one writes code in the subtype for an overriding method, the type checker will ensure that the result has the declared type, but that type might be a subtype of the declared type of the result in the method being overridden.)
). (Note that if one writes code in the subtype for an overriding method, the type checker will ensure that the result has the declared type, but that type might be a subtype of the declared type of the result in the method being overridden.)
To solve this problem, our earlier work [17] used an operator \(\Cap \), defined as follows.
Definition 19
(Restricting Postconditions). Let X be a set of states of type \(State(\varGamma ')\) and let \(post'\) be a J-indexed family of predicates of type \(State(\varGamma ')\). Then \((post' \Cap X)\) is the J-indexed family of predicates defined by:
This operator can be used to define the join of two general specifications with disjoint index sets.
Definition 20
(Inheriting Join of Specifications). Suppose I and J are disjoint non-empty sets. Let  where
where  , and
, and  be general specifications such that
be general specifications such that  . Then the inheriting join of these specifications, a general specification of type
. Then the inheriting join of these specifications, a general specification of type  is defined by:
is defined by:
To illustrate this using the pick method’s specifications as in Example 15, a formal model of those specifications is needed. Since the pick method’s specification involves pure method calls, we define the following notation for evaluating Boolean expressions to help shorten the presentation of these models.

The result of \(\textit{beval}[\![{\varGamma \vdash E}]\!]\) in a given state will thus be either true or false (or \(\bot \)).
To deal with index sets that may have a non-empty intersection, we define [17]:
with injections \(inl: I \rightarrow (I+J)\) and \(inr: J \rightarrow (I+J)\) defined by \(inl(i) = (i,0)\) and \(inr(j) = (j,1)\).
Example 17
Consider the two specification cases for the pick method in Fig. 17.
Ignoring the assignable clauses, the first specification case (from IntSet) can be thought of as the general specification of type  , \((State(\varGamma _{is}),pre_{is},post_{is})\), where the context \(\varGamma _{is}\) is
, \((State(\varGamma _{is}),pre_{is},post_{is})\), where the context \(\varGamma _{is}\) is  ,
,  , and
, and

The second specification case (from Interval) can modeled as the general specification of type  , \((State(\varGamma _{iv}), pre_{iv}, post_{iv})\), where the context \(\varGamma _{iv}\) is
, \((State(\varGamma _{iv}), pre_{iv}, post_{iv})\), where the context \(\varGamma _{iv}\) is  , \(\varGamma _{ir}\) is as above, and (assuming long2int converts a value from a
, \(\varGamma _{ir}\) is as above, and (assuming long2int converts a value from a  to an
to an  ):
):

So the inheriting join of the above two general specifications is
This general specification has type  . The \(\Cap \) operator is not needed to form the postcondition in this case, as the same result context, \(\varGamma _{ir}\), is used for both specifications.
. The \(\Cap \) operator is not needed to form the postcondition in this case, as the same result context, \(\varGamma _{ir}\), is used for both specifications.
Thus the precondition of the join is equivalent to the following.

Similarly the postcondition of the join is equivalent to the following.

\(\blacksquare \)
As in the above example, it is possible to combine the index sets of general specifications as if they were disjoint, by using the operator \(+\) as shown above [17]. Thus the inheriting join can always be used to combine general specifications.
The inheriting join is a “join” in the sense of lattice theory, as it is the least upper bound in the refinement ordering.
Lemma 1
Suppose I and J are disjoint sets (I, pre, post) is a general specification of type  ,
,  , and \((J,pre',post')\) is a general specification of type
, and \((J,pre',post')\) is a general specification of type  such that
such that  . Then the inheriting join \((I,pre,post) \sqcup (J,pre',post')\) is the least upper bound of (I, pre, post) and \((J,pre',post' \Cap State(\varDelta '))\) with respect to the refinement ordering for specifications of type
. Then the inheriting join \((I,pre,post) \sqcup (J,pre',post')\) is the least upper bound of (I, pre, post) and \((J,pre',post' \Cap State(\varDelta '))\) with respect to the refinement ordering for specifications of type  . That is, for all
. That is, for all  ,
,
if and only if the following both hold:
As the above lemma states, the join of two specifications refines both of them. However, satisfying two specifications simultaneously may be impossible.
Example 18
Consider the following JML specification, which has two specification cases.

These specification cases can be modeled formally as follows. Let the type context  . The first specification case is then modeled as \((State(\varGamma _{iv}), true, post_{lb})\), where
. The first specification case is then modeled as \((State(\varGamma _{iv}), true, post_{lb})\), where

The second specification case is similarly modeled as \((State(\varGamma _{iv}, true, post_{ub})\), where

Since the index sets are the same (\(State(\varGamma _{iv})\)), the join is the specification
This is equivalent to the general specification \((State(\varGamma _{iv}) \times \{0,1\}, true, post_c)\), where the family of postconditions \(post_c\) is equivalent to the following.

However, \(post_c\) is unsatisfiable. Why? Because an implementation will need to produce a state with a fixed value for  ; if it makes
; if it makes  be the value of lb, then it will not satisfy \(post_c\) when the state passed is paired with 1, but in the formal model it must satisfy \(post_c\) for all indexes, as the precondition is always satisfied. (One might think of the 0 or 1 passed in a pair with a state as an input that the program cannot observe.) Thus, if the values of lb and ub can be different, then it will not be possible to write a correct implementation of this specification, since the result cannot simultaneously have two different values.
be the value of lb, then it will not satisfy \(post_c\) when the state passed is paired with 1, but in the formal model it must satisfy \(post_c\) for all indexes, as the precondition is always satisfied. (One might think of the 0 or 1 passed in a pair with a state as an input that the program cannot observe.) Thus, if the values of lb and ub can be different, then it will not be possible to write a correct implementation of this specification, since the result cannot simultaneously have two different values.
In more detail, recall that an implementation is modeled as a state transformer, \(\varphi \), which is a function. To satisfy a general specification, such as \((State(\varGamma _{iv}) \times \{0,1\}, true, post_c)\), \(\varphi \) must be such that for each \(((r,h,s),j) \in State(\varGamma _{iv}) \times {0,1}\), if  then
then  . However, if
. However, if  , so that
, so that  is lb’s value, then
is lb’s value, then  , assuming that ub’s value is different. \(\blacksquare \)
, assuming that ub’s value is different. \(\blacksquare \)
Expressed in JML, the join of two specification cases

and

is the JML specification

This combined specification [7, 16, 19, 33], requires the implementation to satisfy both of the separate specification cases (which corresponds to the formal requirement that the specification be satisfied at all indexes). Note that if both  and
and  are true, then both
are true, then both  and
and  must hold.
must hold.
Thus in JML, and in the formal model, the join of two specifications may be unsatisfiable. Another way of looking at this is that joining specifications can only add more constraints to a specification, and that may result in a specification that cannot be correctly implemented [7, 16, 17].
6.2 Constructing the Specification Table
Overall, the goal of specification inheritance, in our formal model, is to construct a specification table that has behavioral subtyping. Thus we can state the goals of a technique for constructing a specification table as follows [17]:
-
1.
It should refine the written specifications,
-
2.
It should have behavioral subtyping.
-
3.
It should be the least refined specification table with these properties.
-
4.
It should provide the most complete modular verification in the sense whenever conclusions are modularly correct, then these conclusions can be verified using the technique.
Our TOPLAS paper [17] discussed several technical approaches to constructing a specification table and compared each against the above goals.
Refinement for specification tables is defined pointwise, that is,

From this definition, it follows that if \(ST' \sqsupseteq ST\), then for all phrases-in-context \(\mathcal{P}\),

One way to formalize the construction of a specification tables with behavioral subtyping is to define a function that takes a specification table argument and returns a specification table based on the argument, which has behavioral subtyping.
Definition 21
(Robust Class Inheritance). Let ST be a specification table. Then the specification table \({{\varvec{rki}}}(ST)\) is defined for class names K and interface names I by:
The following is closest to what JML does.
Definition 22
(Robust RefType Inheritance). Let ST be a specification table. Then the specification table \({{\varvec{rrti}}}(ST)\) is defined for reference types U by:
A variant of the above uses exact restriction instead of a downward restriction.
Definition 23
(Exact RefType Inheritance). Let ST be a specification table. Then the specification table \({{\varvec{erti}}}(ST)\) is defined for reference types U by:
In our prior work, we showed that both of the robust flavors of inheritance produce specification tables that refine the original table: \(\mathbf{rki}(ST) \sqsupseteq ST\) and \(\mathbf{rrti}(ST) \sqsupseteq ST\). However, it is not the case that \(\mathbf{erti}(ST)\) refines ST, because in general exact restrictions do not produce refinements.
Both robust flavors of inheritance produce specification tables with robust behavioral subtyping, although etri only produces a specification table with behavioral subtyping (not robust behavioral subtyping). It turns out [17] that if \(\mathbf{rki}(ST)\) is satisfiable, then it is the least refinement of ST that is satisfiable and has robust behavioral subtyping. So rki satisfies our first three goals. However, rrti also satisfies these first three goals and also provides the most complete modular verification [17].
7 Conclusions
Supertype abstraction allows for modular reasoning about OO programs that is both powerful and simple. In combination with rewriting code to use downcasts, it can be used to reach any conclusions that an exhaustive case analysis could.
Our definition of behavioral subtyping [17] is both necessary and sufficient for sound supertype abstraction.
Robust behavioral subtyping, which itself implies behavioral subtyping, can be obtained by specification inheritance.
7.1 Future Work
Our prior work [17] did not give a modular treatment of framing and how to modularly specify and verify frame conditions in OO programs. Thus an important area of future work is to provide such a modular treatment of framing with supertype abstraction and behavioral subtyping. This work would benefit practical tools. Bao has been working on solving this problem [5].
An interesting line of future work would be to conduct human studies with programmers to see what the true advantages and disadvantages of using supertype abstraction are for reasoning about OO programs.
Notes
- 1.
The size is not specified to decrease, since it can stay the same if the element being removed was not in the set in the pre-state.
- 2.
Recall that a call such as
 is shorthand for
is shorthand for 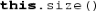 in Java, thus substituting iset for
in Java, thus substituting iset for  in
in  turns it into
turns it into  .
. - 3.
There still are some other details omitted, such as how declarations (e.g., of the variable
 ) are handled.
) are handled. - 4.
Note that the transformation must ensure that any variables declared are fresh.
- 5.
If classes can be created or loaded at runtime, then CT would contain all the classes that might be available to the program at runtime.
- 6.
In Java, and Smalltalk-80 and C#, the values of expressions may be references, but the parameter passing mechanism is call by value, since one cannot write a method that modifies variables passed as actual parameters, such as swap. However, the semantics of method calls would need to be different for a language like C++ where parameters can be declared to be passed by reference (using
 ).
).
References
America, P.: Inheritance and subtyping in a parallel object-oriented language. In: Bézivin, J., Hullot, J.-M., Cointe, P., Lieberman, H. (eds.) ECOOP 1987. LNCS, vol. 276, pp. 234–242. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47891-4_22
America, P.: A behavioural approach to subtyping in object-oriented programming languages. Technical report 443, Philips Research Laboratories, Nederlandse Philips Bedrijven B. V., April 1989. Revised from the January 1989 version
America, P.: Designing an object-oriented programming language with behavioural subtyping. In: de Bakker, J.W., de Roever, W.P., Rozenberg, G. (eds.) REX 1990. LNCS, vol. 489, pp. 60–90. Springer, Heidelberg (1991). https://doi.org/10.1007/BFb0019440
Apt, K.R., Olderog, E.: Verification of Sequential and Concurrent Programs. Graduate Texts in Computer Science Series, 2nd edn. Springer, New York (1997). https://doi.org/10.1007/978-1-4757-2714-2
Bao, Y.: Reasoning about frame properties in object-oriented programs. Technical report CS-TR-17-05, Computer Science, University of Central Florida, Orlando, Florida, December 2017. https://goo.gl/WZGMiB, the author’s dissertation
Cardelli, L.: A semantics of multiple inheritance. Inf. Comput. 76(2/3), 138–164 (1988)
Dhara, K.K., Leavens, G.T.: Forcing behavioral subtyping through specification inheritance. In: Proceedings of the 18th International Conference on Software Engineering, Berlin, Germany, pp. 258–267. IEEE Computer Society Press, Los Alamitos, March 1996. https://doi.org/10.1109/ICSE.1996.493421, a corrected version is ISU CS TR #95-20c, http://tinyurl.com/s2krg
Findler, R.B., Felleisen, M.: Contract soundness for object-oriented languages. In: OOPSLA 2001 Conference Proceedings of Object-Oriented Programming, Systems, Languages, and Applications, 14–18 October 2001, Tampa Bay, Florida, USA, pp. 1–15. ACM, New York, October 2001
Floyd, R.W.: Assigning meanings to programs. Proc. Symp. Appl. Math. 19, 19–31 (1967)
Guttag, J., Horning, J.J.: The algebraic specification of abstract data types. Acta Informatica 10(1), 27–52 (1978). https://doi.org/10.1007/BF00260922
Hennessy, M.: The Semantics of Programming Languages: An Elementary Introduction Using Structural Operational Semantics. Wiley, New York (1990)
Hoare, C.A.R.: An axiomatic basis for computer programming. Commun. ACM 12(10), 576–580, 583 (1969). http://doi.acm.org/10.1145/363235.363259
Huisman, M., Jacobs, B.: Java program verification via a hoare logic with abrupt termination. In: Maibaum, T. (ed.) FASE 2000. LNCS, vol. 1783, pp. 284–303. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-46428-X_20
Landin, P.J.: The mechanical evaluation of expressions. Comput. J. 6, 308–320 (1964). See also Landin’s paper “A Lambda-Calculus Approach” in Advances in Programming and Non-Numerical Computation, L. Fox (ed.), Pergamon Press, Oxford, 1966
Landin, P.J.: The next 700 programming languages. Commun. ACM 9(3), 157–166 (1966)
Leavens, G.T.: JML’s rich, inherited specifications for behavioral subtypes. In: Liu, Z., He, J. (eds.) ICFEM 2006. LNCS, vol. 4260, pp. 2–34. Springer, Heidelberg (2006). https://doi.org/10.1007/11901433_2
Leavens, G.T., Naumann, D.A.: Behavioral subtyping, specification inheritance, and modular reasoning. TOPLAS 37(4), 13:1–13:88 (2015). https://doi.acm.org/10.1145/2766446
Leavens, G.T., Naumann, D.A., Rosenberg, S.: Preliminary definition of Core JML. CS Report 2006–07, Stevens Institute of Technology, September 2006. http://www.cs.stevens.edu/~naumann/publications/SIT-TR-2006-07.pdf
Leavens, G.T., et al.: JML Reference Manual, September 2009. http://www.jmlspecs.org
Leavens, G.T., Weihl, W.E.: Reasoning about object-oriented programs that use subtypes (extended abstract). In: Meyrowitz, N. (ed.) OOPSLA ECOOP 1990 Proceedings. ACM SIGPLAN Notices, vol. 25, no. 10, pp. 212–223. ACM, October 1990. https://doi.org/10.1145/97945.97970
Leavens, G.T., Weihl, W.E.: Specification and verification of object-oriented programs using supertype abstraction. Acta Informatica 32(8), 705–778 (1995). https://doi.org/10.1007/BF01178658
Liskov, B.H., Wing, J.M.: A behavioral notion of subtyping. ACM Trans. Program. Lang. Syst. 16(6), 1811–1841 (1994). https://doi.org/10.1145/197320.197383
Meyer, B.: Object-Oriented Software Construction. Prentice Hall, New York (1988)
Meyer, B.: Object-Oriented Software Construction, 2nd edn. Prentice Hall, New York (1997)
Parkinson, M., Bierman, G.: Separation logic, abstraction and inheritance. In: Wadler, P. (ed.) ACM Symposium on Principles of Programming Languages, pp. 75–86. ACM, New York, January 2008
Sabry, A., Felleisen, M.: Reasoning about programs in continuation passing style. Lisp Symb. Comput. 6(3/4), 289–360 (1993)
Schmidt, D.A.: Denotational Semantics: A Methodology for Language Development. Allyn and Bacon Inc., Boston (1986)
Scott, D.S., Strachey, C.: Toward a mathematical semantics for computer languages. In: Proceedings Symposium on Computers and Automata. Microwave Institute Symposia Series, vol. 21, pp. 19–46. Polytechnic Institute of Brooklyn, New York (1971)
Stoy, J.: Denotational Semantics: The Scott-Strachey Approach to Programming Language Theory. The MIT Press, Cambridge (1977)
Strachey, C.: Towards a formal semantics. In: IFIP TC2 Working Conference on Formal Language Description Languages for Computer Programming, pp. 198–220. North-Holland, Amsterdam (1966)
Strachey, C.: Fundamental concepts in programming languages. In: Notes International Summer School in Computer Programming (1967)
Wills, A.: Capsules and types in Fresco. In: America, P. (ed.) ECOOP 1991. LNCS, vol. 512, pp. 59–76. Springer, Heidelberg (1991). https://doi.org/10.1007/BFb0057015
Wing, J.M.: A two-tiered approach to specifying programs. Technical report TR-299, Massachusetts Institute of Technology, Laboratory for Computer Science (1983)
Acknowledgments
Thanks to David Cok for comments on an earlier draft and for fixing some errors with the IntSet example. Thanks also to David for his work on the OpenJML tool (see http://www.openjml.org/) and his help with using it.
Notations. As an aid to the reader, we present a table of defined notations in Fig. 18 on the next page.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Leavens, G.T., Naumann, D.A. (2018). An Illustrated Guide to the Model Theory of Supertype Abstraction and Behavioral Subtyping. In: Bowen, J., Liu, Z., Zhang, Z. (eds) Engineering Trustworthy Software Systems. SETSS 2017. Lecture Notes in Computer Science(), vol 11174. Springer, Cham. https://doi.org/10.1007/978-3-030-02928-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-02928-9_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-02927-2
Online ISBN: 978-3-030-02928-9
eBook Packages: Computer ScienceComputer Science (R0)









 with a label argument, to reference the prestate of the statement with the given label.
with a label argument, to reference the prestate of the statement with the given label.







 .
. to o (and in general also binding formals to actuals).
to o (and in general also binding formals to actuals). statement evaluates the expression E, copies the value of E to the space allocated for it, and then pops the call’s stack frame off the runtime stack.
statement evaluates the expression E, copies the value of E to the space allocated for it, and then pops the call’s stack frame off the runtime stack.





 is shorthand for
is shorthand for 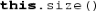 in Java, thus substituting
in Java, thus substituting  in
in  turns it into
turns it into  .
. ) are handled.
) are handled. ).
).