Amplitude Analysis

Abstract

Multi-body decays of unstable particles proceed, where permitted, via various short-lived intermediate resonant states. To probe the interactions that govern these decays, an understanding of the quantum-mechanical amplitude that describes these process is required. The distributions of the angular components of this amplitude are well known and constrained by angular momentum conservation, which permits the separation of various interfering resonant components of differing spin. Interfering components of the same spin result in complicated distributions in the invariant-mass projections that are not as well understood, and are further complicated by the numerous decay channels opening with increasing invariant-mass.

Multi-body decays of unstable particles proceed, where permitted, via various short-lived intermediate resonant states. To probe the interactions that govern these decays, an understanding of the quantum-mechanical amplitude that describes these process is required.

The distributions of the angular components of this amplitude are well known and constrained by angular momentum conservation, which permits the separation of various interfering resonant components of differing spin. Interfering components of the same spin result in complicated distributions in the invariant-mass projections that are not as well understood, and are further complicated by the numerous decay channels opening with increasing invariant-mass. In addition to the construction of the amplitude, there are also various issues related to the implementation and inference of the parameters of the amplitude model that are peculiar to amplitude analyses.

6.1 Introduction

Amplitude analyses are used to decouple the various resonant and non-resonant intermediate states in the decay of a heavy hadron in order to better understand the decay dynamics: e.g., investigations into the relative rates of the intermediate quasi-two-body decays; studying how $C\!P$ violation arises in the production of the intermediate resonances; or to understand the nature of the intermediate resonances themselves. This study of the characteristic enhancement in the inclusive decay rate is the only way to investigate bound states of quarks that decay rapidly via the strong force. As the strong force conserves $C\!P$, only their production in the weak-mediated ${b}$-hadron decay can violate $C\!P$. These resonance states interfere quantum-mechanically with each other, giving sensitivity to potential $C\!P$ violation manifesting in the relative phases between the resonant contributions, additionally permitting inference of the strong and weak phase variations across the phase-space. In general, resonances that do not decay promptly are removed from the phase-space distribution, as their long lifetime implies a very narrow width, resulting in negligible interference with the rest of the resonant contributions.

This Chapter is presented in the context of the amplitude analysis of ${{{{B}} ^+}} \!\rightarrow {{\pi } ^+} {{\pi } ^+} {{\pi } ^-}$, the decay of a scalar ${{{{B}} ^+}}$ meson into three pseudoscalar charged pions, where the results of the analysis of this decay mode with Run 1 LHCb data is presented in Chap. 7.

6.2 Three-Body Kinematics

For a generic three-body decay, there are twelve possible degrees-of-freedom, from the three 4-vectors of the final state particles. Knowledge of the final-state particle masses removes three of these, and energy-momentum conservation removes another four. For a (pseudo)scalar decaying into three (pseudo)scalars, there is no angular dependence to the decay (and therefore no preferred orientation in space) and these can be integrated out, leaving two remaining degrees of freedom. These are commonly taken to be two of the three invariant-mass-pairs squared, $m_{ij}^2 = (p_i^{\mu } + p_j^{\mu })^2$.

Further useful variables are the momentum of one of the resonance daughters in the resonance rest frame, q, the momentum of the ‘bachelor’ ${b}$-hadron daughter (the decay product that does not arise from an intermediate resonance) in the resonance rest frame, p, and the momentum of the bachelor in the ${b}$-hadron rest frame, $p^*$. The helicity angle, $\theta _\mathrm{hel}$, is the angle between one of the resonance daughters and the bachelor meson in the resonance rest frame. These can be related back to the invariant-mass-pairs squared, for example,

$$\begin{aligned} m_{13}^2&= (p_1^{\mu } + p_3^{\mu })^2 = (-2 pq\cos \theta _{13}) + m_1^2 + m_2^2 + 2E_1E_3, \nonumber \\&= (-2 pq\cos \theta _{13}) + m_1^2 + m_3^2 + 2 \sqrt{p + m_1^2}\sqrt{q + m_3^2}, \end{aligned}$$

(6.1)

where here the helicity angle is denoted $\theta _{13}$, and the invariant-masses and energies of the daughter particles are $m_i$ and $E_i$, respectively.

6.3 The Dalitz Plot

The two-dimensional distribution of two invariant-mass pairs squared is known as the Dalitz plot [1]. For the decay of a scalar into three pseudoscalars, where there are only two degrees of freedom, it provides a visualisation of all of the intermediate decay dynamics. A schematic of the Dalitz plot and its kinematical boundaries can be seen in Fig. 6.1.

If there are no intermediate structures, the distribution in this space will be uniform. However, a resonant contribution in, for example, ${{B}} \!\rightarrow R(P_1P_3)P_2$ will produce a band at the invariant-mass-squared of the resonance, R, at $m_{13}^2 = m_R^2$, across the full extent of $m_{23}^2$ (and vice-versa for a decay ${{B}} \!\rightarrow R(P_2P_3)P_1$, however a decay ${{B}} \!\rightarrow R(P_1P_2)P_3$ in this configuration will result in a diagonal band). This band in general is not uniform in $m_{23}^2$, as conservation of total angular momentum enforces a structure in the cosine of the helicity angle, $\cos \theta _{13}$, as described in Sect. 6.4.2. The angular distribution is reflected in $m_{23}^2$, as $m_{23}^2$ can be expressed in terms of the cosine of the helicity angle, per Eq. 6.1. Hence, an isolated resonance’s spin, or more correctly, the relative orbital angular momentum between the resonance and the bachelor meson (where in the case of a scalar meson decaying into three pseuduoscalar mesons, these are equivalent), is uniquely determined by the distribution in the Dalitz plot.

Fig. 6.1

Left: Schematic of the (unsymmetrised) conventional Dalitz-plot, with values corresponding to the boundaries and corners indicated. Right: Distributions of the decay intensities projected on the cosine of the helicity angle, (corresponding to the squares of unnormalised Legendre polynomial angular momentum eigenfunctions), for intermediate resonances exclusively of spin-0 (orange), spin-1 (blue), spin-2 (green), and spin-3 (grey)

6.4 The Isobar Formalism

The main simplifying assumption made in amplitude analyses is that the total three-body amplitude can be expressed as a sum of successive amplitudes of two-body decays. This is known as the isobar formalism, and is in general a good approximation for the decays of B and D mesons.

In this case, the total amplitude is

$$\begin{aligned} \mathcal {A}(m_{13}^2, m_{23}^2) = \sum _{j} c_jF_j(m_{13}^2, m_{23}^2), \end{aligned}$$

(6.2)

where $c_j$ are the complex isobar coefficients that govern the relative magnitudes and interferences between the contributions, and are in general extracted in a fit to the data, and $F_j$ are the normalised dynamical components that describe the properties of the j resonant contribution. The entire K-matrix (described in Sect. 6.5.4), enters as only one of these terms with a single overall magnitude and phase relative to the rest of the contributions, in addition to the other parameters of the K-matrix model that are left free in the fit.

For the decay of a scalar meson, B, into three pseudoscalar mesons $P_1$, $P_2$, and $P_3$, via the decay of an intermediate resonance of arbitrary spin, R, $B \rightarrow R(P_1P_2)P_3$, this matrix element can be written in terms of a matrix element for the production process, a matrix element for the decay process, and a propagator, $T_R(m)$, for an intermediate state with mass m, as

$$\begin{aligned} F = \sum _\lambda \langle P_1P_2|R_\lambda \rangle ~ T_R(m) ~ \langle P_3R_\lambda | B\rangle , \end{aligned}$$

(6.3)

where, as the polarisation states of the intermediate resonance are not observed, there is the sum is over the helicity states, $\lambda$, of the intermediate resonance. This dynamical term can be written as a product of the invariant-mass lineshape, T, the angular distribution, Z, and the Blatt–Weisskopf barrier factors, X, that represent a correction to the amplitude due to the spatial extent of the intermediate resonance and the ${b}$-hadron,

$$\begin{aligned} F(m_{13}^2, m_{23}^2) = T(m_{13}) \cdot Z(\vec {p}, \vec {q}, L) \cdot X(p r_{\text {BW}}, L) \cdot X(q r_{\text {BW}}, L). \end{aligned}$$

(6.4)

6.4.1 Blatt–Weisskopf Form Factors

Fundamental particles are pointlike, however bound states of quarks must have some finite spatial extent (analogous to the semi-classical impact parameter). Due to the potential well that this creates, the maximum angular momentum is limited by 2q, the relative momentum of the decay particles in the resonance rest frame. Decaying particles moving slowly cannot generate sufficient angular momentum to conserve the spin of the resonance, and therefore these decays – both of the parent ${b}$-meson and the resonance – are suppressed, introducing an extra momentum dependence to the lineshape.

Fig. 6.2

Distribution of the $\rho _3(1690)$ resonance, modelled with a spin-3 relativistic Breit–Wigner, in ${{\pi } ^+} {{\pi } ^-}$ invariant mass for various values of the resonance Blatt–Weisskopf barrier radius

This additional dependence is introduced by assuming that the hadron forms a harmonic potential well [2, 3], and are included in the amplitude by multiplicative factors defined in terms of $z=q\,r_\mathrm{BW}$ (or $p\,r_\mathrm{BW}$),

$$\begin{aligned} L = 0 \ : \ X(z)= & {} 1\,, \nonumber \\ L = 1 \ : \ X(z)= & {} \sqrt{\frac{1 + z_0^2}{1 + z^2}}\,, \nonumber \\ L = 2 \ : \ X(z)= & {} \sqrt{\frac{z_0^4 + 3z_0^2 + 9}{z^4 + 3z^2 + 9}}\,, \nonumber \\ L = 3 \ : \ X(z)= & {} \sqrt{\frac{z_0^6 + 6z_0^4 + 45z_0^2 + 225}{z^6 + 6z^4 + 45z^2 + 225}}\,,\nonumber \\ L = 4 \ : \ X(z)= & {} \sqrt{\frac{z_0^8 + 10z_0^6 + 135z_0^4 + 1575z_0^2 + 11025}{z^8 + 10z^6 + 135z^4 + 1575z^2 + 11025}}\,. \end{aligned}$$

(6.5)

where $z_0$ represents the value of z when $m = m_0$. The value of the barrier radius, $r_\mathrm{BW}$, is often taken to be in range 2–4 $\mathrm {\,GeV} ^{-1}$. The effect of this choice on the invariant-mass distribution for the spin-3 $\rho _3(1690)$ resonance can be seen in Fig. 6.2.

An important point to note is that these distributions only result in the correct behaviour of the overall amplitude when combined with the explicit parameterisations of the angular distributions and mass-dependent width of the relativistic Breit–Wigner described in this Chapter (in the Particle Data Group review [4] these are the $B'$ barrier factors), such that all parameters are evaluated in the correct reference frame.

6.4.2 Angular Distributions

The angular distributions in the cosine of the helicity angle, $\cos \theta _{13}$, result from the conservation of angular momentum between the resonance and the bachelor meson, and therefore from the spin of the intermediate resonance. As such these are in terms of the Legendre polynomials that represent the eigenfunctions of angular momentum, which can be seen in Fig. 6.1.

Using the Zemach tensor formalism [5, 6], the angular probability distribution terms $Z(\vec {p},\vec {q})$ are given by

$$\begin{aligned} L = 0 \ : \ Z(\vec {p},\vec {q})= & {} {-}\,1, \nonumber \\ L = 1 \ : \ Z(\vec {p},\vec {q})= & {} -\,2\,\vec {p}\cdot \vec {q},\nonumber \\ L = 2 \ : \ Z(\vec {p},\vec {q})= & {} {-}\,\frac{4}{3} \left[ 3(\vec {p}\cdot \vec {q}\,)^2 - (|\vec {p}\,||\vec {q}\,|)^2\right] , \nonumber \\ L = 3 \ : \ Z(\vec {p},\vec {q})= & {} -\,\frac{24}{15} \left[ 5(\vec {p}\cdot \vec {q}\,)^3 - 3(\vec {p}\cdot \vec {q}\,)(|\vec {p}\,||\vec {q}\,|)^2\right] , \nonumber \\ L = 4 \ : \ Z(\vec {p},\vec {q})= & {} {-}\,\frac{16}{35} \left[ 35(\vec {p}\cdot \vec {q}\,)^4 - 30(\vec {p}\cdot \vec {q}\,)^2(|\vec {p}\,||\vec {q}\,|)^2 + 3(|\vec {p}\,||\vec {q}\,|)^4\right] .\nonumber \\ \end{aligned}$$

(6.6)

The factors of pq form part of the Blatt–Weisskopf form factors described in Sect. 6.4.1.

6.4.3 Interference Effects

All modern amplitude analyses are performed via the construction of a quantitative model of the contributing amplitudes and their interferences, the parameters of which are inferred by some statistical procedure. However, it is instructive to investigate the qualitative features of the Dalitz plot, such that this may guide the physical interpretation of the models in Chap. 7.

Fig. 6.3

Magnitude-squared of the total amplitude (z-axis), in the cosine of the helicity angle and di-hadron invariant mass, for interfering spin-0 (distributed flat in $m_{h^+h^-}$) and spin-1 (distributed with a relativistic Breit–Wigner in $m_{h^+h^-}$) components. The relative isobar phase, $\phi$, is $\pi$ in the bottom-left, and $\frac{\pi }{2}$ in the bottom-right. The magnitude-squared of the amplitude where the decay proceeds purely via the spin-0 contribution can be seen in the top-left, and in the top-right for the decay purely via a spin-1 resonance. Note that regardless of the relative phase, the projection on the di-hadron invariant-mass is the same, but the projection on the cosine of the helicity angle is modified

The sensitivity to the relative phases of each resonant component arises from the interference terms in the amplitude. Considering a very simple amplitude model with only two contributing resonance components (in the same pair of daughter particles), total intensity (magnitude of the total amplitude squared) can be written as

$$\begin{aligned} |\mathcal {A}|^2&= |T_1(m^2) Z_1(\theta ) + T_2(m^2) Z_2(\theta )|^2 \nonumber \\&= Z_1^2 [Re(T_1)^2 + Im(T_1)^2] + Z_2^2 [Re(T_2)^2 + Im(T_2)^2] \nonumber \\&{=~} + 2 Z_1 Z_2 [Re(T_1) Re(T_2) + Im(T_1) Im(T_2)], \end{aligned}$$

(6.7)

where m is the invariant mass of the two daughter particles from the resonance decay, and $\theta$ is the corresponding helicity angle. The factors that do not depend on $\theta$ (such as the Blatt–Weisskopf form factors) have been subsumed into the definition of $T_i(m^2)$, and Z is real. The last term in this expression is the interference term, and gives sensitivity to the physical phase difference between the two contributions. Much like the individual resonance components, this interference term (in the absence of efficiency effects), has a helicity angle distribution proportional to the product of Legendre polynomials when the above expression is integrated over $m^2$. This has important consequences when inferring the properties, or existence, of intermediate resonances.

When the spins of two interfering resonances are different, the interference term from the products of the corresponding Legendre polynomials can be an odd function of $\cos \theta$, and therefore in these cases, when projected on to the invariant-mass axis (i.e., integrating across $\cos \theta$), the effect of the interference vanishes.¹ When projecting on to the helicity angle axis however, a structure appears that is sensitive to the relative isobar phases between the two resonances. An example of this, using toy data sampled from relativistic Breit–Wigner functions representing a broad spin-0 resonance interfering with a narrower spin-1 resonance, can be seen in Fig. 6.3, for two values of the relative isobar phase. Also of note is that this depends on the phase evolution of the relativistic Breit–Wigner: In the case of a relative isobar phase of $\pi$, decays with low values of $\cos \theta$ preferentially occur above the pole mass, denoted by the dotted line, whereas decays with high values of $\cos \theta$ preferentially occur below the pole mass.

Fig. 6.4

Distributions in the cosine of the helicity angle and di-hadron invariant mass for two interfering (and overlapping in mass) spin-1 resonances of equal isobar magnitude, where the relative isobar phase, $\phi$, is $\frac{\pi }{2}$ on the left, and $\pi$ on the right. Note that regardless of the relative phase the projection on the cosine of the helicity angle is invariant, but the projection on the di-hadron invariant mass is modified

For two interfering resonances of the same spin, the interference term is always an even function of $\cos \theta$, and the opposite effect occurs. Projections on the helicity angle do not depend on the relative isobar phase, and instead projections on the invariant-mass distribution are sensitive to this phase. This is visible in Fig. 6.4, where similar projections are shown for two overlapping spin-1 resonances. When the relative isobar phase is zero or $\pi$, the maximum of the mass peak is consistent with the resonance pole mass (dotted line) in the invariant-mass projection. However, when this phase is $\pi /2$, a shift is observed in the position of the invariant-mass distribution relative to the pole mass, due to the constructive and destructive interference resulting from the phase evolution of the relativistic Breit–Wigner. This indicates that correct evaluation of the potential interference contributions from additional contributions is essential when measuring the properties of resonances, and that inspection of the structure in the cosine of the helicity angle and invariant-mass projection can be used to qualitatively interpret the effects of the interferences between various resonant contributions.

This is naturally more complicated when there are multiple interfering resonances of different spins, and hence in practice an automated statistical procedure is required to decouple these contributions (described in Sect. 6.6). However, when few contributions dominate is it often possible to observe these effects in real decays, as in the case of the analysis of the ${{{{B}} ^+}} \!\rightarrow {{\pi } ^+} {{\pi } ^+} {{\pi } ^-}$ decay in Chap. 7.

6.5 Mass Distributions

The component of the amplitude that describes the evolution in the invariant mass of the resonance daughters, often known as the lineshape, is determined by the fundamental parameters of the resonance, such as its mass and width, and is also modulated by the presence of open channels in the same region. The mass lineshape also contains a complex phase, which in concert with the phase from the isobar coefficient determines the interference structure in the Dalitz plot.

Unlike for the angular distributions, enforcing physical constraints such as unitarity and analyticity in the lineshape is difficult. However, for a large number of resonances which are isolated and narrow, the relativistic Breit–Wigner is a sufficient approximation to the true distribution. In the analysis described in Chap. 7, these are used extensively, in addition to the unitarity-conserving K-matrix model for the ${\pi } {\pi }$ S-wave, and the Gounaris–Sakurai model for the $\rho (770)^{\circ }$.

6.5.1 Relativistic Breit–Wigner

The non-relativistic Breit–Wigner form arises from the Fourier transform into the frequency (or energy) domain of a damped driven harmonic oscillator, where the frequency at which the amplitude is at a maximum is known as the resonant frequency. This therefore is a very general physical phenomenon, which is also observed in the exponential decay law of an unstable particle from Fermi’s golden rule, and as the phase-shift of a partial wave in non-relativistic scattering theory.

In quantum field theory, the Feynman rules for a massive intermediate vector resonance prescribe a propagator (disregarding the sum over intermediate polarisations)

$$\begin{aligned} BW_{\text {prop}} = \frac{i}{s- \Pi (s)} \end{aligned}$$

(6.8)

where m is the mass of the propagator, s is the sum of the momenta of the incoming particles squared, and $\Pi (s) = m^2(s) + im(s)\Gamma (s)$ is the self-energy of the intermediate state. In general this self-energy is unknown for hadronic intermediate resonances. For isolated and narrow hadronic resonances, m(s) can be well approximated by a constant.² Therefore, for resonant contributions, the relativistic Breit–Wigner lineshape used is

$$\begin{aligned} T(m) = \frac{1}{(m_0^2 - m^2) - i\, m_0 \Gamma (m)} \,, \end{aligned}$$

(6.9)

where $m_0$ is the mass of the resonance and the dependence of the decay width of the resonance on m is approximated by

$$\begin{aligned} \Gamma (m) = \Gamma _0 \left( \frac{q}{q_0}\right) ^{2S+1} \left( \frac{m_0}{m}\right) X^2(q\,r_\mathrm{BW}) \,, \end{aligned}$$

(6.10)

where $\Gamma _0$ is the nominal width of the resonance, S is the spin of the resonance, X is the Blatt–Weisskopf barrier factor, r is the barrier radius, q is (as before) the magnitude of the momentum of each of the resonance daughters in the resonance rest frame, and $q_0$ denotes the value of q when $m = m_0$.

6.5.2 Gounaris–Sakurai

For the $\rho (770)$ resonance (and often applied to the $\rho (1450)$ resonance), the functional form of the mass-dependent width has been explicitly calculated by Gounaris and Sakurai in Ref. [8], and hence this modification to the relativistic Breit–Wigner is known as the Gounaris–Sakurai model.³ Here the lineshape is defined as

$$\begin{aligned} T(m) = \frac{1+D\cdot \Gamma _0/m_0}{(m_0^2 - m^2) + f(m) - i\, m_0 \Gamma (m)} \,, \end{aligned}$$

(6.11)

where

$$\begin{aligned} f(m) = \Gamma _0 \,\frac{m_0^2}{q_0^3}\, \left[ \; q^2 \left[ h(m)-h(m_0)\right] + \left( \,m_0^2-m^2\,\right) \,q^2_0\, \frac{dh}{dm}\bigg |_{m_0} \;\right] \,, \end{aligned}$$

(6.12)

q is the magnitude of the momentum of one of the daughter particles in the resonance rest-frame,

$$\begin{aligned} h(m) = \frac{2}{\pi }\,\frac{q}{m}\, \ln \left( \frac{m+2q}{2m_\pi }\right) \,, \end{aligned}$$

(6.13)

and

$$\begin{aligned} \frac{dh}{dm}\bigg |_{m_0} = h(m_0)\left[ (8q_0^2)^{-1}-(2m_0^2)^{-1}\right] \,+\, (2\pi m_0^2)^{-1} \,. \end{aligned}$$

(6.14)

The normalisation condition at T(0) fixes the parameter $D=f(0)/(\Gamma _0 m_0)$, and is found to be

$$\begin{aligned} D = \frac{3}{\pi }\frac{m_\pi ^2}{q_0^2}\, \ln \left( \frac{m_0+2q_0}{2m_\pi }\right) + \frac{m_0}{2\pi \,q_0} - \frac{m_\pi ^2 m_0}{\pi \,q_0^3} \,. \end{aligned}$$

(6.15)

A comparison between this and the relativistic Breit–Wigner model for the $\rho (770)^{\circ }$ resonance can be seen in Fig. 6.5 (left).

Fig. 6.5

Left: Relativistic Breit–Wigner (orange) and Gounaris–Sakurai (blue) models for the $\rho (770)^{\circ }$ invariant-mass shape, where the same values of the mass and with are used for both models. Right: The $\rho$–$\omega$ mixing model defined in Eq. 6.16

$\varvec{\rho }$ – $\varvec{\omega }$ Mixing Amplitude

In ${{{{B}} ^+}} \!\rightarrow {{\pi } ^+} {{\pi } ^+} {{\pi } ^-}$, the ${\pi } ^+$ ${\pi } ^-$ invariant-mass spectrum is dominated by a large $\rho (770)^{\circ }$ contribution. A distortion of this lineshape arises from the ${{{{B}} ^+}} \!\rightarrow \omega ({{\pi } ^+} {{\pi } ^-}){{\pi } ^+}$ decay, with the corresponding isospin-violating $\omega \!\rightarrow {{\pi } ^+} {{\pi } ^-}$ decay. Since the $\rho (770)^{\circ }$ and $\omega (782)$ are both vector states and overlap in $m({{\pi } ^+} {{\pi } ^-})$, the relative magnitude and phase of these strongly interfering contributions is included directly in a combined amplitude.

The combined $\rho$–$\omega$ mixing amplitude described in Refs. [9, 10] is modified to replace the relativistic Breit–Wigner with the Gounaris–Sakurai model,

$$\begin{aligned} A_{\rho -\omega } = A_{\rho } \left[ \frac{1 + A_{\omega } \Delta |B| \exp (i \phi _{B})}{1 - \Delta ^2 A_{\rho } A_{\omega }} \right] , \end{aligned}$$

(6.16)

where $A_{\rho }$ is the Gounaris–Sakurai $\rho (770)^{\circ }$ lineshape, $A_{\omega }$ is the relativistic Breit–Wigner $\omega (782)$ lineshape, |B| and $\phi _{B}$ are the relative magnitude and phase of the production amplitudes of $\rho (770)^{\circ }$ and $\omega (782)$, and $\Delta = \delta \,(m_{\rho } + m_{\omega })$, where $\delta$ governs the electromagnetic mixing of $\rho (770)^{\circ }$ and $\omega (782)$. When ignoring the small $\Delta ^2$ term in the denominator of Eq. 6.16, this is equivalent to the parameterisation described in Ref. [11].

From SU(3) symmetry, the $\rho (770)^{\circ }$ and $\omega (782)$ are expected to be produced coherently, giving $|B|\exp (i\phi _B) = 1$. In general $\delta$ is complex, although the imaginary part is expected to be small so this can be neglected. The theory prediction for $\delta$ is around $2 \mathrm {\,MeV}$ [12], and previous analyses have found $|\delta |$ to be $2.15 \pm 0.35 \mathrm {\,MeV}$ [10] and $1.57 \pm 0.16 \mathrm {\,MeV}$, and $\mathrm{{arg}}~\delta$ to be $0.22 \pm 0.06$ [11]. The distribution of this model in the di-pion invariant mass can be seen in Fig. 6.5 (right), under the assumption of coherent production.

6.5.3 Virtual Contributions

Virtual contributions, from the tail of off mass-shell ${B} ^{*0}$ decays can enter the ${{{{B}} ^+}} \!\rightarrow {{\pi } ^+} {{\pi } ^+} {{\pi } ^-}$ Dalitz plot via the decay ${{{{B}} ^+}} \!\rightarrow {B} ^{*0}_{v}({{\pi } ^+} {{\pi } ^-}){{\pi } ^+}$. These are modelled as relativistic Breit–Wigner functions, with a pole mass corresponding to the true pole mass of the excited state. The exception to this is when calculating the $q_0$ parameter in Eq. 6.10, where, as the pole mass is outside of the kinematically allowed region, an effective mass term is used,

$$\begin{aligned} m_R^\mathrm{eff}(m) = m_{{\pi } {\pi }}^\mathrm{min} + (m_{{\pi } {\pi }}^\mathrm{max} - m_{{\pi } {\pi }}^\mathrm{min}) \left[ 1 + \tanh \left( \frac{m - \frac{m_{{\pi } {\pi }}^\mathrm{min} + m_{{\pi } {\pi }}^\mathrm{max}}{2}}{m_{{\pi } {\pi }}^\mathrm{max} - m_{{\pi } {\pi }}^\mathrm{min}} \right) \right] . \end{aligned}$$

(6.17)

In principle, both scalar and vector ${B} ^{*0}$ resonances can contribute, where each of these appears similar to a exponential non-resonant term in the S or P wave, but entering the Dalitz plot from $m_{{\pi } {\pi }}^\mathrm{max}$, rather than from $m_{{\pi } {\pi }}^\mathrm{min}$ as is the case for conventional non-resonant components.

6.5.4 K-Matrix

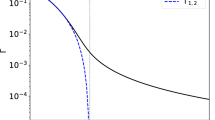
Resonances are associated with poles in the S-matrix, and this alone provides the fundamental, model-independent description. In the special case of a narrow resonance, isolated from other resonances or open channels, there is a close correspondence with the peak observed in experiment (i.e., on the real axis) and the position of the pole – the lineshape of which is given by the relativistic Breit–Wigner distribution. In general however, the parameters of the relativistic Breit–Wigner are not a good representation of the true parameters of the resonance, as can be seen in the comparison between the model for two overlapping resonances using a K-matrix model and two relativistic Breit–Wigner lineshapes in Fig. 6.6.

Fig. 6.6

Comparison between the naïve sum of relativistic Breit–Wigner functions (orange) and relativistic Breit–Wigner propagators within the K-matrix approach (blue), with equal isobar magnitude and phase, in intensity distribution in the di-hadron mass (left), and Argand evolution of the amplitude (right). The K-matrix amplitude remains within the unit circle, whereas the sum of relativistic Breit–Wigner lineshapes violates unitarity

For spin-1 (or higher) resonances decaying to two scalars, the relativistic Breit–Wigner is often a reliable description of the signal shapes, as these are mostly reasonably narrow and isolated. However, in the low di-pion mass region, there are a large number of broad overlapping scalar resonances, which exist in the presence of numerous decay channel openings that distort the lineshapes. Therefore a model is required that simultaneously respects unitarity when resonances interfere strongly, and when additional decay channels for the resonance are possible.

For the interfering resonant $K^{*0}(1430)$, $K^{*0}(800)$, and non-resonant structures in the ${K} {\pi }$ S-wave, the so-called LASS model [13] considerably improves agreement with data by enforcing unitarity in the interference via the phase shifts. Similarly, the Flatté model [14] for the $f_0(980)$ resonance, where the opening of the ${K} {K}$ threshold (at 987$\mathrm {\,MeV}$ for ${{K} ^+} {{K} ^-}$ and 997$\mathrm {\,MeV}$ for ${{K} ^0} {{K} ^0}$) distorts the lineshape in the ${{\pi } ^+} {{\pi } ^-}$ spectrum, likewise models the data well by accounting for the decays into ${K} {K}$ and conserving unitarity.

In general, unitarity conserving amplitude models can be derived from the S-matrix formalism, where resonant contributions appear as poles in the S-matrix. The matrix $S_{fi}$ can be defined as the projection of the initial state on the final state via the scattering operator S,

$$\begin{aligned} S_{fi} = \langle f | S | i \rangle = I + 2iT, \end{aligned}$$

(6.18)

where the identity matrix, I, represents the trivial non-interacting component of the amplitude, and T contains all other scattering information. As the S-matrix is unitary, it then follows that the T-matrix is also unitary and the transition amplitude is bounded by a unit circle in the complex (Re, Im) plane. The factor of 2i is a convention that results in this circle being centred at (0, i / 2). For elastic processes the $\sqrt{s}$ evolution of the amplitude lies exactly on this circle, and for inelastic processes the amplitude exists strictly within the unit circle.

A Hermitian K-matrix and transition amplitude can then be defined as

$$\begin{aligned} \hat{K}^{-1} = \hat{T}^{-1} + i\rho , \ \ \ \ \ \hat{T} = (I - i\hat{K}\rho )^{-1}~\hat{K}, \end{aligned}$$

(6.19)

where the introduction of the phase-space factor, $\rho$, results in these being the Lorentz invariant quantities, $\hat{K}$ and $\hat{T}$, defined such that $T_{uv} \equiv \{ \rho ^{\dagger }_u \}^{\frac{1}{2}} \hat{T}_{uv} \{ \rho _v \}^{\frac{1}{2}}$. For two-body channels the phase-space factor is

$$\begin{aligned} \rho _u = \sqrt{\left( 1 - \frac{(m_{1u} + m_{2u})^2}{s}\right) \left( 1 - \frac{(m_{1u} - m_{2u})^2}{s}\right) } \,, \end{aligned}$$

(6.20)

where $m_{1u}$ and $m_{2u}$ are the rest masses of the two products. When this goes below the production threshold for a particular channel it is analytically continued via the transformation $\rho _u \rightarrow i|\rho _u|$. The more complex parameterisations for multi-body channels can be seen in Ref. [15].

To use this formalism for the production of resonant states in ${B}$ decays, a production-vector, P, is introduced, as described in Ref. [16]. The amplitude for scattering from the ${B}$ decays into a specific final state, u, is then

$$\begin{aligned} \mathcal{{F}}_u = \sum _{v=1}^{n} [I - i \hat{K} \rho ]^{-1}_{uv} \cdot \hat{P}_{v} \,, \end{aligned}$$

(6.21)

where the sum is over all n intermediate states.

There is considerable freedom in the functional forms of K and P, other than that P must have the same pole structure as K. Here the convention of Ref. [15] is followed, and K is the sum over Breit–Wigner propagators for each pole, plus a slowly varying ‘background’ polynomial term,

$$\begin{aligned} \hat{K}_{uv}(s) = \left( \sum _{\alpha =1}^{N}{\frac{g^{(\alpha )}_u g^{(\alpha )}_v}{m^2_{\alpha } - s}} + f^\mathrm{{scatt}}_{uv} \frac{m^2_0 - s^\mathrm{{scatt}}_0}{s - s^\mathrm{{scatt}}_0} \right) f_{A0}(s) \,. \end{aligned}$$

(6.22)

Here, $m_{\alpha }$ is the ‘bare’ pole mass of a resonant contribution; $g^{(\alpha )}_u$ and $g^{(\alpha )}_v$ are the couplings of the resonance $\alpha$ to the ‘out’, u, and, ‘in’, v, channels, respectively; $f^\mathrm{{scatt}}_{uv}$ is the coupling of the slowly varying component to the u and v channels; and $m^2_0$ and $s^\mathrm{{scatt}}_0$ are coefficients of the slowly varying component that are determined from scattering data. The matrix $\hat{K}$ is symmetric, such that it is Hermitian by construction. The ‘Adler zero’ term [17], $f_{A0}(s)$, suppresses the false kinematical singularity when s is below the ${{\pi } ^+} {{\pi } ^-}$ production threshold,

$$\begin{aligned} f_{A0}(s) = \frac{1\,\mathrm{{{\mathrm {\,GeV^2}}}} - s_{A0}}{s - s_{A0}} \left( s - \frac{1}{2}s_A m_{\pi }^2\right) , \end{aligned}$$

(6.23)

where $s_A$ and $s_{A0}$ are constants of order unity.

The P-vector is defined analogously to the K-matrix term in Eq. 6.22,

$$\begin{aligned} \hat{P}_v(s) = \sum _{\alpha =1}^{N}{\frac{\beta _{\alpha } g^{(\alpha )}_v}{m^2_{\alpha } - s} + f^\mathrm{{prod}}_{v}\frac{m_0^2 - s_0^\mathrm{{prod}}}{s - s_0^\mathrm{{prod}}}} \,, \end{aligned}$$

(6.24)

where $\beta _{\alpha }$ and $f^\mathrm{{prod}}_{v}$ are complex parameters that describe the production pole and slowly-varying components, and are to be left free in the fit, and $s_0^\mathrm{prod}$ is a constant. As in previous analyses [18], the P-vector appears without a term to suppress the kinematical singularity.

Fixed Parameters

The most commonly used set of parameters for the K-matrix scattering components that represent the complex ‘bare’ poles present in the K-matrix, as well as the coupling of these poles to the various final state, are those reported in Ref. [19]. These were obtained via private communication with the authors of Ref. [15] as the (then) latest values of their global fit to the available scattering data. These parameters are those used in Chap. 7, and are listed in Table 6.1.

Table 6.1 K-matrix parameters quoted in Ref. [19], which are obtained from a global analysis of $\pi \pi$ scattering data by Anisovich and Sarantsev [15]. Only $f_{1v}$ parameters are listed here, as only the di-pion contributions are observed. Masses, $m_\alpha$, and couplings, $g_u^{(\alpha )}$, are given in $\mathrm {\,GeV}$, while units of $\mathrm {\,GeV} ^2$ for s-related quantities are implied; $s^\mathrm{{prod}}_0$ is taken from Ref. [18]

Typical values for the other coefficients appearing in the K-matrix are $m_0^2 = 1\,{\mathrm {\,GeV^2}}$, $s^\mathrm{{scatt}}_0 = -5\,{\mathrm {\,GeV^2}}$, $s_A = 1$, and $s_{A0} = 0\,{\mathrm {\,GeV^2}}$. There is also a free parameter in the production term in Eq. 6.24, $s_0^{\text {prod}}$, which in previous analyses of $\mathrm {D}$ meson decays has been found to be in the range −3 to 0 [18, 19].

Physical Interpretation

The K-matrix model (with the P-vector ansatz) described in the previous section can be thought of as some initial ${b}$-hadron decay, described by $\hat{P}$, into one of the five K-matrix channels, plus some other hadrons which are sufficiently decoupled via the isobar approximation - in this case a single $\pi$ meson. This state is then propagated via the $[I - i\hat{K}\rho ]^{-1}$ term to another of the five channels to form the final state (the addition of the identity element in this propagator term means that the ‘intermediate’ and final state can be the same), which is often referred to as ‘re-scattering’. In this analysis, only the ${\pi } ^+$ ${\pi } ^-$ final state is observed, and therefore elements in the resulting matrix that describe other final states are discarded.

Fig. 6.7

Left: Absolute magnitude squared of the decay contribution to the ${\pi } ^+$ ${\pi } ^-$ K-matrix, with the positions of the light scalars indicated. It is interesting to note that none of these features resemble a simple relativistic Breit–Wigner peak. Right: Argand diagram of the decay component of the ${\pi } ^+$ ${\pi } ^-$ K-matrix. This is bounded by the unit circle, and elastic until approximately the $f_0(980)$ resonance

Elements of the K-matrix itself, describing the bare resonance poles and couplings to the various final states, can be entirely determined from coupled-channel analyses of scattering data, and these are assumed to universally propagate any state into any other. The P-vector describes the virtual ‘intermediate’ states produced by the ${b}$-hadron decay, and therefore is specific to each ${b}$-hadron decay. These have the same pole structure as the K-matrix, but otherwise there is no requirement on the functional form. Here the P-vector is chosen to have the same form as the components of the K-matrix, with similar pole and slowly-varying components. Specifically, there is no requirement to include any particular pole or slowly-varying component, and therefore inclusion of these is determined by the model selection procedure as with any other resonant contribution.

The physical transition probability and real and imaginary components of the amplitude of the K-matrix only term, given in Eq. 6.19, using parameters determined from the coupled channel analysis in Ref. [15], can be seen in Fig. 6.7. Despite not being included as an explicit pole, the $f_0(500)$ contribution is clear from this plot, and likely arises from the slowly-varying contributions.

6.6 Implementation Details

To extract the physical parameters described in the previous section, along with various derived parameters such as fit fractions and $C\!P$-asymmetries, the amplitude model must be constructed and fitted to the ${b}$-hadron decay data. To this end, the Laura++ amplitude analysis package is used [20]. This package also implements the efficiency, background, and other experimental corrections in order to obtain the best fit quality. There are also various implementation details specific to the analysis described in Chap. 7.

In the ${{{{B}} ^+}} \!\rightarrow {{\pi } ^+} {{\pi } ^+} {{\pi } ^-}$ decay there are two identical (like-sign) pions in the final state, under exchange of which the amplitude is symmetric due to Bose symmetry. The pairs in which to define the amplitude are therefore arbitrary. In this case the two pairs of opposite-sign pions are selected via mass ordering, where the pair with the smaller invariant mass is given the label $m_\mathrm{{low}}$, and the pair with the larger invariant mass is labelled $m_\mathrm{{high}}$. This results in a ‘folding’ of the conventional Dalitz-plot about $m_\mathrm{{low}} = m_\mathrm{{high}}$, and of the square Dalitz-plot about $\theta ^\prime = 0.5$.

Whilst the relative phases between amplitude contributions given by the isobar coefficients are physical, the absolute value of the phase has no meaning, and similarly with the absolute magnitudes of the isobar coefficients. Hence, the magnitude and phase of the dominant contribution (for ${{{{B}} ^+}} \!\rightarrow {{\pi } ^+} {{\pi } ^+} {{\pi } ^-}$ this is the $\rho (770)^{\circ }$) are fixed to be 1 and 0, respectively, and all contributions are measured relative to this. When considering the $C\!P$-conjugate amplitude models, the phase of the dominant contribution is fixed to zero in each case, however the magnitude for one is left free in the fit to incorporate a $C\!P$-asymmetry in the dominant contribution.

6.6.1 Normalisation

The expression in Eq. 6.4 enters the total amplitude with a normalisation factor, $\mathcal {N}$, that ensures that the total integral of the component across the whole Dalitz plot is unity,

$$\begin{aligned} \mathcal {N}\int _{DP}F(m_{13}^2, m_{23}^2) ~m_{13}^2m_{23}^2 = 1. \end{aligned}$$

(6.25)

In Laura++, this integral is performed using Gauss-Legendre numerical integration, where weighted Legendre polynomials are used to approximate the total integral across the transformed domain of $[-1, 1]$. Typically $\mathcal {O}(1000)$ grid points are evaluated in each dimension, however when narrow resonances are present the integration mesh size may be too coarse to correctly evaluate the amplitude. In these cases, an adaptive binning scheme implements a finer mesh in the axis that the resonance is defined in (and in both axes where narrow resonances overlap). Integrals that represent the total ‘rate’ across the Dalitz plot, such as those in the denominator of Eq. 6.26, are also calculated in this way.

When F has no dependence on the resonance parameters (e.g., masses, widths are held constant), and only the isobar, $c_j$, parameters vary, $\mathcal {N}$ can be cached to improve overall execution time.

6.6.2 Efficiency

As true physical distributions are fitted to the distribution of events in the Dalitz plot, any variation in the experimental efficiency (i.e., the probability to observe a decay in a specific point in the phase space), would bias the parameters of the model that are extracted and the statistical significance of any particular component, and therefore such effects need to be corrected for.

Much like in the analysis described in Chap. 5, this is primarily achieved by large samples of simulated decays, with data-driven corrections for the particle identification and level-0 trigger efficiencies. In Laura$++$ (for the analysis described in Chap. 7), the variation of the efficiency is expressed nonparametrically by a histogram in the square Dalitz-plot, which is smoothed by bin-by-bin cubic-spline interpolation.

The efficiency for each decay in the data, $\epsilon (m_{13}^2, m_{23}^2)$, is obtained from the smoothed efficiency histogram, and enters in the definition of the normalised event-wise signal probability-density function,

$$\begin{aligned} \mathcal {P_{\text {sig}}}(m_{13}^2, m_{23}^2) = \frac{|\mathcal {A}(m_{13}^2, m_{23}^2)|^2 \epsilon (m_{13}^2, m_{23}^2)}{\int _{\text {DP}} |\mathcal {A}(m_{13}^2, m_{23}^2)|^2 \epsilon (m_{13}^2, m_{23}^2) ~dm_{13}~dm_{23} }. \end{aligned}$$

(6.26)

The Square Dalitz-Plot

In charmless three-body decays, intermediate resonances predominantly populate the regions around the edges of the conventional Dalitz plot. This effect is exacerbated in the observed distributions by the requirement of the trigger and reconstruction algorithms for a decay to have at least one high transverse-momentum track. Therefore, in an attempt to make the generation of simulated data as efficient as possible for a generic three-body decay, a transformation of the conventional Dalitz-plot, known as the square Dalitz-plot, is introduced, such that generating events uniformly in this transformed phase-space gives more weight to the edges of the conventional Dalitz-plot.

In addition to improving the MC generation efficiency, the uniform phase-space boundaries mean that implementing a binning scheme and performing efficiency corrections is considerably easier, as the boundaries no longer depend on the specific decay and bins can be easily aligned with the boundaries.

The square Dalitz-plot variables, $m'$ and $\theta '$, are a re-scaling of one of the helicity angles and one of the invariant-mass pairs. There are therefore three such square Dalitz-plots for a three-body decay, where the helicity angle and invariant-mass pair are usually chosen to be those where the dominant resonant contributions are expected or to exploit a symmetry in the decay. These variables are defined such that, for $m_{13}$,

$$\begin{aligned} m'&\equiv \frac{1}{\pi }\arccos \left( 2\frac{m_{13}-m_{13}^\mathrm{min}}{m_{13}^\mathrm{max}-m_{13}^\mathrm{min}} - 1 \right) , \end{aligned}$$

(6.27)

$$\begin{aligned} \theta '&\equiv \frac{1}{\pi }\theta _{13}, \end{aligned}$$

(6.28)

which are in the range [0, 1], and similarly defined for the other two invariant-mass combinations.

For the analysis of ${{{{B}} ^+}} \!\rightarrow {{\pi } ^+} {{\pi } ^+} {{\pi } ^-}$ described in Chap. 7, the square Dalitz-plot is chosen to be in $m_{12}$, and has the particularly useful property that the symmetrisation due to the two indistinguishable $\pi$ mesons can be performed by folding about $\theta ' = 0.5$.

6.6.3 Backgrounds

Background in the signal region used to select events for the Dalitz plot fit can arise from random combinations of hadrons from the event (combinatorial background), or where all final state hadrons are from a true ${b}$-hadron decay, but are otherwise mis-identified (cross-feed) or partially reconstructed. Regardless of their origin, the distributions of these background events in the Dalitz plot (conventional or square) is parameterised, much like the efficiency distributions, by a uniformly binned histogram with or without cubic-spline interpolation.

The probability of an event being background is constructed, using the distribution of background events over the Dalitz plot and the total number of background events in the data sample (which is most reliably estimated from a separate fit to the invariant mass distribution of the ${b}$-hadron), and enters the total likelihood in the same way as the efficiency corrected signal probability in Eq. 6.26,

$$\begin{aligned} \mathcal {P_{\text {bkg}}}(m_{13}^2, m_{23}^2) = \frac{\mathcal {B}(m_{13}^2, m_{23}^2)}{\int _{\text {DP}} \mathcal {B}(m_{13}^2, m_{23}^2) ~dm_{13}~dm_{23} }, \end{aligned}$$

(6.29)

where $\mathcal {B}(m_{13}^2, m_{23}^2)$ is the background expectation at the point $(m_{13}^2, m_{23}^2)$.

6.6.4 Parameter Inference

The aim of amplitude analysis is to extract the isobar parameters, $c_j$, that describe the relative magnitudes and interferences between the model components, and other parameters associated to individual resonances, such as masses and widths. Here, this is achieved via a maximum-likelihood fit.

Given an amplitude model probability density function (PDF), $\mathcal {P}(x;\theta )$, which is proportional to the probability that an observation, x, arises from a model P, defined in terms of the model parameters $\theta$, the likelihood function of a vector of independent observations, $\vec {x} = (x_1, x_2, \ldots , x_i)$, can be formed,

$$\begin{aligned} \mathcal {L}(\vec {x};\theta ) = \prod _{x_i} \mathcal {P}(x_i;\theta ). \end{aligned}$$

(6.30)

It follows that the parameters that maximise this likelihood, $\hat{\theta }$ describe a model that is most favoured by the observations.

In practice this is achieved via the non-linear optimisation routines provided by the MINUIT library [21], where instead minimisation is performed on the negative log-likelihood as this is more numerically stable (and as the logarithm is monotonically increasing function, a minimum in the negative log-likelihood coincides with a maximum in the likelihood).

Uncertainties

In most cases in high-energy physics, the maximum-likelihood estimator is unbiased, and asymptotically normal by the central limit theorem (i.e., the estimates are equal to the true parameter plus an uncertainty that is approximately normal, and that the uncertainty decays proportional to $1/\sqrt{N}$, where N is the size of the data).

If this is the case, then the variance, $\text {Var}[\hat{\theta }]$, of a maximum-likelihood estimate of a parameter $\hat{\theta }$ follows the Cramér–Rao bound, which in the univariate case is

$$\begin{aligned} \text {Var}[\hat{\theta }] \ge \frac{1}{I(\theta )}. \end{aligned}$$

(6.31)

Here $I(\theta )$ is the Fisher information,

$$\begin{aligned} I(\theta ) = -E_{\theta }\left[ \frac{\partial ^2\log \mathcal {L}(x;\theta )}{\partial \theta ^2} \right] , \end{aligned}$$

(6.32)

where $E_{\theta }$ denotes the expectation of $\theta$, and $\mathcal {L}(x;\theta )$ is the univariate likelihood function. The maximum-likelihood estimator is these cases is also an efficient estimator, such that the Eq. 6.31 is an equality. The expectation value of $\theta$ can be estimated using the maximum-likelihood value of $\theta$, $\hat{\theta }$, and therefore $\text {Var}[\hat{\theta }]$ can be calculated from the second-derivative of $\mathcal {L}(x;\theta )$ at $\theta = \hat{\theta }$,

$$\begin{aligned} \text {Var}[\hat{\theta }] = - \left( \frac{\partial ^2 \log \mathcal {L}(x;\theta )}{\partial \theta ^2} \right) \Biggr |_{\theta = \hat{\theta }}. \end{aligned}$$

(6.33)

In amplitude analysis, the parameterisation of the models may violate the consistency assumptions that govern Eq. 6.33, resulting in biased estimates of the true parameters and their uncertainties (for example if there are large non-linear correlations between parameters, or the maximum-likelihood estimate of a parameter is near a physical boundary). Alternative methods for calculating the asymmetric uncertainty intervals and the covariance matrix involve scanning the profile likelihood under the assumption of normality, which is performed by MINOS [21].

One can also go one step further and obtain estimates for the statistical uncertainty on the parameters of interest by re-fitting the model on ‘toy’ data generated from the model, where the parameters are set to the maximum-likelihood estimates. The distribution of the central values of the refitted parameter estimates then gives the uncertainty on these parameters. This method is particularly useful for determining uncertainties on derived parameters, such as component fit fractions.

Another similar method that does not assume that the model replicates the data well involves forming a large number of ‘bootstrapped’ samples of the data, which have the same number of events but where the candidates are resampled with replacement [22]. The model is refitted to these bootstrapped distributions and the central values of the parameters used to estimate the uncertainty and bias of the original maximum-likelihood estimates.

6.6.5 Fit Fractions

For each contribution, j, in addition to the isobar parameters defined previously, one can also calculate its fractional contribution to the total amplitude,

$$\begin{aligned} FF_{j} = \frac{ \int _\mathrm{DP} |c_jF_j(m_{13}^2, m_{23}^2)|^2~dm_{13}^2~dm_{23}^2 }{ \int _\mathrm{DP} |\mathcal {A}|^2~dm_{13}^2~dm_{23}^2}. \end{aligned}$$

(6.34)

These fit fractions enable comparison between amplitude analyses that use different amplitude formalisms or parameterisations of the isobar coefficients, and in addition permit extraction of the quasi-two-body branching fractions involving the intermediate resonances. It is also useful to define the interference fit fractions, which express the net constructive or destructive interference contribution to the total amplitude,

$$\begin{aligned} FF_{i>j} = \frac{ \int _\mathrm{DP} 2\mathrm{{Re}} [c_i c_j^{*}F_iF_j] ~dm_{13}^2~dm_{23}^2 }{ \int _\mathrm{DP} |\mathcal {A}|^2~dm_{13}^2~dm_{23}^2}. \end{aligned}$$

(6.35)

Due to constructive and destructive interference, $\sum _j FF_j \not = 1$, however the sum of these and the interference fit fractions is unity.

It is important to note that given the efficiency correction described in Sect. 6.6.2, the isobar parameters extracted from the fit represent the true physical parameters, and therefore subsequent derived quantities need not correct for the efficiency variation across the phase-space.

6.6.6 Extracting $C\!P$-Violating Parameters

To extract parameters that are sensitive to $C\!P$-violation in the intermediate quasi-two-body decays, or in the interferences between them, additional terms are introduced to the isobar coefficients to parameterise this $C\!P$-violation, and the amplitude model must be fitted to $C\!P$-conjugate collision data. In the case of ${{{{B}} ^+}} \!\rightarrow {{\pi } ^+} {{\pi } ^+} {{\pi } ^-}$, described in Chap. 7, charge conservation implies that this split can be performed by separating the data by the charge of the reconstructed ${{{B}} ^+}$ meson, extracting parameters for ${{{{B}} ^+}} \!\rightarrow {{\pi } ^+} {{\pi } ^+} {{\pi } ^-}$ and ${{{{B}} ^-}} \!\rightarrow {{\pi } ^-} {{\pi } ^-} {{\pi } ^+}$ decays separately.⁴ Efficiencies in this case are as described in Sect. 6.6.2, but are separately calculated for ${{{B}} ^+}$ and ${{{B}} ^-}$ to account for any detection asymmetry, and are applied separately to the corresponding model. A production asymmetry is also accounted for using a constant relative efficiency offset between the ${{{B}} ^+}$ and ${{{B}} ^-}$ efficiency models, as this asymmetry has negligible correlation with the decay kinematics [24].

To account for potential $C\!P$-violation, the isobar parameters are modified such that they allow for differences between the ${{{B}} ^+}$ and ${{{B}} ^-}$ amplitudes. For example, the Cartesian parameters are expressed as

$$\begin{aligned} c_{\pm } = x \pm \delta _x + i(y \pm \delta _y), \end{aligned}$$

(6.36)

where taking the positive signs gives the ${{{B}} ^+}$ decay isobar coefficient, and the negative signs give the ${{{B}} ^-}$ decay isobar coefficient. In the absence of $C\!P$-violation, $\delta _x = \delta _y = 0$.

A useful quantity that expresses the degree of $C\!P$-violation in a specific quasi-two-body decay is the $C\!P$-asymmetry, which using the Cartesian isobar coefficient convention is given by

$$\begin{aligned} \mathcal {A}_{{C\!P}} = \frac{|\bar{A}|^2 - |A|^2}{|\bar{A}|^2 + |A|^2} = -2 \left[ \frac{x~\delta _x + y~\delta _y}{x^2 + \delta _x^2 + y^2 + \delta _y^2} \right] . \end{aligned}$$

(6.37)

This in essence gives the degree of $C\!P$-violation in the magnitude of the quasi-two-body contribution, but does not include information on the $C\!P$-violation in the interference between contributions, where the information is contained in the relative phases. The absolute phase difference between the ${{{B}} ^+}$ and ${{{B}} ^-}$ amplitudes cannot be measured in the ${{{{B}} ^+}} \!\rightarrow {{\pi } ^+} {{\pi } ^+} {{\pi } ^-}$, as the final state is not an eigenstate of $C\!P$. However, it is possible to observe $C\!P$-violation in the interference between two quasi-two-body contributions if the relative phases between these contributions are different in the ${{{B}} ^+}$ and ${{{B}} ^-}$ amplitudes.

The branching fraction for a quasi-two-body contribution, $R_j{{\pi } ^+}$, is calculated using an average of the ${{{B}} ^+}$ and ${{{B}} ^-}$ fit-fractions,

$$\begin{aligned} \mathcal {B}({{{{B}} ^+}} \!\rightarrow R_j({{\pi } ^+} {{\pi } ^-}){{\pi } ^+} ) = \mathcal {B}({{{{B}} ^+}} \!\rightarrow {{\pi } ^+} {{\pi } ^+} {{\pi } ^-} ) \cdot FF_{j}^{{C\!P}}. \end{aligned}$$

(6.38)

where $FF_{j}^{{C\!P}}$ is the $C\!P$-conserving fit-fraction,

$$\begin{aligned} FF_{j}^{{C\!P}} = \frac{ \int _{DP} |\bar{c}_j\overline{F}_j(m_{13}^2, m_{23}^2)|^2 + |c_jF_j(m_{13}^2, m_{23}^2)|^2~dm_{13}^2~dm_{23}^2 }{ \int _{DP} |\overline{\mathcal {A}}|^2 + |\mathcal {A}|^2~dm_{13}^2~dm_{23}^2}. \end{aligned}$$

(6.39)