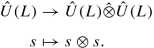Abstract
We relate composition and substitution in pre- and post-Lie algebras to algebraic geometry. The Connes-Kreimer Hopf algebras and MKW Hopf algebras are then coordinate rings of the infinite-dimensional affine varieties consisting of series of trees, resp. Lie series of ordered trees. Furthermore we describe the Hopf algebras which are coordinate rings of the automorphism groups of these varieties, which govern the substitution law in pre- and post-Lie algebras.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Pre-Lie algebras were first introduced in two different papers from 1963. Murray Gerstenhaber [13] studies deformations of algebras and Ernest Vinberg [29] problems in differential geometry. The same year John Butcher [2] published the first in a series of papers studying algebraic structures of numerical integration, culminating in his seminal paper [3] where B-series, the convolution product and the antipode of the Butcher–Connes–Kreimer Hopf algebra are introduced.
Post-Lie algebras are generalisations of pre-Lie algebras introduced in the last decade. Bruno Vallette [28] introduced the post-Lie operad as the Koszul dual of the commutative trialgebra operad. Simultaneously post-Lie algebras appear in the study of numerical integration on Lie groups and manifolds [21, 25]. In a differential geometric picture a pre-Lie algebra is the algebraic structure of the flat and torsion free connection on a locally Euclidean space, whereas post-Lie algebras appear naturally as the algebraic structure of the flat, constant torsion connection given by the Maurer–Cartan form on a Lie group [24]. Recently it is shown that the sections of an anchored vector bundle admits a post-Lie structure if and only if the bundle is an action Lie algebroid [22].
B-series is a fundamental tool in the study of flow-maps (e.g. numerical integration) on Euclidean spaces. The generalised Lie-Butcher LB-series are combining B-series with Lie series and have been introduced for studying integration on Lie groups and manifolds.
In this paper we study B-series and LB-series from an algebraic geometry point of view. The space of B-series and LB-series can be defined as completions of the free pre- and post-Lie algebras. We study (L)B-series as an algebraic variety, where the coordinate ring has a natural Hopf algebra structure. In particular we are interested in the so-called substitution law. Substitutions for pre-Lie algebras were first introduced in numerical analysis [6]. The algebraic structure of pre-Lie substitutions and the underlying substitution Hopf algebra were introduced in [4]. For the post-Lie case, recursive formulae for substitution were given in [18]. However, the corresponding Hopf algebra of substitution for post-Lie algebras was not understood at that time.
In the present work we show that the algebraic geometry view gives a natural way to understand both the Hopf algebra of composition and the Hopf algebra of substitution for pre- and post-Lie algebras.
The paper is organised as follows. In Part 1 we study fundamental algebraic properties of the enveloping algebra of Lie-, pre-Lie and post-Lie algebras for the general setting that these algebras A are endowed with a decreasing filtration A = A 1 ⊇ A 2 ⊇⋯. This seems to be the general setting where we can define the exponential and logarithm maps, and define the (generalised) Butcher product for pre- and post-Lie algebras. Part 2 elaborates an algebraic geometric setting, where the pre- or post-Lie algebra forms an algebraic variety and the corresponding coordinate ring acquires the structure of a Hopf algebra. This yields the Hopf algebra of substitutions in the free post-Lie algebra. Finally, we provide a recursive formula for the coproduct in this substitution Hopf algebra.
Part 1: The Non-algebro Geometric Setting
In this part we have no type of finiteness condition on the Lie algebras, and pre- and post-Lie algebras. Especially in the first Sect. 2 the material will be largely familiar to the established reader.
2 The Exponential and Logarithm Maps for Lie Algebras
We work in the most general setting where we can define the exponential and logarithm maps. In Sect. 2.2 we assume the Lie algebra comes with a decreasing filtration, and is complete with respect to this filtration. We define the completed enveloping algebra, and discuss its properties. This is the natural general setting for the exponential and logarithm maps which we recall in Sect. 2.3.
2.1 The Euler Idempotent
The setting in this subsection is any Lie algebra L, finite or infinite dimensional over a field k of characteristic zero. Let U(L) be its enveloping algebra. This is a Hopf algebra with unit η, counit 𝜖 and coproduct
defined by Δ(ℓ) = 1 ⊗ ℓ + ℓ ⊗ 1 for any ℓ ∈ L, and extended to all of U(L) by requiring Δ to be an algebra homomorphism.
For any algebra A with multiplication map μ A: A ⊗ A → A, we have the convolution product ⋆ on Homk(U(L), A). For f, g ∈Homk(U(L), A) it is defined as
Let 1 be the identity map on U(L), and J = 1 − η ∘ 𝜖. The Eulerian idempotent e: U(L) → U(L) is defined by
Proposition 2.1
The image of e: U(L) → U(L) is L ⊆ U(L), and e is the identity restricted to L.
Proof
This is a special case of the canonical decomposition stated in 0.4.3 in [27]. See also Proposition 3.7, and part (i) of its proof in [27]. □
Let Symc(L) be the free cocommutative conilpotent coalgebra on L. It is the subcoalgebra of the tensor coalgebra T c(L) consisting of the symmetrized tensors
The above proposition gives a linear map \(U(L) \stackrel {e}\longrightarrow L\). Since U(L) is a cocommutative coalgebra, there is then a homomorphism of cocommutative coalgebras
We now have the following strong version of the Poincaré-Birkhoff-Witt theorem.
Proposition 2.2
The map \( U(L) \stackrel {\alpha }\longrightarrow \mathit{\text{Sym}}^c(L)\) is an isomorphism of coalgebras.
In order to show this we expand more on the Euler idempotent.
Again for l 1, …, l n ∈ L denote by (l 1, …, l n) the symmetrized product in U(L):
and let U n(L) ⊆ U(L) be the subspace generated by all these symmetrized products.
Proposition 2.3
Consider the map given by convolution of the Eulerian idempotent:
-
a.
The map above is zero on U q(L) when q ≠ p and the identity on U p(L).
-
b.
The sum of these maps
$$\displaystyle \begin{aligned} \exp^{\star p}(e) = \eta \circ \epsilon + e + \frac{e^{\star 2}}{2} + \frac{e^{\star 3}}{3!} + \cdots \end{aligned}$$is the identity map on U(L). (Note that the map is well defined since the maps e ⋆p∕p! vanish on any element in U(L) for p sufficiently large.)
From the above we get a decomposition
Proof
This is the canonical decomposition stated in 0.4.3 in [27], see also Proposition 3.7 and its proof in [27]. □
Proof of Proposition 2.2
Note that since e vanishes on U n(L) for n ≥ 2, by the way one constructs the map α, it sends the symmetrizer (l 1, …, l n) ∈ U n(L) to the symmetrizer (3) in \(\text{Sym}_n^c(L)\). This shows α is surjective. But there is also a linear map, the surjective section \(\beta : \text{Sym}_n^c(L) \rightarrow U_n(L)\) sending the symmetrizer (3) to the symmetric product (l 1, …, l n). This shows that α must also be injective. □
2.2 Filtered Lie Algebras
Now the setting is that the Lie algebra L comes with a filtration
such that [L i, L j] ⊆ L i+j. Examples of such may be derived from any Lie algebra over k:
-
1.
The lower central series gives such a filtration with L 2 = [L, L] and L p+1 = [L p, L].
-
2.
The polynomials L[h] = ⊕n≥1 Lh n.
-
3.
The power series
 .
.
Let Symn(L) be the symmetric product of L, that is the natural quotient of L ⊗n which is the coinvariants \((L^{\otimes n})^{S_n}\) for the action of the symmetric group S n. By the definition of Symc(L) in (1) there are maps
and the composition is a linear isomorphism. We get a filtration on Symn(L) by letting
The filtration on L gives an associated graded Lie algebra gr L = ⊕i≥1 L i∕L i+1. The filtration on Symn(L) also induces an associated graded vector space.
Lemma 2.4
There is an isomorphism of associated graded vector spaces
Proof
Note first that there is a natural map (where d denotes the grading induced by the graded Lie algebra gr L)
It is also clear by how the filtration is defined that any element on the right may be lifted to some element on the left, and so this map is surjective. We must then show that it is injective.
Choose splittings \(L/L^{i+1} \stackrel {s_i}\longrightarrow L\) of L → L∕L i+1 for i = 1, …p, and let L i = s i(L i∕L i+1). Then we have a direct sum decomposition
This gives an isomorphism \(L \stackrel {\cong }\longrightarrow \text{gr}\, L\) which again gives a graded isomorphism
Since in general Symn(A ⊕ B) is equal to ⊕iSymi(A) ⊗Symn−i(B) we get that
where we sum over all compositions where \(\sum i_j = n\).
Claim
where we sum over all \(\sum i_j = n\) and \(\sum j \cdot i_j \geq d\).
This shows that the composition of (6) and (5) is an isomorphism. Therefore the map in (5) is an isomorphism.
Proof of Claim.
Clearly we have an inclusion ⊇. Conversely let a ∈ F dSymn(L). Then a is a sum of products \(a_{r_1} \cdots a_{r_q}\) where \(a_{r_j} \in L^{r_j}\) and \(\sum r_j \geq d\). But then each \(a_{r_j} \in \oplus _{t \geq r_j} L_t\), and so by the direct sum decomposition in (7), each \(a_{r_1} \cdots a_{r_q}\) lives in the right side of the claimed equality, and so does a.
□
We have the enveloping algebra U(L) and the enveloping algebra of the associated graded algebra U(gr L). The augmentation ideal U(L)+ is the kernel \(\ker U(L) \stackrel {\epsilon }\longrightarrow k\) of the counit. The enveloping algebra U(L) now gets a filtration of ideals by letting F 1 = U(L)+ and
where (L p+1) is the ideal generated by L p+1. This filtration induces again a graded algebra
There is also another version, the graded product algebra, which we will encounter later
Proposition 2.5
The natural map of graded algebras
is an isomorphism.
Proof
The filtrations on each \(\text{Sym}_n^c(L)\) induces a filtration on Symc(L). Via the isomorphism α of (2) and the explicit form given in the proof of Proposition 2.2 the filtrations on U(L) and on \(\text{Sym}^c_n(L)\) correspond. Hence
is an isomorphism of vector spaces. There is also an isomorphism β and a commutative diagram

By Lemma 2.4 the right vertical map is an isomorphism and so also the left vertical map. □
The cofiltration
induces the completion

This algebra also comes with the filtration \(\hat {F}^p\). Let  .
.
Lemma 2.6
The completed algebras are equal:
and so this algebra only depends on the completion \(\hat {L}\).
Proof
The natural map \(L \rightarrow \hat {L}\) induces a natural map \(U(L) \stackrel {\gamma }\longrightarrow U(\hat {L})\). Since L and \(\hat {L}\) have the same associated graded Lie algebras, the two downward maps in the commutative diagram

are isomorphisms, showing that the upper horizontal map is an isomorphism. But given the natural map γ this easily implies that the map of quotients
is an isomorphism, and so the completions are isomorphic. □
We denote the d’th graded part of the enveloping algebra U(gr L) by U(gr L)d. The following gives an idea of the “size” of \(\hat {U}(L)\).
Lemma 2.7
Proof
The left graded product is
But by Proposition 2.5 F p∕F p+1≅U(gr L)p and so the above statement follows. □
Example 2.8
Let V = ⊕i≥1 V i be a graded vector space with V i of degree i, and let Lie(V ) be the free Lie algebra on V . It then has a grading Lie(V ) = ⊕d≥1Lie(V )d coming from the grading on V , and so a filtration F p = ⊕d≥pLie(V )d. The enveloping algebra U(Lie(V )) is the tensor algebra T(V ). The completed enveloping algebra is
Let L p be the quotient L∕L p+1, which is a nilpotent filtered Lie algebra. We get enveloping algebras U(L p) with filtrations F j U(L p) of ideals, and quotient algebras
Lemma 2.9

Proof
First note that if j ≤ p then \(U^p(L_p) \twoheadrightarrow U^j(L_p)\) surjects. If j ≥ p, then \(U^j(L_j) \twoheadrightarrow U^j(L_p)\) surjects. Hence it is enough to show that the natural map
is an isomorphism. This follows since we have an isomorphism of associated graded vector spaces:

□
2.3 The Exponential and Logarithm
The coproduct Δ on U(L) will send
Thus we get a map
Let

be the completed tensor product We then get a completed coproduct
Note that the tensor product
An element g of \(\hat {U}(L)\) is grouplike if Δ(g) = g ⊗ g in \(\hat {U}(L) \otimes \hat {U}(L)\). We denote the set of grouplike elements by \(G(\hat {U}(L))\). They are all of the form 1 + s where s is in the augmentation ideal
The exponential map
is given by
The logarithm map
is defined by
Proposition 2.10
The maps
give inverse bijections. They restrict to inverse bijections
between the completed Lie algebra and the grouplike elements.
Proof
That \(\log (\exp (x)) = x\) and \(\exp (\log (1+s)) = 1+s\), are formal manipulations. If \(\ell \in \hat {L}\) it is again a formal manipulation that
and so \(\exp (\ell )\) is a grouplike element.
The maps \(\exp \) and \(\log \) can also be defined on the tensor products and give inverse bijections
Now let \(s \in G(\hat {U}(L))\) be a grouplike element. Since \(\Delta = \Delta _{\hat {U}(L)}\) is an algebra homomorphism
Since 1 ⊗ s and s ⊗ 1 are commuting elements we also have
Taking logarithms of these two equations, we obtain
and so \(\log (s)\) is in \(\hat {L}\). □
3 Exponentials and Logarithms for Pre- and Post-Lie Algebras
For pre- and post-Lie algebras their enveloping algebra comes with two products • and ∗. This gives two possible exponential and logarithm maps. This is precisely the setting that enables us to define a map from formal vector fields to formal flows. It also gives the general setting for defining the Butcher product.
3.1 Filtered Pre- and Post-Lie Algebras
Given a linear binary operation on a k-vector space A
the associator is defined as:
Definition 3.1
A post-Lie algebra \((P, [,],\rhd )\) is a Lie algebra (P, [, ]) together with a linear binary map \(\rhd \) such that
-
\(x \rhd [y,z] = [x\rhd y,z] + [y, x\rhd z]\)
-
\([x,y] \rhd z = a_{\rhd }(x,y,z) - a_{\rhd }(y,x,z)\)
It is then straightforward to verify that the following bracket

defines another Lie algebra structure on P.
A pre-Lie algebra is a post-Lie algebra P such that bracket [, ] is zero, so P with this bracket is the abelian Lie algebra.
Example 3.2
Let \(\mathcal {X} {\mathbb R}^n\) be the vector fields on the manifold \({\mathbb R}^n\). It comes with the natural Levi-Cevita connection ∇. Write \(f = \sum _{i=1}^n f^i \partial _i\) and \(g = \sum _{i=1}^n g^i \partial _i\) for two vector fields, where ∂ i = ∂∕∂x i. Let
Then \(\mathcal {X} {\mathbb R}^n\) is a pre-Lie algebra with this operation. Hence also a post-Lie algebra with trivial Lie-bracket [, ] equal to zero.
Example 3.3
Let M be a manifold and \(\mathcal {X} M\) the vector fields on M. Let \(\mathfrak {g}\) be a finite dimensional Lie algebra and \(\lambda : \mathfrak {g} \rightarrow \mathcal {X} M\) be a morphism of Lie algebras. Denote by \(\Omega ^0(M,\mathfrak {g})\) the space of smooth maps \(M \rightarrow \mathfrak {g}\). This is a Lie algebra by
The vector fields \(\mathcal {X} M\) act on the functions Ω0(M, k) by differentiation: For \(f \in \mathcal {X} M\) and ϕ ∈ Ω0(M, k) we get fϕ ∈ Ω0(M, k). Hence \(\mathcal {X} M\) acts on \(\Omega ^0(M,\mathfrak {g}) = \Omega ^0(M,k) \otimes _k \mathfrak {g}\).
Now define the operation

Then \(\Omega ^0(M,\mathfrak {g}),[,],\rhd \) becomes a post-Lie algebra by [24, Prop.2.10].
If G × M → M is an action of a Lie group G on M then for each u ∈ M we get a map G → M and on tangent spaces \(\mathfrak {g} \rightarrow T_uM\). This gives a map to the tangent bundle of M: \(\mathfrak {g} \times M \rightarrow TM\) and map of Lie algebras \(\mathfrak {g} \rightarrow \mathcal {X} M\). Hence in this setting we get by the above a post-Lie algebra \(\Omega ^0(M,\mathfrak {g})\).
If M = G and G × G → G is the Lie group operation, then \(\Omega ^0(G,\mathfrak {g})\) naturally identifies with the vector fields \(\mathcal {X} G\) by left multiplication, and so these vector fields becomes a post-Lie algebra. In the special case that \(G = {\mathbb R}^n\) with group operation \({\mathbb R}^n \times {\mathbb R}^n \rightarrow {\mathbb R}^n\) sending (a, b)↦a + b, we get the pre-Lie algebra of Example 3.2 above.
We now assume that P is a filtered post-Lie algebra: We have a decreasing filtration
such that
Then we will also have  . If u and v are two elements of P such that u − v ∈ P
n+1, we say they are equal up to order n.
. If u and v are two elements of P such that u − v ∈ P
n+1, we say they are equal up to order n.
Again examples of this can be constructed for any post-Lie algebra over a field k by letting P 1 = P and
Alternatively we may form the polynomials P[h] = ⊕n≥1
Ph
n, or the power series  .
.
In [10] the enveloping algebra U(P) of the post-Lie algebra was introduced. It is both the enveloping algebra for the Lie algebra [, ] and as such comes with associative product •, and is the enveloping algebra for the Lie algebra  and as such comes with associative product ∗. The triangle product also extends to a product \(\rhd \) on U(P) but this is not associative.
and as such comes with associative product ∗. The triangle product also extends to a product \(\rhd \) on U(P) but this is not associative.
3.2 The Map from Fields to Flows
By Example 3.2 above the formal power series of vector field  is a pre-Lie algebra, and from the last part of Example 3.3 we get a post-Lie algebra
is a pre-Lie algebra, and from the last part of Example 3.3 we get a post-Lie algebra  of series of vector fields. Using this perspective there are several natural ways to think of filtered post-Lie algebras and the related objects.
of series of vector fields. Using this perspective there are several natural ways to think of filtered post-Lie algebras and the related objects.
-
The elements of P may be thought of as formal vector fields, in which case we write P field.
-
The grouplike elements of \(\hat {U}(P)\) may be thought of as formal flows.
-
The elements of P may be thought of as principal parts of formal flows, see below, in which case we write P flow.
Let us explain how these are related. In the rest of this subsection we assume that \(P = \hat {P}\) is complete with respect to the filtration. The exponential map
sends a vector field to a formal flow, a grouplike element in \(\hat {U}(P)\). (Note that the notion of a grouplike element in \(\hat {U}(P)\) only depends on the shuffle coproduct.)
We may take the logarithm
So if \(B \in G(\hat {U}(P))\) we get \(b = \log ^{\bullet }(B)\). We think of b also as a formal flow, the principal part or first order part of the formal flow B. It determines B by \(B = \exp ^{\bullet }(b)\). Note that in (8) the exponential is with respect to the ∗ operation, while in (9) the logarithm is with respect to the • operation.
When P is a pre-Lie algebra A, then \(\hat {U}(P)\) is the completed symmetric algebra \(\widehat {\text{Sym}}(A)\) and \(\log ^{\bullet }\) is simply the projection \(\widehat {\text{Sym}}(A) \rightarrow A\). If B is a Butcher series parametrized by forests (see Sect. 6.3), then b is the Butcher series parametrized by trees. Thus b determines the flow, but the full series B is necessary to compute pull-backs of functions along the flow.
We thus get a bijection

which maps vector fields to principal part flows. This map is closely related to the Magnus expansion [8]. Magnus expresses the exact flow as \(\exp ^*(tv) = \exp ^\bullet (\Phi (tv))\), from which a differential equation for Φ(tv) can be derived.
Example 3.4
Consider the manifold \({\mathbb R}^n\) and let \(\mathcal {X} {\mathbb R}^n\) be the vector fields on \({\mathbb R}^n\). Let f =∑i≥0
f
i
h
i on \({\mathbb R}^n\) be a power series of vector fields where each \(f_i \in \mathcal {X} {\mathbb R}^n\). It induces the flow series \(\exp ^*(hf)\) in  . Since \(\mathcal {X} {\mathbb R}^n\) is a pre-Lie algebra, the completed enveloping algebra is
. Since \(\mathcal {X} {\mathbb R}^n\) is a pre-Lie algebra, the completed enveloping algebra is  . Thus the series
. Thus the series
where the  are d’th order differential operators. (Note that the principal part b is the d = 1 part.) It determines a flow \(\Psi ^f_h: {\mathbb R}^n \rightarrow {\mathbb R}^n\) sending a point P to P(h). For any smooth function \(\phi : {\mathbb R}^n \rightarrow {\mathbb R}\) the pullback of ϕ along the flow is the composition \(\phi \circ \Psi ^f_h : {\mathbb R}^n \rightarrow {\mathbb R}\) and is given by
are d’th order differential operators. (Note that the principal part b is the d = 1 part.) It determines a flow \(\Psi ^f_h: {\mathbb R}^n \rightarrow {\mathbb R}^n\) sending a point P to P(h). For any smooth function \(\phi : {\mathbb R}^n \rightarrow {\mathbb R}\) the pullback of ϕ along the flow is the composition \(\phi \circ \Psi ^f_h : {\mathbb R}^n \rightarrow {\mathbb R}\) and is given by
see [17, Section 4.1] or [23, Section 2.1]. In particular when ϕ is a coordinate function x p we get the coordinate x p(h) of P(h) as given by
since higher derivatives of x p vanish. This shows concretely geometrically why the flow is determined by its principal part.
For a given principal flow b ∈ P flow computing its inverse image by the map (10) above, which is the vector field \(\log ^* \circ \exp ^{\bullet }(b)\) is called backward error in numerical analysis [14, 19].
For a, a ′∈ P field let

a product which is computed using the Baker-Campbell-Hausdorff (BCH) formula for the Lie algebra  . With this product P
field becomes a pro-unipotent group. Transporting this product to P
flow using the bijection Φ in (10), we get for b, b
′∈ P
flow a product
. With this product P
field becomes a pro-unipotent group. Transporting this product to P
flow using the bijection Φ in (10), we get for b, b
′∈ P
flow a product
the composition product for principal flows.
Example 3.5
We continue Example 3.4. Let g =∑i≥0 g i h i be another power series of vector fields, \(\exp ^*(hg)\) its flow series, and \(\Psi _h^g : {\mathbb R}^n \rightarrow {\mathbb R}^n\) the flow it determines. Let c be the principal part of \(\exp ^*(hg)\). The composition of the flows \(\Psi ^g_h \circ \Psi ^f_h\) is the flow sending ϕ to
The principal part of the composed flow is
the Butcher product of c and b.
Denote by  the product in P
flow given by the BCH-formula for the Lie bracket [, ],
the product in P
flow given by the BCH-formula for the Lie bracket [, ],

Proposition 3.6
For x, y in the post-Lie algebra P flow we have

Proof
From [10, Prop.3.3] the product \(A * B = \sum _{\Delta (A)} A_{(1)}(A_{(2)} \rhd B)\). Since \(\exp ^\bullet (x)\) is a group-like element it follows that:
By [10, Prop.3.1] \(A \rhd BC = \sum _{\Delta (A)} (A_{(1)} \rhd B)(A_{(2)} \rhd C)\) and so again using that \(\exp ^\bullet (x)\) is group-like and the expansion of \(\exp ^\bullet (y)\):
Hence
□
In the pre-Lie case [, ] = 0, therefore  and we obtain the formula derived in [9]
and we obtain the formula derived in [9]
3.3 Substitution
Let EndpostLie(P) = HompostLie(P, P) be the endomorphisms of P as a post-Lie algebra. (In the special case that P is a pre-Lie algebra, this is simply the endomorphisms of P as a pre-Lie algebra.) It is a monoid, but not generally a vector space. It acts on the post-Lie algebra P.
Since the action respects the brackets  and \(\rhd \), it also acts on the enveloping algebra U(P) and its completion \(\hat {U}(P)\), and respects the products ∗ and •. Hence the exponential maps \(\exp ^*\) and \(\exp ^\bullet \) are equivariant for this action, and similarly the logarithms \(\log ^*\) and \(\log ^\bullet \). So the formal flow map
and \(\rhd \), it also acts on the enveloping algebra U(P) and its completion \(\hat {U}(P)\), and respects the products ∗ and •. Hence the exponential maps \(\exp ^*\) and \(\exp ^\bullet \) are equivariant for this action, and similarly the logarithms \(\log ^*\) and \(\log ^\bullet \). So the formal flow map
is equivariant for the action. The action on P flow (which is technically the same as the action on P field), is called substitution and is usually studied in a more specific context, as we do in Sect. 7. An element ϕ ∈EndpostLie(P) comes from sending a field f to a perturbed field f ′, and one then sees how this affects the exact flow or approximate flow maps given by numerical algorithms.
Part 2: The Algebraic Geometric Setting
In this part we have certain finiteness assumptions on the Lie algebras and pre- and post-Lie algebras, and so may consider them and binary operations on them in the setting of varieties. The first three subsections of the next Sect. 4 will be quite familiar to the reader who knows basic algebraic geometry.
4 Affine Varieties and Group Actions
We assume the reader is familiar with basic algebraic geometry of varieties and morphisms, like presented in [16, Chap.1] or [7, Chap.1,5]. We nevertheless briefly recall basic notions. A notable and not so standard feature is that we in the last subsection define infinite dimensional varieties and morphisms between them.
4.1 Basics on Affine Varieties
Let k be a field and S = k[x 1, …, x n] the polynomial ring. The affine n-space is
An ideal I ⊆ S defines an affine variety in \({\mathbb A}_k^n\):
Given an affine variety \(X \subseteq {\mathbb A}_k^n\), its associated ideal is
Note that if \(X = {\mathcal Z}(I)\) then \(I \subseteq \mathcal {I}(X)\), and \(\mathcal {I}(X)\) is the largest ideal defining the variety X. The correspondence
is a Galois connection. Thus we get a one-to-one correspondence

Remark 4.1
When the field k is algebraically closed, Hilbert’s Nullstellensatz says that the image of \(\mathcal {I}\) is precisely the radical ideals in the polynomial ring. In general however the image of \(\mathcal {I}\) is only contained in the radical ideals.
The coordinate ring of a variety X is the ring \(A(X) = k[x_1, \ldots , x_n]/\mathcal {I}(X)\). A morphism of affine varieties f: X → Y where \(X \subseteq {\mathbb A}_k^n\) and \(Y \subseteq {\mathbb A}_k^m\) is a a map sending a point a = (a 1, …, a n) to a point (f 1(a), …, f m(a)) where the f i are polynomials in S. This gives rise to a homomorphism of coordinate rings

In fact this is a one-one correspondence:

The zero-dimensional affine space \({\mathbb A}_k^0\) is simply a point, and its coordinate ring is k. Therefore to give a point \(p \in {\mathbb A}_k^n\) is equivalent to give an algebra homomorphism k[x 1, …, x n] → k.
Remark 4.2
We may replace k by any commutative ring \({\Bbbk }\). The affine space \({\mathbb A}_{\Bbbk }^n\) is then \({\Bbbk }^n\). The coordinate ring of this affine space is \({\Bbbk }[x_1, \ldots , x_n]\). A point \(p \in {\mathbb A}_{\Bbbk }^n\) still corresponds to an algebra homomorphism \({\Bbbk }[x_1, \ldots , x_n] \rightarrow {\Bbbk }\). Varieties in \({\mathbb A}_{\Bbbk }^n\) may be defined in the same way, and there is still a Galois connection between ideals in \({\Bbbk }[x_1, \ldots , x_n]\) and subsets of \({\mathbb A}_{\Bbbk }^n\), and a one-one correspondence between morphisms of varieties and coordinate rings.
The affine space \({\mathbb A}_k^n\) comes with the Zariski topology, whose closed sets are the affine varieties in \({\mathbb A}_k^n\) and whose open sets are the complements of these. This induces also the Zariski topology on any affine subvariety X in \({\mathbb A}_k^n\).
If X and Y are affine varieties in \({\mathbb A}^n_k\) and \({\mathbb A}^m_k\) respectively, their product X × Y is an affine variety in \({\mathbb A}^{n+m}_k\) whose ideal is the ideal in k[x 1, …, x n, y 1, …, y m] generated by \(\mathcal {I}(X) + \mathcal {I}(Y)\). Its coordinate ring is
If A is a ring and f ≠ 0 in A, we have the localized ring A f whose elements are all a∕f n where a ∈ A. Two such elements a∕f n and b∕f m are equal if f k(f m a − f n b) = 0 for some k. If A is an integral domain, this is equivalent to f m a − f n b = 0. Note that the localization A f is isomorphic to the quotient ring A[x]∕(xf − 1). Hence if A is a finitely generated k-algebra, A f is also a finitely generated k-algebra. A consequence of this is the following: Let X be an affine variety in \({\mathbb A}_k^n\) whose ideal is \(I = \mathcal {I}(X)\) contained in k[x 1, …, x n], and let f be a polynomial function. The open subset
is then in bijection to the variety \(X^\prime \in {\mathbb A}_k^{n+1}\) defined by the ideal I + (x n+1 f − 1). This bijection is actually a homeomorphism in the Zariski topology. The coordinate ring
Hence we identify A f as the coordinate ring of the open subset D(f) and can consider D(f) as an affine variety. Henceforth we shall drop the adjective affine for a variety, since all our varieties will be affine.
4.2 Coordinate Free Descriptions of Varieties
For flexibility of argument, it may be desirable to consider varieties in a coordinate free context.
Let V and W be dual finite dimensional vector spaces. So V = Homk(W, k) = W ∗, and then W is naturally isomorphic to V ∗ = (W ∗)∗. We consider V as an affine space (this means that we are forgetting the structure of vector space on V ). Its coordinate ring is the symmetric algebra Sym(W). Note that any polynomial f ∈Sym(W) may be evaluated on any point v ∈ V , since v: W → k gives maps Symd(W) →Symd(k) = k and thereby a map Sym(W) = ⊕dSymd(W) → k.
Given an ideal I in Sym(W), the associated affine variety is
Given a variety X ⊆ V we associate the ideal
The coordinate ring of X is \(A(X) = \text{Sym}(W)/\mathcal {I}(X)\).
Let W 1 and W 2 be two vector spaces, with dual spaces V 1 and V 2. A map f: X 1 → X 2 between varieties in these spaces is a map which is given by polynomials once a coordinate system is fixed for V 1 and V 2. Such a map then gives a homomorphism of coordinate rings f ♯: Sym(W 2)∕I(X 2) →Sym(W 1)∕I(X 1), and this gives a one-one correspondence between morphisms f between X 1 and X 2 and algebra homomorphisms f ♯ between their coordinate rings.
4.3 Affine Spaces and Monoid Actions
The vector space of linear operators on V is denoted End(V ). It is an affine space with \(\text{End}(V) \cong {\mathbb A}_k^{n \times n}\), and with coordinate ring Sym(End(V )∗). We then have an action
This is a morphism of varieties. Explicitly, if V has basis e 1, …, e n an element in End(V ) may be represented by a matrix A and the map is given by:
which is given by polynomials.
The morphism of varieties (11) then corresponds to the algebra homomorphism on coordinate rings
With a basis for V , the coordinate ring Sym(End(V )∗) is isomorphic to the polynomial ring k[t ij]i,j=1,…,n, where the t ij are coordinate functions on End(V ), and the coordinate ring Sym(V ∗) is isomorphic to k[x 1, …, x n] where the x i are coordinate functions on V . The map above on coordinate rings is then given by
We may also consider the set GL(V ) ⊆End(V ) of invertible linear operators. This is the open subset \(D(\det (t_{ij}))\) of End(V ) defined by the nonvanishing of the determinant. Hence, fixing a basis of V , its coordinate ring is the localized ring \(k[t_{ij}]_{\det ((t_{ij}))}\), by the last part of Sect. 4.1. The set SL(V ) ⊆End(V ) are the linear operators with determinant 1. This is a closed subset of End(V ) defined by the polynomial equation \(\det ((t_{ij})) -1 = 0\). Hence the coordinate ring of SL(V ) is the quotient ring \(k[t_{ij}]/(\det ((t_{ij})) -1)\).
Now given an affine monoid variety M, that is an affine variety with a product morphism μ: M × M → M which is associative and unital. Then we get an algebra homomorphism of coordinate rings
Since the following diagram commutes

we get a commutative diagram of coordinate rings:

The zero-dimensional affine space \({\mathbb A}_k^0\) is simply a point, and its coordinate ring is k. A character on A(M) is an algebra homomorphism A(M) → k. On varieties this gives a morphism \(P = {\mathbb A}_k^0 \rightarrow M\), or a point in the monoid variety. In particular the unit in M corresponds to a character \(A(M) \stackrel {\epsilon }\longrightarrow k\), the counit. Thus the algebra A(M) with Δ and 𝜖 becomes a bialgebra.
The monoid may act on a variety X via a morphism of varieties
On coordinate rings we get a homomorphism of algebras,
making A(X) into a comodule algebra over the bialgebra A(M).
In coordinate systems the morphism (12) may be written:
If X is an affine space V and the action comes from a morphism of monoid varieties M →End(V ), the action by M is linear on V . Then f i(m, v) =∑j f ij(m)v j. The homomorphism on coordinate rings (recall that V = W ∗)
is then induced from a morphism

where the x j’s are the coordinate functions on V and u are the coordinate functions on M.
We can also consider an affine group variety G with a morphism G → GL(V ) and get a group action G × V → V . The inverse morphism for the group, induces an antipode on the coordinate ring A(G) making it a commutative Hopf algebra.
4.4 Infinite Dimensional Affine Varieties and Monoid Actions
The infinite dimensional affine space \({\mathbb A}^\infty _k\) is ∏i≥1 k. Its elements are infinite sequences (a 1, a 2, …) where the a i are in k. Its coordinate ring is the polynomial ring in infinitely many variables \(S = k[x_i, i \in {\mathbb N}]\).
An ideal I in S, defines an affine variety
Note that a polynomial f in S always involves only a finite number of the variables, so the evaluation f(a) is meaningful. Given an affine variety X, let its ideal be:
The coordinate ring A(X) of X is the quotient ring \(S/\mathcal {I}(X)\). The affine subvarieties of \({\mathbb A}_k^\infty \) form the closed subsets in the Zariski topology on \({\mathbb A}_k^\infty \), and this then induces the Zariski topology on any subvariety of \({\mathbb A}_k^\infty \).
A morphism f: X → Y of two varieties, is a map such that f(a) = (f 1(a), f 2(a), …) where each f i is a polynomial function (and so involves only a finite number of the coordinates of a).
Letting \(k[y_i, i \in {\mathbb N}]\) be the coordinate ring of affine space where Y lives, we get a morphism of coordinate rings

This gives a one-one correspondence
For flexibility of argument, it is desirable to have a coordinate free definition of these varieties also. The following includes then both the finite and infinite-dimensional case in a coordinate free way.
Let W be a vector space with a countable basis. We get the symmetric algebra Sym(W). Let V = Homk(W, k) be the dual vector space, which will be our affine space. Given an ideal I in Sym(W), the associated affine variety is
The evaluation of f on v is here as explained in Sect. 4.2. Given a variety X we associate the ideal
Its coordinate ring is \(A(X) = \text{Sym}(W)/\mathcal {I}(X)\). We shall shortly define morphism between varieties. In order for these to be given by polynomial maps, we will need filtrations on our vector spaces. Given a filtration by finite dimensional vector spaces
On the dual space V we get a decreasing filtration by \(V^i = \ker ( (W)^* \rightarrow (W_{i-1})^*)\). The affine variety V∕V i≅(W i−1)∗ has coordinate ring Sym(W i−1). If X is a variety in V its image X i in the finite affine space V∕V i need not be Zariski closed. Let \(\overline {X_i}\) be its closure. This is an affine variety in V∕V i whose ideal is \(\mathcal {I}(X) \cap \text{Sym}(W_{i-1})\).
A map f: X 1 → X 2 between varieties in these spaces is a morphism of varieties if there exists decreasing filtrations
with finite dimensional quotient spaces, such that for any i we have a commutative diagram

and the lower map is a morphism between varieties in \(V_1/V_1^i\) and \(V_2/V_2^i\).
We then get a homomorphisms of coordinate rings
and the direct limit of these gives a homomorphism of coordinate rings
Conversely given an algebra homomorphism f ♯ above. Let
be a filtration. Write \(W^1 = \oplus _{i \in {\mathbb N}} kw_i\) in terms of a basis. The image of \(W_i^2\) will involve only a finite number of the w i. Let \(W_i^1\) be the f.d. subvector space generated by these w i. Then we get maps (14), giving morphisms

In the limit we then get a morphism of varieties f: X 1 → X 2. This gives a one-one correspondence between morphisms of varieties f: X 1 → X 2 and algebra homomorphisms f ♯.
Let X 1 and X 2 be varieties in the affine spaces V 1 and V 2. Their product X 1 × X 2 is a variety in the affine space V 1 × V 2 which is the dual space of W 1 ⊕ W 2. Its coordinate ring is A(X 1 × X 2) = A(X 1) ⊗k A(X 2).
If M is an affine monoid variety (possibly infinite dimensional) its coordinate ring A(M) becomes a commutative bialgebra. If M is an affine group variety, then A(M) is a Hopf algebra. We can again further consider an action on the affine space
It corresponds to a homomorphism of coordinate rings
making Sym(W) into a comodule algebra over A(M). If the action by M is linear on V , the algebra homomorphism above is induced by a linear map W → A(M) ⊗k W.
5 Filtered Algebras with Finite Dimensional Quotients
In this section we assume the quotients L p = L∕L p+1 from Sect. 2.2 are finite dimensional vector spaces. This enables us to define the dual Hopf algebra U c(K) of the enveloping algebra U(L). This Hopf algebra naturally identifies as the coordinate ring of the completed Lie algebra \(\hat {L}\). In Sect. 5.3 the Baker-Campbell-Hausdorff product on the variety L is shown to correspond to the natural coproduct on the dual Hopf algebra U c(K). In the last Sect. 5.4 the Lie-Butcher product on a post-Lie algebra is also shown to correspond to the natural coproduct on the dual Hopf algebra.
5.1 Filtered Lie Algebras with Finite Dimensional Quotients
Recall that L p is the quotient L∕L p+1 from Sect. 2.2. The setting in this section is k is a field of characteristic zero, and that these quotients L p are finite dimensional as k-vector spaces. We assume that the Lie algebra L is complete with respect to this cofiltration, so we have the inverse limit

The dual K
p = Homk(L
p, k) is a finite dimensional Lie coalgebra. Let  be the direct limit. Recall that the quotient algebra
be the direct limit. Recall that the quotient algebra
The dual U j(L p)∗ is a finite dimensional coalgebra \(U^c_{j}(K^p)\), and we have inclusions

We have the direct limits

Lemma 5.1
Let T c(K) be the tensor coalgebra. It is a Hopf algebra with the shuffle product. Then U c(K) is a Hopf sub-algebra of T c(K).
Proof
U j(L p) is a quotient algebra of T(L p) and T(L), and so \(U_j^c(K_p)\) is a subcoalgebra of T c(K p) and T c(K). The coproduct on U(L p), the shuffle coproduct, does not descend to a coproduct on U j(L p). But we have a well defined map
compatible with the shuffle coproduct on T(L p). Dualizing this we get
and taking colimits, we get U c(K) as a subalgebra of T c(K) with respect to the shuffle product. □
Proposition 5.2
There are isomorphisms
-
a.
L≅Hom k(K, k) of Lie algebras,
-
b.
\(\hat {U}(L) \cong \mathit{\text{Hom}}_k(U^c(K),k)\) of algebras.
-
c.
The coproduct on U c(K) is dual to the completed product on \(\hat {U}(L)\)
$$\displaystyle \begin{aligned} U^c(K) \stackrel{\Delta_\bullet}\longrightarrow U^c(K) \otimes U^c(K), \quad \hat{U}(L) \hat{\otimes} \hat{U}(L) \stackrel{\bullet}\longrightarrow \hat{U}(L). \end{aligned}$$
Proof
-
a.
Since L is the completion of the L p, it is clear that there is a map of Lie algebras Homk(K, k) → L. We need only show that this is an isomorphism of vector spaces.
It is a general fact that for any object N in a category \(\mathcal {C}\) and any indexed diagram \(F : J \rightarrow \mathcal {C}\) then

Applying this to the category of k-vector spaces enriched in k-vector spaces (meaning that the Hom-sets are k-vector spaces), we get

-
b.
This follows as in a. above.
-
c.
This follows again by the above. Since tensor products commute with colimits we have

Then

□
The coalgebra U c(K) is a Hopf algebra with the shuffle product. It has unit η and counit 𝜖. Denote by ⋆ the convolution product on this Hopf algebra, and by 1 the identity map. Write 1 = η ∘ 𝜖 + J. The Euler idempotent
is the convolution logarithm
Proposition 5.3
The image of \(U^c(K) \stackrel {e}\longrightarrow U^c(K)\) is K. This inclusion of K ⊆ U c(K) is a section of the natural map U c(K) → K.
Proof
This follows the same argument as Proposition 2.1. □
This gives a map K → U c(K). Since U c(K) is a commutative algebra under the shuffle product, we get a map from the free commutative algebra Sym(K) → U c(K).
Proposition 5.4
This map
is an isomorphism of commutative algebras. (We later denote the shuffle product by
 .)
.)
Proof
By Proposition 2.2 there is an isomorphism of coalgebras
and the filtrations on these coalgebras correspond. Hence we get an isomorphism
Dualizing this we get
Taking the colimits of this we get the statement. □
In Homk(U c(K), k) there are two distinguished subsets. The characters are the algebra homomorphisms HomAlg(U c(K), k). Via the isomorphism of Proposition 5.2 they corresponds to the grouplike elements of \(\hat {U}(L)\). The infinitesimal characters are the linear maps α: U c(K) → k such that
We denote these as HomInf(U c(K), k).
Lemma 5.5
Via the isomorphism in Proposition 5.2b . these characters correspond naturally to the following:
-
a.
Hom Inf(U c(K), k)≅Hom k(K, k)≅L.
-
b.
\(\mathit{\text{Hom}}_{Alg}(U^c(K),k) \cong G(\hat {U}(L))\).
Proof
-
a.
The map \(U^c(K) \stackrel {\phi }\longrightarrow K\) from Proposition 5.3 has kernel
 , by Proposition 5.4 above, where
, by Proposition 5.4 above, where  denotes the shuffle product. We then see that any linear map K → k induces by composition an infinitesimal character on U
c(K). Conversely given an infinitesimal character α: U
c(K) → k then both k and
denotes the shuffle product. We then see that any linear map K → k induces by composition an infinitesimal character on U
c(K). Conversely given an infinitesimal character α: U
c(K) → k then both k and  are seen to be in the kernel, and so such a map is induced from a linear map K → k by composition with ϕ.
are seen to be in the kernel, and so such a map is induced from a linear map K → k by composition with ϕ. -
b.
That s: U c(K) → k is an algebra homomorphism is equivalent to the commutativity of the diagram
 (17)
(17)But this means that by the map
Conversely given a grouplike element \(s \in \hat {U}(L)\), it corresponds by Proposition 5.2b. to s: U c(K) → k, and it being grouplike means precisely that the diagram (17) commutes. □
On Homk(U c(K), k) we also have the convolution product, which we again denote by ⋆ . Note that by the isomorphism in Proposition 5.2, this corresponds to the product on \(\hat {U}(L)\). Let Homk(U c(K), k)+ consist of the α with α(1) = 0. We then get the exponential map (we write this map without a ⋆ superscript since it is a product on the dual space)
given by
This is well defined since U c(K) is a conilpotent coalgebra and α(1) = 0. Correspondingly we get
given by
Lemma 5.6
The maps
give inverse bijections. They restrict to the inverse bijections
Proof
Using the identification of Proposition 5.2 the \(\exp \) and \(\log \) maps above correspond to the \(\exp \) and \(\log \) maps in Proposition 2.10. □
Since Sym(K) is the free symmetric algebra on K, there is a bijection \(\text{Hom}_{Alg}(\text{Sym}(K),k) \stackrel {\cong }\longrightarrow \text{Hom}_k(K,k)\). The following shows that all the various maps correspond.
Proposition 5.7
The following diagram commutes, showing that the various horizontal bijections correspond to each other:

Proof
That the lower diagram commutes is clear by the proof of Lemma 5.6. The middle (resp. top) map sends K → k to the unique algebra homomorphism ϕ (resp. ϕ ′) such that the following diagrams commute

Since the following diagram commutes where ψ is the isomorphism of algebras

the commutativity of the upper diagram in the statement of the proposition follows. □
5.2 Actions of Endomorphisms
Let E = EndLie co(K) be the endomorphisms of K as a Lie co-algebra, which also respect the filtration on K.
Proposition 5.8
The Euler map in Proposition 5.3 is equivariant for the endomorphism action. Hence the isomorphism Ψ: Sym(K) → U c(K) is equivariant for the action of the endomorphism group E.
Proof
The coproduct on U c(K) is clearly equivariant for E and similarly the product on U c(K) is equivariant, since U c(K) is a subalgebra of T c(K) for the shuffle product. Then if f, g: U c(K) → U c(K) are two equivariant maps, their convolution product f ⋆ g is also equivariant.
Since 1 and η ∘ 𝜖 are equivariant for E, the difference J = 1 − η ∘ 𝜖 is so also. The Euler map e = J − J ⋆2∕2 + J ⋆3∕3 −⋯ must then be equivariant for the action of E.
Since the image of the Euler map is K, the inclusion K↪U c(K) is equivariant also, and so is the map Ψ above. □
As a consequence of this the action of E on K induces an action on the dual Lie algebra L respecting its filtration. By Proposition 5.2 this again induces a diagram of actions of the following sets

5.2.1 The Free Lie Algebra
Now let V = ⊕i≥1 V i be a positively graded vector space with finite dimensional parts V i. We consider the special case of the above that L is the completion \(\widehat {\text{Lie}}(V)\) of the free Lie algebra on V . Note that Lie(V ) is a graded Lie algebra with finite dimensional graded parts. The enveloping algebra U(Lie(V )) is the tensor algebra T(V ).
The graded dual vector space is \(V^\circledast = \oplus V_i^*\) and the graded dual Lie co-algebra is \(\text{Lie}(V)^\circledast \). The Hopf algebra \(U^c(\text{Lie}(V)^\circledast )\) is the shuffle Hopf algebra \(T(V^\circledast )\).
Since Lie(V ) is the free Lie algebra on V , the endomorphisms E identifies as (note that here it is essential that we consider endomorphisms respecting the filtration)
This is a variety with coordinate ring \(\mathcal {E}_V = \text{Sym}( V \otimes \text{Lie}(V)^\circledast )\), which is a bialgebra. Furthermore the diagram (18) with \(L = \widehat {\text{Lie}}(V)\) in this case will be a morphism of varieties: Both E, L and \(\hat {U}(L)\) come with filtrations and all maps are given by polynomial maps. So we get a dual diagram of coordinate rings

But since the action of E is linear on \(\widehat {\text{Lie}}(V)\) and \(\hat {T}(V)\), this gives a diagram

and so the isomorphism \(\text{Sym}(\text{Lie}(V)^\circledast ) \stackrel {\cong }\longrightarrow T^c(V^\circledast )\) is an isomorphism of comodules over the algebra \(\mathcal {E}_V\).
5.3 Baker-Campbell-Hausdorff on Coordinate Rings
The space K has a countable basis and so we may consider Sym(K) as the coordinate ring of the variety L = Homk(K, k). By the isomorphism \(\psi :\text{Sym}(K) \stackrel {\cong }\longrightarrow U^c(K)\) of Proposition 5.4 we may think of U c(K) as this coordinate ring. Then also U c(K) ⊗k U c(K) is the coordinate ring of L × L.
The coproduct (whose dual is the product on \(\hat {U}(L)\))
will then correspond to a morphism of varieties L × L → L. The following explains what it is.
Proposition 5.9
The map L × L → L given by
is a morphism of varieties, and on coordinate rings it corresponds to the coproduct
This above product on L is the Baker-Campbell-Hausdorff product.
Example 5.10
Let V = ⊕i≥1 V i be a graded vector space with finite dimensional graded parts. Let Lie(V ) be the free Lie algebra on V , which comes with a natural grading. The enveloping algebra U(Lie(V )) is the tensor algebra T(V ). The dual Lie coalgebra is the graded dual \(K = \text{Lie}(V)^{\circledast }\), and U c(K) is the graded dual tensor coalgebra \(T(V^{\circledast })\) which comes with the shuffle product. Thus the shuffle algebra \(T(V^\circledast )\) identifies as the coordinate ring of the Lie series, the completion \(\widehat {\text{Lie}}(V)\) of the free Lie algebra on V .
The coproduct on \(T(V^{\circledast })\) is the deconcatenation coproduct. This can then be considered as an extremely simple codification of the Baker-Campbell-Hausdorff formula for Lie series in the completion \(\widehat {\text{Lie}}(V)\).
Proof
If X → Y is a morphism of varieties and \(A(Y) \stackrel {\phi }\longrightarrow A(X)\) the corresponding homomorphism of coordinate rings, then the point p in X corresponding to the algebra homomorphism \(A(X) \stackrel {p^*}\longrightarrow k\) maps to the point q in Y corresponding to the algebra homomorphism \(A(Y) \stackrel {q^*}\longrightarrow k\) given by q ∗ = ϕ ∘ p ∗.
Now given points a and b in L = Homk(K, k). They correspond to algebra homomorphisms from the coordinate ring \(U^c(K) \stackrel {\tilde {a}, \tilde {b}}\longrightarrow k\), the unique such extending a and b, and these are \(\tilde {a} = \exp (a)\) and \(\tilde {b} = \exp (b)\). The pair (a, b) ∈ L × L corresponds to the homomorphism on coordinate rings
Now via the coproduct, which is the homomorphism of coordinate rings,
this maps to the algebra homomorphism \(\exp (a) \bullet \exp (b) : U^c(K) \rightarrow k\). This is the algebra homomorphism corresponding to the following point in L:
□
5.4 Filtered Pre- and Post-Lie Algebras with Finite Dimensional Quotients
We now assume that the filtered quotients P∕P
p+1, which again are post-Lie algebras, are all finite dimensional. Let their duals be Q
p = Homk(P∕P
p+1, k) and  , which is a post-Lie coalgebra. We shall assume \(P = \hat {P}\) is complete with respect to this filtration. Then P = Hom(Q, k), and Sym(Q) is the coordinate ring of P. There are two Lie algebra structures on P, given by [, ] and
, which is a post-Lie coalgebra. We shall assume \(P = \hat {P}\) is complete with respect to this filtration. Then P = Hom(Q, k), and Sym(Q) is the coordinate ring of P. There are two Lie algebra structures on P, given by [, ] and  of Definition 3.1. These correspond to the products • and ∗ on the enveloping algebra of P. We shall use the first product •, giving the coproduct Δ• on U
c(Q). For this coproduct Proposition 5.4 gives an isomorphism
of Definition 3.1. These correspond to the products • and ∗ on the enveloping algebra of P. We shall use the first product •, giving the coproduct Δ• on U
c(Q). For this coproduct Proposition 5.4 gives an isomorphism
Due to the formula in Proposition 3.6 the product
on each quotient P∕P i, is given by polynomial expressions. It thus corresponds to a homomorphism of coordinate rings
Proposition 5.11
Via the isomorphism ψ • in (20) the coproduct Δ ♯ above corresponds to the coproduct
which is the dual of the product ∗ on U(P).
Remark 5.12
In order to identify the homomorphism of coordinate rings as the coproduct Δ∗ it is essential that one uses the isomorphism ψ • of (20). If one uses another isomorphism \(\text{Sym}(Q) \stackrel {\cong }\longrightarrow U^c(Q)\) like the isomorphism ψ ∗ derived from the coproduct Δ∗, the statement is not correct. See also the end of the last remark below.
Remark 5.13 (The Connes-Kreimer Hopf algebra)
For the free pre-Lie algebra T C (see the next Sect. 6) this identifies the Connes-Kreimer Hopf algebra \(\mathcal {H}_{CK}\) as the coordinate ring \(\text{Sym}(T_C^\circledast )\) of the Butcher series \(\hat {T}_C\) under the Butcher product.
As a variety the Butcher series \(\hat {T}_C\) is endowed with the Zariski topology, and the Butcher product is continuous for this topology. In [1] another finer topology on \(\hat {T}_C\) is considered when the field \(k = {\mathbb R}\) or \({\mathbb C}\).
Remark 5.14 (The MKW Hopf algebra)
For the free post-Lie algebra P C (see Sect. 6) it identifies the MKW Hopf algebra \(T(\text{OT}_C^\circledast )\) as the coordinate ring \(\text{Sym}(\text{Lie}(\text{OT}_C)^\circledast )\) of the Lie-Butcher series \(\hat {P}_C = \widehat {\text{Lie}}(\text{OT}_C)\). A (principal) Lie-Butcher series \(\ell \in \hat {P}_C\) corresponds to an element \(\text{Lie}(\text{OT}_C)^\circledast \stackrel {\ell }\longrightarrow k\). This lifts via the isomorphism ψ • of (20) to a character of the shuffle algebra \(T(\text{OT}_C^\circledast ) \stackrel {\tilde {\ell }}\longrightarrow k\). That the lifting from (principal) LB series to character of the MKW Hopf algebra must be done using the inclusion \(\text{Lie}(\text{OT}_C)^\circledast \hookrightarrow T(\text{OT}_C^\circledast )\) via the Euler map of Proposition 5.3 associated to the coproduct Δ•, is a technical point which has not been made explicit previously.
Proof of Proposition 5.11
Given points a, b ∈ P. They correspond to linear maps \(Q \stackrel {a,b}\longrightarrow k\). Via the isomorphism ψ • these extend to algebra homomorphisms \(U^c(Q) \stackrel {\tilde {a}, \tilde {b}}\longrightarrow k\), where \(\tilde {a} = \exp ^\bullet (a)\) and \(\tilde {b} = \exp ^{\bullet }(b)\). The pair (a, b) ∈ P × P then corresponds to a homomorphism of coordinate rings
Now via the coproduct associated to ∗, which is the homomorphism of coordinate rings,
this maps to the algebra homomorphism \(\exp ^\bullet (a) * \exp ^\bullet (b) : U^c(Q) \rightarrow k\). This is the algebra homomorphism corresponding to the following point in P:
□
6 Free Pre- and Post-Lie Algebras
This section recalls free pre- and post-Lie algebras, and the notion of substitution in these algebras. We also briefly recall the notions of Butcher and Lie-Butcher series.
6.1 Free Post-Lie Algebras
We consider the set of rooted planar trees, or ordered trees:

and let kOT be the k-vector space with these trees as basis. It comes with an operation \(\rhd \), called grafting. For two trees t and s we define \(t \rhd s\) to be the sum of all trees obtained by attaching the root of t with a new edge onto a vertex of s, with this new edge as the leftmost branch into the vertex of s.
If C is a set, we can color the vertices of OT with the elements of C. We then get the set OTC of labelled planar trees. The free post-Lie algebra on C is the free Lie algebra P C = Lie(OTC) on the set of C-labelled planar trees. The grafting operation is extended to the free Lie algebra Lie(OTC) by using the relations from Definition 3.1. Note that P C has a natural grading by letting P C,d be the subspace generated by all bracketed expressions of trees with a total number of d vertices. In particular P C is filtered.
The enveloping algebra of P C identifies as the tensor algebra T(OTC). It was introduced and studied in [25], see also [23] for more on the computational aspect in this algebra. Its completion identifies as
6.2 Free Pre-Lie Algebras
Here we consider instead (non-ordered) rooted trees

On the vector space kT we can similarly define grafting \(\rhd \). Given a set C we get the set T C of trees labelled by C. The free pre-Lie algebra is A C = kT C, [5]. Its enveloping algebra is the symmetric algebra Sym(T C), called the Grossman-Larson algebra, and comes with the ordinary symmetric product ⋅ and the product ∗, [26].
6.3 Butcher and Lie-Butcher Series
Recall the pre-Lie algebra \(\mathcal {X} {\mathbb R}^n\) of vector fields from Example 3.2, and the corresponding power series  . Let \(f \in \mathcal {X} {\mathbb R}^n\) be a vector field and A
• the free pre-Lie algebra on one generator •. By sending •↦f we get a homomorphism of pre-Lie algebras \(A_\bullet \rightarrow \mathcal {X} {\mathbb R}^n\) which sends a tree τ to the associated elementary differential f
τ, see [15, Section III.1]. If
. Let \(f \in \mathcal {X} {\mathbb R}^n\) be a vector field and A
• the free pre-Lie algebra on one generator •. By sending •↦f we get a homomorphism of pre-Lie algebras \(A_\bullet \rightarrow \mathcal {X} {\mathbb R}^n\) which sends a tree τ to the associated elementary differential f
τ, see [15, Section III.1]. If  we similarly get a homomorphism of pre-Lie algebras
we similarly get a homomorphism of pre-Lie algebras  . The natural grading on A
• by number of vertices of trees |τ| of a tree τ, gives a filtration and we get a map of complete pre-Lie algebras
. The natural grading on A
• by number of vertices of trees |τ| of a tree τ, gives a filtration and we get a map of complete pre-Lie algebras  . If we let • → f ⋅ h where \(f \in \mathcal {X} {\mathbb R}^n\) is a vector field, then
. If we let • → f ⋅ h where \(f \in \mathcal {X} {\mathbb R}^n\) is a vector field, then
and the latter is called a Butcher series. Often this terminology is also used about the abstract form on the left side above.
In the general setting of a Lie group G. By Example 3.3, \(\mathcal {X} G\) is a post-Lie algebra, and so is also the power series  . Let \(f \in \mathcal {X} G\) be a vector field and P
• the free post-Lie algebra on one generator •. By sending •↦f we get a homomorphism of post-Lie algebras \(P_\bullet \rightarrow \mathcal {X} G\) which sends a tree τ to the associated elementary differential f
τ, see [18, Subsection 2.2]. We also get a map of enveloping algebras \(T(OT_\bullet ) \rightarrow U(\mathcal {X} G)\) which sends a forest ω to an associated differential operator f
ω. The natural grading on P
• by number of vertices of trees |τ| of a tree τ, gives a filtration. Sending •↦f ⋅ h we get a homomorphism of complete post-Lie algebras
. Let \(f \in \mathcal {X} G\) be a vector field and P
• the free post-Lie algebra on one generator •. By sending •↦f we get a homomorphism of post-Lie algebras \(P_\bullet \rightarrow \mathcal {X} G\) which sends a tree τ to the associated elementary differential f
τ, see [18, Subsection 2.2]. We also get a map of enveloping algebras \(T(OT_\bullet ) \rightarrow U(\mathcal {X} G)\) which sends a forest ω to an associated differential operator f
ω. The natural grading on P
• by number of vertices of trees |τ| of a tree τ, gives a filtration. Sending •↦f ⋅ h we get a homomorphism of complete post-Lie algebras  . The image of an element from \(\hat {P_\bullet }\) is a Lie-Butcher series in
. The image of an element from \(\hat {P_\bullet }\) is a Lie-Butcher series in  . Note that there is however not a really natural basis for P
• = Lie(OT
•). Therefore one usually consider instead the map from the completed enveloping algebra to the power series of differential operators (F
• below denotes ordered forests of ordered trees)
. Note that there is however not a really natural basis for P
• = Lie(OT
•). Therefore one usually consider instead the map from the completed enveloping algebra to the power series of differential operators (F
• below denotes ordered forests of ordered trees)

and the latter is a Lie-Butcher series. The abstract form to the left is also often called a LB-series.
6.4 Substitution
In the above setting, we get by Sect. 3.2 a commutative diagram of flow maps

The field f is mapped to the flow \(\Phi _{\mathcal {X} G}(f)\). By perturbing the vector field f → f + δ, it is sent to a flow \(\Phi _{\mathcal {X} M}(f + \delta )\). We assume the perturbation δ is expressed in terms of the elementary differentials of f, and so it comes from a perturbation • →• + δ ′ = s. Since Hom(•, P •) = EndpostLie(P •) this gives an endomorphism of the post-Lie algebra. We are now interested in the effect of this endomorphism on the flow, called substitution of the perturbed vector field, and we are interested in the algebraic aspects of this action. We study this for the free post-Lie algebra P C, but most of the discussions below are of a general nature, and applies equally well to the free pre-Lie algebra, and generalises the results of [4].
7 Action of the Endomorphism Group and Substitution in Free Post-Lie Algebras
Substitution in the free pre-Lie or free post-Lie algebras on one generator gives, by dualizing, the operation of co-substitution in their coordinate rings, which are the Connes-Kreimer and the MKW Hopf algebras. In [4] they show that co-substitution on the Connes-Kreimer algebra is governed by a bialgebra \(\mathcal {H}\) such that the Connes-Kreimer algebra \(\mathcal {H}_{CK}\) is a comodule bialgebra over this bialgebra \(\mathcal {H}\). Moreover \(\mathcal {H}_{CK}\) and \(\mathcal {H}\) are isomorphic as commutative algebras. This is the notion of two bialgebras in cointeraction, a situation further studied in [12, 20], and [11].
In this section we do the analog for the MKW Hopf algebra, and in a more general setting, since we consider free pre- and post-Lie algebras on any finite number of generators. In this case \(\mathcal {H}_{CK}\) and \(\mathcal {H}\) are no longer isomorphic as commutative algebras. As we shall see the situation is understood very well by using the algebraic geometric setting and considering the MKW Hopf algebra as the coordinate ring of the free post-Lie algebra. The main results of [4] also follow, and are understood better, by the approach we develop here.
7.1 A Bialgebra of Endomorphisms
Let C be a finite dimensional vector space over the field k, and P C the free post-Lie algebra on this vector space. It is a graded vector space P C =⊕d≥1 P C,d graded by the number of vertices in bracketed expressions of trees, and so has finite dimensional graded pieces. It has a graded dual
Let {l} be a basis for P C. It gives a dual basis {l ∗} for \(P_C^\circledast \). The dual of \(P_C^\circledast \) is the completion

It is naturally a post-Lie algebra and comes with a decreasing filtration \(\hat {P}_C^{d+1} = \ker (\hat {P}_C \rightarrow P_{C,\leq d})\).
Due to the freeness of P C we have:
Denote the above vector space as E C. If we let {c} be a basis for C, the graded dual \(E_C^\circledast = C \otimes _k P_C^\circledast \) has a basis {a c(l):= c ⊗ l ∗}.
The dual of \(E_C^\circledast \) is \(\hat {E}_C = \text{Hom}_k(E_C^\circledast ,k)\) which may be written as \(C^* \otimes _k \hat {P}_C\). This is an affine space with coordinate ring
The filtration on \(\hat {P}_C\) induces also a filtration on \(\hat {E}_C\).
A map of post-Lie algebras \(\phi :P_C \rightarrow \hat {P}_C\) induces a map of post-Lie algebras \(\hat {\phi }: \hat {P_C} \rightarrow \hat {P}_C\). We then get the inclusion
If \(\phi ,\psi \in \hat {E}_C\), we get a composition \(\psi \circ \hat {\phi }\), which we by abuse of notation write as ψ ∘ ϕ. This makes \(\hat {E}_C\) into a monoid of affine varieties:
It induces a homomorphism on coordinate rings:
This coproduct is coassociative, since ∘ on \(\hat {E}_C\) is associative. Thus \(\mathcal {E}_C\) becomes a bialgebra.
Note that when C = 〈•〉 is one-dimensional, then
as algebras, using Proposition 5.4. The coproduct Δ∘ considered on the shuffle algebra is, however, neither deconcatenation nor the Grossman-Larson coproduct. For the free pre-Lie algebra A • instead of P •, a description of this coproduct is given in [4, Section 4.1/4.2].
7.1.1 Hopf Algebras of Endomorphisms
The augmentation map P C → C gives maps
and dually
Recall that a c(d) are the basis elements of \(\text{Hom}_k(C,C)^\circledast \) (the coordinate functions on Homk(C, C)), where c and d range over a basis for C. We can then invert \(D = \det (a_c(d))\) in the coordinate ring \(\mathcal {E}_C\). This gives a Hopf algebra \(\mathcal {E}_C^{\times }\) which is the localized ring \((\mathcal {E}_C)_D\). Another possibility is to divide \(\mathcal {E}_C\) by the ideal generated by D − 1. This gives a Hopf algebra \(\mathcal {E}_C^{1} = \mathcal {E}_C/(D-1)\). A third possibility is to divide \(\mathcal {E}_C\) out by the ideal generated by the a c(d) − δ c,d. This gives a Hopf algebra \(\mathcal {E}_C^{\text{Id}}\). In the case C = {•} and P • is replaced with the free pre-Lie alegbra A •, both the latter cases give the Hopf algebra \(\mathcal {H}\) in [4, Subsection 4.1/4.2].
7.2 The Action on the Free Post-Lie Algebra
The monoid E C acts on P C, and \(\hat {E}_C\) acts on \(\hat {P}_C\). So we get a morphism of affine varieties
called substitution.
Let \(\mathcal {H}_C = \text{Sym}(P_C^\circledast )\) be the coordinate ring of \(\hat {P}_C\). We get a homomorphism of coordinate rings called co-substitution
Note that the map in (22) is linear in the second factor so the algebra homomorphism (23) comes from a linear map
The action ⋆ gives a commutative diagram

which dually gives a diagram

This makes \(\mathcal {H}_C\) into a comodule over \(\mathcal {E}_C\), in fact a comodule algebra, since all maps are homomorphisms of algebras. The Butcher product ♯ on \(\hat {P}_C\) is dual to the coproduct \(\Delta _\star : \mathcal {H}_C \rightarrow \mathcal {H}_C \otimes \mathcal {H}_C\) by Proposition 5.11. Since \(\hat {E}_C\) gives an endomorphism of post-Lie algebra we have for \(a \in \hat {E}_C\) and \(u,v \in \hat {P}_C\):
In diagrams

which dually gives a diagram

This makes \(\mathcal {H}_C\) into a comodule Hopf algebra over \(\mathcal {E}_C\). We also have
giving corresponding commutative diagrams, making \(\mathcal {H}_C\) into a comodule algebra over \(\mathcal {E}_C\).
7.2.1 The Identification with the Tensor Algebra
The tensor algebra T(OTC) is the enveloping algebra of P C = Lie(OT C). The endomorphism of post-Lie co-algebras \(\text{End}_{\text{postLie} \text{-co}}(P_C^\circledast )\) identifies by Eq. (19) as \(\hat {E}_C = \text{Hom}_{\text{postLie}}(C, \hat {P}_C)\). It is an endomorphism submonoid of \(\text{End}_{\text{Lie}}(P_C^\circledast )\)
By Sect. 5.2.1 the isomorphism \(\mathcal {H}_C = \text{Sym}(P_C^\circledast ) \stackrel {\cong }\longrightarrow T^c(\text{OT}_C^\circledast )\) is equivariant for the action of \(\hat {E}_C\) and induces a commutative diagram

Thus all the statements above in Sect. 7.2 may be phrased with \(T^c(\text{OT}_C^\circledast )\) instead of \(\mathcal {H}_C\) as comodule over \(\mathcal {E}_C\).
7.3 The Universal Substitution
Let K be a commutative k-algebra. We then get \(P_{C,K}^\circledast = K \otimes _k P_C^\circledast \), and correspondingly we get
Let the completion \(\hat {P}_{C,K} = \text{Hom}(P_{C,K}^\circledast ,K)\). (Note that this is not \(K \otimes _k \hat {P}_C\) but rather larger than this.) Similarly we get \(\hat {E}_{C,K}\). The homomorphism of coordinate rings \(\mathcal {H}_{C,K} \rightarrow \mathcal {E}_{C,K} \otimes _K \mathcal {H}_{C,K}\) corresponds to a map of affine K-varieties (see Remark 4.2)
A K-point A in the affine variety \(\hat {E}_{C,K}\) then corresponds to an algebra homomorphism \(\mathcal {E}_{C,K} \stackrel {A^*}\longrightarrow K\), and K-points \(p \in \hat {P}_{C,K}\) corresponds to algebra homomorphisms \(\mathcal {H}_{C,K} \stackrel {p^*}\longrightarrow K\).
In particular the map obtained from (25), using \(A \in \hat {E}_{C,K}\):
corresponds to the morphism on coordinate rings
which due to (26) being linear, comes from a K-linear map
Now we let K be the commutative algebra \(\mathcal {E}_C = \text{Sym}(E_C^\circledast )\). Then
There is a canonical algebra homomorphism
which is simply the product
Definition 7.1
Corresponding to the algebra homomorphism μ of (28) is the point U in \(\hat {E}_{C,K} = \text{Hom}_k(C_K, \hat {P}_{C,K})\). This is the universal map (here we use the completed tensor product):
sending

Using this, (26) becomes the universal substitution, the K-linear map
Let \(H = \text{Hom}(C,P_C)^\circledast \), the degree one part of \(K = \mathcal {E}_C\), and P C,H = H ⊗k P C. Note that the universal map (29) is a map from C to \(\hat {P}_{C,H}\).
If \(a \in \hat {E}_C\) is a specific endomorphism, it corresponds to an algebra homomorphism (character)

Then U ⋆ induces the substitution \(\hat {P}_C \stackrel {a \star }\longrightarrow \hat {P}_C\) by sending each coefficient a c(l) ∈ K to α(c ⊗ l ∗) ∈ k.
The co-substitution \(\mathcal {H}_C \stackrel {\Delta _\star }\longrightarrow \mathcal {E}_C \otimes \mathcal {H}_C\) of (23) induces a homomorphism
which is seen to coincide with the homomorphism (27) when \(K = \mathcal {E}_C\). The universal substitution therefore corresponds to the map on coordinate rings which is the co-substitution map, suitably lifted.
Recall that the tensor algebra T(OTC) identifies as the forests of ordered trees OFC. We may then write \(T^c(\text{OT}_C^\circledast ) = \text{OF}_C^\circledast \). By the diagram (24) the co-substitution \(\mathcal {H}_{C,K} \stackrel {\Delta _\star }\longrightarrow \mathcal {H}_{C,K}\) identifies as a map \(\text{OF}_{C,K}^\circledast \stackrel {U_\star ^T}\longrightarrow \text{OF}_{C,K}^\circledast \) and we get a commutative diagram and its dual

We may restrict this to ordered trees and get
We may also restrict and get
with dual map
For use in Sect. 7.4.1, note that (29) sends C to \(\hat {P}_{C,H}\) where \(H = \text{Hom}_{k}(C,P_C)^\circledast \subseteq K\) is the graded dual of E C. A consequence is that \(\text{OF}_C^\circledast \subseteq \text{OF}_{C,K}^\circledast \) is mapped to \(C_H^* \subseteq C_K^*\) by U t.
7.4 Recursion Formula
The universal substitution is described in [18], and we recall it. By attaching the trees in a forest to a root c ∈ C, there is a natural isomorphism
and dually
Here we denote the image of ω ⊗ ρ as \(\omega \curvearrowright \rho \).
Proposition 7.2 ([18])
The following gives a partial recursion formula for \(\overline {U}^T_\star \) , the universal co-substitution followed by the projection onto the dual ordered trees:
Proof
Recall the following general fact. Two maps \(V \stackrel {\phi }\longrightarrow W\) and \(W^* \stackrel {\psi }\longrightarrow V^*\) are dual iff for all v ∈ V and w ∗∈ W ∗ the pairings
We apply this to \(\phi = \overline {U_\star }\) and
We must then show that
So let \(t = f \rhd c\). Using first the above fact on the map (31) and its dual:

□
We now get the general recursion formula, Theorem 3.7, in [18].
Proposition 7.3
Proof
Given a forest f ⋅ t where t is a tree. We will show
We have:
Since concatenation and deconcatenation are dual maps, this is

Since \(\overline {U}^T_\star (\omega _2)\) is a dual tree, this is:
□
7.4.1 The Case of One Free Generator
Now consider the case that C = 〈•〉 is a one-dimensional vector space. Recall the isomorphism \(\psi : \mathcal {E}_\bullet \cong T(\text{OT}_\bullet ^\circledast )\) as algebras but the coproduct on this is different from \(\mathcal {H}_\bullet \cong T(\text{OT}_\bullet ^\circledast )\). To signify the difference, we denote the former by \(T^\circ (\text{OT}_\bullet ^\circledast )\). It is the free algebra on the alphabet a •(t) where the t are ordered trees. Multiplication on \(\mathcal {E}_\bullet = Sym(P_\bullet ^\circledast )\) corresponds to the shuffle product on \(T^\circ (\text{OT}_\bullet ^\circledast )\).
The coproduct
may then by Sect. 7.2.1 be written as
The two bialgebras \(T(\text{OT}_\bullet ^\circledast )\) and \(T^\circ (\text{OT}_\bullet ^\circledast )\) are said to be in cointeraction, a notion studied in [4, 12, 20], and [11].
The element U t(ω (2)) is in \(C_K^* \cong K\). By the comment following (30) it is in
Then U t(ω (2)) is simply the image of ω (2) by the natural projection \(T(\text{OT}_\bullet ^\circledast ) \rightarrow P_\bullet ^\circledast \). We may consider U t(ω (2)) as an element of \(K \cong T^\circ (\text{OT}_\bullet ^\circledast )\) via the isomorphism ψ above. We are then using the Euler idempotent map
so that U t(ω (2)) = π(ω (2)).
Let B
+ be the operation of attaching a root to a forest in order to make it a tree. By a decorated shuffle  below we mean taking the shuffle product of the corresponding factors in \(K = T^\circ (\text{OT}_\bullet ^\circledast )\). By the decorated ⋅ product we mean concatenating the corresponding factors in \(T(\text{OT}_\bullet ^\circledast )\). Then we may write the recursion of Proposition 7.3 as:
below we mean taking the shuffle product of the corresponding factors in \(K = T^\circ (\text{OT}_\bullet ^\circledast )\). By the decorated ⋅ product we mean concatenating the corresponding factors in \(T(\text{OT}_\bullet ^\circledast )\). Then we may write the recursion of Proposition 7.3 as:
Proposition 7.4

References
Bogfjellmo, G., Schmeding, A.: The Lie group structure of the butcher group. Found. Comput. Math. 17(1), 127–159 (2017)
Butcher, J.C.: Coefficients for the study of Runge-Kutta integration processes. J. Aust. Math. Soc. 3(2), 185–201 (1963)
Butcher, J.C.: An algebraic theory of integration methods. Math. Comput. 26(117), 79–106 (1972)
Calaque, D., Ebrahimi-Fard, K., Manchon, D.: Two interacting Hopf algebras of trees: a Hopf-algebraic approach to composition and substitution of B-series. Adv. Appl. Math. 47(2), 282–308 (2011)
Chapoton, F., Livernet, M.: Pre-Lie algebras and the rooted trees operad. Int. Math. Res. Not. 2001(8), 395–408 (2001)
Chartier, P., Harirer, E., Vilmart, G.: A substitution law for B-series vector fields. Technical Report 5498, INRIA (2005)
Cox, D., Little, J., O’Shea, D.: Ideals, Varieties, and Algorithms, vol. 3. Springer, New York (1992)
Ebrahimi-Fard, K., Manchon, D.: Twisted dendriform algebras and the pre-Lie Magnus expansion. J. Pure Appl. Algebra 215(11), 2615–2627 (2011)
Ebrahimi-Fard, K., Patras, F.: The pre-Lie structure of the time-ordered exponential. Lett. Math. Phys. 104(10), 1281–1302 (2014)
Ebrahimi-Fard, K., Lundervold, A., Munthe-Kaas, H.Z.: On the Lie enveloping algebra of a post-Lie algebra. J. Lie Theory 25(4), 1139–1165 (2015)
Foissy, L.: Chromatic polynomials and bialgebras of graphs. arXiv preprint:1611.04303 (2016)
Foissy, L.: Commutative and non-commutative bialgebras of quasi-posets and applications to ehrhart polynomials. arXiv preprint:1605.08310 (2016)
Gerstenhaber, M.: The cohomology structure of an associative ring. Ann. Math. 78, 267–288 (1963)
Hairer, E.: Backward analysis of numerical integrators and symplectic methods. Ann. Numer. Math. 1, 107–132 (1994)
Hairer, E., Lubich, C., Wanner, G.: Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations, vol. 31. Springer Science & Business Media, Berlin/New York (2006)
Hartshorne, R.: Algebraic geometry. Graduate texts in mathematics, vol. 52. Springer, New York (2013)
Lundervold, A., Munthe-Kaas, H.: Hopf algebras of formal diffeomorphisms and numerical integration on manifolds. Contemp. Math. 539, 295–324 (2011)
Lundervold, A., Munthe-Kaas, H.: Backward error analysis and the substitution law for Lie group integrators. Found. Comput. Math. 13(2), 161–186 (2013)
Manchon, D.: A short survey on pre-Lie algebras. In: Carey, A. (ed.) Noncommutative Geometry and Physics: Renormalisation, Motives, Index Theory, pp. 89–102. Switzerland European Mathematical Society Publishing House, Zuerich (2011)
Manchon, D.: On bialgebras and hopf algebras of oriented graphs. Confluentes Mathematici 4(1), 1240003 (2012)
Munthe-Kaas, H., Krogstad, S.: On enumeration problems in Lie–Butcher theory. Futur. Gener. Comput. Syst. 19(7), 1197–1205 (2003)
Munthe-Kaas, H., Stern, A., Verdier, O.: Past-Lie algebroids and Lie algebra actions. (To appear, 2018)
Munthe-Kaas, H.Z., Føllesdal, K.K.: Lie-Butcher series, Geometry, Algebra and Computation. arXiv preprint:1701.03654 (2017)
Munthe-Kaas, H.Z., Lundervold, A.: On post-Lie algebras, Lie–Butcher series and moving frames. Found. Comput. Math. 13(4), 583–613 (2013)
Munthe-Kaas, H.Z., Wright, W.M.: On the Hopf algebraic structure of Lie group integrators. Found. Comput. Math. 8(2), 227–257 (2008)
Oudom, J.-M., Guin, D.: On the Lie enveloping algebra of a pre-Lie algebra. J. K-theory K-theory Appl. Algebra Geom. Topol. 2(1), 147–167 (2008)
Reutenauer, C.: Free Lie algebras. Handb. Algebra 3, 887–903 (2003)
Vallette, B.: Homology of generalized partition posets. J. Pure Appl. Algebra 208(2), 699–725 (2007)
Vinberg, È.B.: The theory of homogeneous convex cones. Trudy Moskovskogo Matematicheskogo Obshchestva 12, 303–358 (1963)
Acknowledgements
We would like to thank Kurusch Ebrahimi-Fard, Kristoffer Føllesdal and Frédéric Patras for discussions on the topics of this paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Fløystad, G., Munthe-Kaas, H. (2018). Pre- and Post-Lie Algebras: The Algebro-Geometric View. In: Celledoni, E., Di Nunno, G., Ebrahimi-Fard, K., Munthe-Kaas, H. (eds) Computation and Combinatorics in Dynamics, Stochastics and Control. Abelsymposium 2016. Abel Symposia, vol 13. Springer, Cham. https://doi.org/10.1007/978-3-030-01593-0_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-01593-0_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-01592-3
Online ISBN: 978-3-030-01593-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


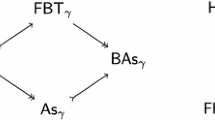

 .
.



 , by Proposition
, by Proposition  denotes the shuffle product. We then see that any linear map K → k induces by composition an infinitesimal character on U
c(K). Conversely given an infinitesimal character α: U
c(K) → k then both k and
denotes the shuffle product. We then see that any linear map K → k induces by composition an infinitesimal character on U
c(K). Conversely given an infinitesimal character α: U
c(K) → k then both k and  are seen to be in the kernel, and so such a map is induced from a linear map K → k by composition with ϕ.
are seen to be in the kernel, and so such a map is induced from a linear map K → k by composition with ϕ.