Rounding Considered Harmful

Abstract

Party-list proportional representation methods aim to allocate seats proportionally to the votes cast for each party. In general, exact proportionality is not possible as it would require a fractional allocation of seats. Therefore several methods have been devised to compute seat allocations that differ in the way they try to achieve proportionality. Examples of such methods include the d’Hondt and Sainte-Laguë methods that allocate seats according to fractional values. These methods are used in many countries. Numerically, these fractions appear harmless, however they are not. Computers do not work with infinite precision floating point numbers, implementations tend to round the fractions to several digits, which can, with a certain probability, lead to incorrect seat allocations.

C. Schürmann—This paper was made possible by grant NPRP 097-988-1-178, Automated verification of properties of concurrent, distributed and parallel specifications with applications to computer security, from the Qatar National Research Fund (a member of the Qatar Foundation). The statements made herein are solely the responsibility of the author.

1 Introduction

Denmark’s electoral law requires a combination of d’Hondt and Sainte-Laguë methods to compute the seat allocation of parliament after a parliamentary election. These methods aim at producing a seat allocation that is proportional and reflects the vote. The methods are deceptively simple as they consist of computing a table of quotients and the selection of the largest those quotients, each of which corresponds to a seat.

However, whenever quotients are computed, one has to be careful with bad numeric effects. Floating point numbers are not represented with infinite precision, and often the digits after the comma are rounded off. In this paper we ask the question if it safe to round quotients, and if rounding can have an effect in real elections. The answer is that it is not safe to round and that rounding can change the outcome of the election (with a certain probability).

For conducting this work, we have been granted access the source code of Denmark’s Seat allocation System (DSAS). While inspecting the software, we observed that DSAS rounds quotients to the next whole number before storing then in the table, and then uses randomness to draw lots to break ties. In the analysis described in this paper, we show that this is highly problematic and that situation can arise where DSAS computes the wrong result. We also conduct a Monte-Carlo experiment to provide some statistical evidence, how likely the error scenario actually is in practice, at least for the Danish case. We estimate that one out of every 66 Danish elections is effected and that DSAS computes the wrong seat allocation in average for one out of 132 elections. The version of DSAS under consideration in this paper was used only since 2007. Seat allocation for elections before 2007 were computed with another system. We have not conducted any further statistical analysis for other countries.

We have written this paper out of concern that similar programming mistakes may be hiding in seat allocations programs used by other countries.

This paper is organized as follows. In Sect. 2 we describe abstractly the d’Hondt method, variants of which are used in dozens countries around the world. In Sect. 3, we describe the effects of rounding and define the probability of how prematurely rounding quotients can effect the result of the seat allocation algorithm. In Sect. 4 we then look at real election data from the Danish 2007 parliament election, and argue, that the effects of rounding are likely and serious. We also provide evidence that the Danish Seat Allocation System, at least in the version examined, rounds quotients to the next whole number and breaks ties by drawing lots. In Sect. 5 we describe briefly how we disclosed the findings to the Ministry, before we we assess results and describe how a fix for the rounding problem in Sect. 6.

Related Work: The subject of this paper touches on several different areas: Party-list proportional representation methods are social choice functions, and their properties have been studied in political science and social choice [1, 5]. The d’Hondt was originally invented by Thomas Jefferson in 1791, and then introduced to Europe by Victor d’Hondt in 1878. The method was designed to be executed by hand. Nowadays, social choice functions such as d’Hondt, single transferable vote (STV) and others are implemented as computer programs. Programming mistakes are common place unless one uses formal methods to verify the implementation of tie breaking rules, which not many implementors do. One of the few works in this area is by Goré and Lebedeva [4], which focuses on verifying implementations of STV and the respective tie-breaking rules. Their reasoning techniques applied to d’Hondt (assuming it is correctly specified) would then automatically recognize programming mistakes such as those that we discuss in this paper. Lastly, even if premature rounding is used in the implementation of d’Hondt and Sainte-Laguë methods, variants of risk-limiting auditing tailored for d’Hondt elections [7] can be used to identify statistically, if seats have been erroneously assigned to the wrong party.

2 The d’Hondt Method

The d’Hondt and Sainte-Laguë methods are a part-list proportional representation methods used for seat allocation in more than 50 countries including Denmark, Germany, and Switzerland. In the following, we focus on d’Hondt. It is defined as follows. Let $t_1 \dots t_n$ represent the vote totals of an election with n parties. The total number of votes cast is therefore $\sum _{1\le i\le n} t_i$, and the goal of the d’Hondt method is to assign the m seats in such a way that they are proportionally allocated in the number of votes obtained by each party: As there are no fractional seats, we cannot expect d’Hondt or any other voting rule for this matter to produce the perfectly proportional seat allocation. The underlying idea of d’Hondt is this: If a party were to pay for a seat with votes then d’Hondt rule allocates the number of seats to each party to maximize the highest (average) price per seat.

Example 1

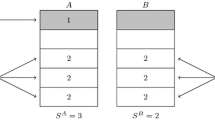
Let A and B be two parties with 10000 and 15000 votes, respectively, and five seats to be allocated.

The algorithm starts with highest price, here 15,000 votes, and reduces the price until all seats are sold! In line (1), the first seat goes to party B, because B is bidding 15,000. In line (2), A obtains the second seat, because at this stage the price is 10,000. B cannot bid, because B has spent all of its money. In line (3), the average price for a seat has dropped to 7,500, which allows B to argue that it should be entitled to a second seat. (B has already spent 15,000 and 2 $\times$ 7,500 = 15,000). After 5 rounds, all seats are sold.

The d’Hondt rule results in a simple algorithm that consists of two steps.

• 1. Construct a table, one column per party, where the first row are initialized with the vote totals $t_1 \dots t_n$. All other rows are identified by a divisor, and the row is computed from the first row by dividing $t_i$ by this divisor. The entries in the table are also called quotients. In the simplest case, the divisors range over $1,2,3,\dots$, but other choices of divisors are used in practice as well, as we will see in Sect. 4.

• 2. To allocate s seats, traverse the table and mark the s highest quotients. The number of markings in each column correspond to the seats assigned for the respective party.

The intended meaning of the table is that the field located at row i and row j is the bidding price for party i for j seats. Note, that if a quotient is marked in a table, all the quotients above (in the same column) are also marked.

Example 2

Back to the example above. The table in this case has the following form. The markings are indicated as check marks.

3 To Round or Not to Round?

Although computing the table is not difficult there are some decision designs that have to be taken when implementing it. The most important perhaps is if and how to round quotients that are not whole numbers. The quotient in Row 3, Party A, for example, is a number with infinitely many digits after the comma. Would it be ok to round these quotients to the nearest whole number? By rounding to the next whole number we mean that if the digits after the “,” $<0.5$ the number will be rounded down and if $\ge 0.5$ it will be rounded up. One may expect the answer is yes, after all, the differences between the tallies of a typical national election are usually quite large, so what could go wrong? Rounding must be considered problematic, if it affects the result of seat allocation, which means that the margin between two quotients in the d’Hondt table are sufficiently close, and this means introducing a tie that has to be resolved by a tie-breaking rule.

Example 3

Consider, for example, a multi-member constituency where three parties A, B and C with tallies 999, 500, 1501, respectively, compete for four constituency seats. Selecting the four highest quotients from the table below

Tallies	A	B	C
	999	500	1501
Divisor 1	999	500	1501
Divisor 2	499.5	250	750.5
Divisor 3	333	$166.\bar{6}$	$500.\bar{3}$

results in the following correct election result: one seat is allocated to A, three seats are allocated to C. In the case with rounding to the next whole number, the table has the following form:

Tallies	A	B	C
	999	500	1501
Divisor 1	999	500	1501
Divisor 2	500	250	750
Divisor 3	333	167	500

The algorithm allocates the first three seats to C, A, and C, and the last seat is drawn by lot, and as each party has a quotient of 500, the probability that the correct result is drawn is only 1/3.

If we were to allocate five seats instead of four, the correct result implies that the fifth seat belongs to B, because $500>499.5$. In the rounded version, however, we would have to draw two seats of the set of three, which means here again, the probability that the correct result is only 1/3.

In real elections there are several factors that impact the margins of the quotient registered in the table: (1) In some countries, d’Hondt is applied not only to the nation-wide totals, but often also on the constituency level, where the tallies are much smaller, which means the likelihood that two quotient are close increases. (2) The choice of divisors varies form country to country. In some countries, for example in Denmark, under certain but rare circumstances, the divisors $1,4,7 \dots$ are being used to construct the d’Hondt table, which means that for large divisors, the quotients, can become quiet close. (3) The size of the elected body plays a big role in how small the margins are between any to quotients in the table.

We distinguish to kinds of errors due to rounding, depending on if they affect allocated seats alone, or allocated and non-allocated seats. The former is called Incorrect Allocation Order is relatively harmless, because it does not affect the overall election result, but only the evidence of how the election result was determined. In some countries already this might be considered an infringement of the law. Things become much more worrisome, when rounding creates an artificial tie situation affecting the last seat(s) to be awarded. In this case, the drawing of the lots may in fact the overall election result. This error is called Incorrect Seat Allocation.

To make our analysis precise, we need to distinguish between two n-way tie situations: We say an n-way tie between n quotients is genuine, if the quotients (before rounding) are all equal. In the case that the quotients (before rounding) are not equal, but they are equal after rounding, we speak of a false n-way tie situation. A genuine tie must be broken by drawing lots, whereas a false tie must not. For the following two definitions, we assume a false tie situation.

Error 1: Incorrect Allocation Order. In the case that the number of seats to be allocated exceeds the number of k quotients rounded to the same number, drawing lots may affect the order in which the seats are allocated, but it does not effect the overall election result. For a false tie, the probability p of allocating seats in the wrong order is

$$\begin{aligned} p = \frac{1}{k!}. \end{aligned}$$

Error 2: Incorrect Seat Allocation. In the case that the number of quotients rounded to the same number exceeds the number of seats to be allocated, lots will have to be drawn, which means that seats may be allocated in error with non-negligible probability. More precisely, if there is a false tie between n rounded quotients and only $k(<n)$ seats are left to be allocated, the probability p that the result of seat allocation is correct result is precisely

$$\begin{aligned} p = \frac{1}{\left( {\begin{array}{c}n\\ k\end{array}}\right) }. \end{aligned}$$

4 Case Study Denmark

In order to learn if this a real or just an academic problem, we describe a case study that we conducted in Denmark. We discuss the Danish legal framework in Sect. 4.1, empirical evidence that Errors 1 and 2 could have actually been encountered in Sect. 4.2, and a discussion of the implementation of Denmark’s seat allocation system, in Sect. 4.3 where we demonstrate that the system actually rounds quotients.

4.1 Legal Framework

Danish election law¹ defines the rules for how mandates are to be distributed. The law distinguishes two kinds of seats, constituency seats kredsmandater and compensatory seats tillægsmandater. In this report, we focus mostly only compensatory seats, but our findings also apply to the calculation of constituency seats. We quote the relevant sections from the Danish Parliamentary Elections Act [3].

Allocation of Constituency Seats

§76. (1) The votes cast for each party in all nomination districts in a multi-member constituency shall be summed up. The votes cast for each individual candidate shall equally be summed up.

(2) Each number of votes appearing as a result of the summation, cf. subsection (1), shall be divided by 1 - 2 - 3 and so on until such number of divisions equivalent to the maximum number of seats expected to be allocated to the party or to the independent candidate has been performed. The party or the independent candidate having the highest resulting quotients shall be given the first seat in the multi-member constituency. The second highest quotient entails the second seat and so on and so forth, until all constituency seats in the multi-member constituency have been distributed among the parties and the independent candidates. If two or more quotients are of equal size, lots shall be drawn.

Allocation of Compensatory Seats to Parties by Region

§78.(1) For each of the parties which are allocated compensatory seats according to section 77, the number of votes cast for the party in each of the three regions shall be computed.

(2) Each of these votes shall be divided by the figures 1 - 3 - 5 - 7 and so on. Next, a number of the largest quotients equivalent to the number of constituency seats obtained by the party in the region according to section 76 shall be omitted.

(3) The region and the party which subsequently has the largest quotient shall have the first compensatory seat. The region and the party which has the second largest quotient shall have the next compensatory seat and so on and so forth. Where a region or a party has obtained the number of compensatory seats it should have, cf. sections 10 and 77, the region or the party shall not be considered any further. The allocation continues for the other regions and the other parties until all compensatory seats have been distributed. If a party which has not received votes in all three regions cannot be allocated the compensatory seats to which the party is entitled by this distribution, these seats shall be allocated in advance to the party in the regions where votes have been cast in its favor.

This law text describes the social choice function to compute the seat allocation for the 135 constituency seats and 40 compensatory seats in the Danish Parliament, called Folketinget. We focus our attention on the allocation of compensatory seats, because the divisors become larger and the quotients smaller than those when allocating constituency seats. Denmark is divided into three regions, Hovedstaden, Sjælland-Syddanmark, and Midtjylland-Nordjylland.

The technique described in the law is a variant of d’Hondt, as described in Sect. 2 (see §10 (2), den største brøks metode). Constituency seats are assigned using divisors $1,2,3, \dots$, and compensatory seats are allocated in a second step using divisors $1,3,5 \dots$ In the case of a tie, lots shall be drawn. We want to emphasize, that neither the published versions of the largest remainder methods, nor the Danish election law permits that rounded versions of the quotients may be considered. This interpretations has been confirmed by the Danish Ministry.

4.2 Empirical Analysis

For our empirical analysis, the interesting step is 3. where the quotients are computed. Consider the seat allocation of compensatory seats 20 and 21 during Denmark’s parliamentary election in 2007, as depicted in Fig. 1, which has been taken from [2, p. 17]. This election is relatively recent and it was chosen, because it demonstrates that Error 1 and 2 do actually arise in real elections. Both seats were awarded with a rounded quotient of 11,097. The seat 20 was awarded to Det Konservative Folkeparti, because

$$\begin{aligned} \frac{122063}{11} = 11,096.6363636 \end{aligned}$$

and seat 21 was awarded to Venstre because

$$\begin{aligned} \frac{366186}{33}= 11,096.5454545. \end{aligned}$$

In Fig. 1, we have marked the important entries using boxes to help the reader identify these more easily.

Fig. 1.

Compensatory seat allocation.

If we were to use instead a seat allocation algorithm that rounds all quotients to the nearest whole number, these two quotients would round to 11,097 and consequently seat 20 and seat 21 can only be allocated by drawing lots. In this situation, the following two outcomes are equally likely.

• 1. Seat 20 will be allocated to Det Konservative Folkeparti and seat 21 to Venstre.

• 2. Seat 20 will be allocated to Venstre and seat 21 to Det Konservative Folkeparti.

Both outcomes are correct, as we have discussed in Sect. 2, however Denmark’s law does regard—strictly speaking—only the first outcome as correct and the second outcome as an instance of Error 1. Evidently, the order in which the seats were assigned was correct, perhaps because it was computed with an earlier version of seat allocation system and not the one we will discuss below.

Regarding Error 2, we notice that the last compensatory seat (Seat 40) was awarded with a quotient of exactly 9404 to the Socialdemokratiet. The next highest quotient in Fig. 1 is 9,389 but what cannot be seen in the table is that there are actually two entries: One for region Hovedstaden, Det Konservative Folkeparti, divisor 13,

$$\begin{aligned} \frac{122063}{13} = 9389.46153846 \end{aligned}$$

and the other for region Sjælland-Syddanmark, Venstre, divisor 39

$$\begin{aligned} \frac{366186}{39} = 9389.38461538. \end{aligned}$$

This means that in the hypothetical situation where the Danish Parliament had 41 compensatory seats, a rounding seat allocation system might have assigned the $41^{\text{ st }}$ seat to the wrong party with a probability of 50%, i.e. to Venstre instead of Det Konservative Folkeparti.

The remaining question is, of course, how big of a problem Error 1 and Error 2 in practice really are. A statistical analysis proves difficult, in part because of the many random variables that need to be considered. Therefore we resort to a Monte-Carlo experiment and develop an election simulator to compute the probabilities of false n-way ties. In our experiment, where we work with 8 parties with tallies chosen at random between 20,000 and 400,000 votes, a situation, which pretty accurately describes the parameters of a Danish election. We then run the simulator 1,000,000 times where we compute a d’Hondt table with 50 rows (which corresponds to a highest divisor of 101).

Error 1: The following table depicts the expected value of n-way ties occurring in a single d’Hondt table.

n =	1	2	3	4
E(false n-way tie)	173.17545	0.904989	0.0048	0.000022

This means that in 9 of 10 d’Hondt tables, there will be in average one false 2-way tie that is decided by drawing lots. However, our experiment also shows that the risk of an Error 1 in the cases of false 3- and 4-way ties are extremely rare. Recall, that Error 1 will not change the election result but only the order in which seats are assigned.

Error 2: In the same statistical experiment, we look at the 175th seat being chosen. The following table depicts the number of false n-way ties observed.

n =	1	2	3	4
# observations	984,089	15,766	144	1

This means, that the probability of a false 2-way tie situation is roughly 1.5%, which means that in one out of 66 elections, the last seat will be awarded with drawing lots.

In summary, rounding while computing the d’Hondt and Sainte-Laguë tables should be considered harmful. We have demonstrated that there is a non-negligible chance that seats are being allocated in the wrong order and/or to the wrong party.

4.3 Implementation

The software for Denmark’s Seat Allocation System (DSAS) has been implemented by Statistics Denmark (Danmarks Statistik), in a programming language called PL/SQL (part of the official ORACLE database distribution) used to program stored procedures. DSAS implements the problematic rounding version of the seat allocation algorithm outlined in the previous section. In a nutshell, the implementation rounds to the nearest number and then generate randomly the digits after the comma as a tie breaker. For the above example, instead of computing the quotients precisely, DSAS rounds and randomly generates after comma digits.

where $r_1, r_2 \in [0,1)$ randomly chosen.

The problematic code can be found in the file packages.sql, dated 16. September 2013, 16:12. The three procedures that support our claim regarding the allocation of compensatory seats are depicted in Fig. 2 that describes how quotients for compensatory seats are computed, Fig. 3 that illustrates how the quotients are introduced into the main table, and Fig. 4 that demonstrates how the quotients are ordered for further computation. The program for allocating the constituency seats is very similar, suffers from the same rounding problem, and can be found elsewhere in this file.

Fig. 2.

Procedure Tillaeg_landsdel_dankvot_ins

Tillaeg_landsdel_dankvot_ins. In Fig. 2, the loop starting in line 23158 ranges over all possible divisors, starting from 1 until the maximal number stored in variable V_antal_divisioner. The body of the loop consists of two steps. In the first step, a temporary table TempTab is defined that stores all possible quotients (in no particular order). In lines 23165–23174 it is determined what precisely is stored in TempTab. The two critical lines here are 23172 and 23173. In the former DSAS uses SQL’s rounding function to compute round (Antal_stemmer/V_divisor), which computes the quotient rounded to the nearest whole number. The string Kvotient tells the ORACLE database engine to name the column Kvotient. In the latter DSAS stores a random value using Oracle’s random generator in a column called Random_nr as a tie breaker. How precisely Oracle’s random generator was seeded, could not be determined. As we will see below, if two quotients are compared and if the Kvotient part is equal, the Random_nr will determine which of the two is ranked higher. In the second step, after computing all quotients, DSAS calls a function to copy the quotients from TempTab into the right table using a stored procedure called Insert_tillaeg_landsdel_kvot (see line 23176), which we discuss next. Note that the first argument to this method is TempTab.

Fig. 3.

Procedure Insert_tillaeg_landsdel_kvot

Insert_tillaeg_landsdel_kvot. Figure 3 depicts a procedure that simply reads all tuples from the table referred to by first argument, i.e. TempTab. The destination table is Tillaeg_man_land_kvotienter, where the attributes for the table are renamed to Tmk_land_kvotient (line 23408) and Tmk_random_nr (line 23409), respectively.

The tuples in the table Tillaeg_man_land_kvotienter are stored in no particular order.

Fig. 4.

Procedure Tillaeg_landsdel_hentpotkvot

Tillaeg_landsdel_hentpotkvot. A fragment of the procedure that accesses and sorts the table Tillaeg_man_land_kvotienter is depicted in Fig. 4. It illustrate how the quotients and random numbers are used for further computation (which we will not discuss here).

All tuples from table Tillaeg_man_land_kvotienter are ordered lexicographically, first by the rounded quotient Tmk_land_kvotient (line 23617) and the random number Tmk_random_nr (line 23618), both in descending order.

5 Responsible Disclosure

Denmark has been using a computer program to compute the seat allocations of the Danish Parliament since for at least two decades [6]. The new version of DSAS (studied in this paper) was introduced only after 2007. We identified the rounding problem in DSAS in 2016 and informed the Ministry immediately about our findings. To the best of our knowledge the software as been updated, and the rounding problem has been addressed and fixed.

6 Conclusion

We have shown, that countries that use d’Hondt or Sainte-Laguë methods for computing the final seat allocation of parliament should be aware that rounding quotients in the table may lead to Error 1, Incorrect Allocation Order, or even worse, Error 2, Incorrect Seat Allocation. We have shown that erroneously rounding can impact an election outcome and that this observation is not just hypothetical, but can with a non-zero probability actually impact real elections. We have also shown that accidental rounding is difficult to detect, after all, on the face of it, how much damage could rounding actually do?

Social choice experts agree that rounding quotients when implementing d’Hondt or Sainte-Laguë methods is a mistake. However, it the election law and relevant election regulations that define the exact rules. The law defines the requirements for seat allocation systems, and if the law requires to round two digits then so be it. The Danish law does is not specific when it comes to rounding, and therefore, it should be the mathematical definition of the voting method that prevails.

Therefore, to implement a d’Hondt or Sainte-Laguë voting rule correctly is easy: One must not store the quotient but instead store both numerator (the Antal_stemmer) and denominator (the V_divisor) in two different fields. Using the following simple rule of arithmetic assuming $b,d \ne 0$

$$\begin{aligned} \frac{a}{b}< \frac{c}{d} \quad \text{ if } \text{ and } \text{ only } \text{ if } \quad a\cdot d < c \cdot b, \end{aligned}$$

it is possible to implement the seat allocation for both constituency and compensatory seats without fractions and rounding guaranteeing that the correct seat allocation is computed.