The Dynamical Analysis of Inter-Trial Fluctuations Near Goal Equivalent Manifolds

Abstract

Using the concept of task manifolds, a number of data analysis methods have been used to explain how redundancy influences the structure of variability observed during repeated motor performance. Here we describe investigations that integrate the task manifold perspective with the analysis of Inter-Trial task dynamics. Goal equivalent manifolds (GEMs), together with optimal control ideas, are used to formulate simple models that serve as experimentally testable hypotheses on how Inter-Trial fluctuations are generated and regulated. In an experimental context, these phenomenological models allow us to show how error-correcting control is spatiotemporally organized around a given GEM. To illustrate our approach, we apply it to study the variability observed in a virtual shuffleboard task. The geometric stability properties of the Inter-Trial dynamics near the GEM are extracted from fluctuation time series data. We find that subjects exhibit strong control of fluctuations in an eigendirection transverse to the GEM, whereas they only weakly control fluctuations in an eigendirection nearly, but not exactly, tangent to it. We demonstrate that our dynamical analysis is robust under coordinate transformations, and discuss how our results support a generalized interpretation of the minimum intervention principle that suggests the involvement of competing costs in addition to goal-level error minimization.

9.1 Introduction

The human body possesses a number of degrees of freedom far in excess of that needed to accurately execute a typical goal-directed movement. It is natural to expect this redundancy to play an important role in the regulation of motor variability as well as to influence its experimentally-observed structure. An important class of data analysis methods, based on the notion of task manifolds (Scholz and Schoner 1999; Müller and Sternad 2004; Cusumano and Cesari 2006), has been developed to examine the effect of this redundancy. In this chapter, we present a data analysis paradigm that integrates a consideration of redundancy at the task level with the dynamical analysis of inter-trial fluctuations arising from repeated goal-directed movements. We ground our discussion by presenting a study of variability in a virtual shuffleboard task, and model inter-trial fluctuations as the output of a perception-action loop whose primary function is to reduce error from one trial to the next. We show that the fluctuation dynamics in the vicinity of the task’s goal equivalent manifold (GEM) (Cusumano and Cesari 2006; John and Cusumano 2007; Dingwell et al. 2010; Dingwell and Cusumano 2010; Dingwell et al. 2013; Cusumano and Dingwell 2013) allow us to characterize not only the “static,” geometrical distribution of the variability, but also its temporal structure. This combined space-time analysis of observed variability yields an improved understanding of how goal-level errors are regulated and generated.

Task manifolds are surfaces in an appropriate body state space (e.g., joint kinematic variables) that contain all possible task solutions. Since, by definition, every point in a task manifold corresponds to body states that result in perfect task execution, only deviations off of the manifold result in error at the goal level. While this same basic idea underlies multiple methods of variability analysis, a different approach has been taken to implement it in each case, largely motivated by a difference in analytical focus. Uncontrolled manifold (UCM) analysis (Scholz et al. 2000; Scholz and Schoner 1999; Latash et al. 2002; Schöner and Scholz 2007) assumes that the task manifold is defined at each instant along a given movement trajectory, and uses an average movement in a time-normalized set of trials to represent the task’s goal. Given the hypothesis that control will only be applied to correct deviations off of the manifold, ratios of normalized variances perpendicular and tangent to a candidate manifold are used as a test: the expectation is that, for a true UCM, there should be greater variance along it than there is normal to it. With a primary focus on motor learning, the tolerance, noise, and covariation (TNC) method (Cohen and Sternad 2009; Müller and Sternad 2004; Ranganathan and Newell 2010; Sternad et al. 2011) statistically decomposes observed variability into the three empirical “costs” in its name, each of which are defined relative to a task manifold. The TNC approach defines the task manifold in a minimal space of variables needed to specify the outcome of a task, such as the position and velocity of a ball at release during a throwing task. TNC analysis does not just focus on the orientation of variability with respect to the task manifold (via the covariation cost) but also takes into consideration the total body-level variability (the noise cost), and relates the goal-level error to variability at the body level (via the tolerance cost).

The GEM concept (Cusumano and Cesari 2006) was initially developed to carry out experimental sensitivity analyses explicitly relating variability at the body and goal levels. The GEM approach defines the task manifold in a manner similar to that of the TNC approach, however it does so by emphasizing the role of a goal function, a mathematical hypothesis on the task strategy that encodes the relationship between the body and goal needed for perfect task execution. The zeros of the goal function are used to analytically define the GEM. In addition, the derivative of the goal function gives the body-goal matrix, the singular values of which characterize the task’s sensitivity to body-level errors (Cusumano and Cesari 2006; John and Cusumano 2007), independent of any control considerations. Motivated by the fact that optimal control, particularly in the form of the minimum intervention principle (MIP), has been proposed as a theoretical basis for modeling the neuromotor system (Scott 2004; Todorov and Jordan 2002; Todorov 2004), optimal control ideas were incorporated with the GEM approach. The resulting dynamical data analysis framework allows one to create models of inter-trial fluctuations that can be tested against movement data from human subjects (Dingwell and Cusumano 2010; Dingwell et al. 2010; Dingwell et al. 2013), providing an analysis of human motor variability data that combines task manifold, optimal control, and time series analysis approaches (Cusumano and Dingwell 2013).

In what follows, we describe GEM-based fluctuation analysis, and, as an illustration, use it to study data from a virtual shuffleboard task. After defining the key concepts, we obtain the geometric stability properties of the inter-trial dynamics for skilled players operating near the shuffleboard GEM. The eigenvalues and eigenvectors of a linear update equation estimated from the data characterize the way inter-trial fluctuations are organized around the GEM. We show that subjects exhibit strong control of fluctuations in an eigendirection transverse to the GEM, but weak control of fluctuations in an eigendirection nearly tangent to it. Furthermore, we demonstrate that our dynamical analysis is robust under coordinate transformations in a way that non-temporal variance-based methods are not. We conclude by discussing how our results support a generalized interpretation of the MIP, and in doing so, suggest the possible involvement of competing costs other than pure goal-level error minimization.

9.2 The Goal Equivalent Manifold

Consider a task for which we can express the goal-level error, $\mathbf{e}$, in terms of a goal function as:

$$\mathbf{f}(\mathbf{x})=\mathbf{e}$$

(9.1)

where $\mathbf{x} \in \mathbb{R}^B$ (the body space), $\mathbf{f} \in \mathbb{R}^E$ (the goal space). For redundant systems, $B> E$, that is the dimension of the body state space is greater than that of the space of goal-level errors. This introduces the possibility that there are many (possibly infinite) $\mathbf{x}$ that result in the goal-level error being zero. This particular set of body states is called the goal equivalent set (GES), and is expressed mathematically as the set $\mathcal{G}$:

$$ \mathcal{G} \triangleq \{\mathbf{x} \, | \, \mathbf{f}(\mathbf{x})=\mathbf{0}\}.$$

If the GES forms a surface in the body space, then it is referred to as a GEM. By definition, changes in the body state variables that remain in $\mathcal{G}$ do not change the performance at the goal, because the error remains zero.

Fluctuations in the body state are mapped to their resulting fluctuations at the goal. Given an operating point on the GEM, $\mathbf{x}^* \in \mathcal{G}$, we write the state for small body-level fluctuations, $\boldsymbol{\xi}$, away from a state on the GEM, $\mathbf{x}^* \in \mathcal{G}$. The sensitivity of the goal-level error to the body-level fluctuations $\boldsymbol{\xi}$ is found using a Taylor series expansion of the error:

$$\mathbf{e} = \mathbf{f}(\mathbf{x}^*+\boldsymbol{\xi}) =\mathbf{f}(\mathbf{x}^*) + D\mathbf{f}(\mathbf{x}^*)\boldsymbol{\xi} + O \!\!\left(||\boldsymbol{\xi}||^2 \right),$$

where $D\mathbf{f}(\mathbf{x}^*) \triangleq{\sf J}$ is the Jacobian of the goal function evaluated at $\mathbf{x}^*$. By hypothesis, $\mathbf{f}(\mathbf{x}^*)=0$, and, for skilled task performance, we expect small errors and, hence, small fluctuations away from the GEM ($\|\boldsymbol{\xi} \| \ll 1$). Thus, the error is expected to be well approximated by the linear relationship:

$$\mathbf{e} \approx D\mathbf{f}(\mathbf{x}^*)\boldsymbol{\xi} ={\sf J} \boldsymbol{\xi}.$$

(9.2)

In this context, ${\sf J}$ is referred to as the body-goal variability matrix (Cusumano and Cesari 2006): it maps the fluctuations at the body level, $\boldsymbol{\xi}$, to the error at the target, $\mathbf{e}$.

Since $B> E$ (by hypothesis), the $E \times B$ matrix ${\sf J}$ has more columns than rows, and so can be decomposed into orthogonal subspaces: the null space, $\mathcal{N}$, and the column space, $\mathcal{C}$ (Poole 2010; Golub and van Loan 1996), where:

$${\cal N} \buildrel \Delta \over = \{ {\bf{\xi }}{\mkern 1mu} \,|{\mkern 1mu} \,{\rm{J}}{\bf{\xi }} = 0\} ,$$

(9.3a)

and

$$\mathcal{C} \triangleq \{\boldsymbol{\xi} \, | \, \boldsymbol{\xi}^T \mathbf{w} = 0 \forall \mathbf{w}\in \mathcal{N}\}.$$

(9.3b)

As defined in Eq. (9.3a), all perturbations away from $\mathbf{x}^*$ that belong to the null space will not cause the error to change from zero, to linear order in $\boldsymbol{\xi}$. In contrast, perturbations in the column space (Eq. 9.3b) will create nonzero error at the target. Thus, in the context of movement variability analysis, we call $\mathcal{N}$ and $\mathcal{C}$, the goal equivalent and goal relevant subspaces, respectively. Geometrically speaking, the null space is tangent to the GEM at $\mathbf{x}^*$, whereas the column space is orthogonal to the GEM.

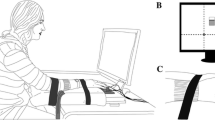
As an illustration, consider the simple shuffleboard task shown in Fig. 9.1, for which B = 2 and E = 1. The goal of this task is to release a puck at some initial distance, x ₀, with some initial velocity, v ₀, and have it stop on the target line that is located at a distance L from the start position, x = 0. Once released, the puck is decelerated by a Coulomb friction force until it comes to rest, so that, by Newton’s second law (Greenwood 1988):

Fig. 9.1

Schematic of shuffleboard task. The subject releases the puck at position x ₀ with an initial velocity v ₀. The goal is for the puck to come to a stop at the target. The coefficient of kinetic friction is constant along the length of the board

$$\ddot{x}(t) = -\mu g,$$

(9.4)

where μ is the coefficient of kinetic friction and g is the local acceleration of gravity. Solving the above differential equation gives the final position, x _f as

$$x_f = x_0 + \frac{v_0^2}{2 \mu g}.$$

(9.5)

For convenience, we rescale the release position and velocity into dimensionless quantities, x and v, using

$$x = \frac{x_0}{L}\quad\text{and} v = \frac{v_0}{\sqrt{2 \mu g L}},$$

(9.6)

which makes our analysis universal for any length of board, coefficient of friction, or local acceleration of gravity. The goal function for the system is then obtained, following Eq. (9.1), by noting that $x_f\, - \, L$ is the scalar error, where x _f is as in Eq. (9.5). After substituting Eq. (9.6), we find the goal-level error, e, in dimensionless form as:

$$e = \frac{x_f-L}{L} = v^2+x-1.$$

(9.7)

Thus, for the shuffleboard task, the goal function is a scalar valued function, $e = f(\mathbf{x}) \equiv f(x,v)$, so that the 2D body state is $\mathbf{x} = (x, v)$. That is, the performance in one trial, as measured by e, is determined exclusively by the value of $(x,v)$, the position and velocity of the puck at release.

The GEM is then obtained from Eq. (9.7) as $\mathcal{G}=\big \{(x,v) \>|\> v = \sqrt{1-x}\> \big\}$ (for $0 \le x \le 1$; see Fig. 9.2), and the 1 × 2 body-goal variability matrix is computed by the gradient of Eq. (9.7) as

$$\sf J = (1, \, 2v).$$

(9.8)

Using the definitions of Eqs. (9.3a) and (9.3b), we find the unit normal and unit tangent, $\hat{\bf n}$ and $\hat{\bf t}$, respectively, to be

$$\hat{\bf n} = \left [\, \frac{1}{\sqrt{1+4 v^2}},\,\frac{2 v}{\sqrt{1+4 v^2}}\, \right]^{\sf T}$$

(9.9a)

and

$$\hat{\bf t} = \left[-\frac{2 v}{\sqrt{1+4 v^2}},\, \frac{1}{\sqrt{1+4 v^2}} \, \right]^{\sf T},$$

(9.9b)

where the superscript ${\sf T}$ indicates the matrix transpose. The unit vectors are shown in Fig. 9.2.

Fig. 9.2

The goal equivalent manifold (GEM) for the shuffleboard task. The solid gray line denotes the GEM (body states $\mathbf{x}=$ (x, v) leading to perfect task performance); dashed gray lines are $\pm 5\,\%$ error contours. Also shown (black arrows) are the unit normal $\hat n$ (Eq. 9.9a) and unit tangent $\hat t$ (Eq. 9.9b) at an operating point $\mathbf{x}^*$. Deviations from the GEM in the $\hat t$ direction cause no error at the target (i.e., they are goal equivalent), whereas deviations in the $\hat n$ direction result in error at the target (i.e., they are goal relevant)

9.3 Inter-Trial Control

Fluctuations in movement arise from inherent physiological noise that is present at multiple scales (Eldar and Elowitz 2010; Faisal et al. 2008; Osborne et al. 2005; Stein et al. 2005; McDonnell and Ward 2011). Thus, during repeated task execution, a subject will strive to make adjustments from one trial to the next in an attempt to maximize performance. We model this behavior as an iterative, error-correcting, perception-action process (Warren 1990, 2006) in which perceived error from trial k is used to estimate the body state at trial k + 1 in an attempt to drive the goal-level error to zero. Among the simplest models are update equations with the form

$$\mathbf{x}_{k+1} =\mathbf{x}_{k} + \left ( I+ N_k \right) \mathbf{u}(\mathbf{x}_{k}) + \boldsymbol{\nu}_k,$$

(9.10)

in which $\mathbf{u}(\mathbf{x}_k)$ is an inter-trial, error-correcting controller depending on the current state $\mathbf{x}_k$, N _k is a matrix representing signal-dependent noise in the motor outputs (Harris and Wolpert 1998), and $\boldsymbol{\nu}_k$ is an additive noise vector representing unmodeled effects from perceptual, sensory, and motor sources. For skilled movements, which are the focus of this chapter and for which the fluctuations $\boldsymbol{\xi}$ are small, similarly small multiplicative noise terms drop out of the leading order analysis (Dingwell    et al. 2010; John and Cusumano 2007; Cusumano and Dingwell 2013), and so the random matrix N _k will not be included in what follows.

To motivate the above model, consider that, for a skilled subject, we expect $\mathbf{x}_k$ to lie very close to the GEM, so if there were no noise there would be no need for control (i.e., $\mathbf{u}=0$), and Eq. (9.10) would give $\mathbf{x}_{k+1} \approx \mathbf{x}_k$. However, some noise, $\boldsymbol{\nu}_k$, is always present, and if there were no control, the fluctuations in $\mathbf{x}_k$ would display a random walk in the body space, which is not observed in experiments. These two extreme limits illustrate that the job of the controller is to keep a multi-trial performance closer to that of a perfect repetition than to a noise-induced random walk. Models of this type implicitly assume a hierarchical structure to the overall motor control system: the controller of Eq. (9.10) makes error-correcting adjustments, between trials, to an approximately “feed forward” controller that executes the task within trials. In this view, the body state $\mathbf{x}_k$ of Eq. (9.10) plays the role of a control parameter for each individual goal-directed action.

Similar models have found use for the study of motor learning (van Beers 2009; Burge et al. 2008; Diedrichsen et al. 2005), with the difference that the controllers were formulated to depend directly on the goal-level error e _k , instead of the body state $\mathbf{x}_k$. However, in our approach, the body and goal-level fluctuations are related by Eq. (9.1), so the fact that Eq. (9.10) depends only on body states yields a system that is amenable to dynamical analysis in the presence of task redundancy. However, it leaves open the question of how the controller incorporates error information, something which we now address.

As before, we let $\boldsymbol{\xi}_{k}$ be a fluctuation (at trial k) from an operating point on the GEM, $\mathbf{x}^* \in \mathcal{G}$, so that $\boldsymbol{\xi}_{k} =\mathbf{x}_{k} - \mathbf{x}^*$. For skilled performance, these fluctuations will be small and so we assume a proportional linear controller

$$\mathbf{u}_{k} = B \boldsymbol{\xi}_{k},$$

(9.11)

where $B$ is a constant proportional gain matrix. Subtracting $\mathbf{x}^*$ from both sides of Eq. (9.10) and substituting in Eq. (9.11), we directly relate the fluctuations from one trial to the next:

$$\boldsymbol{\xi}_{k+1} = ( I+ B) \boldsymbol{\xi}_{k} + \boldsymbol{\nu}_k,$$

(9.12)

where $I$ is the identity matrix. Taking an optimal control approach, we further assume that the controller acts to specify the state at the next trial, $\mathbf{x}_{k+1}$, to minimize the expected value of a cost function ${\rm \Pi}$ with the following general form:

$$ = \alpha_0 e(\mathbf{x}_{k+1})^2 + \sum_{j=1}^M \alpha_j p_j(\mathbf{x}_{k+1})+\boldsymbol{\xi}_{k}^T B^T K B \boldsymbol{\xi}_{k},$$

(9.13)

with terms described as follows. The first term in $e(\mathbf{x}_{k+1})=\| \mathbf{f}(\mathbf{x}_{k+1}) \|$ (via Eq. 9.1), represents the cost of goal-level error. The summation term represents additional possible costs, as appropriate for a given problem, that may arise from biomechanical (e.g., range of motion), physiological (e.g., energy minimization), psychological (e.g., risk avoidance), or other considerations. The last term represents the cost of controller “effort.” Also in Eq. (9.13), the parameters α _j ($j=0,1,\ldots, M$) as well as the matrix $K$, are adjustable weights that can influence details of the system such as, for example, the location of the operating point $\mathbf{x}^*$.

Thus, the goal-level error is incorporated into the controller of Eq. (9.10) implicitly, via the first cost of ${\rm \Pi}$. Furthermore, because the leading terms of ${\rm \Pi}$ are evaluated at the next step, substitution of the update equation (Eq. 9.10) into Eq. (9.13) immediately shows how the noise $\boldsymbol{\nu}_k$ enters into the optimization, explaining why we minimize the expected value, $\mathbb{E}[\, \,]$, to determine the controller.

For an ideal MIP controller, $\alpha_0 \ne 0$ and $\alpha_j =0$ for $j \ge 1$ in Eq. (9.13), so the sole cost being minimized at the next trial is the goal-level error. Since the goal-level error deviates from zero only for goal relevant fluctuations (Fig. 9.2), such a “perfect” MIP controller would push subsequent body states onto the GEM, but would exert absolutely no control along it. The result is that in the presence of noise, the model Eq. (9.10) predicts an unbounded random walk along the GEM. However, such behavior is yet to be observed in multi-trial experiments. For this reason, in Dingwell et al. (2010), an additional cost related to minimizing the distance from a “preferred operating point” on the GEM was included as p ₁ in Eq. (9.13) (with $\alpha_1 \ne 0$ and M = 1 in the sum). This allowed the associated models to capture the localization of multi-trial experimental data around a location on the GEM in a way that an ideal MIP model could not.

9.4 Local Geometric Stability

We can analyze the local geometric stability of the inter-trial control process using Eq. (9.12). For convenience, we let $A= I+ B$ and rewrite Eq. (9.12) slightly as

$$\boldsymbol{\xi}_{k+1} = A \boldsymbol{\xi}_{k} + \boldsymbol{\nu}_k.$$

(9.14)

The eigenvalues and eigenvectors of $A$, which satisfy $A\hat{\bf e} = \lambda \hat{\bf e}$, determine the stability properties of the inter-trial control applied to fluctuations near the GEM. The magnitude of an eigenvalue indicates the action of the system on fluctuations in the direction of its corresponding eigenvectors: after one trial, the size of the fluctuation is reduced by a factor of $(1-|\lambda|) \times 100\,\%$. Thus having at least one eigenvalue with $|\lambda|>1$ indicates instability, whereas if all eigenvalues satisfy $0 \le |\lambda| \le 1$, the system is stable (Guckenheimer and Holmes1983; Hirsch et al. 2004). Heuristically speaking, smaller values of $|\lambda|$ correspond to greater stability. To facilitate our discussion, in the remainder we focus on the case where the body states $\mathbf{x}_k$ (and hence the fluctuations $\boldsymbol{\xi}_k$) are 2D, as is true for the shuffleboard task. In this case, $A$ is a 2 × 2 matrix, so there will be two eigenvalues. We also limit our discussion to the case of real, distinct eigenvalues, which has been found to be sufficient in experimental applications to date.

We label the the eigenvalues as λ _w and λ _s to classify them as “weak” and “strong,” respectively, according to their magnitude, so that $|\lambda_s| < |\lambda_w|$. The corresponding eigenvectors are labeled as $\hat{\bf e}_w$ and $\hat{\bf e}_s$. Thus, after one trial, the size of fluctuations along $\hat{\bf e}_w$ is reduced much less than those along $\hat{\bf e}_s$. A typical situation is shown schematically in Fig. 9.3, which shows the orientation of the eigenvectors with respect to the GEM. Also shown are the weakly and strongly stable subspaces, $\text{span}\{\hat{\bf e}_w\}$ and $\text{span}\{\hat{\bf e}_s\}$, respectively. As illustrated in the figure, in general $\hat{\bf e}_w\cdot\hat{\bf e}_s \ne 0$.

Fig. 9.3

Schematic showing the typical orientation of the weak and strong eigenvectors of matrix $A$ (Eq. 9.12), $\hat{\bf e}_w$ and $\hat{\bf e}_s$, respectively (black arrows) with respect to the goal equivalent manifold (GEM) (gray curve). The weakly and strongly stable subspaces (dashed lines) span the respective eigenvectors. The associated eigenvalues satisfy $|\lambda_s| < \lambda_w$; in general, $\lambda_s \approx 0$ and λ _w is closer to 1. The weakly stable subspace for a generalized minimum intervention principle (MIP) controller will be close to tangent to the GEM. The subspaces are so named because deviations off of the GEM are strongly corrected, whereas deviations along it are only weakly corrected

Note that, in general, the stability subspaces are not aligned with the normal and tangential directions of the GEM. However, for an ideal MIP controller that pushes states onto the GEM but has absolutely no control along it, one finds that $\hat{\bf e}_w$ is identical to $\hat{\bf t}$, the unit tangent to the GEM (Fig. 9.2). Furthermore, the eigenvalues of an ideal single-step MIP controller are $\lambda_w=1$ and $\lambda_s=0$, indicating that fluctuations along the GEM are allowed to persist indefinitely, whereas those transverse to it are, in the absence of noise, eliminated after a single trial. However, as discussed at the end of the last section, such a scenario is not expected in experiments, since in the presence of noise, it would result in a random walk of body states along the GEM from trial to trial. Thus, we do not anticipate the controller to satisfy a strict interpretation of the MIP, or UCM hypothesis, but rather a generalized version for which goal-level error is still the dominant cost to be minimized (Eq. 9.13), but there is at least one additional cost, $p_j(\mathbf{x}_{k+1})$, with a corresponding $\alpha_j \ne 0$. A small perturbation of this type will only slightly change the local stability, so that we still expect $|\lambda_s| \approx 0$ and $0 \ll \lambda_w < 1$. In addition, the eigenvectors will be slightly rotated from those for the ideal MIP controller, so that, in particular, $\hat{\bf e}_w$ will no longer be exactly tangent to the GEM.

As discussed in Cusumano and Dingwell (2013), consideration of the above leads to a set of generic experimental hypotheses. Here, we present only those needed for the experimental study of the 2D shuffleboard task to be discussed in the remainder of the chapter:

H1 :

Consistent with the hypothesis of weak (but not zero) control along the GEM, one of the eigenvectors, $\hat{\bf e}_w$, will be close to the GEM tangent, and so will make an angle $\theta_w \approx 90^\circ$ with $\hat{\bf n}$, the GEM normal. The corresponding eigenvalue, λ _w , will be less than one but much greater than zero ($0 \ll \lambda_w < 1$).

H2 :

The fluctuation dynamics transverse to the GEM are strongly stable: i.e., we expect $0 \approx |\lambda_{s}| \ll \lambda_{w}$. The associated eigenvector, $\hat{\bf e}_s$, will make a much smaller angle with $\hat{\bf n}$ than does $\hat{\bf e}_w$ ($\theta_s \ll \theta_w$).

H3 :

Consistent with the stability properties of H1 and H2, fluctuations in the weakly stable subspace will exhibit statistical persistence, whereas those in the strongly stable subspace will be non-persistent (uncorrelated). In terms of the exponent α from detrended fluctuation analysis (DFA) (Hausdorff et al. 1995; Peng et al. 1992), we expect $0.5 \approx \alpha_s \ll \alpha_w$.

Taken together, these hypotheses can be summarized as the expectation of dynamic anisotropy in the fluctuation dynamics, consistent with the action of a generalized MIP controller that has goal-level error as its main, but not only, cost.

9.5 Experimental Implementation

In this section, we apply the ideas and methods developed in the previous sections to study the experimentally-observed variability in a virtual shuffleboard task.

9.5.1 Apparatus and Protocol

Sixteen subjects (Table 9.1) were recruited as two cohorts, eight subjects between 18 and 35 (“younger”) and eight subjects older than 60 (“older”). Subjects were screened and asked to report any neurological conditions, upper-body arthritis and joint replacement, or uncorrected vision in either eye for exclusion. Subjects were also given the Edinburgh Handedness Inventory (Oldfield 1971), and all participants were deemed right handed, having a score of at least 60 on a -100 to 100 scale. Testing was approved by The Pennsylvania State University Institutional Review Board. No statistically significant differences for the analyses carried out for this chapter were found between the younger and older cohorts, so the results presented below were computed with the cohorts merged.

Table 9.1 Experimental subject demographics (mean ± standard deviation). Assuming normal distributions, no measures, except age, had significantly different means

A custom experimental virtual shuffleboard system was used for the task. The experimental system was composed of a manipulandum on a linear bearing attached to a linear variable differential transformer (LVDT) (Daytronic Corporation; Dayton, OH) that measured the manipulandum’s position. A linear accelerometer (ADXL320; Analog Devices, Inc.; Norwood, MA) was mounted on the manipulandum. Both the LVDT and the accelerometer were routed into a low-pass filter with a 20 Hz cutoff. Out of the filter, the data were sampled by a 12-bit PCMCIA data acquisition card (NI DAQCard-6024E; National Instruments; Austin, TX) at 1 kHz, and sent to a laptop where it was read into simulation and control software written in MATLAB (The Mathworks; Natick, MA).

The control software was used to generate a 2D, top-down view of a virtual shuffleboard court that was projected onto a screen located in front of the subjects’ seat. The projected image displayed a virtual cue that moved in sync with physical motions of the manipulandum, together with a puck and a target line (recall Fig. 9.1). Each trial started with the puck at rest at its zero position. While the puck was being pushed by the cue and subsequently released, its position was displayed in real time. The puck was released when the computed virtual contact force between the puck and cue fell to zero. The velocity at release, v, was found by integrating the acceleration data, and the release position, x, was found directly from the LVDT. A numerical simulation then took over to calculate the released puck’s position and velocity, based on the equation of motion (Eq. 9.4), and the puck’s motion was displayed in real time. After the puck came to a stop, in addition to being able to visually see the puck’s final location, subjects were shown the error e (Fig. 9.1), which was displayed at the top-right of the screen. When the cue was retracted to the start position, the next trial began.

Subjects were asked to adjust the seat to their comfort, but were required to have their forearm parallel to the ground and their right hand above their mid-thigh when the cue was at its initial position. All participants used their right hand to operate the manipulandum. Subjects were given the instruction: “On each trial, have the center of the puck stop on the black target line.” Subjects were given a training session of 50 trials to familiarize themselves with the system, and then were asked to complete 5 blocks of 50 trials each that were used for analysis. Between each block, the subject was given a minimum of 90 s to rest. The release position and velocity, $\mathbf{x}_k=(x_k,v_k)$, and the error e _k (via Eq. 9.7) for each trial were recorded and stored.

9.5.2 Data Processing

All 250 trials were grouped together for each of the 16 subjects. Because we assumed that subjects performed at a skilled steady-state, the first trial of each block after the training block was removed to allow for refamiliarization after a break, and the final trial was removed in case the subject performed differently knowing it was the last trial. Any trials that involved subject errors or technical malfunctions were also removed: there were a total of only six such trials removed across all subjects, with a maximum of three for one subject. All data analyses were performed using MATLAB.

For skilled subjects, we expect the average performance to be nearly perfect. That is, the mean body state over all trials is very nearly on the GEM, and so we defined an empirical operating point as $\mathbf{x}^* = \overline{\mathbf{x}}$. Then the fluctuation time series was computed with respect to this mean operating point (MOP) from $\boldsymbol{\xi}_k = \mathbf{x}_k - \overline{\mathbf{x}}$.

Because of the limited length of each inter-trial time series, as well as the known sensitivity of eigenanalyses for matrices contaminated by noise (Golub and van Loan 1996), bootstrapping (Mooney and Duval 1993; Freedman 1981; Efron and Tibshirani 1994) was used to produce a confidence interval (CI) for the eigenvalue and eigenvector calculations. A set of 250 fluctuations, $\boldsymbol{\xi}_{k}$, and the following fluctuation, $\boldsymbol{\xi}_{k+1}$, was selected randomly with replacement from the original trial data on each iteration of the bootstrap. The matrix $A$ was estimated via least squares, using the pseudo-inverse (Moore and Barnard 1939; Golub and van Loan 1996) for each set of $\boldsymbol{\xi}_{k}$ and $\boldsymbol{\xi}_{k+1}$. The eigenvalues and eigenvectors for each $A$ were then calculated and stored. This process was repeated over 10⁵ iterations of the bootstrapping procedure. Occasionally, an $A$ matrix with imaginary eigenvalues and eigenvectors was produced: in this case, such matrices are numerical artifacts stemming from the fact that we are trying to estimate a nearly-singular matrix with one eigenvalue near zero. However, across all subjects, a mean of only 0.06 % of matrices generated during the bootstrapping iteration fell in this category, with a maximum of 0.93 % for one subject. Because of the relatively small number of instances, these matrices were simply removed from the sample and rerun with new entries.

The above bootstrapped eigenanalyses were used to test hypotheses H1 and H2. To test hypothesis H3, we employed DFA (Hausdorff et al. 1995; Peng et al. 1992). The output of the DFA algorithm is a positive exponent, α: when $\alpha < 0.5$, a time series is said to be “antipersistent,” meaning that fluctuations in one direction are likely to be followed by fluctuations in the opposite direction; when $\alpha> 0.5$, the time series is “persistent,” meaning that fluctuations are likely to be followed by subsequent fluctuations in the same direction; finally, when $\alpha=0.5$, the time series is “non-persistent” or uncorrelated. DFA has been widely used to search for long-range persistence (also called long-range correlations) in experimental time series, a topic that is beyond the scope of this chapter. However, as discussed at some length in Cusumano and Dingwell (2013), when used for this purpose, DFA is prone to false positives (Deligni{è}res and Torre 2009; Maraun et al. 2004; Gao et al. 2006). Accordingly, we emphasize that we are not using DFA to claim that observed fluctuations exhibit long-range persistence, but merely as a convenient tool to characterize persistence in general. In previous work (Dingwell and Cusumano 2010), we have shown that antipersistent time series are consistent with the overcorrecting control of fluctuations normal to a GEM, whereas persistent fluctuations suggest weak or “indifferent” control of fluctuations along it. In this chapter, instead of projecting the fluctuations onto the vectors normal and tangent to the GEM, we examine fluctuations in the weakly and strongly stable directions.

Direct application of DFA within each iteration of bootstrapping was computationally costly, so we first computed the mean value, $\overline{ A}$, of the 10⁵ matrices $A$ generated during the bootstrapping procedure for one subject. Using $\overline{ A}$, we found the “average” weak and strong eigenvectors $\hat{\bf e}_w$ and $\hat{\bf e}_s$. Then we transformed the fluctuations using the linear coordinate transformation

$$\boldsymbol{\xi}= P\boldsymbol{\zeta},$$

(9.15)

where $P$ is the matrix containing $\hat{\bf e}_w$ and $\hat{\bf e}_s$ as its columns. This transformation projects the fluctuations $\boldsymbol{\xi}$, originally expressed in dimensionless position and velocity coordinates, onto the average eigendirections, so that we can write $\boldsymbol{\zeta} = (\zeta_w,\zeta_s)^{\sf T}$. Finally, DFA was performed on the resulting ζ _w and ζ _s fluctuation time series. These results were used to test H3.

While the bootstrapped empirical probability density functions (EPDFs) obtained for this study were close to Gaussian, the aggregate distributions were typically not. Nor were they symmetric about their median. Therefore, across all subjects, a comparison of medians was done using a two-sample, two-sided sign test (Wilcoxon 1945), with significance level set to 0.05. In the box plots used throughout, the center line shows the median value, the lower and upper box edges encompass the interquartile range (IQR), and whiskers extend a maximum of 1.5 IQR. Note, however, that all data, including outliers, were included in the data analyses described above.

9.6 Results

To illustrate the geometrical features of the data analysis, a scatter plot of an ensemble of body states (release positions and velocities), collected for all 250 trials for one subject, is shown in Fig. 9.4. For reference, the GEM and the directions normal and tangential to it are also displayed. We see that the MOP is not located on the GEM, but is close to it, as expected. Also plotted are the weakly and strongly stable eigenvectors, $\hat{\bf e}_w$ and $\hat{\bf e}_s$, respectively, for this figure computed from the average matrix, $\overline{ A}$, estimated during the bootstrapping process. Also displayed are the angles θ _w and θ _s that each eigenvector makes with the normal. Note also that the apparent orientation of the cloud of trials does not align with the normal and tangential axes.

Across all subjects and trials, the goal-level error was e = -0.0204 {$[\!-\!0.1828, 0.1713]$}, where the stated value is the median, and the range in square brackets is the 90 % CI. The corresponding median distance from the GEM in the body space was $\delta =-0.0118$ $[\!-\!0.0221, 0.0046]$. Thus the aggregate performance displayed, roughly speaking, about as much overshooting ($e>0$) as undershooting ($e<0$), though with some indication of a small bias toward undershooting. This small bias is more apparent in the stopping distance, since the CI shows a significant bias toward trials “under” the GEM curve ($\delta < 0$). Nevertheless, these overall results are consistent with the assumption that skilled performance would involve operation close to the GEM.

Fig. 9.4

Plot in the body space of all 250 trials (light gray dots) for one subject, showing the weakly and strongly stable eigenvectors, $\hat{\bf e}_w$ and $\hat{\bf e}_s$, respectively, obtained from the average, $\overline{ A}$, of all 10⁵ matrices $A$ estimated via regression during bootstrapping. Also shown are the mean operating point (MOP, black circle) and goal equivalent manifold (GEM) (dark gray line). Normal and tangential dashed reference lines are spanned by $\hat{\bf n}$ and $\hat{\bf t}$, respectively (Fig. 9.2). The angles θ _w and θ _s to each eigenvector are measured counterclockwise from the normal, as shown

In Fig. 9.5 we show typical results from the bootstrapped local stability analysis using the data from all 250 trials for one subject. Figure 9.5 (top) displays the EPDFs obtained for the eigenvalues, λ _w and λ _s , of the matrix $A$ (Eq. 9.14); in Fig. 9.5 (bottom) are the EPDFs for the angles, θ _w and θ _s that the eigenvectors $\hat{\bf e}_w$ and $\hat{\bf e}_s$ make with $\hat{\bf n}$, the unit normal to the GEM (Fig. 9.4). Observe that the displayed EPDFs are unimodal and symmetric about the median, so that the mean, median, and mode are close to equal: this was found to be true for all bootstrapped distributions generated for this study. For this subject, we find $\lambda_s = -0.1039$ $[-0.2191,0.0143]$ and $\lambda_w = 0.4947$ [0.3997,0.5871], so that $0\approx |\lambda_s| \ll \lambda_w$ as hypothesized. The fact that $\lambda_s < 0$ indicates that this subject slightly overcorrected deviations transverse to the GEM, suggesting a slightly suboptimal controller (Dingwell et al. 2010). We also find $\theta_w = 93.62^\circ$ $[73.68^\circ, 119.74^\circ]$, indicating that $\hat{\bf e}_w$ is nearly tangent to the GEM, whereas $\theta_s = 20.78^\circ$ $[16.82^\circ, 24.45^\circ]$. Thus, again as hypothesized, we find $\theta_s \ll \theta_w \approx 90^\circ$.

Fig. 9.5

Typical empirical probability density functions (EPDFs) for the local stability analysis, obtained via bootstrapping for one subject: (top) eigenvalues λ _w and λ _s ; (bottom) angles θ _w and θ _s made by the eigenvectors $\hat{\bf e}_w$ and $\hat{\bf e}_s$, respectively, with the normal $\hat{\bf n}$ to the gold equivalent manifold (GEM) (see Fig. 9.4 for angle definitions). In the angular EPDFs, the radial direction is the relative frequency, the circumferential direction is the angle, and the italicized numbers represent the relative frequency

Aggregate geometric stability results across all subjects are shown in Fig. 9.6. To compare eigenvalues, we look at their absolute values to directly compare the relative strength of control without regard to possible overcorrection ($\lambda<0$) or undercorrection ($\lambda>0$). Note, however, that for all subjects it was found that the bootstrapped distribution of λ _w was strictly positive, as in Fig. 9.5. As a comparison statistic, for each subject, we used the mean value of the eigenvalues and angles obtained from each subject’s bootstrapped EPDF. In Fig. 9.6 (left) are box plots showing the distribution of $|\overline{\lambda}_s|$ and $|\overline{\lambda}_w|\equiv\overline{\lambda}_w$, whereas Fig. 9.6 (right) displays box plots for the corresponding mean eigenvector angles $\overline{\theta}_w$ and $\overline{\theta}_s$. Applying the two-sided sign test showed that the aggregate median value of $\overline{\lambda}_w$ (0.5597 [0.3026,0.9194]) was significantly larger than that of $\overline{\lambda}_s$ (0.1076 [0.0141,0.3564]), with $p=3.05\times10^{-5}$. It was also found that the aggregate median value of $\overline{\theta}_w$ ($85.83^\circ$ $[53.72^\circ,115.59^\circ]$) was significantly larger than that of $\overline{\theta}_s$ ($20.33^\circ$ $[\!-\!13.39^\circ,33.35^\circ]$), again with $p=3.05\times10^{-5}$. Since $\lambda_w> 0$ in all cases, we find that $0 \approx |\lambda_s| \ll \lambda_w$ and $\theta_s \ll \theta_w \approx 90^\circ$. Taken together, these results confirm hypotheses H1 and H2.

Fig. 9.6

Aggregate geometric stability results: magnitude of mean eigenvalues, $\overline{\lambda}_w$ and $\overline{\lambda}_s$, obtained from each subject’s bootstrapped distributions (left); mean eigenvector angles $\overline{\theta}_w$ and $\overline{\theta}_s$ (right). The median value of $\overline{\lambda}_w$ (0.5597) was significantly larger than that of $\overline{\lambda}_s$ (0.1076), with $p=3.05\times10^{-5}$. The aggregate median value of $\overline{\theta}_w$ ($85.83^\circ$) was significantly larger than that of $\overline{\theta}_s$ ($20.33^\circ$), with $p=3.05\times10^{-5}$. Since λ _w was positive for all subjects, these results confirm hypotheses H1 and H2: $0 \approx |\lambda_s| \ll \lambda_w$ and $\theta_s \ll \theta_w \approx 90^\circ$

The persistence properties of the inter-trial fluctuations, computed using DFA, are presented in Fig. 9.7. For each subject, the average matrix $\overline{ A}$ was obtained from bootstrapping, and the fluctuations $\boldsymbol{\xi}$ were projected onto the average weakly and strongly stable directions using the transformation Eq. (9.15). The DFA algorithm was then applied to the resulting ζ _w and ζ _s fluctuation components. We found that the ζ _w fluctuations were statistically persistent, with an $\alpha_w =0.9433$ $[0.7500, 1.2950]$, suggesting weak control in the weakly stable direction, which Fig. 9.6 shows is nearly tangent to the GEM. In contrast, for ζ _s , we found $\alpha_s=0.4948$ $[0.2773, 0.6863]$, indicating approximately uncorrelated fluctuations. This is consistent with strong control that suppresses substantial deviations from the GEM, leaving only noise. The difference between the median values of α in both cases was significant ($p = 3.06 \times 10^{-5}$). Thus, $0.5 \approx \alpha_s \ll \alpha_w$, confirming hypothesis H3.

Fig. 9.7

Aggregate results for the detrended fluctuation analysis (DFA) exponent α, for fluctuations in the weakly and strongly stable directions, ζ _w and ζ _s , respectively. For ζ _w , we found $\alpha_w =0.9433$ $[0.7500, 1.2950]$ indicating statistical persistence consistent with weak control (Dingwell and Cusumano 2010). For ζ _s we found $\alpha_s=0.4948$ $[0.2773, 0.6863]$, indicating approximately uncorrelated fluctuations, consistent with strong control. The difference between the median values of α in both cases was significant ($p = 3.06 \times 10^{-5}$). These results confirm hypothesis H3: $0.5 \approx \alpha_s \ll \alpha_w$

Taken together, these results demonstrate that subjects exhibited strong dynamical anisotropy around the GEM, precisely as anticipated. This supports the claim that inter-trial error correction for the shuffleboard task is organized around a “GEM aware” generalized MIP controller.

9.7 Comparison with “Static” Variability Analysis

In this section, we contrast our dynamical analysis with an approach that does not consider the temporal order of the data, but instead analyzes only the “static” inter-trial variability structure. Here, we do this by applying principal component analysis (PCA) (Mardia et al. 1979; Daffertshofer et al. 2004) to the ensemble of body states. PCA calculates a new set of coordinates for the data set such that the covariance between the coordinates is zero. A principal component (PC) is an eigenvector of the data’s covariance matrix, and its associated eigenvalue, the principal value (PV) indicates how much variance lies along that direction. Thus, each PV represents a fraction of the total variance that lies in the direction of its associated PC. With 2D data, as was collected for this study, a possible interpretation of PCA results is that the first PC, which has the larger PV and, therefore, the greater variability, indicates a weakly-controlled direction because fluctuations are larger along it. The second, smallest variance PC then indicates a strongly-controlled direction. If true, that would imply that variance analysis alone could identify the organization of inter-trial variability about a candidate GEM. We here show that this interpretation does not hold, in general.

Applying PCA to our fluctuation data, we obtain the aggregate results shown in Fig. 9.8. We labeled the two PVs as λ₁ and λ₂, where $\lambda_1> \lambda_2$, so that the associated PCs are the unit vectors $\hat{\bf p}_1$ and $\hat{\bf p}_2$. We then computed the angles that each PC made with the unit normal to the GEM, as was done for Fig. 9.6. We see that λ₁ accounted for 81.66 % $[61.66\,\%, 95.58\,\%]$ of the total variance, whereas λ₂ accounted for 18.34 % $[4.416\,\%, 38.23\,\%]$. We also see that $\theta_1=27.23^\circ$ $[7.714^\circ, 116.6^\circ]$ and $\theta_2=117.2^\circ$ $[97.71^\circ, 206.6^\circ]$. Thus, neither PC was close to either $\hat{\bf n}$ or $\hat{\bf t}$, and so they did not help locate the GEM. In particular, the angular distance of the first and second PCs from the GEM tangent was roughly $63^\circ$ and $27^\circ$, respectively, thus neither could be said to identify a weakly controlled direction.

Fig. 9.8

Aggregate results of principal component analysis (PCA) applied to each subject’s Inter-Trial data: (left) percent of total variance explained by each PV, λ₁ and λ₂; (right) the angle, θ₁ and θ₂, between each PC and $\hat{\bf n}$ (Fig. 9.2). We see that the first principal value (PV) explains about 80 % of the total variance (81.66 % $[61.66\,\%, 95.58\,\%]$), however, both PCs are approximately the same angular distance (about 27°) from the tangent, $\hat{\bf t}$, and hence do not locate the goal equivalent manifold (GEM) in body space

To further explore this issue, we transformed the data from one subject using a coordinate transformation that rendered the variability isotropic, for which, that is, the variance ellipse would be a circle. This is easily accomplished using a linear transformation similar to Eq. (9.15), however instead of constructing the matrix $P$ by using the eigenvectors $\hat{\bf e}_w$ and $\hat{\bf e}_s$ as its columns, we use the eigenvectors of the covariance matrix, that is, the PCs, $\hat{\bf p}_1$ and $\hat{\bf p}_2$. This projects the original fluctuations ${\boldsymbol \xi}$ onto the principal directions. After this step, each coordinate was normalized to unit variance, giving fluctuations in rescaled principal coordinates, $\mathbf{q}=(q_1,q_2)^{\sf T}$.

Figure 9.9 shows the effect of this transformation on a typical geometric stability analysis, carried out using the data from one subject. In Fig. 9.9 (left), we see the results for the data in the original position–velocity fluctuation coordinates. For this figure, the eigenvectors $\hat{\bf e}_w$ and $\hat{\bf e}_s$ were computed from a single, typical matrix $A$, as would be estimated during a single bootstrap iteration. Also included in the figure is the standard variance ellipse, which, as would be expected from the results of Fig. 9.8, is not particularly well aligned with the GEM. However, the weakly and strongly stable subspaces are oriented in a way that helps understand how control is organized around the GEM. In Fig. 9.9 (right), we see the same data, however transformed into $(q_1,q_2)$ coordinates, together with the eigenvectors. These eigenvectors were not merely transformed from Fig 9.9 (left), rather, the transformed data were used to estimate a new matrix $A$, and a new eigenanalysis was then performed. In the transformed picture, it is clear that the variability cloud provides no useful information about the location of the GEM since, by design, its variability ellipse is circular. However, the new eigenvectors continue to define weakly and strongly stable subspaces that correctly demonstrate how control is organized about the GEM.

Fig. 9.9

Illustration showing the effect of a coordinate transformation that renders the variability ellipse circular: (left) data from one subject (light gray dots) together with the weakly and strongly stable eigenvectors, $\hat{\textrm{e}}_w$ and $\hat{\textrm{e}}_s$ (black arrows), for a matrix $A$ estimated via regression during a single iteration of the bootstrap; (right) the same ensemble (gray dots) after transforming into rescaled principal coordinates $(q_1,q_2)$ that have isotropic variance. In the right plot, the eigenvectors were calculated from a new matrix $A$ estimated from the transformed data. Also shown in both figures is the goal equivalent manifold (GEM) (dark gray line) in the local coordinates, and the variance ellipse (dashed line). We observe that while the variability is radically changed by the transformation, the local geometry of the inter-trial dynamics is fundamentally preserved

9.8 Discussion

In this chapter, we have described a dynamical approach to the experimental analysis of inter-trial variability in skilled movement tasks. Our approach combines consideration of task manifolds, in the particular form of GEMs, with optimal control concepts, to formulate experimentally testable models of inter-trial fluctuations. Because of this fundamentally dynamical perspective, we are not forced to make inferences about control based solely on the “static” structure of variability observed in some body-level state space, but rather can characterize the way variability, at both the body and goal levels, is organized and generated in time.

While the general GEM-based framework discussed in this chapter can be used to create mathematical models suitable for theoretical analysis, our approach is phenomenological and experimentally oriented. Thus, the primary significance of the theoretical discussion presented here is that it allows us to arrive at a set of quite generic hypotheses on the structure of variability observed with skilled performers: namely, that we expect to see strong evidence of dynamic anisotropy in the inter-trial fluctuations near a GEM. Furthermore, while motivated by both the MIP and the UCM hypothesis, consideration of our relatively simple mathematical models in the light of available experimental evidence leads us to the conclusion that neither can be true in an ideal form, since “perfect” MIP controllers would result in nonlocalized fluctuations that drift randomly along the GEM. Thus, our hypotheses include the assumption of a generalized MIP for which control along the GEM is not zero, but weak. This seemingly minor observation has an important experimental consequence: while this weakly controlled direction might be expected to be nearly tangent to the GEM, it will not, in general, be perfectly so.

To illustrate the theory, as well as its experimental implementation, we applied our analysis approach to study the variability observed in a virtual shuffleboard experiment. We found that all of our general hypotheses regarding dynamic anisotropy were supported by the analysis results. In particular, we found that subjects exhibited strong control of fluctuations in a direction transverse, but not typically normal, to the GEM, whereas they only weakly controlled fluctuations in a direction nearly, but not exactly, tangent to it. The assessment of control “strength” in these two directions was not determined by the relative magnitude of variances, but was provided both by local stability analysis and DFA. In both of these cases, the differences between the weakly and strongly stable directions were found to be as predicted and highly significant.

We compared our dynamical analysis with a non-temporal, variance-based analysis carried out using PCA. We found that the orientation of the variability cloud did not help identify how inter-trial control was organized around the GEM. Furthermore, we showed that our dynamical approach is robust to coordinate changes that result in isotropic variability. Under such circumstances, variability alone provides no information about the GEM, whereas the orientation of weakly and strongly stable subspaces still helps explain how variability is structured around a GEM, as well as how control is temporally organized.

The theoretical discussion in this chapter, together with the experimental demonstration that the weakly stable directions are not exactly directed along the GEM, suggest that while goal-level error minimization is likely a dominant cost being minimized by the human motor system, it is not the only one. In particular, our work suggests that there are relatively small additional costs—such as might be related to ergonomic, physiological, or even psychological needs of the performer—that need to be considered in combination with error reduction so that we might completely characterize experimentally-observed motor variability. It is hoped that dynamical data analysis methods like those presented here might help us to identify such costs in future experiments.