Keywords

Introduction

On a geological time scale, our planet has experienced a relatively stable environment for the last 10,000 years (Petit et al. 1999), known to geologists as the Holocene, but for the last couple of centuries, also termed the Anthropocene (Crutzen 2002), human activities have become the main driver of environmental change at the global scale and also at the local scale throughout most regions of the earth (Rockström et al. 2009). These anthropogenic drivers have exerted increased pressure on world’s ecosystems (Vitousek et al. 1997), and the acknowledgment and scientific documentation of the associated deleterious effects have prompted political responses to alleviate these pressures in an attempt to restore ecosystem functioning. Action plans addressing various sources of emissions were established on the pervasive belief that ecosystem responses to increasing pressures could be reversed and that a previously observed and desired ecosystem state could be restored. The fundamental tenet was that ecosystem decline and recovery would follow the same pathway, linear or nonlinear , and that such relationships between driver and response were time invariant.

There is growing observational evidence that this tenet is essentially flawed. The ozone layer has not been restored to past levels after the implementation of the Montreal Protocol in 1987 for reducing emissions of chlorofluorocarbon (CFC) gases and this lack of recovery is believed to be caused by climate warming and release of new chemicals with a yet unknown effect to the ozone layer (Weatherhead and Andersen 2006). Commercial fish stocks have not recovered following reduced fishing pressure, and climate change and complex food-web interactions have been suggested as plausible explanations (Botsford et al. 1997). Nutrient reductions in coastal areas have not reduced phytoplankton biomass (Duarte et al. 2009) nor the extent of hypoxia (Conley et al. 2007), and this is mainly attributed to climate change and altering of the food web. Thus, many of the world’s ecosystems fail to return to previously observed states after pressure reduction, because changes in other drivers have shifted the baseline. This evidently leads to nonuniform time trajectories in the relationship between pressure and response.

The concept that ecosystems respond nonlinearly to changes in the drivers, displaying hysteresis-like behavior with alternative stable states , is not new (Holling 1973; May 1977). Lakes exhibit shifts between a clear state with dominance of submerged aquatic vegetation and a turbid state dominated by phytoplankton (Scheffer et al. 1997; Carpenter et al. 1999). The shift is typically driven by enhanced nutrient input (mostly phosphorus) from human activity leading to increased phytoplankton growth and subsequently shading of the submerged aquatic vegetation (Jeppesen et al. 1999). Tropical reefs alternate between corals states and states where macroalgae overgrow the corals and prevent the settlement of coral larvae for continued recruitment (Knowlton 1992). The resilience of the coral reefs has been eroded through nutrient enrichment and overfishing (Scheffer et al. 2001), whereas the shift between states appears to be triggered by events such as hurricanes and outbreak of diseases affecting sea urchins (Mumby et al. 2007). The complex interactions in food webs may similarly lead to regime shifts through cascading effects driven by eutrophication , overfishing, and invasive species (Daskalov et al. 2007; Casini et al. 2008). Outbreaks of hypoxia can also lead to a sudden change in the biogeochemical processes causing a positive feedback of nutrients to the water column through reduced nitrification-denitrification, releases of ironbound phosphate, and reduced transfer of energy to higher trophic levels (Conley et al. 2009b). Loss of benthic macrofauna with hypoxia and thresholds associated with recolonization suggests a hysteresis-like behavior (Diaz and Rosenberg 2008). Thus, there are several examples from the literature of ecosystems displaying hysteresis behavior and the conceptual understanding of the positive feedback mechanisms required for the existence of alternative stable states has largely been established.

However, there is a gap in the literature between apparent regime shifts and the application of a rigorous mathematical-statistical framework for the actual demonstration of such threshold effects and hysteresis responses (Andersen et al. 2009). Moreover, most quantitative analyses of regime shifts are theoretical studies that examine the behavior of a simple nonlinear model that is believed to capture the essential mechanisms of the ecosystem (e.g., Carpenter et al. 1999; Ludwig et al. 2003; Guttal and Jayaprakash 2008). Although such models may mimic ecosystem observations to a reasonable degree and hence provide support for the existence of regime shifts , they do not offer statistical confidence in the existence of bistability, i.e., in terms of quantifying the probability of a hysteresis response relative to a simpler and uniform relationship.

Statistical tests can, in principle, be employed by comparing the likelihood of two such competing models, but in practice this is more complicated as it requires relatively simple mathematical representation of the ecosystem in question (i.e., few parameters) and sufficient data to estimate these models and calculate their likelihood. Consequently, scientists have resorted to simpler statistical procedures, typically identification of change-points in time (e.g., Zeileis et al. 2003; Rodionov 2004), as an exploratory data analysis indicating if abrupt changes may have occurred. Such statistical methods have started to populate the ecological literature recently and are the natural first step towards identifying potential drivers and mechanisms but do not describe any driver-response relationship as time can never be the underlying driver (Andersen et al. 2009). Moreover, change-point detection methods can identify abrupt changes, both with respect to time and potential drivers although the latter is rarely seen in the literature, but they do not provide inference for alternative stable states . Therefore, the objective here is to supplement the growing set of statistical methods used to analyze for potential regime shifts in ecosystems with a method indicative of alternative stable states. The idea is to examine the time trajectory of an ecosystem response variable relative to a hypothesized driver and test if this trajectory is time invariant, i.e., the relationship is uniform across time.

Conceptualizing Ecosystem Responses

The literature is populated with conceptual figures displaying different categories of driver-response relationships. May (1977) formulated a nonlinear differential equation and showed graphically that this model would exhibit two alternative stable states for a specific parameter setting and one unstable state constituting a divide between the two stable attractors. A perhaps better illustration of this concept was the marble rolling in a rugged landscape that could have several attractors (Scheffer 1990; Scheffer et al. 1993; Scheffer et al. 2001). The ridge between the two basins of attraction constituted the unstable state where the ball would roll either direction. Carpenter et al. (1999) presented a simple lake model with a sigmoid phosphorus influx for the sources and a linear efflux for the sinks, and graphically demonstrated how this could lead to alternative stable states and hysteresis responses. The main conclusion from these studies was that the bistability figures could actually be derived mathematically from the simple models exhibiting hysteresis.

On the other hand, the statistical approach to conceptualizing driver-response relationship has been based on experiences from data exploration. De Young et al. (2004) proposed three different types of responses: (1) linear, (2) abrupt change and reversible, and (3) abrupt change and not directly reversible, the latter representing a hysteresis-type behavior. Andersen et al. (2009) extended these to also consider the time dimension, showing that abrupt changes in time series can occur even if the driver-response relationship is strictly linear, because an abrupt change in the driver is directly mediated to the response. They cautioned about over-interpreting abrupt changes in biological time series , if the cause of the change was not within the biological system itself.

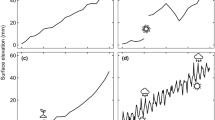
A broad range of possible responses to increasing followed by decreasing pressures on the ecosystem , derived from theory and observations, has been proposed and synthesized into a few generic classes of responses (e.g., Duarte et al. 2009; Kemp et al. 2009). Here, I will consider the four different response types presented in Duarte et al. (2009) (Fig. 12.1). The uniform relationship between response and pressure variable is an idealized situation (Fig. 12.1a), where nothing else changes over time (termed “Return to Neverland” in Duarte et al. 2009). This is the fundamental type of relationship that managerial frameworks are built around, despite increasing observational evidence that pressure-response relationships are not static. The hysteresis relationship (Fig. 12.1b) resembles those obtained from theoretical studies (e.g., May 1977; Scheffer et al. 2001) with alternative stable states within a range of the pressure variable. It involves a resistance to return to the original state when the pressure is alleviated. A shift in the ecosystem baseline (Fig. 12.1c) typically occurs in a multi-pressure system, which essentially includes all ecosystems, and illustrates that the outcome, after reducing the main pressure on the system, is different from the starting point, because other pressures have induced a shift (for most ecosystems a shift to a less desirable state). Finally, ecosystems can display combinations of hysteresis and shifting baselines (Fig. 12.1d).

Fig. 12.1
figure 1

Different types of ecosystem responses to increasing and decreasing pressure. (Redrawn from Duarte et al. 2009)

Full size image

One major problem in analyzing observations of pressure versus response and identifying the most appropriate relationship is that Fig. 12.1 displays a steady-state relationship, whereas observations do not necessarily represent a steady-state situation. The steady state can be assessed when all pressures and other perturbations remain at a constant level for over a sufficiently long time for the ecosystem variables to stabilize. However, ecosystem dynamics are often associated with lags and memory effects having a time scale exceeding that of the sampling. Essentially, this implies that it can be difficult to distinguish hysteresis and shifting baselines from the dynamic output of a linear system. To exemplify this, responses of four linear dynamical systems are shown for an increasing followed by decreasing input (Fig. 12.2). If there are no accumulating effects, the dynamical response to an increasing/decreasing input equals the steady-state solution (Fig. 12.2a), but there can be a delay (delayed exponential response) if the ecosystem variable linearly depends on the input as well as previous states of the response (Fig. 12.2b). Lagged responses or simple delays (i.e., the ecosystem variable depends on past and not present values of the input variable) also give rise to delays, albeit less smooth, in the response (Fig. 12.2c). Finally, a linear dynamical system combining lag and memory effects can display almost hysteresis-like behavior (Fig. 12.2d). Thus, the example illustrates that separating nonlinear dynamics leading to hysteresis and alternative stable states from linear dynamical systems can indeed be difficult.

Fig. 12.2
figure 2

Linear system responses to increasing and decreasing driver. a Direct response or simple gain, b memory effect (response equals 90 % weight on previous state and 10 % on driver), c lagged response to the driver, and d combination of memory effect and lagged response

Full size image

Methods for Identifying Pressure-Response Relationships

The theory for identification of linear dynamical systems is well described and involves estimating the impulse response function from which the structure of the transfer function can be inferred and subsequently estimated (Box and Jenkins 1976). These standard-identification procedures are applicable only to input-output relationships (open loop) and should not be employed when there is feedback in the system (closed loop) (see e.g., Chatfield 1984 for discussion). However, I will refer to the literature for more details on identification of linear systems.

The framework for nonlinear model selection is less rigorous than for linear models, and essentially boils down to formulating a number of candidate models that are subsequently compared by various goodness-of-fit criteria. Two of the most common are Akaike’s Information Criterion (AIC) (Akaike 1974) and Bayes Information Criterion (BIC) (Schwarz 1978) that combine the maximum likelihood with a penalty for the number of parameters in the model. Application of these criteria may lead to different optimal models and they should be used only as a guideline in the model selection process. Hence, nonlinear modeling involves a large degree of subjectivity in the formulation of alternative models, and for ecosystem modeling this implies careful consideration of the mechanisms underlying the observations. It should also be stressed that the use of information criteria selects for the best-fitting model, but it does not provide a formal testing to determine if one model is significantly better than another.

The above-mentioned methods for identification of linear systems and selection of the most appropriate nonlinear model underlie the assumption that the observations can be described by a parametric distribution and that the residuals are independent. This also implies that the residuals should be uncorrelated with time. Many ecosystem studies have suggested that pressure-response relationships are changing with time (see above), but few have provided statistical inference to support these conclusions (e.g., Hagy et al. 2004; Conley et al. 2009a; Carstensen and Weydmann 2012). There are many model diagnosis tools available to test the assumptions of proposed regression models (e.g., cross-validation, autocorrelation, correlation with time, Portmanteau lack-of-fit), but I will focus on examining the time trajectory of the ecosystem response to the pressure and provide a test for the significance of departures from a proposed uniform relationship using the statistical framework of Generalized Additive Models (GAM) (Hastie and Tibshirani 1990).

Let us assume that there is a uniform relationship between the pressure (x) and the response given by the parametric function denoted f(x). Let us also assume that we can describe potential departures from this relationship with a smooth nonparametric function of time, denoted s(t). Consequently, we are interested in testing if the combination of f(x) and s(t) gives a significantly better description of the response variable than just f(x) alone. This can be formalized such as: Given there are n pairs of observations for the pressure and response variables (x i , y i ; i = 1…n), where y i belongs to the exponential family of distributions (e.g., Normal, Binomial, Poisson, Gamma) with location parameter (µ) that is linked (through a link function g(µ)) to f(x) and s(t), we can test the null hypothesis

$${\rm{H}}0:g(\mu ) = f(x)$$

versus the alternative

$${\rm{H1}}:g(\mu ) = f(x) + s(t).$$

Both the parametric (f(x)) and the nonparametric (s(t)) functions are estimated by means of the backfitting algorithm (see Hastie and Tibshirani 1990) that iteratively finds an optimal fit for both functions. The significance of the alternative hypothesis is tested by calculating the log ratio of the two models’ maximum likelihood values (likelihood ratio test), which is approximately χ 2 (df)-distributed with df equal to the approximate degrees of freedom of the smoothing function s(t). The likelihood ratio test applies only because the model under H0 is a submodel of the full model (H1). A simple example of the test above is a normal distributed response with f(x) being linear and the identity function used as link function, i.e., g(µ) = µ (Fig. 12.3). The pressure-response relationship appears linear when the time dependency of the observations is disregarded (Fig. 12.3a), but if observations are connected to constitute a time trajectory a slightly more complicated relationship emerges (Fig. 12.3b). Thus, the test formulated above examines if the likelihood of the alternative hypothesis is larger than the likelihood of the null hypothesis with sufficient confidence.

Fig. 12.3
figure 3

Illustration of the linear model hypothesis (a) versus the time trajectory hypothesis (b). Observations were simulated from the trajectory model in (b) with a relatively small noise added. To illustrate the time dependency of the alternative hypothesis observations were connected in time (b)

Full size image

The smoothness of s(t) is governed by df with lower degrees of freedom leading to rather smooth fit, whereas higher degrees of freedom result in wiggly curves. GAM normally offers to estimate the optimal degrees of freedom by cross-validation, and this is the recommended setting. However, occasionally GAM does overfit the data using cross-validation and this is reflected in high degrees of freedom in the smoothing function. Thus, if the degrees of freedom gets high (> 4 as a rule of thumb) it is recommended to constrain the degrees of freedom to a maximum of four.

The trajectory of the pressure-response relationship can be graphically shown by predicting the response variable as function of f(x) and s(t). This will produce a smooth trajectory, provided that the pressure is a smooth function of time (continuously increasing/decreasing). If the trend in the pressure variable is noisy, in the sense that there are temporal fluctuations in addition to the overall trend, the resulting trajectory based on predictions from a fluctuating input will result in less smooth trajectory. Consequently, for displaying the trajectory it can be recommended to smooth the pressure-input variable first and subsequently use the smoothed pressure time series for predicting (scoring) responses. The trajectory analysis will be exemplified in the following with a simulation example and by means of observations from four coastal ecosystems.

Noise Contamination Simulation

The noise added to the trajectory model for illustrating the difference between the two hypotheses in the previous section was small and the trajectory of the pressure-response relationship was still apparent from the observations (Fig. 12.3b). In such cases the observations themselves convincingly demonstrate a departure from the simple linear model. This is not necessarily the case if more noise is added to the relationship. To investigate the behavior of the method with more noisy data I have considered the following alternative situations: (1) the underlying relationship between pressure and response is linear versus time trajectory, (2) the pressure is increasing and decreasing linearly without versus with random variation (e.g., interannual variation), and (3) observations of the response variable are noisy versus observations of both pressure and response variables are noisy. These eight combinations were analyzed for different magnitudes of random variation. For this purpose I used the normal distribution for simulating random variates and defined a noise ratio as the standard error of the random variation divided by the range of variation in the pressure and response variables. Moreover, as many simulations and estimations were carried out without user intervention the risk of overfitting GAM was tackled by fixing the degrees of freedom of the GAM to four. However, it is important to stress that the idea was not to perform a complete power analysis to decipher when the method successfully identifies an existing trajectory for various combinations of random variation and number of observations.

One might expect that the GAM would be significant only for the four cases based on an underlying trajectory model, but two out of the four simulated examples with an underlying linear model also had a significant trajectory (Fig. 12.4c, g). At first glance this might seem surprising; however, both examples had observational noise on the observed values of the pressure variable, whereas the two other examples, with an underlying linear model and observation noise in the response variable only, did not result in significant departures from linearity (Fig. 12.4a, e). An explanation is that ordinary regression methods do not account for uncertainty in the independent (or explanatory) variable, so observation noise may lead to significant departures from linearity by sheer coincidence. Secondly, it should be noticed that the linear model in Fig. 12.4c is not significant (regressions slope not different from zero) and the linear slope in Fig. 12.4g is significant, albeit with less confidence than Fig. 12.4a, e. Moreover, the method also failed to identify the linear part of the trajectory with observation noise on both pressure and response (Fig. 12.4d) and the estimated linear component in Fig. 12.4h had a slope substantially lower than the linear part of the simulated trajectory (slope = 1). In fact, all the simulations with observational noise on the pressure resulted in slope estimates significantly lower than 1 (P < 0.0001 in Fig. 12.4c, d, g, and h, assessed by t-tests of the parameter estimates), whereas the simulations without observational noise all had slopes not significantly different from 1 (P > 0.1 in Fig. 12.4a, c, e, g). These results show that the nonparametric smooth curve is actually capable of explaining the linear relationship with the pressure variable as part of the smooth trend, and that the GAM to some extent render the linear model insignificant, when observation noise is added to the pressure variable, whereas this does not seem to be the case when there is no observation noise on the pressure.

Fig. 12.4
figure 4figure 4

Simulated observations from a linear (left panel) and trajectory (right panel) pressure-response relationship. a and b have observation noise on the response variable only. c and d have observation noise on both pressure and response variables. e and f have observation noise on the response variable and random variation added to the increasing and decreasing pressure trend. g and h have observation noise on the response variable and both random variation and observation noise on the pressure variable. The underlying linear model and the linear component of the trajectory had slopes equal to 1 and no intercept. The smooth component was simulated with a sine function of time. Noise ratio was set to 10 %

Full size image

The results exemplified in Fig. 12.4 did not represent a single isolated case but were confirmed by numerous simulations. For each of the eight different combinations in Fig. 12.4, the probability of finding a significant time trajectory was estimated as the proportion of 10,000 replications having a significant time component (s(t)) in the GAM. The linear model with observation noise only (Fig. 12.4a) had about 10–11 % probability for a significant time trajectory, whereas the linear model that also included random variation in the pressure (Fig. 12.4e) had about 17–19 % probability for a significant time trajectory (Table 12.1). These probabilities did not decrease with increasing noise ratio, as was the case for all the other models. Both the linear model and the trajectory model with observation noise on both pressure and response (Fig. 12.4c, d) generally gave higher probabilities for a significant time trajectory than the other linear and trajectory models (Table 12.1). The probabilities for identifying a time trajectory decreased the most with the noise ratio for the models that included the most uncertainty components, i.e., observation noise on both pressure and response and random variation in pressure (Fig. 12.4g, h). Overall, there was a high probability for finding a significant time trajectory, when present, for noise ratios up to 60 %, yielding a power of approximately 80 % (Table 12.1). Even when the noise approached the range of variation in the data (noise ratio ~1) there was still a considerable probability (> 40 %) for identifying a significant time trajectory, when present (Table 12.1).

Table 12.1 Probability of identifying a significant time trajectory (GAM) for the eight simulation models exemplified in Fig. 12.4 (cf. letters in first column)
Full size table

Coastal Ecosystem Recovery Example

Duarte et al. (2009) brought the concept of regime shifts and shifting baselines from theory to practice by showing that these phenomenas actually take place and should be considered in ecosystem management . Four coastal ecosystems with long-term monitoring data, all having experienced increasing nutrient inputs in the 1970s and 1980s followed by decreasing nutrient inputs during the last two decades, demonstrated idiosyncratic trajectories of phytoplankton biomass versus nutrient inputs. In all these systems, nutrient inputs approximately doubled from the 1970s to the 1980s and then returned to the level of the 1970s. It was anticipated that the management measures to reduce nutrient inputs would return the ecosystems to their original status, i.e., phytoplankton biomass levels similar to that observed in the 1970s. However, in all four systems, recent phytoplankton biomass concentrations were almost double that of the 1970s despite similar levels of nutrient inputs. The trajectories in Duarte et al. (2009) were computed as 5-year moving averages on both nutrient inputs and phytoplankton annual means to reduce the variation in the data. Thus, although the trajectories in Duarte et al. (2009) graphically displayed departures from an anticipated linear relationship (based on the eutrophication concept originally developed for lakes, see Vollenweider 1968; Dillon and Rigler 1974), there was no statistical evidence of this. Therefore, I reanalyzed these data to examine if the time trajectories were significantly different from a linear pressure-response relationship.

All four coastal ecosystems had considerable variation in both pressure and response variables, without any visually discernible pressure-response relationship from the annual means (Fig. 12.5). None of the four systems actually had a distinctive linear response to changing nutrient inputs (null hypothesis), although the Helgoland and Gulf of Riga data (Fig. 12.5b, d) were borderline significant with P values close to the standard significance level of 5 % (Table 12.2). For the Marsdiep data the chlorophyll yield to increasing nutrient input was still positive under H0, albeit nonsignificant (Fig. 12.5a), and the Odense Fjord data actually gave rise to a weak negative linear relationship (Fig. 12.5c). In fact, testing for a linear model only in these four systems would suggest that there is no relationship between phytoplankton biomass and nutrient input, a result that is in contrast to our general conceptual understanding of coastal ecosystem behavior. Such analyses, based on the assumption of a time-invariant relationship between nutrient input and phytoplankton biomass, could potentially lead to erroneous conclusions for nutrient management in the coastal watersheds. The lack of explanatory power under the null hypothesis was also seen in low R2-values (< 22 %, Table 12.2).

Fig. 12.5
figure 5

Reanalysis of trajectories from Duarte et al. (2009) using the GAM method presented here. For comparison the linear model under the null hypothesis is also given. The sample trajectories represent four intensively studied Northern European coastal ecosystems that experienced significant eutrophication followed by oligotrophication. The full black symbols show the annual average values and the red line shows the smooth trajectory developed here. Initial and final years of the time series are indicated. Inserts show the time series and smooth GAM trend of total nitrogen inputs to the ecosystems. Note the difference in scaling across ecosystems

Full size image
Table 12.2 Statistics for the null hypothesis (H0: linear pressure-response model) versus the alternative hypothesis. H1: linear pressure-response model and smooth time departure for the four coastal ecosystem exemplifying the method. For the linear models (both H0 and H1) the parametric regression line (f(x)) and the probability for zero slope are given. For the nonparametric time smoother (s(t)) the degrees of freedom (d.f.) for the smoother and its significance are given. Coefficients of determination were calculated from the model deviance
Full size table

The alternative hypothesis, including both a linear pressure-response model and a smooth time trend, explained considerably more variation in data (R2~50–65 %) but the linear component did not change much from that of the null hypothesis (Table 12.2). Thus, the smooth time trend accounted for most of the explained variation, and the P values associated with s(t) indicated a high significance. The smooth trend was selected by general cross-validation for the Marsdiep and Gulf of Riga data, whereas the degrees of freedom for the smoother were constrained to be less than four for Helgoland and Odense Fjord data. The general cross-validation method resulted in degrees of freedom equal to 9.11 and 6.54 for these two ecosystems , respectively, and therefore, the wiggliness of the smoother had to be constrained. The estimated time trajectories (Fig. 12.5) generally showed the same behavior as those found by moving averages in Duarte et al. (2009), although considerably smoother, and the statistics confirmed that there was indeed a significant departure from the simple linear pressure-response relationship across time (Table 12.2). Thus, the method delivered statistical inference to further support the theory of shifting baselines and regime shifts in coastal-ecosystem responses to nutrient input.

Discussion

Observations from ecosystem monitoring can be quite variable, often spanning several orders of magnitude, resulting in a cloud of scattered observations as the basis for identifying relationships between drivers and responses (e.g., Guildford and Hecky 2000; Ptacnik et al. 2008). The implication of the large data scatter is that many observations are required to identify potential relationships and that the true nature of the relationship is not visible. Today, many ecosystem monitoring programs have been in operation for several decades, thereby alleviating the data requirements for identifying relationships in the presence of noisy data. Despite the substantial source of information that large data sets typically offer, most studies analyze for simple and static relationships only, despite the availability of a large toolbox of statistical methods to gain further insight into the data (Andersen et al. 2009). The trajectory analysis in this study presents a specific application of the wide class of GAM, specifically designed to identify significant time departures from a proposed static relationship in data. As such, the approach does not present a novel statistical development but it documents the usefulness of analyzing time series by means of GAM to test the implicit assumption of time invariance underlying most pressure-response relationship in the literature. Therefore, this study fulfills the intended goal of providing scientists, that are less experienced with the wide variety of statistical methods, a standard approach for exploring structures in their data that may potentially lead to further model development beyond the most common and simple relationships.

The trajectory analysis provides both a general exploratory tool to uncover changes in pressure-response relationships that may not be visible from plotting the data, and a model diagnosis tool. If there are significant time departures from a proposed parametric relationship then clearly the assumption of independence across the residuals is violated and the estimated parametric relationship will be biased. Secondly, systematic deviations may give hints to refining the parametric relationship or extending the parametric component by including additional explanatory variables. For instance, plotting the smooth trend component (s(t)) against various explanatory factors may identify other pressures potentially affecting the ecosystem , and subsequently include these as part of the functional relationship (f(x)) and reassess if significant time departures are still present. Hence, the trajectory analysis becomes part of a model identification framework. Essentially, such an iterative process can continue until there are no more suggestions for model improvements and/or there are no more systematic time departures from the relationship. This identification framework may also include process-based models, although there are limitations to the number of parameters that can be identified based on statistical principles. For example, the smooth trend component for the four coastal ecosystems (Fig. 12.5) could be plotted against temperature or grazing pressure to develop an improved functional description of phytoplankton biomass responses to multiple pressures. In fact, Jurgensone et al. (2011) showed that the increasing phytoplankton biomass in the Gulf of Riga could be attributed to declines in zooplankton biomass.

The potential confounding of combined lag and memory effects with the smooth trend component was not considered for the four coastal ecosystems above, although these effects could mimic, to some extent, the observed trajectories (cf. Figs. 12.3 and 12.5). Here, model intuition should also play an important role, because phytoplankton regeneration times and the residence times are substantially shorter than the time resolution of the observations (annual values) for all systems. Although internal inputs of nutrient regenerated from sedimenting organic material could have responses on the interannual scale, the processes involved are more subtle and functional relationships to describe these would go beyond the scope of introducing the trajectory-analysis approach. However, it will be important to consider lag and memory effects for other types of ecosystem responses to recovery efforts, particularly those involving long-lived organisms (Jones and Schmitz 2009).

Another issue of confounding effects was revealed in the simulation study , where the smooth trend was also capable of explaining the underlying simulated linear relationship when observational noise was added to the pressure variable (Fig. 12.4c, d, g, h), whereas both the functional relationship and the smooth time trajectory were nicely separated when the pressure variable had no observational noise (Fig. 12.4a, b, e, f). These tendencies were further confirmed from the multiple simulations with different noise ratios (Table 12.1). Thus, the GAM is sufficiently flexible to overrule an existing functional relationship when the exact value of the pressure variable is not known. The simulations indicated that this phenomenon is pronounced only for noise ratios above 10 % on the pressure variable. Most pressure variables are relatively well determined compared to the ecosystem response . Emission estimates for various substances may have noise ratios below 10 % and climate effects, such as temperature increases, can be measured with high precision and consequently, the noise on pressure variables associated with climate change is likely considerably less than 10 %. Thus, for most pressure-response relationships the noise on the pressure variable is such that the underlying relationship can be separated from the smooth trend.

The trajectory analysis assumes separability of the functional relationship and the smooth time trajectory (additive factors under H1), but it could be argued that time interacts with the functional relationship such that the functional shape changes with time. Such models can also be analyzed within the GAM framework using thin plate splines. However, for the principle of parsimony such an avenue of analysis should be pursued only, if the separability assumption is first invalidated. The good thing about separability is that the significance of the functional relationship and smooth time trend can be tested separately, which is not the case with a thin plate spline. Furthermore, there can be an increased risk of overfitting data with a thin plate spline, which requires a less heuristic constraining of the degrees of freedom, compared to an additive form of the functional relationship and smooth time trend.

In summary, the trajectory analysis is a general exploratory tool that identifies time departures in a proposed functional relationship. It can be used in an iterative manner for model diagnosis and development. However, it should be stressed that there are many other tools that have similar objectives, and that all these tools should be used for guidance rather than providing a rigorous modeling framework.