Abstract
Formal and computational models within the effectively unpaired electron (EUE) theory are reviewed and extended. In the first part, we analyze open-ended aspects of the existing EUE measures and find additional advantages of the Head-Gordon index (2003) over the very first (Yamaguchi et al. 1978) index. In particular, for ground states the Head-Gordon index estimates an average occupation of virtual holes and particles, which occur due to electron correlation. Additional hole-particle indices for describing EUE are proposed and analyzed. The second part of the paper is focuses on practical aspects and EUE computational schemes in small molecules (at the ab initio level) and large-scale polyaromatic and graphene-like structures (at the semi-empirical level). Here the unrestricted Hartree-Fock (UHF) schemes and their recently proposed simplistic versions turn out to be a suitable tool producing meaningful EUE characteristics for the extended π-electron systems (with number of carbon atoms ~103 and more) in a fast and simple way. We emphasize that UHF solutions should be regarded not as invalid spin-contaminated states but as precursors of the appropriate spin-projected states of the Lowdin’s extended Hartree-Fock type. The influence of the static and variable electric fields on π-electron systems is also studied. It is shown that strong perturbations drastically increase the electron unpairing in aromatic hydrocarbons, especially those with the initially stable Clar-type structure.
Dedicated to Late Prof. O.V. Shishkin.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
6.1 Introduction
The notion of effectively unpaired electrons (EUE) in molecules originates from the seminal paper of Yamaguchi and colleague [1]. The EUE analysis of wave functions has become a very useful tool for understanding electronic structure of complex in particular, conjugated molecules. In case of singlet states all the approaches to EUE are inevitably rooted in high-level many-electron theories because no unpaired electrons are possible in a one-electron picture of closed-shell systems. Indeed, by construction, each electron pair (with opposite spins) occupies exactly one suitable MO, as prescribed by any correct independent-particle model. Hence, only bona fide wave functions accounting for electron correlation should be employed for treating EUE. This makes the problem interesting and difficult simultaneously.
It should be also emphasized that there exist no spin density effects in spin-singlet (diamagnetic) molecules if relativistic effects are neglected (see Eqs. (5.2) and (5.3) in Ref. [2]). Hence, “effectively unpaired electrons” (as in the dissociated hydrogen molecule or in radical pairs) remain, as a whole, in the singlet state due to the total spin conservation law. This fact indicates some type of spin correlation between particles, particularly between spatially separated ones, as it is in the classical Einstein-Podolsky-Rosen pair [3, 4]. At the same time, systems with large unpairing effects behave as singlet diradicaloids or even polyradicals which feature many unusual properties. The problem is significant because a considerable occurrence of the effectively unpaired electrons is an instability factor of the system of interest. In particular, an EUE analysis of wave functions can easily point to a diradical or, generally, polyradical character of electronic states. In this respect, the EUE problem is also important for designing new molecular-based materials containing giant molecules. A separate issue is electron unpairing in excited states, which has attracted attention only recently.
There exist various quantum chemical approaches to define and quantify “odd” electrons (this very term is used in [1] for effectively unpaired electrons). Obviously, it is important to rightly choose the scheme describing EUE. Two key approaches are now popular in this field. The first employs the so-called Yamaguchi index from [1]; the other uses the Head-Gordon indices from [5]. A noteworthy progress was recently made in ab initio applications of the EUE theory [6–11]. And yet, high-level electron correlation methods are very computationally demanding or, more frequently, not available for large-scale and super-large-scale systems. Therefore, it was important to develop a simplified semi-empirical, but at the same time physically meaningful EUE theory for huge systems such as \( \pi \)-electron-containing graphene-like structures and finite-sized carbon nanotubes. Preliminary attempts in this direction were made in [12, 13]. It is worth mentioning some interesting results produced for giant graphene molecules obtained by the density functional theory (DFT) [14]. At the same time, in practice standard DFT approaches typically fail to produce correctly formed density matrices, which presents a stumbling block for the consistent analysis of molecular electronic structures.
In light of the above, the goal of the present contribution is to describe main trends in this field and to give a comparable analysis of different approaches as well as to demonstrate the utility of the EUE indices for interpreting complex structures—up to covalent polymeric networks. In our applications of the EUE theory the stress will be on strongly correlated molecular states, in particular large \( \pi \)-conjugated systems. Here, we revisit the EUE problem in the context of previous studies [12, 15, 16], and find the Head-Gordon index to be more appropriate and more consistent from a physical viewpoint as well. We also describe new applications of EUE indices for molecules in strong static and nonstationary electric fields. We aim to provide a self-contained introduction to and a concise overview of the EUE theory.
6.2 General Definitions and Yamaguchi’s Index
We start with paper [1]. This work had put forward a first possible definition of the EUE density for an arbitrary wave function with any permitted spin value \( s \ge 0 \). As mentioned in the introduction, our main interest is the case of singlet states, and for them the EUE effects are really important and interesting. Indeed, for nonzero spin states (doublet-state radicals, triplet-state diradicals etc.), the manifestations of unpaired electrons can be described even within the restricted open-shell Hartree-Fock (ROHF) theory. The latter characterizes the unpaired spins by standard spin density matrices. In the singlet state, the spin density matrix disappears [2], and yet, electron correlation enforces electrons to be unpaired if physical and chemical circumstances require it (e.g., in bond breaking processes).
First, we provide the main EUE definitions using the conventional reduced density matrix (RDM) methods. In singlet states, the first-order RDM (1-RDM) can be defined as a spin-free matrix which is also termed the charge density matrix. Throughout the paper, the capital letter D will be denoted the charge density matrix. In Dirac’s bra-ket notation, D conveniently takes a compact form of a spectral resolution, that is the following diagonal form:
with \( \left| {\varphi_{k} } \right\rangle \) being the eigenvectors (natural orbitals), and \( \lambda_{k} ( \ge 0) \) being the respective eigenvalues. The quantities \( \lambda_{k} \) are usually called natural orbital occupancy numbers (NOON). Due to Pauli’s principle, \( 0 \le \lambda_{k} \le 2 \). Furthermore, NOON are usually normalized to a total (always even in our case) number of electrons, \( N = 2n \), where n is a number of electron pairs in the given spin-singlet molecule. Thus,
If unpaired electrons are absent then all molecular orbitals are doubly occupied. Obviously, for the fully closed-shell system the all nonzero NOON are equal to 2:
(pair orbital occupancies), other \( \lambda_{k > n} = 0 \). In this case one deals actually with the customary independent-particle model, more exactly, the restricted Hartree-Fock (RHF) approach. The RHF density matrix is denoted as \( D_{0} \). Explicitly,
The structure (6.4) is certainly changed under the influence of electron correlation. So, expression (6.1) with a more involved NOON spectrum \( \{ \lambda_{k} \} \) is generally valid, and a deviation of a realistic NOON distribution from Eq. (6.3) properly characterizes EUE. In [1] this simple reasoning was the underlying rationale for introducing the EUE notion and the corresponding deviation measure.
Proceeding in a more formal fashion, we introduce the EUE density matrix, \( D^{\text{eff}} \), as a function of density matrix D (in the operatorial sense). It means that
and the new, also nonnegative, ‘occupation numbers’ \( \lambda_{k}^{\text{eff}} \) are generated by a certain function of the initial NOON spectrum, that is
(see [5]). The total EUE number, or better still, the EUE index, \( N_{\text{eff}}\), can be identified with a sum of these \( \lambda_{k}^{\text{eff}} \):
For singlet states, the natural requirement is \( f(\lambda_{k} ) \equiv 0 \) for any one-determinant wave function satisfying Eq. (6.3). In this case \( \lambda_{k}^{2} = 2\lambda_{k}^{{}} \), and this can be condensed into the matrix identity
(the duodempotency relation). Thus, function \( f(\lambda ) = 2\lambda - \lambda^{2} \) provides an admissible choice for a function which vanishes in the case of singlet state determinants. This leads to the simplest solution of the EUE problem: \( \lambda_{k}^{\text{eff}} = \lambda_{k}^{\text{odd}} \) where
Here and elsewhere superscript and subscript ‘odd’ denote that the Yamaguchi index and related quantities are considered. As a result, the matrix representation of Eq. (6.5) takesthe form
and we can easily specify Eq. (6.6) as
The above approach gained more attention after this method was restated in [17] (see also [18] about the history of \( N_{\text{odd}}^{{}} \) and related measures in earlier literature on valency). We now understand that for singlet states, Yamaguchi’s index \( N_{\text{odd}}^{{}} \) is merely a possible measure of the wave function departure from a single determinant. In a different context, a closely related nonidempotency measure of 1-RDM was independently introduced in Mestechkin’s book [19]. Furthermore, \( N_{\text{odd}}^{{}} \) was examined, carefully analyzed and extended in many later works, such as [6, 20–24].
Let us now give a simple example of using \( N_{\text{odd}}^{{}} \). Following mainly [1, 5, 12], we consider the unrestricted Hartree-Fock (UHF) method for singlet states. In this case Eqs. (6.8) and (6.9) can be easily rewritten, based on the known UHF relation
where \( \rho_{\alpha } \) and \( \rho_{\beta } \) are usual one-electron density matrices for α - и β-shells of the UHF determinant. Then, the working equation is
that is equivalent to
as a result of idempotency relations \( \rho_{\alpha } = (\rho_{\alpha } )^{2} \) and \( \rho_{\beta } = (\rho_{\beta } )^{2} \). The equivalent representation is
where \( \left\| Z \right\| = ({\text{Tr }}Z^{ + } Z)^{1/2} \) is the familiar Euclidean (Frobenius) matrix norm for an arbitrary matrix Z. When \( \rho_{\beta } = \rho_{\alpha } \) (no spin polarization ) we return to RHF, and \( N_{\text{odd}}^{{}} = 0 \), as it should be. Another form of Eq. (6.11) is
with \( \left\langle {{\mathbf{S}}^{2} } \right\rangle \) being an average value of the squared spin [18].
6.3 Head-Gordon’s Index
In spite of many useful applications of Yamaguchi’s index, it fails in many cases. It was first shown in [5] where one interesting example (dissociation of the triplet oxygen molecule) was considered, and an incorrect behavior of \( N_{\text{odd}}^{{}} \) was observed for the dissociation limit. In this work a new approach was formulated in such a way that could handle difficult cases as well. We will further refer to the EUE index from [5] as the Head-Gordon index, and use the more compact term “H-G index”, denoting it simply by \( N_{\text{eff}}^{{}} \). This index is based on the following choice:
so that
By construction, the index satisfies the inequality
(see Fig. 1 in [5]). The inequality is rather easy to demonstrate by considering the UHF model. Using the corresponding spectrum \( \{ \lambda_{k} \} \) from [25] an explicit expression is derived to be
where \( \lambda_{j}^{\alpha \beta } \) are eigenvalues of \( \rho_{\beta } \rho_{\alpha } \rho_{\beta } \). We see that indeed \( N_{\text{eff}} [{\text{UHF}}] \le N_{\text{odd}}^{{}} [{\text{UHF}}] \) because eigenvalues of the product of idempotent matrices are less than 1, and moreover, in the same notation we have from Eq. (6.12)
There are many researchers who exploit H-G index (e.g., see [6–12, 26, 27]). In several papers, indices \( N_{\text{odd}}^{{}} \) and \( N_{\text{eff}} \) are considered concurrently, and only few authors advocate a preference of \( N_{\text{odd}}^{{}} \). Notice the polemic papers [28, 29] which present conficting viewpoints on the EUE problem. We will discuss a difference between \( N_{\text{odd}}^{{}} \) and \( N_{\text{eff}} \) in Sects. 6.5, 6.14, and Appendix C. Based on this consideration it appears that \( N_{\text{eff}} \) provides a more consistent way to quantify the diradical (or polyradical) character in terms of traditional NOON. It is worth mentioning the earlier works [30] where NOON have been applied for a qualitative identification of diradical states and diagnostics of multiconfigurational character.
Let us review some common properties of the \( N_{\text{odd}}^{{}} \) and \( N_{\text{eff}} \) measures and the corresponding EUE occupancies, that is numbers \( \lambda_{k}^{\text{odd}} \) in Eq. (6.7′) and \( \lambda_{k}^{\text{eff}} \) in Eq. (6.14). Returning to Eq. (6.5′) we write understandable requirements of the nonnegative EUE function \( f(\lambda ) \) to be defined only in the closed interval [0, 2], so that
Of course, \( N_{\text{odd}}^{{}} \) and \( N_{\text{eff}} \) obey these equations. Less trivial is that \( f(\lambda ) \) is symmetric with respect to axis \( \lambda = 1 \), that is
In other words, Eq. (6.18) is satisfied by an appropriate function \( f(\lambda ) = F(|\lambda - 1|) \). Obviously, \( \lambda_{k}^{\text{odd}} \) and \( \lambda_{k}^{\text{eff}} \) obey the above relations. The reason for symmetry (6.18) will be explained in Appendix A in terms of a duality transformation well-known in the multilinear algebra literature. In Appendix A one can also find a possible generalization of indices \( N_{\text{odd}}^{{}} \) and \( N_{\text{eff}} \). Various examples of \( N_{\text{eff}} \) and related indices will be given throughout the rest of this chapter.
6.4 Unpairing Indices from Collectivity and Entropy Numbers
Another EUE quantification scheme appeared in [15, 31]. This scheme is based on the so-called collectivity numbers first introduced in [32] for describing electronic excitations within the single configuration interaction (CIS) method. More general collectivity numbers were subsequently given in [33] for the full configuration interaction (FCI). The related logarithmic measures are considered in [15, 34, 35]. Below we follow [15] from which a few illustrations (with a slight modification) are taken as well.
The collectivity number can be treated as a statistical measure. A similar statistical measure has been defined before in [36] for analyzing localization of vibrational modes. It was named the participation ratio. We define it as an average rank, \( \kappa \), of the given normalized probability distribution \( \{ w_{k} \} \):
(for more detail see [15, 32, 37]). The squared expansion coefficients can be used as a possible \( \{ w_{k} \} \) set. Generally, the resulting \( \kappa \) will be crucially dependent of the representation chosen (the AO or MO representation, for instance). To make Eq. (6.19) basis-independent, a matrix construction is required. The result is automatically attained within the FCI matrix theory [38] based on the conventional determinant FCI method [39].
For singlet states the FCI wave function \( \left|\Psi \right\rangle \) can be cast as follows:
Here real-valued (for simplicity) expansion coefficients \( X_{IJ} \, \) are normalized, and \( \left| {I;J} \right\rangle \) symbolizes the N-electron Slater determinants comprised of spin-up orbital subset \( \{ \mathop {\chi_{{i_{1} }} }\limits^{ + } , \ldots ,\mathop {\chi_{{i_{n} }} }\limits^{ + } \} \) and spin-down orbital subset \( \{ \bar{\chi }_{{p_{1} }} , \ldots ,\bar{\chi }_{{p_{n} }} \} \). The orbitals are all taken from the chosen “full” basis set
Furthermore, in Eq. (6.20) indices I and J are in fact ordered multi-indices (strings in [39]) of the form
As a consequence of the determinantal nature of the basis set \( \{ \left| {I;J} \right\rangle \} \) used in Eq. (6.20), the matrix
has regular transformation properties, and thus all matrix invariants of X are basis-independent. Moreover, for singlet states X should be a symmetric (\( X_{IJ} \, = X_{J\,I} \, \)) and normalized matrix (due to \( \left\langle {\Psi } \mathrel{\left | {\vphantom {\Psi \Psi }} \right. \kern-0pt} {\Psi } \right\rangle = 1 \)), so that \( \sum\nolimits_{I,J} {(X_{IJ} )^{2} } = {\text{Tr(}}X^{2} ) = 1 \). The eigenvalues \( \{ x_{k} \} \) of X produce a normalized probability distribution, that is \( \{ w_{k} \} = \{ x_{k}^{2} \} \). Thus, the counterpart of Eq. (6.19) for FCI is
This is just the collectivity number which was introduced in [33] and systematically studied in [15]. For single-determinant models we have \( X^{2} = X \). In this case, \( \left| {\Psi \,} \right\rangle \) in Eq. (6.19) can be reduced to one term, that is to a single determinant, so \( \kappa = 1 \). More preferable is a logarithmic quantity which we define by the expression:
We term this quantity as the EUE \( \kappa \)-index, or simply \( \kappa \)-index. As shown in [15, 31], this index provides the needed properties (nonnegativity, additive separability, and clearly interpreted results for simple chemical systems in extreme cases).
Consider two examples. The first is the two-electron hydrogen molecule treated in a minimal basis of two atom-centred orthonormal AOs, {\( \left| {\chi_{1} } \right\rangle \), \( \left| {\chi_{2} } \right\rangle \)}. From the symmetry and normalization we directly obtain matrix \( X \), as follows
with z being a variational parameter. This z has a meaning of a covalency parameter (a weight of the Heitler-London geminal \( \left| {\chi_{1} \,\chi_{2} \, + \chi_{2} \,\chi_{1} } \right\rangle /\sqrt 2 \) in the total wave function). Elementary computations on Eq. (6.22) give
It can be compared with the respective values of \( N_{\text{odd}}^{{}} \) and \( N_{\text{eff}} \) indices:
(they follow from the respective density matrix \( D[{\text{H}}_{2} ] = 2(X[{\text{H}}_{2} ])^{2} \). Notice that there is a misprint for \( \kappa [{\text{H}}_{2} ] \) in [15, 31]. The value \( z = 1/2 \) describes the Hartree-Fock ground state. All indices, Eqs. (6.24) and (6.25), go to 2 when \( z \to 1 \), that corresponds to the dissociation limit of the hydrogen molecule (see Fig. 6.1).
We see from Fig. 6.1 that the \( \kappa \)-index is intermediate between Yamaguchi’s and Head-Gordon’s indices: \( N_{\text{eff}} \le N_{\kappa }^{{}} \le N_{\text{odd}}^{{}} \). As our experience testifies, this is, in fact, the typical result.
As a second more complex example, consider the insertion reaction:
(see [40] for the molecular geometry in the selected 10 points on the reaction path). For reaction (6.26) the results (partially taken from [15]) are presented in Fig. 6.2. Evidently, each of the approaches gives a similar picture with a maximum near a transition region (the fifth and sixth points in Fig. 6.2). A more detailed analysis reveals that the transition state (TS) corresponds, only very approximately, to a diradicaloid state in which unpaired electrons should be significantly localized on the H-atoms. Really, from the NOON spectrum (the right panel in Fig. 6.2) it is clear that there are no NOON near 1. Only the values 1.45 and 0.51 in this spectrum appear to give a quasi open-shell TS structure. The value \( N_{\text{eff}} = 1. 2 6 \) for the fifth point is quite compatible with this situation. At the same time, the diradical character of this TS appears to be overestimated by the corresponding values \( N_{\text{odd}}^{{}} = 1. 9 4 \) and \( N_{\kappa }^{{}} = 1. 7 5 \). The fact that \( N_{\text{odd}}^{{}} \) and \( N_{\kappa }^{{}} \) overestimate the radicaloid character is typical.
Left panel \( N_{\text{odd}}^{{}} \) (in blue), \( N_{\kappa }^{{}} \) (in green), and \( N_{\text{eff}}^{{}} \) (in red) for insertion reaction (6.26) within FCI/6-31G. Right panel the NOON spectrum corresponding to the region near the transition state (for point 5 on the reaction path)
6.5 Hole-Particle Densities and Head-Gordon’s Index
We now look at the EUE problem from the viewpoint of the general theory of hole-particle distributions given in [16]. The related indices (in a different disguise) appeared in [15, 31]. In these works, Kutzelnigg’s original idea [41] about an openness measure of electronic shells was discussed as well. A suitable description of EUE follows from a direct analysis of the RDM hole-particle components [16]. We introduce the latter by considering the general type of wave functions in terms of the so-called excitation operators [39, 42]. They create the CI (configuration interaction) wave-function of arbitrary order, up to FCI. Expansions of this type are well known long ago [43, 44]. But only in [45] the one-electron and two-electron RDMs were presented explicitly in terms of excitation operator matrices, more exactly, elementary transition matrices (see also [16, 46]).
As usual, we must choose an appropriate reference determinant \( \left|\Phi \right\rangle \) from which one can generate singly excited \( \{ \left| {\Phi _{i}^{a} } \right\rangle \} \), doubly excited \( \{ \left| {\Phi _{ij}^{ab} } \right\rangle \} \), and so on configurations (as usually, indices i, j,… refer to occupied orbitals of the reference, and indices a, b,… refer to virtual orbitals). Thus, the k-excited configurations are taken from the set \( \{ \left| {\Phi _{{i_{1} \ldots i_{k} }}^{{a_{1} \ldots a_{k} }} } \right\rangle \} \), and all possible k must be taken into account in an exact (FCI) consideration. Each configuration contributes, to the considered FCI function, with a respective configuration coefficient, \( C_{{a_{1} \ldots a_{k} ;i_{1} \ldots i_{k} }} \), or explicitly
For our formal consideration, the full set
is assumed to be fully known for a while. As usual, it is normalized to 1. Coefficients (6.28) can be packed into the corresponding multi-index matrices
The same quantities (6.28) are identified with hole-particle amplitudes which are just equal to matrix elements of hole-particle excitation operators \( \hat{C}_{k} \, \). By definition, \( \hat{C}_{k} \, \) generates the superposition of k-excited configurations of the corresponding order k (for more detail see [39, 42]). Within the customary hole-particle formalism, the first k indices \( a_{1} \ldots a_{k} \) in \( C_{{a_{1} \ldots a_{k} ;\,i_{1} \ldots i_{k} }} \) are related to states of ‘particles’ which are excited above a ‘sea’ of occupied states, whereas the second k indices \( i_{1} \ldots i_{k} \) (occupied orbitals) are related to the possible hole states in the same sea. This well-known interpretation is also suitable for designing correlation indices. To this end, let us consider the normalization condition which is, evidently,
where obviously
The squared norm \( ||C_{k} ||^{2} \) can be presented in two equivalent forms: as \( ||C_{k} ||^{2} = {\text{Tr }}C_{k} (C_{k} )^{ + } \), and as \( ||C_{k}^{ + } ||^{2} = {\text{Tr (}}C_{k} )^{ + } C_{k} \). Evidently, the first form is relevant to the particles, whereas the second to the holes.
Now look at an average number of holes, that is index \( N^{\text{h}} \) (in notations from [16]):
But the same expression is valid for the average number of particles:
so
Thus, we find the sum
as an admissible hole-particle EUE measure [16, 31]. It remains to add that the reference determinant \( \left|\Phi \right\rangle \) in expansion (6.27) should be built up from natural orbitals of the state in question. But sometimes another choice can be also informative.
No practical difficulties exist in calculating \( N_{\text{h - p}}^{{}} \) because in terms of spin-free RDMs we have the explicit relations
and \( D_{{}}^{\text{h}} \) and \( D_{{}}^{\text{p}} \) are the hole, and, respectively, particle components of D. These components, as defined in [16], are
Here and elsewhere, \( \rho = D_{0} /2 \), that is the spin-free projector on \( n \) maximally occupied natural orbitals of the reference determinant:
(the Dirac-Fock density matrix , in other terms). In the same notations the total hole-particle density matrix is \( D^{\text{hp}} = \, D_{\text{h}} + D_{\text{p}} \), or
Within the given hole-particle approach, \( D^{\text{hp}} \) is a counterpart of the corresponding EUE density matrix (6.5). Technical details for computing FCI and closed-shell CCSD (singles and doubles coupled cluster) approaches are given in [16, 47]. We write here only the simplest relation
following from Eqs. (6.37). The corresponding spectral sum is
It is this quantity from in [15] which was derived based on [41]. More than that, the numerical experience revealed that our hole-particle index (6.39) actually provides the same characterization of EUE, as H-G index does. This fact was recently subject to closer scrutiny [12]. The main inference from the analysis [12] is that the identity
is true for ‘normal’ ground states, which have no pathology in the NOON spectrum \( \{ \lambda_{k} \} \) (see below). This becomes transparent if one considers the spectral representation
The latter follows from Eqs. (6.1) and (6.37), as moment’s inspection of definitions shows it. In the same fashion one can rephrase the matrix \( D^{\text{eff}} \), Eq. (6.5), which is associated with H-G index by Eq. (6.14):
Here \( n' \) is a number of NOONs greater than 1. If \( n' = n \) we have, by definition, the normal state, and then
Otherwise the state in question falls into the category of ‘pathological’ states. In practice, the excited states can be such ones, and in Sect. 6.10 (Table 6.4) we will provide an example of the pathological state.
As usual, the ground state is normal in this categorization. It means that in reality, identities (6.40) and (6.43) are valid even for highly correlated ground states. This fact serves as additional argument in favor of \( N_{\text{eff}}^{{}} \) since a clear physical meaning can be ascribed to this index within the conventional hole-particle picture. Namely, for the normal ground states the \( N_{\text{eff}}^{{}} \) index is the average number of holes and particles which are excited in the reference one-determinant state due to electron correlation. As for molecular excited states themselves, the situation is generally more involved, and will be addressed in Sect. 6.10. Incidentally, from Eq. (6.41) it follows that the hole and, respectively, particle occupancy spectra are of the form
where \( \lambda_{i}^{{}} \) are related to ‘occupied’ natural orbitals (\( \lambda_{i} > 1 \)), and \( \lambda_{a}^{{}} \) to ‘vacant’ natural orbitals (\( \lambda_{a}^{{}} \le 1 \)). A possible generalization of hole-particle EUE measure (6.39) is postponed to Sect. 6.14.
6.6 Using the High-Order Density Matrices
The fact that the EUE theory [1, 5, 15] can be chiefly founded on the one-electron RDM is remarkable per se. However, electron correlation effects are at least two-electron in nature, and it is no wonder that the second-order RDM was applied for quantifying EUE and related electron-correlation properties. Seemingly, the first investigation in this direction was presented in book [19] where in Sect. 6.5 a special operator named ‘correlation operator’ was introduced. Actually, in [19] the two-electron counterpart of \( D^{\text{eff}} \) was examined. In this section we will denote RDMs of order k by \( D_{k}^{\text{so}} \). The superscript ‘so’ shows that the full RDM (in spin-orbital basis) is considered. For instance, \( D_{1}^{\text{so}} \) and \( D_{2}^{\text{so}} \) are the conventional one-electron and two-electron RDMs.
As well known, for the single Slater determinant (SD), that is for independent-particle models, the two-electron RDM is the antisymmetrized product of one-electron RDMs [48, 49]:
where \( P_{12}^{{}} \) represents the full (with spin variables) transposition operator. Following [19], we introduce the correlation operator \( \Delta _{2}^{\text{so}} \) as a difference between the exact two-electron RDM and the SD approximation (6.44):
By contracting \( \varDelta_{2}^{\text{so}} \) over variables of the second electron, we find
that is but a ‘nonidempotency matrix’. This fact was independently discovered later in [21] (the first paper in this reference entry). Really, contracting Eq. (6.46) over spin variables just produces the EUE density matrix \( D^{\text{odd}} \) in Eq. (6.8). We see that using Eq. (6.46) does not provide us a new quantification scheme, not to mentioning that Eq. (6.8) gives not very good approach, as argued previously.
A significant advance has been made in [50] where the completely two-electron measure was introduced. In this work the squared norm of \( \varDelta_{2}^{\text{so}} \), that the quantity \( ||\varDelta_{2}^{\text{so}} ||^{2} \), was proposed as a new correlation and entanglement measure. Admittedly, the EUE aspect was not within the scope of [50]. This aspect is discussed in [35] (among other approaches). An appropriate rescaling, by constant factor 8/7, guarantees a correct number of unpaired electrons in the dissociated H2 molecule and in arbitrary cluster of dissociated two-electron systems. Therefore, it is simply to modify the above-mentioned measure, as follows:
Here subscript ‘cum’ in \( N_{\text{cum}} \) means that this EUE index is produced by the so-called cumulant density matrix (6.45), as such RDM constructions are termed in the current RDM theory [51]. For practical computations, within FCI or RAS-CI (restricted active space CI), more suitable is a spin-free expression from [35].
Some results (the data partially from [35]) are presented in Table 6.1. We see that \( N_{\text{cum}} \) gives the values which are somewhat close to \( N_{\text{eff}}^{{}} \) than other indices. We also observe that all the indices provide a similar qualitative picture. For instance, in a case of the fully dissociated BeH2, we must obtain \( N_{\text{eff}}^{{}} [{\text{Be}} + {\text{H}} + {\text{H}}] = N_{\text{eff}}^{{}} [{\text{Be}}] + 2 \) where \( N_{\text{eff}}^{{}} [{\text{Be}}] \) is a non-zero value which results from the effect of intra-atomic electron correlation in a free Be atom. At the FCI/6-31G level, we obtain \( N_{\text{odd}}^{{}} [{\text{Be}}] \) = 0.74 and \( N_{\text{eff}} [{\text{Be}}] \) = 0.39. Thus, it is expected that for the full dissociation \( N_{\text{odd}}^{{}} \) = 2.74 and \( N_{\text{eff}} \) = 2.39, as it is the case, judging from Table 6.1. We note also that at present using \( N_{\text{cum}}^{{}} \) is rather restricted because a direct handling with 2-RDM is avoided as a rule when treating large scale problems.
6.7 Algorithmic Aspects
Several schemes are possible for practical calculations of the main EUE indices. Frequently, all the elements of D are needed, e.g. for computing \( N_{\text{odd}}^{{}} \) by Eq. (6.9) and \( N_{\text{eff}} \) by Eq. (6.15). In a number of cases we can simply exploit the explicit expressions, as in the case of the rather easily performed UHF-like models. When sophisticated multiconfigurational models are used, it is necessary to employ the technique which is elaborated for obtaining D within the restricted active space CI (RAS-CI) and coupled cluster schemes [39, 42]. However, the direct way is too demanding when large-scale systems need to be addressed. Sometimes, one can employ the RDM-free scheme from [52] that avoids the tedious computations of all matrix elements of D. This scheme (see Eqs. (107) and (111) in [52]) can be applied to the hole-particle quantification scheme described above. The respective technique is based on reverting the obvious relationship which connects expectation values to RDM. Namely, for the given spinless one-particle operator Z we have
Then the \( N_{\text{eff}}^{{}} \) index is simply computed in the equivalent form of \( N_{\text{h - p}}^{{}} \), Eq. (6.38), that is as usual one-electron average (6.48) with
In this case we imply that \( \rho \) is known. This is a case when the Hartree-Fock reference determinant can be approximately used in the EUE analysis. Another case is the Brueckner coupled-cluster method [42] producing the reference molecular orbitals, almost the same as natural orbitals.
Additional indices which can by obtained by using Eq. (6.48) are the hole-particle atomic localization indices \( \{ D_{A}^{\text{eff}} \} \) which are related to \( N_{\text{h - p}}^{{}} \) (in practice, \( N_{\text{eff}}^{{}} \)). They can be defined by the customary partition procedure well known for other atomic indices [53, 54]. Let us introduce projector \( I_{A} \) on atomic orbitals belonging to the given atom (or fragment) A:
Then
where index \( \mu \) numbers the standard orthonormalized AOs. Here the full orthonormalized AO basis is
(dim is a size of the basis set). Hence, performing calculations using Eq. (6.48) with \( Z = I_{A} + \frac{1}{n}({\text{Tr}}\,I_{A} \rho )\,I - I_{A} \,\rho - \rho \,I_{A} \, \) for each atom A, we find the full atomic distribution of the unpaired electrons in molecule. Obviously, the identity
is guaranteed. For computing D and \( \{ D_{A}^{\text{eff}} \} \) in case of the CCSD model one can apply a suitable algorithm which resembles that of the CISD (CI singles and doubles) method (see Appendix in [47]).
6.8 Spin Correlations
In the introduction, we mentioned that the presence of unpaired electrons in singlet states gives indirect evidence in favor of the essential spin correlations between the electrons, especially when they are strongly localized. The following discussion highlights this issue. It is well known from the quantum theory of magnetism that spin correlations can be interpreted consistently by invoking the spin correlator formalism. In quantum chemistry, spin correlators had been introduced by Penny [55]. In the last two decades the interest to them revived (see [35, 56–60] and many others). We follow the notations and techniques from [35, 59].
For the given atoms or molecular subunits A and B, spin correlator \( \left\langle {{\mathbf{S}}_{A} \cdot {\mathbf{S}}_{B} } \right\rangle \) is an average of the form
where the local spin operator \( {\mathbf{S}}_{A} \) can be taken as follows: \( {\mathbf{S}}_{A} = \sum\limits_{1 \le i \le N} {{\mathbf{s}}(i)} \,I_{A} (i) \). Here \( {\mathbf{s}}(i) \) is the spin operator for the ith electron, and \( I_{A} (i) \) is a local projector (6.49) for the ith electron. The diagonal correlators \( \left\langle {{\mathbf{S}}_{A} \cdot {\mathbf{S}}_{A} } \right\rangle \equiv \left\langle {{\mathbf{S}}_{A}^{2} } \right\rangle \) are usually named the (squared) local spins. The useful identity is
where \( Q_{A} \) is a spin density localized on A, and \( s \) is the total spin value for the state in study [35, 59]. For singlet states, spin densities identically dissappear, so
Obviously, the full sum rule is
When analyzing spin correlators it is also suitable to pack the correlators into the matrix
where subscripts A and B run over all atoms in molecule.
As a simple application of these rules, consider the system divided into two parts (subsystems) A and B. From Eq. (6.55) it follows
Thus, the spin-correlator matrix is of the form
where local correlator \( \left\langle {{\mathbf{S}}_{A}^{2} } \right\rangle \) takes the specific values. If the subsystems A and B are in a singlet state (as in the case of a van der Waals (vdW) dimer of singlet molecules) then the spin-correlator matrix is evidently
Now let A and B be subsystems which we assume to be in a triplet state. Then for a resulting singlet state of the entire system, matrix (6.57) is
This case occurs when we treat the singlet excited states of the vdW dimers and complexes (the so-called triplet-triplet (TT) excitations). The spin-correlator analysis for the vdW dimers was shortly mentioned in [61] where the singlet fission models are discussed. In context of the EUE problems we can connect spin correlators with the \( N_{\text{eff}}^{{}} \) measure of the TT-type excited states. For instance, when no charge transfer effects are involved, the local spins \( \left\langle {{\mathbf{S}}_{A}^{2} } \right\rangle \equiv \left\langle {{\mathbf{S}}_{B}^{2} } \right\rangle \) provide an estimate of a weight of double excitations \( \left| {A_{s = 1}^{*} B_{s = 1}^{*} } \right\rangle \) in the total excited state of dimer AB (see Appendix C in [61]). Then \( N_{\text{eff}}^{{}}\,\approx\,2\left\langle {{\mathbf{S}}_{A}^{2} } \right\rangle \) because the singlet excitation \( \left| {A_{s = 1}^{*} B_{s = 1}^{*} } \right\rangle \) has four unpaired electrons. In more general situation we must take into account interfragment charge-transfer states. It leads to a more complicated analysis which will be given in a forthcoming paper in collaboration with D. Casanova and A. Krylov. Additional aspects of the EUE analysis for excited states are considered in Sect. 6.10.
6.9 Spin-Polarization Indices and Antiferromagnetic Image of Molecule
We briefly considered in Sects. 6.2 and 6.3 how to treat EUE within the UHF approximation which admits to different orbitals for different spin (DODS). For singlet states the UHF scheme is usually called the spin-polarized HF method (then \( \rho_{\alpha } \ne \rho_{\beta } \), unlike RHF where \( \rho_{\alpha } = \rho_{\beta } \)). Here we look at the problem from the more general viewpoint which allow us to introduce relevant spin-polarization indices for any singlet many-electron states [62].
It is well known that for singlet states, the UHF solutions with \( \rho_{\alpha } \ne \rho_{\beta } \) are really possible when electron correlations become sufficiently strong. More exactly, the spin-polarized HF determinant \( \left|\Phi \right\rangle \) appear only under the non-singlet (triplet) instability which was defined by Cizek and Paldus in [63]. At the same time, solutions of the spin-projected variational HF method (the Löwdin’s extended HF scheme) always exist [19]. The wave functions of this type will be signified by \( \left| {\Phi ^{\text{ext}} } \right\rangle \). This is usually defined by (apart from a normalization factor)
with \( O_{s} \) being a projection operator onto a spin-pure N-electron state with the spin z-projection \( s_{z} = s \) and the total spin value \( s \).
In this context, it is pertinent to recall that in many cases one can obtain the so-called best overlap orbitals [64] of DODS type which are produced by the given many-electron wave function. These orbitals were considered in [65] where they were identified with spin-polarized Brueckner orbitals. However, they exist if and only if the so-called nonsinglet Brueckner instability conditions are satisfied. At last, if the correct spin-projected determinant \( \left| {\Phi ^{\text{ext}} } \right\rangle \) is involved in the consideration, then it is always possible to construct the best overlap orbitals of DODS type for the given exact or approximate state vector \( \left|\Psi \right\rangle \). These orbitals were recently introduced [62] and named the spin-polarized extended Brueckner (SPEB) orbitals. By construction, they maximize \( \left\langle {{\,\Phi ^{\text{ext}} }} \mathrel{\left | {\vphantom {{\,\Phi ^{\text{ext}} }\Psi }} \right. \kern-0pt} {\Psi } \right\rangle \).
Typical overlap integrals between \( \left| {\Phi ^{\text{ext}} } \right\rangle \) and \( \left|\Psi \right\rangle \) are found to be around 0.98 even for dissociated covalent molecules [62]. The corresponding EUE measures (6.1) and (6.5) were also studied in [62] along with appropriate spin-polarization indices. The latter are computed for \( \left| {\Phi ^{\text{ext}} } \right\rangle \) from matrices \( \rho_{\alpha } \) and \( \rho_{\beta } \) in another way than in Eqs. (6.11) or (6.17). Following the cited work, let us introduce the intermediate matrices
and define for SPEB the special spin-polarization matrices
Then the indices
and the total spin-polarization index
serve for the spin-up and spin-down characterization of EUE in the singlet states. Additionally, we can introduce the associated EUE α-and β-distributions which are composed of the atomic contributions, viz.,
They are also helpful for the visual interpretation of the ESPB computations. Here, A is a selected atom in molecule, and subscript μμ, as previously in Eq. (6.50), indicates a diagonal element of the matrix in the orthonormal AO basis. The total spin polarization index assigned to atom A is evidently equal to
so that summing \( \Pi _{A} \) over all A reproduces \( N_{\text{pol}} \).
Let us look at Table 6.2 to understand what one can gain from this analysis. In the table, along with the above indices and distributions, we also give coefficient \( C_{\text{nat}} \equiv \left\langle {{\,\Phi ^{0} }} \mathrel{\left | {\vphantom {{\,\Phi ^{0} }\Psi }} \right. \kern-0pt} {\Psi } \right\rangle \) at the reference determinant \( \left| {\Phi ^{0} } \right\rangle \) (the latter is taken as is the closed-shell natural orbital determinant). From Table 6.2 we see that \( \left\langle {{\,\Phi ^{\text{ext}} }} \mathrel{\left | {\vphantom {{\,\Phi ^{\text{ext}} }\Psi }} \right. \kern-0pt} {\Psi } \right\rangle \cong C_{\text{nat}} \) (so that \( C_{\text{nat}} \cong 1 \)) only for normal molecules which are far from quasi-degeneracy (H6, CH2 etc. in the table). In the H8 cluster, due to the frontier orbital degeneracy, the ground state allows no symmetrical closed-shell structure, and it leads to the fact that even \( C_{\text{nat}} \) is not large. At the same time, the SPEB orbitals generate the spin-projected determinant which provides a sufficiently high overlap with the exact wave function. The same is true for dissociative states in Table 6.2. Interestingly, in this table the \( N_{\text{pol}} \) indices turn out, as a rule, to be more close to the \( N_{\text{eff}}^{{}} \) values than to the \( N_{\text{odd}}^{{}} \) ones. The spin–polarization diagrams (two columns in Table 6.2) deserve attention too. From them we see that the spin-up EUE distributions are preferably localized in those parts of molecules where the spin-down EUE distributions are localized poorly, and vice versa. This behaviour outwardly resembles features of the alternant MOs introduced by Löwdin (e.g., see Fig. 3 in [66]). The distinction between the two descriptions is in the fact that the \( \{\Pi _{A}^{\alpha } \} \) and \( \{\Pi _{A}^{\beta } \} \) describe the “spin” localization of EUE, that is purely correlation effects, whereas the spin-up and spin-down orbitals in UHF, EHF etc. correspond to individual one-electron states without specifying correlations per se. In particular, UHF orbitals are always nonzero whereas the spin-polarization indices can disappear (e.g. in ‘one-electron’ limit). It is a matter of no small importance that the SPEB orbitals and corresponding distributions \( \{\Pi _{A}^{\alpha } \} \), \( \{\Pi _{A}^{\beta } \} \) are generated by exact (FCI or RAS-CI) wave functions or high-level many-electron approximations. Opposite to the latter, UHF and EHF frequently provide only a small part of correlation effects for molecules in equilibrium or not too far from it (e.g., see [67]).
Alternatively, the EUE structure (within the SPEB) can be depicted by the special spin-arrow diagrams representing together the \( \{\Pi _{A}^{\alpha } \} \) and \( \{\Pi _{A}^{\beta } \} \) distributions. One may think of such diagrams as giving the antiferromagnetic EUE images of molecules. Some examples are given in Fig. 6.3. Notice that the interpretation of molecular structures in terms of antiferromagnetic coupling has a long history. Implicitly, it was used in the Hartmann work [68]. Usually this terminology is invoked when analyzing \( \pi \)-conjugated polymers and atomic clusters [69–75]. However, the nature of antiferromagnetism for the overall singlet state in molecules is not so simple as in the case of the solid state ferromagnetism [69, 70]. We return to this issue in Sect. 6.11.
6.10 Unpairing in Excited States
The molecular excited states are just those in which the electron unpairing is one of the key points in understanding the nature and properties of the electronic transitions. But only in few works, such as [15, 62, 76–78], the EUE characteristics were explicitly invoked for analyzing excited states. Recall that the simplified approximations are typically based on CIS (CI singles) and TDDFT (time-dependent DFT) models. For singlet excitations the CIS density matrices were first derived by McWeeny [79]. Then they were generalized [80] and extended to RPA (random phase approximation) and TDDFT [81, 82].
The CIS wave function, as a particular case of Eq. (6.27), can be written as follows:
with \( \,\left| {\Phi _{i}^{a} } \right\rangle \) being the singly excited configurations, and \( C_{ai} \) the normalized amplitudes (configurational coefficients). For our purposes we will use the equivalent form of Eq. (6.66) which is based on spinless amplitudes \( \tau_{ai} \), so that
where
are the standard spin-singlet configurations [83]. The charge density matrix for this \( \left| {\Psi ^{\text{CIS}} } \right\rangle \) is
where the spin-free transition matrix \( \tau \) is defined by the formula
and \( \rho \) is the previously defined projector (6.36) on occupied spin-free MOs of the reference determinant (e.g., the RHF determinant). To guarantee the normalization condition \( \left\langle {{\Psi ^{\text{CIS}} }} \mathrel{\left | {\vphantom {{\Psi ^{\text{CIS}} } {\Psi ^{\text{CIS}} }}} \right. \kern-0pt} {{\Psi ^{\text{CIS}} }} \right\rangle = 1 \) we impose the condition \( {\text{Tr}}\tau_{{}}^{ + } \tau = 1 \).
Having at disposal density matrix (6.69) it is easy to perform the hole-particle analysis of the CIS method. In this case, Eqs. (6.40) and (6.43) are valid because the CIS states have no anomalies in the density matrix spectrum. Simple manipulations on Eq. (6.37) lead to
so
for any CIS state [15]. The result is quite natural, and it is in agreement with the standard spin structure of each singlet-spin configuration \( \left| {\varPhi_{i \to a} } \right\rangle \), Eq. (6.68). The same result is obtained for \( \kappa \)-index (6.22): \( N_{eff}^{\kappa } [{\text{CIS}}] = 2 \). On the other hand, computations on Eq. (6.9) give
From this it follows that \( 2 \le N_{\text{odd}}^{{}} [{\text{CIS}}] < 4 \). Thus, we see that again Yamaguchi’s index overestimates the EUE measure even for the discussed (very restricted) CI wave function. More important is the result (6.71). This EUE density matrix exactly coincides with the excitation localization operator, which was first introduced in [84] (see also Eq. (6.5) in [82]). In the notation adopted here this is of the form
Thus, in terms of Eq. (6.5),
We see that within the CIS approximation the excitation localization indices can be additionally treated as the localization indices (6.50) of the unpaired electrons occurring under excitation:
This aspect of the EUE theory for CIS and CIS-like models was briefly outlined in the recent review [76] (in Sect. 14.4). It would be interesting to understand to what extend this holds true for more general models. We provide here only preliminary insight on this rather difficult question.
For the lowest transitions, the CIS and the related TDDFT excitation energies are often found in satisfactory or even good agreement with more refined theoretical estimates. Nevertheless, there are low-lying transitions that cannot be usefully studied in these popular approximations. Among such are the so-called double-excitation transitions for which the excited-state wave function has a significant proportion of a doubly excited configurations. Even sometimes, more efficient methods may fail as in the case presented for the methylene CH2 in [85]. The methylene singlet excited states were also examined in terms of spin-polarization diagrams [62]. Here relevant supplementary results are added (Table 6.3). In the table, along with excitation energies and EUE indices, we present the most important squared norms \( ||C_{k} ||^{2} \) defined by Eq. (6.31). These norms are computed in the basis of the ground-state natural orbitals.
From the table we observe that 1B1 and 1A2 terms are CIS-like states (\( \left\| {C_{1} } \right\|^{2} \cong 1 \), all \( N_{\text{eff}}^{{}} \cong 2 \)). The 2A1, excited state is the doubly excited state (\( \left\| {C_{2} } \right\|^{2} \cong 1 \)), which, however, has almost the same small \( N_{\text{eff}}^{{}} \) value as that of the ground state (see Tables 6.2 and 6.3). Thus, the EUE indices may not reflect the multiconfigurational character of excited states. To elucidate this issue, let us consider the main part of the NOON spectrum for the ground and excited states of CH2 (Table 6.4). In the table we omitted the maximal NOON value 2, which is due to the \( (1s)_{ 2}^{{}} \) frozen core of the carbon atom. Additionally, we included in Table 6.4 the main hole-particle index \( N_{{{\text{h}} - {\text{p}}}} \), Eq. (6.39), and the related index \( N_{{{\text{h}} - {\text{p}}}}^{{({\text{ref}})}} \). The latter was computed by Eq. (6.38) with \( \rho \) taken as the projector on the occupied MO of the reference determinant used in the CI expansion (6.27). Recall that in agreement with definitions (6.32) and (6.33), hole-particle index \( N_{{{\text{h}} - {\text{p}}}}^{{}} \) can serve as a suitable measure for multiconfigurational character in the corresponding CI expansion (6.27). From Table 6.4 it is clear that the 1A1 and 2A1 states are very similar in their NOON spectrum. Only in the case of the 2A1 state its closed-shell nature is combined with the high multiconfigurational character when \( \left\| {C_{2} } \right\|^{2} \cong 1 \) (see Table 6.3). This picture is in accordance with \( \,N_{{{\text{h}} - {\text{p}}}}^{{({\text{ref}})}} \,\,[ 2 {\text{A}}_{ 1} ] \) = 3.997. The example demonstrates a usefulness of the hole-particle indices as supplementary characteristics of excited states. Incidentally, one can observe from Table 6.4 that the 1B1 state of CH2 provides an example of the pathological state (for definition, see Sect. 6.4).
The above outlined peculiarities in using EUE indices for the multiconfigurational states return us to the problem of constructing excitation localization indices for arbitrary excitations. We can proceed in many ways. In the scheme [82, 84] the operator modulus of density matrix difference, \( \varDelta \,D \), is used. Namely, the normalized excitation operator, \( \hat{L}^{ *} \), can be naturally introduced as follows:
where \( D^{ *} \) is the charge density matrix for the excited state of interest, and by definition, \( |\varDelta D|\, = [(\varDelta D)^{2} ]^{1/2} \). Then, as usual, the atomic indices
furnish the excitation localization measure assigned to each atom of the excited molecule. Doing so for CIS-type states (6.67) we automatically produce indices (6.76).
To solve the same problem by another way, take atomic EUE distributions (6.50) and compute the corresponding normalized indices
These indices characterize the excitation localization in its own manner. For CIS-like states the distributions \( \{ L_{A}^{ *} \} \) and \( \{ \mathop {L_{A}^{{*({\text{eff}})}} }\} \) are sufficiently close, as the methylene molecule example shows. In particular, we have
However, for the double excited state the compared results are markedly different:
We conclude that for the depiction of excitation localization, the EUE indices should be used with a certain care.
6.11 Conjugated Hydrocarbons in π-Electron Schemes
In this section we consider computations of the EUE indices for moderate-sized systems within the easily implementable semi-empirical methods. Before doing so, we briefly touch on simplified ab initio approaches to polyaromatic hydrocarbons (PAHs). Many of the ab initio studies are based on various UHF and unrestricted DFT schemes [86–88]. By these schemes, crude estimates of EUE effects can be made even from the \( \left\langle {{\mathbf{S}}^{2} } \right\rangle_{\text{UHF}} \) values. Really, for slightly correlated systems the semi-quantitative relation
holds (e.g., compare with the results of Table 6.2 for equilibrium geometries). As an additional example, take the benzene molecule for which we have (in 6-31G basis set): \( N_{\text{odd}}^{{}} [{\text{UHF}}] \) = 1.101, and \( N_{\text{eff}}^{{}} [{\text{UHF}}] \) = 0.584. Recalling Eq. (6.13), we can expect that the rough estimate
can be utilized for a simplistic description in other moderately correlated systems. Such estimates are easy because the needed data can be routinely obtained by most quantum chemical programs. Besides, in the current literature, the \( \left\langle {{\mathbf{S}}^{2} } \right\rangle^{\text{UHF}} \) data are available for many PAHs (e.g., see [87, 88]).
To be more specific, consider linear polyacenes for which a model geometry will be used here and throughout the paper: the carbon backbone is formed by regular hexagons with the C-C bond length of 1.4 Å and the C-H bond length of 1.09 Å. Using the Gaussian program package [89], we computed \( \left\langle {{\mathbf{S}}^{2} } \right\rangle^{\text{UHF}} \) for the first ten linear polyacenes C4n+2H2n+4 at the UHF/6-31G level. The results are conveniently expressed via the linear regression
with residual variance \( 10^{ - 3} \), thus reflecting a size-consistent behavior of the index.
In the case of large carbon-containing systems it is suitable to compare the EUE index value per carbon atom. For instance, we introduce
where \( N_{\text{c}} \) is a number of carbon atoms (\( N_{\text{c}} \; = \;4n + 2 \) for Eq. (6.82)). For large linear acenes we have from Eq. (6.82)
Likewise, other EUE indices per carbon atom are defined:
Returning to Eqs. (6.81) and (6.83) we suggest a rough estimate,
is reasonable for sufficiently large linear polyacenes treated with the 6-31G basis set.
An interesting point is a measure of the participation of π-electrons in the total unpairing . Our experience with small conjugated systems tells that usually \( \approx 2/3 \) of the average \( D_{\text{C}}^{\text{eff}} \) value is from π-electrons. Together with Eq. (6.85) it gives a crude estimate
This approach is in concordance with the fact that in large conjugated systems, electron correlation largely influences the outer π- electron shells. That is why most physical models of conjugated polymers are based on one or another version of the π-electron approximation (most often in the form of a many-electron Hubbard model, see reviews [69, 90]). Furthermore, previous non-empirical studies [8, 9, 11] in large conjugated molecules (by using DMRG and MR-AQCC) have considered only π-electron contribution to EUE. All this has motivated us to undertake a detailed study [12] of the EUE effects within the conventional π-electron theory. Below we shortly outline the main results of this study.
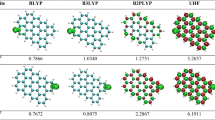
For the selected PAHs, the results are presented in Table 6.5 where in the structural formulas the EUE atomic distributions are displayed in a qualitative manner. All EUE indices (except for \( \overline{{\left\langle {{\mathbf{S}}^{2} } \right\rangle }}^{\text{UHF}} \)) are computed within the hole-particle approach, Eqs. (6.37) and (6.38), which, for ground states, is equivalent to the Head-Gordon approach. Here, the Parizer-Parr-Pople (PPP) π-electron approximation is employed. We see that again the UHF scheme based on Eqs. (6.10) and (6.17) works well (in respect to the CCD results), and this fact was emphasized in [12]. The π-electron UHF scheme (π-UHF) is favorable because of its simplicity of computation, and ease of interpretation. However, this method is not recommended for systems with a relatively small π-electron correlation effects, e.g. in the peropyrene molecule (the third entry in Table 6.5). In the case of too little electron correlation, the half-projected Hartree-Fock (HPHP) [91] and EHF schemes are applicable. We remark that the EHF results in Table 6.5 are sufficiently close to the CCD ones even for the peropyrene and pyranthrene molecules which have modest electron correlation effects. These observations are the basis on which the UHF method, with obligatory use of Eq. (6.17) or more refined indices, can be recommended for studying EUE effects in large graphene-like molecules [12]. The usefulness of this approach shows Table 6.6 containing two examples taken from the cited paper. To the previously defined quantities, Eqs. (6.83) and (6.85), we have included in the table one additional characteristic index, \( \aleph_{{}}^{\text{loc}} \). The index \( \aleph_{{}}^{\text{loc}} \) gives a mean number of atoms (sites) on which the unpaired electrons are preferentially localized. Explicitly,
This equation is a generalization of the participation ratio (6.19) and gives a more sharp estimate for a number of strongly localized atomic centers (sites). The related index was employed in [92] where it is shown that the index can well distinguish between localized and extended states. From Table 6.6 we see that indeed \( \aleph_{{}}^{\text{loc}} \) gives an acceptable average number of the essentially localized unpaired electrons. When using \( \aleph_{{}}^{\text{loc}} \) one must keep in mind that this index is informative if \( \aleph_{{}}^{\text{loc}} \ll N_{\text{c}} \), that is in the case of a sufficiently sharp EUE localization.
Now we remark on the NOON spectrum \( \{ \lambda_{k} \} \) given in the fourth column of Table 6.6. Similar plots are frequently displayed when considering the nature of EUE in large molecules [8, 9, 11–13, 26]. The first system in the table belongs to the so-called periacene family. The earlier theoretical study of this family was given in [93] where a simplified Hubbard-like π-UHF method was applied. In the recent papers [8, 9, 11] the EUE analysis for the periacenes was given at the high-level ab initio level. Here, we can directly compare these reliable ab initio results and ours, thanking to the fact that the needed ab initio data were kindly provided by the authors of [9, 11]. The results are displayed in Fig. 6.4, where the same nomenclature of periacenes, as in [9, 11], is used. Comparing the corresponding plots, we observe their really close similarity. More specifically, the same localization of few NOON in the vicinity of 1 is found in the ab initio as well as the π-electron calculations, and this localization corresponds to a genuine open-shell (polyradical) singlet structure. A general view of the plots is also similar. Moreover, in the (5a, 6z) periacene the EUE atomic localization is comparable (see [12] for detail). On this account, we suggest that the π-electron EUE model, which is based on the simple UHF expression (6.17), should be useful for other large-scale conjugated systems, at least at a qualitative level. The symmetry (exact or approximate) of the NOON in respect to point \( \lambda = 1 \) is also deserve attention. For alternant hydrocarbons within any correct PPP scheme this symmetry is exact, and it is easy to prove (see the last paragraph in Appendix B). The ab initio results [9, 11] approximately fulfil this symmetry which implicitly reflects the physical equivalence of the holes and the particles in alternant π-systems [94] (see again plots in Fig. 6.4).
Comparison of the ab initio [9] (violet color), and semi-empirical (green color) NOON spectra for (5a, nz) periacenes
Notice that the above cited EUE ab initio study was performed for active π-orbitals. Thus, the EUE indices obtained from corresponding NOON spectra, are related to respective π-electron contributions. In case of the periacenes (5a, 4z), (5a, 5z), and (5a, 6z), we find, from the respective NOON spectra, the following ab initio \( \bar{N}_{\text{eff}} [\pi ] \) values: 0.111, 0.108, 0.108, in agreement with rough estimation (6.87). The analogous π-electron PPP data will be given in Sect. 6.14, Table 6.11. They are approximately twice less than the ab initio values. At the same time, if we exploit the so-called Mataga formula for two-electron two-center integrals \( \gamma_{\mu \nu } \) (with a Coulomb-like distance dependence), then we obtain the results closer to the ab initio ones. In particular, for the (5a, 6z) periacene the π-UHF scheme with Mataga’s \( \gamma_{\mu \nu } \) gives \( \bar{N}_{\text{eff}} \) = 0.129. Nevertheless, the standard π-parametrization we use (\( \gamma_{\mu \nu } \) by Ohno’s formula) is more appropriate for π-electron correlation effects, as was established long ago. We also computed index \( \overline{{\left\langle {{\mathbf{S}}^{2} } \right\rangle }}^{\text{UHF}} \) (by using the program package [89]) and get a crude ab initio estimate via Eqs. (6.81) and (6.83). For the (5a, 6z) periacene at the 6-31G level we thus obtained \( \bar{N}_{\text{eff}} [\pi ] \cong 0.09 \) which seems quite reasonable in comparison with the above non-empirical value \( \bar{N}_{\text{eff}} [\pi ] \cong 0.108 \) from [9].
As mentioned in Sect. 6.9, the EUE structure can be interpreted in somewhat notional terms of antiferromagnetism [95, 96]. Indeed, a local spin density is absent in any correctly defined singlet state, and, strictly speaking, the Néel-like spin structure is not possible for the single spin-singlet molecule. Thence, we cannot introduce, as usual, the antiferromagnetic order parameter (such as average difference of spin density between neighboring atoms). For the correlated singlet states, spin density matrix can be substituted with EUE density matrix (6.5). Consequently, index \( \bar{N}_{\text{eff}}^{{}} \) might serve as an appropriate order parameter for polymer structures,. This index satisfies inequality: \( 0 \le \bar{N}_{\text{eff}}^{{}} \le 1 \), that is natural to expect from the order parameter. In our case, \( \bar{N}_{\text{eff}}^{{}} = 1 \) corresponds to the ordered Néel state with the maximal ‘spin’ value in each sublattice of the bipartite structure. The given interpretation introduces an obviousness in understanding EUE for bipartite network structures. By adopting this reasoning, one can, moreover, invoke the best spin-polarized orbitals, that is the SPEB solutions discussed in Sect. 6.9. It allows us to reinterpret \( \bar{N}_{\text{eff}}^{{}} \) as a “spin” order parameter for exact or almost exact wave functions too.
Before closing this section let us comment on the UHF calculations presented above. From the formal viewpoint, UHF is the one-electron model which deals with a single determinant wave function \( \left|\Phi \right\rangle \). However, for strongly correlated systems the UHF wave function well mimics many properties of the spin-projected determinant \( \left| {\Phi ^{\text{ext}} } \right\rangle \) which is, of course, many-determinant state and which takes into account electron correlation. The closeness between \( \left|\Phi \right\rangle \) and \( \left| {\Phi ^{\text{ext}} } \right\rangle \) had been demonstrated long ago [70] with the infinite polyene chain treated analytically within the ‘diagonal’ Hubbard Hamiltonian approximation. The authors had suggested that it is a general feature of UHF solutions in polymeric π-problems. Our experience with EHF computations on large π-systems confirms these expectations. In particular, for the large systems the UHF charge RDM, \( D^{\text{uhf}} \), as in Eq. (1.10), is a good approximation to the EHF charge RDM, \( D^{\text{ext}} \), which is provided by the variational \( \left| {\Phi ^{\text{ext}} } \right\rangle \) state. Nevertheless, the UHF spin density matrix does not vanish for the UHF (spin-polarized) singlet ground state. Therefore, upon obtaining the UHF solution, the spin density matrix should be ignored (fixed to zero) what corresponds to an implicit purification of the spin-contaminated singlet state. At the same time, charge density \( D^{\text{uhf}} \) is well defined, and indeed very close to the EHF counterpart. For instance, we find the following squared norms, \( ||D^{\text{ext}} - D^{\text{uhf}} ||^{2} /N \) (deviation of \( D^{\text{uhf}} \) from \( D^{\text{ext}} \) per π-electron): 0.0007 for decacene C42Hc4, and 0.0002 for acene C102H54, respectively. These and many other examples (recall also Table 6.5) allow us to consider, for large systems, the usual spin-contaminated UHF solutions as a good approximation to main properties of the spin-adapted EHF solutions.
6.12 Giant Hydrocarbons and Nanographenes in a Spin-Polarized Hückel-like Scheme
In case of huge conjugated systems with several thousands of atoms, even the π-electron UHF method, in its full version, necessitates using high-performance computer clusters. Meanwhile, many important problems of nanoelectronics require studying novel molecular materials, including graphene nanoribbons, nanoislands, nanowiggles and other unusual giant honeycomb structures [74, 97–100]. Most of these structures are based on the so-called bipartite lattices. By definition, the bipartite lattice is formed by two interpenetrating sublattices, and each of these sublattices contains only one kind of atoms. Following [101], we will use the term “lattice” in an extended meaning, allowing the term for finite lattices and even for any finite-size atomic structures. In the theory of π-conjugated molecules, the standard term “alternant system” is a full counterpart of the term “bipartite lattice”.
There are many remarkable theorems dealing with abstract and realistic models of bipartite lattices [94, 101–104]. The well-known Coulson-Rushbrooke pairing theorem [102] is one of them. Additionally, the pairing theorem has a nice and useful matrix representation due to Hall [105]. The Hall formula (see below Eq. (6.90)) is valid within the Hückel method, and there is its analogue within the PPP one-electron approximation. In solid state physics, the counterpart of the Hückel approach is known as the tight-binding (TB) model. TB schemes, now more refined than before in the old solid-state physics days, are very popular because they have advantages to handle atomic cluster with thousands of atoms, reaching experimental sizes [106, 107]. Unfortunately, all these methods ignore electron correlation. In [13] we modified the TB model for bipartite lattices in such a way that it can handle strongly correlated bipartite lattices, and describe in them the relevant EUE effects. Below we sketch the main results of this work, and leave most formal details to Appendix B.
We recall few simple facts from the TB (or Hückel) theory of bipartite lattices. For the carbon-containing conjugated systems, the usual basis set \( \{ \left| {\chi_{\mu } } \right\rangle \} \) of the orthonormalized \( 2p_{z} \)-orbitals is employed. The corresponding one-electron Hamiltonian can be represented by the \( 2 \times 2 \) block-structure matrix
where all entries are expressed in units of \( |\beta_{0} | \) with \( \beta_{0} \) being the standard hopping (resonance) integral between nearest-neighbor sites (π-centers). The block B in Eq. (6.89) is the biadjacency matrix, that is \( B_{\mu \nu } = 1 \), if \( \mu \) and \( \nu \) are nearest-neighbor sites, otherwise \( B_{\mu \nu } = 0 \). Obviously, due to a bipartite structure of the considered lattices we can always renumber lattice sites in such a way that Eq. (6.89) holds true. From Eq. (6.89) it is not difficult to deduce the Hall formula [105] for the charge density matrix (or Coulson’s bond-order matrix):
This and somewhat more general relations are rederived in Appendix B.
Certainly, Eq. (6.89) is only a specific case of Eq. (6.4), and no EUE effects are possible at this level of description. It would be important to extend the Hückel model in order to somehow account for electron correlation effects without oversimplifying the model. The approximation of this kind was given in [108] and applied to EUE problems in [13]. The most important expressions of this work are reproduced here (see cit. loc. for the argumentation and precursors of the model). The model was referred as to the quasi-correlated tight-binding (QCTB) method. Within QCTB, we construct the effective Hamiltonians matrices
where \( \delta \) is treated as a fixed auxiliary parameter. The \( h^{\alpha } \) and \( h^{\beta } \) matrices are the counterparts of common Fock matrices for spin-up and spin-down electrons, respectively. Unlike UHF, no self-consistency procedure is needed for obtaining the corresponding density matrices \( \rho_{\alpha } \) and \( \rho_{\beta } \). The approach used is the most similar to the earlier approximate one-parameter UHF theory (e.g., see [101], the second citation). However, we can always obtain nonzero correlation effects by a suitable choice of the fitting parameter \( \delta \), and it allows to extend the applicability of the whole approach. Only for very strongly correlated systems, QCTB and the one-parameter UHF theory scheme are virtually equivalent.
Now turn to computational aspects. For matrices \( \rho_{\alpha } \) and \( \rho_{\beta } \), a block representation is easy to find by simple algebra (see Appendix B). As a result, we get charge density matrix of the QCTB model, Eq. (B4), and the respective NOON spectrum, Eq. (B5). It comes to a suitable working formula for the main EUE index:
Here \( \varepsilon_{i} \equiv \left| {\varepsilon_{i} } \right| \) are eigenvalues of \( (B^{ + } B)^{1/2} \), that is \( \{ \varepsilon_{i} \} \) is precisely the Hückel energy spectrum (in modulus) of the respective alternant system (the bipartite graph spectrum). In specific computations we will use value \( \delta = 7/24 \) which was found by fitting. Incidentally, remark that for small \( \delta \) it is easy to check that with second-order accuracy in \( \delta \), \( N_{\text{odd}}^{{}} = 2N_{\text{eff}}^{{}} \), as suggested before from a numerical experience (see Eq. (6.80)).
The above quasi-Hückel approach to EUE turns out to be reasonable and sufficiently close to the UHF and even CCD schemes (see Table 1 in [12]). Here we extract from this reference two kind of representative examples. One kind of them is related to the conjugated polymer structures (Table 6.7), the other to the finite-size graphene nanoflakes (Table 6.8). Before considering Table 6.7, let us make brief preliminary remarks. For many π-electron structure, particularly, with translation symmetry the analytical solution of the Hückel band spectrum is well known. For instance, consider a long polyene chain [–(CH=CH)–]n (polyacetylene) as a paradigmatic example of strong correlation in the physics of conjugated polymers [69, 109]. In case of the finite polyene chain the Hückel spectrum is \( \varepsilon_{k} = 2\cos [\pi \,k/(2n + 1)] \)(see any quantum chemistry textbook). For the asymptotic case, \( n \to \infty \), straightforward computations on Eq. (6.92) (with approximating a sum by integration method) lead to
We see from this equation that in the limit of large \( \delta \) (very strong correlation effects) the EUE index \( N_{\text{eff}}^{{}} \to N \), as it should be. Evidently, the value \( N_{\text{eff}}^{{}} = N \) corresponds to breaking each of π-bonds, when all \( \pi \)-electrons are unpaired. Remark that for infinite polymer chains the NOON spectrum \( \{ \lambda_{k} \} \) generally covers a whole interval [0, 2]. Therefore, instead of discrete set \( \{ \lambda_{k} \} \), the continuous (more exactly, quasi-continuous) function \( \lambda (k) \) of the continuous variable k makes its appearance. For convenience we make using the unity interval [0, 1] for continuous variable k.
A more general case is the polyene chain with alternating resonance integrals \( \beta_{\mu ,\mu + 1} = [1 + ( - 1)^{\mu + 1} \eta ]\beta_{0} \), where η is usually small quantity (we put \( \eta = 0.07 \)). The Hückel spectrum is of the form [110]: \( \varepsilon (k) = \sqrt 2 \,[1 + \eta^{2} + \,(1 - \eta^{2} )\cos \pi \,k]^{1/2} \), where \( 0 \le k \le 1 \). This case is intractable analytically, but numerical computations are easily performed, and the results are given in Table 6.7 (the first two systems in the table). Another interesting example is the linear polyacene (the third system in Table 6.7), for which in accordance with Coulson [111] we have \( \varepsilon (k) = [1 \pm (9 + 8\cos \pi \,k)^{1/2} \,]/2 \). In order to present a more complete comparison we add in the table the results for the graphene nanoribbon (4-ZGNR in the standard nomenclature) and for the poly(perianthracene) chain. The π-electron band structure of these two systems is computed by a code from [112].
As seen from Table 6.7, only the polyacetylene with alternating bonds and poly(perianthracene) molecules exhibit a gap in their NOON spectra. In contrast, the polyacene and 4-ZGNR demonstrate a quasi-continuous NOON spectrum covering the whole interval [0, 2]. Furthermore, crowding \( \lambda (k) \) near a ‘polyradical range’, that is near \( \lambda = 1 \), is observed in these spectra. A significant difference, in the \( \bar{N}_{\text{eff}}^{{}} \) index, between the 4-ZGNR and poly(perianthracene) can be simply understood in terms of Clar’s aromatic sextet theory (for the latter see, e.g., [74, 113]).
Now we will discuss in brief the QCTB results for three graphene nanoclusters with \( N \propto 10^{3} \), presented in Table 6.8. We only note that an unprecedented rise of interest in the graphene engineering researches generated the enormous literature in which recent books [74, 114, 115] only minimally reflect this graphene popularity. The first two systems in Table 6.8 are of a nanoflake family with the D 6h symmetry (hexagonal graphene nanoflakes). The cluster system, C1302, is with the armchair-shaped edge, and the second, C1350, with the zigzag-shaped edge. From the table we see that these two clusters have a small difference in energy stability (within QCTB), but a significant difference in the EUE characteristics. In zigzag-edge nanocluster C1350, the third system in Table 6.8, more electrons are unpaired, and again these unpaired electrons are preferentially localized on edge atoms. It is revealed by localization index \( \bar{N}_{\text{eff}}^{\text{bord}} \,\, \) (sum of atomic EUE occupancies divided by a number of the border atoms). On this account the zigzag edge atoms should be more unstable, or more reactive than the armchair edge atoms, and thereby the armchair nanoflakes be more stable in accordance with experiment (see [116], p. 382) and a model DFT study [117]. Chemical reactivity of graphene structures is a rather frequent issue discussed in current chemical literature [74, 118–122], and the principal inference we can make is that the major reactivity contribution comes from the edge states of nanoclusters. The very different models, from simplistic semiempirical to high-level nonempirical ones, predict the same qualitative trends. Notice that in the case of graphene nanoribbons with zigzag edges the strongly localized edge states were first reported almost 20 years ago [72] where the Hubbard π-UHF model was used. Apparently, in all models the characteristic effects of chemical topology are exhibited, and this fact demonstrates the practical usefulness of even naive models for studying large conjugated systems. We close this chapter by noting that the proposed π-electron QCTB scheme can be modified for an all valence-electron treatment by using the extended Hückel MO theory [123]. In this case the ionization potentials of 2p-electrons in the respective Wolfsberg-Helmholtz relation should be changed similar to Eq. (6.89).
6.13 Electron Unpairing in Strong Fields
The behavior of molecules under external perturbation shows the interesting, but not unexpected, fact that the electron unpairing greatly increases in strong fields. We consider here some representative examples carried over from [124, 125]. First, we discuss the effects of static electric fields for small molecules. A typical illustration is provided by an example of the rhombic cluster of Li4 in an atomic-scale electric field (\( {\mathbf{\sim }}0.1 \) atomic units). The results of the FCI/STO-3G calculations are shown in Fig. 6.5 where we plotted, in atomic units, the dipole moment \( d_{x} \) and \( N_{\text{eff}}^{{}} \) as functions of the electric field strength E, and the static field is applied along the longest diagonal (x-direction) of the rhombus.
By inspecting the plots, we see a strong increase of the dipole moment in the field, but \( N_{\text{eff}}^{{}} \) behaves more unpredictably, particularly in the region where the dipole moment curve undergoes a small inflection. A sharp maximum of \( N_{\text{eff}}^{{}} \) in this region corresponds to a diradical state (\( N_{\text{eff}}^{{}} \cong 2.04 \)). Interestingly, in this extremal state the most unpaired atom (judging from \( D_{A}^{\text{eff}} \)) is the ending atom on the longest diagonal, whereas the opposite atom on the same diagonal has zero EUE density and net atomic charge +1 (that is, locally it is \( {\text{Li}}^{ + } \)). This corresponds to the valence scheme of the form

Practically the same field dependency is obtained within the CISD and EHF schemes. Furthermore, passing from the STO-3G basis set to the 6-31G basis set, we obtain similar plots. For other small systems, see [125]. As one can see from [124], the analogous treatment (at the FCI/PPP level) of small conjugated hydrocarbons, such as the naphthalene and biphenylene molecules, gives the results resembling those of the Li4 case. For extended conjugated molecules the results are even more pronounced. Notice that in [124] we preferred using \( \kappa \)-index, Eq. (6.22), to using other EUE measures because the \( N_{\kappa }^{{}} \) index requires no computations of D, and this gives a certain advantage when it is necessary to calculate, at the FCI/PPP level, the \( \kappa \)-index for hundreds or more electric-field points.
It is interesting to see a typical difference in behavior between strongly and slightly correlated systems in a strong static field. For definiteness, we examine two molecules with the same numbers of carbon atoms. These are the linear decacene molecule, C42H24, and Clar’s type aromatic hydrocarbon C42H20 (see Table 6.9). Recall that Clar’s hydrocarbon is described by a structural formula which consists exclusively of benzenoid rings interlinked by quasi-single bonds [126]. It is quite natural that the PAHs of the Clar type have significantly less diradical (polyradical) character. The data from Table 6.9 for the decacene and Clar’s system C42H20 in zero electric field agree with this. However, the situation is somewhat different in the case of strong field. Namely, the maximal \( N_{\text{eff}}^{{}} \) index of the Clar system is more than six times larger than that in the field’s absence, and this value becomes still greater than the maximal \( N_{\text{eff}}^{{}} \) index for the decacene molecule. In the latter, we observe only a modest increase of the electron unpairing in the field (the maximal \( N_{\text{eff}}^{{}} \) is about 1.5 times larger than that in the field’s absence). Note that the dipole moment shows the qualitatively similar behavior for both systems.
We would like to stress that the observed enhancing of EUE effects in the stable PAHs under strong fields is not confined to the static electric field. Somewhat similar effects were reported in [127] where the action of strong magnetic field on small acenes and antiaromatic systems was examined at the FCI/PPP level (within London’s model of magnetic field effects). It turned out that in the strong magnetic field, aromatic molecules usually become diradicaloid and non-aromatic. Accordingly, the antiaromatic systems dramatically reduce their initial diradicaloid character, and thus lose their initial antiaromaticity. The interconnection between EUE and singlet-triplet splitting (STS) was also discussed for these π-problems [127]. At the ab initio level, a more extended study of STS and the polyradical character was presented in [11].
Let us return to the external field effects. Other cases are given in [27] where we studied small molecules in laser fields which generate transient diradical or more complex structures. Below we extend this study to the conjugated systems by using the π-electron time-dependent UHF (TD-UHF) method. We take again the decacene molecule, and the same pulsed laser field, as in [27], the first entry in Table 6.1. The corresponding pulse field is of the form E(t) cos(ωt), where E(t) is an enveloping function, and ω = 0.06 atomic units. The pulse field and temporal dependencies of dipole moment, \( d_{x}^{{}} \), and \( N_{\text{eff}}^{{}} \) index are given in Table 6.10. These data show that, unlike the static field (see Table 6.9), the pulse laser field produces the enormous electron unpairing in the linear decacene molecule. The similar results are obtained for other PAHs.
The above considered effects are implicitly connected with other strong perturbation effects reported in the literature. For instance, distorted graphene-like structures are really observed after irradiation generating lattice irregularities, e.g. vacancies. It leads to appearance the dangling carbon bonds, and thereby to the electron unpairing . The recent semiempirical study of surface states at a many-electron (UHF-type) level was given in [128]. In our context, paper [129] is presented even more relevant as giving the ab initio model of single defects and treating the EUE effects simultaneously. Summing this section we would like stress a nontrivial role of electron unpairing in various physical phenomena taking place in molecular materials.
6.14 In Search of Better EUE Measures
Now we address a difficult issue what is good and what is not for the EUE theory. The first discussions were started in papers [28, 29]. In the present work the Yamaguchi index [1] is treated mainly as a historically valuable first quantity for the EUE characterization, but not recommended for wide practical use (works [130] are a rare example of using \( N_{\text{eff}}^{\text{Yam}} \) now). Instead, we advocate the H-G index [5] for which a clear hole-particle physical nature, Eq. (6.40), is established [12]. Nevertheless, one can encounter intrinsic interpretational problems when judging the adequacy of any quantitative EUE measure, and the \( N_{\text{eff}}^{{}} \) index is not the exception. For instance, we obtained in the anthracene molecule a nonempirical estimate \( N_{\text{eff}}^{{}} \cong 1.9 \). Given the well known stability of anthracene, is it a reasonable magnitude? Before going on, we must ones again consider a formal side of the issue.
For this, we will include into consideration the second index proposed by Head-Gordon in [5]. This index denoted by \( N_{\text{odd}} [2] \) (as in Appendix A) is defined as follows:
Equation (6.94) was intensively applied in papers [9, 11, 129, 131] as even more preferable tool for quantifying EUE. By using \( N_{\text{odd}} [2] \), a not so important part of the NOON spectrum (mainly due to dynamical electron correlation) is effectively cut off. Another way to approach the EUE problems is to use matrix invariants of the deviation matrix
This matrix has a meaning of a hole-particle correction to \( 2\rho \) (see Appendix C for detail). Following the same procedure presented earlier for CIS states [76, 82, 84], we define the matrix modulus
and introduce the hole-particle invariants in form of traces of the \( |\varDelta D| \) powers:
The formal analysis of \( N_{\text{h - p}}^{{}} [q] \) is given in Appendix C. In particular, for ground state we have
The second-order index \( N_{\text{h - p}}^{{}} [2] \) has a meaning of the squared norm of the density matrix deviation \( \varDelta D \):
Our experience shows that the special case q = 3/4, which produced the hole-particle invariant \( N_{\text{h - p}}^{{}} [4/3] \), can also serve as a good EUE measure. In this case, as in the case of the above \( N_{\text{odd}}^{{}} \,\,[2] \) index, nonsignificant contributions from dynamical correlation are effectively suppressed. Apparently, the dynamical correlation has no direct relation to diradicality and polyradicality. However, the considered procedure may be not well suitable for dissociation states, as one example in [5] had shown this for the \( N_{\text{odd}}^{{}} \,\,[2] \) measure. Nevertheless, for typical equilibrium molecular states, such a suppression seems to be quite sensible if one is interesting in an estimation of polyradicality. In Table 6.11 we present the results of using \( N_{{{\text{h}} - {\text{p}}}}^{{}} \) (for the ground state \( \,N_{\text{h - p}}^{{}} = N_{eff}^{{}} \, \)), \( N_{\text{odd}}^{{}} \,\,[2] \) and \( N_{{{\text{h}} - {\text{p}}}}^{{}} [4/3] \) for periacenes discussed in Sect. 6.11. We supplement the table by the values of average locality index \( \aleph_{\text{loc}}^{{}} \) (6.88) for the each EUE measure. It is seen that the \( N_{\text{odd}}^{{}} \,\,[2] \) and \( N_{\text{h - p}}^{{}} [4/3] \) data differ nonsignificantly. With this, \( \,\,N_{\text{h - p}}^{{}} [4/3] \) is of the hole-particle origin, as the initial \( \,\,N_{{{\text{h}} - {\text{p}}}}^{{}} \) index. Moreover, judging from the \( \aleph_{\text{loc}}^{{}} \) magnitudes in Table 6.11, both measures, \( N_{\text{odd}}^{{}} \,\,[2] \) and \( N_{{{\text{h}} - {\text{p}}}}^{{}} [4/3] \) are associated with more localized EUE distributions than in the \( N_{\text{eff}}^{{}} \) case. This fact gives additional support for using the special measures \( N_{\text{odd}}^{{}} \,\,[2] \) and \( \,\,N_{{{\text{h}} - {\text{p}}}}^{{}} [4/3] \) for describing a polyradical character in conjugated hydrocarbons and related carbon-based networks.
Seemingly, it would be more preferable to perform EUE studies by invoking several quantification schemes. One needs also to take into account the specific features of the problem before deciding what the scheme should be taken as a more relevant in the problem context. For instance, if we are interesting in the EUE spatial localization, then the locality index \( \aleph_{\text{loc}}^{{}} \) (6.88) can be quite appropriate. If the localization measure of the NOON spectrum \( \{ \lambda_{k} \} \) near \( \lambda = 1 \) is in question then, then indices \( N_{\text{h - p}}^{{}} [q] \) and \( N_{\text{odd}}^{{}} \,\,[q] \) with large \( q \), e.g., \( q = 4 \), are more preferable.
6.15 Concluding Remarks
The initial intent of this chapter was to provide a broad overview and a critical assessment of various trends in the theory of effectively unpaired electrons. In the process of preparing the manuscripts some accents were shifted, and we would unavoidably restrict ourselves to a narrow set of issues and examples for discussion. For instance, we only slightly touched on the electron unpairing analysis in structures with a spatial separation of molecular subunits. These are bichromophore systems, molecular dimers and complexes, radical and ion–radical pairs, etc. The recent papers [77, 78, 125] are dedicated just to these problems. Besides, many interesting systems, e.g., semiconductor quantum dots, fell beyond the scope of this review. Indeed, many-electron aspects of the multiple exciton generation (MEG) in quantum dots are closely related to the EUE theory, but only circumstantial evidence about EUE effects in MEG can be found in the current literature [127, 128].
Before closing, we briefly reiterate the basic points. The conventional formalism of density matrices was used here in such a way that it helped us to understand some essential features and interrelations between different EUE measures. In particular, in Sect. 6.5 we see that the hole-particle index, which was introduced in [15, 16], is identical, for ground states, to the previously proposed H-G index [5]. We also examined excited states where the situation is more complicated, so that the H-G and hole-particle indices should be considered concurrently.
We must admit that the EUE theory is a little trickier than it seems. Indeed, rigorously speaking, the EUE problem is not well-defined, because it does not have a unique solution [5]. Nevertheless, we tried to understand what are the most appropriate definitions of the EUE measures. Now, we could report only preparatory results until a subsequent, more substantial analysis. Nevertheless, possible directions to modifying the existing measures are discussed here. In particular, we could retain the same hole-particle description for the modified (‘q-extended’) EUE measures in which unwanted small contributions to EUE are suppressed, as it was previously done in the case of the second Head-Gordon index, Eq. (6.94). Another way to produce better EUE indices is to somehow estimate an average localization of the unpaired electron. This leads to a possible measure \( \aleph_{\text{loc}}^{{}} \), Eq. (6.88), giving the results which are closer to those expected from a ‘common chemistry sense’.
In our specific applications the stress is put on large-scale carbon-containing molecules. For those we propose a simple semiempirical scheme [13] which has the same complexity as the ordinary Hückel method. It allows us to make quick and easy estimates of EUE effects even in gigantic conjugated networks which cannot be rigorously treated by high-level ab initio methods. It is important that the proposed elementary model yields the results which are qualitatively in agreement with the existing ab initio data [9, 11] for relatively small systems. The influence of external perturbations on EUE is another attractive field of application. It turns out that the systems which have a small polyradical character (hydrocarbons of the Clar type) become extremely polyradicaloid in a strong static electric field (Sect. 6.14). The laser field effects on the polyaromatic systems are even more pronounced, as preliminary studies show.
In sum, we would like to stress that during the last decade or so, the unpaired electron theory came up with new fruitful insights and techniques. In future, the semiempirical models and concrete results for large systems should be carefully examined by more rigorous approaches. We believe that a physical side of the existing simplified EUE theories remains, and plenty of new intriguing results for electrons in the conjugated molecules will be revealed.
References
Takatsuka K, Fueno T, Yamaguchi K (1978) Theor Chim Acta 48:175
McWeeny R, Kutzelnigg W (1968) Int J Quant Chem 2:187
Einstein A, Podolsky B, Rosen N (1935) Phys Rev 47:777
Afriat A, Selleri F (1999) The Einstein, Podolsky, and Rosen paradox in atomic, nuclear, and particle physics. Plenum Press, New York; McWeeny R (2000) Adv Quant Chem 36:365
Head-Gordon M (2003) Chem Phys Lett 372:508
Hachmann J, Dorando JJ, Aviles M, Chan GK-L (2007) J Chem Phys 127:134309
Yoneda K, Nakano M, Fukuda K, Champagne B (2012) J Phys Chem Lett 3:3338
Mizukami W, Kurashige Y, Yanai T (2012) J Chem Theor Comp 9:401
Plasser F, Pašalić H, Gerzabek MH, Libisch F, Reiter R, Burgdörfer J, Müller T, Shepard R, Lischka H (2013) Angew Chem Int Ed 52:2581
Casanova D (2014) J Comput Chem 35:944
Horn S, Plasser F, Müller T, Libisch F, Burgdörfer J, Lischka H (2014) Theor Chem Acc 133:1511
Luzanov AV (2014) J Struct Chem 55:799
Luzanov AV (2014) Funct Mater 21:437 [http://www.isc.kharkov.com/journal/contents/21-4/fm214-12.pdf]
Barnard AS, Snook IK (2011) Modelling Simul Mater Sci Eng 19:054001; Shi H, Barnard AS, Snook IK (2012) Nanotechnology 23:065707
Luzanov AV, Zhikol OA (2005) Int J Quant Chem 104:167
Luzanov AV, Prezhdo OV (2006) J Chem Phys 124:224109
Staroverov VN, Davidson ER (2000) Int J Quant Chem 77:316
Staroverov VN, Davidson ER (2000) Chem Phys Lett 330:161
Mestechkin MM (1977) Metod Matritsy Plotnosti v Teorii Molekul. Naukova Dumka, Kiev
Staroverov VN, Davidson ER (2000) J Am Chem Soc 122:7377
Lain L, Torre A, Bochicchio RC, Ponec R (2002) Chem Phys Lett 346:283; Alcoba DR, Bochicchio RC, Lain L, Torre A (2006) Chem Phys Lett. 429:286; Lain L, Torre A, Alcoba DR, Bochicchio RC (2009) Chem Phys Lett 476:101
Yamaguchi K, Kawakami T, Takano Y, Kitagawa Y, Yamashita Y, Fujita H (2002) Int J Quant Chem 90:370
Cheng M-J, Hu C-H (2003) Mol Phys 101(9):1319
Proynov EI (2006) J Mol Struct (Theochem) 762:159; Proynov E, Liu F, Kong J (2013) Phys Rev A 88:032510
Amos AT, Hall GG (1961) Proc Roy Soc A 263:483
Stück D, Baker TA, Zimmerman P, Kurlancheek W, Head-Gordon M (2011) J Chem Phys 135:194306
Luzanov AV (2013) Int J Quant Chem 113:2489
Bochicchio RC, Torre A, Lain L (2003) Chem Phys Lett 380:486
Head-Gordon M (2003) Chem Phys Lett 380:488
Döhnert D, Koutecký J (1980) J Am Chem Soc 102:1789; Gordon MS, Schmidt MW, Chaban G M, Glaesemann KR, Stevens WJ, Gonzalez C (1999) J Chem Phys 110:4199
Luzanov AV (2004) Kharkov University Bulletin. Chemical Series Issue 11(34):195 [http://chembull.univer.kharkov.ua/archiv/2004/12.pdf]
Luzanov AV, Umanski VE (1977) Theor Experim Chem 13:162
Luzanov AV, Pedash YF, Mohamad S (1990) Theor Experim Chem 26:513
Grobe R, Rzazewski K, Eberly JH (1994) J Phys B 27:L503
Luzanov AV, Prezhdo OV (2007) Mol Phys 105:2879
Bell RJ, Dean P, Hibbins-Butler DC (1970) J Phys C 32:111
Zyczkowski K (1999) Phys Rev A 60:3496
Luzanov AV (1989) Theor Experim Chem 25:19; Luzanov AV, Wulfov AL, Krouglov VO (1992) Chem Phys Lett 197:614
Helgaker T, Jørgensen P, Olsen P (2000) Molecular Electronic-Structure Theory. Wiley, New York
Purvis GD, Sheppard R, Brown BR, Bartlett RJ (1983) Int J Quant Chem 23:835
Kutzelnigg W, Smith VH (1968) Int J Quant Chem 2(531):553
Shavitt I, Bartlett RJ (2009) Many-body methods in chemistry and physics. Cambridge University Press, Cambridge
Nesbet RK (1958) Phys Rev 109:1632
Kumar K (1962) Perturbation theory and the nuclear many body problem. North-Holland, Amsterdam
Luzanov AV (1977) Theor Math Phys 30:232
Luzanov AV (2008) Int J Quant Chem 108:671
Luzanov AV, Prezhdo OV (2006) J Chem Phys 125:154106
Dirac PAM (1931) Cambr Phil Soc 27:240
Davidson ER (1976) Reduced density matrices in quantum chemistry. Academic, New York
Juhasz T, Mazziotti DA (2006) J. Chem. Phys. 125:174105
Mazziotti DA (ed) (2007) Advances in Chemical Physics, vol 134. Wiley, New York
Luzanov AV, Prezhdo OV (2005) Int J Quantum Chem 102:582
Roby KR (1974) Mol Phys 27:81
Clark AE, Davidson ER (2003) Int J Quantum Chem 93:384
Penney WG (1937) Proc Roy Soc A 158:306
Raos G, Gerratt J, Cooper DL, Raimondi M (1994) Chem Phys 186:233; Clark AE, Davidson ER (2001) J Chem Phys 115:7382; (2002) Mol Phys 100:373; (2002) J Phys Chem A 106:7456
Herrmann C, Reiher M (2006) J Comput Chem 27:1223; Podewitz M, Reiher M (2010) Adv Inorg Chem 62:177
Alcoba DR, Torre A, Lain L, Bochicchio RC (2011) J Chem Theory Comput 7:3560
Luzanov AV (2012) Int J Quantum Chem 112:2915
Ramos-Cordoba E, Matito E, Mayer I, Salvador P (2012) Phys Chem Chem Phys 14:15291
Matsika S, Feng X, Luzanov AV, Krylov AI (2014) J Phys Chem A 118:11943
Luzanov AV, Prezhdo OV (2011) J Chem Phys 135:094107
Cížek J, Paldus J (1967) J Chem Phys 47:3976
Kutzelnigg W, Smith VH (1964) J Chem Phys 41:896
Paldus J, Cížek J, Keating BA (1973) Phys Rev A 8:640
Mayer I (1980) Adv Quantum Chem 12:189
Klimo V, Tino J (1980) Mol Phys 43:477; Henderson TM, Tsuchimochi T, Scuseria GE (2012) J Chem Phys 136:164109; Luzanov
Hartmann H (1947) Z Naturforsch A 2:259
Ovchinnikov AA, Ukrainskii II, Kvenzel’ GF (1973) Sov Phys Uspekhi 15:575
Misurkin IA, Ovchinnikov AA (1974) Mol Phys 27:237; Misurkin IA, Ovchinnikov AA (1977) Russ Chem Rev 46:96
Macêdo AMS, dos Santos MC, Coutinho-Filho MD, Macedo CA (1995) Phys Rev Lett 74:1851
Fujita M, Wakabayashi K, Nakada K, Kushakabe K (1996) J Phys Soc Jap 65:1920
Jiang D-E, Chen X-Q, Luo W, Shelton WA (2009) Chem Phys Lett 483:120; Jiang DE, Sumpter BG, Dai SJ (2007) Chem Phys 126:134701; Das M (2014) J Chem Phys 140:124317
Jiang DE, Chen Z (eds) (2013) Graphene chemistry: theoretical perspectives. Wiley, Puerto Rico
Jiménez-Hoyos CA, Rodríguez-Guzmán R, Scuseria GE (2014) J Phys Chem A 118:9925
Luzanov AV, Zhikol OA (2012) In: Leszczynski J, Shukla MK (eds) Practical aspects of computational chemistry I: an overview of the last two decades and current trends. Springer, Heidelberg, p 415
Minami T, Iton S, Nakano M (2013) J Phys Chem Lett 4:2133
Feng X, Luzanov AV, Krylov AI (2013) J Phys Chem Lett 4:3845
McWeeny R (1968) In: Reports on the Density Matrix Seminar. Queen’s University. Ontario; p 25; Dacre PD, Watts CJ, Williams GRJ, McWeeny R (1975) Mol Phys 30:1203
Luzanov AV (1975) Theor Experim Chem 9:567
Ipatov A, Cordova F, Doriol LJ, Casida ME (2009) J Mol Struct (Theochem) 914:60
Luzanov AV, Zhikol OA (2010) Int J Quant Chem 110:902
Murrell JN, McEwen KL (1956) J Chem Phys 25:1143
Luzanov AV, Sukhorukov AA, Umanski VE (1976) Theor Experim Chem 10:354
Krylov AI, Sherrill CD, Head-Gordon M (2000) J Chem Phys 113:6509
Bendikov M, Duong H M, Starkey K, Houk KN, Carter EA, Wudl F (2004) J Am Chem Soc 126:7416; Son Y-W, Cohen ML, Louie SG (2006) Nature 444:347; Pisani L, Chan JA, Montanari B, Harrison NM (2007) Phys Rev B 75:064418; Hod O, Barone V, Scuseria GE (2008) Phys Rev B 77:035411
San-Fabian E, Moscardy F (2013) Int J Quantum Chem 113:815
Torres A, Guadarrama P, Fomine S (2014) J Mol Modeling 20:1
Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA Jr., Vreven T, Kudin KN, Burant JC, MillamJM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA (2004) Gaussian 03, Revision A.01. Gaussian, Inc., Wallingford
Gebhard F (1997) The Mott metal insulator transition: models and methods. Springer, Berlin; Yazyev OV (2013) Acc Chem Res 46:2319
SmeyersYG, Doreste-Suarez L (1973) Int. J. Quantum Chem 7:687
Murphy NC, Wortis R, Atkinson WA (2011) Phys Rev B 83:184206
Tyutyulkov N, Dietz F, Müllen K, Baumgarten M (1992) Chem Phys 163:55
McLachlan AD (1961) Mol Phys 4:49
Vonsovskii SV, Svirskii MS (1970) JETP 30:140; Vonsovskii SV (1974) Magnetism. vol 2. Wiley, New York
Majlis N (2000) The quantum theory of magnetism. World Scientific, Singapore
Luo Z, Kim S, Kawamoto N, Rappe AM, Johnson AT (2011) ACS Nano 5:9154
Girão EC, Cruz-Silva E, Liang L, Filho AGS, Meunier V (2012) Phys Rev B 85:235431
Fujihara M, Miyata Y, Kitaura R, Nishimura Y, Camacho C, Irle S, Iizumi Y, Okazaki T, Shinohara H (2012) J Phys Chem C 116:15141
Zhang X, Xin J, Ding F (2013) Nanoscale 5:2556
Lieb EH, Mattis DC (1962) J Math Phys 3:749; Langer WD, Mattis DC (1971) Phys Lett 36A:139; Lieb EH (1989) Phys Rev Lett 62:1201
Coulson CA, Rushbrooke GS (1940) Proc Cambridge Phil Soc 36:139; Brickstock A, Pople JA (1954) Trans Farad Soc 59:901
Kasteleyn P (1967) In: Harary F (ed) Graph theory and theoretical physics. Academic Press, London, p 43
Harary F (1972) Graph theory. Addison-Wesley, London; Cvetkovic´ DM, Doob M, Sachs H (1980) Spectra of graphs, theory and application. Academic Press, New York
Hall GG (1955) Proc Roy Soc A 229:251
Boykin TB (2009) J Comput Electron 8:142; Goringe CM, Bowler DR (1997) Hernández E Rep Prog Phys 60:1447
Mariscal M.M, Oviedo OA, Leiva EPM (eds) (2011) Metal clusters and nanoalloys: from modeling to applications. Springer, Berlin
Ivanov VV, Kisil IP, Luzanov AV (1996) J Struct Chem 37:537
Chien JCW (1984) Polyacetylene: chemistry, physics and materials science. Academic Press, New York
Lennard-Jones JE (1937) Proc Roy Soc A 158:280
Coulson CA (1948) Proc Phys Soc A 60:257
Luzanov AV (2002) J Struct Chem 43:711
Petersen R, Pedersen TG, Jauho A-P (2011) ACS Nano 5:523
Foa Torres LEF, Roche S, Charlie J-C (2014) Introduction to graphene-based nanomaterials: from electronic structure to quantum transport. Cambridge Uiversity Press, Cambridge
Wolf EL (2014) Graphene: a new paradigm in condensed matter and device physics. Oxford University Press, Oxford
Cresti A, Nemec N, Biel B, Nieble G, Triozon F, Cuniberti G, Roche S (2008) Nano Research 1:361
Wei D, Wang F (2012) Surf Sci 606:485
Baldoni M, Sgamellotti A, Mercuri F (2008) Chem Phys Lett 464:202; Selli D, Mercuri F (2014) Carbon 75:190; Baldoni M, Mercuri F (2015) Phys Chem Chem Phys 17:2088
Sharma R, Nair N, Strano MS (2009) J Phys Chem C 113:14771
Dinadayalane TC, Leszczynski J (2010) Struct Chem 21:1155
Wassmann T, Seitsonen AP, Saitta AM, Lazzeri M, Mauri F (2010) J Am Chem Soc 132:3440
Radovic R, Silva-Villalobos AF, Silva-Tapia AB, Vallejos-Burgos F (2011) Carbon 49:3471
Hoffmann R (1963) J Chem Phys 39:1397; Lowe JP (1978) Quantum chemistry. Academic, New York
Luzanov AV (2013) J Struct Chem 54:835
Luzanov AV (2013) Kharkov University Bulletin. Chemical Series Issue 22(45):9
Clar E, Zander M. (1958) J Chem Soc 1861; Clar E (1972) Aromatic sextet. Wiley, London
Luzanov AV (2013) J Struct Chem 54:277
Tyutyulkov N, Drebov N, Mu1llen K, Staykov A, Dietz F (2008) J Phys Chem C 112: 6232
Machado FBC, Aquino AJA, Lischka H (2014) ChemPhysChem 15:3334
Sheka EF (2012) Int J Quantum Chem 112:3076; Sheka EF (2015) Adv Quantum Chem 70:111
Cui Z-h, Lischka H, Mueller T, Plasser F, Kertesz M (2014) ChemPhysChem 15:165; Cui ZH, Lischka H, Beneberu, HZ, Kertesz M (2014) J Am Chem Soc 136:12958
Mardsen JE, Ratiu T, Abraham R (2001) Manifolds, tensor analysis, and applications. Springer, New York
Mestechkin MM (1969) Theor Math Phys 1:221
Ruskai MB (1970) J Math Phys 11:3218
Valdemoro C (1992) Phys Rev A 45:4462
Dirac PAM (1934) Proc Cambr Phil Soc 30:150
Davydov AS (1965) Quantum mechanics. Pergamon Press, Oxford [see Eqs. (61.12) and (61.29)]
Rebane TK (1963) Vestn Leningr Gos Univ 22:30; Mestechkin MM (1965) Theor Experim Chem 1:388
Li W, Chen F (2014) J Nanopart Res 16:2498
Löwdin P-O (1955) Phys Rev 97:1505
Fischer SA, Prezhdo OV (2011) J Phys Chem C 115:10006; Jaeger HM, Hyeon-Deuk K, Prezhdo OV (2012) Acc Chem Res 46:1280
Acknowledgment
Many people influenced the author’s work directly or indirectly, and most valuable were nice contacts with colleagues and coauthors Art Bochevarov, David Casanova, Anna Krylov, Hans Lischka, Felix Plasser, and Oleg Zhikol. The receipt of the ab initio π-NOON spectra for the (5a, 4z), (5a, 5z), and (5a, 6z) periacenes from H. Lischka and F. Plasser is also greatly acknowledged.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix A: Duality Symmetry and Generalized EUE Indices
In this Appendix we clarify the cause for postulating symmetry relation (6.18). For this aim we introduce a formal operation which can be named the duality transformation and which is well known in multilinear algebra as the Hodge star operation, or Hodge dual [132]. In the RDM theory an equivalent transformation was applied in [19, 133], without recognizing it as a Hodge dual. The following simple example helps to explain this notion in the more familiar terms of many-electron state vectors.
We consider a two-electron problem in the basis of five spin-orbitals
Let the ket
be the two-electron Slater determinant built from \( \left| {\chi_{1} } \right\rangle \) and \( \left| {\chi_{2} } \right\rangle \). By definition, the dual ket, \( \left| {\Psi _{[3]}^{ *} } \right\rangle \), is built up from the rest spin-orbitals, giving the three-electron determinant:
In the same basis (A1), the maximal Slater determinant \( \left| {\Psi _{ \hbox{max} } } \right\rangle \) is
It is not difficult understand that we can produce \( \left| {\Psi _{[3]}^{ *} } \right\rangle \) from \( \left| {\Psi _{ \hbox{max} } } \right\rangle \) by annihilating in Eq. (A4) the state vector (A2). More exactly, apart from a prefactor we have
They say that the obtained three electron state \( \left| {\Psi _{[3]}^{ *} } \right\rangle \) is the Hodge dual of the two-electron state \( \left| {\Psi _{{^{ [ 2 ]} }} } \right\rangle \).
Now consider the respective 1-RDMs. In notation of Sect. 6.6, we have from determinants (A2) and (A3) the usual \( D_{1}^{\text{so}} \) matrices in the form of projectors on occupied spin-orbitals of the respective determinants:
We see that
where unity operator I is a projector on all five spin-orbitals from Eq. (A1).
This line of reasoning can be directly extended to a general case including exact state vectors as well. It the general case we start with a r-dimensional spin-orbital basis \( \{ \left| {\chi_{k} } \right\rangle \}_{1 \le k \le r} \) and build the respective maximal determinant \( \left| {\Psi _{ \hbox{max} } } \right\rangle = \left| {\chi_{1} \ldots \chi_{r} } \right\rangle \) (clearly, the only r-electron state vector is \( \left| {\Psi _{ \hbox{max} } } \right\rangle \equiv \left| {\Psi _{ [r ]} } \right\rangle \, \)). The given exact (or approximate) state-vector \( \Psi _{ [N ]} \) produces the Hodge dual, as previously:
Accordingly, relation (A6) is generalized to be
This is the duality transformation in terms of 1-RDM. The analogous relation for \( D_{2}^{\text{so}} (\Psi _{ [r - N ]}^{ *} ) \) is somewhat more involved [133, 134]. The remarkable property of the Hodge duality transformation is its ability to preserve correlation operator \( \varDelta_{2}^{\text{so}} \) in Eq. (6.45), as it is first shown in [19]. The related expression is given in [135]. Thus, the other correlation matrices, e.g., \( D^{\text{eff}} \), must be the same as well. It is worth mentioning in passing that in [128] and many subsequent papers, a somewhat inconvenient terminology is used for RDMs \( D_{{}}^{\text{so}} (\Psi _{ [r - N ]}^{ *} ) \)—the latter are loosely identified with hole RDMs. Certainly, it leads to confusion and even misinterpretation, since generally such RDMs have no relation to the genuine, ‘physical’, hole RDMs discussed in Sect. 6.4 and in [16]. We prefer to refer to them as the dual RDMs [16].
We now have to sum over spin indices, making spin trace in Eq. (A8). As a result, the dual charge density matrix is yielded, viz.
Then the NOON spectrum of the dual charge density matrix is simply a set \( \{ 2 - \lambda_{k} \} \) where we imply that the initial NOON spectrum is the set \( \{ \lambda_{k} \} \). Recalling that EUE characteristics of the dual state (A7) should be the same as in the initial state \( \Psi _{ [N ]} \), the identity
is necessitated. Taking into account Eqs. (6.1), (6.5) and (6.5′) we arrive at the relation
from whence Eq. (6.18) immediately follows, that is
The requirement (A12) allows us to specify a general dependence \( \lambda_{{}}^{\text{eff}} = f(\lambda_{{}} ) \), namely, \( \lambda_{{}}^{\text{eff}} \) is a nonnegative definite function of argument \( |\lambda - 1| \), with boundary values \( f(0) = f(2) = 0. \) Eqs. (6.7′) and (6.14) are evidently of this type. Rather general types of the functions can be proposed as ‘q-extensions’ of Eqs. (6.9) and (6.15). These are
where \( q \ge 1 \). We see that \( N_{\text{odd}}^{{}} \,[1] \) and \( N_{{{\text{eff}}\,}}^{{}} \,[1] \) produce the usual \( N_{\text{odd}}^{{}} \) and \( N_{\text{eff}}^{{}} \) measures, respectively. The choice \( q = 2 \) in Eq. (A13) leads to
which is the modified Head-Gordon index from [5]. This expression is trivially equivalent to Eq. (6.94).
Appendix B: Density Matrix and NOON for QCTB
We consider here in more detail the QCTB model described in Sect. 6.13. Having at hand the effective Hamiltonian matrices (6.91), we straightforwardly derive projector matrices \( \rho_{\alpha } \) and \( \rho_{\beta } \) by using the well known expressions connecting Hamiltonians and respective projectors [19, 136, 137]). Let h be the Hermitian operator, such that exactly n eigenvalues of h lie below zero, and P be the projector on the corresponding eigenvectors. Then
where \( |h| = \,\,\,[(h)^{2} ]^{1/2} \) is the modulus of operator h. Further, let one-electron Hamiltonian matrix \( h^{\delta } \) be defined as follows:
In particular, \( h^{\alpha } = h^{[\delta ]} \), \( h^{\beta } = h^{[ - \delta ]} \). Then, by applying Eq. (B1) to \( h = h^{[\delta ]} \), we obtain the corresponding projector
In derivation, the block-diagonal structure of \( (h^{[\delta ]} )^{2} \) is used, that is
Equation (B2) was earlier derived by another technique for the special closed π-shells with alternating electronegativity [138]. Obviously, setting \( \delta = 0 \), we return to the Hall formula (6.90). By recalling Eq. (6.91) we have
Putting together Eqs. (B2) and (B3), we get from Eq. (6.10) the main result:
The problem of diagonalizing this \( D \) is a quite elementary, and the full NOON spectrum takes the form
where \( 1 \le i,\,a \le n \), and nonnegative quantities \( \varepsilon_{i} \equiv \left| {\varepsilon_{i} } \right| \), as well as \( \varepsilon_{a} \equiv \left| {\varepsilon_{a} } \right| \), are eigenvalues of \( (B^{ + } B)^{1/2} \), that is \( \{ \varepsilon_{i} \} \) is the bipartite graph spectrum. From Eq. (B5) the main EUE indices within QCTB are easily deduced. For instance,
Remark also an evident symmetry of the corresponding hole and particle occupancies, defined by Eq. (6.41′):
that follows from Eq. (B5). In other words, the hole and particle occupancy spectra are identical for this π-model.
As a matter of fact, the hole and particle occupancies are identical for any bipartite networks treated within π-approximation, up to FCI/PPP. This is a simple corollary of the generalized pairing theorem of McLachlan [94] stating that the π-electron charge density matrix of the alternant hydrocarbons is of the form
where the \( 2p_{z} \) AO basis set is ordered as in Eq. (6.89), and \( \partial \) defines the inter-sublattice bond order matrix. Clearly, the corresponding NOON spectrum \( \{ \lambda_{k} \} \) is
where \( \mu_{i} \) (or \( \mu_{a} \)) are eigenvalues of \( \partial^{ + } \partial \), and \( 1 \le i,\,a \le n \). As a result, the initial π-NOON spectrum is symmetrical in respect to the point \( \lambda = 1 \). From Eq. (B9) we deduce that indeed the respective hole and particle π-occupancies, defined as in Eq. (6.41′), are identically the same:
Interestingly, an initio data [9, 11] approximately follow Eqs. (B9) and (B10). Incidentally, it follows, from this discussion, that the hole occupancy distribution \( \{ 1 - \sqrt {\mu_{i} } \} \) (generally \( \{ 2 - \lambda_{i} \}_{1 \le i \le n} \)) is sufficient for considering EUE problems. For instance, instead of plotting NOON spectrum \( \{ \lambda_{k} \} \), one can plot only hole occupancy spectrum \( \{ 2 - \lambda_{i} \} \) as even more suitable in the EUE context. This occupancy spectrum is in fact the second half of the typical π-NOON spectra which were presented in Tables 6.6, 6.7, and Fig. 6.4.
Appendix C: Generalized Hole-Particle Indices
Here we analyze the main EUE indices in terms of hole-particle quantities. We begin with the representation
where \( \rho \) is of the form (6.36), and \( \left| {\varphi_{i} } \right\rangle \) are the natural orbitals of the state in question, so \( \varDelta D \) commutes with \( \rho \). Then, using the same notation, as in Eq. (6.41), we obtain the spectral resolution
where
are new nonnegative quantities (\( 0 \le \varDelta_{i} < 1 \), and \( i \le n \)), and \( \lambda_{a}^{{}} \) are related to ‘virtual’ natural orbitals. We see that correlation correction matrix \( \varDelta D \) has a clear hole-particle structure: \( \varDelta_{i} \, \) are the occupancy numbers for the holes, and \( \lambda_{a}^{{}} \) are the same for the particles. In manipulations the identity
will be useful as well. It follows from Eqs. (C1), (C2), and normalization (6.2).
Due to the diagonal form (C2) we trivially have the diagonal form of the matrix \( |\varDelta D|\, \) defined by Eq. (6.96):
But this is the same as the hole-particle density in Eq. (6.41), that is
It is essential that under duality transformation (A9) the holes and particles in Eq. (C2) change place, so identity (A10) satisfies automatically for \( D^{\text{eff}} = D^{\text{h - p}} \).
The appropriate q-extended (\( q \ge 1 \)) hole-particle indices can be cast explicitly into the form
Particularly,
The previously defined EUE indices can be rewritten in terms of the correlation-dependent quantities {\( \varDelta_{i} \), \( \lambda_{a} \)}:
where we used identity (C4).
For slightly correlated systems, the most important are the first order terms in \( \varDelta_{i} \) and \( \lambda_{a} \). It gives \( N_{\text{odd}}^{{}} \cong 4\sum {\varDelta_{i} } \), so
and this goes back to the rude estimation, Eq. (6.80). It is interesting that the exact interrelation \( 2N_{\text{eff}}^{{}} - N_{\text{odd}}^{{}} = \,||\varDelta D\,||^{2} \) is true. Likewise, the first-order estimation of the modified Head-Gordon index (6.94), that is Eq. (C11), is null:
Indeed, Eq. (C11) contains only the second-order and higher-order terms:
The above simple analysis now elucidates how small contributions from \( \varDelta_{i} \) and \( \lambda_{a} \) are essentially suppressed in the \( N_{\text{odd}}^{{}} \,\,\,[2] \) and \( N_{\text{h - p}}^{{}} [2] \) indices. As a rule, these small contributions appear mainly from dynamical correlations. For instance, MP2 (the Moller-Plesset second-order perturbation theory) normally produce the contributions of this kind. Evidently, they have no direct relation to diradicality and polyradicality, and the \( N_{\text{odd}}^{{}} \,\,\,[2] \) and \( N_{\text{h - p}}^{{}} [2] \) indices should be rather small without a significant contribution from non-dynamical correlation. This is a good property of the generalized indices such as (6.94) and (C8), and apparently, this is the basic reason why \( N_{\text{odd}}^{{}} \,\,\,[2] \) is systematically employed in papers [9, 11, 122, 124] for analyzing the unpaired electrons in large PAHs. At the same time, the dynamical correlation cannot fully ignored, and the problem of an optimal quantification remains.
Rights and permissions
Copyright information
© 2016 Springer Science+Business Media New York
About this chapter
Cite this chapter
Luzanov, A.V. (2016). Effectively Unpaired Electrons for Singlet States: From Diatomics to Graphene Nanoclusters. In: Leszczynski, J., Shukla, M. (eds) Practical Aspects of Computational Chemistry IV. Springer, Boston, MA. https://doi.org/10.1007/978-1-4899-7699-4_6
Download citation
DOI: https://doi.org/10.1007/978-1-4899-7699-4_6
Published:
Publisher Name: Springer, Boston, MA
Print ISBN: 978-1-4899-7697-0
Online ISBN: 978-1-4899-7699-4
eBook Packages: Chemistry and Materials ScienceChemistry and Material Science (R0)