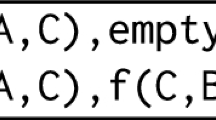FormalPara Synonyms

Learning in logic; Multi-relational data mining; Relational data mining; Relational learning

FormalPara Motivation

The first motivation and most important motivation for using inductive logic programming is that it overcomes the representational limitations of attribute-value learning systems. Such systems employ a table-based representations where the instances correspond to rows in the table, the attributes to columns, and for each instance, a single value is assigned to each of the attributes. This is sometimes called the single-table single-tuple assumption. Many problems, such as the Bongard problem shown in Fig. 1, cannot elegantly be described in this format. Bongard (1970) introduced about a hundred concept learning or pattern recognition problems, each containing six positive and six negative examples. Even though Bongard problems are toy problems, they are similar to real-life problems such as structure–activity relationship prediction, where the goal is to learn to predict whether a given molecule (as represented by its 2D graph structure) is active or not. It is hard – if not, impossible – to squeeze this type of problem into the single-table single-tuple format for various reasons. Attribute-value learning systems employ a fixed number of attributes and also assume that these attributes are present in all of the examples. This assumption does not hold for the Bongard problems as the examples possess a variable number of objects (shapes). The singe-table single-tuple representation imposes an implicit order on the attributes, whereas there is no natural order on the objects in the Bongard problem. Finally, the relationships between the objects in the Bongard problem are essential and must be encoded as well. It is unclear how to do this within the single-table single-tuple assumption. First-order logic and relational representations allow one to encode problems involving multiple objects (or entities) as well as the relationships that hold them in a natural way.

Inductive Logic Programming, Fig. 1
figure 91figure 91

A complex classification problem: Bongard problem 47, developed by the Russian scientist Bongard (1970). It consists of 12 scenes (or examples), 6 of class \(\oplus \) and 6 of class \(\ominus \). The goal is to discriminate between the two classes

Full size image

The second motivation for using inductive logic programming is that it employs logic, a declarative representation. This implies that hypotheses are understandable and interpretable. By using logic, inductive logic programming systems are also able to employ background knowledge in the induction process. Background knowledge can be provided in the form of definitions of auxiliary relations or predicates that may be used by the learner. Finally, logic provides a well-understood theoretical framework for knowledge representation and reasoning. This framework is also useful for machine learning, in particular, for defining and developing notions such as the covers relation, generality, and refinement operators; see also Logic of Generality.

FormalPara Theory

Inductive logic programming is usually defined as concept learning using logical representations. It aims at finding a hypothesis (a set of rules) that covers all positive examples and none of the negatives, while taking into account a background theory. This is typically realized by searching a space of possible hypotheses. More formally, the traditional inductive logic programming definition reads as follows:

Given

  • A language describing hypotheses \(\mathcal{L}_{h}\)

  • A language describing instances \(\mathcal{L}_{i}\)

  • Possibly a background theory B, usually in the form of a set of (definite) clauses

  • The covers relation that specifies the relation between \(\mathcal{L}_{h}\) and \(\mathcal{L}_{i}\), that is, when an example e is covered (considered positive) by a hypothesis h, possibly taking into account the background theory B

  • A set of positive and negative examples \(E = P \cup N\)

Find a hypothesis \(h \in \mathcal{L}_{h}\) such that for all p ∈ P : covers(B, h, p) = true and for all n ∈ N : covers(B, h, n) = false.

This definition can, as for Concept-Learning in general, be extended to cope with noisy data by relaxing the requirement that all examples be classified correctly.

There exist different ways to represent learning problems in logic, resulting in different learning settings. They typically use definite clause logic as the hypothesis language \(\mathcal{L}_{i}\) but differ in the notion of an example. One can learn from entailment, from interpretations, or from proofs, cf. Logic of Generality. The most popular setting is learning from entailment, where each example is a clause and covers(B, h, e) = true if and only if \(B \cup h\models e\).

The top leftmost scene in the Bongard problem of Fig. 1 can be represented by the clause:

positive :- object(o1),             object(o2),             circle(o1),             triangle(o2),             in(o1, o2),             large(o2).

The other scenes can be encoded in the same way. The following hypothesis then forms a solution to the learning problem:

positive :- object(X),             object(Y),             circle(X),             triangle(Y),             in(X,Y).

It states that those scenes having a circle inside a triangle are positive. For some more complex Bongard problems, it could be useful to employ background knowledge. It could, for instance, state that triangles are polygons.

 polygon(X) :- triangle(X).

Using this clause as background theory, an alternative hypothesis covering all positives and none of the negatives is

positive :- object(X),             object(Y),             circle(X),             polygon(Y),             in(X,Y).

An alternative for using long clauses as examples is to provide an identifier for each example and to add the corresponding facts from the condition part of the clause to the background theory. For the above example, the facts such as

object(e1,o1). object(e1,o2). circle(e1,o1). triangle(e1,o2). in(e1,o1,o2). large(e1,o2).

would be added to the background theory, and the positive example itself would then be represented through the fact positive(e1), where e1 is the identifier. The inductive logic programming literature typically employs this format for examples and hypotheses.

Whereas inductive logic programming originally focused on concept learning – as did the whole field of machine learning – it is now being applied to virtually all types of machine learning problems, including regression, clustering, distance-based learning, frequent pattern mining, reinforcement learning, and even kernel methods and graphical models.

FormalPara A Methodology

Many of the more recently developed inductive logic programming systems have started from an existing attribute-value learner and have upgraded it toward the use of first-order logic (Van Laer and De Raedt 2001). By examining state-of-the-art inductive logic programming systems, one can identify a methodology for realizing this (Van Laer and De Raedt 2001). It starts from an attribute-value learning problem and system of interest and takes the following two steps. First, the problem setting is upgraded by changing the representation of the examples, the hypotheses as well as the covers relation toward first-order logic. This step is essentially concerned with defining the learning setting, and possible settings to be considered include the already mentioned learning from entailment, interpretations, and proofs settings. Once the problem is clearly defined, one can attempt to formulate a solution. Thus, the second step adapts the original algorithm to deal with the upgraded representations. While doing so, it is advisable to keep the changes as minimal as possible. This step often involves the modification of the operators used to traverse the search space. Different operators for realizing this are introduced in the entry on the Logic of Generality.

There are many reasons why following the methodology is advantageous. First, by upgrading a learner that is already effective for attribute-value representations, one can benefit from the experiences and results obtained in the propositional setting. In many cases, for instance, decision trees, this implies that one can rely on well-established methods and findings, which are the outcomes of several decades of machine learning research. It will be hard to do better starting from scratch. Second, upgrading an existing learner is also easier than starting from scratch as many of the components (such as heuristics and search strategy) can be recycled. It is therefore also economic in terms of man power. Third, the upgraded system will be able to emulate the original one, which provides guarantees that the output hypotheses will perform well on attribute-value learning problems. Even more important is that it will often also be able to emulate extensions of the original systems. For instance, many systems that extend frequent item-set mining toward using richer representations, such as sequences, intervals, the use of taxonomies, graphs, and so on, have been developed over the past decade. Many of them can be emulated using the inductive logic programming upgrade of Apriori (Agrawal et al. 1996) called Warmr (Dehaspe and Toivonen 2001). The upgraded inductive logic programming systems will typically be more flexible than the systems it can emulate but typically also less efficient because there is a price to be paid for expressiveness. Finally, it may be possible to incorporate new features in the attribute-value learner by following the methodology. One feature that is often absent from propositional learners and may be easy to incorporate is the use of a background theory.

It should be mentioned that the methodology is not universal, that is, there exist also approaches, such as Muggleton’s Progol (1995), which have directly been developed in first-order logic and for which no propositional counterpart exists. In such cases, however, it can be interesting to follow the inverse methodology, which would specialize the inductive logic programming system.

FormalPara FOIL: An Illustration

One of the simplest and best-known inductive logic programming systems is FOIL (Quinlan 1990). It can be regarded as an upgrade of a rule learner such as CN2 (Clark and Niblett 1989). FOIL’s problem setting is an instance of the learning from entailment setting introduced above (though it restricts the background theory to ground facts only and does not allow functors).

Like most rule-learning systems, FOIL employs a separate-and-conquer approach. It starts from the empty hypothesis, and then repeatedly searches for one rule that covers as many positive examples as possible and no negative example, adds it to the hypothesis, removes the positives covered by the rule, and then iterates. This process is continued until all positives are covered. To find one rule, it performs a hill-climbing search through the space of clauses ordered according to generality. The search starts at the most general rule, the one stating that all examples are positive, and then repeatedly specializes it. Among the specializations, it then selects the best one according to a heuristic evaluation based on information gain. A heuristic, based on the minimum description length principle, is then used to decide when to stop specializing clauses.

The key differences between FOIL and its propositional predecessors are the representation and the operators used to compute the specializations of a clause. It employs a refinement operator under \(\theta\)-subsumption (Plotkin 1970) (see also Logic of Generality). Such an operator essentially refines clauses by adding atoms to the condition part of the clause or applying substitutions to a clause. For instance, the clause

    positive :- triangle(X),                 in(X,Y),                 color(X,C).

can be specialized to

    positive :- triangle(X),                 in(X,Y),                 color(X,red).

    positive :- triangle(X),                 in(X,Y),                 color(X,C),                 large(X).     positive :- triangle(X),                 in(X,Y),                 color(X,C),                 rectangle(Y). ...

The first specialization is obtained by substituting the variable C by the constant red, the other two by adding an atom (large(X), rectangle(Y), respectively) to the condition part of the rule. Inductive logic programming systems typically also employ syntactic restrictions – the so-called – that specify which clauses may be used in hypotheses. For instance, in the above example, the second argument of the color predicate belongs to the type Color, whereas the arguments of in are of type Object and consist of object identifiers.

FormalPara Application

Inductive logic programming has been successfully applied to many application domains, including bio- and chemo-informatics, ecology, network mining, software engineering, information retrieval, music analysis, web mining, natural language processing, toxicology, robotics, program synthesis, design, architecture, and many others. The best-known applications are in scientific domains. For instance, in structure–activity relationship prediction, one is given a set of molecules together with their activities, and background knowledge encoding functional groups, that is particular components of the molecule, and the task is to learn rules stating when a molecule is active or inactive. This is illustrated in Fig. 2 (after Srinivasan et al. 1996), where two molecules are active and two are inactive. One then has to find a pattern that discriminates the actives from the inactives. Structure–activity relationship (SAR) prediction is an essential step in, for instance, drug discovery. Using the general purpose inductive logic programming system Progol (Muggleton 1995) structural alerts, such as that shown in Fig. 2, have been discovered. These alerts allow one to distinguish the actives from the inactives – the one shown in the figure matches both of the actives but none of the inactives – and at the same time they are readily interpretable and provide useful insight into the factors determining the activity. To solve structure–activity relationship prediction problems using inductive logic programming, one must represent the molecules and hypotheses using the logical formalisms introduced above. The resulting representation is very similar to that employed in the Bongard problems: the objects are the atoms and relationships the bonds. Particular functional groups are encoded as background predicates.

Inductive Logic Programming, Fig. 2
figure 92figure 92

Predicting mutagenicity (Srinivasan et al. 1996)

Full size image
FormalPara State-of-the-Art

The upgrading methodology has been applied to a wide variety of machine learning systems and problems. There exist now inductive logic programming systems that:

  • Induce logic programs from examples under various learning settings. This is by far the most popular class of inductive logic programming systems. Well-known systems include Aleph (Srinivasan 2007) and Progol (Muggleton 1995) as well as various variants of FOIL (Quinlan 1990). Some of these systems, especially Progol and Aleph, contain many features that are not present in propositional learning systems. Most of these systems focus on a classification setting and learn the definition of a single predicate.

  • Induce logical decision trees from examples. These are binary decision trees containing conjunctions of atoms (i.e., queries) as tests. If a query succeeds, then one branch is taken, else the other one. Decision tree methods for both classification and regression exist (see Blockeel and De Raedt 1998; Kramer and Widmer 2001).

  • Mine for frequent queries, where queries are conjunctions of atoms. Such queries can be evaluated on an example. For instance, in the Bongard problem, the query ?- triangle (X), in (X, Y) succeeds on the leftmost scenes and fails on the rightmost ones. Therefore, its frequency would be 6. The goal is then to find all queries that are frequent, that is, whose frequencies exceed a certain threshold. Frequent query mining upgrades the popular local pattern mining setting due to Agrawal et al. (1996) to inductive logic programming (see Dehaspe and Toivonen 2001).

  • Learn or revise the definitions of theories, which consist of the definitions of multiple predicates, at the same time (cf. Wrobel 1996), and the entry in this encyclopedia. Several of these systems have their origin in the model inference system by Shapiro (1983) or the work by Angluin (1987).

FormalPara Current Trends and Challenges

There are two major trends and challenges in inductive logic programming. The first challenge is to extend the inductive logic programming paradigm beyond the purely symbolic one. Important trends in this regard include:

  • The combination of inductive logic programming principles with graphical and probabilistic models for reasoning about uncertainty. This is a field known as statistical relational learning, probabilistic logic learning, or probabilistic inductive logic programming. At the time of writing, this is a very popular research stream, attracting a lot of attention in the wider artificial intelligence community, cf. the entry Statistical Relational Learning in this encyclopedia. It has resulted in many relational or logical upgrades of well-known graphical models including Bayesian networks, Markov networks, hidden Markov models, and stochastic grammars.

  • The use of relational distance measures for classification and clustering (Ramon and Bruynooghe 1998; Kirsten et al. 2001). These distances measure the similarity between two examples or clauses, while taking into account the underlying structure of the instances. These distances are then combined with standard classification and clustering methods such as k-nearest neighbor and k-means.

  • The integration of relational or logical representations in reinforcement learning, known as Relational Reinforcement Learning (Dzeroski et al. 2001).

The power of inductive logic programming is also its weakness. The ability to represent complex objects and relations and the ability to make use of background knowledge add to the computational complexity. Therefore, a key challenge of inductive logic programming is tackling this added computational complexity. Even the simplest method for testing whether one hypothesis is more general than another – that is, θ-subsumption (Plotkin 1970) – is NP-complete. Similar tests are used for deciding whether a clause covers a particular example in systems such as FOIL. Therefore, inductive logic programming and relational learning systems are computationally much more expensive than their propositional counterparts. This is an instance of the expressiveness versus efficiency trade-off in computer science. Because of these computational difficulties, inductive logic programming has devoted a lot of attention to efficiency issues. On the theoretical side, there exist various results about the polynomial learnability of certain subclasses of logic programs (cf. Cohen and Page 1995, for an overview). From a practical perspective, there is quite some work on developing efficient methods for searching the hypothesis space and especially for evaluating the quality of hypotheses. Many of these methods employ optimized inference engines based on Prolog or database technology or constraint satisfaction methods (cf. Blockeel and Sebag 2003 for an overview).

Cross-References

Footnote 1