Mutual Fund Industry Performance: A Network Data Envelopment Analysis Approach

Abstract

The objective of this chapter is twofold. First, we present a comprehensive review of the DEA literature that has evaluated mutual fund performance. Second, we present a two-stage DEA model that decomposes the overall efficiency of a decision-making unit into two components and demonstrate its applicability by assessing the relative performance of 66 large mutual fund families in the US over the period 1993–2008. By decomposing the overall efficiency into operational management efficiency and portfolio management efficiency components, we reveal the best performers, the families that deteriorated in performance, and those that improved in their performance over the sample period. We also make frontier projections for poorly performing mutual fund families and highlight how the portfolio managers have managed their funds relative to the others during financial crisis periods.

7.1 Introduction

The mutual fund industry in the US is by far the largest such industry in the world, managing US$14.3 trillion in assets by the end of the calendar year 2012. Research on performance at the mutual fund family level is limited (Tower and Zheng 2008; Elton et al. 2007), possibly due to the complex nature of the analysis involved. Despite the limited existing research to date, an understanding of performance (absolute and relative) at the fund family level is important as investors tend to invest in funds within the same mutual fund family rather than across a number of families. The reasons for investing within one mutual fund family include convenience in searching for investment opportunities and recordkeeping (Kempf and Ruenzi 2008) and flexibility of switching funds without additional sales charges and restrictions imposed by the fund family (Elton et al. 2006, 2007).

Mutual fund performance receives substantial coverage in much of the US financial press due to the rapid growth of the mutual fund industry as well as the vital role it plays in the financial market . Investors and media commentators are keen to acquire an enhanced understanding of operational aspects at both the fund level and the fund family level given the recent turmoil experienced in the US financial market. This chapter gives an overview of the US mutual fund industry for open funds and respond to the line of criticism faced by the standard DEA-models by using a two-stage network DEA model that decomposes the overall efficiency of a fund family into two components; an operational management efficiency and portfolio management efficiency and thereby making a contribution to the mutual fund performance appraisal literature and mutual fund industry at large. We demonstrate the application of the proposed DEA model by examining the relative performance of 66 large mutual fund families in the US over the period 1993–2008.

We conceptualise the activities of mutual fund management as a two-stage process as follows. In the first stage, we focus on the operational management aspect and investigate how efficiently the managers at the fund family level make use of inputs such as marketing and distribution expenses and management fees in producing the output, which is the net asset value. In the second stage, the focus is on the portfolio management aspect where we determine how efficiently the fund managers make use of inputs such as fund size, standard deviation of the returns, turnover ratio, expense ratio and net asset value in producing the output, which is fund family average return. Brown et al. (2001) point out that even though relative performance appears to be the overriding concern of fund managers as well as their clients, considerably less attention is directed towards the equally important question of relative performance appraisal of portfolios.

We treat net asset value (NAV) which is considered as the output variable at the first stage as an input variable in the second stage; that is, net asset value is modeled as an intermediate variable that links stage 1 with stage 2. Holod and Lewis (2011) treat deposits in the same way in the two-stage network DEA model they use in assessing bank performance. Our modelling framework aligns with the network structure of Färe and Whittaker (1995). Although we consider only one output from the first stage and one output from the second stage in this particular application, the DEA model that we use here allows multiple inputs, outputs and intermediate measures (Premachandra et al. 2012).

Our model splits the overall process of a DMU into two stages and assesses the efficiencies of both stages simultaneously. Our two-stage network DEA model not only assesses the overall performance of the DMUs, but also decomposes the overall efficiency into two components associated with the performance in the two stages. Such a decomposition of overall efficiency is not possible in the previous network approach by Färe and Whittaker (1995). Furthermore, our modelling framework allows assessments under the variable returns to scale (VRS) as well as constant returns to scale (CRS) assumptions and as such it is not restrictive in terms of orientation as in Kao and Hwang’s (2008) two-stage model, which is valid only under the CRS assumption. Usually, in the two-stage DEA models, the intermediate variables that link stage 1 with stage 2 become the inputs of stage 2. Our model allows new variables as inputs in the second stage in addition to the intermediate variables. Interested reader is referred to Cook and Zhu (2014) for recent developments in network DEA modeling techniques.

The chapter is structured as follows: Sect. 7.2 provides an overview of the US mutual fund industry, Sect. 7.3 examines the literature on mutual fund performance appraisal, Sect. 7.4 formulates the two-stage DEA model and in Sect. 7.5 the data used in the application are presented. Section 7.6 analyses the fund family performance and Sect. 7.7 presents concluding remarks.

7.2 Background to US Mutual Fund Industry

According to the Investment Company Institute (ICI 2013), the mutual fund industry (MFI) in the United States is by far the largest such industry in the world (see Fig. 7.1), managing $13.1 trillion in assets as at the end of 2012 which accounts for 48.9 % of the $26.8 trillion worldwide value of assets under management in the industry. There has been a significant growth in US mutual fund industry over the 10 years from 2003 having almost doubled the total market value of assets under management to $7.4 trillion. The total value of funds under management in the US industry has rebounded since the onset of the global financial crisis ; increasing by 25 % since 2006. Measuring the growth of the MFI is much more complex than simply looking at the growth in dollar value of assets under management. Other dynamic measures such as net flow of funds into mutual funds (MFs) also matter.

Fig. 7.1

Global significance of United States Mutual Fund Asset Pool (December 2012). Source of data: Investment Company Fact Book 2010, Worldwide Total Net Assets of Mutual Funds. This figure reports the size of investment fund industries around the world. All dollar values are represented in billions of US dollars at the end of the 2012 calendar year

At year-end 2012 (ICI 2013), the number of fund products constituting the US MFI was approximately 7596 sponsored by more than 700 fund families. Nevertheless, since the dawn of the new millennium the percentage of industry assets invested in larger fund complexes has increased. The share of the assets managed by the largest ten US fund families in 2012 was 53 %, up from the 44 % in 2000. Long run competitive dynamics have prevented any single fund or family of funds from dominating the market. For example, out of the largest 25 fund complexes in 1995, only 15 remained at the top level in 2012. The composition of the assets held in the top 25 fund complexes has changed significantly with a relative reduction in domestic equity holdings and an increase in money market funds. Nevertheless, this could be representative of the financial situation that prevail post 2008 meltdown. The Herfindahl Hirschman Index for the US MFI is 465 (ICI 2013, p. 25) which is well below the 1000 that is considered as the cutoff for a concentrated industry. To this end, it is deemed that the US MFI still offers to investors products that vary significantly in size, number of investment classes, investment horizon, and management style.

7.3 Prior Research on Performance Appraisal of Mutual Funds and Mutual Fund Families

One of the major motivations for mutual fund managers, whether at the fund family level or at the fund product level , is to maintain high standard of performance compared to their peers so that in the event of a temporary setback they are able to manage possible cash outflows and potential job losses better. This is a vital challenge for fund family managers in the US due to the increasing competition within the mutual fund industry. Maintaining high standard of performance is consistent with fund family managers minimizing controllable efforts (inputs) to achieve the highest possible level of return (outputs) defined by a production frontier (Charnes et al. 1978). This phenomenon which is consistent with the economic theory on optimization provides a strong motivation for adopting the production frontier concept in performance appraisal of mutual funds.

Fund family managers aim for their products to lie on the outer extremities of the production frontier so that their funds are more efficient than the other funds of comparable type. However, in reality, they may fall short due to reasons within and sometimes beyond their control. It is this notion of a shortfall of performance of some mutual funds relative to other funds in the sample that aligns with the concept of production inefficiency which is a measurable quantity.

In the past 25 years, innovative approaches have been introduced to measure mutual fund performance at both the individual fund product level (Murthi et al. 1997; McMullen and Strong 1998) and more recently at the fund family level (Premachandra et al. 2012). In general, the findings support the assertion that fund managers should be concerned about inefficiencies not only in managing funds but also in their operations. Table 7.1 presents a summary of the used DEA model, the input and output variables and the key findings of some of the significant studies conducted on mutual fund performance appraisal since the pioneering work in the investment funds area by Murthi et al. (1997).

Table 7.1 Summary of relevant literature

DEA has the following unique features . First, DEA does not require a priori assumption on the relation between inputs and outputs. It can handle multiple performance measures classified as inputs and outputs in a single mathematical model without the need for trade-off between the inputs and outputs associated with performance. The literature has shown DEA to be a valuable instrument for performance evaluation and benchmarking (Zhu 2002; Cooper et al. 2004). Second, DEA examines each DMU independently by generating individual performance (efficiency) scores that are relative to the DMUs in the entire sample under investigation. Misspecification, a recurring problem in regression analysis, is not a concern with DEA models since DEA creates the best practice frontier based on comparison of the peers in the sample. Third, it has been documented that DEA can assist with the study of a frontier shift over a time horizon, using for example, the DEA-based Malmquist index of Fare et al. (1997). This allows exploration of the dynamic change of fund family failure or success over time. The fourth advantage is that DEA does not need a large sample size (usually required by statistical and econometric approaches ) for the evaluation of mutual funds or mutual fund families. The need for large sample sizes is a significant drawback when investment decisions have to be made using smaller samples. DEA can bypass such practical difficulties (see Premachandra et al. 2009).

Selection of performance measures or input and output factors is an important issue in DEA application (see Cook et al. 2014). For risk-averse investors , the capital market theory dictates that the higher the risk that you take in the investment, the greater is the return. This implies a functional relationship between risk and return. Hence, in principle, it follows that risk measures may be considered as inputs in the DEA model and return measures as outputs. McMullen and Strong (1998) document the relation between risk and return and highlight that investors are concerned about risk and return over various time horizons as that allows investors to obtain greater information about a fund than simply looking at performance over a single time period. In addition to the risk–return trade-off, Murthi et al. (1997) report that investors are equally concerned about transaction costs such as subscription and redemption fees. Basso and Funari (2001, 2005) document that some investors also consider ethical criteria in their decisions. Thus, there is no consensus among researchers as to what input and output variables should be included in a DEA model when investigating the relative performance of mutual fund products.

In mutual fund performance appraisal, some of the input output factors considered in the DEA model such as the annual average return of a fund may take negative values. This problem can easily be resolved by translating such variables into positive values by adding a constant and then using an appropriate translation invariant DEA model. For example, the input-oriented BCC model (BCC-I) is translation invariant with respect to outputs, but not inputs. Similarly, the output oriented BCC model (BCC-O) is invariant under the translation of inputs, but not outputs. The additive DEA model is translation invariant in both inputs and outputs (See for example Cooper et al. (2006) for details). Table 7.1 lists various DEA models that have been used for mutual fund performance appraisal in the past. The standard DEA models do not account for the activities involved in transforming inputs into outputs and instead consider the DMU operation as a black box. In our case, we look inside this black box and consider the process of overall management of mutual fund families (the DMUs of our empirical application) as a combination of two sub processes namely; operational management and portfolio management.

7.4 Development of the Two-Stage DEA Model

Cook et al. (2010) document that in many instances, the underlying process of generating outputs from inputs may have a two-stage network structure with intermediate measures where outputs from the first stage become the inputs to the second stage. Chilingerian and Sherman (2004) describe such a two-stage process used in measuring physician care. Their first stage is a manager-controlled process and the second stage is a physician-controlled process . In their model, the output of the first-stage is considered as input to the second stage. The factors that link the two stages are called intermediate measures . Kao and Hwang (2008) consider the process of Taiwanese non-life-insurance companies as a two-stage process of premium acquisition and profit generation. In our application, we assume that the activities of mutual fund families can be viewed as a two-stage process where stage 1 represents the operational management process and stage 2 represents the portfolio management process. In the current application, the overall efficiency of a mutual fund family is conceptualized as made up of two components; operational management efficiency (hereinafter referred to as operational efficiency) and portfolio management efficiency (hereinafter referred to as portfolio efficiency). A schematic diagram of the mutual fund family management process is given in Fig. 7.2. In stage 1, the fund family management makes an attempt to attract funds from the investors and therefore outgoings such as management fees (I ₁) and marketing and distribution expenses (I ₂) that contribute directly towards generating funds are considered as the input variables. In stage 1 of Fig. 7.2, we consider the net asset value labeled O ₁ as the output variable. Hence, a mutual fund family that produces the highest net asset value with the least amount of management fees and marketing and distribution expenses is considered to be operationally more efficient than the other families in the sample. Stage 2 is the portfolio management stage. Here we treat net asset value (O ₁), fund size (I ₃), net expense ratio (I ₄), turnover ratio (I ₅) and standard deviation of the returns of the family portfolio over the last 3 years (I ₆) as the input variables and mean return of the family portfolio (O ₂) as the output variable. Since net asset value (O ₁), which is an output variable of stage 1 is also an input variable of stage 2 (I ₇), it becomes an intermediate variable. I ₇ is not observable; it is obtained by adjusting O ₁ which is observed. In stage 2, a fund family that produces the highest average family portfolio return with the least amount of net asset value, fund size, net expense ratio, turnover ratio, and standard deviation is deemed more efficient compared to the other families in the sample.

Fig. 7.2

The proposed two-stage DEA model for evaluating the efficiency of mutual fund families . At stage 1, the operational management efficiency will be estimated, and at stage 2 the portfolio management efficiency will be estimated. The overall efficiency of the fund family is decomposed into the operational management efficiency (stage 1) and the portfolio management efficiency (stage 2). Variables I ₁ and I ₂ are the input variables and O ₁ is the output variable at stage 1 and I ₃, I ₄, I ₅, I ₆ and I ₇ are the input variables and O ₂ is the output variable at stage 2. Net asset value is an intermediate variable and therefore I ₇ is the expected value of O ₁ estimated in stage 1

A common approach to solving two-stage network problems illustrated in Fig. 7.2 is to assume that the two stages operate independently and apply a standard DEA model separately in each stage. Various problems could arise due to this approach. For example, in stage 1, a fund may attempt to maximize its outputs in order to achieve its performance in the best possible light. As these outputs from stage 1 become inputs to the second stage, high output from stage 1 may lead to poor assessment of performance in the second stage if the optimization criterion at stage 2 is maximization type where more output with less input is preferred. Kao and Hwang (2008) and Liang et al. (2008) overcome this problem under the CRS assumption by assessing that the overall efficiency of the two-stage process as the product of the efficiencies of the two stages. Chen et al. (2009) extend Kao and Hwang (2008) approach by using additive efficiency decomposition under both the CRS and VRS . In the proposed model, we use the VRS assumption, as one of the output variables (average return) used in our empirical application can be negative. The standard VRS DEA model has the translation invariance property so that a constant may be added to all values of the negative valued output variable to make them positive without altering the efficient frontier and the position of the funds relative to the efficient frontier (see Ali and Seiford 1990).

The two stage process proposed in Fig. 7.2 is different from the two-stage process considered in Kao and Hwang (2008), Liang et al. (2008), and Chen et al. (2010) in the sense that we allow new inputs to the second stage in addition to the intermediate measures. The network DEA approach of Färe and Whittaker (1995) and Färe and Grosskopf (1996), the slack-based network DEA approach of Tone and Tsutsui (2009) and the dynamic effects in production networks of Chen (2009) are more general versions of the two-stage process described in Fig. 7.2. However, they do not yield efficiencies at individual stages. We have overcome this problem in the network DEA model used in this chapter. For a review of the relevant recent literature on modeling of network processes, see Cook et al. (2010) and Cook and Zhu (2014). An application of the network DEA approach is available in Lewis and Sexton (2004). The existing approaches cannot be readily adopted to model the situation depicted in Fig. 7.2 and therefore in this study we present a new network DEA approach.

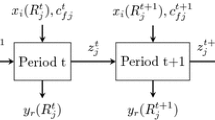
In order to understand the basic concepts behind the proposed two-stage DEA model, consider the simplified version presented in Fig. 7.3. Suppose we have one input (x1) to stage 1, one intermediate measure (z), one additional input (x2) to stage 2 and one output (y) from stage 2. To measure the overall efficiency of the two-stage process, we first calculate the expected (efficient) output y from stage 2 using input x1 indirectly and input x2 directly with an intermediate measure z. Assume that the DMU should have produced an output z* with input x1 had it operated efficiently in stage 1 and should have produced an output y* with inputs z* and x2 in stage 2. Then a measure of overall efficiency is y/y*, a measure of stage 1 efficiency is z/z* and a measure of stage 2 efficiency is (z* + x2)/(z + x2).

Fig. 7.3

A simplified two-stage framework of mutual fund family performance . This is a simplified version of the complete two-stage DEA model illustrated in Fig. 7.1. x1 and x2 are the input variables for stage 1 and 2, respectively, and z is the intermediate variable that links the two stages. y is the output variable in stage 2

When calculating the expected (efficient) output of stage 2, we require the intermediate measure to be the expected (efficient) output of stage 1. When this concept is generalized to the case with multiple intermediate measures, the “aggregate” value of intermediate measures must remain the same. According to Liang et al. (2008), such a modeling process treats the two stages as players in a cooperative game where both players “negotiate” on the expected value of intermediate measures. Such a modeling process does not fit into a standard DEA approach. Rather, it optimizes a joint efficiency of the two stages subject to the condition that the intermediate input to stage 2 is the expected output from stage 1. In that regard, the approach used in the two-stage DEA model proposed in this chapter is different from the iterative process used by Holod and Lewis (2011). Their two-stage process is based upon a non-oriented standard DEA model and does not provide separate efficiency estimates for each stage.

Next, we describe the DEA-based procedure used in this chapter to model the relationship between the overall efficiency and the efficiencies at stage 1 and stage 2 in a single mathematical model under the VRS assumption.

Consider a general two-stage DEA network structure for DMU-j with i ₁ inputs to stage 1 denoted by ${X}_j^1 = \left\{{x}_{1j}^1,{x}_{2j}^1,\dots, {x}_{i_1j}^1\right\}$, i ₂ inputs to stage 2 denoted by ${X}_j^2 = \left\{{x}_{1j}^2,{x}_{2j}^2,\dots, {x}_{i_2j}^2\right\}$, D intermediate measures denoted by z _dj (d = 1, … , D), and s outputs from stage 2 denoted by y _rj (r = 1, … , s). With respect to our mutual fund family example in Fig. 7.1, X ¹ has two input variables, X ² has four input variables, z has one variable, and y has one variable. Following Banker et al. (1984), the VRS efficiency score of DMU _o at the first and second stages can be calculated using models (7.1) and (7.2), respectively.

$$ \begin{array}{l} Max\kern0.6em \frac{{\displaystyle \sum_d{\eta}_d^1{z}_{do}}+{u}^1}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}}\\ {}s.t.\kern1em \frac{{\displaystyle \sum_d{\eta}_d^1{z}_{dj}}+{u}^1}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1j}^1}}\le 1,\kern1.1em j=1,2,\dots, n\\ {}\kern2em {v}_{i_1}^1,{\eta}_d^1\ge \varepsilon; \kern0.5em {u}^1\ \mathrm{free}\end{array} $$

(7.1)

$\left({v}_{i_1}^1,{\eta}_d^1\right)$ are decision variables (weights) associated with the inputs to the first stage and the intermediate measures (outputs from the first stage). u ¹ is a free variable associated with returns to scale (RTS) in DEA for stage 1.

$$ \begin{array}{l} Max\kern0.6em \frac{{\displaystyle \sum_r{u}_r{y}_{ro}}+{u}^2}{{\displaystyle \sum_d{\eta}_d^2{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}\\ {}s.t.\kern1em \frac{{\displaystyle \sum_r{u}_r{y}_{rj}}+{u}^2}{{\displaystyle \sum_d{\eta}_d^2{z}_{dj}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2j}^2}}\le 1,\kern1.1em j=1,2,\dots, n\\ {}\kern2em {v}_{i_2}^2,\kern0.1em {u}_r\kern0.1em ,{\eta}_d^2\ge \varepsilon; \kern0.6em {u}^2\kern0.5em \mathrm{free}\end{array} $$

(7.2)

(${v}_{i_2}^2\kern0.1em ,\kern0.2em {u}_r\kern0.1em ,\kern0.2em {\eta}_d^2$) are decision variables (weights) associated with the inputs to the second stage, the intermediate measures and outputs from the second stage. u ² is a free variable associated with RTS in DEA for stage 2.

Note that if we assume ${u}^1={u}^2=0$, then the above models become the CRS models of Charnes et al. (1978) and therefore the following discussion is applicable to the CRS case as well. Similar to Kao and Hwang’s (2008) assumption and the centralized model in Liang et al. (2008), we assume that ${\eta}_d^1={\eta}_d^2={\eta}_d$ (d = 1, … , D) in models (7.1) and (7.2). This assumption ensures that in both stages the same multipliers (weights) are applied to the intermediate measures. Then, as far as the intermediate variables are concerned, the expected outputs from stage 1 will be equal to the expected inputs to the second stage.

As in Chen et al. (2009), we compute the overall efficiency as a weighted average of the efficiency scores from stages 1 and 2 as

$$ {w}_1\cdot \frac{{\displaystyle \sum_d{\eta}_d{z}_{do}}+{u}^1}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}}+{w}_2\cdot \frac{{\displaystyle \sum_r{u}_r{y}_{ro}}+{u}^2}{{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}} $$

(7.3)

where w ₁ and w ₂ are user-specified weights such that ${w}_1+{w}_2=1$. If the geometric average as in Kao and Hwang (2008) is used, the product of $\frac{{\displaystyle \sum_d{\eta}_d{z}_{do}+{u}^1}}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}}$ and $\frac{{\displaystyle \sum_r{u}_r{y}_{ro}+{u}^2}}{{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}$ will not yield a linear objective function due to the fact that ${\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}$ cannot be cancelled. If we assume that ${X}_j^2=\left\{\right\}$ and u ¹ = 0, the model would reduce to the CRS version and then the approach of Kao and Hwang (2008) can be applied.

In Sect. 7.4.1 we present further details on how the 2-stage model can be generalised by converting (7.3) along with models (7.1) and (7.2) when ${\eta}_d^1={\eta}_d^2={\eta}_d$ (d = 1, … , D). We also show how to decompose the overall efficiency and develop a procedure to determine whether the decomposed efficiency scores are unique.

7.4.1 DEA Model for Two-Stage Network and Efficiency Decomposition

Since w ₁ and w ₂ in (7.3) are intended to reflect the relative importance or the contribution of the performance in the first and the second stage to the overall performance, a reasonable choice of weights is the proportion of total resources devoted to each stage. To be more specific, we define

$$ {w}_1=\frac{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}+{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}\kern1em \mathrm{and}\kern1em {w}_2=\frac{{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}+{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}} $$

(7.4)

where ${\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}+{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}$ represents the total amount of resources (inputs) consumed by the entire two-stage process and ${\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}$ and ${\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}$ represents the amount of resources consumed in the first and the second stage, respectively. These weights are functions of the decision variables of models (7.1) and (7.2).

Hence, under VRS, the overall efficiency score of DMU _o in the two-stage process can be evaluated by solving the following fractional program (7.5). The constraints in (7.5) ensure that the efficiency scores of a DMU in both stages are non-negative and no greater than unity.

$$ \begin{array}{l}{\theta}_o^{*}= Max\kern0.5em \frac{{\displaystyle \sum_d{\eta}_d{z}_{do}}+{u}^1+{\displaystyle \sum_r{u}_r{y}_{ro}}+{u}^2}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}+{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}\\ {}\kern2em s.t.\kern1em \frac{{\displaystyle \sum_d{\eta}_d{z}_{do}}+{u}^1}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1j}^1}}\le 1,\kern1.1em j=1,2,\dots, n\\ {}\kern4em \frac{{\displaystyle \sum_r{u}_r{y}_{ro}}+{u}^2}{{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2j}^2}}\le 1,\kern1.1em j=1,2,\dots, n\\ {}\kern4em 1\ge {w}_1=\frac{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}+{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}\ge {w}_1^o\\ {}\kern4em 1\ge {w}_2=\frac{{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}+{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}\ge {w}_2^o\\ {}\kern4em {v}_{i_1}^1\kern0.1em ,\kern0.1em {v}_{i_2}^2\kern0.1em ,\kern0.3em {u}_r\kern0.1em ,\kern0.2em {\eta}_d\ge \varepsilon, \kern1em {u}^1,\kern0.1em {u}^2\kern0.5em \mathrm{free}\end{array} $$

(7.5)

Sensitivity analysis of the weights w ₁ and w ₂ can be performed by adding lower bounds w ^o₁ and w ^o₂ on w ₁ and w ₂. In this study, we substitute 50 % for both w ^o₁ and w ^o₂ assuming that operational management and portfolio management are equally important functions.

By applying the Charnes–Cooper transformation , the above fractional programming model (7.5) can be transformed into the following linear programming model (7.6).

$$ \begin{array}{l}{\theta}_o^{*}= Max\kern0.5em {\displaystyle \sum_d{\pi}_d{z}_{do}}+{\displaystyle \sum_r{\mu}_r{y}_{ro}}+{u}^A+{u}^B\\ {}\kern2em s.t.\kern1em {\displaystyle \sum_d{\pi}_d{z}_{dj}}+{u}^A\le {\displaystyle \sum_{i_1}{\omega}_{i_1}^1{x}_{i_1j}^1}\kern0.2em ,\kern1em j=1,2,\dots, n\\ {}\kern4em {\displaystyle \sum_r{\mu}_r{y}_{rj}}+{u}^B\le {\displaystyle \sum_d{\pi}_d{z}_{dj}}+{\displaystyle \sum_{i_2}{\omega}_{i_2}^2{x}_{i_2j}^2},\kern1.1em j=1,2,\dots, n\\ {}\kern4em {\displaystyle \sum_{i_1}{\omega}_{i_1}^1{x}_{i_1o}^1}+{\displaystyle \sum_d{\pi}_d{z}_{do}}+{\displaystyle \sum_{i_2}{\omega}_{i_2}^2{x}_{i_2o}^2}=1\\ {}\kern4em 1\ge {\displaystyle \sum_{i_1}{\omega}_{i_1}^1{x}_{i_1o}^1}\ge {w}_1^o\\ {}\kern4em 1\ge {\displaystyle \sum_d{\pi}_d{z}_{do}}+{\displaystyle \sum_{i_2}{\omega}_{i_2}^2{x}_{i_2o}^2}\ge {w}_2^o\\ {}\kern4em {\omega}_{i_1}^1\kern0.1em ,{\omega}_{i_2}^2\kern0.1em ,{\mu}_r,\kern0.1em {\pi}_d\ge \varepsilon, \kern1em {u}^A,{u}^B\kern0.5em \mathrm{free}\end{array} $$

(7.6)

7.4.1.1 Efficiency Decomposition

Once we obtain an optimal solution to (7.6), the efficiency scores for the two individual stages can be calculated as ${\theta}_o^{1*}=\frac{{\displaystyle \sum_d{\pi}_d^{*}{z}_{do}+{u}^{A*}}}{{\displaystyle \sum_{i_1}{\omega}_{i_1}^{1*}{x}_{i_1o}^1}}$ and ${\theta}_o^{2*}=\frac{{\displaystyle \sum_r{\mu}_r^{*}{y}_{ro}+{u}^{B*}}}{{\displaystyle \sum_d{\pi}_d^{*}{z}_{do}}+{\displaystyle \sum_{i_2}{\omega}_{i_2}^{2*}{x}_{i_2o}^2}}$. We can also obtain a set of weights as ${w}_1^{*}={\displaystyle \sum_{i_1}{\omega}_{i_1}^{1*}{x}_{i_1o}^1}$, ${w}_2^{*}=1-{w}_1^{*}$. However, since model (7.6) can have multiple optimal solutions, the θ ^1 * _o and θ ^2 * _o components of overall efficiency may not be unique. Therefore, we follow the procedure adopted by Kao and Hwang (2008) and Chen (2009) to obtain a set of multipliers that would produce the highest first- or second-stage efficiency score while maintaining the overall efficiency score of the entire process fixed. Denote the overall efficiency score of DMU _o obtained by model (7.6) as θ ^* _o . We maximize the first-stage efficiency score first while maintaining the overall efficiency score at θ ^* _o and the weighted first- and second-stage efficiency scores at no greater than unity as

$$ \begin{array}{l}{\theta}_o^{1\kern0.2em *}= Max\kern1em \frac{{\displaystyle \sum_d{\eta}_d{z}_{do}}+{u}^1}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}}\kern3.75em \\ {}\kern2em \mathrm{s}.\mathrm{t}.\ \frac{{\displaystyle \sum_d{\eta}_d{z}_{dj}}+{u}^1}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1j}^1}}\le 1\kern0.1em ,\kern1em j=1,2,\dots, n\kern1em \left(\mathrm{a}\right)\\ {}\kern3em \frac{{\displaystyle \sum_r{u}_r{y}_{rj}}+{u}^2}{{\displaystyle \sum_d{\eta}_d{z}_{dj}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2j}^2}}\le 1,\kern1.1em j=1\kern0.1em ,2\kern0.1em ,\dots, n\kern1em \left(\mathrm{b}\right)\\ {}\kern3em \frac{{\displaystyle \sum_d{\eta}_d{z}_{dj}}+{u}^1+{\displaystyle \sum_r{u}_r{y}_{ro}}+{u}^2}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}+{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}={\theta}_o^{*}\kern1em \left(\mathrm{c}\right)\\ {}\kern3em 1\ge {w}_1=\frac{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}+{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}\ge {w}_1^o\\ {}\kern3em 1\ge {w}_2=\frac{{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}{{\displaystyle \sum_{i_1}{v}_{i_1}^1{x}_{i_1o}^1}+{\displaystyle \sum_d{\eta}_d{z}_{do}}+{\displaystyle \sum_{i_2}{v}_{i_2}^2{x}_{i_2o}^2}}\ge {w}_2^o\\ {}\kern3em {v}_{i_1}^1\kern0.1em ,\kern0.1em {v}_{i_2}^2\kern0.1em ,\kern0.3em {u}_r,\kern0.2em {\eta}_d\ge \varepsilon, \kern1em {u}^1,\kern0.1em {u}^2\kern0.5em \mathrm{free}\end{array} $$

(7.7)

In model (7.7), the constraints (a) and (b) ensure that the efficiency scores of all DMUs at both stages are no greater than unity and the constraint (c) maintains the overall efficiency score at θ ^* _o . Model (7.7) can be converted into the following equivalent linear program (7.8).

$$ \begin{array}{l}{\theta}_o^{1\kern0.2em *}= Max\kern0.5em {\displaystyle \sum_d{\pi}_d{z}_{do}}+{u}^A\\ {}\kern2.5em s.t.\kern1em {\displaystyle \sum_d{\pi}_d{z}_{dj}}+{u}^A\le {\displaystyle \sum_{i_1}{\omega}_{i_1}^1{x}_{i_1j}^1}\kern0.2em ,\kern1em j=1,2,\dots, n\\ {}\kern4.5em {\displaystyle \sum_r{\mu}_r{y}_{rj}}+{u}^B\le {\displaystyle \sum_d{\pi}_d{z}_{dj}}+{\displaystyle \sum_{i_2}{\omega}_{i_2}^2{x}_{i_2j}^2},\kern0.1em j=1,2,\dots, n\\ {}\kern4.5em {\displaystyle \sum_d{\pi}_d{z}_{do}}+{\displaystyle \sum_r{\mu}_r{y}_{rj}}+{u}^A+{u}^B-{\theta}_o^{*}\kern0.2em \left(\kern0.2em 1+{\displaystyle \sum_d{\pi}_d{z}_{do}}+{\displaystyle \sum_{i_2}{\omega}_{i_2}^2{x}_{i_2o}^2}\right)=0\\ {}\kern4.5em {w}_1^o\kern0.2em \left(1+{\displaystyle \sum_d{\pi}_d{z}_{do}}+{\displaystyle \sum_{i_2}{\omega}_{i_2}^2{x}_{i_2o}^2}\right)\le 1\\ {}\kern4.5em \left(1-{w}_2^o\right)\kern0.3em \left({\displaystyle \sum_d{\pi}_d{z}_{do}}+{\displaystyle \sum_{i_2}{\omega}_{i_2}^2{x}_{i_2o}^2}\right)\ge {w}_2^o\\ {}\kern4.5em {\displaystyle \sum_{i_1}{\omega}_{i_1}^1{x}_{i_1o}^1}=1\\ {}\kern4.5em {\omega}_{i_1}^1\kern0.1em ,{\omega}_{i_2}^2\kern0.1em ,\kern0.1em {\mu}_r,\kern0.1em {\pi}_d\ge \varepsilon, \kern1em {u}^A\kern0.1em ,{u}^B\kern0.5em \mathrm{free}\end{array} $$

(7.8)

Let ${\omega}_{i_1}^{1\kern0.1em *}\kern0.1em ,\kern0.1em {\omega}_{i_2}^{2\kern0.1em *}\kern0.1em ,\kern0.3em {\mu}_r^{*}\kern0.1em ,\kern0.2em {\pi}_d^{*},\kern0.3em {u}^{A\kern0.2em *},\kern0.3em {u}^{B\kern0.2em *}$ represent the optimal values of ${\omega}_{i_1}^1\kern0.1em ,\kern0.1em {\omega}_{i_2}^2\kern0.1em ,\kern0.3em {\mu}_r\kern0.1em ,\kern0.2em {\pi}_d\kern0.1em ,\kern0.2em {u}^A,\kern0.2em {u}^B$ in model (7.8). Then the first-stage efficiency score is ${\theta}_o^{1\kern0.2em *}={\displaystyle \sum_d{\pi}_d^{*}{z}_{do}}+{u}^{A\kern0.2em *}$ and the optimal weights for the two stages are ${w}_1^{*}=\frac{1}{1+{\displaystyle \sum_d{\pi}_d^{*}{z}_{do}}+{\displaystyle \sum_{i_2}{\omega}_{i_2}^{2\kern0.1em *}{x}_{i_2o}^2}}$ and ${w}_2^{*}=1-{w}_1^{*}$, respectively. The second-stage efficiency score for DMU _o is calculated as ${\theta}_o^2=\frac{\theta_o^{*}-{w}_1^{*}{\theta}_o^{1\kern0.2em *}}{w_2^{*}}$. Note that (*) is used in θ ^1 * _o to indicate that the first-stage efficiency score is optimized first. In this case, the resulting efficiency score for the second stage is denoted by θ ² _o (without *).

Similarly, the following linear program can be formulated to maximize the second-stage efficiency score while maintaining the overall efficiency score at θ ^* _o and the weighted first- and second-stage efficiency score at no greater than unity as

$$ \begin{array}{l}{\theta}_o^{2\kern0.2em *}= Max\kern0.5em {\displaystyle \sum_r{\mu}_r{y}_{ro}}+{u}^B\\ {}\kern2.5em s.t.\kern1em {\displaystyle \sum_d{\pi}_d{z}_{dj}}+{u}^A\le {\displaystyle \sum_{i_1}{\omega}_{i_1}^1{x}_{i_1j}^1}\kern0.1em ,\kern1em j=1,2,\dots, n\\ {}\kern4em {\displaystyle \sum_r{\mu}_r{y}_{rj}}+{u}^B\le {\displaystyle \sum_d{\pi}_d{z}_{dj}}+{\displaystyle \sum_{i_2}{\omega}_{i_2}^2{x}_{i_2j}^2}\kern0.2em ,\kern1.1em j=1,2\kern0.1em ,\dots, n\\ {}\kern4em {\displaystyle \sum_d{\pi}_d{z}_{do}}+{\displaystyle \sum_r{\mu}_r{y}_{ro}}+{u}^A+{u}^B-{\theta}_o^{*}\kern0.2em \left(\kern0.2em {\displaystyle \sum_{i_1}{\omega}_{i_1}^1{x}_{i_1o}^1}+1\right)=0\\ {}\kern4em \left(\kern0.2em 1-{w}_1^o\right)\kern0.2em {\displaystyle \sum_{i_1}{\omega}_{i_1}^1{x}_{i_1o}^1}\ge {w}_1^o\\ {}\kern4em {w}_2^o\kern0.2em \left(\kern0.2em {\displaystyle \sum_{i_1}{\omega}_{i_1}^1{x}_{i_1o}^1}+1\right)\le 1\\ {}\kern4em {\displaystyle \sum_d{\pi}_d{z}_{do}}+{\displaystyle \sum_{i_2}{\omega}_{i_2}^2{x}_{i_2o}^2}=1\\ {}\kern4em {\omega}_{i_1}^1\kern0.1em ,\kern0.1em {\omega}_{i_2}^2\kern0.1em ,\kern0.3em {\mu}_r\kern0.1em ,\kern0.2em {\pi}_d\ge \varepsilon, \kern1em {u}^A,\kern0.1em {u}^B\kern0.5em \mathrm{free}\end{array} $$

(7.9)

Let ${\omega}_{i_1}^{1\kern0.1em *}\kern0.1em ,\kern0.1em {\omega}_{i_2}^{2\kern0.1em *}\kern0.1em ,\kern0.3em {\mu}_r^{*}\kern0.1em ,\kern0.3em {\pi}_d^{*},\kern0.3em {u}^{A\kern0.2em *},\kern0.3em {u}^{B\kern0.2em *}$ represent the optimal values of ${\omega}_{i_1}^1\kern0.1em ,\kern0.1em {\omega}_{i_2}^2\kern0.1em ,\kern0.3em {\mu}_r\kern0.1em ,\kern0.2em {\pi}_d\kern0.1em ,\kern0.2em {u}^A,\kern0.2em {u}^B$ in model (7.9). Then the second-stage efficiency score is ${\theta}_o^{2\kern0.2em *}={\displaystyle \sum_r{\mu}_r^{*}{y}_{r0}}+{u}^{B\kern0.2em *}$ and the optimal weights for the two stages are ${w}_2^{*}=\frac{1}{{\displaystyle \sum_{i_1}{\omega}_{i_1}^{1\kern0.1em *}{x}_{i_1o}^1}+1}$ and ${w}_1^{*}=1-{w}_2^{*}$, respectively. The first-stage efficiency score is calculated as ${\theta}_o^1=\frac{\theta_o^{*}-{w}_2^{*}{\theta}_o^{2\kern0.2em *}}{w_1^{*}}$. If the results satisfy ${\theta}_o^1={\theta}_o^{1*}$ and ${\theta}_o^2={\theta}_o^{2*}$, then we may conclude that the decomposed efficiency scores are unique.

As in the conventional DEA models , the efficiency scores obtained for stages 1 and 2 provide information on how an inefficient unit can improve its performance. However, because the optimal (frontier projection) intermediate measures need to be determined, as noted in Chen et al. (2010), one needs to rely on the envelopment form of the DEA model to derive the DEA frontier for the two-stage process. Note that our two-stage network structure is different from the one discussed in Chen et al. (2010) with added additional multiple inputs to the second stage. Therefore, in Sect. 7.4.1.2 we develop a new model for providing information on how to improve the DMUs’ performance under our newly developed two-stage DEA network model.

7.4.1.2 Frontier Projection

Model (7.6) does not yield information on optimal intermediate measures. Therefore, following Chen et al. (2010), we develop a model for frontier projection of the DMUs as follows:

$$ \begin{array}{l} \min\ \left({w}_1^{*}\alpha +{w}_2^{*}\beta \right)-\varepsilon \left({\displaystyle \sum_{i_1}{s}_{i_1}^{1-}}+{\displaystyle \sum_{i_2}{s}_{i_2}^{2-}}+{\displaystyle \sum_r{s}_r^{+}}\right)\\ {}s.t.\kern1em {\displaystyle \sum_{j=1}^n{\lambda}_j{x}_{i_1j}^1}+{s}_{i_1}^{1-}=\alpha {x}_{i_1o}^1,\kern1.1em {i}_1=1,2\kern0.1em ,\dots, \\ {}\kern2em {\displaystyle \sum_{j=1}^n{\lambda}_j{z}_{dj}}={\displaystyle \sum_{j=1}^n{\mu}_j{z}_{hj}}\kern0.1em ,\kern1em d=1,\kern0.1em 2,\dots, D\\ {}\kern2em {\displaystyle \sum_{j=1}^n{\lambda}_j}=1\\ {}\kern2em {\displaystyle \sum_{j=1}^n{\mu}_j{x}_{i_2j}^2}+{s}_{i_2}^{2-}=\beta {x}_{i_2o}^2,\kern1em {i}_2=1,\kern0.1em 2,\dots, \\ {}\kern2em {\displaystyle \sum_{j=1}^n{\mu}_j{y}_{rj}}-{s}_r^{+}={y}_{ro},\kern1em r=1\kern0.1em ,2,\dots, s\\ {}\kern2em {\displaystyle \sum_{j=1}^n{\mu}_j}=1\\ {}\kern2em {\lambda}_j,{\mu}_j,{s}_{i_1}^{1-},{s}_{i_2}^{2-},{s}_r^{+}\ge 0\end{array} $$

(7.10)

where w ^*₁ , w ^*₂ are obtained from the two-stage network DEA model developed in Sect. 7.4.1.

The above model is based on the production possibility set with ${\displaystyle \sum_{j=1}^n{\lambda}_j}=1$ and ${\displaystyle \sum_{j=1}^n{\mu}_j}=1$ indicating that both stages exhibit VRS, as in the standard DEA model. ${\displaystyle \sum_{j=1}^n{\lambda}_j{z}_{dj}}={\displaystyle \sum_{j=1}^n{\mu}_j{z}_{hj}}\kern0.1em ,\kern0.5em d=1,\kern0.1em 2,\dots, \kern0.1em D$ ensures that both stages determine the optimal (frontier projection) intermediate measures.

If we fix α and β in the above model as θ ^1 * _o and θ ^2 * _o obtained from our two-stage model, model (7.10) adopts the principle of the “second-stage” model for calculating DEA slacks (Cooper et al. 2004). In that case, the model becomes

$$ \begin{array}{l} \max\ {\displaystyle \sum_{i_1}{s}_{i_1}^{1-}}+{\displaystyle \sum_{i_2}{s}_{i_2}^{2-}}+{\displaystyle \sum_r{s}_r^{+}}\\ {}s.t.\kern1em {\displaystyle \sum_{j=1}^n{\lambda}_j{x}_{i_1j}^1}+{s}_{i_1}^{1-}={\theta}_o^{1*}{x}_{i_1o}^1,\kern1.1em {i}_1=1,\kern0.1em 2,\kern0.1em \dots, \\ {}\kern2em {\displaystyle \sum_{j=1}^n{\lambda}_j{z}_{dj}}={\displaystyle \sum_{j=1}^n{\mu}_j{z}_{dj}}\kern0.1em ,\kern1em d=1,2,\dots, D\\ {}\kern2em {\displaystyle \sum_{j=1}^n{\lambda}_j}=1\\ {}\kern2em {\displaystyle \sum_{j=1}^n{\mu}_j{x}_{i_2j}^2}+{s}_{i_2}^{2-}={\theta}_o^{2*}{x}_{i_2o}^2,\kern1em {i}_2=1,\kern0.1em 2,\dots, \\ {}\kern2em {\displaystyle \sum_{j=1}^n{\mu}_j{y}_{rj}}-{s}_r^{+}={y}_{ro},\kern1em r=1\kern0.1em ,2,\dots, s\\ {}\kern2em {\displaystyle \sum_{j=1}^n{\mu}_j}=1\\ {}\kern2em {\lambda}_j,{\mu}_j,{s}_{i_1}^{1-},{s}_{i_2}^{2-},{s}_r^{+}\ge 0\end{array} $$

(7.11)

Both stages determine the best projection levels for the intermediate measures as ${\displaystyle \sum_{j=1}^n{\lambda}_j^{*}{z}_{hj}}={\displaystyle \sum_{j=1}^n{\mu}_j^{*}{z}_{hj}}$. The frontier projection point is given by (${\theta}_o^{1*}{x}_{i_1o}^1$ $-{s}_{i_1}^{1-*}$, ${\displaystyle \sum_{j=1}^n{\lambda}_j^{*}{z}_{hj}}$, ${\theta}_o^{2*}{x}_{i_2o}^2$ $-{s}_{i_2}^{2-*}$, y _ro $+{s}_r^{+*}$).

7.5 Data and Sampling

The data on US mutual funds are obtained from the Morningstar Direct database. The sample consists of 66 large mutual fund families with total funds under management in each family exceeding $1 billion USD. The sample period is January 1993 to December 2008 (a total of 1056 family years). The 66 families comprise 1269 individual mutual funds, adding up to 20,304 fund years. For each of these individual funds, we compute monthly return and monthly standard deviation over the 16-year sample period.

Some funds have multiple share classes depending on the fee structure and we consider them as separate mutual funds. Furthermore, we found that some families may offer the same fund to different investors under different names. We treated them as separate funds as well. We included all the funds in the family irrespective of their investment policy or classification, such as money market funds, bond funds, equity funds, and index funds.

During our survey period, some funds may have ceased operations and some funds mostly small funds, do not report all the data that we require. Therefore, we consider only large mutual fund families with total funds under management in each family of at least $1 billion USD. Out of a total of 198 fund families reported in 2008, 101 families (51 %) have a total fund size of at least $1 billion USD. Out of these 101 families, 35 families (34.7 %) are dropped from the study due to non-availability of data on all the input and output variables given in Fig. 7.2.

Our final sample contains 66 mutual fund families. Most of the families that we dropped from the study are small; that is, the fund size of 19 out of the 35 families dropped (54.3 %) is less than $4 billion USD. The two largest families dropped from the study are PIMCO Funds (fund size of $217 billion USD with three mutual funds in it) and Dodge and Cox (fund size of $71 billion USD with three mutual funds in it). Total funds under management in each of the other 14 families dropped from the analysis are between $4 billion USD and $40 billion USD. In DEA, the efficiencies of mutual fund families are assessed relative to the other families in the sample and therefore dropping large families from the sample may affect efficiency scores. However, as only a very small percentage of the dropped funds are large, their impact on the overall assessment is minimal.

Even though the primary focus of this paper is to introduce a novel two-stage DEA model for efficiency decomposition, we make a significant effort to minimize the survivorship bias in the numerical example that we use here to demonstrate the applicability of the proposed model. In mutual fund research, survivorship bias is an important issue. According to Carhart (1997), data used in mutual fund research may often be incomplete due to the following reasons. During the sample period, some funds may have ceased operations or some funds may not report data in poorly performing years. The availability of all the individual fund-level data for the 66 families in our sample throughout the entire survey period implies that all the funds in those selected families are healthy funds and none of them have ceased operations during the survey period.

Summary statistics for the 66 mutual fund families selected in our sample and sorted by total funds under management as of 2008 are presented in Table 7.2. American Funds is by far the largest in terms of funds under management ($1490 billion USD). Vanguard is the next largest with $579 billion USD worth of funds under its control. In our sample, the fund family that offers the greatest number of individual mutual funds is Fidelity Investments, with 94 mutual funds worth $418 billion USD under its management. We consider each mutual fund family in the sample as a separate DMU.

Table 7.2 Summary statistics of mutual fund families

The list of input and output variables used in the DEA model is given in Table 7.3. As illustrated in Fig. 7.2, stage 1 has two inputs and one output and stage 2 has five inputs and one output. These variables are selected following previous studies of mutual fund performance such as Malhotra et al. (2007), Choi and Murthi (2001), Murthi et al. (1997), Nguyen-Thi-Thanh (2006) and Wilkens and Zhu (2005). For each family, the values of the input and output variables are calculated for each year from 1993 to 2008 using the data collected on the individual mutual funds in the family.

Table 7.3 Input–output variables used in DEA models

Summary statistics of the input and output variables are given in Panel A of Table 7.4 and the maximum correlation (Pearson correlation coefficient) between each pair of the variables over the sample period 1993–2008 are given in Panel B. The minimum Pearson correlation coefficient is given in Panel C.

Table 7.4 Summary measures of variables used in the two-stage DEA

7.6 Analysis of the Results

In this section we demonstrate application of the two stage DEA model proposed in Sect. 7.4 by examining the relative performance of the US fund families listed in Table 7.2. In Sect. 7.6.1 we analyze the overall performance of the mutual fund families using the overall efficiency scores estimated in model (7.5). Thereafter, to gain insights on the source of efficiency/inefficiency of the fund families, we analyze the operational efficiency scores in Sect. 7.6.2 and the portfolio efficiency scores in Sect. 7.6.3.

7.6.1 Overall Efficiency Estimated in the Two-Stage DEA Model

Table 7.5 lists the 16 families that have performed consistently well overall over the most recent 3-year period from 2006 to 2008 based on the overall efficiency estimated in the two-stage DEA model. We judge the consistency of performance of a mutual fund family by the number of times a family has been ranked in the top 2, top 3, and so on up to top 10 during the 3-year period. Since the investigation period is 3 years, the maximum frequency possible under each category is 3.

Table 7.5 Top-performing mutual fund families in the 3-year period from 2006 to 2008 based on their overall efficiency estimated in the two-stage DEA procedure

Vanguard is clearly the best performing fund family over the investigation period (ranked top 2 in all 3 years), followed by Fidelity Investments (ranked top 3 twice), Hartford Mutual Funds (ranked top 4 twice and top 5 three times), Allegiant (ranked top 4 twice and top 6 three times), and American Funds (ranked top 6 twice). It is not surprising that the Vanguard family of funds is the top performer over the most recent 3-year sample period, given its dominance with respect to the market share in terms of funds under passive management (Smith 2010) and adherence to the fund family gospel that low-cost investments deliver the best returns (Dunstan 2012). The Vanguard Group provides the necessary services to run the funds on an at-cost basis (Bogle 2004). As a result, Vanguard has the reputation within the fund management industry as having the lowest operating expenses. In 2008, the Vanguard funds cost, on average, 0.27 % of assets or about 25 % of the industry average (Morningstar 2012). Vanguard is well known among investors for offering mutual funds with the lowest or close to the lowest annual operating expenses and hence the high overall efficiency is not surprising. All the five fund families identified above (Vanguard, Fidelity, Hartford, Allegiant, and American) have substantial market share and a long history averaging over 80 years. Further, they received rankings in the top quartile in the 2007 fund family rankings released by Barron’s based on the performance in 2006.

On the other hand, American Century Investments and Neuberger Berman are ranked in the top 2 in one of the 3 years and in the other 2 years both are ranked below 10 showing inconsistency in their performance from 2006 to 2008. The poor performance of Neuberger Berman after 2006 can be linked to the fallout of the global financial crisis.

Now we discuss consistency in the performance over a longer period- the 5 years from 2004 to 2008. Table 7.6 shows the 17 best performing mutual fund families based on overall performance over the 5-year period. As seen in Table 7.6, during this period Vanguard is always ranked in the top 2 and is clearly the best performer. Neuberger Berman is the next best, followed by Fidelity investments, Hartford Mutual Funds and T. Rowe Price. Two out of these five families, Neuberger Berman and T. Rowe Price, do not feature in the list of the five best performers over the most recent 3-year period. The same 16 families reported in Table 7.5 also performed better than the other sampled families over the 5-year period from 2004 to 2008.

Table 7.6 Top-performing mutual fund families in the 5-year period from 2004 to 2008 based on their overall efficiency estimated in the two-stage DEA procedure

Similarly, we investigated the overall performance of the mutual fund families over the 10-year period from 1999 to 2008. The results obtained for the 35 best performing fund families over the ten-year period are presented in Table 7.7. When the window is extended to a longer time horizon, no fund family ranks consistently in the top-10 100 % of the time. The results reveal that Vanguard continues its dominance over the other fund families listed in Tables 7.5 and 7.6 with its performance ranked consistently in the top ten 80 % of the time. The most consistent fund family over the longer term horizon is TransAmerica with 1.5 billion funds under management. TransAmerica which is ranked among the top ten 90 % of the time is considerably smaller in size than Vanguard and as a result is not able to offer a low fee structure in terms of Marketing and Management fees as Vanguard does. However, through effective asset allocation and close attention to its investment mandate, TransAmerica consistently performs well relative to the other fund families in the sample over the 10-year period. Other fund families that demonstrate persistence in overall relative performance in the long term are; Aquila, Sun America, and Barron Capital Group.

Table 7.7 Overall consistent performance of mutual fund families in the 10-year period from 1993 to 2008

One of the main contributions of the proposed two-stage DEA model compared with the conventional DEA models is the decomposition of overall efficiency into two components, namely, operational efficiency and portfolio efficiency. In the next section, we discuss how the fund families have performed over the sample period with respect to operational and portfolio efficiency.

7.6.2 Operational Management Efficiency

Table 7.8 lists the 13 fund families that perform relatively better from 2006 to 2008 based on the operational efficiency scores estimated in the proposed two-stage DEA model. The operational efficiency score reflects how well a fund family has managed its resources in securing or generating funds for that family. Here, we observe that three families have been ranked top 2 in all 3 years of assessment; Vanguard, T. Rowe Price, and American Century Investments. According to the overall efficiency score rankings reported in Table 7.5, only Vanguard performs at this level. The next-best performer under operational efficiency is Neuberger Berman, with rankings of 3 or better in all 3 years, followed by American Funds and Fidelity Investments.

Table 7.8 Top-performing mutual fund families in the 3-year period from 2006 to 2008 based on their operational efficiency estimated in the proposed two-stage DEA procedure

The top-performing families in terms of operational efficiency over the 5-year period 2004–2008 reported in Table 7.9 reveal that the same 13 families reported in Table 7.8 also performed better than the other sampled families over this 5-year period. The top 5 performers from 2006 to 2008 are also the top 5 performers over the 5-year period. Once again, when the window is extended to reflect the long term nature of investing (1999–2008) as shown in Table 7.10, the same mutual fund families continue to demonstrate their comparative advantage with low fee structures. Not surprisingly, the two fund families that are ranked 1 or 2 in any calendar year on the basis of operational efficiency throughout the 10-year window; Vanguard (100 %) and T. Rowe Price (100 %) are both among the top 6 in terms of funds under management having portfolios exceeding 100 billion USD. The fee structure of these two fund families reveal that they are able to keep the costs significantly below industry average. This is evident especially in the case of marketing fees where Vanguard and T. Rowe Price both have fees less than 2.3 % compared to the industry average of 44.4 %.

Table 7.9 Top-performing mutual fund families in the 5-year period from 2004 to 2008 based on their operational efficiency estimated in the proposed two-stage DEA procedure

Table 7.10 Top-performing mutual fund families in the 10-year period from 1999 to 2008 based on their operational efficiency estimated in the proposed two-stage DEA procedure

Seven additional fund families join Vanguard and T. Rowe Price by consistently outperforming the other families in terms of operational efficiency. The continually dominating top 10 families are; American Century Investments, Wells Fargo Advantage, American funds, Neuberger Berman, Fidelity investments, Allegiant and Dreyfus. All these fund families have realized high levels of net asset values given their levels of management and marketing fees. We were not able to obtain data on variables such as salaries and rent that may be relevant for operational performance assessment. If it were possible, one could easily include them in the model to further improve the discriminatory power of mutual fund families based on their operational performance.

7.6.3 Portfolio Management Efficiency

Portfolio management efficiency measures how well a mutual fund family manages its investment portfolio to realize high returns subject to a chosen set of factors that may influence returns. Portfolio efficiency is important information not only for investors in making their investment decisions but also for fund family administrators in assessing the performance of their portfolio managers. The fund family administrators may be able to judge how well their fund managers have performed relative to their competitors using the proposed portfolio management efficiency score (measure). The benefits of the proposed efficiency measure do not stop there. Relative performance at the portfolio management level is vital information for recruiting agencies to identify the best-performing fund managers and those who are underperforming.

As in the previous cases, Tables 7.11 and 7.12 lists the fund families that have been ranked at or above different levels of ranking in the last three- and 5-year periods respectively based on portfolio efficiency. According to Table 7.11, Hartford Mutual Funds, Vanguard, Nuveen, Aquila, Davis Funds and Sun America have managed their portfolios relatively better securing a rank of at least 2 during the 3-year period beginning 2006. High performance in stage 2 implies that the mutual fund family has gained relatively high returns with their existing level of fund size, transaction costs (net expense ratio), turnover ratio, risk exposure (standard deviation) and net asset value. The next-best set of mutual fund families in Table 7.11 includes Principal Funds, Van Eck, Fidelity Investments, American Funds, Thornburg, Baron Capital Group, Evergreen, Jennison Dryden, Security Funds, Selected Funds, Transamerica and US Global Investors. Under the portfolio efficiency measure, the top 5 performers from 2006 to 2008 (see Table 7.11) are also the top 5 performers over the 5-year period from 2004 to 2008 (see Table 7.12).

Table 7.11 Top-performing mutual fund families in the 3-year period from 2006 to 2008 based on their portfolio efficiency estimated in the proposed two-stage DEA procedure

Table 7.12 Top-performing mutual fund families in the 5-year period from 2004 to 2008 based on their portfolio efficiency estimated in the proposed two-stage DEA procedure

Fiduciary Insight, using Morningstar Direct data, produces quarterly research reports on the major managed fund families in the US. These reports rank fund families by the percentage of individual funds within the family that have either “passed” the fiduciary score or the “appropriate” classification. The ranking of fund families based on our stage 2 portfolio efficiency scores and the ranking by Fiduciary Insight (Fiduciary Insight 360 2009) for the period ending December 2008 are remarkably similar. Fiduciary Insight reports that Aquila, American Funds, American Century Investments, Baron Capital Group, Eagle Funds, Franklin Templeton Investments and Vanguard belong to the top quartile of the funds as of December 31, 2008. In this, we observe that the traditional approaches used by the fund family ranking organizations may rely only on portfolio efficiency rather than on an overall efficiency measure that covers both the operational management and portfolio management aspects of performance. In recognition of performance over the 3-year period from 2008 to 2010, Transamerica received four 2008 Lipper Fund awards. Transamerica also received for the eighth consecutive year dating back to 2001, the DALBAR Mutual Fund Service Award for excellence in customer service. However, according to Table 7.12, Transamerica is not one of the top performers. A plausible reason for the differences in the rankings of some families, such as Transamerica, based on the overall efficiency scores estimated in the two-stage DEA model and those offered by family ranking organizations may be that these organizations consider a small sample of fund families that satisfy specific investment criteria. Their selection criteria may also vary from time to time.

Table 7.13 presents a summary of the results for long term performance over the window 1999–2008. Table 7.13 only presents fund families that rate in the top 10 at least 60 % of the time. Sixty out of the 66 fund families are ranked within the top 10 at some stage of the 10-year period beginning 1999. The families that are not ranked at least once in the top 10 in any given calendar year are; Seligman (top ranking 13th in 1999), Calvert (top ranking 14th in 2002), Victory (top ranking 16th in 2003), Morgan Stanley (top ranking 19th in 2006), Wells Fargo Advantage (top ranking 22nd in 2000) and Allianz Funds (top ranking 35th in 1999). In terms of portfolio performance over the long run, Vanguard, Nuveen and Aquila are the best.

Table 7.13 Top-performing mutual fund families in the 10-year period from 1999 to 2008 based on their portfolio efficiency estimated in the proposed two-stage DEA procedure

Table 7.14 provides the rankings of individual fund families each year from 1993 to 2008 based on the overall, operational, and portfolio efficiencies estimated in the two-stage DEA model. We report only the top 10 mutual fund families listed in Table 7.14 to conserve space. It is clear in Table 7.14 that the overall efficiency of mutual fund families may be affected by their portfolio and operational efficiencies being at varying degrees. For example, Vanguard is both operationally and portfolio efficient with a rank of 1 and hence is overall efficient throughout the period 1994–2008. T. Rowe Price, on the other hand, is operationally efficient during the period 1994–2008 maintaining a rank of 1. However, T. Rowe Price is not portfolio efficient (except in 2003 and 2004) and therefore is not overall efficient in most of the years. More on the effect of portfolio and operational efficiencies on overall efficiency for a set of fund families is discussed and illustrated graphically in the next section.

Table 7.14 Rankings of a sample of mutual fund families in each year from 1993 to 2008 based on the efficiency estimated in the proposed two-stage DEA procedure

7.6.4 Variation in Efficiency Across Time and Fund Families

Selecting a few families as examples, we now illustrate graphically how operational efficiency and portfolio efficiency may affect the overall efficiency of fund families over time. Panels (a) and (b) of Fig. 7.4 give the graphs for Allianz Funds and Morgan Stanley, respectively. Both these funds perform consistently poorly overall, due to consistent poor operational and portfolio performance. Panel (c) shows that Vanguard’s continual overall performance is due to the excellent performance in both the operational and portfolio fronts. The graph in panel (d) of Fig. 7.4 for Aquila indicates that the reason for its continued good overall performance is mainly due to the consistency in its portfolio management efficiency. Panels (a) and (b) of Fig. 7.5 show the corresponding graphs for Hartford Mutual Funds and Allegiant. These are examples of fund families that have improved their performance after 2003. The improvement of Hartford Mutual Funds family after 2003 is mainly due to the improvement in operational and portfolio efficiencies, and in the case of Allegiant more or less due to the improvement in portfolio efficiency. On the other hand, Putnam and Franklin Templeton Investments, whose graphs are shown in Panels (c) and (d), respectively, in Fig. 7.5, reveal that the poor portfolio efficiency appears to be the main contributor to their declining overall performance towards the end of the sample period.

Fig. 7.4

Impact of operational efficiency and portfolio efficiency on the overall efficiency for Allianz, Morgan Stanley, Vanguard and Aquila fund families. This figure illustrates how the rankings of Allianz Funds, Morgan Stanley, Vanguard, and Aquila fund families based on their overall, operational and portfolio efficiency change over the period 1993–2008. (a) Allianz Funds. (b) Morgan Stanley. (c) Vanguard. (d) Aquila

Fig. 7.5

Impact of operational efficiency and portfolio efficiency on the overall efficiency for Hartford, Allegiant, Putnam and Franklin Templeton fund families. This figure illustrates how the rankings of Hartford Mutual Fund, Allegiant, Putnam, and Franklin Templeton Investments on their overall, operational and portfolio efficiency change over the period 1993–2008. (a) Hartford Mutual Fund. (b) Allegiant. (c) Putnam. (d) Franklin Templeton Investments

Four families (Allianz Funds, Morgan Stanley, Hartford Mutual Fund, and Putnam), illustrated in Figs. 7.4 and 7.5, show relatively poor portfolio performance in 1993. We notice similar performance in several other mutual fund families in the sample as well. This is clear evidence of the effect of the 1991 currency crisis on the portfolios managed by some mutual fund families. The improvement shown in the relative rankings after 1994 suggests quick recovery from the crisis in 1991. Vanguard and Aquila have managed their mutual funds relatively efficiently during all financial crisis periods from 1993 to 2008.

During the last two quarters of 1990 and the first quarter of 1991, the US economy experienced a sustained period of negative growth. Other significant shocks to the market during the sample period include the collapse of Long-Term Capital Management in 1998, the dotcom bubble and the subsequent market crash in March 2000, the market meltdown following the September 11 attacks in New York and the Enron debacle, and the recent global financial crisis (GFC) that impacted the markets post July 2007. The effects of the GFC continued well into the years that followed. In Figs. 7.4 and 7.5, we observe that the portfolio efficiency of Allianz Funds, Morgan Stanley, and Putnam families have been seriously affected (low portfolio efficiency ranking) by the recessions of 1990–1991 and 2000–2002 and the fallout from the GFC over the period 2007–2009. These three fund families have high exposure investment across domestic and international equity markets: Allianz Funds (94 %), Morgan Stanley (79 %), and Putnam (68 %). In contrast, even though Hartford Mutual Fund has been affected by the downturn in market activity in 1991 and 2000 to an extent similar to that of the three aforementioned fund families, it has not been affected as much by the problems resulting from the GFC in 2007. The better showing of Hartford Mutual Fund in the later period may be attributed to improved operational and portfolio efficiencies in part driven by an appropriate fee structure. The performance of Allegiant has been affected by the 1998 Long-Term Capital Management collapse and the 2000 recession and has survived the impact of the 2007 crisis. The standout fund family within our sample, Vanguard, as far as operational, portfolio, and overall efficiencies are concerned, has been exceptional throughout the full sample period.

Aquila performs extremely well in terms of portfolio efficiency, but due to its poor operational efficiency its overall efficiency is also low. The Franklin Templeton Investments family has done extremely well in its portfolio management until 2006. As far as operational efficiency is concerned, it has not done well, with a rank of around 10. The operational and portfolio management performance of the Hartford Mutual Fund family is not relatively satisfactory up to 2003, but has shown tremendous improvement in these areas thereafter. The Allegiant family’s operational efficiency is relatively satisfactory over the sample period, but its portfolio efficiency is relatively weak. However, Allegiant’s overall performance shows an improvement after 2005. Allianz Funds and Morgan Stanley show inferior overall performance due to their poor performance in both operational and portfolio management areas and show no sign of improvement over the sample period. The Putnam family’s operational management performance is relatively poor throughout the sample period. Its portfolio management performance has been relatively satisfactory until 2000 and has deteriorated thereafter. Overall, the above analysis clearly shows that the proposed DEA model is able to capture the dynamics of the operational and portfolio management efficiencies and overall efficiency of mutual fund families.

7.6.5 Frontier Projection of DMUs

Another important feature of DEA is its ability to provide information to make inefficient DMUs efficient. In this subsection, we demonstrate this feature in a selected set of mutual fund families. Such information is very important for a fund family’s management decision making.

In Sect. 7.4.1.2, following Chen et al. (2010) we develop a model for frontier projection of mutual fund families deemed inefficient according to the proposed two-stage DEA model. We apply the frontier projection model with the values of the input, output and intermediate variables corresponding to the year 2008. The input, output and intermediate variable changes required for making the inefficient mutual fund families efficient are illustrated in Table 7.15 for a selected set of families. Under the column “NAV” (the intermediate measure), a positive percentage indicates that NAV should be increased, and a negative percentage indicates that NAV should be decreased in order to make the fund family efficient. Positive values with respect to the other input variables in Table 7.15 indicate that they should be decreased by the corresponding percentages.

Table 7.15 Frontier projections of mutual fund families

According to Table 7.15, no changes are required for any of the input (I ₁, I ₂, I ₃, I ₄, I _5, and I ₆), output (O ₂) and intermediate (NAV) variables of Vanguard and Fidelity Investments, as they are operational, portfolio and overall efficient in year 2008. This observation tallies with the 2008 ranking of these two families in Table 7.14, where they are ranked within the top three as far as overall, operational, and portfolio efficiencies are concerned. The percentage changes of the variables in the second stage for Davis Funds are all zero, indicating that it is portfolio efficient in 2008. This is evident in Tables 7.11 and 7.12, where this family has been ranked within the top 2 during the period 2004–2008. However, Davis Funds is operationally inefficient and therefore it has to decrease the marketing and distribution fee and the management fee by 51 and 40 % in the first stage, respectively, to become operationally efficient. These changes will make Davis Funds overall efficient as well. Evidence presented in Tables 7.5 and 7.6 supports this finding, as Davis Funds appears at the bottom of these tables as far as overall efficiency is concerned. On the other hand, American Century Investments is operationally efficient but not efficient in managing the portfolio. This family needs to increase its return by 4 % and decrease its inputs at stage 2—I _3, I ₄, I _5, and I ₆ by the following percentages: 34 %, 34 %, 52 %, and 34 %, respectively—in order to become portfolio efficient and thereby become overall efficient. According to the entries in Table 7.15, Morgan Stanley is a poor performer in 2008 with inefficient operational and portfolio management. This is evident in Fig. 7.4b with the overall, operational and portfolio rankings of this family lying in the range 20–60. For Morgan Stanley to be overall efficient, it needs to reduce all its inputs at stage 1 and stage 2 by the percentages given in Table 7.15 and increase its stage 1 output or the intermediate measure (NAV) by 16 % and increase the return (output) by 19 %. On the other hand, Oppenheimer Funds may decrease all its inputs at stages 1 and 2 (and NAV) by the percentages given in Table 7.15 and increase its return by 23 % in order to become efficient. These two examples (Morgan Stanley with a positive change in NAV and Oppenheimer Funds with a negative change in NAV) demonstrate an interesting feature of the proposed DEA model; that is, the model treats the intermediate variable, NAV, as both an input as well as an output. In the proposed DEA model, the optimal NAV is determined by both stages through coordination in such a way that the performances of both stages are maximized. Technique such as a stochastic frontier approach cannot treat a variable as an input and as an output within the same model.

7.7 Concluding Remarks

The main objective of this chapter is to present a two-stage network DEA model and demonstrate its application by assessing the relative performance of large mutual fund families in the US. It is well documented that the mutual fund industry in the US is the largest such industry in the world and its well being is important to a strong global economy . Hence a heightened understanding at both the operational level and portfolio performance level of fund families is of importance as we move forward to a time of increased numbers in retirement relying upon their investment income for day-to-day living costs. Unlike traditional performance measures such as the Sharpe, Treynor and Sortino measures, the DEA model proposed in this chapter allows a combination of several factors of performance such as; returns, fees and charges, risk of investment, stock selection style, portfolio management skills and operational management skills into a single measure in evaluating the overall performance of a mutual fund family relative to the other families included in the sample.

The presented two-stage DEA model provides greater insight into the performance of mutual fund families by decomposing the overall efficiency into two components: operational efficiency and portfolio efficiency. In addition to mutual fund families, the proposed DEA model can also be applied to other financial institutions such as banks, insurance companies, credit unions, etc.

The performance of the mutual fund families assessed over the period 1993–2008 using the proposed DEA model reveals that the two-stage model is able to highlight those mutual fund families that may have managed their portfolios well during financial crisis periods as well as which of the two components; operational management and portfolio management may have been the contributory factor for their superior/inferior performance. This is useful information as it can aid individual and institutional investors when making investment decisions and also enables administrators of fund families to judge how well their portfolio managers have performed relative to their competitors.