Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Mathematics has often been eclipsed by literacy in academic intervention research, despite the importance of both skills for a child’s overall success (Methe et al. 2011). Knowledge of early mathematics concepts was one of the most powerful predictors of future academic achievement (Duncan et al. 2007). More broadly, mathematics proficiency is necessary for individuals to successfully navigate the modern world. Principles of mathematics are embedded in simple daily tasks such as cooking or a trip to the grocery store, and also in more advanced, yet equally important, tasks like paying taxes or balancing a household budget. Competence in mathematics is fundamental in science and engineering careers, which are predicted to outpace general job growth in the coming years (National Mathematics Advisory Panel 2008). Additionally, those with poor skills in mathematics are less likely to be involved within their communities, have difficulty managing finances, and experience various employment challenges (Methe et al. 2011). It is critical that schools address mathematics intervention through evidence-based methods to support positive student outcomes in such a foundational skill.

This chapter reviews previous research that identifies types of mathematics challenges experienced by students, and provides a general overview of the status of mathematics interventions that focus on whole number knowledge. Specific discussion of interventions that address rational numbers or applied problem-solving extends beyond the scope of this chapter. Second, the chapter describes core features of tier 3 intervention packages that can be utilized across mathematics topics, while highlighting their application to number combinations and computation fluency using examples from our own intervention work. Finally, the chapter discusses future areas of needed research.

Review of Previous Research

Mathematics is a complex content area consisting of many topics that are reflected in the challenges experienced by students. As many as 30 different behaviors differentiated children with mathematics difficulties from typically performing peers (Bryant et al. 2000). Thus, let us begin by discussing student mathematics difficulties and provide an overview of mathematics interventions.

Description of Student Mathematics Difficulties

Solving word problems represents a commonly cited area of difficulty, and some of the best predictors of mathematics challenges include procedural difficulty with multi-step problems and borrowing errors (Bryant et al. 2000; Geary 1993). Children with mathematics learning disabilities also tend to use less mature counting strategies, such as guessing and the sum procedure (e.g., in the problem 3 + 4, children line up two sets of items and count all objects starting from 1) and make more counting errors than their peers (Geary et al. 2004). This may result because children are not familiar with the magnitude sequence of numerals and can only determine which number comes first (e.g., 3 or 4) by counting from one (Baroody et al. 2009).

A series of longitudinal studies illustrated that knowledge of and fluency with number words, numerals and their quantities, as well as number lines represent critical components that underlie mathematics learning (Geary 2011; Geary et al. 2009; Jordan et al. 2009). Difficulties in these core areas have been shown to be stable through the elementary school years, and mathematics competency in kindergarten is highly predictive of later school achievement (Duncan et al. 2007; Jordan et al. 2009; Morgan et al. 2009).

A robust finding in the literature is that challenges with automatic fact retrieval and calculation fluency may be the unifying feature of children who struggle in mathematics (e.g., Geary 2011; Gersten et al. 2005). Research has illustrated that students without mathematics learning disabilities recall as many as three times the number of basic facts as their peers with learning disabilities even though accuracy of basic fact performance is equivalent (Hasselbring et al. 1988; Gersten and Chard 1999), which is consistent with research that found that poor performance with simple arithmetic tasks at the end of kindergarten predicts learning disabilities by the end of third grade (Mazzocco and Thompson 2005).

Students without basic fact fluency may be less able to grasp underlying mathematics concepts or access higher-level mathematics curricula (Gersten and Chard 1999). Students that have to allocate more cognitive resources to retrieving the solution to 9 + 6 (for example) may experience interference with higher-order thinking or problem-solving because directing conscious attention towards multiple tasks simultaneously is challenging (Barrouillet and Fayol 1998; Dahaene 1997). Evidence also exists to suggest that students with low number combination fluency may exhibit greater anxiety for mathematics tasks than students with more fluent skills (Cates and Rhymer 2003). Whether it is the additional effort required, anxiety, or a combination of the two, collectively this evidence suggests that students without number combination fluency may engage in less frequent practice with mathematics content and complete fewer mathematics-related tasks (Billington et al. 2004; Skinner et al. 1997).

Overview of Mathematics Interventions

With the recognition that computational fluency is a key aspect of mathematics learning, as well as research supporting that its absence represents a hallmark feature of mathematics learning disabilities (Gersten et al. 2005), the NMAP report (2008) indicated that automaticity with number combinations is a necessary goal for all children. Mathematics computation and applications have been shown to be distinct albeit highly related ( r = 0.83) constructs suggesting that skills in one area are necessary for success in the other (Thurber et al. 2002). Jordan et al. (2003) illustrated that students with low mastery of mathematics facts make minimal, if any, progress on a variety of other tasks compared to higher-mastery groups suggesting the critical role that computation fluency has on building procedural and conceptual knowledge of mathematics principles. More intervention research has been conducted on this aspect of mathematics than with rational numbers, early number knowledge, or word problem-solving.

Preliminary intervention research targeting early numeracy has focused on developing individualized and small-group interventions that include instruction on strategic counting (e.g., counting up; doubles + 1) and magnitude representations through practice with magnitude comparisons (e.g., which number is bigger?), number games, and number-line estimation tasks (Bryant et al. 2011; Fuchs et al. 2005; Seigler and Ramani 2009). Research examining word problem-solving interventions has produced convincing evidence implicating the use of schema-based instruction, which directly teaches underlying structures of word problems through problem mapping and diagramming (Fuchs et al. 2007; Jitendra 2007). These data suggest that there are promising protocols that interventionists can incorporate within their school systems; however, more research on intervention effectiveness is needed.

In a review of the literature on mathematics computation intervention research between 1980 and 2007, the 12 different strategies listed in Table 1 were identified, 50 % of which were analyzed in more than one study (Codding et al. 2009b). These interventions were categorized as either simple intensity interventions that improve the academic learning environment, or moderate intensity reflecting a specific alteration in the form or type of instruction provided (Barnett et al. 2004; Shapiro 2011). All of these interventions are resource friendly requiring minimal training and materials. Generally, these interventions were effective, but for some improvement depended on the outcome measure (i.e., percentage accuracy, fluency (digits correct), or general mathematics achievement (according to criterion- or norm-referenced tests)). These findings suggest that replication of effectiveness findings is warranted and that knowing what intervention strategy to implement is necessary but not sufficient. Knowledge of student-specific skill levels and appropriate treatment match according to level of skill proficiency might also be useful, particularly for students experiencing the most difficulty.

Table 1 Selected mathematics intervention strategies and descriptions
Full size table

Given the paucity of standard protocol mathematics interventions (Fuchs et al. 2008; National Mathematics Advisory Panel 2008), this chapter will emphasize common intervention features that have been broadly supported in the literature and can be used to generate individualized treatment plans for students in need of tier 3 supports. Examples are used from our research on whole-number computation fluency and instructional decision-making to illustrate conceptualization and application of relevant treatment components.

Key Features of Tier 3 Interventions

Common intervention features identified through the extant literature offer promising guidelines for generating treatment packages for use with students exhibiting some of the greatest problems in mathematics (Burns et al. 2010; Codding et al. 2011a; Fuchs et al. 2008; Baker et al. 2002; Gersten et al. 2009; Swanson 2009; Swanson and Sachse-Lee 2000). These core components include: (a) matching treatment to skill needs, (b) explicit instruction, (c) self-instruction, (d) concrete–representational–abstract (C–R–A) instructional sequencing, (e) providing productive opportunities to practice, and (f) incorporating motivation (Table 2). Independently, these intervention components seldom demonstrate efficacy; however, combinations of these strategies have consistently led to positive student outcomes among children struggling with mathematics (Codding et al. 2011a; Fuchs et al. 2008; Gersten et al. 2009; Swanson 2009).

Table 2 Key components of tier 3 mathematics interventions
Full size table

Treatment by Skill Match

Additional assessment and analysis is recommended when developing tier 3 supports, given previous challenges these students have experienced in core instruction and potential lack of response to tier 2 interventions. Rather than simply identifying available interventions, it might be useful to apply a problem-solving approach so that treatment selection matches student level of skill development. Selecting treatments according to their match with students’ level of skill proficiency requires two steps: (a) identify students’ specific skill strengths and weaknesses and (b) use a decision-making heuristic to match skill level with an intervention strategy (Burns et al. 2010; Codding et al. 2007; Daly et al. 2000). Tier 3 interventions should use the hierarchical nature of mathematics content to emphasize prerequisite skills that may not necessarily match grade-level content (Gersten et al. 2009; Swanson 2009). For example, fourth-grade students with unmastered addition and subtraction skills should receive intervention support that addresses these skill weaknesses prior to focus on multiplication or division (Shapiro 2011). Within a tiered system of service delivery, all students will have access to grade-level content during core instruction and the provision of tiered services emphasizing key foundational skills will facilitate access to this content.

Curriculum-based assessment (CBA) is a useful tool for intervention planning (Burns 2004). CBA-instructional design (Gickling and Havertape 1981) requires a survey-level assessment be constructed with a range of single-skill mathematics facts reflective of Common Core State Standards (National Governers Associaton Center for Best Practices, Council of Cheif State School Officers 2010) and/or National Council of Teachers of Mathematics (2006) focal point scope and sequence recommendations. CBA worksheets are administered beginning with grade-level skills and continue down the skill hierarchy with the goal of identifying skills that fall in the mastery, frustration, and instructional ranges of proficiency according to specified criteria. For example, Burns et al. (2006) derived criteria experimentally which resulted in scores below 14 (grades 2 and 3) and 24 (grades 4 and 5) digits correct per minute (DCPM) representing the frustration level, scores between 14 and 31 DCPM (grades 2 to 3) and 24 to 49 (grades 4 and 5) DCPM representing the instructional level, and mastery performance exceeding the highest score of those ranges (see Table 3). The skill selected for treatment focus will depend on the number of skills identified in the frustration and instructional ranges with a potential starting point being the unmastered skill lowest in the skill hierarchy.

Table 3 Treatment by skill interaction: Combining CBA-ID and the instructional hierarchy for treatment selection. (CBA-ID criteria according to Burns et al. 2006)
Full size table

Although there are a number of decision-making heuristics that could be selected to make an appropriate skill by treatment match (Christ 2008), our research has focused on the application of the instructional hierarchy (IH) as defined by Haring and Eaton (1978) and adapted to mathematics by Rivera and Bryant (1992). The IH suggests that skill development consists of four stages: acquisition, fluency, generalization, and adaption. Initially, students focus on acquiring new skills by developing accuracy. Therefore, performance of students in this stage is slow and inaccurate. Once students have achieved accuracy, the next step is to build fast and accurate performance with the skill. Haring and Eaton (1978) postulated that accurate and fluent skill performance permits generalization of skill use over time, under different conditions, and with new stimuli (the third stage of skill development), and, lastly, skill proficiency results in adaption of skills to novel mathematics tasks. When used with CBA-ID, performance that falls in the frustration range may represent the acquisition stage of skill development and performance in the instructional range may represent the fluency stage (Burns et al. 2010).

Intervention techniques for students in the acquisition stage of skill development might include modeling, guided practice, think-alouds, and immediate corrective feedback using concrete manipulatives, visual representation, and numerals (Rivera and Bryant 1992). However, once students have attained accuracy, continued use of these strategies may be counterproductive for building fluency, as students may become strategy dependent (Poncy et al. 2006). Characteristics of interventions for students in the fluency stage of skill development include novel and frequent opportunities to practice recently acquired skills through the use of timed drills, peer tutoring, reinforcement, goal setting, reinforcement, and computers.

The manner in which skill generalization can be facilitated is less clear. In fact, 38 % of studies included in recent meta-analytic research-measured skill retention and only 11 % measured generalization (Codding et al. 2009b). There is some evidence that suggests high rates of skill fluency result in subsequent proficiency on nationally normed achievement tests (VanDerHeyden and Burns 2008) and strong correspondence has been yielded between single and multiple-digit multiplication fluency (Lin and Kubina 2005). We have also found that higher rates of fluency in single-skill subtraction resulted in generalization with 2 × 1 digit subtraction with regrouping problems as compared to students displaying lower levels of fluency (Codding et al. 2009a) and that improved performance on multiplication flash cards using a drill procedure resulted in improved fluency on multiplication and fraction curriculum-based measurement (CBM) probes (Codding et al. 2010). These data suggest that adequate levels of fact fluency on key component skills might facilitate problem-solving on composite skills (Johnson and Layng 1992; Skinner and Daly 2010). It may also be that arranging intervention opportunities to facilitate generalization such as through the use of multiple examples or training hierarchical skill elements simultaneously promotes generalized learning (Codding and Poncy 2010; Skinner and Daly 2010). Applied practice activities within learning centers or instructional games could also prove effective (Rivera and Bryant 1992).

Two studies were conducted that offer some preliminary support for using a skill by treatment (CBA−ID + IH) approach to intervention selection. In our initial study (Codding et al. 2007), second- and third-grade students were randomly assigned to one of three groups: Explicit Timing, Cover–Copy–Compare (CCC), or Control. Explicit timing was hypothesized to be an intervention that would benefit students in the fluency stage of the IH, and CCC was selected to represent the acquisition phase of the IH. The length of practice time was held constant and occurred twice weekly for 6 weeks. Using multilevel modeling, an interaction between initial CBA score and treatment was found whereby students whose performance fell in the instruction range (i.e., fluency stage of IH) prior to inception of the study and received explicit timing made more growth during the project and achieved higher final performance than students with comparable performance receiving either no treatment or CCC. Students whose initial scores fell in the frustration range (i.e., acquisition stage of the IH) and received explicit timing had lower scores at the end of treatment and flatter rates of growth than comparable students also in the acquisition stage of the IH assigned to the control condition or receiving the CCC treatment. This supported the notion that students performing in the instruction range of the skill selected for treatment (i.e., fluency stage of IH) benefited from a treatment procedure that contained strategies consistent with fluency building but this intervention was not effective when applied to students whose skills were in the frustration range (i.e., acquisition stage of IH).

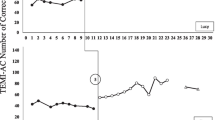
Next, (Burns et al. 2010) a meta-analysis was conducted using single-case design studies that employed mathematics computation interventions. Intervention strategies were categorized as consistent with building accuracy (i.e., acquisition stage of IH) or fluency (i.e., fluency stage of IH) using criteria from Rivera and Bryant (1992). Baseline scores were analyzed to determine whether each participant’s CBA score fell in the frustration or instructional range. We were interested in determining whether the indicated treatment (e.g., acquisition strategies applied when CBA score fell in frustration range) would result in better performance than the contraindicated treatment (e.g., acquisition strategies applied when CBA skill level was instructional). The obtained studies included 55 participants in grades 2–6 with 65.5 % displaying CBA scores in the frustration range and 34.5 % displaying CBA scores in the instructional range. We were unable to evaluate the effect of fluency-building interventions on students whose performance was in the instructional range of CBA (indicated treatment) due to a limited number of participants that fell in this category. Our hypotheses were partially supported (see Fig. 1). It was found that acquisition building strategies applied to students with CBA scores in the frustration range resulted in large effect sizes (indicated treatment) whereas fluency building strategies applied to students with similar performance resulted in small to moderate effect sizes (contraindicated treatment). For students with CBA scores in the instruction range receiving an acquisition intervention a small effect size was yielded (contraindicated treatment).

Fig. 1
figure 1

Mean phi coefficient for skills of students falling in the frustration and instructional ranges and receiving intervention strategies consistent with either acquisition or fluency stages of the instructional hierarchy. (Burns et al. 2010)

Full size image

Collectively, these data suggest that using CBA-ID with the IH may be a useful guide to select an appropriate treatment match for students. That being said additional research is warranted in this area. It is unclear whether skill development occurs in the discrete stages suggested by the IH (Martens and Eckert 2007). It also remains to be seen whether treatment strategies should be applied sequentially so that when a skill is in the acquisition stage one set of techniques is provided but once achieved another set of techniques is employed for fluency building, or, whether treatment packages should be developed with both sets of techniques applied simultaneously (Skinner and Daly 2010).

Explicit Instruction

In no uncertain terms, explicit instruction has been described as a critical instructional method for helping children acquire basic skills in mathematics, particularly when providing tier 3 services (Baker et al. 2002; Fuchs et al. 2008; Gersten et al. 2009; Swanson 2009; Swanson and Sachse-Lee 2000). Explicit instruction includes the teaching of specific skills and strategies by breaking them down into smaller, more manageable steps in a planned sequence with the incorporation of many examples. Typically, this process begins with modeling, error correction, and guided practice and gradually shifts to independent practice using teacher modeling and corrective feedback. This intervention feature provides an effective foundation for helping students understand concepts that underlie number combinations such as quantity discrimination, counting, and mental use of number lines (Gersten et al. 2005; Poncy et al. 2006).

Self-Instruction

Self-instruction, also considered a self-regulation or meta-cognitive strategy, is intended to teach students to monitor their own problem-solving through the use of teacher-modeled visual and verbal prompts (Goldman 1989). These interventions are often implemented by students themselves or in conjunction with support from a teacher and have demonstrated large effect sizes, as opposed to treatments implemented solely by a teacher (Codding et al. 2011a). Specific self-instruction strategies for students often consist of “think-alouds,” self-questioning, and simple heuristics; for example, the “Say–Ask–Check” method encourages students to read a problem, ask themselves questions about the problem, and check their work at each step (Kroesberg and Van Luit 2003; Montague 2008). Similarly, steps for solving different types of problems can be stated aloud by students in action terms, such as “read the problem first, next find the bigger number,” followed by students repeating and completing successive steps (Kroeger and Kouche 2006; Tournaki 2003). Accurate verbalization of problem-solving steps is particularly important for struggling students (Gersten et al. 2009; Siegler and Booth 2004; Swanson 2009), as such strategies help students to focus attention to the task, prevent impulsive responding, and manage frustration (Meichenbaum and Goodman 1971).

C–R–A Sequence

Mathematics learning opportunities that incorporate the use of visual representations and concrete manipulatives along with numerals is an important feature of effective interventions with struggling students (Flores 2010; Gersten et al. 2009; Miller and Mercer 1993; Mercer and Miller 1992; Swanson 2009). The use of manipulatives such as counters, chips, and blocks is common in mathematics instruction; however, current recommendations suggest that manipulatives are most effective when used sequentially with concrete examples, visual representations, and abstract numerical symbols (Baroody et al. 2009). Mercer and Miller (1992) demonstrated that students with mathematics learning disabilities benefited from using concrete manipulatives an average of three times before practicing the same concept using visual displays such as pictures of objects, number lines, tally marks, and/or ten frames. It is essential that the use of visuals and manipulatives be implemented according to a progression, such that manipulatives are used first and faded to proceed to the use of visual representations, which serve as an intermediate step. When students are able to accurately and independently solve problems with visual representations, more advanced practice with abstract symbols (i.e., numerals) should be initiated (Flores 2010).

Productive Opportunities to Practice

US students cannot solve basic facts as quickly or efficiently as their international peers which is due, in part, to the quantity and quality of practice provided within the classroom and offered via traditional mathematics textbook curricula (National Mathematics Advisory Panel 2008). Educators tend to focus on accurate mathematics performance as opposed to rates of responding and tend to emphasize complex composite mathematics skills at the expense of component prerequisite skills (Daly et al. 2007). This has resulted in rapid introduction of new mathematics concepts without supplying sufficient opportunities to master content and ensure retention of previously learned skills (Daly et al. 2007; National Mathematics Advisory Panel 2008). However, development and implementation of carefully constructed direct practice opportunities is widely supported in the literature (Codding et al. 2011a; Daly et al. 2007; Powell et al. 2009; Swanson 2009). Practice has been described as a necessary treatment component for students receiving tier 3 services (Binder 1996; Fuchs et al. 2008) and treatment packages that contain direct opportunities for practice produce better outcomes that those without (Powell et al. 2009). Binder (1996) suggested that fluency building might be facilitated by allocating as much as 70 % of instructional time to practice activities.

Practice consists of a number of activities including drill, practice, and cumulative review. Drill has been defined by Haring and Eaton (1978) as the rehearsal of isolated items such as with flash cards, whereas practice requires the use of newly learned responses in a different context (i.e., worksheets, word problems; Daly et al. 2007; Fuchs et al. 2008) or combined with previously learned responses as might be seen in a mathematics worksheet. Cumulative review can be conceptualized as rehearsal of learned responses, such as practicing all one by one digit addition number combinations (Fuchs et al. 2008) or sequenced review of skills previously learned to a criterion until all skills in a hierarchy or components of a more complex skill are mastered (Engelmann and Carnine 1982). In our (Codding et al. 2011a) meta-analysis of basic fact fluency interventions, the impact of various practice activities on student outcomes were coded and isolated. Our findings demonstrated that for students in need of intensive interventions, practice that incorporated modeling of the problem with the correct answer or a flash-card drill procedure where the ratio of known to unknown facts was controlled resulted in median gains of 9.75 DCPM and 25.33 DCPM, respectively, compared to median gains of 2 DCPM for practice without modeling. However, this does not necessarily mean that only one type of practice activity should be used. It has been postulated that drill facilitates skill fluency, whereas as other practice activities lead to retention, maintenance, and generalization (Daly et al. 2007; Haring and Eaton 1978) and our study only evaluated immediate effects of treatment.

Development of effective practice opportunities requires that students be presented with material that matches their instructional level. In mathematics, this means that students should perform skills with approximately 70–85 % accuracy (Gickling and Thompson 1985) and/or exhibit rates of performance that range from 14 to 31 DCPM (grades 2 and 3), or 24 to 49 DCPM (grades 4 and 5; Burns et al. 2006). Practice sessions should be organized to be brief and frequent lasting approximately 10 min (Daly et al. 2007; Gersten et al. 2009). Practice should be sequenced systematically in small sets and according to student progress (Fuchs et al. 2008; Martens and Eckert 2007; Woodward 2006). There is some evidence to suggest that constructing small practice sets according to fact families (i.e., 2 × 3 = 6; 6/2 = 3) or introducing facts sequentially is beneficial (i.e., 0, 1, 2s, etc.; Hasselbring et al. 2006).

Motivation

The NMAP report (2008) highlighted the importance of incorporating strategies that facilitate motivation within treatment packages in order to encourage engagement in mathematics tasks. As students become accurate in mathematics, reinforcement for continued practice (as is recommended to build fluency) in the natural environment may diminish (Skinner et al. 1997). Students may in turn be less motivated to engage in overlearning, and rates of responding may not improve to levels necessary for skill retention and generalization (Daly et al. 2007). These problems are exacerbated for students in need of more intensive interventions (Fuchs et al. 2008) who are at increased risk of experiencing mathematics anxiety (Cates and Rhymer 2003) and less likely to persist on mathematics tasks given their difficult educational history (Billington et al. 2004). Encouragement provided to students engaging in mathematics tasks can be directly associated with mathematics performance (e.g., meeting a specified criterion, beating a score) or indirect, focusing instead on self-regulation with mathematical tasks (e.g., task persistence, initiation, or completion). The can’t do/won’t do assessment (VanDerHeyden and Witt 2008) can distinguish among students displaying skill deficits, performance deficits, and combined skill and performance deficits.

Token economies with and without response cost, where points or tokens are earned (or removed) and exchanged for prizes, can be incorporated into a treatment package. For example, Math FLASH (Fuchs et al. 2003), a computer-assisted program focusing on fact families, incorporates reinforcement by awarding students with stars for participating, attending, and providing effort toward each element of the intervention package. These stars are recorded on a chart after each treatment session and when 16 stars are accumulated, an assortment of prizes is presented from which the student selects one (Fuchs et al. 2008). Prizes could also be provided directly for improvement on performance such as digits or problems correct.

Providing students with feedback on their performance also improves student outcomes (Gersten et al. 2009). Performance feedback can consist of informing students of the number of correctly completed or answered problems, graphs depicting mathematics scores, or number and type of mastered skills. When feedback is linked to praise for effort, the effects are particularly powerful (Gersten et al. 2009). A series of studies have been conducted examining the added value of performance feedback with goal setting (PFGS) applied to treatment packages for kindergarteners (Codding et al. 2011b), third (Codding et al. 2009a), and fourth graders (Codding et al. 2005). For kindergarteners, a vertical bar chart was created with the scores indicated on the left side of the chart. Students were instructed to color in the bar chart after each session. In effect, the chart served as a thermometer with students getting closer to the top of the bar with each session of improved performance. A variety of crayons were used so that students could visualize not only the overall increased progress but also gains made each session.

For third and fourth graders, written and graphic performance feedback was provided. A PowerPoint generated graphic display of student progress using a bar chart with sessions on the x-axis and digits or problems correct on the y-axis were constructed. A praise statement was provided at the top of the graph when the student beat their score (e.g., “Way to go, you completed 2 more problems correct!”). A star was inserted on the graph at the point where the new performance goal ( y-axis) met with the session number ( x-axis). A text box below the star provided a goal statement (“Let’s see if you can complete 30 problems correctly today!”). Students were shown the bar graph prior to each session, informed of their current performance levels, and provided with a performance goal that was visually depicted. In all cases, treatment packages with PFGS (i.e., Kindergarten Peer-Assisted Learning Strategies—KPALS + PFGS; Cover–Copy–Compare–CCC + PFGS) yielded significantly greater growth and higher final scores by study termination than treatment packages without PFGS (i.e., KPALS; CCC).

Summary and Areas for Future Research

Current research efforts are underway to develop new standard protocol mathematics interventions and refine existing ones to meet evidence-based expectations. Evaluation of general and specific intervention strategies that can improve whole and rational number knowledge, number combination fluency, and word problem-solving are needed. Fortunately, individualized treatment packages for students in need of tier 3 supports in mathematics can be generated through a problem-solving approach and developed according to the core treatment elements described in this chapter. These treatment components are resource friendly, offering options that require minimal additional training or materials for implementation.

Questions remain regarding the specific combination of treatment elements that are most effective including whether strategies to promote acquisition and fluency are introduced simultaneously or whether treatment strategies are altered depending on skill development. The extent to which existing strategies promote generalization, which is the ultimate goal of all tiered supports, or the manner in which to program for generalization when building treatment packages is unclear. Additional research is needed on the importance of skill sequences (easy to hard; component to composite) and how these arrangements might alter intervention efficiency. The interplay between outcomes (final performance, growth, trials to criterion) and treatment dose defined as number of treatment sessions per week, session duration, and total length of treatment is imperative for determining appropriate and efficient treatment options.