DEA Based Benchmarking Models

Abstract

Data envelopment analysis (DEA) is a methodology for identifying the efficient or best-practice frontier of decision making units (DMUs). It is required that all DMUs under consideration be evaluated against each other in a same pool. Adding or deleting an inefficient DMU does not alter the efficient frontier and the efficiencies of the existing DMUs. The inefficiency scores change only if the efficient frontier is altered. Benchmarking is the process of comparing a DMU’s performance to the best practices formed by a set of DMUs. DEA is also called “balanced benchmarking”, because DEA considers multiple performance metrics in a single model. Under such a notion, the best practices are the benchmarks identified by DEA. However, in a more general sense, best practices do not have to be identified by DEA—they can be existing “standards”. This chapter presents two DEA-based benchmarking approaches where one set of DMUs is compared (or benchmarked) against another. One approach is called “context-dependent” DEA where a set of DMUs is evaluated against a particular evaluation context. Each evaluation context represents an efficient frontier composed by DMUs in a specific performance level. The context-dependent DEA measures the attractiveness and the progress when DMUs exhibiting poorer and better performance are chosen as the evaluation context, respectively. The other approach consists of a fixed benchmark model and a variable benchmark model where each (new) DMU is evaluated against a set of given benchmarks (standards).

10.1 Introduction

Data envelopment analysis (DEA) uses the linear programming technique to evaluate the relative efficiency of decision making units (DMUs) with multiple performance metrics. These performance metrics are classified as DEA outputs and inputs. DEA classifies a set of DMUs into a set of efficient DMUs which form a best-practice frontier and a set of inefficient DMUs. Adding or deleting an inefficient DMU does not alter the efficient frontier and the efficiencies of the existing DMUs. The inefficiency scores change only if the efficient frontier is altered. The performance of DMUs depends only on the identified efficient frontier characterized by the DMUs with a unity efficiency score.

If the performance of inefficient DMUs deteriorates or improves, the efficient DMUs still may have a unity efficiency score. Although the performance of inefficient DMUs depends on the efficient DMUs, efficient DMUs are only characterized by a unity efficiency score. The performance of efficient DMUs is not influenced by the presence of inefficient DMUs, once the DEA frontier is identified.

In this sense, all DMUs under consideration are being benchmarked against the “identified” DEA efficient frontier or best practice. Note that the best practices are part of the DMUs under evaluation. In other words, DEA simultaneously identifies the best practices and measures the performance of under-performing DMUs. As such, DEA is called “balanced benchmarking” where multiple performance metrics are integrated in a single model (Sherman and Zhu 2013).

However, benchmarking can refer to a situation where a set of DMUs is compared to a set of given standards or DMUs. The setup in the conventional DEA does not allow such benchmarking to be performed using DEA. There are two DEA-based approaches that benchmark DMUs against a given set of standards represented by a set of DMUs.

One approach is called “context-dependent” DEA (Seifrod and Zhu 2003) where a set of DMUs is evaluated against a particular evaluation context. Each evaluation context represents an efficient frontier composed by DMUs in a specific performance level. The context-dependent DEA measures the attractiveness and the progress when DMUs exhibiting poorer and better performance are chosen as the evaluation context, respectively.

The other approach consists of a fixed benchmark model and a variable benchmark model where each (new) DMU is evaluated against a set of given benchmarks (standards) (Cook et al. 2004).

10.2 Context-Dependent Data Envelopment Analysis

Performance evaluation is often influenced by the context. A DMU’s performance will appear more attractive against a background of less attractive alternatives and less attractive when compared to more attractive alternatives. Researchers of the consumer choice theory point out that consumer choice is often influenced by the context. e.g., a circle appears large when surrounded by small circles and small when surrounded by larger ones. Similarly, a product may appear attractive against a background of less attractive alternatives and unattractive when compared to more attractive alternatives (Tversky and Simonson 1993).

Considering this influence within the framework of DEA, one could ask “what is the relative attractiveness of a particular DMU when compared to others?” As in Tversky and Simonson (1993), one agrees that the relative attractiveness of DMU$x$ compared to DMU$y$ depends on the presence or absence of a third option, say DMU$z$ (or a group of DMUs). Relative attractiveness depends on the evaluation context constructed from alternative options (or DMUs).

In fact, a set of DMUs can be divided into different levels of efficient frontiers. If we remove the (original) efficient frontier, then the remaining (inefficient) DMUs will form a new second-level efficient frontier. If we remove this new second-level efficient frontier, a third-level efficient frontier is formed, and so on, until no DMU is left. Each such efficient frontier provides an evaluation context for measuring the relative attractiveness. e.g., the second-level efficient frontier serves as the evaluation context for measuring the relative attractiveness of the DMUs located on the first-level (original) efficient frontier. On the other hand, we can measure the performance of DMUs on the third-level efficient frontier with respect to the first or second level efficient frontier.

The context-dependent DEA (Seiford and Zhu 2003) is introduced to measure the relative attractiveness of a particular DMU when compared to others. Relative attractiveness depends on the evaluation context constructed from a set of different DMUs.

The context-dependent DEA is a significant extension to the original DEA approach. The original DEA approach evaluates each DMU against a set of efficient DMUs and cannot identify which efficient DMU is a better option with respect to the inefficient DMU. This is because all efficient DMUs have an efficiency score of one. Although one can use the super-efficiency DEA model (Andersen and Petersen 1993; Seiford and Zhu 1999b) to rank the performance of efficient DMUs, the evaluation context changes in the evaluation of each efficient DMU, and the efficient DMUs are not evaluated against the same reference set.

In the context-dependent DEA, the evaluation contexts are obtained by partitioning a set of DMUs into several levels of efficient frontiers. Each efficient frontier provides an evaluation context for measuring relative attractiveness and progress. When DMUs in a specific level are viewed as having equal performance, the attractiveness measure allows us to differentiate the “equal performance” based upon the same specific evaluation context. A combined use of attractiveness and progress measures can further characterize the performance of DMUs.

Context-dependent DEA has been used for the ranking and benchmarking of the Asian Games achievements (Wu et al. 2013). Lu and Lo (2012) construct the China regions’ benchmark-learning ladders for those inefficient regions to improve progressively and to identify real benchmark for those efficient regions to rank ascendant by incorporating the stratification DEA method, attractiveness measure, and progress measure.

Chiu and Wu (2010) adopt the context-dependent DEA model to analyze the operating efficiencies of 49 international tourism hotels in Taiwan from 2004 through 2006. Ulucan and Atici (2010) evaluate the efficiency of a World Bank supported Social Risk Mitigation Project in Turkey through context-dependent DEA. Yang et al. (2007) use context-dependent DEA to explore the operating efficiency and the benchmark-learning roadmap of military retail stores for Taiwan’s General Welfare Service Ministry. Chen et al. (2005) also provide an illustrative application to measuring the performance of Tokyo public libraries.

Context-dependent DEA has been extended to use with cross efficiency (Lim 2012). Lu and Hung (2008) propose an alternative context-dependent DEA technique to explore the managerial performance and the benchmarks of 24 global leading telecom operators. Tsang and Chen (2013) present a revised context-dependent DEA model to identify multilevel strategic groups in the case of International Tourist Hotels in Taiwan. Brissimis and Zervopoulos (2012) develop a step-by-step effectiveness assessment model for customer-oriented service organizations based upon the context-dependent DEA.

10.2.1 Stratification DEA Model

The first step in the context-dependent DEA is to identify the performance levels or contexts. Assume that there are $n$ DMUs which have $s$ outputs and $m$ inputs. We define the set of all DMUs as ${J^1}$ and the set of efficient DMUs in ${J^1}$ as ${E^1}$. Then the sequences of ${J^l}$ and ${E^l}$ are defined interactively as ${J^{l + 1}}= {J^l}-{E^l}$. The set of ${E^l}$ can be found as the DMUs with optimal value $\phi_k^l$ of 1 to the following linear programming problem:

$$ \begin{matrix} {\mathop {{\text{minimize}}}_{\lambda,\theta } }&{\theta_k^l = \theta } \\ {{\text{subject to}}}&{\sum_{j\in {J^l}}{{\lambda_j}{x_{ij}}}\le \theta {x_{ik}},i = 1,\ldots,m} \\ {}&{\sum_{j\in {J^l}}{{\lambda_j}{y_{rj}}}\ge {y_{rk}},r = 1,.\ldots s} \\ {}&{{\lambda_j}\ge 0,j\in {J^l}} \end{matrix} $$

(10.1)

where ${x_{ij}}$ and ${y_{rj}}$ are $i$-th input and $r$-th output of DMU$j$respectively. When $l = 1$, model (10.1) becomes the original input-oriented CCR model (Charnes et al. 1978) and ${E^1}$ consists of all the radially efficient DMUs. A radially efficient DMU may have non-zero input/output slack values. The DMUs in set ${E^1}$ define the first-level efficient frontier. When $l = 2$, model (10.1) gives the second-level efficient frontier after the exclusion of the first-level efficient DMUs. In this manner, we identify several levels of efficient frontiers. We call ${E^l}$ the $l$-th level efficient frontier. The following algorithm accomplishes the identification of these efficient frontiers by model (10.1).

Step 1

Set $l = 1$. Evaluate the entire set of DMUs, ${J^1}$, by model (10.1) to obtain the first-level efficient DMUs, set ${E^1}$ (the first-level efficient frontier).

Step 2

Let ${J^{l + 1}}= {J^l}-{E^l}$ to exclude the efficient DMUs from future DEA runs. If ${J^{l + 1}}= \O$ then stop.

Step 3

Evaluate the new subset of "inefficient" DMUs, ${J^{l + 1}}$, by model (10.1) to obtain a new set of efficient DMUs ${E^{l + 1}}$ (the new efficient frontier).

Step 4

Let $l = l + 1$. Go to step 2.

Stopping rule

If ${J^{l + 1}}= \O$, the algorithm stops.

Model (10.1) yields a stratification of the whole set of DMUs, which partitions the DMUs into different subgroups of efficiency levels characterized by ${E^l}$. It is easy to show that these sets of DMUs have the following properties:

• 1. ${J^1} = \bigcup {{E^l}}$ and ${E^l}\cap {E^{l'}}= \phi$ for $l\ne l'$;

• 2. The DMUs in ${E^{l'}}$ are dominated by the DMUs in ${E^l}$ if $l'>l$;

• 3. Each DMU in set ${E^l}$ is efficient with respect to the DMUs in set ${J^{l'}}$ for all $l'>l$.

Figure 10.1 plots the three levels of efficient frontiers of 10 DMUs with two inputs and one single output as shown in Table 10.1.

Fig. 10.1

Efficient Frontiers in Different Levels

Table 10.1 Numerical example

10.2.2 Attractiveness and Progress

Based upon the evaluation context ${E^l}$, the context-dependent DEA measures the relative attractiveness of DMUs. Consider a specific DMU$q$ in ${E^{l}}$. The following model is used to characterize the attractiveness with respect to levels exhibiting poorer performance in ${E^{l'}}$ for $l'>l$.

$$ \begin{matrix} {\mathop {{\text{minimize}}}_{\lambda,\theta } }&{\theta_q^{l'} = \theta } \\ {{\text{subject to}}}&{\sum_{j\in {J^{l'}}}{{\lambda_j}{x_{ij}}}\le \theta {x_{iq}},i = 1,\ldots,m} \\ {}&{\sum_{j\in {J^{l'}}}{{\lambda_j}{y_{rj}}}\ge {y_{rq}},r = 1,\ldots,s} \\ {}&{{\lambda_j}\ge 0,j\in {J^{l'}}} \end{matrix} $$

(10.2)

It is easy to show that $\theta_q^{l'}>1$ for $l'>l$, and $\theta_q^{{l_1}}>\theta_q^{{l_2}}$ for ${l_1}>{l_2}$. Then $\theta_q^{l'}$ is called the input-oriented $d$-degree attractiveness of DMU$q$ from a specific level ${E^{l}}$, where $d = l'-l$.

In model (10.2), each efficient frontier represents an evaluation context for evaluating the relative attractiveness of DMUs in ${E^{l}}$. Note that the bigger the value of $\theta_q^{l'}>1$, the more attractive DMU$q$ is, because DMU$q$ makes itself more distinctive from the evaluation context ${E^{l'}}$. We are able to rank the DMUs in ${E^{l}}$ based upon their attractiveness scores and identify the best one.

To obtain the progress measure for a specific DMU$q$ in ${E^{l}}$, we use the following context-dependent DEA, which is used to characterize the progress with respect to levels exhibiting better performance in ${E^{l'}}$ for $l'<l$.

$$ \begin{matrix} {\mathop {{\text{minimize}}}_{\lambda,\varphi } }&{\varphi_q^{l'} = \varphi } \\ {{\text{subject to}}}&{\sum_{j\in {J^{l'}}}{{\lambda_j}{x_{ij}}}\le \varphi {x_{iq}},i = 1,\ldots,m} \\ {}&{\sum_{j\in {J^{l'}}}{{\lambda_j}{y_{rj}}}\ge {y_{rq}},r = 1,\ldots,s} \\ {}&{{\lambda_j}\ge 0,j\in {J^{l'}}} \end{matrix} $$

(10.3)

We have that $\varphi_q^{l'}<1$ for $l'<l$, and $\varphi_q^{{l_1}}<\varphi_q^{{l_2}}$ for ${l_1}>{l_2}$. Then $\varphi_q^{l'}$ is called the input-oriented $g$-degree progress of DMU$q$ from a specific level ${E^{l}}$, where $g = l-l'$.

10.2.3 Output Oriented Context-Dependent DEA Model

Here we provide the output-oriented context-dependent DEA model. Consider the following linear programming problem for DMU$q$ in specific level ${E^{l}}$ based upon the evaluation context ${E^{l'}}$ for $l'>l$.

$$ \begin{matrix} {\mathop {{\text{maximize}}}_{\lambda,H} }&{H_q^{l'} = H} \\ {{\text{subject to}}}&{\sum_{j\in {J^{l'}}}{{\lambda_j}{x_{ij}}}\le {x_{iq}},i = 1,\ldots,m} \\ {}&{\sum_{j\in {J^{l'}}}{{\lambda_j}{y_{rj}}}\ge H{y_{rq}},r = 1,\ldots,s} \\ {}&{{\lambda_j}\ge 0,j\in {J^{l'}}} \end{matrix} $$

(10.4)

This problem is used to characterize the attractiveness with respect to levels exhibiting poorer performance in ${E^{l'}}$. Note that dividing each side of the constraint of (10.4) by $H$ gives

$$ \begin{gathered} \sum_{j\in {J^{l'}}}{{{\tilde{\lambda }}_j}{x_{ij}}}\le \frac{1}{H}{x_{iq}} \\ \sum_{j\in {J^{l'}}}{{{\tilde{\lambda }}_j}{y_{rj}}}\ge {y_{rq}} \\ {{\tilde{\lambda }}_j} = \frac{{{\lambda_j}}}{H}\ge 0,j\in {J^{l'}} \end{gathered}$$

Therefore, (10.4) is equivalent to (10.2), and we have that $H_q^{l'}<1$ for $l'>l$ and $H_q^{l'} = 1/\theta_q^{l'}$. Then $H_q^{l'}$ is called the output-oriented $d$-degree attractiveness of DMU$q$ from a specific level ${E^{l}}$, where $d = l'-l$. The smaller the value of $H_q^{l'}$ is, the more attractive DMU$q$ is. Model (10.4) determines the relative attractiveness score for DMU$q$ when inputs are fixed at their current levels.

To obtain the progress measure for DMU$q$ in ${E^{l}}$, we develop the following linear programming problem, which is used to characterize the progress with respect to levels exhibiting better performance in ${E^{l'}}$ for $l'<l$.

$$ \begin{matrix} {\mathop {{\text{maximize}}}_{\lambda,G} }&{G_q^{l'} = G} \\ {{\text{subject to}}}&{\sum_{j\in {J^{l'}}}{{\lambda_j}{x_{ij}}}\le {x_{iq}},i = 1,\ldots,m} \\ {}&{\sum_{j\in {J^{l'}}}{{\lambda_j}{y_{rj}}}\ge G{y_{rq}},r = 1,\ldots,s} \\ {}&{{\lambda_j}\ge 0,j\in {J^{l'}}} \end{matrix} $$

(10.5)

We have that $G_q^{l'}>1$ for $l'<l$ and $G_q^{l'} = 1/\varphi_q^{l'}$. Then $G_q^{l'}$ is called the output-oriented $g$-degree progress of DMU$q$ from a specific level ${E^{l}}$, where $g = l-l'$.

To improve the performance of inefficient DMU, the target of improvement should be given among the efficient DMUs. The reference set suggests the target of improvement for the inefficient DMUs. Actually, when $l = 1$, model (10.1) gives the reference set of DMUs from the efficient DMUs for inefficient DMUs. It may be a final goal of improvement; however, for some inefficient DMUs, this goal may be quite different from the current performance and difficult to achieve. Therefore, it is not appropriate to set a benchmark target for improvement from the efficient DMUs directly. Step-by-step improvement is a useful way to improve the performance, and the benchmark target at each step is provided based on the evaluation context at each level of efficient frontier.

10.2.4 Context-Dependent DEA With Value Judgment

Both attractiveness and progress are measured radially with respect to different levels of efficient frontiers. The measurement does not require a priori information on the importance of the attributes (input/output) that feature in the performance of DMUs. However different attributes play different roles in the evaluation of a DMU’s overall performance. Therefore, we introduce value judgment into the context-dependent DEA.

In order to incorporate such a priori information into our measures of attractiveness and progress, we first specify a set of weights related to the $m$ inputs, ${v_i},i = 1,\ldots,m$such that $\sum_{i = 1}^m {{v_i}}= 1$. Based upon Zhu (1996), we develop the following linear programming problem for DMU$q$ in ${E^l}$.

$$ \begin{matrix} {\mathop {{\text{Maximize}}}_{{\lambda_j},\Theta_{iq}} }&{\Theta {{_q^{l'}}^*} = \sum_{r = 1}^s {{v_i}{\Theta_{iq}}}}\\ {{\text{subject to}}}&{\sum_{j\in {E^{l'}}}{{\lambda_j}}{x_{ij}}\le {\Theta_{iq}}{x_{iq}}{,}i = 1,\ldots,m} \\ {}&{\sum_{j\in {E^{l'}}}{{\lambda_j}}{y_{rj}}\ge {y_{rq}}{,}r = 1,\ldots,s} \\ {}&{{\Theta_{iq}}\geq 1{,}i = 1,\ldots,m} \\ {}&{{\lambda_j}\ge 0,j\in {E^{l'}}} \end{matrix}{} $$

(10.6)

$\Theta {_q^{l}{\prime}^*}$ is called the input-oriented value judgment $d$ -degree attractiveness of DMU$q$ from a specific level ${E^{l}}$, where $d = l'-l$. Obviously, $\Theta {_q^{l}{\prime}^*}> 1$. The larger the $\Theta {_q^{l}{\prime}^*}$ is, the more attractive the DMU$q$ appears under the weights ${v_i},i = 1,\ldots,m$. We now can rank DMUs in the same level by their attractiveness scores with value judgment which are incorporated with the preferences over outputs.

If one wishes to prioritize the options (DMUs) with higher values of the ${i_o}$-th input, then one can increase the value of the corresponding weight ${v_{{i_o}}}$. These user-specified weights reflect the relative degree of desirability of the corresponding outputs. For example, if one prefers a printer with faster printing speed to one with higher print quality, then one may specify a larger weight for the speed. The constraints of ${\Theta_{iq}}\geq 1,i = 1,\ldots{},m$ ensure that in an attempt to make itself as distinctive as possible, DMU$q$ is not allowed to decrease some of its outputs to achieve higher levels of other preferred outputs.

Note that $\Theta ^{l{\prime}*}{_q}$ is an overall attractiveness of DMU$q$ in terms of inputs while keeping the outputs at their current levels. On the other hand, each individual optimal value of ${\Theta_{iq}},i = 1,\ldots,m$ measures the attractiveness of DMU$q$ in terms of each input dimension. $\Theta_{iq}^*$ is called the input-oriented value judgment input-specific attractiveness measure for DMU$q$.

With the input-specific attractiveness measures, one can further identify which inputs play important roles in distinguishing a DMU’s performance. On the other hand, if $\Theta_{{i_o}q}^* = 1$, then other DMUs in ${E^{l'}}$ or their combinations can also produce the same amount as the ${i_o}$-th input of DMU$q$, i.e., DMU$q$ does not exhibit better performance with respect to this specific input dimension. Therefore, DMU$q$ should improve its performance on the ${i_o}$-th input to distinguish itself in the future.

Similar to the development in the previous section, we can define the input-oriented value judgment progress measure:

$$ \begin{matrix} {\mathop {{\text{Maximize}}}_{{\lambda_j},{\Phi_{iq}}}}&{\Phi {{_q^{l'}}^*} = \sum_{r = 1}^s {{v_i}{\Phi_{iq}}}}\\ {{\text{subject to}}}&{\sum_{j\in {E^{l'}}}{{\lambda_j}}{x_{ij}}\le {\Phi_{iq}}{x_{iq}}{,}i = 1,\ldots,m} \\ {}&{\sum_{j\in {E^{l'}}}{{\lambda_j}}{y_{rj}}\ge {y_{rq}}{,}r = 1,\ldots,s} \\ {}&{{\Phi_{iq}}\leq 1,i = 1,\ldots,m} \\ {}&{{\lambda_j}\ge 0,j\in {E^{l'}}} \end{matrix} $$

(10.7)

The optimal value $\Theta^{l{\prime}{*}} _{q}$ is called the input-oriented value judgment $g$ -degree progress DMU$q$ from a specific level ${E^{l}}$, where $g = l-l'$. The larger $\Theta^{l{\prime}{*}} _{q}$ is, the greater the amount of progress is expected for DMU$q$. Here the user-specified weights reflect the relative degree of desirability of improvement on the individual output levels. Let $\Phi_{iq}^*,i = 1,\ldots,m$ represent the optimal value of (10.7) for a specific level $l$. By Zhu (1996), we know that $\sum_{j\in {E^{l'}}}{\lambda_j^*{x_{ij}}}= \Phi_{iq}^*{x_{iq}}$ holds at optimality for each $i = 1,\ldots,m$. Consider the following linear programming problem:

$$ \begin{matrix} {\mathop {{\text{Maximize}}}_{} }&{\sum\limits_{r = 1}^s {S^{+}{{_r}}}}\\ {{\text{subject to}}}&{\sum_{j\in {E^{l'}}}{{\lambda_j}}{x_{ij}}= {\Phi^*}_{iq}{x_{iq}}{,}i = 1,\ldots,m} \\ {}&{\sum_{j\in {E^{l'}}}{{\lambda_j}}{y_{rj}}-S_r^ += {y_{rq}},r = 1,\ldots,s} \\ {}&{S_r^ + \ge 0,r = 1,\ldots,s} \\ {}&{{\lambda_j}\ge 0,j\in {E^{l'}}} \end{matrix} $$

(10.8)

The following point

$$\left\{ \begin{aligned} & {{{\hat{x}}}_{iq}}=\Phi _{iq}^{*}{{x}_{iq}},i=1,\ldots ,m \\ & {{{\hat{y}}}_{rq}}={{y}_{rq}}+s{{_{r}^{+}}^{*}},r=1,\ldots ,s \\\end{aligned} \right.$$

is called a preferred global efficient target for DMU$q$ in level ${E^l}$ for $l' = l-1$; otherwise, if $l'<l-1$, it represents a preferred local efficient target, where $\Phi_{iq}^*$ is the optimal value in (10.7), and $s{{_{r}^{+}}^{*}}$ represent the optimal values in (10.8).

10.3 Variable and Fixed Benchmarking Models

Cook et al. (2004) develop DEA-based models for use in benchmarking where multiple performance measures are needed to examine the performance and productivity changes. The standard data envelopment analysis method is extended to incorporate benchmarks through (i) a variable-benchmark model where a unit under benchmarking selects a portion of benchmark such that the performance is characterized in the most favorable light, and (ii) a fixed-benchmark model where a unit is benchmarked against a fixed set of benchmarks. Cook et al. (2004) apply these models to a large Canadian bank where some branches’ services are automated to reduce costs and increase the service speed, and ultimately to improve productivity. Their empirical investigation indicates that although the performance appears to be improved at the beginning, productivity gain has not been discovered. The models can facilitate the bank in examining its business options and further point to weaknesses and strengths in branch operations. The current chapter presents the benchmarking models developed by Cook et al. (2004).

10.3.1 Variable-Benchmark Model

Let ${E^*}$ represent the set of benchmarks or the best-practice identified by the DEA. Based upon the input-oriented Constant Returns to Scale (CRS) DEA model, we have

$$ \begin{gathered} \min\; \delta_{}^{CRS} \\ {\text{subject to}} \\ \sum_{j\in E*} {{\lambda_j}}{x_{ij}}\le \delta_{}^{CRS}x_i^{new} \\ \sum_{j\in E*} {{\lambda_j}}{y_{rj}}\ge y_r^{new} \\ {\lambda_j}\ge 0,j\in {E^*} \end{gathered}$$

(10.9)

where a new observation is represented by $DM{U^{new}}$ with inputs $x_i^{new}({i = 1,\ldots,m})$ and outputs $y_r^{new}({r = 1,\ldots,s})$. The superscript of CRS indicates that the benchmark frontier composed by benchmark DMUs in set ${E^*}$ exhibits CRS.

Model (10.9) measures the performance of $DM{U^{new}}$ with respect to benchmark DMUs in set ${E^*}$ when outputs are fixed at their current levels. Similarly, based upon the output-oriented CRS envelopment model, we can have a model that measures the performance of $DM{U^{new}}$ in terms of outputs when inputs are fixed at their current levels.

$$ \begin{gathered} \max\; \tau_{}^{CRS} \\ {\text{subject to}} \\ \sum_{j\in E*} {{\lambda_j}}{x_{ij}}\le x_i^{new} \\ \sum_{j\in E*} {{\lambda_j}}{y_{rj}}\ge \tau_{}^{CRS}y_r^{new} \\ {\lambda_j}\ge 0,j\in {E^*} \end{gathered}$$

(10.10)

Note that $\delta_{}^{CRS*} = {1/{{\tau^{CRS*}}}}$, where $\delta_{}^{CRS*}$ is the optimal value to model (10.9) and $\tau_o^{CRS*}$ is the optimal value to model (10.10).

Model (10.9) or (10.10) yields a benchmark for $DM{U^{new}}$. The ith input and the rth output for the benchmark can be expressed as

$$ \left\{\begin{gathered} \sum_{j\in E*} {\lambda_j^*} {x_{ij}}{}(ith{}input) \\ \sum_{j\in E*} {\lambda_j^*} {y_{ij}}{}(rth{\text{ }}output) \end{gathered} \right. $$

(10.11)

Note also that although the DMUs associated with set ${E^*}$ are given, the resulting benchmark may be different for each new DMU under evaluation. For each new DMU under evaluation, (10.11) may represent a different combination of DMUs associated with set ${E^*}$. Thus, models (10.9) and (10.10) represent a variable-benchmark scenario.

We have

• 1. $\delta_{}^{CRS*}<1$ or $\tau_{}^{CRS*}>1$ indicates that the performance of $DMU_o^{new}$ is dominated by the benchmark in (10.11).

• 2. $\delta_{}^{CRS*} = 1$ or $\tau_{}^{CRS*} = 1$ indicates that $DM{U^{new}}$ achieves the same performance level as the benchmark in (10.11).

• 3. $\delta_{}^{CRS*}>1$ or $\tau_{}^{CRS*}<1$ indicates that input savings or output surpluses exist in $DMU_o^{new}$ when compared to the benchmark in (10.11).

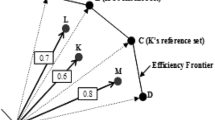
Figure 10.2 illustrates the three cases. ABC (A'B'C') represents the input (output) benchmark frontier. D, H and G (or D', H', and G') represent the new DMUs to be benchmarked against ABC (or A'B'C'). We have $\delta_D^{CRS*}>1$ for DMU D ($\tau_{D'}^{CRS*}<1$ for DMU D') indicating that DMU D can increase its input values by $\delta_D^{CRS*}$ while producing the same amount of outputs generated by the benchmark (DMU D' can decrease its output levels while using the same amount of input levels consumed by the benchmark). Thus, $\delta_D^{CRS*}>1$ is a measure of input savings achieved by DMU D and $\tau_{D'}^{CRS*}<1$ is a measure of output surpluses achieved by DMU D'.

Fig. 10.2

Variable-benchmark Model

For DMU G and DMU G', we have $\delta_G^{CRS*} = 1$ and $\tau_{G'}^{CRS*} = 1$ indicating that they achieve the same performance level of the benchmark and no input savings or output surpluses exist. For DMU H and DMU H', we have $\delta_H^{CRS*}<1$ and $\tau_{H'}^{CRS*}>1$ indicating that inefficiency exists in the performance of these two DMUs.

Note that for example, in Fig. 10.2, a convex combination of DMU A and DMU B is used as the benchmark for DMU D while a convex combination of DMU B and DMU C is used as the benchmark for DMU G. Thus, models (10.9) and (10.10) are called variable-benchmark models.

We can define $\delta_{}^{CRS*}-1$ or $1-\tau_{}^{CRS*}$ as the performance gap between $DM{U^{new}}$ and the benchmark. Based upon $\delta_{}^{CRS*}$ or $\tau_{}^{CRS*}$, a ranking of the benchmarking performance can be obtained.

It is likely that scale inefficiency may be allowed in the benchmarking. We therefore modify models (10.9) and (10.10) to incorporate scale inefficiency by assuming variable returns to scale (VRS).

$$ \begin{gathered} \min\; \delta_{}^{VRS} \\ {\text{subject to}} \\ \sum_{j\in E*} {{\lambda_j}}{x_{ij}}\le \delta_{}^{VRS}x_i^{new} \\ \sum_{j\in E*} {{\lambda_j}}{y_{rj}}\ge y_r^{new} \\ \sum_{j\in E*} {{\lambda_j}}= 1 \\ {\lambda_j}\ge 0,j\in {E^*} \end{gathered}$$

(10.12)

$$ \begin{gathered} \max\; \tau_{}^{VRS} \\ {\text{subject to}} \\ \sum_{j\in E*} {{\lambda_j}}{x_{ij}}\le x_i^{new} \\ \sum_{j\in E*} {{\lambda_j}}{y_{rj}}\ge \tau_{}^{VRS}y_r^{new} \\ \sum_{j\in E*} {{\lambda_j}}= 1 \\ {\lambda_j}\ge 0,j\in {E^*} \end{gathered}$$

(10.13)

We have

• 1. $\delta_{}^{VRS*}<1$ or $\tau_{}^{VRS*}>1$ indicates that the performance of $DM{U^{new}}$ is dominated by the benchmark in (10.11).

• 2. $\delta_{}^{VRS*} = 1$ or $\tau_{}^{VRS*} = 1$ indicates that $DM{U^{new}}$ achieves the same performance level as the benchmark in (10.11).

• 3. $\delta_{}^{VRS*}>1$ or $\tau_{}^{VRS*}<1$ indicates that input savings or output surpluses exist in $DM{U^{new}}$ when compared to the benchmark in (10.11).

Note that model (10.10) is always feasible, and model (10.9) is infeasible only if certain patterns of zero data are present (Zhu 1996b). Thus, if we assume that all the data are positive, (10.9) is always feasible. However, unlike models (10.9) and (10.10), models (10.12) and (10.13) may be infeasible.

We have

• 1. If model (10.12) is infeasible, then the output vector of $DM{U^{new}}$ dominates the output vector of the benchmark in (10.11).

• 2. If model (10.13) is infeasible, then the input vector of $DM{U^{new}}$ dominates the input vector of the benchmark in (10.11).

The implication of the infeasibility associated with models (10.12) and (10.13) needs to be carefully examined. Consider Fig. 10.3 where ABC represents the benchmark frontier. Models (10.12) and (10.13) yield finite optimal values for any $DM{U^{new}}$ located below EC and to the right of EA. Model (10.12) is infeasible for $DM{U^{new}}$ located above ray E''C and model (10.13) is infeasible for $DM{U^{new}}$ located to the left of ray E'E.

Fig. 10.3

Infeasibility of VRS Variable-benchmark Model

Both models (10.12) and (10.13) are infeasible for $DM{U^{new}}$ located above E''E and to the left of ray EF. Note that if $DM{U^{new}}$ is located above E''C, its output value is greater than the output value of any convex combinations of A, B and C.

Note also that if $DM{U^{new}}$ is located to the left of E'F, its input value is less than the input value of any convex combinations of A, B and C.

Based upon Fig. 10.3, we have four cases:

Case I::

When both models (10.12) and (10.13) are infeasible, this indicates that $DM{U^{new}}$ has the smallest input level and the largest output level compared to the benchmark. Thus, both input savings and output surpluses exist in$DM{U^{new}}$.

Case II::

When model (10.12) is infeasible and model (10.13) is feasible, the infeasibility of model (10.12) is caused by the fact that $DM{U^{new}}$ has the largest output level compared to the benchmark. Thus, we use model (10.13) to characterize the output surpluses.

Case III::

When model (10.13) is infeasible and model (10.12) is feasible, the infeasibility of model (10.13) is caused by the fact that $DM{U^{new}}$ has the smallest input level compared to the benchmark. Thus, we use model (10.12) to characterize the input savings.

Case IV::

When both models (10.12) and (10.13) are feasible, we use both of them to determine whether input savings and output surpluses exist.

10.3.2 Fixed-Benchmark Model

Although the benchmark frontier is given in the variable-benchmark models, a $DM{U^{new}}$ under benchmarking has the freedom to choose a subset of benchmarks so that the performance of $DM{U^{new}}$ can be characterized in the most favorable light. Situations when the same benchmark should be fixed are likely to occur. For example, the management may indicate that DMUs A and B in Fig. 10.2 should be used as the fixed benchmark. i.e., DMU C in Fig. 10.2 may not be used in constructing the benchmark.

To couple with this situation, Cook et al. (2004) turn to the multiplier DEA models. For example, the input-oriented CRS multiplier DEA model determines a set of referent best-practice DMUs represented by a set of binding constraints in optimality. Let set $B = \left\{{DM{U_j}:j\in {I_B}}\right\}$ be the selected subset of benchmark set ${E^*}$. i.e., ${{\mathbf{I}}_B}\subset E*$ Based upon the input-oriented CRS multiplier model, we have

$$ \begin{gathered} \tilde{\sigma }_{}^{{\text{CRS*}}}= {}\max \sum_{r = 1}^s {{\mu_r}y_r^{new}} \\ {\text{subject to}} \\ \sum_{r = 1}^s {{\mu_r}{y_{rj}}}-\sum_{i = 1}^s {{\nu_i}{x_{ij}}}= 0{\text{ }}j\in {{\mathbf{I}}_B} \\ \sum_{r = 1}^s {{\mu_r}{y_{rj}}}-\sum_{i = 1}^s {{\nu_i}{x_{ij}}}\le 0{}j\notin {{\mathbf{I}}_B} \\ \sum_{i = 1}^m {{\nu_i}x_i^{new}}= 1 \\ {\mu_r},{\nu_i}\ge 0. \end{gathered}$$

(10.14)

By applying equalities in the constraints associated with benchmark DMUs, model (10.14) measures $DM{U^{new}}$’s performance against the benchmark constructed by set B. At optimality, some DMU _j $j\notin {{\mathbf{I}}_B}$, may join the fixed-benchmark set if the associated constraints are binding.

Note that model (10.14) may be infeasible. For example, the DMUs in set B may not be fit into the same facet when they number greater than m + s-1, where m is the number of inputs and s is the number of outputs. In this case, we need to adjust the set B.

Three possible cases are associated with model (10.14). $\tilde{\sigma }_{}^{CRS*}>1$ indicating that $DM{U^{new}}$ outperforms the benchmark. $\tilde{\sigma }_{}^{CRS*} = 1$ indicating that $DM{U^{new}}$ achieves the same performance level of the benchmark. $\tilde{\sigma }_{}^{CRS*}<1$ indicating that the benchmark outperforms $DM{U^{new}}$.

By applying returns to scale (RTS) frontier type and model orientation, we obtain the fixed-benchmark models in Table 10.2.

Table 10.2 Fixed-benchmark Models

A commonly used measure of efficiency is the ratio of output to input. For example, profit per employee measures the labor productivity. When multiple inputs and outputs are present, we may define the following efficiency ratio

$$ \frac{{\sum_{r = 1}^s {{u_r}{y_{ro}}}}}{{\sum_{i = 1}^m {{v_i}{x_{io}}}}}$$

where ${v_i}$ and ${u_r}$ represent the input and output weights, respectively.

DEA calculates the ratio efficiency without the information on the weights. In fact, the multiplier DEA models can be transformed into linear fractional programming problems. For example, if we define ${\nu_i} = {\text{t}}{v_i}$ and ${\mu_r} = {\text{t}}{u_r}$, where ${\text{t}}= {1/{\sum {{\nu_i}{x_{io}}}}}$, the input-oriented CRS multiplier model can be transformed into

$$ \begin{gathered} \max \frac{{\sum_{r = 1}^s {{u_r}{y_{ro}}}}}{{\sum_{i = 1}^m {{v_i}{x_{io}}}}} \\ {\text{subject to}} \\ \frac{{\sum_{r = 1}^s {{u_r}{y_{rj}}}}}{{\sum_{i = 1}^m {{v_i}{x_{ij}}}}}\le 1{\text{ }}j = 1,2,\ldots,n \\ {u_r},{v_i}\ge 0{}\forall r,i \end{gathered}$$

(10.15)

The objective function in (10.15) represents the efficiency ratio of a DMU under evaluation. Because of the constraints in (10.15), the (maximum) efficiency cannot exceed one. Consequently, a DMU with an efficiency score of one is on the frontier. It can be seen that no additional information on the weights or tradeoffs are incorporated into the model (10.15).

If we apply the input-oriented CRS fixed-benchmark model to (10.15), we obtain

$$ \begin{gathered} \max \frac{{\sum_{r = 1}^s {{u_r}y_r^{new}}}}{{\sum_{i = 1}^m {{v_i}x_i^{new}}}} \\ {\text{subject to}} \\ \frac{{\sum_{r = 1}^s {{u_r}{y_{rj}}}}}{{\sum_{i = 1}^m {{v_i}{x_{ij}}}}}= 1{\text{ }}j\in {{\mathbf{I}}_{\text{B}}}\end{gathered}$$

(10.16)

$$ \begin{gathered} \frac{{\sum_{r = 1}^s {{u_r}{y_{rj}}}}}{{\sum_{i = 1}^m {{v_i}{x_{ij}}}}}\le 1{\text{ }}j\notin {{\mathbf{I}}_{\text{B}}} \\ {u_r},{v_i}\ge 0{}\forall r,i \end{gathered}$$

It can be seen from (10.16) that the fixed benchmarks incorporate implicit tradeoff information into the efficiency evaluation. i.e., the constraints associated with ${{\mathbf{I}}_{\text{B}}}$ can be viewed as the incorporation of tradeoffs or weight restrictions in DEA. Model (10.16) yields the (maximum) efficiency under the implicit tradeoff information represented by the benchmarks.

As more DMUs are selected as fixed benchmarks, more complete information on the weights becomes available.

10.4 Concluding Remarks

This chapter presents the context-dependent DEA and benchmarking DEA approaches. Morita et al. (2005) show that non-zero slacks can be incorporated into the context-dependent DEA. Zhu (2014) provides spreadsheet models for calculating the presented DEA models. The benchmarking models developed by Cook et al. (2004) provide tools needed to monitor the performance change and further facilitates the development of the best strategic option for the organization with regard to DMU makeup. The interested reader is referred to Cook et al. (2004).