Keywords

1 Introduction

Rapid distribution of medical supplies plays a critical role in assuring the effectiveness and efficiency of the healthcare system. The medical supply distribution involves the movement of a large volume of different items that usually must be delivered rapidly. For example, in the USA, the distribution system must serve more than 130,000 pharmacy outlets every day on demand and a typical pharmacy relies on the distributors to have more than 10,000 SKUs accessible for delivery, often within 12 h (HDMA 2005).

In broad terms, most pharmaceuticals distributed in the USA go through a supply chain that comprises the following steps (Belson 2005):

  • Manufacturers produce various pharmaceuticals necessitated by demand.

  • Distributors manage large warehouses and control the movement of supplies from manufacturers to the retailers.

  • Retailers, including hospitals, clinics, independent pharmacies, chain pharmacies, and grocery stores, sell or dispense the pharmaceuticals to customers.

The pharmaceutical supply chain is relatively complex compared to the supply chains for other products, particularly when considering the strict deadline and sufficiency requirements. Different information technologies such as product identification, bar coding, usage related information, and electronic identification have been applied to facilitate the rapid distribution of the pharmaceuticals in the supply chain (Belson 2005). Furthermore, logistic and inventory control of the pharmaceuticals have also been widely investigated in the research community in the past decades; for example, see Rebidas et al. (1999), Rubin and Keller (1983), and McAllister (1985).

It is the design of the distribution system in particular, that most significantly affects the rapid disbursement of pharmaceuticals, directly impacting the quality of healthcare. The design of an effective distribution system comprises the careful consideration of two strategic planning issues:

  • Where to place the facilities including warehouses and inventories in support of rapid distribution of the medical supplies

  • What is the best strategy to distribute the medical supplies and what routes need to be used?

Operations research models play an important role in addressing these logistical problems for distribution systems. At the heart of both questions there is a transportation network to distribute the medical supplies. The question of where to place warehouses/inventories is essentially a facility location problem within this supply network, while the disbursement of supplies can be posed as a vehicle routing problem (VRP) on this network. The benefits of modeling and solving the facility location problem and vehicle routing problem are twofold. First, from a planning perspective, the models and solutions can aid planners to optimally determine the facility locations and vehicle routes and thus maximize the efficiency and effectiveness of the pharmaceutical supply chain system as a whole. Second, these plans can become well tested operating policies, which can further improve performance. Clearly, the plans need to be flexible enough to accommodate contingencies of daily operations. For the plans to be robust, they must take into consideration the stochastic nature of the problem such as uncertain demand, traffic conditions, etc.

Large-scale emergencies create situations that demand a rapid distribution of medical supplies and thus require an efficient and coordinated solution to both the facility location and vehicle routing problems. In particular, the response to a large-scale emergency must take into consideration that:

  • A huge demand for medical supplies appears within a short time period and thus large quantities of medical supplies must be brought to the affected area.

  • The local first-responders and resources will be overwhelmed.

  • Although tremendous in their magnitude, large-scale emergencies occur with low frequency.

An additional parallel distribution system is envisioned in response to large-scale emergencies such as earthquakes, terrorist events, etc. as massive supplies that are brought to the affected area have to be rapidly disbursed among the affected population. Indeed, many countries maintain national stockpiles of medical supplies that can be delivered in push packages to the Emergency Staging Area (ESA) in case of a large-scale emergency. For example, to address emergencies of infectious disease outbreak, the federal government of the USA maintains a Strategic National Stockpile (SNS) which contains about 300 million doses of smallpox vaccines and enough antibiotic to treat 20 million people for anthrax (CDC website 2005). Furthermore, a vendor managed inventory system (VMI) has also been developed to augment the SNS from pharmaceutical vendors to ESAs within 21–36 h. During a large-scale emergency, the medical supplies at the national stockpile and VMI require direct delivery and disbursement to ESAs and dispensing centers from which the population could receive the medical supplies. Rapid delivery and disbursement of the large volume of supplies need careful planning and professional execution to save lives, particularly in high-density urban regions like Southern California.

In this chapter, we analyze the facility location and vehicle routing problems, which are crucial for a rapid distribution of medical supplies in response to large-scale emergencies. We use the anthrax disease as an emergency example to investigate the problems of determining where to locate the staging areas to receive the national stockpile and how to route the vehicles to distribute the medical supplies. The rest of the chapter is organized as follows: Section 2 presents a literature review of the facility location and vehicle routing problems that are related to emergency services. In Section 3, we describe an anthrax emergency example in a metropolitan area and then analyze the requirements for locating the facilities and routing the vehicles for rapid medical supply distribution. In Section 4, we propose a facility location model and a vehicle routing model that address the characteristics of an anthrax emergency. In Section 5, we demonstrate how the proposed models can be used to solve the facility location problem and the VRP. The solutions, including the selected staging areas and vehicle routes to store and distribute the medical supplies, are discussed. Finally, we conclude the chapter and give future research directions in Sect. 6.

2 Literature Review

Facility location problems and VRPs have been extensively investigated by different researchers and practitioners. In this section, we review the prior work that is related to different emergencies settings.

2.1 Review of Facility Location Problems

Various location models have been proposed to formulate different facility location problems for emergency services. Based on the objectives, these location models can be classified into covering models, P-median models, and P-center models.

2.1.1 Covering Models

Covering models are the most widespread location models for formulating the emergency facility location problem. The objective of covering models is to provide “coverage” to the demand points. A demand point is considered as covered only if a facility is available to service the demand point within a distance limit. Figure 16.1 presents an illustration of an infeasible covering problem, where the coverage area of a facility is indicated by circles around the four selected locations.

Fig. 16.1
figure 1

Covering problem example

Full size image

Toregas et al. (1971) first proposed the location set covering problem (LSCP), aiming to locate the least number of facilities to cover all demand points. Since all the demand points need to be covered in the LSCP, the resources required for facilities could be excessive. Recognizing this problem, Church and ReVelle (1974) and White and Case (1974) developed the MCLP model that does not require full coverage to all demand points. Instead, the model seeks the maximal coverage with a given number of facilities. The MCLP and different variants of it have been extensively used to solve various emergency service location problems (see e.g., Benedict 1983, and Hogan and ReVelle 1986).

Research on emergency service covering models has also been extended to incorporate the stochastic and probabilistic characteristics of emergency situations so as to capture the complexity and uncertainty of these problems. Examples of these stochastic models can be found in recent papers by Goldberg and Paz (1991), ReVelle et al. (1996), and Beraldi and Ruszczynski (2002). There are several approaches to model stochastic emergency service covering problems. The first approach is to use chance constrained models (Chapman and White 1974). Daskin (1983) used an estimated parameter (q) to represent the probability that at least one server is free to serve the requests from any demand point. He formulated the Maximum Expected Covering Location Problem (MEXCLP) to place P facilities on a network with the goal to maximize the expected value of population coverage. ReVelle and Hogan (1986) later enhanced the MEXCLP and proposed the Probabilistic Location Set Covering Problem (PLSCP). In the PLSCP, a server busy fraction and a service reliability factor are defined for the demand points. Then the locations of the facilities are determined such that the probability of service being available within a specified distance is maximized. The MEXCLP and PLSCP later were further modified to tackle other EMS location problems by ReVelle and Hogan (MALP) (1989a), Bianchi and Church (MOFLEET) (1988), Batta et al. (AMEXCLP) (1989), Goldberg et al. (1990), and Repede and Bernardo (TIMEXCLP) (1994). A summary and review to the chance constrained emergency service location models can be found in ReVelle (1989).

Another approach to modeling stochastic emergency medical service (EMS) covering problems is to use scenario planning to represent possible values for parameters that may vary over the planning horizon in different emergency situations. A compromise decision is made to optimize the expected/worst-case performance or expected/worse-case regret across all scenarios. For example, Schilling (1982) extended the MCLP by incorporating scenarios to maximize the covered demands over all possible scenarios. Individual scenarios are respectively used to identify a range of good location decisions. A compromise decision is made to the final location configuration that is common to all scenarios in the horizon.

2.1.2 P-Median Models

Another important way to measure the effectiveness of facility location is by evaluating the average (total) distance between the demand points and the facilities. When the average (total) distance decreases, the accessibility and effectiveness of the facilities increase. This relationship applies to both private and public facilities such as supermarkets, post offices, as well as emergency service centers, for which proximity is desirable. The P-median problem takes this measure into account and is defined as: minimize the average (total) distance between the demands and the selected facilities. We illustrate a P-median model in Fig. 16.2. The total cost of the solution presented is the sum of the distance between demand points and selected locations represented by the black lines.

Fig. 16.2
figure 2

P-median/P-center problem example

Full size image

Since its formulation, the P-median model has been enhanced and applied to a wide range of emergency facility location problems. Carbone (1974) formulated a deterministic P-median model with the objective of minimizing the distance traveled by a number of users to fixed public facilities such as medical or day-care centers. Recognizing the number of users at each demand node is uncertain, the author further extended the deterministic P-median model to a chance constrained model. The model seeks to maximize a threshold and meanwhile ensure the probability that the total travel distance is below the threshold is smaller than a specified level a. Paluzzi (2004) discussed and tested a P-median based on a heuristic location model for placing emergency service facilities for the city of Carbondale, IL. The goal of this model is to determine the optimal location for placing a new fire station by minimizing the total aggregate distance from the demand sites to the fire station.

One major application of the P-median models is to dispatch EMS units such as ambulances during emergencies. For example, Carson and Batta (1990) proposed a P-median model to find the dynamic ambulance positioning strategy for campus emergency service. Mandell (1998) developed a P-median model and used priority dispatching to optimally locate emergency units for a tiered EMS system that consists of advanced life-support (ALS) units and basic life-support (BLS) units.

Uncertainties have also been considered in many P-median models. Mirchandani (1980) examined a P-median problem to locate fire-fighting emergency units with consideration of stochastic travel characteristics and demand patterns. Serra and Marianov (1998) implemented a P-median model and introduced the concept of regret and minmax objectives. The authors explicitly addressed in their model the issue of locating facilities when there are uncertainties in demand, travel time or distance.

2.1.3 P-Center Models

In contrast to the P-median models, which concentrate on optimizing the overall (or average) performance of the system, the P-center model attempts to minimize the worst performance of the system and thus is also known as minimax model. The P-center model considers a demand point is served by its nearest facility and therefore full coverage to all demand points is always achieved. In the last several decades, the P-center model and its extensions have been investigated and applied in the context of locating facilities such as EMS centers, hospitals, fire station, and other public facilities, The objective function for the P-center model of the location solution in Fig. 16.2 quantifies only the longest distance between a demand point and a selected location.

In order to locate a given number of emergency facilities along a road network, Garfinkel et al. (1977) examined the fundamental properties of the P-center problem. He modeled the P-center problem using integer programming and the problem was successfully solved by using a binary search technique and a combination of exact tests and heuristics. ReVelle and Hogan (1989b) formulated a P-center problem to locate facilities so as to minimize the maximum distance within which EMS service is available with α reliability. System congestion is considered and a derived server busy probability is used to constrain the service reliability level that must be satisfied for all demands. Stochastic P-center models have also been formulated for EMS location problems. For example, Hochbaum and Pathria (1998) considered the emergency facility location problem that must minimize the maximum distance on the network across all time periods. The cost and distance between the locations vary in each discrete time period. The authors used k underlying networks to represent different periods and provided a polynomial time 3-approximation algorithm to obtain the solution for each problem. Talmar (2002) utilized a P-center model to locate and dispatch three emergency rescue helicopters to serve the growing EMS demands from accidents of tourist activities such as skiing, hiking and climbing at the north and south end of the Alpine mountain ranges. One of the model’s aims is to minimize the maximum (worst) response times and the author used effective heuristics to solve the problem.

2.2 Review of VRPs

Routing vehicles in response to a large-scale emergency typically include various uncertainties such as stochastic demands and/or travel times. In this section, we first review the literature on the stochastic vehicle routing problem (SVRP). We then review other vehicle routing/dispatching problems in the literature that have been formulated for emergency situations.

2.2.1 Stochastic Vehicle Routing Problems (SVRPs)

SVRPs differ from the deterministic VRPs in several aspects, such as problem formulations and solution techniques. SVRPs are usually divided, according to the uncertainties in consideration, into SVRPs with stochastic customers and/or demands, and SVRPs with stochastic travel time and/or service time.

The VRP with stochastic customers (VRPSC) addresses the probabilistic presence of customers (see e.g., Jezequel (1985), Jaillet (1987), and Jaillet and Odoni (1988). Bertsimas (1988) gave a systematic analysis to this problem. The properties, the bounds, and the heuristics to solve the problem were also presented.

The VRP with stochastic demand (VRPSD) captures the uncertainty of customer demands (i.e., the demands at the individual delivery (pickup) locations behave as random variables). An early investigation on the VRPSD comes from Stewart and Golden (1983), who applied the chance constraint modeling and resource methods to model the problem. Dror and Trudeau (1986) later illustrated the effects of route failure on the expected cost of a route, as well as the impact that a redirection of the predesigned route has on the expected cost. In the late 1980s and early 1990s, along with the conventional stochastic programming framework, Markovian Decision Processes for single-stage and multi-stage stochastic models were introduced by Dror (1989, 1993) to investigate the VRPSD. Another major contribution to the study of VRPSD comes from Bertsimas (1988, 1992). Their work illustrates different recourse policies that could be applied to re-optimize the routes. More recently, a re-optimization based routing policy for the VRPSD has been demonstrated by Secomandi (2001). In their work, a rollout algorithm is proposed to improve a given a priori solution.

The vehicle routing problem with stochastic customers and demands (VRPSCD) combines the VRPSC and the VRPSD. Early work on this topic includes Jezequel (1985), Jaillet (1987), and Jaillet and Odoni (1988). Motivated by applications in strategic planning and distribution systems, Bertsimas (1992) constructed an a priori customer visit sequence with minimal expected total distance and analyzed the problem using a variety of theoretical approaches. Gendreau et al. (1995) proposed a L-shaped method for the VRPSCD and solved it to optimality for instances of up to 46 customers. Another strategy to account for the demand uncertainties is to develop a waiting strategy for vehicles to strategically wait at predetermined locations in order to maximize the probability of meeting any future anticipated demand (Branke et al. 2005).

VRP with stochastic travel time (VRPSTT) addresses the unknown knowledge of the road conditions. Systematic research on the VRP with service time and travel time (VRPSSTT) has been done by Laporte et al. (1992). They proposed three models for the VRPSTT: chance constrained model, 3-index recourse model, and 2-index recourse model. The VRPSSTT model was also applied by Lambert et al. (1992), and Hadjiconstrantinou and Roberts (2002) to optimize the customer service in the banking and other commercial systems. Jula et al. (2005) has developed an approximate solution approach for random travel times with hard time windows. Their approximation approach is based on developing estimations for the first two moments of the arrival time distribution.

2.2.2 Vehicle Locating/Routing/Dispatching for Emergency Services

Emergency service systems (e.g., police, fire, etc.) need to dispatch their response units to service requests. In an emergency, the primary objective is to save lives, and thus sending response units to the incident site at the earliest time has the highest priority. However the requests for emergency services are usually unpredictable and furthermore they come with a relatively low frequency. Therefore the planner is generally faced with two major problems. First, an allocation problem in which the response units that are sent for service need to be determined; and second, a re-deployment problem in which the available response units need to be deployed at the potential sites in preparation to incoming requests needs to be determined.

One important thrust and cornerstone in vehicle locating/routing/dispatching for emergency services is the development and application of the queuing approach. The most well known queuing models for emergency service problems are the hypercube and the approximated hypercube by Larson (1974, 1975), which consider the congestions of the system by calculating the steady-state busy fractions of servers on a network. The hypercube model can be used to evaluate a wide variety of output performance such as vehicle utilization, average travel time, inter-district service performance, etc. Particularly important in the hypercube models is the incorporation of state-dependent interactions among vehicles that preclude applications of traditional vehicle locating/routing/dispatching models. Larson (1979) and Brandeau and Larson (1986) further extended and applied the hypercube models with locate-allocate heuristics for optimizing many realistic EMS systems. For example, these extended models have been successfully used to optimize the ambulance deployment problems in Boston and the EMS systems in New York. Based on the hypercube queuing model, Jarvis (1977) developed a descriptive model for operation characteristics of an EMS system with a given configuration of resources and a vehicle locating/dispatching model for determining the placement of ambulances to minimize average response time or other geographically based variables. Marianov and ReVelle (1996) created a realistic vehicle locating/dispatching model for emergency systems based on results from queuing theory. In their model, the travel times or distances along arcs of the network are considered as random variables. The goal is to place a limited numbers of emergency vehicles, such as ambulances, in a way as to maximize the calls for service. Queueing models formulating other theoretical and practical problems have also been reported by Berman and Larson (1985), Batta (1989), and Burwell et al. (1993).

3 A Large-Scale Emergency: An Anthrax Attack

In this section, we use an anthrax attack emergency to demonstrate the characteristics of a large-scale emergency. We then derive the requirements for the facility location problem and vehicle routing problem for the medical supply distribution in a large-scale emergency. Note that different emergency scenarios may require different response plans. The area in which we consider the anthrax attack emergency is Los Angeles (LA) County, which consists of 2054 census tracts and a total population of 9.5 million. In addition, we identify a number of potential eligible medical supply facility sites (see Fig. 16.3) and the goal is to select some of these eligible facility sites as the staging areas to dispense the vaccinations.

Fig. 16.3
figure 3

Los Angeles county

Full size image

3.1 Characteristics of an Anthrax Emergency

Anthrax is an acute infectious disease caused by a spore-forming bacterium. The anthrax spores can be used as a bioterrorist weapon, as was the case in 2001, when Bacillus anthracis spores had been intentionally distributed through the postal system causing 22 cases of anthrax emergency, including 5 deaths (CDC website 2005). If the anthrax spores had been disseminated in an airborne manner through airplanes or from high buildings, thousands of people and hundreds of blocks would have been severely affected. Anthrax causes disease after inoculation of open or minor wounds, ingestion, or inhalation of the spores. At the earliest sign of disease, patients should be treated with antibiotics and other necessary medications to maximize patient survival. Otherwise, shock and death could ensue within 24–48 h. Although no cases of person-to-person transmission of inhalation anthrax have ever been reported, cutaneous transmissions have occurred. Early treatment of anthrax disease is usually curative and significant for recovery. For example, patients with cutaneous anthrax have reported case fatality rates of 20 % without antibiotic treatment and less than 1 % with it (CDC website 2005).

The impact of an anthrax attack to the population can be tremendous. First, thousands of people could be directly infected by the disease at the incident site. Second, the affected area could quickly spread from the original incident site to a much larger region by the movement of the infected but unaware people because the anthrax attack is usually covert and the appearance of the disease symptom may lag the attack from hours to days. Third, after an anthrax disease emergency becomes known in public, people may panic and become scared. They may request medical treatment or vaccination even if they are not actually infected or not in a high-risk situation.

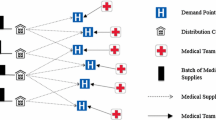
Huge demands for medical supplies could occur in a short time period after the anthrax attack. Blanket medical service coverage and mass vaccination may be necessary to all the population in a region. As such, a large amount of vaccines may be required. However an anthrax emergency has a low occurrence frequency and it is very expensive for any local region to maintain massive medical supplies for such a rare event. Therefore, large volumes of medical supplies for such an emergency are usually not stored at local sites. Instead, they are inventoried by the government at national stockpiles which consist of large quantities of medications, vaccines, and antibiotics to protect the public. The national stockpile is organized as push packages for flexible response and immediate deployment to a designated site within 12 h (e.g., the SNS of the USA). Once delivered to the local areas, the stockpiles can be repackaged and distributed to various demand points though the local dispensing centers (staging areas). The overall process of a rapid medical supply distribution for a large-scale emergency can be depicted as follows in Fig. 16.4. The details for each procedure in this process are described in the following sections.

Fig. 16.4
figure 4

Medical supply distribution process

Full size image

It should be noted that anthrax is not contagious from person to person and the medical service coverage should depend on the actual disease spreading pattern. For example, if the attack can be detected at an early stage and the infected people can be identified and quarantined in a timely manner, then only the areas near the incident site need to be serviced with medical supplies. In this example we consider the worst case scenario and assume that the delayed detection of the attack has caused intractable population movements, and thus a blanket medical service coverage to all the areas is required. The logistical problem for such a worst case scenario is much more challenging than other scenarios in which only a portion of a region needs to be provided with medical supplies. Also note that the blanket medical service coverage is similarly applicable to contagious emergencies such as smallpox. During a contagious disease outbreak, it is possible that some areas are more critical than others due to certain disease spreading pattern. However, a mass vaccination to all the areas may be desired since it could effectively stem the disease transmission among the population (CDC 2005).

3.2 Requirements to Facility Location Deployment

As mentioned in the last section, the medical supplies are usually not stored at the local level, and during an anthrax emergency the national stockpile will be called to service the demands at the local areas. Therefore, the primary goal of the facility location problem is to determine a number of local staging areas so that the supplies from the national stockpile can be received, repackaged, and distributed.

The deployment of medical facility sites (staging areas) in response to a large-scale emergency must account for massive service requirements. In most traditional facility location problems, each individual demand point is covered only by one facility given the fact that demand does not appear in large amounts. However, in the event of an anthrax emergency, if a mass vaccination to the population is necessary, the demands for medical services will be significant. As a result, a redundant and dispersed placement of the facilities (staging areas) is required so that more medical supplies could be mobilized to service different demand points to reduce mortality and morbidity.

Another important aspect of the facility locations for the anthrax emergency is the fact that given the occurrence of the emergency at an area, the resources of a number of facilities will be applied to quell the impact of the emergency, not only those located closest to the emergency site. This implies that there are different types of coverage, or quality of coverage, which can be classified in terms of the distance (time) between facilities and demand points. Thus, a facility that is close to a demand point provides a better quality of coverage to that demand point than a facility located far from that demand point. When planning the emergency medical services, it is important to consider adequate staging areas of various qualities for each demand point.

Furthermore, potential demand areas for medical services need to be categorized in a different way than other regular emergencies. Each demand area has distinct attributes, such as population density, economic importance, geographical feature, weather pattern, etc. Therefore, different requirements of facility quantity and quality should be assigned for each demand point so that all demand points can be serviced in a balanced and optimal manner. For example, for the demand points at a downwind and populous downtown area, a larger quantity of facilities should be located at a relatively better quality level, as opposed to the demand points at an upwind and/or less populous area.

Moreover, the facility location objective for an anthrax disease emergency should be carefully defined. An anthrax emergency is bound to impact lives regardless of the solution. Thus care should be taken in prioritizing one solution over another. Since the blanket medical service coverage and mass vaccination may be carried out, all the demand points in the affected areas need to be serviced simultaneously. To optimize the overall performance of the medical distribution system, it is desirable that the total (average) distance from all demand points to the staging areas be minimized. Thus, a P-median model with multiple facility quantity-of- coverage and quality-of-coverage requirements is applicable. It is important to note the model that is selected should be in accordance with the characteristics of the emergency, and different models may be suitable for different emergency scenarios. For example, for the emergency of a dirty bomb attack in which only a portion of a region needs be serviced by the medical supplies, the covering model may be more applicable since the model ensures a maximal population coverage by the medical supply facilities.

Finally, the selection of eligible staging area sites for the anthrax emergency must consider a different set of criteria that are used for regular emergencies. For instance, the facilities should have easy access to more than one major road/highway including egress and ingress. The sites should be secure and invulnerable to damages caused by the emergencies. In this paper we consider eligible staging area sites as given.

3.3 Requirements to Vehicle Routing

In an anthrax emergency, the primary goal of vehicle routing is to deliver the medical supplies to the affected areas as soon as possible. To reach this goal, a fast and efficient vehicle routing/dispatching plan needs to be executed. To maximize life-saving in an anthrax emergency, medications, antibiotics, and vaccines should be administered to the affected population within a specified time limit (within 24–36 h). This implies that vehicles need to have a hard time-window for medical supply delivery. To minimize the loss of life at any demand area, the medical supplies must be sent to the demand area within this hard time-window. Note that although a hard time-window is used to model the VRP for the anthrax emergency, it may not always be applicable to other emergencies. For example, for a contagious disease outbreak, such as smallpox, the demand for medical supplies could be a continuous function of time. In such a case, a soft time- window approach may be more suitable to model the VRP.

The input parameters to the vehicle routing problem in the anthrax emergency have a probabilistic/stochastic nature. For example, the traffic conditions may change and therefore the vehicle travel times can be highly uncertain. In addition, the demands for medical services may be stochastic because of the way the disease disseminates, the wind direction, the geographic conditions, etc. As such, the vehicle routing problem needs to capture the demand uncertainties and provide a robust solution that performs well in a variable environment.

Moreover, because of the massive service requirements, the demand at a location is not necessarily satisfied by a single truckload. As such, the vehicle routing problem for the anthrax emergency should allow for split delivery (i.e., a point can be visited more than once if the demand exceeds the load capacity of available vehicles). Also, the VRP for the anthrax emergency should be a multi-depot problem since many local depots are dispersed across a region. However, unlike the traditional multi-depot VRP, which requires each vehicle to return to its origination depot, the vehicles are now allowed to return to any depot for reloading and then continue serving other demand points. This requirement enables the vehicles to distribute the medical supplies in a more flexible manner.

Finally, the primary objective of the vehicle routing problem during the emergency should be the minimization of loss of lives, which is caused by minimizing the unmet demands for the medical service.

As mentioned before, the facility location and vehicle routing models can be used as a planning tool to determine the optimal staging areas and vehicle routes considering the probabilistic/stochastic nature of the emergency. These plans can serve as practical drills for the first responders to prepare and train them for a possible emergency, and they may be to be altered in the event that an emergency has occurred once the characteristics of the emergency become known.

4 Mathematical Model Formulations

Based on the analysis stated in the last section, we now formulate a facility location model and a vehicle routing model that take into account the characteristics of the anthrax disease emergency. Generalizations of the models discussed in this section can found in Jia et al. (2005) for the facility location problem and Shen et al. (2005) for the vehicle routing problem.

4.1 Formulation of the Facility Location Model

To formulate the facility location model, we use I to denote the set of demand points and J to denote the set of eligible facility sites (staging areas). Indexed on these sets we define two types of integer variables:

Decision variables:

\( {x}_j=\left\{\begin{array}{c}\hfill 1\hfill \\ {}\hfill 0\hfill \end{array}\right. \)

if a facility is placed at site j; otherwise

\( {z}_{ij}=\left\{\begin{array}{c}\hfill 1\hfill \\ {}\hfill 0\hfill \end{array}\right. \)

if a facility j services demand point i; otherwise

Furthermore, we define the following parameters:

Input Parameters:

Pop i  = the population of demand point i

d ij  = the distance between demand point i and facility location j

D t  = the distance limit within which a facility could service demand point i

N i  = {j|d ij  ≤ D i }, the set of eligible facility sites that are located within the distance limit and thus are able to service demand point i

Q i  = the required number of facilities that must be assigned to demand point i so that i is considered as covered

P = the maximal number of facilities that can be placed in J

We can now formulate the model to locate P facilities to service the population during an anthrax emergency, requiring that Q i facilities service demand point i with the same quality.

$$ \mathrm{Minimize}\;{\displaystyle \sum_{i\in I}{\displaystyle \sum_{j\in J}{\mathrm{Pop}}_i{d}_{ij}\;{z}_{ij}}} $$
(16.1)

Subject to:

$$ {\displaystyle \sum_{j\in J}{x}_j\le P} $$
(16.2)
$$ {\displaystyle \sum_{j\in {N}_i}{z}_{ij}\ge {Q}_i\kern0.4em \forall i\in }I, $$
(16.3)
$$ {z}_{ij}\le {x}_j\kern0.4em \forall i\in I,j\in J, $$
(16.4)
$$ {x}_j,{z}_{ij}=\left\{0,1\right\}\kern0.4em \forall i\in I,j\in J, $$
(16.5)

The objective (16.1), as mentioned in Sect. 3.2, is to minimize the total demand-weighted distance between the demand points and the facilities. Constraint (16.2) states that there are P facilities to be located in a set J of possible locations. Constraint (16.3) ensures that demand point i is assigned with a required quantity (Q i ) of facilities servicing it. This constraint also requires that all the facilities assigned to demand point i need to be located within the given distance limit. Constraint (16.4) allows assignment only to the sites at which facilities have been located. Finally constraint (16.5) enforces the integrality of variables Z ij and x i

Consider now the problem with multiple quality-of-coverage requirements at each demand point. Let us assume that at demand point i we must have Q 1 i , Q 2 i , …, Q q i , facilities for each quality from 1 to q, where quality Q 1 i represents the facilities that are closest to demand point i, Q 2 i are the facilities located farther than those of quality 1, and so on. Thus the facility location model needs to be modified as follows:

  1. 1.

    Objective function: Since multiple quality-of-coverage is considered, the objective function needs to be optimized across different quality levels. Because the facilities with a higher quality level (i.e., closer to the demand points) are usually considered to be more crucial in servicing the demand points, as opposed to the facilities with lower quality levels (i.e., farther from the demand points), we introduce a weight parameter, h r, to prioritize the importance of the facilities at each different quality level r. Also we modify Z ij to z r ij in order to differentiate the facilities that are servicing the demand points at different quality levels. Thus, we obtain the modified objective function:

    $$ \mathrm{Minimize}\kern0.24em {\displaystyle \sum_r{\displaystyle \sum_{i\in I}{\displaystyle \sum_{j\in J}{h}^r{\mathrm{Pop}}_i{d}_{ij}{z}_{ij}^r}}} $$
    (16.6)
  2. 2.

    Constraints: First, the group of constraints (16.3) needs to be changed to:

    $$ {\displaystyle \sum_{j\in {N}_i^r}{z}_{ij}^r\ge {Q}_i^r\kern0.4em \forall i\in I,r=1,\dots q} $$
    (16.7)

    The modified constraints state that, for each demand point, there must be more than a required quantity of facilities at each quality level so that this demand point can be considered as properly serviced. In addition, to avoid repeated assignment of a facility to any demand point for different quality requirements, we introduce another group of constraints:

    $$ {\displaystyle \sum_r{z}_{ij}^r\le 1\kern0.4em \forall i\in I,j\in J} $$
    (16.8)

As such, the modified objective (16.6), together with the constraints (112), (16.4), (16.5), (16.7), and (16.8), can be used to formulate the facility location problem for the anthrax emergency with multiple facility quantity- of-coverage and quality-of-coverage requirements. Note that in the problem formulation, all the Z ij ,Q i and N i need to be correspondingly changed to z r ij , Q r i and N r i .

Exact algorithms have been developed in the literature to solve different facility location problems; for example, see Holmberg (1999). However exact algorithms can only solve small problem instances in a reasonable computational time. Therefore, to solve the location problems for large-scale emergencies, efficient heuristics, such as greedy algorithms, genetic algorithms, or Tabu search, should be used. References to the heuristics for traditional location problems can be found in Jain et al. (2002) and Jaramillo et al. (2002).

4.2 Formulation of the Vehicle Routing Model

To formulate the vehicle routing model, we use K, I, J, and A to denote the sets of vehicles, demand points, facility sites, and medical supply items. In addition, we use node 0 as a dummy node to represent a virtual/imaginary central depot that is linked to each real depot (facility site). The cost or travel times on these links is set to be a large number. The dummy node is useful in representing the availability of vehicles. To conveniently denote different node combinations in the medical supply network, we further define set C = I ∪ J ∪ {node _ 0}, and set RO = I ∪ J. Furthermore, indexed on these sets, we define the following deterministic parameters. Note that different from the facility location problem, in which the index i is defined as demand point i and the index j is defined as facility site j, here the indices i and j are defined as any node from set C, which could be either a demand point or a facility site (depot).

Deterministic Parameters:

n i  = the initial number of vehicles at facility site (depot) i

W a  = the unit weight of medical supply item a

C a,k  = the load capacity of vehicle k for medical supply item a

e a,i  = the earliest service start time for medical supply item a at demand point i

l a,j  = the latest service start time for medical supply item a at demand point i

S a,i  = the amount of medical supply item a supplied at facility site (depot) i

r i  = the service (loading/unloading) time at node i, including both the demand points and the facility sites

We use M as a large constant to transform nonlinear terms to linear ones for the time window constraints. In addition, the parameter α D is used to represent the upper bound of unsatisfactory rate for demands at each demand point and α T is used to denote the upper bound of total traveling time for each vehicle. These two parameters represent the probabilistic violation on the demand and travel time constraints.

As mentioned in the previous section, uncertainties exist in the anthrax emergency. We consider the following two parameters as stochastic variables.

Stochastic Parameters:

τ i,j,k  = the time required for vehicle k to travel from point i to j

ζ a,i  = the demand for medical supply item a at demand point i

Finally, four groups of decision variables are defined as follows:

Decision variables:

\( {X}_{i,j,k}=\left\{\begin{array}{c}\hfill 1\hfill \\ {}\hfill 0\hfill \end{array}\right. \) if vehicle k traverses arc (ij):otherwise

Y a,i,j,k  = the amount of medical supply item a traversing arc (i,j) using vehicle k

U a,t  = the amount of unsatisfied demand for medical supply item a at demand point i

T i,k  = the service start time for vehicle k at demand point i

Based on these parameters and variables, we are now in a position to formulate the stochastic vehicle routing problem, with the objective to minimize the unmet demands over all the demand points.

$$ \mathrm{Minimize}\kern0.24em {\displaystyle \sum_{a\in A}{\displaystyle \sum_{i\in I}{U}_{a,i}}} $$
(16.9)

Subject to:

$$ {\displaystyle \sum_{k\in K}{X}_{0,i,k}\le {n}_i\kern0.4em \forall i\in J} $$
(16.10)
$$ {\displaystyle \sum_{j\in 1}{X}_{i,j,k}=1}\kern0.4em \forall i\in J,k\in K, $$
(16.11)
$$ {\displaystyle \sum_{j\in I}{X}_{j,i,k}=1}\kern0.4em \forall i\in J,k\in K, $$
(16.12)
$$ {\displaystyle \sum_{j\in \mathrm{RO}}{X}_{i,j,k}}={\displaystyle \sum_{j\in \mathrm{RO}}{X}_{j,i,k}}\kern2em \forall i\in I,k\in K, $$
(16.13)
$$ P\left\{\tau \left|\left({T}_{i,k}+{r}_i+{\tau}_{i,j,k}-{T}_{j,k}\right)\right.\le \left(1-{X}_{i,j,k}\right)M\right\}\ge 1-{\alpha}_T\kern1em \forall i,j\in C $$
(16.14)
$$ {s}_{a,i}-{\displaystyle \sum_{k\in K}\left[{\displaystyle \sum_{j\in C}{Y}_{a,i,j,k}}-{\displaystyle \sum_{j\in C}{Y}_{a,j,i,k}}\right]}\ge 0\kern0.4em \forall a\in A,\forall i\in J $$
(16.15)
$$ {Y}_{a,0,i,k}+{Y}_{a,i,0,k}=0\kern0.4em \forall a\in A,\forall i\in \mathrm{RO},k\in K $$
(16.16)
$$ {X}_{i,j,k}{c}_k\ge {\displaystyle \sum_a{w}_a{Y}_{a,i,j,k}\kern0.4em \forall \left\{i,j\right\}\subseteq \mathrm{RO},k\in K,a\in A} $$
(16.17)
$$ {e}_{a,i}\;{\displaystyle \sum_{j\in {\varDelta}^{+}(i)}{X}_{i,j,k}\le {T}_{i,k}\le {l}_{a,i}\kern0.24em {\displaystyle \sum_{j\in {\varDelta}^{+}(i)}{X}_{i,j,k}\kern0.4em \forall a\in A,\forall i,j\in C}} $$
(16.18)
$$ \begin{array}{l}P\left\{\zeta \left|{\displaystyle \sum_{k\in K}\left[{\displaystyle \sum_{j\in C}{Y}_{a,j,i,k}}-{\displaystyle \sum_{j\in C}{Y}_{a,i,j,k}}\right]}\right.-{U}_{a,i}-{\zeta}_{a,i}\ge 0\right\}\ge 1-{\alpha}_D\\ {}\forall a\in A,\forall i\in I\end{array} $$
(16.19)
$$ {X}_{i,j,k}=\left\{0,1\right\};{Y}_{a,i,j,k}\ge 0;{U}_{a,i}\ge 0;{T}_{i,k}\ge 0; $$
(16.20)

Constraints (16.10)–(16.14) characterize the vehicle flow on the medical distribution network. Constraint (16.10) states that the number of vehicles in service should not exceed the number of vehicles available at each depot at the beginning of the planning horizon. The number of vehicles in service is the total number of vehicles flowing from the dummy central depot 0 to each facility site. Constraints (16.11) and (16.12) specify that each vehicle can flow from and to only one facility site (depot). Constraint (16.13) states that all vehicles that flow into any demand point must also flow out of it. Constraint (16.14) is a chance constraint for the service start times at the demand points. The inner part, (T i,k  + r i + τ i,j,k  − T j,k ) ≤ (1 − X i,j,k )M guarantees the schedule feasibility with respect to time considerations. Constraint (16.15) gives the balanced material flow requirement for the facility sites. Constraint (16.16) prohibits the medical supply items flow from and to the dummy node. Constraint (16.17) allows the medical supply item to flow as long as there are sufficient vehicle capacities. It establishes the connection between the medical supply flow and vehicle flow. Constraint (16.18) gives the hard time window constraint on each demand point. Chance constraint (16.19) enforces the balanced material flow requirement for the demand points from a probabilistic perspective. It states that a small probability of unmet demands at each demand point is allowed within a threshold level. Finally constraint (16.20) enforces the integrality and non-negativity constraints on the variables.

5 Problem Solution and Analyses

In the preceding section, the facility location problem and the VRP for the anthrax disease emergency have been formulated. In this section, we first specify illustrative values for the input parameters and then we show how these proposed models could be applied to solve the facility location problem and the VRP for the anthrax emergency.

5.1 Facility Location Problem

5.1.1 Parameter Specification

There are 2054 census tracts and 9.5 million people in Los Angeles County. To define the demand distribution for medical services during an anthrax disease emergency, we use the day-time population density pattern that is available for Los Angeles County (ESRI website 2005). Furthermore, we use the centroid of each census tract as a demand point to represent the aggregated population in this tract. Thus we obtain 2054 discrete demand points that have different population densities. We assume that, in the anthrax emergency, the people at different demand points need to visit the selected facilities (staging areas) for vaccination. Note that although we assume that all the population at the demand points need to be serviced by the medical supplies, during an emergency, a more accurate demand pattern for medical supplies can be obtained by using schools, shopping malls and offices as indicators to assess the actual disease exposure.

To determine the staging areas that can be used to receive, repackage, and distribute the medical supplies from the national stockpile to the demand points, we identify 30 eligible facility sites. We assume that the resource limitation allows only 10 eligible facility sites to be selected to services the demand points (P = 10). To ensure effective and efficient medical supply distribution, each demand point needs to be serviced by a required quantity of facilities that are located at each quality level. In practice, different quality levels should be defined for different demand points, based on the attributes of each point such as population density, political/economic importance, etc. In this example, for simplicity, we define a uniform quality requirement for all demand points; that is, each demand point needs two quality levels and the distance requirements for the first and second quality levels are 35 miles and 60 miles, respectively.

Furthermore, we specify the facility quantity requirement at each quality level for each demand point as follows:

  1. 1.

    Q i  = 1 if the population of demand point i is less than 4,000.

  2. 2.

    Q i  = 2, if the population of demand point i is between 4,000 and 8,000.

  3. 3.

    Q i  = 3, if the population of demand point i is greater than 8,000.

Finally, we specify the distances (times) between each pair of demand point and facility site. In practice, the roadway system should be used to define the distances since the medical supplies will be transported by vehicles during the emergency. However, for simplicity, in this illustrative example, we use the straight line distances between the demand points and facility sites.

5.1.2 Solution and Analyses

Based on the input parameters defined above, we solve the facility location problem for the anthrax emergency. The solution is depicted in Fig. 16.5 . The problem was solved to optimality using a commercial integer program solver, CPLEX 8.1. The stars in the diagram represent the selected facilities.

Fig. 16.5
figure 5

Solution to the facility location problem

Full size image

In this solution, each demand point is covered by a required quantity of facilities at each of the two quality levels. Therefore, the demand points can be sufficiently serviced by the facilities in an efficient manner. The average distance from the demand points to their servicing facilities at quality level 1 is 25.8 miles; and the average distance at quality level 2 is 50.2 miles. Since the weighted total distance between the demand points and the facilities has been minimized (as defined by the objective function), the effectiveness of facility service performance is optimized.

It should be noted that a tight definition of the input parameters may lead to the facility location problem being infeasible; that is, no subset of P facilities is able to service all demand points within the defined quality levels (distance requirements). In this case, any one of the following four adjustments in the parameters can be made to make the problem feasible:

  1. 1.

    Increase the parameter P, i.e., the number of facilities that can be selected.

  2. 2.

    Relax the distance requirements, within which the facilities need to be located to service the demand points.

  3. 3.

    Drop the insignificant demand points (e.g., the ones with a low population density) from the problem constraints so that the limited resources (facilities) can be leveraged to the other demand points.

5.2 Vehicle Routing Problem (VRP)

5.2.1 Parameter Specification

After the facility sites (staging areas) have been determined, the solution is used as input parameters for the vehicle routing problem. In the anthrax emergency example, the 10 selected facility sites from the location problem are the demand points for the vehicle routing problem. To illustrate the VRP, for simplicity, we will use a single depot (i.e., Los Angeles International Airport as the central distribution warehouse) and a uniform capacity for each of a total of three vehicles to route and service the 10 staging facilities.

We calculate the demand on each selected facility by summing up the population in the tracts that are covered by the facility. The population size will be used as the criterion to specify the demand size; for example, 1 box of 100,000-dose anthrax vaccine is needed for every 100,000 people. As we stated in the previous section, the demand of each facility is stochastic. The exponential distribution, p(x) = e(A–x)/B IB (where the mean is A + B and variance is B 2), is assumed with the mean value set according to the population density. The standard deviation is set to be 20 % of its mean value at each facility.

Furthermore, we assume an exponential distribution for the travel times between each pair of facility and central depot. Their mean values are specified as proportional to the Euclidean distances between them. We also set the standard deviation to be 20 % of the mean value of the travel time on each leg of the connection. Such an exponential distribution gives a lower bound and an upper bound for the travel time, which reasonably reflects the fact that travel time is constrained by the physical distance and the maximal speed of the vehicle, and could be prolonged by different traffic conditions.

Shock and death caused by untreated anthrax exposure could ensue within 24–48 h, and the dispatching from the central warehouse to the 10 selected local staging facilities is just one chain of the whole process of dispensing medical supplies. Hence we use a hard time window constraint of up to half of the required time for treatment (i.e., 12 h) to finish this placement.

Finally, we assume the total supply at the depot can meet 120 % of the summation of the mean value of the demand quantity at all points. However, since the demand is stochastic, it is possible that the demand cannot be fully satisfied in some cases.

5.2.2 Solution and Analyses

The routing problem is solved based on the parameters specified in the previous section and its result is compared with that of a deterministic formulation to show the advantage of our chance-constraint model.

The CPLEX solver was used to optimally solve both the deterministic and chance-constraint models to optimality with the given parameters. The deterministic model uses the mean value of the demand quantity and travel time to eliminate uncertainties.

To compare the routing solutions, we generate exponential random variables with the mean and variance specified above for the demand and travel time. For each generated scenario we solve a linear optimization problem to obtain the quantities of supply that minimize the total unmet demand with fixed routing solutions obtained above and constrained by the deadline and the total available quantity at the depot. The comparison shows that out of the 50 test cases, the deterministic routes generate 18 unmet demand cases with an average unmet demand of 9.94 while the chance-constraint routes only generate 2 unmet demand cases with an average unmet demand of 5.50. The chance-constraint routes outperform the deterministic ones because of the conservative nature of the chance-constraint model, which leads to balanced routes with similar number of nodes. The deterministic routes are more prone to have uneven number of nodes on different paths. We observe that this property makes the chance-constraint solution more robust and competitive than the deterministic one especially for the test cases that deviate far away from the mean value.

6 Conclusions and Future Directions

Facility location and vehicle routing are important issues in designing the medical supply distribution system, particularly for large-scale emergencies. This chapter has two primary goals. The first is to review different location models and vehicle routing models in the literature that are related to regular emergency services such as police, fire, etc. The second goal is to present tailored location and vehicle routing models to design rapid distribution systems of medical supplies in response to a large-scale emergency. An illustrative example of an anthrax emergency was discussed to show how the proposed models can be used to determine the facilities locations and vehicle routes for rapid medical supply distribution during the emergency.

In this chapter, we consider an emergency due to an anthrax attack as a representative large-scale emergency. We discuss the characteristics of large-scale emergencies and their requirements for the facility location and vehicle routing problems in the context of this particular emergency. However, other types of emergencies (e.g., chemical incident, dirty bomb attack, contagious disease outbreak) may involve different characteristics and thus will lead to different requirements on the problem formulations and solutions. For example, an emergency caused by a dirty bomb attack may impact not only the population, but also the medical supply facilities themselves. Therefore, reduced service capability of the facilities needs to be taken into account. A chemical incident may need instantaneous medical service to the infected people, and therefore medical supplies may need to be pre-positioned at a local level for immediate deployment. An open research question is how to develop an overall response plan that takes into consideration all the different possible scenarios. Is it more efficient and cost effective to develop a single strategy that is robust to the different possibilities or is it better to develop a separate plan for each possible emergency?

Another research direction is to develop efficient algorithms to solve the facility location and vehicle routing problems. In this chapter, the formulated problems were of relatively small size (i.e., 30 eligible facility sites, 10 selected staging areas, 1 central depot, and 3 vehicles) so the optimal solutions could be readily found using commercially available optimization software. However, for modeling more realistic and larger scenarios, the problem size of the models will increase significantly so that it becomes computationally prohibitive to obtain an optimal solution. Future research direction should also focus on developing efficient heuristics which can identify near optimal solutions to the large problems within a reasonable computational time.