Distance-Based Clique Relaxations in Networks: s-Clique and s-Club

Abstract

The concept of the clique, originally introduced as a model of a cohesive subgroup in the context of social network analysis, is a classical model of a cluster in networks. However, the ideal cohesiveness properties guaranteed by the clique definition put limitations on its applicability to situations where enforcing such properties is unnecessary or even prohibitive. Motivated by practical applications of diverse origins, numerous clique relaxation models, which are obtained by relaxing certain properties of a clique, have been introduced and studied by researchers representing different fields. Distance-based clique relaxations, which replace the requirement on pairwise distances to be equal to 1 in a clique with less restrictive distance bounds, are among the most important such models. This chapter surveys the up-to-date progress made in studying two common distance-based clique relaxation models called s-clique and s-club, as well as the corresponding optimization problems.

1 Introduction

In 1949, Luce and Perry [42] introduced the clique concept to model the notion of a cohesive subgroup in social network analysis. Since then, cliques and the associated maximum clique problem have become ubiquitous and have been studied extensively in graph theory [13, 14, 28], theoretical computer science [32, 39] and operations research [9, 15, 20] from different perspectives. In graph-theoretic terms, a clique is a subset of vertices that are pairwise adjacent. The clique definition ensures the perfect reachability between the group’s entities, as they are directly linked to each other. Moreover, it also ensures that a clique has the highest possible degree of each vertex, the highest possible connectivity, and the largest possible number of edges in the induced subgraph among all subsets of vertices of the same cardinality. However, the ideal cohesiveness properties of a clique put limitations on its applicability to situations where enforcing such properties is unnecessary or even prohibitive. For example, in transportation and telecommunication networks easy reachability between the members of a group (or a cluster) is of utmost importance, whereas a large number of edges is either costly to construct and maintain or results in operating inefficiencies, such as excessive interference.

To address particular practical aspects that cannot be suitably modeled by cliques, numerous clique relaxation models have been introduced in the literature that enforce certain elementary properties of cliques to be present, in a relaxed form, in the model of a cluster. The long list of the proposed models includes the distance-based clique relaxations called s-clique [41] and s-club [49], degree-based relaxations called s-plex [62] and k-core [61], and an edge density-based model known as quasi-clique [1] among many others. The focus of this chapter is on distance-based clique relaxations, s-clique and s-club.

Originally proposed by Luce [41] in 1950, s-clique was the historically first clique relaxation concept. This structure relaxes the requirement of having an edge (distance 1) between any pair of vertices from the group by allowing them to be at most distance s apart, thus ensuring that they can communicate via a path of at most s−1 intermediate vertices. Note that these intermediate vertices, while guaranteeing the reachability in at most s hops between vertices from an s-clique, do not have to be a part of the s-clique themselves, which may be considered a drawback from the cohesiveness standpoint. This was first pointed out by Alba [3], who proposed a definition of the so-called sociometric clique of diameter s, which was later refined by Mokken [49] under the name of s-club. Any two members of an s-club are required to be connected by a path of length at most s, where all intermediate vertices belong to the s-club.

The objective of this chapter is to provide an up-to-date survey of known results concerning s-clique, s-club, and the corresponding optimization problems, as well as to identify related open questions for future work. The remainder of the chapter is organized as follows. We start by introducing the formal definitions and notations used throughout the chapter in Sect. 2. In Sect. 3, we discuss some basic structural properties of s-cliques and s-clubs and the complexity results for the optimization problems associated with these models in order to have a better understanding of the computational challenges one has to overcome in order to solve the problems of interest. Section 4 provides integer programming formulations proposed for the optimization problems. Known polyhedral combinatorics results associated with these formulations are reviewed in Sect. 5. An overview on the solution methods that have been proposed for these problems, along with a brief review of the computational results, is presented in Sect. 6. Selected applications of the problems of interest are discussed in Sect. 7. Finally, the article concludes by discussing some possible research directions for future work in Sect. 8.

2 Definitions and Notations

We consider a simple undirected graph G=(V,E) with the set of vertices V and the set of edges E corresponding to pairs of vertices. Two vertices v and v′ in G are said to be adjacent or neighbors if (v,v′)∈E, in which case the edge (v,v′) is said to be incident to v and v′. Let N _G (v)={v′∈V:(v,v′)∈E} denote the neighborhood of a vertex v in G, and let N _G [v]={v}∪N _G (v) be the closed neighborhood of v. The cardinality of the neighborhood, |N _G (v)|, is called the degree of v in G and is denoted by deg _G (v). Let δ(G) and Δ(G) denote the minimum and the maximum degree of a vertex in G, respectively. We call a graph G′=(V′,E′) a subgraph of G=(V,E) if V′⊆V and E′⊆E. For a subset of vertices S⊆V, the subgraph induced by S, G[S], is given by G[S]=(S,E∩(S×S)), where “×” denotes the Cartesian product.

A path of length r between vertices v and v′ in G is a subgraph of G given by an alternating sequence of distinct vertices and edges v≡v ₀,e ₀,v ₁,e ₁,…,v _r−1,e _r−1,v _r ≡v′ such that e _i =(v _i ,v _i+1)∈E for all 1≤i≤r−1. A cycle of length r is defined similarly, by assuming that v≡v′ in the definition of a path. If there is at least one path between two vertices v and v′ in G, then we say that v and v′ are connected in G. A graph is called connected if any pair of its vertices is connected. Otherwise, a graph is called disconnected. The length of a shortest path between two connected vertices v and v′ in G is called the distance between v and v′ in G and is denoted by d _G (v,v′). If v and v′ are not connected in G, then d _G (v,v′)=∞. The diameter diam(G) of a graph G is given by the maximum distance between any pair of vertices in G, that is, diam(G)=max _v,v′∈V d _G (v,v′).

The vertex connectivity κ(G) of G is the minimum number of vertices that need to be deleted from G in order to obtain a disconnected or a trivial graph. The density ρ(G) of G is given by $\rho(G)=|E|/{|V|\choose2}$. A complete graph K _n on n vertices is a graph that contains all possible edges, that is, ρ(K _n )=1. The complement $\bar{G}$ of G is $\bar{G}=(V,\bar{E})$, where $\bar{E}$ is the complement of E, that is, $E\cap \bar{E}=\emptyset$ and $K_{|V|}=(V,E\cup\bar{E})$. A clique C is a subset of vertices such that G[C] is a complete graph. An independent set I is a subset of vertices such that G[I] has no edges. Clearly, S⊆V is a clique in G if and only if S is an independent set in $\bar{G}$. A clique (independent set) is called maximal if it is not a subset of a larger clique (independent set). A maximum clique (independent set) of G is a clique (independent set) of the largest size in G, and the problem of finding a maximum clique (independent set) in a graph is called the maximum clique (independent set) problem. The size of a maximum clique in G is called the clique number of G and is denoted by ω(G). The size of a maximum independent set in G is called the independence number of G and is denoted by α(G). We have $\omega(G)=\alpha(\bar{G})$.

Some of the well known clique relaxation models are defined next. We assume that s and k are positive integer constants and λ,γ∈(0,1] are real constants. Let S⊆V. S is an s-plex if δ(G[S])≥|S|−s. S is an s-defective clique if G[S] contains at least ${|S| \choose2} - s$ edges. S is a k-core if δ(G[S])≥k. S is a k-block if κ(G[S])≥k. S is a γ-quasi-clique if ρ(G[S])≥γ. S is a (λ,γ)-quasi-clique if δ(G[S])≥λ(|S|−1) and ρ(G[S])≥γ. D⊆V is called a distance s-dominating set if for any v∈V∖D there exists v′∈D such that d _G (v,v′)≤s. Distance 1-dominating set is called simply a dominating set.

In [54], the motivation behind some of the most popular clique relaxation models was analyzed in a systematic fashion, and a set of simple rules for defining meaningful clique relaxation structures was identified, yielding a methodical taxonomic framework for clique relaxations. The framework is based on the observation that the clique can be defined using alternative equivalent descriptions via other basic graph concepts, such as distance, diameter, domination, degree, density, and connectivity. The corresponding equivalent definitions are referred to as elementary clique defining properties. Then, by applying some simple modifications to the elementary clique defining properties, one can reproduce the known clique relaxation models, as well as define new structures of potential practical interest. We will adhere to this framework in defining the distance-based clique relaxations formally as follows.

First, note that a subset of vertices C is a clique in G if and only if d _G (v,v′)=1, for any v,v′∈C or, equivalently, diam(G[C])=1. These equivalent clique definitions constitute the elementary clique defining properties based on distance and diameter, respectively. In both cases, we have an equivalent characterization of a clique by setting a certain parameter (pairwise distance or diameter) to its minimum possible value. We can define the corresponding clique relaxations by restricting the violation of the respective elementary clique defining property, that is, by allowing the pairwise distance or diameter to be greater than 1, but no greater than a constant positive integer s>1. As a result, we obtain the following definitions.

Definition 1

(s-clique)

Given a simple undirected graph G=(V,E) and a positive integer constant s, a subset of vertices S⊆V is called an s-clique if d _G (v,v′)≤s, for any v,v′∈S.

Definition 2

(s-club)

Given a simple undirected graph G=(V,E) and a positive integer constant s, a subset of vertices S⊆V is called an s-club if diam(G[S])≤s.

An s-clique (s-club) is called maximal in G if it is not a subset of a larger s-clique (s-club) in G, and maximum in G if there is no larger s-clique (s-club) in G. The maximum s-clique (s-club) problem asks to find a maximum s-clique (s-club) in G. The size of the largest s-clique in G is called the s-clique number and is denoted by $\tilde{\omega}_{s}(G)$. The size of the largest s-club in G is called the s-club number and is denoted by $\overline{\omega}_{s}(G)$.

According to the taxonomy in [54], clique relaxations based on restricting the violation of an elementary clique defining property can be standard or weak; absolute or relative; and structural or statistical. For a standard relaxation, we require the relaxed clique-defining property to hold in the induced subgraph, whereas the corresponding weak relaxation requires the same property to be satisfied within the original graph instead of the induced subgraph. Since s-clique is defined by restricting pairwise distances for its members in G, it is a weak relaxation, whereas s-club, which restricts distances in the induced subgraph, is a standard relaxation. Both s-clique and s-club are absolute relaxations, since the value of the constant s refers to the absolute bound on the distance in G or G[S] and does not depend on the size of S. However, their relative version could easily be introduced by replacing the constant s in the definitions of s-clique and s-club with γ|S|, where γ∈(0,1) is a constant. Finally, both s-clique and s-club are structural clique relaxations and their statistical counterparts could be defined by requiring that the average pairwise distance between vertices for S in G or G[S] is at most s. It should be noted that, in contrast to the structural relaxations, statistical relaxations generally impose little in terms of the group structure.

Higher-order clique relaxation models, which relax more than one elementary clique defining properties simultaneously, could also be defined using distance or diameter restrictions in addition to other requirements. Since the graph-theoretic notion of distance relies on paths, in addition to the simple higher order relaxations that combine multiple properties in a straightforward fashion, s-clique and s-club could also be involved in the so-called k-hereditary higher-order relaxations, with k-connectivity embedded within their structure. Namely, k-hereditary s-club and s-clique can be defined as follows. Given G=(V,E) and positive integers s and k, S⊆V is called a k-hereditary s-club if diam(G[S∖S′])≤s for any S′⊂S such that |S′|≤k. Similarly, S is a k-hereditary s-clique if d _G (v,v′)≤s for all v,v′∈S∖S′ for any S′⊂S such that |S′|≤k.

While the variations of distance-based relaxations just defined may potentially find interesting applications, in the remainder of this chapter, we focus on the s-clique and s-club models, which were referred to as canonical clique relaxation models for distance and diameter, respectively, in [54].

Next, we introduce some graph classes for which the problems of interest have been explored in the literature. Consider a graph G=(V,E). Given a cycle in G, its chord is an edge between two vertices of the cycle that is not a part of the cycle. A graph is called chordal if any cycle on at least 4 vertices has a chord. G is called a k-partite graph if V can be partitioned into k non-overlapping independent sets. If k=2, a k-partite graph is bipartite. G is a split graph, if V=V ₁∪V ₂, where V ₁ is a clique and V ₂ is an independent set such that V ₁∩V ₂=∅. G is an interval graph if there exists a set of intervals on the real line such that I _v ∩I _v′≠∅ iff (v,v′)∈E.

3 Structural Properties and Computational Complexity

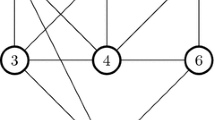
From the definitions, it is clear that an s-club is also an s-clique, however, the converse is not true in general. Even though the s-clique and s-club models appear to be very similar, there are some fundamental differences in their structural properties that have important implications for the associated optimization problems. To highlight these differences, consider a simple example in Fig. 1 that originally appeared in [3]. In the graph in this figure, a subset of vertices {1,2,3,4,5} is a 2-clique, but not a 2-club, since the distance between vertices 1 and 5 is 3 in the induced subgraph. Moreover, {1,2,4} is a 2-clique and a 2-club, {1,2,4}∪{5} and {1,2,4}∪{6} are both 2-cliques but not 2-clubs, whereas {1,2,4}∪{5,6} is again a 2-clique and a 2-club. This shows the lack of any type of heredity for s-clubs, which is formally defined as follows [54]. A graph property Π is called hereditary on induced subgraphs, if for any graph G with property Π deleting any subset of vertices does not produce a graph violating Π. A graph property Π is called weakly hereditary, if for any graph G=(V,E) with property Π all subsets of V posses the property Π in G.

Fig. 1

A graph illustrating structural differences of 2-cliques and 2-clubs

Unlike s-clubs, s-cliques posses weak heredity, which allows to reduce the problem of finding an s-clique to the problem of finding a clique in an auxiliary power graph defined as follows. Given a graph G=(V,E) , the sth power of G, denoted by G ^s, is given by G ^s=(V,E ^s), where E ^s={(v,v′):0<d _G (v,v′)≤s}. Then S⊆V is an s-clique in G if and only if S is a clique in G ^s. Heredity on induced subgraphs is the core property implicitly exploited by some of the most successful combinatorial algorithms for the maximum clique problem [21, 51], which can also be applied to G ^s in order to solve the maximum s-clique problem in G. Because of the presence of weak heredity, s-clique has advantage over s-club in terms of applicability of the variety of existing techniques available for the maximum clique problem to solving the maximum s-clique problem. However, this comes at a price. The fact that the s-clique is defined by restricting the distances in the original graph rather than the induced subgraph leads to the possibility of absence of any cohesiveness in the subgraph induced by an s-clique. For example, the subset of vertices {1,3,5} in the graph on Fig. 1 is a 2-clique that induces an independent set, a structure that can hardly be considered cohesive by any standards. In terms of cohesiveness, the worst-case example of an s-club is a star graph, where one “central” vertex is adjacent to all other vertices, which have no neighbors other than the central vertex. While this structure appears to be quite fragile, as removing the central vertex makes it an independent set, it is still more cohesive than the worst-case example of an s-clique, which is an independent set to begin with. Since s-clique does not have to be connected in general, it makes sense to consider a connected s-clique, which is an s-clique that induces a connected subgraph.

Since s-clubs do not have any form of heredity defined above, the maximum clique algorithms cannot be easily adapted for the maximum s-club problem. In fact, the problem of finding a maximal s-club, which is very easy for clique and s-clique, becomes challenging. Indeed, the problem of checking whether a given clique (s-clique) is maximal reduces to checking whether there is a vertex from outside that can be added to the clique (s-clique). However, the example above clearly shows that this strategy will not work for s-clubs. In fact, Mahdavi and Balasundaram [44] have recently shown that testing whether an s-club is maximal is NP-hard for any fixed integer s≥2. They have also identified sufficient conditions for every connected 2-clique to be a 2-club based on the concept of a partitionable cycle, which can be defined as follows. Consider two nonadjacent vertices v and v′ in a cycle C in G. Removing these two vertices breaks the cycle into two paths, P ₁(v,v′) and P ₂(v,v′) with the vertex sets V ₁(v,v′) and V ₂(v,v′), respectively. If there exist v,v′ such that G[V ₁(v,v′)]=P ₁(v,v′) and G[V ₂(v,v′)]=P ₂(v,v′) then C is called a partitionable cycle. If, in addition, |V ₁(v,v′)|≠|V ₂(v,v′)| then the partitionable cycle C is called asymmetric. Mahdavi and Balasundaram [44] have proved that if no subset of 5≤c≤2s+1 vertices induces an asymmetric partitionable cycle in G, where s≥2, then every connected s-clique is an s-club. This implies, in particular, that in a bipartite graph every connected 2-clique is a 2-club, which induces a complete bipartite subgraph. In cases where every connected s-clique is an s-club, checking maximality of an s-club reduces to checking maximality of a connected s-clique and hence is easy. Thus, discovering more of such cases is an interesting future research direction, which will provide further insights towards understanding the complexity of the problem.

The maximum clique problem is a classical NP-hard problem [32, 39], which is also hard to approximate. Recall that for a maximization problem with an optimal objective value given by $\operatorname {opt}(G)$ on an input graph G, an algorithm is called σ-approximation algorithm (or algorithm with approximation ratio σ) if for every input graph G, where is the objective value output by when applied to G. It is known that the maximum clique size cannot be approximated in polynomial time within a factor of n ^1−ε for any ε>0 unless P=NP [5, 6, 67]. Since clique is a special case of s-clique and s-club, where s=1, all these results apply to the versions of the maximum s-clique and maximum s-club problems that allow for arbitrary (non-fixed, instance-dependent) s. However, these results do not directly extend to the maximum s-clique and maximum s-club problems for the fixed constant parameter s>1, which is given as a part of the problem definition rather than as an instance-dependent parameter. Therefore, in recent years there has been a considerable amount of research towards characterizing these problems in terms of their computational complexity in general and restricted graph classes.

Bourjolly et al. [17] use a reduction from clique to show that the maximum s-club problem is NP-hard for any fixed s. Balasundaram et al. [10] use an alternative reduction from clique to prove that both the maximum s-clique and maximum s-club problem are NP-hard, even if restricted to graphs of fixed diameter s+1. Note that both problems are trivial when the graph’s diameter is bounded above by s, therefore the transition in complexity is sudden.

Asahiro et al. [7] proved that for any ε>0 and a fixed s≥2 the maximum s-club problem is NP-hard to approximate within a factor of n ^1/2−ε in general graphs, improving on the hardness of n ^1/3−ε-approximation result of Marinček and Mohar [45]. They also designed a simple polynomial-time algorithm that approximates the maximum s-club within a factor of n ^1/2 for an even s, and within a factor of n ^2/3 for an odd s. Given a graph G=(V,E), the algorithm finds a maximum degree vertex in the power-⌊s/2⌋ graph G ^⌊s/2⌋=(V,E ^⌊s/2⌋) and outputs its closed neighborhood in G ^⌊s/2⌋, which forms an s-club C _s of size Δ(G ^⌊s/2⌋)+1 in G. To establish the approximation ratio, they consider two cases, Δ(G)≥n ^1/s and Δ(G)<n ^1/s. Then in the first case we have:

$$\frac{\overline{\omega}_{s}(G)}{|C_s|}=\frac{\overline{\omega}_{s}(G)}{\varDelta (G^{\lfloor s/2\rfloor})+1}\le\frac{\overline{\omega}_{s}(G)}{\varDelta (G)+1}<n^{1-1/s}. $$

In the second case, noting that $\overline{\omega}_{s}(G)\le1+\varDelta (G)+\varDelta (G)^{2}+\cdots+\varDelta (G)^{s}$, the following holds:

$$\frac{\overline{\omega}_{s}(G)}{|C_s|}\le\frac{\varDelta (G)^{s}+O(\varDelta (G)^{s-1})}{\varDelta (G)+1}=O\bigl(\varDelta (G)^{s-1}\bigr)=O \bigl(n^{1-1/s}\bigr). $$

Thus, in both cases the approximation ratio of the algorithm is O(n ^1−1/s), which becomes O(n ^1/2) for s=2 and O(n ^2/3) for s=3. To show that the algorithm is, in fact O(n ^1/2)-approximate for any even s≥4, observe that

$$ \overline{\omega}_{s}(G) \le\overline{\omega}_{2} \bigl(G^{s/2}\bigr), $$

(1)

while the output of the approximation algorithm applied to the maximum s-club problem on G and to the maximum 2-club problem on G ^s/2 is the same. Thus, the approximation ratio of O(n ^1/2) holds for any even s.

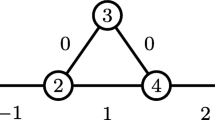
It should be noted that [7] uses a stronger claim, $\overline{\omega}_{s}(G) = \overline{\omega}_{2}(G^{s/2})$ instead of (1) in the proof of the approximation ratio. However, the equality does not hold in general, that is, we may have $\overline{\omega}_{s}(G) < \overline{\omega}_{2}(G^{s/2})$ as in the graph in Fig. 2. The proof still holds using the inequality (1) instead.

Fig. 2

A graph with $\overline{\omega}_{s}(G)=14$ (a maximum 2-club is given by, e.g., C={5,6,7,8,9,12,13,14,16,17,18,19,20,21}) and $\overline{\omega}_{2}(G^{s/2})=16$ (all vertices excluding 2,4,6,8,10 form the maximum 2-club in G ²), where s=4

In addition to the above results, Asahiro et al. [7] proved that for any ε>0 the maximum s-club problem is NP-hard to approximate within a factor of n ^1/3−ε for chordal and split graphs with even s, for bipartite graphs with s≥3, and for k-partite graphs (k≥3) with s≥2. On the other hand, the problem can be solved in polynomial time for chordal and split graphs with odd s, as well as for trees and interval graphs [7, 58]. Unlike the maximum s-club problem with s≥3, the maximum 2-club problem can be solved in O(n ⁵) on bipartite graphs [58]. In addition, the maximum 2-club can be approximated within a factor of n ^1/3 for split graphs.

In several recent papers, the maximum s-club problem was approached from the parameterized complexity perspective [23, 36, 37, 59]. In this framework, one considers a parameter k (such as the size of a structure sought) in addition to the traditional input size n [31]. A parameterized problem is fixed-parameter tractable if there exists an algorithm (referred to as an fpt-algorithm) that solves the parameterized problem in time f(k)⋅n ^O(1), where f is a computable (typically exponential) function that depends only on the parameter k.

It is known that deciding if a given graph contains a clique of size k is W[1]-complete [24], meaning that an fpt-algorithm is unlikely to exist. In contrast, Chang et al. [23] have shown that the problem of deciding if a given graph contains an s-club of size k is fixed-parameter tractable for s>1. The proof is as follows. Let G=(V,E) be the given graph. If G ^⌊s⌋ has a vertex v such that $|N_{G^{\lfloor s/2\rfloor }}[v]|\ge k$ then $N_{G^{\lfloor s/2\rfloor}}[v]$ is an s-club of size at least k in G. Otherwise, $|N_{G^{\lfloor s/2\rfloor}}[v]| < k$ for any v∈V, and it can be shown that $|N_{G^{s}}[v]| < k^{2}$ when s is even and $|N_{G^{s}}[v]| < k^{3}$ when s is odd [23]. Since any s-club C is a subset of $N_{G^{s}}[v]$ for any v∈C, in order to check whether G has an s-club of size k it suffices to check all k-element subsets of $N_{G^{s}}[v]$ for each v∈V. There are at most ${k^{3}\choose k}n$ such subsets, and checking whether a k-element vertex set forms an s-club can be done in k ³ time. Thus, the overall run time is O(k ^3(k+1) n).

Schäfer et al. [59] have shown that the maximum s-club problem is fixed-parameter tractable not only with the solution size k used as the parameter, but also when parameterized by the so-called dual parameter d=|V|−k. The algorithm they propose for this case runs in O(2^d nm), where m is the number of edges in the graph. These ideas are extended to develop a practical algorithm for 2-club in [36], as will be discussed in more detail in Sect. 6. In addition, Hartung et al. [36] analyzed parameterized complexity of s-club with other parameters, such as the size of a vertex cover, feedback edge set size, size of a cluster editing set, and treewidth of the graph.

4 Mathematical Programming Formulations

In this section, mathematical programming formulations for the maximum s-clique and maximum s-club problems are presented. The maximum clique problem is one of the well studied problems in discrete optimization, with a number of known integer, as well as continuous non-convex formulations [15]. Similar formulations can be applied to the maximum s-clique problem on a graph G by reducing it to the maximum clique problem on the sth power of G, G ^s=(V,E ^s), constructed from the original graph as mentioned above. Let $\overline{E^{s}}$ denote the complement set of edges in G ^s, that is, $\overline{E^{s}}=\lbrace(i,j): i,j\in V, i<j, d_{G}(i,j) > s\rbrace$. Then the following formulation of the maximum clique problem written for the power-s graph G ^s can be used for the maximum s-clique problem on G:

(2)

(3)

(4)

The first mathematical program for computing the s-club number of a graph was proposed in [17]; see also [10]. In the following, we explain this general integer programming model first and then describe special cases for s=2,3 that are of highest practical interest and have received more attention in the literature. For S⊆V the vector x∈{0,1}ⁿ such that x _i =1 if and only if i∈S is called the characteristic vector of S. In the general model (5)–(8) below, which is often referred to as chain formulation, the vector of decision variables x is the characteristic vector of the s-club sought. For every pair of vertices i,j∈V, let $P_{ij}^{s}$ be the set of all paths of length at most s between i and j in G. We will denote by $\mathbb{P}$ the set of all such paths in G, i.e., $\mathbb{P}=\bigcup_{i,j\in V}P_{ij}^{s}$. Let V _P be the set of vertices included in a path P. Also let y _P be the auxiliary binary variable associated with every path $P\in\mathbb{P}$. If this variable is equal to 1 in a feasible solution, this implies that all the vertices in the path P are included in the corresponding s-club. Then the following finds the maximum cardinality s-club in G:

(5)

(6)

(7)

(8)

In this formulation, constraint (6) ensures that two vertices i and j such that d _G (i,j)>s cannot both belong to the same s-club (in this case $P_{ij}^{s}=\emptyset$ and the constraint becomes x _i +x _j ≤1). It also guarantees that if two nonadjacent vertices are included in the s-club sought, then there must be at least one path of length at most s such that all the vertices from this path are also included in the s-club. In addition, constraint (7) forces y _P to be 0 whenever a vertex from P is not included in the s-club. For s=2 the above chain formulation becomes:

(9)

(10)

(11)

This model ensures that any two nonadjacent vertices that are in the same 2-club must have at least one common neighbor inside the 2-club.

Considering the number of possible distinct paths of length at most s between every pair of vertices, the chain formulation may have an excessive number of variables when s>2. In general, we may have $|P_{ij}^{s}|=O(n^{s-1})$ for every pair of vertices, so $|\mathbb {P}|=O(n^{s+1})$. Therefore, this model does not scale well when s increases, and even solving small instances using this formulation is challenging when s≥3 [65].

To formulate the maximum 3-club problem using a smaller number of variables, the neighborhood formulation (13)–(16) was proposed in [4] that has |V|+|E| variables. Note that a pair of nonadjacent vertices i and j in G can be a part of the same 3-club S only if they have a common neighbor k in S or there are two adjacent vertices {p,q}∈S such that p∈N _G (i) and q∈N _G (j). The first condition holds if and only if d _G[S](i,j)=2. If the first condition does not hold and the second condition holds, then p∈{N _G (i)∖N _G (j)} and q∈{N _G (j)∖N _G (i)}. Let E _ij denote the set of edges that connect such intermediate nodes for i and j:

$$ \begin{aligned}[b] & E_{ij}=\bigl\{(p,q)\in E:p\in\bigl \{N_G(i)\setminus N_G(j)\bigr\}, q\in\bigl\{ N_G(j)\setminus N_G(i)\bigr\}\bigr\}\\ & \quad\forall i,j: d_G(i,j)=3.\end{aligned} $$

(12)

Now associate a binary variable x _i with each vertex i∈V and a binary variable z _ij with each edge (i,j)∈E. Then the maximum 3-club problem in G=(V,E) can be formulated using the following binary program:

(13)

(14)

(15)

(16)

Neighborhood constraints (14) ensure that two nonadjacent vertices i and j cannot be both in the solution unless their common neighbor is in the solution or a pair of their neighbors p and q, linked by an edge, are in the solution. The constraints in (15) guarantee that an edge (i,j) is used if and only if both its endpoints belong to the solution. The neighborhood formulation has |V|+|E| variables and $\frac{|V|^{2}-|V|}{2}+2|E|$ constraints.

Almeida and Carvalho [4] also proposed another formulation for the maximum 3-club problem that is based on identifying minimal node cut sets for every pair of vertices with d _G (i,j)=3. Consider a pair of nonadjacent vertices i,j∈G and let E _ij be defined as in (12). Recall that E _ij is the set of inner edges of chains with length 3 connecting i and j with no common neighbors. Let V _ij represent the set of vertices incident to edges from E _ij . We associate with i and j a subgraph $G_{ij}=(V'_{ij},E'_{ij})$ where $V'_{ij}=V_{ij}\cup\{i,j\}$ and $E'_{ij}=E_{ij}\cup\{(i,v)\in E:v\in V_{ij}\}\cup\{(j,v)\in E:v\in V_{ij}\}$. Figure 3 is an example of a subgraph G _ij in which E _ij ={(1,2),(1,5),(3,4)}, V _ij ={1,2,3,4,5} and $E'_{ij}=\{(1,2),(1,5),(3,4),(i,1),(i,3),(2,j),(4,j),(5,j)\}$. Let S _ij be an i–j node cut set and define to be the set of all minimal S _ij . For our example in the figure, . These sets separate i and j in G _ij , therefore, to include nodes i and j with d _G (i,j)=3 in the same 3-club S, it is necessary to include a node of each set . Thus, the node cut set formulation (17)–(19) for the maximum 3-club problem can be stated as follows:

(17)

(18)

(19)

In this formulation, inequalities (18) are the node cut set constraints described above. The formulation has |V| variables, but potentially exponential number of constraints. Note that constraints associated with non-minimal cut sets are dominated by constraints (18) and are not necessary.

Fig. 3

Subgraph G _ij illustrating the node cut set formulation

Next, we present an integer programming formulation for the maximum s-club problem recently proposed by Veremyev and Boginski [65]. We first discuss the formulation for s=2 and then extend it to the higher s values. Let V={1,…,n} and let $A=[a_{ij}]_{i,j=1}^{n}$ be the adjacency matrix of G=(V,E). Then the characteristic vector x of a 2-club S must satisfy the following nonlinear constraint:

$$ a_{ij}+\sum_{k\in V} a_{ik}a_{kj}x_{k} \geq x_{i}x_{j} \quad\forall i,j\in V. $$

(20)

Linearizing this constraint, we formulate the maximum 2-club problem as follows:

(21)

(22)

(23)

The above formulation can be simplified as follows:

(24)

(25)

(26)

Similarly, the characteristic vector x of a 3-club must satisfy the following nonlinear constraints:

$$ \sum_{k=1}^{n} a_{ik}a_{kj}x_{k}+ \sum_{k=1}^{n}\sum _{m=1}^{n}a_{ik}a_{km}a_{mj}x_{k}x_{m} \geq x_{i}x_{j}\quad\forall (i,j)\notin E. $$

(27)

Letting w _ij =x _i x _j for all i,j∈V and linearizing the constraints, we obtain the following formulation for the maximum 3-club problem:

(28)

(29)

(30)

(31)

This formulation contains O(n ²) binary variables and O(n ²) constraints. Similarly, one can develop the model and linearize it using the standard approaches for the general case of the maximum s-club problem. However, the resulting formulation will have O(n ^s−1) variables. Veremyev and Boginski [65] exploit the special structure of s-club and propose an efficient linearization technique that reduces the number of variables substantially. We discuss their compact binary formulation next.

Consider a subset of vertices S and its characteristic vector x. Let $v_{ij}^{(l)}\ (i,j=1,\ldots,n; l=2,\ldots,s)$ be a binary variable taking the value 1 if there exists at least one path of length l from i to j in G[S] and 0 otherwise. Note that for l=2 we have $v_{ij}^{(2)}=\min\{x_{i}x_{j}\sum_{k=1}^{n}a_{ik}a_{kj}x_{k},1\}$, which can be linearized using the following set of constraints:

$$\left\{ \begin{aligned} &v_{ij}^{(2)}\leq x_{i},\quad v_{ij}^{(2)}\leq x_{j} \\ & v_{ij}^{(2)}\leq\sum_{k=1}^{n}a_{ik}a_{kj}x_{k}, \quad v_{ij}^{(2)}\geq\frac{1}{n} \Biggl(\sum _{k=1}^{n}a_{ik}a_{kj}x_{k} \Biggr)+(x_{i}+x_{j}-2). \end{aligned} \right. $$

Other variables for higher values of l=3,…,s can be found recursively using $v_{ij}^{(l)}=\min\{x_{i}\sum_{k=1}^{n}v_{kj}^{(l-1)}a_{ik},1\}$ and linearized by applying the following set of inequalities:

$$\left\{ \begin{aligned} & v_{ij}^{(l)}\leq x_{i},\quad v_{ij}^{(l)}\leq\sum _{k=1}^{n}a_{ik}v_{kj}^{(l-1)} \\ & v_{ij}^{(l)}\geq\frac{1}{n} \Biggl(\sum _{k=1}^{n}a_{ik}v_{kj}^{(l-1)} \Biggr)+(x_{i}-1). \end{aligned} \right. $$

Therefore the maximum s-club problem can be formulated as the following binary linear program:

(32)

(33)

(34)

(35)

(36)

(37)

(38)

The above model is the most compact known formulation for the maximum s-club problem with O(sn ²) variables and constraints. For more information about compact formulation and its properties, we refer the reader to [65].

5 Polyhedral Results

Due to the structure of the problem and its dependence on the value of parameter s, most of the research in this area has been focused on the 2-club polytope and, partially, 3-club polytope and not on the s-club polytope in general. In this section, we review the polyhedral results available for the 2-club polytope.

Consider a nontrivial simple undirected connected graph G=(V,E). A subset of vertices I⊆V is a 2-independent set in G if d _G (i,j)>2 ∀i,j∈I. Let M ₁ be the edge-vertex incidence matrix of the complement graph $\bar{G}$. The rows of M ₁ correspond to edges $(i,j)\in\bar{E}$ and the columns correspond to vertices i∈V. The entries in the row corresponding to an edge (i,j) are 1 in columns i and j and are 0 otherwise. Let M ₂ be the matrix representing the common neighborhood of i,j for every $(i,j)\in\bar{E}$. The rows of M ₂ correspond to edges $(i,j)\in\bar{E}$ and the columns correspond to vertices i∈V. The entries in the row corresponding to an edge (i,j) are 1 in columns k∈N _G (i)∩N _G (j) and are 0 otherwise. Let A=M ₁−M ₂, then the maximum 2-club problem formulation (9)–(11) can be written as [10]:

$$\bar{\omega}_{2}(G)= \max\bigl\lbrace\mathbf{1}^{T}x: Ax \leq\mathbf{1}, x\in\lbrace0,1 \rbrace^{|V|}\bigr\rbrace, $$

where 1 is the vector of all ones of appropriate dimension and $\bar{\omega}_{2}(G)$ is the 2-club number of G. Let Q be the set of feasible binary vectors defined as Q={x∈{0,1}^|V|:Ax≤1}, then the 2-club polytope P _2C is given by the convex hull of Q: P _2C =conv(Q). The following results were established in [10].

• 1. dim(P _2C )=|V|.

• 2. x _i ≥0 induces a facet of P _2C for every i∈V.

• 3. For any i∈V, x _i ≤1 induces a facet of P _2C if and only if d _G (i,j)≤2 ∀j∈V.

• 4. Let I be a maximal 2-independent set in G. Then ∑ _i∈I x _i ≤1 induces a facet of P _2C .

Note that each neighborhood constraint is associated with two vertices v and v′ such that d _G (v,v′)=2. For any node i∈V∖{v,v′} such that min{d _G (i,v),d _G (i,v′)}>2, the inequality $x_{v}+x_{v'}+x_{i}-\sum_{j\in\{N_{G}(v)\cap N_{G}(v')\}}x_{j}\leq1$ is valid for P _2C because neither v nor v′ can be included in a 2-club that includes node i, and to include nodes v and v′, at least one of their common neighbors must also be included in the 2-club. This inequality is a lifted version of the neighborhood constraint (10). Carvalho and Almeida [22] used this observation to establish the following valid inequality for P _2C :

$$ \sum_{i\in I\cup\{v,v'\}}x_{i}- \sum_{j\in N_G(v)\cap N_G(v')}x_{j}\leq1, $$

(39)

where I⊆V∖{v,v′} is such that I∪{v} and I∪{v′} are 2-independent sets in G. They also extended this result to triples of vertices as follows. Let v,v′,v″ be given. For a vertex j denote by a _j =(|N _G (j)∩{v,v′,v″}|−1)⁺, where a ⁺=max{a,0}, i.e., a _j =2 if j neighbors all three vertices; a _j =1 if j neighbors two of the three vertices; and a _j =0, otherwise. Let R={v,v′,v″} be an independent set in G. Let I⊆V∖{v,v′,v″} be such that I∪{v}, I∪{v′} and I∪{v″} are 2-independent sets in G. Then the inequality

$$ \sum_{i\in I\cup\{v,v',v''\}}x_{i}- \sum_{j\in V}\bigl(\bigl|N_G(j)\cap\bigl\{ v,v',v''\bigr\}\bigr|-1\bigr)^+ x_{j}\leq1 $$

(40)

is valid for P _2C .

More recently, Mahdavi [43] developed a family of valid inequalities that subsume both (39) and (40).

Theorem 1

([43])

Let I be an independent set in G. Then the inequality

$$ \sum_{i\in I}x_{i}- \sum_{j\in V\setminus I} \bigl(\bigl|N_G(j)\cap I\bigr|-1\bigr)^+ x_{j}\leq1 $$

(41)

is valid for P _2C . If, in addition, I is a distance 2-dominating set, i.e., I is an independent distance 2-dominating set (I2DS), then this inequality defines a facet for P _2C referred to as I2DS facet.

Mahdavi [43] also proved that given a noninteger feasible point $\tilde{x}$ in P _2C deciding whether this point violates an I2DS inequality is NP-complete, that is, the I2DS inequalities separation problem is NP-complete. On a positive note, I2DS inequalities are sufficient to derive the complete description of the 2-club polytope of trees. See [43] for a more detailed discussion on the 2-club polytope.

As for the maximum 3-club problem, Almeida and Carvalho [4] developed some non-trivial valid inequalities based on ideas similar to those used to develop (39) and (40) above. An interesting future research question is whether the valid inequalities they developed for 3-club can be generalized to develop a class of facets similar to I2DS above.

6 Exact and Heuristic Algorithms

The correspondence between the maximum clique and maximum s-clique problems implies that the heuristic and exact algorithms for maximum clique problem can be applied to the sth power of the graph to solve the maximum s-clique problem. In such cases, the performance of these algorithms may be poor as the edge density is higher in G ^s. Unlike the maximum clique problem, the maximum s-clique problem has not been the subject of extensive research and we are not aware of any computational results for this problem to date. This may be due to the above-mentioned correspondence between the two problems which facilitates the use of proposed algorithms for clique detection to solve the later case. Therefore, in this section our focus will primarily be on the existing algorithms for the maximum s-club problem.

Due to the NP-hardness of checking whether an s-club is maximal, developing sufficient conditions for an s-club to be maximal is of importance for designing effective algorithmic procedures for the maximum s-club problem. One such condition, which was proposed in [63], is outlined next.

For a positive integer k, the k-neighborhood $N_{G}^{k}(v)$ of v∈V is given by $N_{G}^{k}(v)=\{v': d_{G}(v,v')\leq k\}$. Note that $v\in N_{G}^{k}(v)$ for any k≥1, thus $N_{G}^{1}(v)=N_{G}[v]$. The k-neighborhood $N_{G}^{k}(S)$ of a given subset of vertices S is defined as follows: $N_{G}^{k}(S)=\bigcap_{v \in S}N_{G}^{k}(v)$. Given an s-club S and a positive integer p, we recursively define N ^s(G,S,p) as the s-neighborhood of S in G[N ^s(G,S,p−1)]:

$$N^s(G,S,p)=\left \{ \begin{array}{l@{\quad}l} N_G^s(S), & \mbox{if}\ p=1, \\ N^{s}(G[N^{s}(G,S,p-1)],S,1), & \mbox{if}\ p\geq2. \end{array} \right . $$

Then the following properties hold [63]:

• 1. If S⊆S ^∗⊆V, then we have N ^s(G[S],S,p)⊆N ^s(G[S ^∗],S,p)⊆N ^s(G,S,p) for any p≥1.

• 2. If S is an s-club, then we have S=N ^s(G[S],S,p)⊆N ^s(G,S,p+1)⊆N ^s(G,S,p) for any p≥1.

• 3. Let S be an s-club that is not maximal. Then for any maximal s-club S ^∗ containing S we have: S ^∗⊆N ^s(G,S,p) for any p≥1.

Theorem 2

([63])

Let S be an s-club. If there exists a positive integer p such that N ^s(G,S,p)=S, then S is a maximal s-club.

The sufficient condition in Theorem 2 is not necessarily satisfied by a maximal s-club, as illustrated by the example in Fig. 4. In the graph G=(V,E) in this figure, the subset of vertices S={1,2,3,4,5,6,7} is a maximal 2-club, however, for any p>1, N ²(G,S,p)=N ²(G,S,1)=V⊃S. Since the distance between vertices 8 and 11 is 3, V is not a 2-club.

Fig. 4

A graph with a maximal s-club S={1,2,3,4,5,6,7} that does not satisfy the condition of Theorem 2

6.1 Heuristic Algorithms

Due to computational intractability of the maximum s-club problem, heuristics become the method of choice for solving the maximum s-club problem in practice. Several construction heuristics have been proposed in the literature. In 2000, Bourjolly et al. [16] proposed three simple heuristic algorithms for the maximum s-club problem called DROP, CONSTELLATION and s-CLIQUE-DROP. Among these, DROP, which runs in O(|V|³|E|) time, was reported to produce the best result in terms of solution quality specially in graphs with higher density. DROP works as follows: we start with the whole graph G and at each iteration the vertex i with most infeasibility is deleted where infeasibility is defined as the number q _i of vertices of G whose shortest distance to i has a length of at least s+1. If there is a tie, a vertex of minimum degree is then selected for elimination and the graph is updated. The procedure continues until no infeasible vertex can be found. CONSTELLATION is based on identifying the largest star graph in the first step. In the next iteration, the vertex having the largest number of neighbors in the remaining graph is selected and added to the s-club provided that the total number of iterations does not exceed s−1. CONSTELLATION runs in O(s(|V|+|E|)) time and was reported to perform well solving the maximum 2-club problem on low density graphs. The third algorithm, s-CLIQUE-DROP, proceeds by identifying the largest s-clique in G and removing all vertices not belonging to s-clique from G along with their incident edges. Then DROP is called to find a feasible solution. To obtain the largest s-clique, the maximum clique problem is solved on G ^s using one of the existing algorithms. The recently proposed EXPAND algorithm [63] proceeds by taking the closed neighborhood of each vertex i in G, computing its s-neighborhood and applying DROP procedure on the subgraph induced by s-neighborhood of a vertex to obtain a feasible solution. Recall that the closed neighborhood of a vertex provides a 2-club, which is used to obtain the s-neighborhood for s≥2. To increase the chance of obtaining larger s-clubs in the initial steps of EXPAND, vertices are sorted based on a non-increasing order of their degrees in the initialization step. Therefore at each iteration i, DROP is called only if the size of the s-neighborhood of vertex i is larger than the best s-club found so far. A similar version of EXPAND, named IDROP, was independently used in [23].

Recently, a variable neighborhood search (VNS) meta-heuristic has been proposed for the maximum s-club problem [63]. VNS is based on the idea that a local optimum for one neighborhood structure is not necessarily a local optimum for another neighborhood structure [48]. Hence, to avoid being trapped in a poor-quality local optimum, the VNS explores, in a systematic fashion, multiple neighborhood structures. As a part of the procedure, the sufficient condition described in Theorem 2, has been used to test the maximality of a given solution to search the solution space more effectively. Computational experiments for s=2,3 using VNS algorithm were conducted on two sets of instances. The first testbed included the same set of random instances used in [44] to facilitate the comparison between the two methods. The second set included some of the large-scale instances from the tenth DIMACS implementation challenge [30]. For more detail on the proposed algorithm, neighborhood structures and computational results see [63].

6.2 Exact Algorithms

The first exact algorithm for the maximum s-club problem was proposed by Bourjolly et al. [17]. The proposed branch-and-bound (B&B) algorithm employs DROP heuristic to direct its branching process. For the bounding process, algorithm relies on the solutions to the maximum stable set problem solved on an auxiliary graph. Two branches are generated at the root node of the search tree that correspond to removing or keeping the vertex selected by a single iteration of DROP. The algorithm first explores the branch that removes the vertex. The process is then recursively applied until a terminal node is reached, yielding a depth first search. Note that deciding to remove or keep a vertex during the branching process may increase the shortest chains length and this affects the whole subtree rooted at the node in which this decision has been made. As a result, a pair of vertices in the current solution at some node of the subtree may appear too far away from each other. This leads to an infeasible solution and thus the corresponding branch is pruned. For the upper bounding procedure, let G′=(V′,E′) be the graph induced by the current solution at a given node of the B&B tree and let H=(V′,F) be an auxiliary graph associated with G′, where there is an edge between any two vertices in H only if the shortest path connecting these two vertices in G′ has length greater than s. Obviously, if there is an edge between two vertices in H, they cannot both belong to the same s-club in G′. Therefore, the largest independent set in H provides an upper bound on the size of the largest s-club in G′. In their computational results, authors report the average solution size and CPU time for s=2,3,4 on randomly generated instances with different edge densities. Instances were generated using the method proposed in [33].

Recently, Chang et al. [23] have shown that the B&B algorithm of Bourjolly et al. [17] runs in O(1.62ⁿ) time and proposed a variation of this algorithm that uses IDROP procedure to find the initial feasible solution and computes the s-coloring number of the graph associated with each node of the B&B tree to obtain an upper bound on the size of the s-club for that node. Observe that the chromatic number χ(G) of G is the minimum number of colors required to color the vertices of G properly, that is, so that no two neighbors are assigned the same color and the s-coloring number of G is the minimum number of colors required to color all vertices such that no two vertices of distance at most s are assigned the same color. Note that the s-coloring number of G provides an upper bound on the s-club number of G and one can compute the chromatic number χ(G ^s) of the sth power graph G ^s to obtain the s-coloring number of G. The authors report the results of computational experiments with a set of randomly generated instances, Erdös collaboration networks [11, 35], and some benchmark graphs from the second DIMACS implementation challenge [29].

More recently, Mahdavi and Balasundaram [44] proposed another B&B algorithm to compute the s-club number of a graph. Their algorithm employs two methods for computing a lower bound. The first method selects the larger of the two solutions found using DROP and CONSTELLATION heuristics, and the second method is a bounded enumeration-based technique. This lower-bounding scheme proceeds by finding an initial s-club S followed by a bounded search that enumerates s-clubs containing S. The idea behind this bounded search is to improve the initial solution in a reasonable amount of time. The best solution found by these two methods initializes the incumbent. Two methods are used to derive an upper bound for the B&B algorithm. The first one, proposed independently of [23], is based on obtaining the s-coloring number of graph associated with every node in the B&B tree. To obtain this upper bound a combination of greedy heuristic and DSATUR heuristic, proposed in [18], is used. The second method computes the maximum s-clique to serve as an upper bound for the s-club number of a given graph G. To obtain this upper bound, the algorithm proposed by [51] is employed to find the maximum clique on sth power graph G ^s. For branching, a vertex dichotomy is used, where a vertex is selected and fixed to be included or deleted from the solution. To traverse the search tree, best bound search (BBS) strategy has been considered. Authors report extensive computational results, for s=2,3, using four different combinations of lower-bounding and upper-bounding techniques on a set of randomly generated instances of order n=50, 100, 150 and 200 with seven different densities ranging from 0.0125 up to 0.25. They report on the effectiveness of the bounding techniques used in the B&B algorithm and their relation with the topological structure of the randomly generated instances. The general B&B framework for solving the maximum s-club problem outlined in [44] can be easily adapted to include alternative lower- and upper-bounding schemes. One such enhancement has been proposed in [63], where the B&B framework was used in conjunction with the VNS heuristic mentioned above.

Veremyev and Boginski [65] solved the maximum s-club problem for s=2,…,7, using the compact formulation (32)–(38) on a set of randomly generated instances of order n=100,200,300 with different edge densities. For every combination, 10 instances are generated and the average maximum s-club size, average CPU time and the average tightness for each group of problem instances have been reported. The advantage of the compact formulation is that it contains a reasonable number of entities that grows linearly as s increases, thus providing an opportunity to solve the problem for higher values of s. Computational results show that the compact formulation is rather tight and the relative gap between the exact and the LP relaxation objective values decreases for larger values of s. The results of experiments with IP-based approaches for s=2,3 have also been reported in [4, 22].

Hartung et al. [36] used their theoretical findings concerning parameterized algorithms for 2-clubs based on the dual parameter d=|V|−k to develop a B&B strategy in conjunction with a kernelization proposed in [59]. The results of experiments with the proposed algorithm for the maximum 2-club problem that they report are very encouraging. In particular, their implementation significantly outperforms other known exact approaches on small to medium-size random graphs and large-scale real-life networks from the tenth DIMACS implementation challenge [30].

7 Applications and Extensions

The introduction of the concepts of s-clique and s-club was originally motivated by applications in social networks analysis, where these distance-based clique relaxations are used to model cohesive subgroups [3, 49]. A social network can be formalized by a simple undirected graph G=(V,E). The vertex set V can represent people, or actors, in a social network and the mutual relationships between pairs of actors can be naturally modeled using edges. For example, in a collaboration network the edges could represent collaborations between researchers. For mathematicians and computational geometers [11, 35], such collaboration networks are used to determine the collaborative distance between researchers which was first popularized by the concept of Erdös numbers [34].

Studying cohesive or “tightly knit” subgroups, which describe groups of actors that tend to share certain features of interest [60, 66], finds applications in different branches of sociology, including epidemiology of sexually transmitted diseases [55], organizational management [27], and crime detection/prevention and terrorist network analysis [12, 56, 57] among many others. For example, in [46], s-cliques and s-clubs are used to analyze 9/11 terrorist network.

Even though the distance-based clique relaxation structures may not be characterized by a very high overall degree of interaction between their members that is typical for some other models, the low distances between all group members make them appropriate models of cohesive subgroups in situations where easy reachability is most crucial. This is the case, in particular, when one deals with various types of flows in the network, such as flows of information, spread of diseases, or transportation of commodities. It is therefore not surprising that s-cliques and s-clubs appear naturally in many real-life complex systems, including biological and social systems, as well as telecommunication, transportation, and energy infrastructure systems.

In social networks, the proliferation of low-diameter structures manifests itself in catch-phrases “small world phenomenon” and “six degrees of separation” that made their way to the mainstream popular culture. A low diameter is a key characteristic of many other massive-scale complex networks that tend to have power-law degree distribution, or the so-called scale-free property [50]. Such networks typically have a small number of high-degree nodes, which are most likely to be “central vertices” in the largest s-clubs. In biology, it has been observed that groups of proteins where interactions occur via a central protein often represent similar biological processes [8]. This phenomenon makes computing 2-clubs, especially those that induce star graphs, particularly interesting [10, 52].

In transportation, hub-and-spoke model is the most popular network architecture used by major airlines [2, 38]. One of the main advantages of this model is that it is optimal in the sense that it ensures a 2-hop reachability while using the minimum possible total number of direct connections. Under this model, most of the flights are routed through several hub airports. This provides passengers a convenient access (via hubs) to numerous destinations that would not be able to support many direct connections, as well as allows to facilitate a wide variety of services, thus attracting more customers.

Another application is in computer and communication networks security [26]. A bot is a malicious program carrying out tasks for other programs or users and a botnet is a network of bots. Botnets are usually controlled by members of organized crime groups, called botmasters, for many different purposes. Almost all computers can host malicious programs that belong to a particular botnet and only a few of them might be immune to becoming a host. Distribution of spam and Distributed Denial-of-Service Attacks (DDoS) are among the malicious tasks performed by botnets. Naturally, the botmaster would like to maximize the effect of attack, damage, to the network and is therefore interested in selecting the densest subnetwork to initiate the attack. Identifying the densest subnetwork would help the botmaster to pick the minimum number of nodes to attack. This strategy leads to the greatest possible damage to the network and, at the same time, minimizes the chance of detection and regulation. Therefore to protect the network and minimize the damage and, at the same time, reduce the cost of taking defensive steps, it is essential to locate cohesive subgraphs and nodes through which such malicious programs can propagate all over the network very quickly.

In internet research, 2-clubs have been used for clustering web sites to facilitate text mining in hyper-linked documents [47], as well as search and retrieval of topically related information [64]. In wireless networks, small-diameter dominating sets, or the so-called dominating s-clubs offer an attractive alternative to usual connected dominating sets as a tool to model virtual backbones used for routing [19, 40]. Since wireless networks are often modeled using geometric graphs known as unit disk and unit ball graphs, studying the distance-based relaxations restricted to such graphs is of special interest. It is well known that a maximum clique in unit disk graphs can be found in polynomial time [9, 25]. However, the complexity of maximum 2-clique and 2-club problems restricted to unit disk graphs remains open. A 0.5-approximation algorithm for the maximum 2-clique problem in unit-disk graphs that is based on geometric arguments is given in [53].

8 Concluding Remarks

Applications in large-scale social, telecommunication, biological, and transportation networks, where easy accessibility between the system’s entities is of utmost importance, stimulated a significant activity in studying distance-based clique relaxation models, s-clique and s-club. This chapter presented an up-to-date survey of the literature of these models and the corresponding optimization problems. Due to its stronger cohesiveness properties and non-hereditary nature, which results in interesting research challenges, the maximum s-club problem has attracted much more attention. The lack of results for the maximum s-clique problem can also be explained by the fact that this problem is equivalent to the maximum clique problem in the corresponding power-s graph, and the maximum clique problem has been studied extensively in the last several decades. While solving the maximum s-clique problem by reducing it to the maximum clique problem is, perhaps, most natural and straightforward approach, it is not clear whether it is most effective. The power-s graph G ^s typically has a much higher edge density than the original graph G, and the maximum clique problem is known to be particularly difficult to solve on dense graphs in practice. Moreover, clique is W[1]-hard, and, given that s-club is fixed-parameter tractable for s>1, reducing s-clique to clique does not appear to be appealing from the parameterized complexity viewpoint. Therefore, investigating the maximum s-clique problem from alternative perspectives may be of interest.