Keywords

62.1 Introduction

Stochastic volatility (SV) models are workhorses for the modelling and prediction of time-varying volatility on financial markets and are essential tools in risk management, asset pricing, and asset allocation. In financial mathematics and financial economics, stochastic volatility is typically modelled in a continuous time setting which is advantageous for derivative pricing and portfolio optimization. Nevertheless, since data is typically only observable at discrete points in time, in empirical applications, discrete-time formulations of SV models are equally important.

Volatility plays an important role in determining the overall risk of a portfolio and identifying hedging strategies that make the portfolio neutral with respect to market moves. Moreover, volatility forecasting is also crucial in derivatives trading.

Recently, SV models allowing the mean level of volatility to “jump” have been used in the literature; see Chang et al. (2007), Chib et al. (2002), and Eraker et al. (2002). The volatility of financial markets is a subject of constant analysis movements in the price of financial assets which directly affects the wealth of individual, companies, charities, and other corporate bodies. Determining whether there are any patterns in the size and frequency of such movements, or in their cause and effect, is critical in devising strategies for investments at the micro level and monetary stability at the macro level. Shephard and Pitt (1997) used improved and efficient Markov Chain Monte Carlo (MCMC) methods to estimate the volatility process “in block” rather than one point of time such as highlighted by Jacquier et al. (1994), for a simple SV model. Furthermore, Hsu and Chiao (2011) analyze the time patterns of individual analyst’s relative accuracy ranking in earnings forecasts using a Markov chain model by treating two levels of stochastic persistence.

Least squares and maximum likelihood techniques have long been used in parameter estimation problems.

However, those techniques provide only point estimates with unknown or approximate uncertainty information. Bayesian inference coupled with the Gibbs sampler is an approach to parameter estimation that exploits modern computing technology. The estimation results are complete with exact uncertainty information. Section 62.2 presents the Bayesian approach and the MCMC algorithms. The SV model is introduced in Sect. 62.3, whereas empirical illustrations are given in Sect. 62.4.

62.2 The Bayesian Approach and the MCMC Algorithm

The Bayesian approach is a classical methodology where we assume that there is a set of unknown parameters. Alternatively, in the Bayesian approach the parameters are considered as random variables with given prior distributions. We then use observations (the likelihood) to update these distributions and obtain the posterior distributions.

Formally, let X = (X1, … , X T ) denote the observed data and θ a parameter vector:

$$ P\left(\frac{\theta }{X}\right)\propto P\left(\frac{X}{\theta}\right)\ast P\left(\theta \right) $$

The posterior distribution P(θ/X) of a parameter θ/ given the observed data X, where P(X/θ) denotes the likelihood distribution of X and P(θ) denotes the prior distribution of θ.

It would seem that in order to be as subjective as possible and to use the observations as much as possible, one should use priors that are non-informative. However, this can sometimes create degeneracy issues and one should choose a different prior for this reason. Markov Chain Monte Carlo (MCMC) includes the Gibbs sampler as well as the Metropolis-Hastings (M-H) algorithm.

62.2.1 The Metropolis-Hastings

The Metropolis-Hastings is the baseline for MCMC schemes that simulate a Markov chain θ (t) with P(θ/Y) as the stationary distribution of a parameter θ given a stock price index X. For example, we can define θ 1, θ 2, and θ 3 such that θ = (θ 1, θ 2, θ 3) where each θ 1 can be scalar, vectors, or matrices. MCMC algorithms are iterative, and so at iteration t we will sample in turn from the three conditional distributions. Firstly, we update θ 1 by drawing a value θ 1 (t) from p(θ 1/Y, θ (t−1)2 , θ (t−1)3 ). Secondly, we draw a value for θ 2 (t) from p(θ 2/Y, θ (t)1 , θ (t−1)3 ), and finally, we draw θ 3 (t) from p(θ 3/Y, θ (t)1 , θ (t)2 ).

We start the algorithm by selecting initial values, θ i (0), for the three parameters. Then sampling from the three conditional distributions in turn will produce a set of Markov chains whose equilibrium distributions can be shown to be the joint posterior distributions that we require.

Following Hastings (1970), a generic step from a M-H algorithm to update parameter θ i at iteration t is as follows:

  1. 1.

    Sample θ * i from the proposal distribution p t (θ i /θ (t−1) i ).

  2. 2.

    Calculate f = p t (θ (t−1) i /θ * i )/p t (θ * i /θ (t−1) i ) which is known as the Hastings ratio and which equals 1 for symmetric proposals as used in pure Metropolis sampling.

  3. 3.

    Calculate s t = fp(θ * i /Y, ϕ i )/p(θ (t−1) i /Y, ϕ i ), where ϕ i is the acceptance ratio and gives the probability of accepting the proposed value.

  4. 4.

    Let θ (t) i = θ * i with probability min(1, s t ); otherwise let θ (t) i = θ (t − 1) i .

A popular and more efficient method is the acceptance-rejection (A-R) M-H sampling method which is available. Whenever the target densities are bounded by a density from which it is easy to sample.

62.2.2 The Gibbs Sampler

The Gibbs sampler (Casella and Edward 1992; Gelfand and Smith 1990; Gilks et al. 1992) is the special M-H algorithm whereby the proposal density for updating θ j equals the full conditional p(θ * j /θ j ) so that proposals are acceptance with probability 1.

The Gibbs sampler involves parameter-by-parameter or block-by-block updating, which when completed from the transaction from θ (t) to θ (t+1):

  1. 1.

    θ (t+1)1 ≈ f 1(θ 1/θ t2 , θ (t)3 , … θ (t) D )

  2. 2.

    θ (t+1)2 ≈ f 2(θ 2/θ t+11 , θ (t)3 , … θ (t) D )

    .

    .

    .

    .

D. θ (t+1) D ≈ f D (θ D /θ t+11 , θ (t+1)2 , … θ (t+1) D − 1 )

Repeated sampling from M-H samplers such as the Gibbs samplers generates an autocorrelated sequence of numbers that, subject to regularity condition (ergodicity, etc.), eventually “forgets” the starting values θ 0= (θ 1 (0), θ 2 (0), ……, θ D (0)) used to initialize the chain and converges to a stationary sampling distribution p(θ/y).

In practice, Gibbs and M-H algorithms are often combined, which results in a “hybrid” MCMC procedure.

62.3 The Stochastic Volatility Model

62.3.1 Autoregressive SV Model with Student’s Distribution

In this paper, we will consider the pth order ARSV-t model, ARSV(p)-t, as follows:

$$ \left\{\begin{array}{l}{Y}_t=\sigma \xi exp\left({V}_t/2\right)\\ {}{V}_t={\phi}_1{V}_{t-1}+....+{\phi}_p{V}_{t-p}+{\eta}_{t-1}\end{array}\right. $$
$$ {\xi}_t=\frac{\varepsilon_t}{\sqrt{\kappa_t/\left(\nu -2\right)}} $$
$$ {\kappa}_t\approx {\chi}^2\left(\nu \right) $$

where κ t is independent of (ɛ t , η t ), Y t is the stock return for market indexes, and V t is the log-volatility which is assumed to follow a stationarity AR(p) process with a persistent parameter ∣ϕ∣ ≺ 1. By this specification, the conditional distribution, ξ t , follows the standardized t-distribution with mean zero and variance one. Since κ t is independent of (ɛ t , η t ), the correlation coefficient between ξ t and η t is also ρ.

If ϕ ≈ N(0, 1), then

$$ {\phi}_1=\frac{\left({\displaystyle \sum_{t=1}^T{V}_t{V}_{t-1}}\right)-{\phi}_2\left({\displaystyle \sum_{t=1}^T{V}_{t-1}{V}_{t-2}}\right)+\overline{\phi_1}}{\left({\displaystyle \sum_{t=1}^t{V}_{t-1}^2}\right)-1} $$

and

$$ {\phi}_2=\frac{\left({\displaystyle \sum_{t=2}^T{V}_t{V}_{t-2}}\right)-{\phi}_1\left({\displaystyle \sum_{t=2}^T{V}_{t-1}{V}_{t-2}}\right)+\overline{\phi_2}}{\left({\displaystyle \sum_{t=2}^T{V}_{t-2}^2}\right)-1} $$

The conditional posterior distribution of the volatility is given by

$$ \begin{array}{l}p\left(V/\Theta, Y\right)\propto {e}^{\left(\frac{1}{2*{\sigma}^2}\left({\displaystyle \sum_{t=1}^T{Y}_t^2{e}^{-{V}_t}}\right)\kern-0.7em -\frac{1}{2}\displaystyle \sum_{t=1}^T{\left({V}_t-{\phi}_1{V}_{t-1}-{\phi}_2{V}_{t-2}\right)}^2 \right.}\\ \left. \quad -\frac{1}{2}{\displaystyle \sum_{t=1}^T{\left({V}_{t+1}-{\phi}_1{V}_t-{\phi}_2{V}_{t-2}\right)}^2}\right)\end{array} $$

The representation of the SV-t model in terms of a scale mixture is particularity useful in a MCMC context since it allows for sampling a non-log-concave sampling problem into a log-concave one. This allows for sampling algorithms which guarantee convergence in finite time (see Frieze et al. 1994). Allowing log returns to be student-t-distributed naturally changes the behavior of the stochastic volatility process; in the standard SV model, large value of ∣Y t ∣ induces large value of the V t .

62.3.2 Basic Svol Model

Jacquier, Polson, and Rossi (1994), hereafter JPR, introduced Markov chain technique (MCMC) for the estimation of the basic Svol model with normally distributed conditional errors:

$$ \left\{\begin{array}{l}{Y}_t=\sqrt{V_t}{\varepsilon}_t^s\\ {} \log \left({V}_t\right)=\alpha +\delta log\left({V}_{t-1}\right)+{\sigma}_{\nu }{\varepsilon}_t^{\nu}\end{array}\right. $$
$$ \left({\varepsilon}_t^s,{\varepsilon}_t^{\nu}\right)\approx N\left(0,{I}_2\right) $$

Let Θ = (α, δ, σ v ) be the vector of parameters of the basic SVOL, and \( V={\left({V}_t\right)}_{t=1}^T \), where α is the intercept. The parameter vector consists of a location α, a volatility persistence δ, and a volatility of volatility σ ν .

The basic Svol specifies zero correlation, the errors of the mean, and variance equations.

Briefly, the Hammersley-Clifford theorem states that having a parameter-set Θ, a state V t , and an observation Y t , we can obtain the joint distribution p(Θ, V/Y) from p(Θ, V/Y) and p(V/Θ, Y), under some mild regularity conditions. Therefore by applying the theorem iteratively, we can break a complicated multidimensional estimation problem into many sample one-dimensional problems.

Creating a Markov chain Θ(t) via a Monte Carlo process, the ergodic averaging theorem states that the time average of a parameter will converge towards its posterior mean.

The formula of Bayes factorizes the posterior distribution likelihood function with prior hypotheses:

$$ P\left(\Theta, V/Y\right)\alpha P\left(Y/V,\Theta \right)P\left(V/\Theta \right)P\left(\Theta \right) $$

where α is the intercept, δ the volatility persistence, and σ v is the standard deviation of the shock to log V t .

We use a normal-gamma prior, so, the parameters α, δ ≈ N, and σ v 2 ≈ IG, (Appendix 1)

Then

$$ P\left(\alpha, \delta /{\sigma}_v,V,Y\right)\approx {\displaystyle \prod P\left({V}_t/{V}_{t-1},\alpha, \delta, {\sigma}_v\right)}P\left(\alpha, \delta \right)\alpha N $$

And for σ v , we obtain

$$ P\left({\sigma}^2/\alpha, {\sigma}_v,V,Y\right)\alpha {\displaystyle \prod P\left({V}_t/{V}_{t-1},\alpha, \delta, {\sigma}_v\right)}P\left({\sigma}_v^2\right)\alpha IG $$

62.4 Empirical Illustration

62.4.1 The Data

Our empirical analysis focuses on the study of five international financial indexes: the Dow Jones Industrial, the Nikkei, the CAC 40, the S&P500, and the Nasdaq. The indexes are compiled and provided by Morgan Stanley Capital International. The returns are defined as y t = 100 * (log S t − log S t−1). We used the last 2,252 observations for all indexes except the Nikkei, when we have only used 2,201 observations due to lack of data. The daily stock market indexes are for five different countries over the period 1 January 2000 to 31 December 2008.

Table 62.1 reports the mean, standard deviation, median, and the empirical skewness as well as kurtosis of the five series. All series reveal negative skewness and overkurtosis which is a common finding of financial returns.

Table 62.1 Summary statistics for daily returns
Full size table

62.4.2 Estimation of SV Models

The standard SV model is estimated by running the Gibbs and A-R M-H algorithm based on 15,000 MCMC iterations, where 5,000 iterations are used as burn-in period.

Tables 62.2 and 62.3 show the estimation results in the basic Svol model and the SV-t model of the daily indexes. α and δ are independent priors.

Table 62.2 Estimation results for the Svol model
Full size table
Table 62.3 Estimation results for the SV-t model
Full size table

The prior in δ is essentially flat over [0, 1]. We impose stationarity for log(V t ) by truncating the prior of δ. Other priors for δ are possible.

Geweke (1994a, b) proposes alternative priors to allow the formulation of odds ratios for non-stationarity. Whereas Kim et al. (1998) center an informative Beta prior around 0.9.

Table 62.2 shows the results for the daily indexes. The posterior of δ are higher for the daily series. The highest means are 0.782, 0.067, 0.611, 0.85, and 0.722, for the full sample Nikkei.

This result is not a priori curious because the model of Jacquier et al. (1994) can lead to biased volatility forecast.

Well, as the basic SVOL, there is no apparent evidence of unit of volatility. There are other factors that can deflect this rate such exchange rate (O’Brien and Dolde 2000).

Deduced from this model, against the empirical evidence, positive and negative shocks have the same effect in volatility.

Table 62.3 shows the Metropolis-Hastings estimates of the autoregressive SV model.

The estimates of ϕ are between 0.554 and 0.643, while those of σ are between 0.15 and 0.205.

Against, the posterior of ϕ for the SV-t model are located higher.Footnote 1 This is consistent with temporal aggregation (as suggested by Meddahi and Renault 2000). This result confirms the typical persistence reported in the GARCH literature. After the result, the first volatility factors have higher persistence, while the small values of Φ2 indicate the low persistence of the second volatility factors.

The second factor Φ2 plays an important role in the sense that it captures extreme values, which may produce the leverage effect, and then it can be considered conceivable.

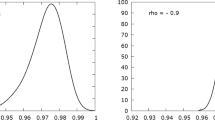
The estimates of ρ are negative in most cases. Another thing to note is that these estimates are relatively higher than that observed by Asai et al. (2006) and Manabu Asai (2008). The estimated of ρ for index S&P using Monte Carlo simulation is −0.3117, then it is −0.0235 using Metropolis-Hasting. This implies that for each data set, the innovations in the mean and volatility are negatively correlated.

Negative correlations between mean and variance errors can produce a “leverage” effect in which negative (positive) shocks to the mean are associated with increases (decreases) in volatility.

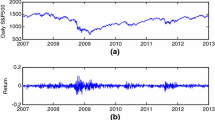
The return of different indexes not only is affected by market structure (Sharma 2011) but also is deeply influenced by different crises observed in international market, i.e., the Asian crises detected in 1987 and the Russian one in 2002. The markets in our sample are subject to several crises that directly affect the evolution of the return indexes. The event of 11 September 2002 the Russian crisis and especially the beginning of the subprime crisis in the United States in July 2007 justify our results. These results explored in Fig. 62.1 suggest that periods of market crisis or stress increase the volatility. Then the volatility at time (t) depends on the volatility at (t−1) (Engle 1982).

Fig. 62.1
figure 1

Return for indexes

Full size image

When the new information comes in the market, it can be disrupted and this affects the anticipation of shareholders for the evolution of the return.

The resulting plots of the smoothed volatilities are shown in Fig. 62.2. We take our analysis in the Nikkei indexes, but the others are reported in Appendix 2.

Fig. 62.2
figure 2

Smoothed estimates of Vt, basic SVOL, and SV-t model

Full size image

The convergence is very remarkable for the Nikkei, like Dow Jones, Nasdaq, and the CAC 40 indexes. This enhances the idea that the algorithm used for estimated volatility is a good choice.

The basic Svol model mis-specified can induce substantial parameter bias and error in inference about V t ; Geweke (1994a, b) showed that the basic Svol has the same problem with the largest outlier, October 1987 “Asiatique crisis.” The V t for the model Svol reveal a big outlier on period crises.

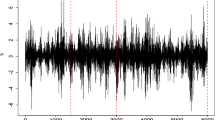
The corresponding plots of innovation are given by Fig. 62.3 for two models basic Svol and SV-t for Nikkei indexes. Appendix 3 shows the QQ plot for the other indexes, respectively, for the Nasdaq, S&P, Dow Jones, and CAC 40 for the two models. The standardized innovation reveals a big outlier when the market in stress (Hwang and Salmon 2004).

Fig. 62.3
figure 3

QQ plot of normalized innovation based on the basic Svol model (left) and the SV-t model (right)

Full size image

The advantages of asymmetric basic SV is able to capture some aspects of financial market and the main properties of their volatility behavior (Danielsson 1994; Chaos 1991; Eraker et al. 2000).

It is shown that the inclusion of student-t errors improves the distributional properties of the model only slightly. Actually, we observe that basic Svol model is not able to capture extreme observation in the tail of the distribution. In contrast, the SV-t model turns out to be more appropriate to accommodate outliers. The corresponding plot of innovation for the basic model is unable to capture the distribution properties of the returns. This is confirmed by the Jarque-Bera normality test and the QQ plot revealing departures from normality, mainly stemming from extreme innovation.

Finally, in order to detect which of the two models is better, we opt for two indicators of performance, such as the likelihood and the MSE. Likelihood is a function of the parameters of the statistical model that plays a preponderant role in statistical inference. MSE is called squared error loss, and it measures the average of the square of “error.” Table 62.4 reveals the results for this measure and indicates that the SV-t model is much more efficient than the other. Indeed, in terms of comparison, we are interested in the convergence of two models. We find that convergence to the SV-t model is fast.

Table 62.4 MSE and likelihood for two models
Full size table

Table 62.4 shows the performance of the algorithm and the consequence of using the wrong model on the estimates of volatility. The efficiency is at 60 %.

The MCMC is more efficient for all parameters used in these two models. In a certain threshold, all parameters are stable and converge to a certain level. Appendices 4 and 5 show that the α, δ, σ, ϕ converge and stabilize; this shows the power for MCMC.

The results for both simulated show that the algorithm of SV-t model is fast and converges rapidly with acceptable levels of numerical efficiency. Then, our sampling provides strong evidence of convergence of the chain.

62.5 Conclusion

We have applied these MCMC methods to the study of various indexes. The ARSV-t models were compared with Svol models of Jacquier et al. (1994) models using the S&P, Dow Jones, Nasdaq, Nikkei, and CAC 40.

The empirical results show that SV-t model can describe extreme values to a certain extent, but it is more appropriate to accommodate outliers. Surprisingly, we have frequently observed that the best model is the Student’s t-distribution (ARSV-t) with their forecast performance. Our result confirms the finding from Manabu Asai (2008), who indicates, first, that the ARSV-t model provides a better fit than the MFSV model and, second, the positive and negative shocks do not have the same effect in volatility. Our result proves the efficiency of Markov chain for our sample and the convergence and stability for all parameters to a certain level. This paper has made certain contributions, but several extensions are still possible. To find the best results, opt for extensions of SVOL.