Gauss–type quadrature

Abstract

Walter Gautschi’s work in this area has had a profound impact, especially on the computational and practical aspects of Gauss quadrature. I have heard people refer to it as Gautschian quadrature, just to emphasize Walter’s many contributions to the theory and computation.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Walter Gautschi’s work in this area has had a profound impact, especially on the computational and practical aspects of Gauss quadrature. I have heard people refer to it as Gautschian quadrature, just to emphasize Walter’s many contributions to the theory and computation.

To fix notation, suppose one wants to approximate the integral of a function f by a sum using only n evaluations of the function:

$$\displaystyle{ \int _{a}^{b}f(x)\,d\mu (x) =\sum _{ k=1}^{n}\lambda _{ k,n}f(x_{k,n}) + E_{n}(f). }$$

(15.1)

Here the general case is considered where integration is with respect to a positive measure μ on the real line, supported on the finite or infinite interval [a, b], but quite often only a weight function w on [a, b] is used. If {x _k, n : 1 ≤ k ≤ n} are the zeros of the nth-degree orthogonal polynomial p _n for the measure μ, i.e.,

$$\displaystyle{ \int\nolimits_{a}^{b} p_{n}(x){x}^{k} \; d \mu (x) = 0, \qquad 0 \leq k \leq n - 1,} $$

one can find weights $\{\lambda_{k,n} : 1 \leq k \leq n \}$ such that E _n (f) = 0 for every polynomial f of degree at most 2n − 1, and hence the quadrature gives the exact value of the integral for polynomials of degree less than or equal to 2n − 1. These weights are known as Christoffel weights or Christoffel numbers, and the quadrature formula is known as the Gauss quadrature formula or, as Walter Gautschi usually calls it, the Gauss–Christoffel quadrature formula. In his book [GAB3, §1.4.2] Gautschi uses the term Gauss-type quadrature to refer to this class of quadrature formulas, including those modified by Radau and Lobatto (cf. Section 15.2). Carl Friedrich Gauss originally (1816 [5]) considered the case where μ is the uniform measure on [ − 1, 1], for which the corresponding quadrature nodes are the zeros of the Legendre polynomial P _n ; Elwin Bruno Christoffel [2] in 1877 extended this to more general weight functions. Szegő calls it Gauss–Jacobi mechanical quadrature in his book [10, §3.4], whereas Stroud and Secrest [9] refer to it as Gaussian quadrature formulas in their book (which contains many tables).

1 Construction of Gauss quadrature formulas

For the construction of Gauss quadrature formulas one basically needs to compute the n zeros $x_{1,n} < \cdots < x_{n,n}$ of the orthogonal polynomial p _n and the Christoffel numbers $\{\lambda_{j,n} : 1 \leq j \leq n \}$. The measure μ is given and one needs the first 2n moments $(\mu_{k})_{0 \leq k \leq 2n-1}$ of μ to find the zeros and the Christoffel numbers:

$$\displaystyle{ \mu_{k} = \int_{a}^{b}{x}^{k}\,d\mu (x) = \sum _{j=1}^{n}{(x_{j,n})}^{k} \lambda_{ j,n},\qquad 0 \leq k \leq 2n - 1. }$$

Gautschi shows in [GA31] that the map $(\mu_{k})0\leq k\leq 2n-1 \:\mapsto\: (x_{j,n}, \lambda_{j,n}) 1\leq j \leq n$ is ill conditioned and gives some lower bounds for the condition number κ _n showing that for a large class of weights on [ − 1, 1] this κ _n grows exponentially like $(17 + 6 \sqrt{8})^{n} = (1 + \sqrt{2})^{4n}$ and he concludes that

“The lesson to be learned from this analysis is evident: the moments are not suitable, as data, for constructing Gauss–Christoffel quadrature formulas of large order n. Apart from the fact that they are not always easy to compute, small changes in the moments (due to rounding, for example) may result in very large changes in the Christoffel numbers.”

He proposes an alternative procedure in which the inner product involving the measure μ (or weight w) is replaced by a discrete inner product

$$\displaystyle{\langle f,g\rangle _{N} =\sum _{ k=1}^{N}w_{ k,N}f(y_{k,N})g(y_{k,N}),\qquad w_{k,N} > 0,}$$

in such a way that

$$\displaystyle{\lim _{N\rightarrow \infty }\langle f,g\rangle _{N} =\int _{ a}^{b}f(x)g(x)\,d\mu (x)}$$

for all polynomials f and g. In his later work he refers to this as the discretized Stieltjes procedure [GA81, §2.2], [GA117, §4.2]; it has since become known as the discretized Stieltjes–Gautschi procedure (cf. Section 11.2.2). The orthogonal polynomials (π _n, N ) _{n ∈ ℕ} for this discrete inner product then have the property that

$$\displaystyle{\lim _{N\rightarrow \infty }\pi _{n,N}(x) = p_{n}(x),}$$

and the corresponding zeros and Christoffel numbers converge to the required quantities for the Gauss quadrature,

$$\displaystyle{\lim _{N\rightarrow \infty }x_{j,n}^{(N)} = x_{ j,n},\quad \lim _{N\rightarrow \infty }\lambda _{j,n}^{(N)} =\lambda _{ j,n}.}$$

In order to be practical, one needs to find a suitable discrete inner product $\langle \cdot\,, \cdot \rangle_{N\cdot}$ Gautschi suggests using the Fejér quadrature formula (introduced by Fejér in 1933 [4] and studied by Gautschi in 1967 [GA30]) or the Gauss–Chebyshev quadrature formula to do the discretization. The convergence can be accelerated by Newton’s method.

Another procedure was proposed by Sack and Donovan in 1969 and quickly picked up by Gautschi in [GA40]. Instead of starting from the moments

$$\displaystyle{\mu _{k} =\int _{ a}^{b}{x}^{k}\,d\mu (x),}$$

it uses modified moments

$$\displaystyle{\nu _{k} =\int _{ a}^{b}q_{ k}(x)\,d\mu (x),}$$

where the (q _n ) _{n ∈ ℕ} are given orthogonal polynomials for a measure ν on [α, β], 

$$\displaystyle{\int _{\alpha }^{\beta }q_{k}(x)q_{n}(x)\,d\nu (x) =\delta _{k,n},}$$

and hence satisfy a three-term recurrence relation

$$\displaystyle{xq_{k}(x) =\alpha _{k+1}q_{k+1}(x) +\beta _{k}q_{k}(x) +\alpha _{k}q_{k-1}(x).}$$

If one chooses the measure ν close to the measure μ (in particular with the same support [a, b] = [α, β]), the mapping from the modified moments to the zeros and Christoffel numbers is often well conditioned. In [GA40] Gautschi gives an upper bound for the condition number and various asymptotic estimates for Jacobi weights. He also gives an algorithm for generating orthogonal polynomials (p _n ) _{n ∈ ℕ} for the measure μ, starting from the modified moments. Numerical examples (and tables of Gaussian quadrature on an accompanying microfiche supplement) show that this is indeed a very convenient way to construct Gauss quadrature formulas.

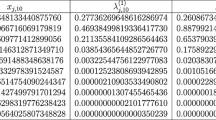
A very convincing way to show people that the mapping from moments to zeros and Christoffel numbers is ill conditioned is given in [GA84] where Gautschi displays a table for the nodes $\{ x_{j,n} : 1 \leq j \leq n\}$ and Christoffel numbers $\{ \lambda_{j,n} : 1 \leq j \leq n\}$ for n = 15 and weight $w(x) = e^{-x^{3}/3}$ on [0, ∞), which appeared in the Journal of Chemical Physics in 1980. Table 1 shows 16 decimals but only the first two are correct. Gautschi also gives Table 2 with his own computation using a discretized Stieltjes procedure and a suitable partition of the infinite interval [0, ∞) into eight subintervals. Instead of saying that the first table is wrong, Gautschi describes four tests which can be used to check the accuracy of the table and leaves it to the reader to decide that the second table is accurate to 16 decimals. He also explains why Table 1 was thought to be accurate: it passes two of the tests. The first test is to check the quadrature formula on the moments, i.e., on the functions f(x) = x ^k with 0 ≤ k ≤ 2n − 1, and indeed both tables show that the quadrature formula produces the moments accurately to about 15 correct decimals. But this is an extreme case of correlation of errors. Test 2 suggested by Gautschi is to compute the coefficients in the recurrence relation

$$\displaystyle{xp_{k}(x) = a_{k+1}p_{k+1}(x) + b_{k}p_{k}(x) + a_{k}p_{k-1}(x),\qquad k \geq0,}$$

of the orthogonal polynomials using the quadrature formula, and then to check whether

$$\displaystyle{\mu _{2n} =\sum _{ j=1}^{n}\lambda _{ j,n}x_{j,n}^{2n} + a_{ 1}^{2}a_{ 2}^{2}\cdots a_{ n}^{2},}$$

which follows from the formula for the error term E _n (x ²ⁿ) of the Gauss quadrature formula. This test too does not distinguish between the two tables. The two other tests show that Table 1 is not accurate but Table 2 is. Test 3 is to compute the recurrence coefficients using the quadrature formula and to check them with the explicit formulas in terms of Gram determinants (cf. Eq. (11.5) of Section 11.1). This test indeed shows that the accuracy of the recurrence coefficients decreases by one decimal in each step for Table 1, but remains stable for Table 2. Test 4 is to compute the sum of the nodes, which is the trace of the Jacobi matrix and which can be computed as the ratio of two determinants. This test also shows that Table 1 is only accurate to two decimals, whereas Table 2 gives 12 accurate decimals. I have computed the nodes and Christoffel numbers for this weight and n = 15 using Maple (which nowadays is a convenient way to perform multiprecision computations) and found that one needs to work with a precision of 45 decimals (Digits:=45) to produce Table 2 if one starts from the moments and uses the method with which Table 1 was generated. Gautschi’s approach requires only double precision and hence is to be preferred. A Matlab suite for generating orthogonal polynomials and related quadrature rules can be found on his website http://www.cs.purdue.edu/archives/2002/wxg/codes/ under the heading OPQ.

2 Gauss–Radau and Gauss–Lobatto quadrature

The Gauss quadrature formulas can be extended somewhat to include information of the function at the endpoints of the interval [a, b]. For Gauss–Radau quadrature one uses a fixed node at one of the endpoints a or b, and then n nodes in (a, b) are taken such that for every polynomial f of degree ≤ 2n

$$\displaystyle{\int _{a}^{b}f(x)w(x)\,dx =\lambda _{ a}f(a) +\sum _{ j=1}^{n}\lambda _{ j,n}f(x_{j,n}),}$$

which is the Gauss–Radau quadrature rule with fixed left endpoint, or

$$\displaystyle{\int _{a}^{b}f(x)w(x)\,dx =\lambda _{ b}f(b) +\sum _{ j=1}^{n}\lambda _{ j,n}f(x_{j,n}),}$$

which is the Gauss–Radau quadrature rule with fixed right endpoint. Even though these formulas use n + 1 quadrature points, the effect of fixing one quadrature point is to reduce the degree of the polynomials which can be correctly integrated by one. Recall that the Gauss quadrature rule with n + 1 points has degree of exactness 2n + 1, which is one higher than the Gauss–Radau rule. The n other nodes are all in the open interval (a, b) and turn out to be zeros of the orthogonal polynomial of degree n for the modified weight function (x − a)w(x) when one fixes the left endpoint a, or (b − x)w(x) when one fixes the right endpoint b. These orthogonal polynomials are known as kernel polynomials [1, §1.7] and can be expressed in terms of the Christoffel–Darboux formula.

For Gauss–Lobatto quadrature one uses both endpoints as fixed nodes and one looks for n nodes in (a, b) such that

$$\displaystyle{\int _{a}^{b}f(x)w(x)\,dx =\lambda _{ a}f(a) +\lambda _{b}f(b) +\sum _{ j=1}^{n}\lambda _{ j,n}f(x_{j,n})}$$

for every polynomial f of degree ≤ 2n + 1. There are n + 2 quadrature nodes, but two nodes are now fixed at a and b, resulting in the reduction of the polynomial degree of exactness by 2 (Gauss quadrature with n + 2 nodes has degree of exactness 2n + 3). The n remaining nodes turn out to be the zeros of the orthogonal polynomial of degree n for the modified weight (x − a)(b − x)w(x). These orthogonal polynomials can be expressed in terms of the orthogonal polynomials for the weight w by means of a formula of Christoffel [10, §2.5].

An e-mail from someone inquiring how to fix an underflow problem when computing high-order Gauss–Lobatto quadrature rules for the Legendre case w(x) = 1 on [ − 1, 1] prompted Walter Gautschi to investigate the more general case of Jacobi weights w(x) = (1 − x)^α(1 + x)^β on [ − 1, 1] in [GA163]. The Gauss–Lobatto formula then uses the quadrature nodes ± 1 and the zeros of the orthogonal polynomials for the weight (1 − x ²)w(x), which is again a Jacobi weight but now with parameters (α + 1, β + 1). Gautschi first notes that underflow can be avoided by computing the two modified elements of the Jacobi matrix directly as functions of α and β, rather than by solving the usual 2 ×2 system of linear equations (which for large n becomes singular, numerically). He then gives explicit formulas for the weights $\lambda_{1}$ and $\lambda_{1}$ and for the interior weights in terms of the Jacobi polynomials $P_{n}^{\alpha,\beta}$ evaluated at the interior nodes. He compares the results obtained by direct computation using his formulas with the results obtained by computing the modified Jacobi matrix and the first components of the eigenvectors. The conclusion is that the direct computation using the explicit formulas is more accurate in 90% of all the 8,400 cases he investigated.

Gauss–Radau quadrature for the Jacobi weight is investigated in [GA164] where again explicit formulas are found for the weight at the boundary and for the interior weights in terms of the Jacobi polynomials evaluated at the interior nodes. No numerical results are presented but the explicit formula for the boundary weight is said to be more accurate than the result computed using the eigenvector of the modified Jacobi matrix. For the interior weights, however, in about two-thirds of the cases computed, the results of the direct computation are found less accurate than the results obtained by using the eigenvectors of the modified Jacobi matrix. [GA164] also deals with the Gauss–Radau formula for the Laguerre measure w(x) = x ^α e ^− x on [0, ∞) and an explicit formula for the weight $\lambda_{0}$ is given, together with a formula for the interior weights in terms of the Laguerre polynomials evaluated at the interior nodes. Again no numerical results are presented but the conclusion is said to be much like in the case of the Jacobi weight, i.e., the boundary weight is always considerably more accurate by means of direct computation than via eigenvectors, whereas for the interior weights the result using the eigenvectors is generally more accurate than the explicit formula.

In [GA126] Walter Gautschi and Shikang Li extend the Gauss–Radau and Gauss–Lobatto idea by allowing the endpoints to appear with multiplicity 2. This amounts to using also the derivatives of f at the endpoints, i.e., for Gauss–Radau quadrature with fixed left endpoint

$$\displaystyle{\int _{a}^{b}f(x)w(x)\,dx =\lambda _{ 0}f(a) +\lambda _{1}f^{\prime}(a) +\sum _{ j=1}^{n}\lambda _{ j,n}f(x_{j,n}) + E_{n}^{R}(f).}$$

If one takes for the n nodes x _j, n the zeros of the orthogonal polynomial of degree n for the modified weight (x − a)² w(x), then E _n ^R(f) = 0 can be achieved for every polynomial of degree at most 2n + 1. Of course a similar formula can be constructed for the right endpoint. Gautschi and Li show that the weights in this quadrature formula are all positive and they give explicit formulas for the weights $\lambda_{0}$ and $\lambda_{1}$ when w is the Chebyshev weight function on [ − 1, 1] of any of the four kinds,

$$\displaystyle{w(x) = {(1 - x)}^{\pm 1/2}{(1 + x)}^{\pm 1/2}.}$$

They also handle the extension of Gauss–Lobatto quadrature, where

$$\displaystyle{\int _{a}^{b}f(x)w(x)\,dx =\lambda _{ 0}f(a) +\lambda _{1}f^{\prime}(a) +\sum _{ j=1}^{n}\lambda _{ j,n}f(x_{j,n}) +\mu _{0}f(b) -\mu _{1}f^{\prime}(b) + E_{n}^{L}(f).}$$

Note the negative sign before μ ₁ f ′(b). Choosing the n nodes x _j, n as the zeros of the orthogonal polynomial of degree n for the weight (x − a)²(b − x)² w(x) then results in E _n ^L(f) = 0 for every polynomial of degree at most 2n + 3. All the weights are again positive and the weights $\lambda_{0}$, $\lambda_{1}$, μ ₀, μ ₁ are explicitly given for the four Chebyshev weights. Their paper ends with various examples.

There is nothing really special about multiplicity two in Gauss–Radau or Gauss–Lobatto quadrature, so the natural next step is to consider having nodes of arbitrary multiplicity at one or both endpoints of the interval [a, b]. This is worked out in [GA173] in a general setting, and in [GA194] for Jacobi and Laguerre weight functions. The generalized Gauss–Radau formula has the form

$$\displaystyle{\int _{a}^{b}f(x)w(x)\,dx =\sum _{ k=0}^{r-1}\lambda _{ a}^{(k)}{f}^{(k)}(a) +\sum _{ j=1}^{n}\lambda _{ j,n}f(x_{j,n}) + E_{n,r}^{R}(f),}$$

where r > 1 is the multiplicity of the endpoint a. The degree of exactness is 2n − 1 + r, i.e., one has E _n, r ^R(f) = 0 for every polynomial of degree at most 2n − 1 + r, if one takes for the internal nodes $\{ x_{j,n} : 1 \leq j \leq n\}$ the zeros of the orthogonal polynomial of degree n for the weight function (x − a)^r w(x). For the generalized Gauss–Lobatto quadrature, similarly,

$$\displaystyle{\int _{a}^{b}f(x)w(x)\,dx =\sum _{ k=0}^{r-1}\lambda _{ a}^{(k)}{f}^{(k)}(a)+\sum _{ j=1}^{n}\lambda _{ j,n}f(x_{j,n})+\sum _{k=0}^{r-1}{(-1)}^{k}\lambda _{ b}^{(k)}{f}^{(k)}(b)+E_{ n,r}^{L}(f),}$$

where E _n, r ^L(f) = 0 for every polynomial f of degree at most 2n − 1 + 2r when the internal nodes are the zeros of the orthogonal polynomial of degree n for the weight (x − a)^r(b − x)^r w(x). Note the alternating sign for the weights at the endpoint b. This is useful in the case of a symmetric weight w( − x) = w(x) on a symmetric interval, where $\lambda_{a}^{k} = \lambda_{b}^{k}$ for $0 \leq k \leq r - 1$. For questions regarding the positivity of the weights, see Section 7.6.2, Vol. 1.

Gautschi developed in [GA173] a routine for computing these generalized Gauss–Radau and Gauss–Lobatto formulas for arbitrary r, and Matlab routines are downloadable from his website http://www.cs.purdue.edu/archives/2002/wxg/ codes/ under the heading HOGGRL.

3 Error bounds for Gauss quadrature

So far we witnessed Gautschi’s skills in constructing Gauss quadrature formulas. He also is a very skillful analyst able to find sharp bounds for the error E _n (f) in Gauss quadrature on [ − 1, 1] for functions f which are analytic in a domain D containing [ − 1, 1]. Together with Richard Varga he starts in [GA85] from the contour integral representation

$$\displaystyle{E_{n}(f) = \frac{1} {2\pi i}\int _{\Gamma }K_{n}(z)f(z)\,dz,}$$

where the kernel is

$$\displaystyle{K_{n}(z) = \frac{1} {p_{n}(z)}\int _{-1}^{1}\frac{p_{n}(t)} {z - t}\,d\mu (t),}$$

and Γ is a contour in D surrounding [ − 1, 1]. A straightforward estimation gives

$$\displaystyle{\vert E_{n}(f)\vert \leq \frac{\ell(\Gamma )} {2\pi } \max _{z\in \Gamma }\vert K_{n}(z)\vert \max _{z\in \Gamma }\vert f(z)\vert,}$$

where ℓ(Γ) is the length of the contour Γ. The first maximum depends only on μ and the second maximum only on the function f, thus separating the dependence of the error on the quadrature rule and on the function to be integrated. If Γ is the circle { | z |  = r} with r > 1, then Gautschi and Varga show that for a large class of measures μ the maximum of $|K_{n}(Z)|$ is attained on the real line and is either K _n (r) or | K _n ( − r) | , and they show that it can be evaluated accurately and efficiently by recursion. This class of measures includes the Jacobi weights d μ(x) = (1 − x)^α(1 + x)^β  d x for arbitrary α, β >  − 1. They also investigate elliptic contours $\Gamma = \{z = \frac{1}{2} (re^{i\theta} + \frac{1}{r} e^{-i\theta}), 0 \leq \theta \leq 2 \pi \}$ for which they show that in the case of Chebyshev weights $\alpha = \beta = \pm \frac{1}{2}$ and $\alpha = -\frac{1}{2},\; \beta = \frac{1}{2}$ the maximum of $|K_{n}(Z)|$ is attained on the real positive axis, hence equal to K _n ((r + 1 ∕ r) ∕ 2), except for the Chebyshev weight of the second kind $(\alpha = \beta = \frac{1}{2})$ for which the maximum is located on the imaginary axis when n is odd, and near the imaginary axis when n is even. The problem is much more complicated for general Jacobi weights; in this case some empirical results are worked out.

The problem for the elliptic contour and Chebyshev weights is taken up again in [GA119] with Tychopoulos and Varga, and a more detailed analysis is made for the Chebyshev weight $\alpha = \beta = \frac{1}{2}$ and n even. They show that for r ≥ r _n + 1, where r _n + 1 > 1 is the root of an explicitly stated algebraic equation, the maximum of $|K_{n}(Z)|$ occurs on the imaginary axis while for r < r _n + 1 it is near the imaginary axis within an angular distance less than π ∕ (2n + 2). Furthermore, the sequence (r _n ) _n ≥ 2 decreases monotonically to 1.

A similar error bound analysis is done in [GA123] and [GA121] for Gauss–Radau quadrature and Gauss–Lobatto quadrature where the endpoints have multiplicity one and two, respectively, and integration is with respect to any of the Chebyshev weight functions. The original analysis can be carried over fairly well since most of the ingredients still involve orthogonal polynomials, albeit with a modified weight function. Furthermore, if one starts with a Chebyshev weight function, then the modified weights are still Jacobi weights and the corresponding orthogonal polynomials are linear combinations of Chebyshev polynomials.

4 Gauss quadrature for rational functions

The quadrature formulas so far are designed to integrate functions that are close to polynomials. If one deals with functions having poles (outside the interval of integration) or other singularities, then the best thing to do is to absorb that information in the weight function, or, which amounts to the same thing, to construct quadrature formulas that exactly integrate rational functions with prescribed location of the poles. This kind of rational quadrature is something I was interested in myself through the thesis of one of the PhD students in my department; see [12], where we studied the case of poles of multiplicity one or two. The following characterization appears in [GA137] and [GA167]:

Theorem 1.

Let {ζ _k : 1 ≤ k ≤ M} be complex numbers such that − 1∕ζ _k ∉[a,b] and define

$$\displaystyle{\omega _{m}(x) =\prod _{ k=1}^{M}{(1 +\zeta _{ k}x)}^{s_{k} },\qquad m =\sum _{ k=1}^{M}s_{ k},}$$

where s _k ∈ ℕ. Assume that the weight w(x)∕ω _m (x) admits the n-point Gaussian quadrature formula

$$\displaystyle{\int _{a}^{b}f(x)\frac{w(x)} {\omega _{m}(x)}\,dx =\sum _{ j=1}^{n}w_{ j,n}^{G}f(x_{ j,n}) + E_{n}^{G}(f),}$$

with E _n ^G (f) = 0 for every polynomial f of degree at most 2n − 1. Then

$$\displaystyle{ \int _{a}^{b}g(x)w(x)\,dx =\sum _{ j=1}^{n}\lambda _{ j,n}g(x_{j,n}) + E_{n}(g),\qquad \lambda _{j,n} = w_{j,n}^{G}\omega _{ m}(x_{j,n}), }$$

(15.2)

has the property that

$$ E_{n}(g) = 0\quad \text{if}\quad X\left\{ \begin{array}{@{}l@{\quad }l@{}} g(x) = {(1 +\zeta _{k}x)}^{-s},\quad &k = 1,2,\ldots\;,M,\ s = 1,2,\ldots\,,s_{k}, \\ g(x) = {x}^{k}, \quad &k = 0,1,2,\ldots\,,2n - m - 1. \end{array} \right.\; $$

Hence one can construct n-point quadrature formulas for rational functions by using the n-point Gaussian quadrature formula for the weight w(x) ∕ ω _m (x) which has prescribed poles outside [a, b] with given multiplicities. Furthermore, Gautschi describes in [GA137] and [GA167] a way to compute the quadrature formula (15.2), either by a partial fraction decomposition and modification algorithms, or by the discretization method, which we described earlier. A number of examples illustrate the efficiency of the quadrature rule. Some other types of rational quadrature rules are also given in [GA167] such as the rational Fejér quadrature rule, rational Gauss–Kronrod quadrature, rational Gauss–Turán quadrature, and rational Cauchy principal value quadrature. The latter three are described in more detail in [GA162], where many numerical examples are given.

5 Gauss quadrature for special weights

The methods for constructing orthogonal polynomials, their recursion coefficients and the corresponding Gaussian quadrature, which were proposed by Gautschi, have been applied to a number of interesting explicit cases. In [GA93] Walter Gautschi and Gradimir Milovanović worked out the details for the weights

$$\displaystyle{\epsilon _{r}(x) = \frac{{x}^{r}} {{({e}^{x} - 1)}^{r}},\quad \varphi _{r}(x) = \frac{1} {{({e}^{x} + 1)}^{r}},\qquad x \in[0,\infty ),}$$

for r = 1 and r = 2. The weight ε ₁ is known as the Einstein function and φ ₁ as the Fermi function. Integrals involving the functions ε _r occur in phonon statistics, lattice specific heats, and in the study of radiative recombination processes. Integrals involving the functions φ _r are encountered in the dynamics of electrons in metals and heavy doped semiconductors. For the weights ε _r (r = 1, 2) they propose to compute the recursion coefficients of the orthogonal polynomials by means of a discretized Stieltjes–Gautschi procedure based on the Gauss–Laguerre quadrature rule, which uses the zeros of the Laguerre polynomial L _n as quadrature nodes. This indeed makes a lot of sense since ε ₁(x) ∼ x e ^− x and ε ₂(x ∕ 2) ∼ x ² e ^− x as x → ∞, so that these weights behave near infinity as the weight w(x) = e ^− x for Laguerre polynomials, up to polynomial growth. A different procedure is suggested for the weights φ _r because the poles ± i π of these weights are closer to the real axis. Instead a composite Fejér quadrature rule is proposed where the interval [0, ∞) is decomposed into four subintervals [0, 10] ∪[10, 100] ∪[100, 500] ∪[500, ∞]. These methods are illustrated by a number of numerical results. Tables of the recursion coefficients are included in the appendix of [GA93] and the quadrature nodes and quadrature weights are included in a supplement to [GA93]. A particularly interesting application is the summation of certain series $\sum\nolimits_{n=1}^{\infty}(\pm1)^{n}a_{n}$ where a _n is expressible as a Laplace transform or the derivative of a Laplace transform. Indeed, if

$$\displaystyle{a_{n} =\int _{ 0}^{\infty }f(t){e}^{-nt}\,dt,}$$

then

$$\displaystyle{\sum _{n=1}^{\infty }{(-1)}^{n-1}a_{ n} =\int _{ 0}^{\infty } \frac{f(t)} {{e}^{t} + 1}\,dt =\int _{ 0}^{\infty }f(t)\varphi _{ 1}(t)\,dt,}$$

and when

$$\displaystyle{ a_{n} =\int _{ 0}^{\infty }tf(t){e}^{-nt}\,dt = -\left. \frac{d} {dx}\int _{0}^{\infty }f(t){e}^{-xt}\,dt\right \vert _{ x=n}, }$$

then

$$\displaystyle{ \sum _{n=1}^{\infty }a_{ n} =\int _{ 0}^{\infty }f(t) \frac{t} {{e}^{t} - 1}\,dt =\int _{ 0}^{\infty }f(t)\epsilon _{ 1}(t)\,dt.}$$

Several examples of infinite series of this type are worked out, showing the efficiency of Gauss quadrature for evaluating slowly converging infinite series. Particularly useful is the advice they give for each example and ways to circumvent problems that occur.

In [GA154] Gautschi and Milovanović join forces again, but now their interest is in constructing Gauss–Turán quadrature rules, which are of the form

$$\displaystyle{\int _{-1}^{1}f(x)\,dx =\sum _{ i=0}^{k-1}\sum _{ j=1}^{n}A_{ i,j}{f}^{(i)}(x_{ j,n}) + E_{n,k}(f),}$$

using the derivatives f ⁽ⁱ⁾ for 0 ≤ i ≤ k − 1 at the quadrature nodes. Turán showed that for k = 3 the nodes can be chosen in such a way that the formula is exact for polynomials f of degree at most 4n − 1. In general one can choose the nodes $\{ x_{j,n} : 1 \leq j \leq n\}$ in such a way that E _n, k (f) = 0 for polynomials of degree ≤ (k + 1)n − 1 whenever k = 2s + 1 is odd, but this does not work when k is even. The nodes are zeros of the monic polynomial π _n that minimizes the L ^k + 1 norm

$$\displaystyle{\int _{-1}^{1}{[\pi _{ n}(x)]}^{k+1}\,dx.}$$

This can be extended to positive measures d μ on the real line and Gauss–Turán quadrature is possible for k = 2s + 1 odd, with nodes being the zeros of the monic polynomial π _n minimizing the L ^k + 1(μ) norm. This minimization is equivalent to the conditions

$$\displaystyle{\int _{}\mathbb{R}{[\pi _{n}(x)]}^{2s+1}{x}^{r}\,d\mu (x) = 0,\qquad r = 0,1,\ldots\;,n - 1,}$$

and the corresponding polynomials π _n are known as s-orthogonal polynomials. Gautschi and Milovanović observe that these s-orthogonal polynomials are the polynomials π _n, n from a sequence of orthogonal polynomials (π _k, n ) _k ≤ n for the varying weight [π _n (x)]^2s  d μ(x):

$$\displaystyle{\int _{}\mathbb{R}{[\pi _{n}(x)]}^{2s}\pi _{ k,n}(x){x}^{j}\,d\mu (x) = 0,\qquad j = 0,1,\ldots\;,k - 1.}$$

Note, however, that the s-orthogonal polynomials π _n are implicitly defined in this way, since the varying measure involves the polynomial π _n . Gautschi and Milovanović propose a method for computing the recurrence coefficients of the orthogonal polynomials starting from an initial guess for the unknown polynomial π _n and then applying an iterative procedure (Newton-Kantorovič method) to compute the recursion coefficients of the orthogonal polynomials (π _k, n )_{0 ≤ k ≤ n} , which in the end gives the required π _n  = π _n, n . The elements in the Jacobian, which one needs for the Newton method, are integrals which can all be computed exactly by using Gaussian quadrature for the (nonvarying) measure μ taking (s + 1)n quadrature nodes. The procedure is illustrated with numerical examples. For the Chebyshev measure of the first kind on [ − 1, 1], the monic polynomials minimizing

$$\displaystyle{\int _{-1}^{1}\frac{\vert \pi _{n}(x){\vert }^{k+1}} {\sqrt{1 - {x}^{2}}} \,dx,\qquad k \geq0,}$$

are the monic Chebyshev polynomials of the first kind T _n (x) ∕ 2^n − 1, hence the nodes for the Gauss–Turán formula are cos(2j − 1)π ∕ 2n (1 ≤ j ≤ n).

In his most recent paper [GA211], Gautschi returns to Gauss–Turán quadrature, suggesting an improvement of the procedure described above in the case of Laguerre and Hermite weight functions.

Another example where Gautschi’s construction of Gauss quadrature rules works well is Gauss quadrature for refinable weight functions, which appear in multiresolution analysis and wavalet analysis in particular. In [GA161] Gautschi worked with Laura Gori and Francesca Pitolli on Gaussian quadrature for a weight ϕ satisfying

$$\displaystyle{\phi (x) =\sum _{j\in \mathbb{Z}}a_{j}\phi (2x - j),}$$

where

$$ a_{j} = {2}^{-h}\left [\binom{m + 1}{j} + 4({2}^{h-m} - 1)\binom{m - 1}{j - 1}\right ],\qquad h \geq m \geq2. $$

The function ϕ is only computable at dyadic points

$$\displaystyle{x_{k} = -\frac{m + 1} {2} + k \cdot{2}^{-r},\qquad k = 0,1,2,\ldots\;,(m + 1){2}^{r},}$$

hence these points are used for the discrete inner product needed for the discretization method. The inner product is taken as Simpson’s quadrature. Numerical results and examples illustrate the proposed procedure.

The more recent paper [GA198] deals with weight functions with logarithmic factors, such as v(x) = x ^α e ^− x(x − 1 − logx) on [0, ∞) and w(x) = (1 − x)^α(1 + x)^β log(2 ∕ (1 + x)) on [ − 1, 1], which are logarithmic modification of the Laguerre weight and the Jacobi weight, respectively. The procedure is to use a (symbolic) modified Chebyshev algorithm based on ordinary as well as modified moments executed with sufficiently high precision. The natural choice for modified moments for the weight v is to use Laguerre polynomials,

$$\displaystyle{\nu _{k} =\int _{ 0}^{\infty }{x}^{\alpha }{e}^{-x}(x - 1 -\log x)L_{ k}^{\alpha }(x)\,dx,}$$

and for w it is natural to make the change of variable x = 2t − 1 and use the shifted Jacobi polynomials,

$$\displaystyle{\nu _{k} =\int _{ 0}^{1}{t}^{\beta }{(1 - t)}^{\alpha }\log (1/t)P_{ k}^{(\alpha\;,\beta )}(2t - 1)\,dt.}$$

These modified moments can be expressed explicitly in terms of special functions and evaluated to arbitrary precision. As usual, a number of examples illustrate the numerical results.

6 The circle theorem for Gauss-type quadrature

If one plots the n Gaussian weights (suitably normalized) against the n Gaussian nodes, one finds that, asymptotically as n → ∞, they come to lie on a half circle when the weight is supported on a finite interval and satisfies a mild condition. This is known as the circle theorem and was first established by Davis and Rabinowitz [3] in 1961 for Jacobi weights w(x) = (1 − x)^α(1 + x)^β on [ − 1, 1].

Theorem 2.

Let w be a weight function on [−1,1] in the Szegő class, i.e.,

$$\displaystyle{\int _{-1}^{1}\log w(x) \frac{dx} {\sqrt{1 - {x}^{2}}} > -\infty }$$

and suppose that 1∕w ∈ L ₁($\Delta$) for a compact interval $\Delta$ $\subset$ (−1,1). Then

$$\displaystyle{ \frac{n\lambda _{j,n}} {w(x_{j,n})} \sim \pi \sqrt{1 - x_{j,n }^{2}},\qquad n \rightarrow \infty,}$$

for all nodes x _j,n (and corresponding weights $\lambda_{j,n}$ ) that lie in $\Delta$.

This theorem is useful if one wants to check whether the quadrature weights that one computed for a certain weight w are indeed reliable: if they don’t follow the circle theorem, then one cannot trust the computed results. The circle theorem basically follows as a corollary of the asymptotic behavior of Christoffel functions

$$\displaystyle{\lambda _{n}(x) = \frac{1} {\sum _{k=0}^{n-1}p_{k}^{2}(x)}}$$

of a weight w, where (p _n ) _{n ∈ ℕ} are the orthonormal polynomials for w. Indeed, Nevai proved that

$$\displaystyle{ \lim _{n\rightarrow \infty }n\lambda _{n}(x) =\pi w(x)\sqrt{1 - {x}^{2}} }$$

(15.3)

holds almost everywhere in $\Delta$ under the conditions given in the theorem. The relation $\lambda_{j,n} = \lambda_{n}(x_{j,n})$ then gives the circle theorem. See [8, §4.5] for a discussion on asymptotics for the Christoffel functions, which shows that the idea of the circle theorem predates Davis and Rabinowitz [3]. The asymptotic behavior in (15.3) for weights w on [ − 1, 1] holds almost everywhere on an open interval $\Delta$  $\subset$ [ − 1, 1] under the weaker condition [7, Thm. 8]

$$\displaystyle{\int _{\Delta }\log w(x)\,dx > -\infty\;.}$$

Gautschi extends this circle theorem in [GA180] to Gauss–Radau and Gauss–Lobatto quadrature for weights w satisfying the conditions in Theorem 2. He also considers Gauss–Kronrod quadrature

$$\displaystyle{\int _{-1}^{1}f(x)w(x)\,dx =\sum _{ j=1}^{n}\lambda _{ j,n}f(x_{j,n}) +\sum _{ k=1}^{n+1}\lambda _{ k,n}^{{\ast}}f(x_{ k,n}^{{\ast}}) + E_{ n}(f),}$$

where $\{ x_{j,n} : 1 \leq j \leq n\}$ are the Gaussian nodes and the Kronrod nodes {x _k, n ^∗ : 1 ≤ k ≤ n + 1} and the weights $\{ \lambda_{j,n} : 1 \leq j \leq n \}$ and $\{ \lambda_{k,n}^{\ast} : 1 \leq k \leq n + 1 \}$ are such that E _n (f) = 0 whenever f is a polynomial of degree at least 3n − 1. (For Gauss–Kronrod quadrature, see also Section 14.1.) The Kronrod nodes are the zeros of the polynomial π _n + 1 which is the orthogonal polynomial of degree n + 1 for the (nonpositive) weight p _n (x)w(x), with p _n the orthogonal polynomial of degree n for the weight w:

$$\displaystyle{\int _{-1}^{1}\pi _{ n+1}(x){x}^{k}p_{ n}(x)w(x)\,dx = 0,\qquad k = 0,1,2,\ldots\;,n.}$$

The Kronrod nodes are not necessarily in the interval [ − 1, 1] and may in fact be complex, but when all the Kronrod nodes are real, distinct, in the interval ( − 1, 1), and different from the Gauss nodes, there is indeed a chance for a circle theorem to hold. Gautschi proves such a circle theorem for Gauss–Kronrod quadrature for a restricted class of weights.

The function $\pi \sqrt{1-x ^{2}}$ in the circle theorem and in }(15.3) is in fact the reciprocal of the density of the equilibrium measure for the interval [ − 1, 1] (the Chebyshev weight of the first kind). If one considers weights on a compact set E of the real line, then a variant of the circle theorem would be

$$\displaystyle{ \frac{n\lambda _{j,n}} {w(x_{j,n})} \sim\frac{1} {w_{E}(x_{j,n})}\,,}$$

where w _E is the density of the equilibrium measure of the compact set E. This holds, for instance, almost everywhere on $\Delta$  $\subset$  E when E is a regular set and [11, Thm. 1]

$$\displaystyle{\int _{\Delta }\log w(x)\,dx > -\infty\;.}$$

Gautschi illustrates this when the weight w is supported on two disjoint intervals and remarks that the equilibrium measure is explicitly known for a set E = T ^− 1([ − 1, 1]), where T is a polynomial, referring to my joint work [6] with Jeff Geronimo in 1988.

Before concluding this presentation, this may be a good place to reaffirm that Walter Gautschi has written quite a few nice and interesting papers on Gauss-type quadrature, which are very influential and even essential when one plans to make numerical computations. Furthermore, he is very well aware of the existing literature, has a good taste in the choice of specific problems and examples, and his papers are a pleasure to read. Some of the codes are available on his website http://www.cs.purdue.edu/archives/2002/wxg/codes/ showing that he is willing to share his knowledge and results with the international community.