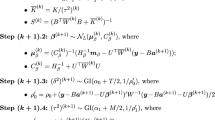Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

3.1 Introduction

Longitudinal research has an important role in various fields of science, for example in medicine, economics, social sciences, and engineering. The aim is to analyze the change caused, e.g., by growth, degradation, maturation, and ageing when individuals are followed over time or according to some other ordered sequence of measurements. In this paper the focus is on complete and balanced data. One of the most important statistical models for these data is the growth curve model of Potthoff and Roy (1964). The early development of this model was mainly based on the unstructured MANOVA assumption of the covariance matrix of independent random vectors (e.g., Khatri 1966 and Grizzle and Allen 1969). Later, however, more attention has been paid to modeling the covariance matrix by using parsimonious covariance structures (see, e.g., Azzalini 1987, Lee  1988 and Nummi 1997). For excellent reviews of the growth curve model we refer to the books by Kshirsagar and Smith (1995) and Pan and Fang (2002).

Our approach is to use cubic smoothing splines to model the mean growth curve. As is very well known cubic smoothing splines are very flexible curves with interesting mathematical properties (see, e.g., Green and Silverman 1994). For an up-to-date summary of recent methods of smoothing splines and nonparametric regression we refer to Wu and Zhang (2006). Approximate inference with smoothing splines have been studied, e.g., in Eubank and Spiegelman (1990), Schimek (2000), and Cantoni and Hastie (2002). In their simulation study Liu and Wang (2004) compared six testing statistics. Nummi et al. (2011) provided a test of a regression model against spline alternative for correlated data. The main focus in these studies have been on testing the order of the polynomial model against a spline alternative. However, testing if two or more splines are equal would be very important in many applications. Nummi and Koskela (2008) introduced some results for the estimation and rough testing of growth curves when the analysis is based on spline functions. However, very little research about testing equality of smoothing splines, especially for correlated data, has been carried out so far. In this paper we focus on testing if the progression in time is equal over the set of correlated observations.

In Sect. 3.2 we introduce the basic growth model and its estimation using cubic smoothing splines. In Sect. 3.3 a spline approximation is introduced and a test for mean curves is developed. In Sect. 3.4 a computational example of Glucose data is presented and the method is also investigated by simulation experiments.

3.2 Basic Spline Growth Model and Some Properties

One of the most important statistical models for balanced complete multivariate repeated measures data is the GMANOVA (Generalized Multivariate Analysis of Variance Model) of Potthoff and Roy (1964). The model is often also refered to as the growth curve model. This model can be written as

$$\displaystyle{ \mathbf{Y} = \mathbf{T}\mathbf{B}\mathbf{A}^{\prime} + \mathbf{E}, }$$
(3.1)

where \(\mathbf{Y} = (\mathbf{y}_{1},\mathbf{y}_{2},\ldots,\mathbf{y}_{n})\) is the matrix of independent response vectors, T is a q ×p within-individual design matrix, A is an n ×m between-individual design matrix, B is an unknown p ×m parameter matrix to be estimated, and E is a q ×n matrix of random errors. It is assumed that the columns \(\mathbf{e}_{1},\ldots,\mathbf{e}_{n}\) of E are independently normally distributed as \(\mathbf{e}_{i} \sim N(\mathbf{0},\boldsymbol{\Sigma }),\ i = 1,\ldots,n.\) In the original model formulation \(\boldsymbol{\Sigma }\) was assumed to be an unstructured covariance matrix and the analyses were mainly based on the methods developed for linear models and multivariate analysis.

Often when analyzing growth data the true growth function is more or less unknown and there may not be any theoretical justification for any specific parametric form of the curve. Parametric models are then used for descriptive purposes rather than interpretative to summarize the information of development profile. A natural first choice in such situations is a low order polynomial curve. However, in many cases these models may fail to reveal important features of the growth process and more complicated models are therefore also needed.

Our approach is to use the cubic smoothing splines to model the mean growth curve. As is very well known cubic smoothing splines are very flexible curves with interesting mathematical properties (see, e.g., Green and Silverman 1994). We can write the model (3.1) in a slightly more general form as (see also Nummi and Koskela 2008)

$$\displaystyle{ \mathbf{Y} = \mathbf{G}\mathbf{A}^{\prime} + \mathbf{E}, }$$
(3.2)

where \(\mathbf{G} = (\mathbf{g}_{1},\ldots,\mathbf{g}_{m})\) is the matrix of smooth mean growth curves in time points \(t_{1},t_{2},\ldots,t_{q}\). We assume that the covariance matrix \(\boldsymbol{\Sigma }\) takes certain type of parsimonious structure \(\boldsymbol{\Sigma } {=\sigma }^{2}\mathbf{R}(\theta )\) with covariance parameters \(\theta\). In sequel we refer to this model as the spline growth model (SGM). The growth curve model of Potthoff and Roy (1964) is now the special case G = T B. The smooth solution for G can be obtained by minimizing the penalized least squares (PLS) criterion

$$\displaystyle{ Q = \mbox{ tr}[(\mathbf{Y} -\dot{\mathbf{G}})^{\prime}\mathbf{H}(\mathbf{Y} -\dot{\mathbf{G}}) +\alpha \dot{ \mathbf{G}}^{\prime}\mathbf{K}\dot{\mathbf{G}}], }$$
(3.3)

where we denote \(\dot{\mathbf{G}} = \mathbf{G}\mathbf{A}^{\prime}\), \(\mathbf{H} ={ \mathbf{R}}^{-1}\), and K is the so-called roughness matrix arising from the common roughness penalty R P = ∫ g ′ 2 and α is a fixed smoothing parameter. For cubic smoothing splines the roughness matrix is

$$\displaystyle{ \mathbf{K} = \nabla {\boldsymbol{\Delta }}^{-1}\nabla ^{\prime}, }$$
(3.4)

where the nonzero elements of banded q ×(q − 2) and \((q - 2) \times (q - 2)\) matrices ∇ and \(\boldsymbol{\Delta }\), respectively, are

$$\displaystyle{ \nabla _{k,k} = \frac{1} {h_{k}},\ \nabla _{k+1,k} = -\left ( \frac{1} {h_{k}} + \frac{1} {h_{k+1}}\right ),\ \nabla _{k+2,k} = \frac{1} {h_{k+1}} }$$
(3.5)

and

$$\displaystyle{ \boldsymbol{\Delta }_{k,k+1} = \boldsymbol{\Delta }_{k+1,k} = \frac{h_{k+1}} {6},\ \boldsymbol{\Delta }_{k,k} = \frac{h_{k} + h_{k+1}} {3}, }$$
(3.6)

where \(h_{j} = x_{j+1} - x_{j},j = 1,2,\ldots,(q - 1)\), and \(k = 1,2,\ldots,(q - 2)\). It can be shown that Q can be rewritten in an alternative form

$$\displaystyle{ Q = \mbox{ tr}[\{\dot{\mathbf{G}} - {(\mathbf{H} +\alpha \mathbf{K})}^{-1}\mathbf{H}\mathbf{Y}\}^{\prime}(\mathbf{H} +\alpha \mathbf{K})\{\dot{\mathbf{G}} - {(\mathbf{H} +\alpha \mathbf{K})}^{-1}\mathbf{H}\mathbf{Y}\} + c], }$$
(3.7)

where c is a constant and (H + α K) is a positive definite matrix. The function Q is minimized for given α and H when \(\dot{\mathbf{G}} = {(\mathbf{H} +\alpha \mathbf{K})}^{-1}\mathbf{H}\mathbf{Y}.\) This gives the spline estimator

$$\displaystyle{ \tilde{\mathbf{G}} = {(\mathbf{H} +\alpha \mathbf{K})}^{-1}\mathbf{H}\mathbf{Y}\mathbf{A}{(\mathbf{A}^{\prime}\mathbf{A})}^{-1}. }$$
(3.8)

However, the covariance matrix H may not be known and therefore the estimator (3.8) maybe difficult to use in practical situations. Fortunately, it can be shown that in certain important special cases the general spline estimator (3.8) simplifies to simple linear functions of the original observations Y. One obvious condition for such kind of simplification is

$$\displaystyle{ \mathbf{K}\mathbf{R} = \mathbf{K} }$$
(3.9)

and since now K = K H the spline estimators \(\tilde{\mathbf{G}}\) can be simplified as

$$\displaystyle{ \hat{\mathbf{G}} = {(\mathbf{I} +\alpha \mathbf{K})}^{-1}\mathbf{Y}\mathbf{A}{(\mathbf{A}^{\prime}\mathbf{A})}^{-1} = \mathbf{S}\mathbf{Y}\mathbf{A}{(\mathbf{A}^{\prime}\mathbf{A})}^{-1}, }$$
(3.10)

where the smoother matrix is \(\mathbf{S} = {(\mathbf{I} +\alpha \mathbf{K})}^{-1}\). Covariance matrices satisfying the condition (3.9) have been studied in Nummi and Koskela (2008) and Nummi et al. (2011). Some important special cases of these structures useful for growth data are R = I, \(\mathbf{R} = \mathbf{I} +\sigma _{ d}^{2}\mathbf{1}\mathbf{1}^{\prime}\), \(\mathbf{R} = \mathbf{I} +\sigma _{ d^{\prime}}^{2}\mathbf{X}\mathbf{X}^{\prime}\)  and \(\mathbf{R} = \mathbf{I} + \mathbf{X}\mathbf{D}\mathbf{X}^{\prime}\), where X = (1, x) and x is a vector of q measuring times.

If we apply the result \(\mbox{ vec}(\mathbf{A}\mathbf{B}\mathbf{C}) = (\mathbf{C}^{\prime} \otimes \mathbf{A})\mbox{ vec}(\mathbf{B})\), where the vec operation rearranges the columns of a matrix underneath each other, we can write the basic model (3.2) in a vector form

$$\displaystyle{\mathbf{y} = (\mathbf{A} \otimes \mathbf{I}_{q})\mathbf{g},}$$

where y = vec(Y) and g = vec(G). If the spline estimates are written in vector form we have

$$\displaystyle{\hat{\mathbf{g}} = [{(\mathbf{A}\mathbf{A}^{\prime})}^{-1}\mathbf{A}^{\prime} \otimes \mathbf{S}]\mathbf{y}}$$

and the smoother of the whole data is

$$\displaystyle{ \hat{\mathbf{y}} = (\mathbf{P}_{a} \otimes \mathbf{S})\mathbf{y} = \mathbf{S}_{{\ast}}\mathbf{y}, }$$
(3.11)

where we denote \(\mathbf{P}_{a} = \mathbf{A}{(\mathbf{A}^{\prime}\mathbf{A})}^{-1}\mathbf{A}^{\prime}\) and \(\mathbf{S}_{{\ast}} = (\mathbf{P}_{a} \otimes \mathbf{S})\). The effective degrees of freedom of the smoother can now be given as

$$\displaystyle{ \mathit{edf }_{{\ast}} = \mbox{ tr}(\mathbf{S}_{{\ast}}) = \mbox{ tr}(\mathbf{P}_{a} \otimes \mathbf{S}) = \mbox{ tr}(\mathbf{P}_{a})\mbox{ tr}(\mathbf{S}) = m \times \mathit{edf }, }$$
(3.12)

where edf  = tr(S) is the effective degrees of freedom of the smoother S. It is further easy to see that the generalized cross-validation criteria for choosing the smoothing parameter α take the form

$$\displaystyle{ \mathit{GCV }(\alpha ) = \frac{ \frac{1} {\mathit{nq}}\sum _{i=i}^{\mathit{nq}}{[y_{ i} -\hat{ y}_{i}]}^{2}} {{(1 -\frac{m\times \mathit{edf }} {\mathit{nq}} )}^{2}}, }$$
(3.13)

where y i and \(\hat{y}_{i}\) are individual elements of the observed and smoothed vectors y and \(\hat{\mathbf{y}}\), respectively.

3.3 Testing of Mean Curves

It is very well known that exact tests may be difficult to develop when making statistical inference based on smoothing splines. Our interest in this study focuses on testing if the progression in time is the same in treatment groups considered. In this study an exact test based on spline approximations for testing growth curves is developed.

3.3.1 Spline Approximation

It has been demonstrated by Nummi et al. (2011) that the approximation discussed in this paper is quite good for relatively smooth data. More detailed consideration of spline approximations can be found, e.g., in Hastie (1996). In a general case the smoother matrix S is not a projection matrix and therefore certain results, e.g. in testing, developed for general linear models are not directly applicable. Our approach is to utilize an approximation for the smoother matrix S with the properties of a projection matrix. As discussed by Hastie (1996) the smoother matrix can be written as

$$\displaystyle{ \mathbf{S} = \mathbf{M}{(\mathbf{I} +\alpha \Lambda )}^{-1}\mathbf{M}^{\prime}, }$$
(3.14)

where M is the matrix of q orthogonal eigenvectors of K and \(\Lambda \) is a diagonal matrix of corresponding q eigenvalues. It is easily seen that K and S share the same set of eigenvectors \(\mathbf{m}_{1},\mathbf{m}_{2},\ldots,\mathbf{m}_{q}\) and the eigenvalues are connected such that the eigenvalues of S are \(\gamma = 1/(1+\alpha \lambda )\). In sequel we assume that eigenvectors \(\mathbf{m}_{1},\mathbf{m}_{2},\ldots,\mathbf{m}_{q}\) are ordered according to the eigenvalues of S. It is well known that the sequence of eigenvectors appears to increase in complexity like a sequence of orthogonal polynomials. The first two eigenvalues of S are always 1. We can set \(\mathbf{m}_{1} = \mathbf{1}/\sqrt{n}\) and \(\mathbf{m}_{2} = \mathbf{t}_{{\ast}},\) where \(\mathbf{t}_{{\ast}} = (\mathbf{t} -\bar{ t}\mathbf{1})/S_{t},\) \(\bar{t}\) is the mean and \(S_{t} = \sqrt{\sum _{i=1 }^{q }{(t_{i } -\bar{ t})}^{2}}\) is the square root of the sum of squares of the time points \(t_{1},\ldots,t_{q}\). Therefore the first two eigenvectors m 1 and m 2 span the subspace corresponding to the straight line model. In the mixed model formulation of the spline solution (e.g. Verbyla et al. 1999) this corresponds to the fixed part of the model. It is also easily observed that if the value of the smoothing parameter α increases the fit approaches the straight line model and the fitted line (fixed part) is not influenced by any specific choice of α.

Clearly, one obvious approximation of the spline fit (3.10) is the spline model

$$\displaystyle{ \bar{\mathbf{G}} = \mathbf{P}_{m}\mathbf{Y}\mathbf{A}{(\mathbf{A}^{\prime}\mathbf{A})}^{-1}, }$$
(3.15)

where \(\mathbf{P}_{m} = \mathbf{M}_{{\ast}}\mathbf{M}_{{\ast}}^{\prime}\) and M  ∗  contains the c( ≤ q) first eigenvectors of M. This corresponds to minimizing the least squares (LS) criteria

$$\displaystyle{ Q^{\prime} = \mbox{ tr}(\mathbf{Y} -\dot{\mathbf{G}})^{\prime}(\mathbf{Y} -\dot{\mathbf{G}}), }$$
(3.16)

where \(\dot{\mathbf{G}} = \mathbf{G}\mathbf{A}^{\prime}\). Note that the smoother matrix S and the smoothing parameter need not be computed here. However, the number of eigenvectors c from K used in the approximation needs to be estimated. This is easily done by, for example, using a modified generalized cross-validation criteria

$$\displaystyle{{ \mathit{GCV }}^{{\ast}}(c) = \frac{ \frac{1} {\mathit{nq}}\sum _{i=i}^{\mathit{nq}}{[y_{ i} -\bar{ y}_{i}]}^{2}} {{(1 -\frac{m\times c} {\mathit{nq}} )}^{2}}, }$$
(3.17)

where \(\bar{y}_{i}\) is now computed using the formula (3.11) with S replaced by P m .

3.3.2 Constructing a Test for Mean Spline Curves

First, consider the set of fitted spline curves

$$\displaystyle{ \hat{\mathbf{Y}} =\hat{ \mathbf{G}}\mathbf{A}^{\prime}. }$$
(3.18)

As discussed in the previous section we may use the approximation

$$\displaystyle{ \hat{\mathbf{Y}} =\bar{ \mathbf{G}}\mathbf{A}^{\prime} = \mathbf{M}_{{\ast}}\hat{\Omega }\mathbf{A}^{\prime}, }$$
(3.19)

where we denoted \(\hat{\Omega } = \mathbf{M}_{{\ast}}^{\prime}\mathbf{Y}\mathbf{A}{(\mathbf{A}^{\prime}\mathbf{A})}^{-1}\). All the relevant information for testing mean profiles is now in the matrix \(\hat{\Omega }\), which can now be considered to be an unbiased estimate of the unknown parameter matrix of the statistical model \(E(\mathbf{Y}) = \mathbf{M}_{{\ast}}\Omega \mathbf{A}^{\prime}\). Therefore in sequel we confine in testing linear hypothesis of the form

$$\displaystyle{H_{0}: \mathbf{C}\Omega \mathbf{D} = \mathbf{0},}$$

where C and D are known ν ×c and m ×g matrices with ranks ν and g, respectively. Since \(\mbox{ vec}(\mathbf{A}\mathbf{B}\mathbf{C}) = (\mathbf{C}^{\prime} \otimes \mathbf{A})\mbox{ vec}(\Omega )\), the vector form of H 0 is given by

$$\displaystyle{H_{0}: (\mathbf{D}^{\prime} \otimes \mathbf{D})\omega = \mathbf{0},}$$

where \(\omega = \mbox{ vec}(\Omega )\). If we take the vector form of \(\hat{\Omega }\), we get

$$\displaystyle{ \hat{\omega }= \mbox{ vec}(\hat{\Omega }) = [{(\mathbf{A}^{\prime}\mathbf{A})}^{-1}\mathbf{A}^{\prime} \otimes \mathbf{M}_{ {\ast}}^{\prime}]\mathbf{y}. }$$
(3.20)

It is now easily seen that the covariance matrix of \(\hat{\omega }\) is

$$\displaystyle{ \mathit{Var}(\hat{\omega }) {=\sigma }^{2}[{(\mathbf{A}^{\prime}\mathbf{A})}^{-1} \otimes \mathbf{M}_{ {\ast}}^{\prime}\mathbf{R}\mathbf{M}_{{\ast}}]. }$$
(3.21)

If we denote \(\mathit{Var}(\mathbf{D}^{\prime} \otimes \mathbf{C})\hat{\omega } = \mathbf{W}\), it is then obvious that under the null hypothesis

$$\displaystyle{{\mathbf{W}}^{-1/2}(\mathbf{D}^{\prime} \otimes \mathbf{C})\hat{\omega } \sim N_{\nu g}(\mathbf{0},\mathbf{I})}$$

and

$$\displaystyle{{\sigma }^{-2}Q_{ {\ast}} =\hat{\omega } ^{\prime}(\mathbf{D} \otimes \mathbf{C}^{\prime}){\mathbf{W}}^{-1}(\mathbf{D}^{\prime} \otimes \mathbf{C})\hat{\omega } \sim \chi _{\nu g}^{2}.}$$

By using the results \(\mbox{ tr}(\mathbf{A}\mathbf{Z}^{\prime}\mathbf{B}\mathbf{Z}\mathbf{C}) = (\mbox{ vec}\ \mathbf{Z})^{\prime}(\mathbf{C}\mathbf{A} \otimes \mathbf{B})\mbox{ vec}\ \mathbf{Z}\), it is further easy to see that Q  ∗  can be rewritten as

$$\displaystyle{ Q_{{\ast}} = \mbox{ tr}\{{[\mathbf{D}^{\prime}{(\mathbf{A}^{\prime}\mathbf{A})}^{-1}\mathbf{D}]}^{-1}[\mathbf{C}\hat{\Omega }\mathbf{D}]^{\prime}{[\mathbf{C}\mathbf{M}_{ {\ast}}^{\prime}\mathbf{R}\mathbf{M}_{{\ast}}\mathbf{C}^{\prime}]}^{-1}[\mathbf{C}\hat{\Omega }\mathbf{D}]. }$$
(3.22)

If σ 2 is estimated by

$$\displaystyle{{ \hat{\sigma }}^{2} = \frac{1} {n(q - c)}\mbox{ tr}\mathbf{Y}^{\prime}(\mathbf{I} -\mathbf{P}_{m})\mathbf{Y}, }$$
(3.23)

it can be shown that \(n(q - c) {\times \hat{\sigma }}^{2} \sim \chi _{n(q-c)}^{2}\) and since Q  ∗  and \({\hat{\sigma }}^{2}\) are independent testing can be based on the F-ratio. Then under the null hypothesis

$$\displaystyle{ F ={ \frac{Q_{{\ast}}/\nu g} {\hat{\sigma }}^{2}} \sim F[\nu g,n(q - c)]. }$$
(3.24)

Testing can then be based on the quantiles of the F-distribution. However, in practical situations the matrix R contains unknown parameters that need to be estimated and therefore the distribution of F in general case is only approximate. However, if we are only interested in progression in time we can drop the first eigenvector m 1 corresponding to the constant term in the approximation model (see Sect. 3.3.1). Therefore we can take C = [0, I], and if we assume the uniform covariance model \(\mathbf{R} = {d}^{2}\mathbf{1}\mathbf{1}^{\prime} + \mathbf{I}\), it can be shown that

$$\displaystyle{ \mathbf{C}\mathbf{M}_{{\ast}}^{\prime}\mathbf{R}\mathbf{M}_{{\ast}}\mathbf{C}^{\prime} = \mathbf{C}\{{d}^{2}\mathbf{e}_{ 1}\mathbf{e}_{1}^{\prime} + \mathbf{I}\}\mathbf{C}^{\prime} = \mathbf{I}, }$$
(3.25)

where \(\mathbf{e}_{1} = (1,0,\ldots,0)^{\prime}\). Therefore the term Q  ∗  simplifies to

$$\displaystyle{ Q_{{\ast}} = \mbox{ tr}[\mathbf{C}\hat{\Omega }\mathbf{D}]\{{[\mathbf{D}^{\prime}{(\mathbf{A}^{\prime}\mathbf{A})}^{-1}\mathbf{D}]}^{-1}[\mathbf{C}\hat{\Omega }\mathbf{D}]^{\prime}, }$$
(3.26)

which does not contain unknown parameters of the covariance matrix and therefore for this special case the distribution of the F-statistic is exact. This is an important result since the uniform covariance model is quite common and a good approximation in many situations. The F-test proposed here provides means to test if the progression in time is the same over treatment groups when the models are based on spline curves. Following the same kind of considerations it would be easy to develop an exact F-statistic to test if the progression around the fitted straight line (the so-called random part in mixed model formulation) is the same over treatment groups with the more general assumption of linear correlation structure \(\mathbf{R} = \mathbf{X}\mathbf{D}\mathbf{X}^{\prime} + \mathbf{I}\).

3.4 Computational Examples

3.4.1 Standard Glucose Tolerance Test

As the first computational example we consider the glucose data of Zerbe (1979). In these data glucose tolerance tests were administered to 13 control and 20 obese patients. Plasma inorganic phosphate measurements determined from blood samples drawn 0, 0.5, 1, 1.5, 2, 3, 4, and 5 h after standard oral glucose dose were taken. The curves plotted for the control and obese patients are plotted in Fig. 3.1. In Fig. 3.1, two features of the plotted curves are quite obvious. First, there is a considerable variation in patient’s individual levels. Secondly, the functional form of the dependency of plasma inorganic phosphate and time is quite complicated and possibly different for control and obese patients. In Zerbe (1979) a polynomial of degree of 4 was used to model this relationship.

Fig. 3.1
figure 1

Plasma inorganic phosphate measurements for control and obese patients

Full size image

To set up the spline growth model the between-individual design matrix A was first defined. For 13 control patients the rows of A are \((1,0),\ i = 1,\ldots,13\) and for 20 obese patients the rows of A are \((0,1),\ i = 14,\ldots,33\). The minimum value of G C V = 0. 4484152 is obtained at α = 0. 09410597. This gives the total effective degrees of freedom e d f  ∗  = 9. 310273. The fitted curves are plotted in Fig. 3.1. It can be observed that the fitted spline curves very nicely depict the mean performance of measurements in both groups.

To test if the progression in time is the same in both groups we first determined the dimension c needed in the spline approximation. Minimizing the modified generalized cross-validation criterion gives c = 5. To test the null hypothesis we took

$$\displaystyle{\mathbf{C} = [\mathbf{0},\mathbf{I}_{4}]\quad \mbox{ and}\quad \mathbf{D} = [1,-1]^{\prime}.}$$

Next we calculated the estimate \(\mathbf{C}\hat{\Omega }\mathbf{D}\). This yields

$$\displaystyle{\mathbf{C}\hat{\Omega }\mathbf{D} = (0.74897422,\ -0.03613939,\ 0.46201190,\ 0.54998030)^{\prime}}$$

and the residual variance estimate for this setup is \({\hat{\sigma }}^{2} = 0.09408348.\) For the covariance matrix R we assumed the uniform correlation model and therefore the exact version of the test statistics can be used. Then the value of Q  ∗  is given as

$$\displaystyle{Q_{{\ast}} = \mbox{ tr}[\mathbf{C}\hat{\Omega }\mathbf{D}]\{{[\mathbf{D}^{\prime}{(\mathbf{A}^{\prime}\mathbf{A})}^{-1}\mathbf{D}]}^{-1}[\mathbf{C}\hat{\Omega }\mathbf{D}]^{\prime} = 8.494923}$$

and the value of the test statistics is then

$$\displaystyle{F ={ \frac{Q_{{\ast}}/\nu g} {\hat{\sigma }}^{2}} = \frac{8.494923/4} {0.09408348} = 22.57283.}$$

If this is compared to the critical value F 0. 95(4, 99) = 2. 447, the null hypothesis of equal progression in mean plasma inorganic phosphate for control and obese patients is clearly rejected.

3.4.2 A Simulation Study

In order to demonstrate the advances of the methodology presented we conducted a simulation study. In this study two models were tested

$$\displaystyle{ y = 1 + 0.5 \times t+\epsilon, }$$
(3.27)
$$\displaystyle{ y = 1 + 0.5 \times t + a \times \cos (0.4\pi t)+\epsilon, }$$
(3.28)

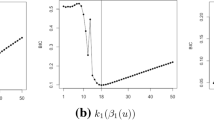
with \(t = 1,\ldots,10\) and independent random errors ε i  ∼ N(0, 1). The coefficient a takes the values 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, and 0.7. The first group of growth curves consists of 100 random vectors generated from model 3.27 and the second consists of 100 random vectors generated from model 3.28. So, for each value of a these two sets of growth curves were generated. The mean growth curves are then tested against the null hypothesis that the progression in time is the same in both groups. Two methods were utilized. The spline testing method presented in this paper and the second method utilized here was the basic parametric least squares fit of the third degree polynomial model. The power was estimated with the significance level 0.05 by counting the percentage of rejections in the 1,000 repetitions.

The results are shown in Fig. 3.2. Clearly, the spline test presented in this paper performed better than the test based on the least squares fit of the third degree polynomial. This is obviously due to the fact that the fit provided by the splines better depicts the peculiarities of the unknown growth function.

Fig. 3.2
figure 2

Proportion of the rejections in 1,000 repetitions under models (3.27) and (3.28)

Full size image

3.5 Concluding Remarks

Traditional analyses of growth curves are often based on simple parametric curves, which may not satisfactorily depict all the features of the growth process during the testing period. The method presented in this paper is based on cubic smoothing splines, which provides a very flexible modeling tool for the analysis. However, very little research on the statistical inference (especially testing) of cubic smoothing splines for correlated data has been carried out. The novel test presented in this paper seems to provide a good alternative, especially when more accurate modeling of growth process is required.