Keywords

1 Introduction

A variety of methods have been developed for extracting modal parameters from structures undergoing ambient vibration. Ibrahim [1] applied the random decrement technique coupled with a time-domain parameter identification method [2] to process ambient vibration data. James et al. [3] developed the so-called natural excitation technique using the correlation technique coupled with time-domain parameter extraction. In the previous studies of modal-parameter identification from ambient vibration data, the assumption usually made is that the input excitation is a broadband stochastic process modeled by stationary white or filtered white noise. In this chapter, it is shown that if the input signals can be modeled as nonstationary white noise, which is a product of white noise and a deterministic time-varying function, the practical problem of insufficient data samples available for evaluating nonstationary correlation can be approximately resolved by first extracting the amplitude-modulating function from the response and then transforming the nonstationary responses into stationary ones. The correlation functions and randomdec signatures of the stationary response are treated as free-vibration response, and so the Ibrahim time-domain method can then be applied to identify modal parameters of the system. Numerical simulations will be performed to demonstrate a comparison of correlation technique and random decrement algorithm for modal identification and to confirm the validity of the proposed method for identification of modal parameters from nonstationary ambient vibration data.

2 Correlation Technique

James et al. [3] developed the so-called natural excitation technique (NExT) using the correlation technique. It was shown that the cross-correlation between two response signals of a linear system with classical normal modes and subjected to white-noise inputs is of the same form as free-vibration decay or impulse response. In combination with a time-domain parameter extraction scheme, such as the ITD method, this concept becomes a powerful tool for the identification analysis of structures under stationary ambient vibration. When a system is excited by stationary white noise, the cross-correlation function \( {R_{ij }}(\tau ) \) between two stationary response signals \( {x_i}(t) \) and \( {x_j}(t) \) can be shown to be [3]

$$ {R_{ij }}(\tau )=\sum\limits_{r=1}^n {\frac{{{\phi_{ir }}{A_{jr }}}}{{{m_r}{\omega_{dr }}}}\exp (-{\zeta_r}{\omega_r}\tau )\;\sin\;({\omega_{dr }}\tau +{\theta_r})} $$
(1)

where \( {\phi_{ir }} \) denotes the ith component of the rth mode shape, \( {A_{jr }} \) a constant, and \( {m_r} \) the rth modal mass. The result above shows that \( {R_{ij }}(\tau ) \) in Eq. (1) is a sum of complex exponential functions (modal responses), which is of the same mathematical form as the free-vibration decay or the impulse response of the original system. Thus, the cross-correlation functions evaluated of responses data can be used as free-vibration decay or as impulse response in time-domain modal extraction schemes so that measurement of white-noise inputs can be avoided.

3 Random Decrement Algorithm

The random decrement technique is a method that has been studied extensively for signature analysis of vibrating systems. Vandiver et al. [4] and Bedewi [5] showed that when excitation force is zero-mean, stationary, Gaussian white noise, the random decrement signature \( {\delta_{ij }}(\tau ) \) of response, could be denoted as follows:

$$ {\delta_{ij }}(\tau )=\frac{{{R_{ij }}(\tau )}}{{{R_{ij }}(0)}}{x_s}, $$
(2)

where \( {R_{ij }}(0)={R_{ij }}(\tau =0) \). Note that \( {x_s} \) is the threshold level for the acquisition of sample time history and generally defined as the root-mean-square value of system’s stationary displacement response. Equation (2) signifies that the random decrement signature is in proportion to the cross-correlation function \( {R_{ij }}(\tau ) \). Since the correlation function has the same mathematical form as that of free-vibration response [3], the random decrement signature can also be treated as a free-vibration signal for modal-parameter identification.

4 Practical Treatment of Nonstationary Data

It has been shown in the previous studies [3–5] that by assuming the ambient excitation to be stationary white noise, the cross-correlation functions or randomdec signatures evaluated at a fixed time instant of responses can be used as free-vibration decay or as impulse response in time-domain modal extraction schemes. However, the practical problem for evaluating nonstationary randomdec signatures is that usually very limited data samples are available in engineering practice. The problem can be resolved by first extracting the modulating function from the response if the nonstationary excitation can be modeled approximately as the product model [6]. It has been shown in a previous paper of the authors [6] that the temporal root-mean-square functions of the response histories describe the same time variation as given by the envelope function. If the original nonstationary data could be represented by the product model with a slow varying envelope function, the temporal root-mean-square functions of the data also have the same nonstationary trends as that of the original data. The temporal root-mean-square function, and so the envelop function, can thus be determined by using the interval average and then applying curve fitting. This gives us the deterministic envelope function which describes the slow variation in the amplitude of the ambient excitations. The approximate stationary responses can thus be acquired by dividing the nonstationary responses of each DOF with the associated modulating functions obtained through curve fitting. Then the randomdec signatures of the stationary response data can be obtained, which are in turn treated as the free decay responses corresponding to each DOF. The modal parameters of a system can then be obtained via a time-domain modal identification method, such as the ITD method [4].

5 Numerical Simulation

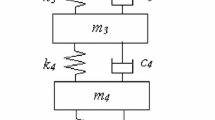
To demonstrate the effectiveness of the proposed method, we consider a linear 6-DOF chain model with viscous damping. A schematic representation of this model is shown in Fig. 1. The mass matrix M, stiffness matrix K, and the damping matrix C of the system are given as follows:

$$ \boldsymbol{M}=\left[ {\begin{array}{*{20}{c}} 2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0 & 4 \\ \end{array}} \right]\;\mathrm{N}\cdot {{\mathrm{s}}^2}/\mathrm{m},\quad \boldsymbol{K}=600\cdot \left[ {\begin{array}{*{20}{c}} 1 & {-1} & 0 & 0 & 0 & 0 \\ {-1} & 2 & {-1} & 0 & 0 & 0 \\ 0 & {-1} & 2 & {-1} & 0 & 0 \\ 0 & 0 & {-1} & 2 & {-1} & 0 \\ 0 & 0 & 0 & {-1} & 3 & {-2} \\ 0 & 0 & 0 & 0 & {-2} & 5 \\ \end{array}} \right]\;\mathrm{N}/\mathrm{m},\quad \boldsymbol{C}=0.05\;\boldsymbol{M}+0.001\;\boldsymbol{K}+0.2{{\left[ {\begin{array}{*{20}{c}} 1 & \ldots & 1 \\ \vdots & \ddots & \vdots \\ 1 & \ldots & 1 \\ \end{array}} \right]}_{{6\times 6}}}\mathrm{N}\cdot \mathrm{s}/\mathrm{m}. $$
Fig. 1
figure 00871

Schematic plot of the 6-DOF chain system

Full size image

Note that the system has nonproportional damping (and so complex modes in general), since the damping matrix C cannot be expressed as a linear combination of M and K. Consider that the ambient vibration input can be modeled as nonstationary white noise as represented by the product model. The stationary white noise is generated using the spectrum approximation method [7] as a zero-mean band-pass noise, whose standard deviation is \( 0.02\;{\mathrm{{N}}^2}\cdot \operatorname{s}/\mathrm{rad} \) with a frequency range from 0 to 50 Hz. The sampling interval is chosen as \( \Delta t=0.01\;\mathrm{s} \), and the sampling period is\( T={N_t}\cdot \Delta t=1,310.72 \operatorname {s} \). The stationary white noise simulated is then multiplied by an amplitude-modulating function \( \Gamma (t)=4\cdot \left( {{e^{-0.002t }}-{e^{-0.004t }}} \right)\), as shown in Fig. 2, to obtain the nonstationary white noise, which serves as the excitation input acting on the 6th mass point of the system. The time signal of a simulated sample of the nonstationary white noise and the power spectrum of the corresponding stationary part are shown in Figs. 3 and 4, respectively.

Fig. 2
figure 00872

A typical plot of the amplitude-modulating function

Full size image
Fig. 3
figure 00873

A sample function of nonstationary white noise in time domain

Full size image
Fig. 4
figure 00874

Power spectrum associated with the stationary part of the simulated nonstationary white noise

Full size image

The simulated displacement responses of the system were obtained using Newmark’s method [8]. By examining the Fourier spectra associated with each of the response channel, we chose the response of the 6th channel, \( {X_6}(t)\), which contains rich overall frequency information, as the reference channel to compute the correlation functions and randomdec signatures, respectively, of the system. According to the theory presented in the previous sections, the nonstationary problem may reduce to a stationary problem if we extract the amplitude-modulating function from the original nonstationary data. Therefore, we can follow the same procedures as those for stationary problems and the correlation functions and randomdec signatures, respectively, thus obtained are treated as free-vibration data. The Ibrahim time-domain method could then be applied to identify modal parameters of the system.

The results of modal-parameter identification are summarized in Tables 1 and 2, which shows that the errors in natural frequencies are less than 2 % and the maximum error in damping ratios is less than 40 %. Note that the “exact” modal damping ratios listed in Table 1 are actually the equivalent modal damping ratios obtained by utilizing ITD from the simulated free-vibration data of the nonproportionally damped structure. It is remarkable that the modes identified by the ITD generally include the vibrating modes of the structural system and some fictitious modes due to numerical computation. To keep track of the target modes, we utilize the Modal Assurance Criterion (MAC) [9] that has been extensively used in the experimental modal analysis. The value of MAC varies between 0 and 1. When the MAC value is equal to 1, the two mode-shape vectors represent exactly the same mode shape. In addition, we can distinguish the fictitious modes from the vibrating modes of the structural system if the mass matrix or the stiffness matrix of the structural system is available according to the orthogonality conditions, which show that vibrating shapes are orthogonal with respect to the stiffness matrix as well as to the mass matrix.

Table 1 Results of modal-parameter identification of a 6-DOF system subjected to nonstationary white-noise input in the form of a product model through the correlation technique in conjunction with a technique of curve fitting
Full size table
Table 2 Results of modal-parameter identification of a 6-DOF system subjected to nonstationary white-noise input in the form of a product model through the random decrement algorithm in conjunction with a technique of curve fitting
Full size table

The identified mode shapes are also compared with the exact values in Fig. 5, where good agreement is observed. The errors of identified damping ratios and mode shapes are somewhat higher due to the fact that the system response generally has lower sensitivity to these modal parameters than to the modal frequencies. It should be mentioned that the choice of the reference channel for computing the correlation functions and randomdec signatures is important to the identification results. The reference channel is chosen as a response channel for which the Fourier spectrum has rich frequency content around the structure modes of interest. The richer the frequency content of the reference channel, the better the modal-parameter identification that can be achieved. It is remarkable that for the random decrement algorithm to be effective, we need generally more than 500 samples of time history for each response channel. We can then perform averaging over the samples to obtain good quasi free-vibration data for further modal-parameter identification. For this purpose, the random decrement algorithm generally requires response data to be much longer in time and therefore is practically less efficient when compared with the correlation technique.

Fig. 5
figure 00875

Comparison between the identified mode shapes and the exact mode shapes of the 1st, 3rd, and 5th modes of the 6-DOF system subjected to nonstationary white-noise input. (a) Correlation technique. (b) Random decrement algorithm

Full size image

6 Conclusions

Identification of modal parameters is considered from response data of structural systems under nonstationary ambient vibration. It is shown that if the original nonstationary data could be represented by the product model with a slowly varying envelope function, the temporal root-mean-square functions of the data also have the same nonstationary trend as that of the original data. The temporal root-mean-square function, and so the envelope function, can thus be determined by using interval average and then applying curve fitting. The practical problem of insufficient data samples available for evaluating nonstationary correlation functions and randomdec signatures, respectively, can be approximately resolved by first extracting the amplitude-modulating function from the response and then transforming the nonstationary responses into stationary ones. The correlation functions and the randomdec signatures of the stationary response are treated as free-vibration response, and so the Ibrahim time-domain method can then be applied to identify modal parameters of the system. The selection of reference channel for computing correlation functions and randomdec signatures is also important to the identification results. The richer frequency content the reference channel has, the better results of modal-parameter identification can be achieved. In addition, the random decrement algorithm generally requires response data to be much longer in time and therefore is practically less efficient when compared with the correlation technique.