Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Brain shift severely compromises the fidelity of image-guided neurosurgery (IGNS). Most studies use a biomechanical model to estimate the brain shift based on sparse intra-operative data after the dura is opened [1–3]. Very few studies in the literature address brain deformation during and after tumor resection. The difficulty originates from the fact that resection creates a cavity, which renders the biomechanical model defined on pre-operative MRI inaccurate due to the existence of the additional part of the model corresponding to the resection region. In this work, the model accuracy will be improved by (1) removing the tetrahedra in the model corresponding to the resection region and (2) building a heterogeneous biomechanical model, which is facilitated by our multi-tissue mesh generation method [4].

In [5], Miga et al. investigated tissue retraction and resection using sparse operating room (OR) data and a finite element model. They developed a two-step method: (1) remove tissue volume by manual deletion of model elements that coincide with the targeted zone and then (2) apply boundary conditions to the new surfaces created during the excision process. Determining the cavity is challenging because a portion of it will be filled by surrounding tissues [6]. Our method eliminates the manual removal step by treating the resection region as a variable, which is able to be automatically resolved by a Nested Expectation and Maximization (EM) framework, an extension of traditional EM optimization [7]. Based on the bijective Demons algorithm, Risholm et al. presented an elastic FEM-based registration algorithm and evaluated it on the registration of 2D pre- with intra-operative images, where a superficial tumor has been resected [8]. Ding et al. [6] presented a semi-automatic method based on postbrain tumor resection and laser range data. Vessels are identified in both pre-operative MRI and laser range image; then the robust point matching (RPM) method [9] is used to force the corresponding vessels to exactly match each other under the constraint of the bending energy of the whole image. RPM uses thin-plate splines (TPS) as the mapping function. The basis function of TPS is a solution of the biharmonic [10], which does not have compact support and will therefore lead to, in real application, unrealistic deformation in the region far away from the matching points. In other words, RPM is not suitable for estimating deformation using sparse data. We use a heterogeneous biomechanical model to realistically simulate the underlying movement of the brain, which extends our previous work using a homogeneous model [11].

In this work, we target the specific feature point-based non-rigid registration (NRR) problem, which can be stated as:

Given a heterogeneous patient-specific brain model, a source point set in pre-operative MRI and a target point set in intra-operative MRI, find point correspondence, deformation field and resection region.

To resolve this problem, the three variables are incorporated into one cost function, which is minimized by a Nested EM strategy. The deformation field is represented by a displacement vector defined on the mesh nodes, the correspondence between two point sets is represented by a correspondence matrix, and the resection region is represented by a connected submesh.

2 Method

In this section, we first develop the cost function step by step from a simple point-based non-rigid registration cost function to the three-variable cost function and then present a Nested Expectation and Maximization framework to resolve it.

2.1 Cost Function

Given a source point set S = { s i } i = 1 N ∈ ℜ 3 and a target point set T = { t i } i = 1 N ∈ ℜ 3, with known correspondence, i.e., s i corresponding to t i , the point-based non-rigid registration problem can be formulated as:

$$\bar{u} = \arg \min _{u}\left (\displaystyle\int \limits _{\Omega }R(u)\mathrm{d}\Omega + \lambda \displaystyle\sum \limits _{s_{i}\in \Omega }{\left \|s_{i} + u(s_{i}) - t_{i}\right \|}^{2}\right )$$
(1)

where the first term is regularization or smoothing energy, and the second term is similarity energy. u is the deformation field and λ controls the trade-off between these two energies. Ω is the problem domain, namely the segmented brain. The removed tumor influences Ω and therefore influences both terms in Eq. (1). We extend Eq. (1) to (2) by specifying the regularization term with the strain energy of a linear elastic model, removing the limitation of correspondence between S and T, and accommodating tumor resection.

$$\displaystyle\begin{array}{rcl} (\bar{u},\bar{c}_{\mathit{ij}},\bar{{\Omega }}^{{\prime}})& =& \arg \min \limits _{ u,c_{\mathit{ij}},{\Omega }^{{\prime}}}\left (\displaystyle\int \limits _{\Omega -{\Omega }^{{\prime}}}\sigma (u)\epsilon (u)d(\Omega - {\Omega }^{{\prime}})+\lambda _{ 1}\displaystyle\sum _{s_{i}\in \Omega -{\Omega }^{{\prime}}}\vert \vert s_{i} + u(s_{i})\right. \\ & & -\left.\displaystyle\sum \limits _{t_{j}\in \Omega _{R}}c_{\mathit{ij}}t{_{j}\vert \vert }^{2}\right ) + \lambda _{ 2} \displaystyle\int \displaystyle\int \displaystyle\int \limits _{{\Omega }^{{\prime}}}\mathrm{d}x\mathrm{d}y\mathrm{d}z \end{array}$$
(2)

where variable Ω ′ represents the resection region, and variable c ij reflects the degree to which point s i corresponds to t j . The c ij is defined as in RPM [9] with soft assignment. The Classic Iterative Closest Point (ICP) method [12] treats the correspondence as a binary variable and assigns the value based on the nearest-neighbor relationship. However, this simple and crude assignment is not valid for non-rigid registration, especially when large deformation and outliers are involved [13]. We define a range Ω R , a sphere centered at the source point with radius R, and only take into account: (1) the target points, which are located in Ω R of the source point, and (2) the source points, which have at least one target point in Ω R . Thus, with this simple extension of RPM, our method is capable of eliminating outliers existing in both point sets. The first two terms come from the extension of Eq. (1), and the last term is used to prevent too much regions from being rejected.

The homogeneous model employed in the regularization term in Eq. (2) is further extended to the following heterogeneous model:

$$\displaystyle\begin{array}{rcl} (\bar{u},\bar{c}_{\mathit{ij}},\bar{{\Omega }}^{{\prime}})& =& \arg \min \limits _{ u,c_{\mathit{ij}},{\Omega }^{{\prime}}}\left (\displaystyle\sum \limits _{\Omega _{i}\in \Omega -{\Omega }^{{\prime}}}\displaystyle\int \limits _{\Omega _{i}}\sigma _{i}(u)\epsilon _{i}(u)d\Omega _{i} + \lambda _{1}\displaystyle\sum _{s_{i}\in \Omega -{\Omega }^{{\prime}}}\vert \vert s_{i} + u(s_{i})\right. \\ & & -\left.\displaystyle\sum \limits _{t_{j}\in \Omega _{R}}c_{ij}t{_{j}\vert \vert }^{2}\right ) + \lambda _{ 2} \displaystyle\int \displaystyle\int \displaystyle\int \limits _{{\Omega }^{{\prime}}}\mathrm{d}x\mathrm{d}y\mathrm{d}z \end{array}$$
(3)

where ∪Ω i  = Ω − Ω ′, i = 1…n. 

Remark.

If n = 1, Ω ′ = Empty, and c ij  = 1 then Eq. (3) is reduced to Eq. (1), which means the proposed method can be viewed as a general point-based NRR method characterized by (1) employing a heterogeneous biomechanical model as the regularization, (2) accommodating incomplete data, and (3) without correspondence requirement.

Equation (3) is approximated by Eq. (4) using finite element method:

$$J(U,C,M_{\mathrm{Rem}}) =\displaystyle\sum {U}^{\mathrm{T}}K_{ i}U + \lambda _{1}{(HU - D(C))}^{\mathrm{T}}W(HU - D(C)) + \lambda _{ 2}\left \vert M_{\mathrm{Rem}}\right \vert $$
(4)

where U T K i U approximates \(\int _{\Omega _{i}}\sigma _{i}(u)\epsilon _{i}(u)d\Omega _{i}\) as in [14, 15]. C is a point correspondence matrix with entries c ij . The equation to calculate c ij will be given later. The entries of the vector D are defined as: d i (c ij ) = s i  − ∑ t j  ∈ Ω R c ij t j ,  ∀s i  ∈ M ∖ M Rem, where M is the non-resected mesh that approximates Ω, and M Rem is the removed mesh that approximates Ω ′. The first term of Eq. (4) is the strain energy assembled on all elements in M ∖ M Rem, the second term is similarity energy defined on all source points s i  ∈ M ∖ M Rem, and the third term prevents too much tetrahedral from being rejected.

W in the second term is a weighted matrix of size 3S ×3 | S | . W is a block-diagonal matrix whose 3 ×3 submatrix W k is defined as \(\frac{m} {\vert S\vert }S_{k}^{\mathrm{avg}}\), where m is the number the vertices of the mesh. \(\frac{m} {\vert S\vert }\) makes the matching term independent of the numbers of the vertices and the registration (source) points. S k avg is the average stiffness tensor for k-th registration point. S k avg makes the registration point behavior like an elastic node of the finite element model. Assume the k -th registration point is located in the tetrahedron defined by vertices c i , i ∈ [0 : 3]. S k avg is calculated by \(S_{k}^{\mathrm{avg}} =\sum _{ i=\mathrm{0}}^{\mathrm{3}}h_{i}K_{c_{i}}\), where \(K_{c_{i}}\) is a 3 ×3 sub-matrix of the global stiffness matrix K. h i is the interpolation factor, the element of the global linear interpolation matrix H [16].

Finding C and M Rem is equivalent to outlier rejection. We developed a Nested Expectation and Maximization method to iteratively reject point and element outliers.

2.2 Nested Expectation and Maximization

The Expectation and Maximization (EM) algorithm [7] is a general algorithm for maximum-likelihood [17] estimation of the model parameter (unknowns) in the presence of missing or hidden data. EM proceeds iteratively to estimate the model parameters. Each iteration of the EM algorithm consists of two steps: The E step and the M step. In the E step, the missing data is estimated given the observed data and current estimate of the model parameters. In the M step, the likelihood function is maximized under the assumption that the missing data is known. The estimate of the missing data from the E step is used in lieu of the actual missing data. Convergence is assured since the algorithm is guaranteed to increase the likelihood at each iteration [7].

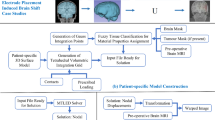
The proposed Nested EM framework is shown in Fig. 1. The inner EM is used to resolve ⟨U, C⟩ with M Rem fixed, and the outer EM is used to resolve M Rem. M Rem is approximated as a collection of tetrahedra located in a region of the model, which corresponds to the resection region in the intra-operative MRI. M Rem is initialized as empty and updated at each iteration of the outer EM. If all the tetrahedra contained in the resection region are collected, the outer EM stops.

Fig. 1
figure 1

Nested expectation and maximization framework

Full size image

2.2.1 Inner EM

Inner EM is used to resolve ⟨U, C⟩ given M Rem.

For each source point s i , assume its correspondences are subject to Gaussian distribution, so c ij can be estimated (E step) by Eq. (5).

$$c_{\mathit{ij}} = \frac{c_{\mathit{ij}}^{{\prime}}} {\displaystyle\sum _{k=1}^{m}c_{\mathit{ik}}^{{\prime}}},\mathrm{}c_{\mathit{ij}}^{{\prime}} = \frac{1} {R\sqrt{2\pi }}{\mathrm{e}}^{\frac{-{(t_{j}-s_{i})}^{2}} {2{R}^{2}} },\mathrm{}\forall t_{j} \in \Omega _{R},\mathrm{}j = 1\ldots m$$
(5)

Once C is estimated, U can be resolved by solving the minimization equation obtained by setting the derivative of functional (4) to zero, i.e., dJ ∕ dU = 0. λ2 can be ignored because the last term becomes a constant. The resolved U is used to warp S closer to T, and then the correspondence C is estimated again. The pseudo code of the inner EM is presented in Alg. 1.

Alg. 1
figure 2

Feature point outlier rejection (inner EM)

Full size image

2.2.2 Outer EM

Outer EM is used to find M Rem. In M step, ⟨U, C⟩ is resolved by the inner EM. In E step, M Rem is resolved by an element outlier rejection algorithm. M Rem is approximated by a collection of tetrahedron outliers, which fall in the resection region of the intra-operative MRI. The resection region does not need to be identified in the intra-operative MRI, and it is in fact impossible to distinguish the resection region from the background. The Background Image BGI including the resection region and the background can be very easily segmented by a simple threshold segmentation method. However, we cannot determine if a tetrahedron is an outlier based only on whether it is located in the BGI because this tetrahedra might happen to fall in the background rather than the resection region. To make the element outlier rejection algorithm robust, we utilize the fact that the resection region is a collection of tetrahedra, which not only fall in the BGI of intra-operative MRI but also connect with each other and constitute a maximal connected submesh. The collection of the outliers proceeds iteratively, and at each iteration, more specifically the E step of outer EM, additional outliers will be added into M Rem if they fall in the BGI and connect with the maximal connected submesh identified in previous iteration.

The element outlier rejection algorithm is presented in Alg. 2.

Alg. 2
figure 3

Element outlier rejection

Full size image

The outer EM iteratively rejects element outliers using Alg. 2 and computes ⟨U, C⟩ using Alg. 1 until no additional element outliers are detected. Algorithm 3 presents the whole pseudo code of the Nested EM algorithm.

Alg. 3
figure 4

Nested expectation and maximization

Full size image

3 Results

We conducted experiments on 14 clinical cases using MRI data, which were acquired with the protocol: T1-weighted magnetization-prepared rapid gradient echo (MPRAGE) sagittal images with [dimension = 256 ×256 ×176, in plane resolution = 1. 0 ×1. 0 mm, thickness = 1. 0 mm, FOV = 256 ×256].

Figure 2a shows the multi-tissue mesh we used to build the heterogeneous model.

Fig. 2
figure 5

(a) Multi-tissue mesh: brain and ventricle. (b) Deformation field of resected heterogeneous model

Full size image

Figure 2b shows the result of element outlier rejection produced by Alg. 2 and the deformation field of the heterogeneous model. A portion of the brain is cut off to expose the ventricle and its deformation field. The largest deformation reaches 18.2 mm, still in the effective range of the linear elastic biomechanical model. The larger deformation occurs in the region near the resection, and the ventricle on the tumor side is squeezed inward as the arrows show.

Figure 3 shows the results of point outlier rejection produced by Alg. 1. Comparing to the edges before outlier rejection, most point outliers are removed after outlier rejection.

Fig. 3
figure 6

Point outlier rejection. The blue points are edge detected by canny edge detection. The top two figures are edge points before outlier rejection. The bottom two figures are remaining edge points after outlier rejection

Full size image

Figure 4 shows the results of the Nested EM method. We superimpose edges detected on iMRI onto preMRI and warped preMRI, respectively, to illustrate the improvement of the boundary matching after registration.

Fig. 4
figure 7

Qualitative evaluation regarding canny edges. The blue points are edge detected by canny edge detection on iMRI. The detected edge points are superimposed on the preMRI (left) and warped preMR (right)

Full size image

To quantitatively evaluate the proposed method, Hausdorff Distance (HD) [18] is employed as the measurement of the registration accuracy. We use outlier rejected edge points in preMRI and iMRI to calculate HD before non-rigid registration (after rigid registration) and use outlier rejected edge points in iMRI and warped preMRI to calculated the HD after registration. Both homogeneous model and heterogeneous model are used for the registration. As shown in Table 1, both models can significantly improve the accuracy.

Table 1 Quantitative evaluation of Nested EM NRR regarding edge points using HD for 14 cases
Full size table

“Rigid” denotes the error after rigid registration, “Homo” denotes the error after non-rigid registration using a homogeneous model, “Hete” denotes the error after non-rigid registration using a heterogeneous model, and the “Homo-Hete” denotes the improvement brought by the heterogeneous model. The unit of the error is mm. λ1 = 1. 0. R = 10. 0 mm

We also conducted experiments to compare the homogeneous model and the heterogeneous model. To specifically measure the influence of the model on the registration, we employ the multi-tissue mesh, as shown in Fig. 2a, in both models. As a result, the influence of the discrepancy of the geometry and topology between single mesh and multi-tissue mesh can be eliminated. The only difference between the two models is the biomechanical attributes of the ventricle. The homogeneous model uses Young’s modulus E = 3, 000 Pa, Poisson’s ratio ν = 0. 45 for all tetrahedra, and the heterogeneous model replaces Young’s modulus with E = 10 Pa and Poisson’s ratio with ν = 0. 1 for the ventricle [19]. We compared the two models regarding edge points with HD as the measurement. The evaluation results show the magnitude improvement brought by the heterogeneous model is not large, but statistically significant (Two tailed t test, P-value 0.04).

4 Conclusion and Future Work

We present a novel non-rigid registration method to compensate for brain deformation induced by tumor resection. This method does not require the point correspondence to be known in advance and allows the input data to be incomplete, thus producing a more general point-based NRR.

This method uses strain energy of the biomechanical model to regularize the solution. To improve the fidelity of the simulation of the underlying deformation field, we build a heterogeneous model based on a multi-tissue mesher. To resolve the deformation field with unknown correspondence and resection region, we develop a Nested EM framework, which can effectively resolve these three variables simultaneously.

The heterogeneous model, embedded in the proposed registration method, can incorporate as many tissues as possible. In this work, we use a simple two-tissue model to perform the evaluation. Compared to rigid registration, the proposed method can significantly improve the accuracy. Compared to the homogeneous model, the improvement of the accuracy brought by the heterogeneous model is statistically significant. We believe as more tissues are incorporated into the model, such as the falx of the brain, the improvement of the accuracy regarding the magnitude will become noticeable.