Keywords

Introduction

Worldwide recommendations for the reform of school mathematics suggest an important role for problem posing. For example, the Principles and Standards for School Mathematics in the United States (National Council of Teachers of Mathematics, 2000) calls for students to “formulate interesting problems based on a wide variety of situations, both within and outside mathematics” (p. 258). In addition, that document recommends that students should make and investigate mathematical conjectures and learn how to generalize and extend problems by posing follow-up questions. Likewise, Compulsory Education Mathematics Curriculum Standards (Ministry of Education of The People’s Republic of China, 2012) pays attention to students’ acquisition of problem-posing abilities, emphasizing that students should learn to discover and pose problems from the perspective of mathematics (p. 9). So, according to these reform documents, the development of problem-posing competency is an important goal of mathematics teaching and learning that lies at the heart of mathematical activity. Moreover, the potential value of problem posing in developing students’ problem-solving abilities, creativity, and mathematical understanding has been recognized by several researchers (Brown & Walter, 1990; English, 1997a, 1997b, 1998; Kilpatrick, 1987; Lavy & Bershadsky, 2003; Lowrie, 2002; Silver, 1994; Yuan & Sriraman, 2011).

Theoretical and Empirical Background

Since the late eighties, there has been growing interest in problem posing among researchers. First, some studies revealed that many students suffer from some difficulties in posing problems (Cai & Hwang, 2002; Chen, Van Dooren, Chen, & Verschaffel, 2005, 2007; Ellerton, 1986; English, 1997a, 1997b, 1998; Silver & Cai, 1996; Verschaffel, Van Dooren, Chen, & Stessens, 2009). Other studies revealed that some teachers also face difficulties in posing problems (Chen, Van Dooren, Chen, & Verschaffel, 2011; Leung & Silver, 1997; Silver, Mamona-Downs, Leung, & Kenney, 1996). Researchers have found that there is a close relationship between students’ abilities to pose and solve problems (Cai & Hwang, 2002; Chen et al., 2005, 2007; Ellerton, 1986; Silver & Cai, 1996; Verschaffel et al., 2009). Second, several design experiments aimed at implementing and testing new instructional approaches that incorporate problem-posing activities into the mathematics curriculum have been carried out. These experiments were designed to improve students’ mathematical understanding, problem-posing and problem-solving abilities, as well as their beliefs about and attitudes toward problem posing and problem solving (Bonotto & Baroni, 2008; English, 1997a, 1997b, 1998; Lavy & Bershadsky, 2003; Rudnitsky, Etheredge, Freeman, & Gilbert, 1995; Verschaffel, De Corte, Lowyck, Dhert, & Vandeput, 2000; Winograd, 1997).

Rudnitsky et al. (1995) implemented a “structure-plus-writing” instruction with third-grade and fourth-grade students to test whether the instruction, intended to help students construct knowledge about addition and subtraction story problems, could be transferred to helping them to solve problems. Children were instructed with the concept of a mathematics story (i.e., any story, happening, or event that has to do with quantities or amounts) and its relationship to a mathematics problem, and were engaged in creating their own mathematics stories, categorizing their own stories, and making up mathematics problems from these mathematics stories. It was found that children with structure-plus-writing instruction outperformed children who only received a problem-solving treatment based on practice and provision of explicit heuristics, and children who received no explicit instruction in arithmetic word problem solving. Winograd (1997) implemented a problem-posing training program with fifth-grade students, wherein different ways of sharing student-authored word problems (i.e., posing and solving mathematics problems like a mathematician, publishing their problems on worksheets) were attempted. Classroom observations revealed that students were highly motivated to pose problems that their classmates would find interesting or difficult, and that their personal interest was sustained during the process of sharing posed problems.

In a study by Verschaffel et al. (2000), problem posing was integrated into a computer-supported learning environment in which upper elementary school children were guided and supported in becoming more strategic, motivated, communicative, mindful, and self-regulated mathematical problem solvers. Various problem posing and solving activities were integrated, such as solving mathematical application problems and putting them on a networked knowledge forum, learning to pose and solve mathematical application problems, and so on. It was found that learning environments in which problem posing played an important role, had a positive effect on the problem-solving competency of the sixth-graders, but not on that of the fifth-graders. It also yielded a positive influence on all pupils’ beliefs about, and attitudes toward, collaborative learning in general. In the study of Lavy and Bershadsky (2003), a What-if-not strategy was adapted into two learning workshops for preservice teachers on complex solid geometry. The results showed that the preservice teachers strengthened their understanding of geometrical concepts and the connections between the given and new concepts while creating new problems. In a study involving problem-posing and problem-critiquing activities (Bonotto & Baroni, 2008), children were able to create problem situations that were more original, complex, and realistic in their content than traditional word problems after the training.

In many studies, problem posing is not only considered as a vehicle to develop students’ problem-solving abilities, but also as one of the central aims of mathematics teaching in itself, and, consequently, is treated as a critical, if not the most important, dependent variable in the evaluation. English (1997a, 1997b, 1998) carried out a 3-year study in which various (related) problem-posing programs were implemented with third-, fifth-, and seventh-grade students who displayed different profiles of achievement in number sense and mathematical problem solving. English (1998) found that third-grade students had difficulties in posing a range of problems in informal contexts (e.g., a picture or a piece of literature) and even more difficulties in formal contexts (e.g., a standard addition and subtraction number sentence). Furthermore, the program was effective in increasing the number of problems generated in general and the number of multi-step problems in particular, but not effective in increasing the diversity of the third-grade students’ self-generated problem types. In problem-posing training programs with fifth- and seventh-grade students (English, 1997a, 1997b), it was found that, compared to children in a control group, students who followed the programs displayed an increase in their abilities to generate more diverse and more semantically and computationally complex problems, to identify problem structures, and to model new problems on the structure of a given problem. English also found an increase in the range of problems that students indicated they would like to solve.

Taken as a whole, the intervention studies reviewed above suggest that engaging students in instructional activities related to problem posing has a positive influence on their mathematical understanding (e.g., Lavy & Bershadsky, 2003), word problem-posing abilities (e.g., English, 1997a, 1997b, 1998), and problem-posing motivation (e.g., Winograd, 1997), as well as on their word problem-solving abilities (e.g., Rudnitsky et al., 1995; Verschaffel et al., 2000) and beliefs (e.g., Verschaffel et al., 2000). However, these intervention studies have some limitations. First, the ecological validity of some studies can be questioned because (a) the intervention involved only selected subgroups of children and not intact classes (e.g., English, 1997a, 1997b, 1998); (b) the training program was conducted separately from normal mathematics lessons (e.g., Verschaffel et al., 2000); or (c) the participants were selected only from preservice teachers (Lavy & Bershadsky, 2003). Second, some studies do not allow strong conclusions because of the lack of an appropriate control group (e.g., Verschaffel et al., 2000; Winograd, 1997). Third, some studies only address one type of problem-posing activity, for example, making up mathematics problems from mathematics stories (e.g., Rudnitsky et al., 1995), when in fact many forms of problem-posing activities are available—such as posing problems from a symbolic expression, or from verbal statements (English, 1997a, 1997b, 1998).

The present study tries to overcome the shortcomings described above. First, apart from an initial set of training units that was separated from normal mathematics lessons and was given by the researcher, the training program involved a second series of experimental lessons—taught by the regular classroom teacher—in which problem-posing activities were integrated. Second, we worked with intact classes instead of specifically chosen subgroups of students. Third, rather than doing only one kind of problem-posing activity, various problem-posing situations and activities were used. Finally, we developed and used a systematic assessment battery to examine students’ problem-posing and problem-solving capacities, as well as problem-posing and problem-solving beliefs and attitudes. More particularly, as far as problem-posing capacity is concerned, we made use of an assessment tool that evaluated the problems posed along four dimensions: appropriateness, complexity, originality, and diversity.

Description of the Intervention Program

Aims of the Intervention Program

The first aim of the intervention program was that students would acquire problem-posing skills, and positive beliefs about and attitudes toward problem posing. Given the claimed close relationship between problem posing and problem solving, a second aim of the program was to develop students’ problem-solving abilities and positive beliefs about and attitudes toward problem solving.

With respect to problem-posing skills, we intended that students would acquire metacognitive strategies for generating problems from a given situation or by reformulating a given problem, which consists of four steps, namely: (a) understanding the problem-posing task presented; (b) identifying the category of the problem-posing task presented; (c) applying appropriate strategies to pose problems; and (d) evaluating the posed problems (for more details, see Figure 15.2). With respect to the development of positive beliefs and attitudes toward problem posing, we intended that students would be more explicitly aware of their erroneous beliefs about and their negative attitudes toward problem posing (e.g., “I will give up immediately if I can’t pose a mathematical problem in a given situation” or “I don’t like communicating my problem-posing strategies with peers”), and that, after the intervention, they would be more inclined to change them into more positive beliefs and attitudes.

Major Design Principles of the Intervention Program

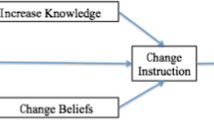
The intervention program incorporated three design principles—drawn from the above aims—related to the learning tasks, instructional techniques, and socio-mathematical norms (English, 1997a, 1997b, 1998; Rudnitsky et al., 1995; Verschaffel et al., 2000; Winograd, 1997). These three principles, which are depicted in Figure 15.1, were the basic pillars of the training program that, together and in close mutual interaction, guided the activities of and interactions between the teacher and students.

Figure 15.1.
figure 1

Three design principles of the training program.

Full size image

  • In a typical lesson, the teacher presented a meaningful and realistic task and asked students to pose mathematics problems starting from that task (principle 1).

  • During this problem-posing task, the teacher encouraged students to pose appropriate problems using powerful instructional techniques. For example, if students posed a nonmathematical problem, the instructor would scaffold the students by means of a series of focused questions to help them realize that this problem was not a good word problem although it was a meaningful one (e.g., “Is it a mathematical problem?”, “What do we need to have a mathematical problem?”, or “What are the givens and the requirements?”) (principle 2).

  • Meanwhile, the teacher created a classroom climate conducive to the development of students’ appropriate dispositions toward mathematical problem posing (principle 3).

Below, we discuss and illustrate these three design principles in greater detail.

First, a varied set of meaningful and realistic learning tasks (i.e., problem-posing situations) was used. The problem-posing tasks were presented in various formats including stories, formulae, pictures, tables, and games. Problems were generated in various semantic structures, different problem-posing strategies were applied to pose problems, and attention was paid to the meaningful and realistic nature of the problem-posing situations.

Some examples of problem-posing tasks are:

  • Writing appropriate problems for the following symbolic expressions and equations

    • 76 + 28, 96 − 24, 11 × 3, and 24 ÷ 3

    • 100 ÷ 8 = 12.5, 100 ÷ 8 = 12, and 100 ÷ 8 = 13

  • Writing a problem based on the following story, “Teddy Bear Sells Fish.”

    “Teddy bear’s mother was ill, so he must earn money to cure his mother’s disease by selling fish. One day, a fox, a dog, and a wolf wanted to buy fish from Teddy bear. They asked: ‘How much is the fish per kilo? … so he sold the fish to the fox, dog, and wolf. 35 kilos of bellies were sold for 70 yuan, 15 kilos of heads were sold for 15 yuan, and 10 kilos of tails were sold for 10 yuan”;

  • Solving the following word problem and posing some new problems based on the given problem using the what-if-not strategy, modifying the attributes of the given problem by replacing them with more general or more restricted ones (Brown & Walter, 1993);

  • “Calculate the area of a rectangle given that its width is 2 m and its length is 3 m.”

Second, a varied set of instructional techniques was used (Collins, Brown, & Newman, 1989; Verschaffel et al., 2000). Most of the experimental lessons/training units followed an instructional model consisting of the following sequence of classroom activities: (a) a short whole-class introduction; (b) posing problems in fixed heterogeneous groups; (c) solving problems generated by other groups; and (d) an individual problem-posing task, followed by a final whole-class discussion. During all of these activities, the instructor’sFootnote 1 role was to stimulate and scaffold students in the problem-posing and problem-solving activities. We relied heavily on the list of six instructional techniques distinguished in the cognitive apprenticeship model of Collins et al. (1989) to help ensure that the problem-posing instruction would have the features of a powerful instructional environment: modeling, coaching, scaffolding, fading, articulation, and reflection. For example, assuming that initially students do not know how to pose problems, modeling was used by the instructor at the outset to show how a problem-posing process unfolds and explains why it happens that way (Collins et al., 1989) to allow the students to follow and see what and how an expert problem poser thinks and to pay special attention to the overall strategy of posing problems. During the process of posing a problem, the students were given an instruction card, as shown in Figure 15.2, with scaffolding instructions that they were to follow sequentially. This card was initially used intensively and systematically and was gradually removed as students began to internalize its contents.

Figure 15.2.
figure 2

Problem-posing instruction card.

Full size image

The third principle of the intervention program was the establishment of socio-mathematical norms concerning mathematical problem posing aimed at creating a classroom climate conducive to the development of students’ appropriate dispositions toward mathematical problem posing (English, 1997a, 1997b; Silver, 1997; Verschaffel et al., 2000; Winograd, 1997; Yackel & Cobb, 1996). Norms about problem posing included (a) thinking of problem posing as a genuine and valuable mathematical activity; (b) agreements about what makes a problem (sufficiently) different from another one, why more challenging and/or more realistic problems are better, how problem posing and problem solving are related, etc. and (c) expectations of the role that students and teachers should play in the problem-posing activities. Examples of such norms are: “Just increasing the size of the given numbers is not the best way to increase the complexity of a problem” or “There is not a single best problem for a given problem-posing task.”

Content and Organization of the Intervention Program

The training program consisted of eleven 90-minute training units taught by the first author (LC) with one training unit per week, and twenty-four 45-minute lessons taught by the regular classroom teacher of the experimental class wherein problem-posing activities were integrated into the regular mathematics lessons, with two lessons per week. An overview of the 11 training units is presented in Table 15.1.

Table 15.1 Overview of the Intervention Program
Full size table

According to the influential instructional theory of Kaiipob (Ma, 2003), there are five steps in a typical mathematics lesson in a Chinese classroom: (a) introduction; (b) new knowledge introduction; (c) new knowledge exploration; (d) practice and consolidation; and (e) summary. In the experimental program, problem posing was integrated into three of these five instructional steps in the regular lessons taught by the classroom teacher, namely, steps (b), (d), and (e).

Teacher Support

Because the second series of experimental lessons of the training program was not taught by the researcher but by the experimental teacher, the experimental teacher was prepared for and supported in implementing the program. The model of teacher development used was inspired by Verschaffel et al. (2000) and emphasized the creation of a social context wherein the teacher and researcher learn from each other, rather than a model whereby the researcher directly transmits knowledge to the teacher. The teacher support involved three elements: (a) provision of a general teacher guide containing an extensive description of the experimental program; (b) provision of a description of one exemplified lesson showing what each lesson looks like and how it differs (precisely) in terms of the problem posing tasks between the experimental and control class; and (c) the presence of the researcher during one lesson per week, and feedback to the teacher with suggestions for possible improvements.

The experimental teacher’s preparation was implemented during the months that preceded the actual intervention and consisted of three meetings—each lasting 1 hour—attended by the teacher and the researcher, wherein (a) the theory of problem posing; (b) different instructional techniques of integrating problem posing into the three instructional steps of the mathematics lessons; (c) an extensive description of the training program; and (d) a description of one exemplified lesson for the experimental and the control group was introduced to the experimental teacher, and wherein a try-out lesson on problem posing (with the researcher being the only audience) was presented and feedback was given. During a fourth meeting, held shortly after the end of the intervention, the researcher obtained some feedback and suggestions from the teacher about the experimental program and the way she had been coached.

Method

Participants

The training program took place in two mixed-gender 4th-grade classes with 69 students (average age = 12.2 years) of a primary school located in the countryside near Shenyang City, China. One of the 2 classes, with 33 students, was designated to be the experimental class, and the other class, with 36 students, acted as the control group. The socioeconomic and educational level of most students’ parents was relatively low in both groups. An experimental class teacher with about 12 years of teaching experience and a control class teacher with about 34 years of teaching experience participated in the program. Each of them was in charge of one class, and their duty included teaching mathematics, teaching Chinese, and some daily managerial tasks. Before participating in this study, the students had had some occasional experiences in problem-posing activities since a few problem-posing situations appear in the regular textbooks to meet the goal of problem posing described in the Compulsory Education Mathematics Curriculum Standards in China (Ministry of Education of The People’s Republic of China, 2012).

Instruments

Before and after the intervention, five instruments—a problem-posing test (PPT), a problem-solving test (PST), a problem-posing questionnaire (PPQ), a problem-solving questionnaire (PSQ), and a standard achievement test (SAT)—were collectively administered in the two participating classes. The first four instruments were administered in two sessions on two successive days, shortly before and after the intervention, and each session lasted for about 1 hour. In the first session, the experimental and control classes were administered the PPT, and in the next session, they were administered the PST, PPQ, and PSQ. The SAT was administered to the students as the final exam in the first and the second term of the academic year in which the experiment was implemented, respectively.

Problem-posing test. Two parallel PPTs were designed, consisting of 12 problem-posing items aimed to assess students’ problem-posing abilities. They were administered before and after the intervention. The problem-posing items were selected from different curricular subfields (arithmetic, geometry, and statistics). In each item students were asked to pose two problems. When administering the PPT, one half of the experimental and control classes were administered PPT 1 and the other half of each class was administered PPT 2. Before administering the actual PPT, all students were introduced to the test by means of one example of a problem-posing item.

Problems posed in the PPT were evaluated along four dimensions, i.e., appropriateness,Footnote 2 complexity, originality, and diversity. Appropriateness refers to the number of appropriate mathematics problems posed. A posed problem was awarded 1 point if it was scored as appropriate or 0 points if scored as inappropriate. Since two problems were required to be posed in each item, each item was awarded a maximum of 2 points, resulting in a total score for the dimension of appropriateness of 0–24 (2 × 12) points. All the appropriate problems were also scored along the other three dimensions (i.e., complexity, originality, and diversity) with a higher score reflecting a higher level of problem-posing ability.

Complexity refers to the linguistic complexity—whether the word problem involved propositions with an assignment, a relational and/or a conditional structure (Silver & Cai, 1996)—and the semantic complexity—combine, change, compare, and equalize structure for addition and subtraction word problems (Fuson, 1992) and equal group, multiplicative comparison, rectangular pattern, and Cartesian product for multiplication and division word problems (Verschaffel & De Corte, 1996)—of an appropriately posed mathematics problem. More specifically, in line with Silver and Cai (1996), a problem with conditional and/or relational propositions was considered to be more complex than a problem containing only assignment propositions (e.g., a conditional problem “The price for 1 scarf is 20 yuan. If Xiaoming bought 3 scarves and gave the seller 70 yuan, how much was returned?” was considered more complex than an assignment problem “The price for 1 scarf is 20 yuan, and for 1 pair of gloves is 10 yuan. How much is 2 scarves and 1 pair of gloves?”). A problem involving a greater variety of semantic relationships was considered to be more complex than a problem involving fewer semantic relationships (e.g., the posed problem “The price for 1 scarf is 20 yuan, and for 1 pair of gloves is 10 yuan. How much is 2 scarves and 3 pairs of gloves?” was scored as more complex than “The price for 1 scarf is 20 yuan. How much is 2 scarves?”).

Originality refers to the uncommon or rare nature of the appropriate mathematics problems being posed. More specifically, a problem belonging to a problem type (defined and operationalized in terms of its linguistic, semantic, and mathematical structure) that occurred with a smaller frequency in our data set was considered to be more original than a problem that occurred with a larger frequency.

For the dimensions of complexity and originality, each self-generated problem was awarded from 1 to 5 points, and so each item (consisting of two problems) was awarded from 2 to 10 points. So the total score for the dimension of complexity and originality ranged from 24 (2 × 12) to 120 (10 × 12) points.

The first three criteria can be applied to each individual self-generated problem, whereas the fourth criterion, diversity, addresses the relationship between the two problems that had to be generated in a given problem-posing item. More specifically, it assesses how much variation there is for the two posed problems in terms of their semantic, linguistic, and mathematical features. For the dimension of diversity, each item (except for oneFootnote 3) was awarded from 1 to 5 points, so the total score for the dimension of diversity was from 11 (1 × 11) to 55 (5 × 11) points.

To assess the reliability of the scoring method, ten students were randomly selected and their posed problems in the pre-test and post-test were independently scored by two researchers based on the scoring system described above (complemented with a note with more detailed scoring instructions and examples). Inter-rater agreement for the dimension of appropriateness, complexity, originality, and diversity was 1.00, 0.86, 0.93, and 0.93, respectively. The two researchers then met, jointly examined the posed problems that had yielded different scores, and reached an agreement on the final scores for those problems. Finally, 1 researcher scored all of the problems posed by the remaining 59 students based on the assessment criteria and asked for advice if any uncertainties occurred during this coding process. As another test of the reliability of the scoring system, we also computed the correlation between the control group students’ total scores on the two parallel versions of the PPT for each of the four scoring dimensions. This correlation analysis showed that the PPT has a sufficiently high positive and statistically significant parallel forms reliability (Nunnally & Bernstein, 1994) for all four dimensions: appropriateness (r = .51, p = .00), complexity (r = .32, p < .001), originality (r = .31, p < .001), and diversity (r = .29, p < .001).

Problem-solving test. Two parallel PSTs were designed, consisting of ten problem-solving items aimed at assessing students’ problem-solving abilities. They were administered before and after the intervention. They were also selected from three different curricular subfields (arithmetic, geometry, and statistics). In each item, students were required to answer one or two questions. A similar procedure to the PPT was used for the administration of the PST. Each answer was scored either as a correct answer, a wrong answer (i.e., an answer using one or more faulty arithmetic operations), a technical error (i.e., an answer with a purely technical mistake in the execution of the arithmetic operation), or no answer. However, because the intervention especially aimed at the improvement of students’ problem-solving abilities (rather than at students’ computational proficiency), purely technical errors were ultimately also considered correct. So, items consisting of 2 questions were awarded 2 points if the 2 questions were answered correctly, 1 point if only 1 question was answered correctly, and 0 points when neither of the questions was answered correctly, whereas items consisting of only 1 question were awarded 2 points if that question was answered correctly, and 0 points in all other cases. This resulted in a maximum total score of 20 points for the PST. The PST had relatively high parallel forms reliability (Nunnally & Bernstein, 1994); the correlation between the control group students’ total score on the two parallel versions of the PST was r = .76, p < .001.

Problem-posing and problem-solving questionnaires ( PPQ and PSQ ). The PPQ and PSQ were designed to assess students’ beliefs about and attitudes toward problem posing and solving, and were administered before and after the intervention.Footnote 4 The PPQ consisted of twenty 5-point Likert-scale items dealing with students’ values about, preference for, perseverance in, and confidence in mathematical problem posing (e.g., “I think pupils can learn a lot from posing mathematical problems,” “I like to pose mathematical problems similar to those in textbooks,” or “I don’t have the confidence that I can improve my problem-posing ability by effort”). With respect to each item of the PPQ students had to respond by indicating whether they strongly agreed, agreed, were uncertain, disagreed, or strongly disagreed with the statement. The PSQ had a similar content and design to the PPQ, except that the statements were about problem solving instead of problem posing. A similar procedure to the PPT was used for the administration of the PPQ and PSQ. Each response to the problem-posing/solving questionnaire was awarded 1–5 points with a higher score reflecting a more positive belief about or attitude toward problem posing/solving. For a positively formulated item like “In most cases, I can pose/solve mathematical problems successfully in a given situation,” the option “strongly disagree” was awarded 1 point, “disagree” 2 points, “uncertain” 3 points, “agree” 4 points, and “strongly agree” 5 points. In case of a negatively formulated item like “I am not very sure whether I can pose mathematical problems in a given situation,” or “I don’t like solving mathematical problems,” the scores were reversed. This resulted in a total score from 20 to 100 points for the PPQ and for the PSQ. Cronbach’s (1951) α for the PPQ and PSQ was 0.81 and 0.87, respectively, which is considered to be a sufficient level of internal consistency (Nunnally & Bernstein, 1994).

Standard achievement test. To assess students’ general mathematical knowledge and skills, two SATs developed by the Shenyang Municipal Educational Committee were used to assess students’ general mathematical knowledge and skills before and after the intervention. As stated above, the two SATs were administered as the final exams in the first and second terms. The items on the final exam administered in each term related to the various curricular subfields being covered in the program, such as number, addition and subtraction of fractions, solving equations, area of plane or solid figures, word problem solving, probability, and statistics. The two SATs collected from the experimental and control groups were scored by the experimental teacher and control group teacher with each teacher being responsible for her own class. The maximum score for each SAT was 100 points.

Hypotheses and Research Questions

A first hypothesis was that the experimental program would result in a positive effect on students’ problem-posing abilities based on the results of some intervention studies (English, 1997a, 1997b, 1998; Winograd, 1997). We predicted in the experimental group—as compared to the control group—that there would be a significantly larger increase from pre-test to post-test of the global score on the PPT in the four dimensions, appropriateness, complexity, originality, and diversity.

A second hypothesis was that the experimental program would result in a positive effect on students’ problem-solving abilities because of the close relationship between problem posing and problem solving revealed by some investigations (Cai & Hwang, 2002; Chen et al., 2005, 2007; Ellerton, 1986; Silver & Cai, 1996; Verschaffel et al., 2009). Therefore, a significantly larger increase of the global score on the PST from pre-test to post-test was predicted for the experimental group than for the control group.

Third, based on the results of previous intervention studies (English, 1997a, 1997b, 1998; Verschaffel et al., 2000; Winograd, 1997), we hypothesized that the experimental program would result in a positive effect on students’ problem-posing/solving beliefs and attitudes. More specifically, we expected a significantly larger increase of the global score on the problem-posing/solving questionnaire from pre-test to post-test for the experimental group than for the control group.

Finally, for the same reasons as argued by Verschaffel et al. (1999), no prediction was formulated for the results of the SAT after the intervention.

Results

The impact of the training program on the students’ results on the five assessment instruments was analyzed by means of independent sample t-tests and an alpha level of .05 for all statistical tests was used. The outcomes of these analyses are presented below.

First, the results of the problem-posing pre-test (see Table 15.2) revealed that there was no significant difference between the experimental and control groups in the four dimensions, i.e., appropriateness (t-test, two-tailed, t(1,652.29) = 1.37, p = .70), complexity (t-test, two-tailed, t(1,220) = 0.68, p = .50), originality (t-test, two-tailed, t(1,220) = 0.23, p = .82), and diversity (t-test, two-tailed, t(563.58) = 0.51, p = .61), which indicates that the two groups were comparable for the PPT before the intervention.

Table 15.2 Mean Score (and Standard Deviation) on the Problem-Posing Pre-test for the Dimensions of Appropriateness, Complexity, Originality, and Diversity in the Experimental and Control Group
Full size table

Furthermore, there was significantly different progress from pre-test to post-test between the experimental and control group in the dimension of originality (t-test, one-tailed, t(1,198.77) = 1.99, p = .02) in favor of the experimental group, but not in the dimensions of appropriateness (t-test, one-tailed, t(1,654) = −0.44, p = .33), complexity (t-test, one-tailed, t(1,187.64) = 1.13, p = .13), and diversity (t-test, one-tailed, t(479) = 1.15, p = .13). The effect size for the dimension of originality was 0.114, which is considered small (Cohen, 1988). So, the first hypothesis was confirmed only for one of the four problem-posing dimensions and only to some extent. The progress from the problem-posing pre-test to post-test in the four dimensions is provided in Table 15.3.

Table 15.3 Progress (and Standard Deviation) from the Problem-Posing Pre-test to Post-test for the Dimensions of Appropriateness, Complexity, Originality, and Diversity in the Experimental and Control Group
Full size table

Second, the results of the problem-solving pre-test revealed there was no significant difference between the experimental and control groups (t-test, two-tailed, t(67) = –0.28, p = .78). The mean score for the experimental group was 14.39 (SD = 3.86) and 14.64 (SD = 3.33) for the control group, which indicates that the two groups were comparable for the PST before the intervention. Results further revealed that there was significantly different progress from the problem-solving pre-test to the post-test between the experimental and control groups in favor of the experimental group (t-test, one-tailed, t(67) = 2.46, p = .01). The effect size was 0.57, which is relatively large (Cohen, 1988). The change of the mean score for the experimental and for the control groups was 1.26 (SD = 2.51) and −0.18 (SD = 2.54), respectively. So, the second hypothesis was confirmed.

Third, before the start of the experimental intervention, for both PPQ and PSQ, the mean score for the control group tended to be higher than that for the experimental group, and it was significantly different for the PPQ (t-test, two-tailed, t(67) = −2.00, p = .049), but not for the PSQ (t-test, two-tailed, t(67) = −1.27, p = .21) (see Table 15.4).

Table 15.4 Mean Score (and Standard Deviation) on the PPQ and PSQ in the Experimental and Control Group at the Pre-test
Full size table

After the intervention, the control group declined in its scores quite strongly, whereas the experimental group made limited progress which led to a significant difference for the PPQ from the pre-test to the post-test between the two groups (t-test, one-tailed, t(67) = 4.21, p < .001) and for the PSQ (t-test, one-tailed, t(67) = 5.28, p < .001) in favor of the experimental group (see Table 15.5). The effect size was 1.02 and 1.27, respectively, each of which is very large (Cohen, 1988).

Table 15.5 Progress (and Standard Deviation) from the Problem Posing Pre-test to Post-test on the PPQ and PSQ in the Experimental and Control Group
Full size table

Fourth, the results of the two SATs revealed that there was no significant difference either on the mean score of the two SATs between the experimental and control group before the intervention (t-test, two-tailed, t(67) = −0.35, p = .73), nor on the gain from pre-test to post-test (t-test, one-tailed, t(67) = −0.33, p = .37).

Discussion

In the present study, a training program aimed at developing Chinese students’ problem-posing abilities and indirectly developing their problem-solving abilities and beliefs about and attitudes toward mathematical problem posing and problem solving, given the claimed close relationship between problem posing and problem solving, was designed, implemented, and evaluated. The study focused on the impact of the program on students’ problem-posing and problem-solving abilities and beliefs, rather than on the interaction processes between teacher and students and/or between the researcher and the teacher, or on the impact of the involvement in the program on the teachers’ professional knowledge and beliefs about mathematical problem posing and problem solving. First, we found that, compared to students from the control group, students who followed the program demonstrated more improvement in their abilities in posing original problems, but not in posing appropriate, complex, or diverse problems after the training. Second, the students in the experimental group also showed better performance on a problem-solving test. Finally, they also improved more in their beliefs about and attitudes toward problem posing and problem solving.

We end this contribution with a reflection on some restrictions of the present study and some theoretical, methodological, and educational issues that need to be addressed in further research. First, the present study sheds some light on the complex relationship between students’ problem-posing and problem-solving abilities. More specifically, it confirms the close relationship between students’ problem-posing and problem-solving abilities using an intervention study since we found that experiences with problem posing had a positive effect on students’ problem-solving abilities. In other words, even if the experimental group students were not explicitly and systematically instructed with any problem-solving strategies, they still made more progress in problem solving than the students from the control group. However, the students from the experimental group were also frequently asked to solve the problems they posed in some training units, and some lessons given by the regular classroom teacher might have had a positive impact on their problem-solving abilities. So, in order to detect the relationship between problem posing and problem solving more accurately, in future research, it might be necessary to involve an experimental group with only problem-posing activities in addition to one experimental group with both problem-posing and problem-solving activities and one control group with only regular lessons.

Second, we developed a self-made PPT together with a problem-posing coding system to assess students’ problem-posing abilities. This assessment tool evaluates the problems that the students posed along four dimensions, namely appropriateness, complexity, originality, and diversity. However, some intriguing questions remain, such as: Are these four dimensions sufficient to assess the quintessence of students’ problem-posing abilities? And how should the (meta) cognitive processes underlying students’ problem-posing performance be assessed? Indeed, the four dimensions described in the assessment tool only focused on evaluating the students’ performance in the problem-posing tasks, but the assessment tool was unable to assess students’ underlying (meta) cognitive processes. The four-step problem-posing model (see Figure 15.2) that was developed for and used in the intervention program could be taken as a starting point for developing a more process-oriented measure.

Third, the students who participated in our study were all selected from one particular, relatively small region in China. Moreover, the sample size was small and involved only one experimental and one control class. Both elements evidently jeopardize the external validity of the results. So, follow-up studies should involve a larger sample of classes randomly selected from both the countryside and inner cities from different regions in China.

Fourth, while we made a detailed lesson plan for the first series of lessons taught by the researcher and prepared a detailed teacher guide for the teacher for the second series of lessons, together with an individual preparation and coaching program, we have to acknowledge that a detailed picture of what actually occurred in the experimental class in terms of the realization of the three design principles, is largely lacking. Therefore, future studies need to analyze the specific effects of these various design principles and the relative contribution of more specific instructional features within each principle. This requires the unraveling of the “black box” of the experimental treatment by means of videotaped lessons and/or systematic observations of what happens during these lessons.

Fifth, the training program was evaluated with only a pre-test and a post-test, but without a retention test. Therefore, it is impossible to know whether the observed positive effects of the experimental program on the development of students’ problem-posing and problem-solving abilities, beliefs, and attitudes would last after the program had stopped. So, in future research, a repeated measurement design should be used to allow assessment of lasting effect. Moreover, only paper-and-pencil tests and questionnaires were used to assess students’ abilities in and beliefs about problem posing and problem solving. Interviews could have allowed us to know more about students’ problem-posing and problem-solving abilities and beliefs. So, it might also be interesting in future research to supplement the tests and questionnaires with interviews. In particular, there is a specific challenge in measuring students’ problem-posing skills by means of collective tests which is different from measuring problem-solving skills.

In an exploration of individual student profiles, we were surprised to find that some experimental group students posed quite complex problems on the pre-test and easier ones on the post-test. This might be due to the fact that problem-posing tasks are—according to the students’ beliefs—a kind of activity with more openness and freedom since it typically elicits multiple possible results and more divergent thinking processes (Çildir & Sezen, 2011). So, given the rather “open” nature of most problem-posing tasks (as compared to typical word problem-solving tasks), students may not always try to pose difficult or original problems and tend to be satisfied with easy and familiar ones. Therefore, we recommend including in future problem-posing tasks and tests, more instructions like “Pose complex problems” or warnings like “Complex problems will get a higher score.” It may also be interesting to supplement the paper-and-pencil test with an interview with a carefully selected subgroup sample in order to explore why students who received training in problem posing may not do their very best to come up with the most complex and unfamiliar problems they can think of.

Sixth, some other recent intervention studies on problem posing revealed that a training program on problem posing can improve students’ problem-posing abilities, problem-solving abilities, and students’ standardized mathematics achievement test performance to a greater extent than found in our study (e.g., Chen & Ye, 2007; Xia, Lü, Wang, & Song, 2007). As noted above, our training program, first, only had a significant positive effect on the originality of the problems posed by the students (but not on the appropriateness, complexity, and diversity of the problems posed), second, the decreased performance of the control group between pre-test and post-test resulted in augmenting the gains for the experimental group, so the positive effect on students’ problem-solving ability was more due to the negative effect for the control group than to a significant increased performance in the experimental group, and, third, the program did not have a significant positive effect on the experimental students’ standardized mathematics achievement test performance. Therefore, to conclude, we list some factors that may help to explain the rather modest effects of our intervention. First, there is the small sample size of the experimental and control groups. As a result, the regular absence of two students during the intervention (who were kept in the analysis because of the small sample size), might have had a negative effect on the post-test results of the experimental group. Second, as a consequence of the new Chinese mathematics curriculum, most teachers already pay some attention to problem posing. Because of the lack of systematic control over the experimental teacher’s actual implementation of the three design principles during the problem-posing moments, the actual instructional difference between the two classes with respect to the intensity and quality of the problem-posing moments may have been less extreme than intended by the researchers. Finally, even though much attention was paid to the selection and construction of the assessment instruments, it is possible that some instruments were unable to detect possible (positive) learning and transfer effects in the students of the experimental class.