Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

2.1 Introduction

This chapter presents the max-pressure feedback policy for the control of an arbitrary network of signalized intersections. The cycle length at each intersection is fixed, although it may be different at different intersections. The policy determines at the beginning of each cycle, the fraction of the cycle that is allocated to each stage. (A stage is a set of permissible simultaneous movements.) The movement of traffic is modeled as a store and forward (SF) queuing system (Aboudolas et al. 2009a). Feedback policies based on queue measurements to control an SF model have been extensively studied, including in (Aboudolas et al. 2009b; Cai et al. 2009; Heydecker 2004; Mirchandani and Head 2001; Robertson and Bretherton 1991). There are two major differences between the max-pressure policy and those proposed in these studies.

First, the max-pressure policy is decentralized: the decision at any intersection depends only on the queues adjacent to that intersection; the policies in the other studies are centralized: the decision at each intersection depends on the queues at all intersections. This distinction may be practically important, since the communication infrastructure required to implement max pressure is much simpler to build. More significantly perhaps, max pressure may be implemented incrementally: remarkably, if a new intersection is added to the network, the max pressure policy for the original network does not change. In the centralized control of the cited studies, an expansion of the controlled network leads to changes in the policy of all intersections.

Second, the max-pressure policy is provably stable. That is, if external arrivals and turn ratios are stationary, and if there is any policy that keeps all queues bounded, then max-pressure also keeps all queues bounded. None of the cited studies provides such a stability guarantee. Also, max-pressure requires no knowledge of the external arrivals (but it does require knowledge of turn ratios, which can be estimated from the queue measurements), whereas the other studies require knowledge of the external arrivals. Consequently, max-pressure automatically adapts to slow changes in demand patterns.

Analysis of the SF queuing system is carried out using network calculus, which was developed to model, analyze, and control communication networks. (The fundamental reference is (Cruz 1991); we quote results from (Chang 2000); for a brief description see (Wikipedia 2009).) Network calculus is equally well suited for signal control studies, as the calculus describes traffic flows in terms of cumulative counts, commonly used in traffic studies. A flow is characterized by its average rate \(\rho \) and the maximum burst (or platoon) size \(\sigma \). The service that an intersection provides to a flow is also characterized by two parameters: the saturation rate s and the maximum duration r (effective red) for which no service is provided. These parameters are easier to estimate empirically than parameters of stochastic queuing models. (The max-pressure policy for stochastic queueing models is studied in Varaiya (2009), which also proves stochastic stability.)

This chapter is organized as follows. The basic theory of the calculus for a single queue is recalled in Sect. 2.2 and used in Sect. 2.3 to study an isolated signalized intersection. The simplest case of the queue formed by a single constant flow of arriving vehicles and its dependence on the green duration is well known (Newell 1989, pp. 33–37). But even for this case, as seen in Sect. 2.3.1, network calculus offers a deeper analysis by providing bounds on queue length and busy period when vehicles arrive in bursts or platoons. This analysis readily extends to an intersection with multiple phases. The treatment in Sect. 2.3.2 of the fixed-cycle controller extends that of (Allsop 1972) and (Newell 1989, §2.2) by including the impact of traffic bursts.

A fixed-cycle controller is inevitably wasteful because sometimes it actuates phases with no queue even though other phases have queues. This waste is eliminated by the work-conserving controllers considered in Sect. 2.3.3. In the case that only one phase can be actuated at a time, work-conserving controllers are always superior to fixed-cycle controllers in the sense that the former minimize a weighted sum of queue lengths (Sect. 2.3.3.1, Theorem 3).

Two counter-examples in Sect. 2.3.3.2 show that obvious extensions of Theorem 3 are false. The first example presents an unstable work-conserving single-phase controller for a two-intersection network. The second example exhibits an unstable work-conserving controller for a single intersection in which each stage activates two phases. In both examples, there exist stabilizing fixed-time controllers.

These counterexamples motivates the problem: Construct a stable, adaptive, work-conserving controller. For an isolated intersection the “max-pressure” controller of Sect. 2.3.3.3 is one solution. It works as follows. At each time, the controller calculates the pressure exerted by each stage. The pressure is defined as the sum of the queue lengths multiplied by the saturation rates of all the phases actuated by the stage. The max-pressure controller selects the stage that exerts the maximum pressure. Theorem 5 states that the max-pressure controller is stabilizing whenever there exists a stabilizing fixed-cycle controller.

The problem for an arbitrary network of signalized intersections is treated in Sect. 2.4. The network calculus model is developed in Sect. 2.4.1. Once the model is laid out, Corollary 1 yields performance bounds for a fixed-cycle control scheme in Sect. 2.4.2. The max-pressure controller is described in Sect. 2.4.3. The pressure exerted by a stage is now different: it is the sum of the upstream queue lengths minus the downstream queue lengths (weighted by the turn ratio) multiplied by the saturation rates of all the phases actuated by the stage. Theorem 7 extends Theorem 5 to networks. This appears to be the first adaptive, provably stable controller in the literature.

The discussion in Sect. 2.5 provides the mathematical intuition underlying the max-pressure controller; compares it to other controllers presented in the literature; outlines the major limitations of the store and forward model; and poses some questions.

2.2 Network Calculus for a Single Queue

Time is discrete: \(t = 0,1,\cdots \). \(\mathcal{F}\) (\(\mathcal{F}_{0}\)) denotes the set of all nonnegative, increasing functions f (with f(0) = 0). Consider a queuing system with cumulative arrivals \(A \in \mathcal{F}_{0}\), cumulative departures \(B \in \mathcal{F}_{0}\), and cumulative (virtual) service completions \(C \in \mathcal{F}_{0}\). See Fig. 2.1. Let q(t) denote the queue size at time t, with q(0) = 0. q(t) satisfies Lindley’s equation,

$$q(t + 1) = [q(t) - c(t)]_{+} + a(t + 1),\;\;t \geq 0.$$
(2.1)

(Notation: \([x]_{+} =\max \{ 0,x\}\).) In (2.1) \(a(t) = A(t) - A(t - 1)\) and \(c(t) = C(t) - C(t - 1)\) are respectively the numbers of arrivals and (virtual) service completions in period t. (Take \(A(-1) = C(-1) = 0\).)

Fig. 2.1
figure 1

A queuing system with arrivals A, departures B, service C

Full size image

For \(f \in \mathcal{F}\) and \(s \leq t\), let f(t, s) = f(t) − f(s). Recall that q(0) = 0. Lemma 1 is proved in Appendix A.

Lemma 1 ((Chang 2000, Lemma 1.3.1)). 

For all \(t \geq 0\) the queue size is

$$q(t) =\max \limits_{0\leq s\leq t}[A(t,s) - C(t - 1,s)],$$
(2.2)

and the cumulative departures \(B(t) = A(t) - q(t)\) are

$$B(t) =\min \limits_{0\leq s\leq t}[A(s) + C(t - 1,s)].$$
(2.3)

Definition 1.

The arrival process \(A \in \mathcal{F}_{0}\) is upper-bounded by \(f_{1} \in \mathcal{F}_{0}\) if \(A(t,s) \leq f_{1}(t - s)\) for all \(t \geq s\). The service process \(C \in \mathcal{F}_{0}\) provides service \(f_{2} \in \mathcal{F}_{0}\) if \(C(t - 1,s)\geq f_{2}(t - s)\) for all \(t \geq s\).

Theorem 1 is proved in Appendix B.

Theorem 1 ((Chang 2000, Theorem 2.2.8)). 

If A is upper-bounded by f 1 and C provides f 2,

$$q(t) \leq \max _{0\,\leq \,\tau \,\leq \,t}[f_{1}(\tau ) - f_{2}(\tau )],$$
(2.4)
$$B(t,s) \leq A(t) - B(s) \leq \max _{0\,\leq \,\tau }[f_{1}(t - s + \tau ) - f_{2}(\tau )].$$
(2.5)

The delay d(t) of the last arrival before t is bounded by

$$d(t) \leq \min \{ d \geq 0\ \vert \ f_{1}(\tau ) \leq f_{2}(\tau + d - 1),\tau = 1,\cdots \,,t\}.$$
(2.6)

The duration of any busy period is bounded by

$$BP =\max \{ b\ \vert \ f_{1}(\tau ) > f_{2}(\tau ),\tau = 1,\cdots \,,b\}.$$
(2.7)

Remark.

From (2.4) and (2.6) the queue size and delay are respectively bounded by the vertical and horizontal distances between f 1 and f 2, and from (2.7) the busy period is bounded by the first time the graphs of \(f_{1},f_{2}\) intersect, as in Fig. 2.2a. Thus the most important performance measures are captured by the curves f 1 and f 2.

Fig. 2.2
figure 2

Maximum queue size and delay: (a) general case, (b) Corollary 1

Full size image

Definition 2.

The arrival process A is \((\sigma, \rho )\) upper-bounded if it is upper-bounded by \(f_{1}(t) = \sigma + \rho t\). The service process C provides (c, r) service if it provides service \(f_{2}(t) = c[t - r]_{+}\). One also says that A is bounded by rate \(\rho \) with burst size \(\sigma \) and \(\sigma \) serves at rate c with delay r.

Theorem 1 is used in the paper in the simpler setting of Corollary 1.

Corollary 1.

Suppose A is \((\sigma, \rho )\) upper-bounded, C provides service (c,r), and \(c \geq \rho \) . Then

$$\displaystyle\begin{array}{rcl} & q(t) \leq \sigma + \rho \min \{t,r\} \leq (\sigma + \rho r),&\end{array}$$
(2.8)
$$\displaystyle\begin{array}{rcl}& B\mbox{ is $(\sigma + \rho r,\rho )$} \ bounded.&\end{array}$$
(2.9)

The maximum queue size, delay, and busy period are bounded as

$$q(t) \leq \sigma + \rho r,\;\;d(t) \leq r + \sigma /c,\;\;BP \leq (\sigma + cr)/(c - \rho ).$$
(2.10)

Proof.

Using \(f_{1}(t) = \sigma + \rho t\) and f 2(t) = c[t − r] +  in (2.4), (2.5), (2.6), and (2.7) yield (2.8)–(2.10) as can be seen from Fig. 2.2b.

2.3 Performance Bounds for a Single Intersection

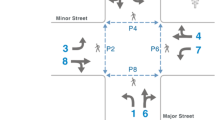
Consider a signalized intersection with input links \(l \in I\), and output links \(m \in O\). A vehicle arriving on input link l can cross the intersection and move to one of several output links m. A phase is any movement, denoted by the associated input–output pair (l, m). Not every movement is permitted, e.g., U-turns or left turns may be prohibited. A set of phases may be simultaneously permitted. Such a set U is called a stage; \(\mathcal{U}\) denotes the set of all stages.

For example, the standard intersection of Fig. 2.3 (left) has four input and four output links, both labeled \(1,\ldots, 4\); eight permitted phases, \(\phi _{1},\ldots, \phi _{8}\); and eight stages, each actuating two phases:

$$\{\phi _{1},\phi _{5}\},\{\phi _{1},\phi _{6}\},\{\phi _{2},\phi _{5}\},\{\phi _{2},\phi _{6}\},\{\phi _{3},\phi _{7}\},\{\phi _{3},\phi _{8}\},\{\phi _{4},\phi _{7}\},\{\phi _{4},\phi _{8}\}.$$
(2.11)
Fig. 2.3
figure 3

The eight phases of a standard intersection (left) and the matrix representation for the stage \(\{\phi _{1},\phi _{5}\}\) (right)

Full size image

An intersection controller selects one stage \(u(t) \in \mathcal{U}\) for each \(t = 0,1,\cdots \). If the sequence u(t) is periodic, the controller is called pre-timed or fixed-cycle and the period T is the cycle. No vehicle movement is permitted for some portion of the cycle. This enforced idleness of duration L is required for pedestrian movement or for an amber light between successive transitions in u(t). Thus within each cycle T − L periods are available for vehicle movement.

A periodic control sequence selects stage u(t) = U for duration \(d_{U} \geq 0\) within each cycle. For performance analysis using network calculus, the parameters that matter are the durations \(\{d_{U},U \in \mathcal{U}\}\), whereas the order within a cycle in which u(t) takes these values is not relevant. (The order is crucial in designing signal offsets.) Consequently, one may assume that each cycle is comprised of a fixed order of all phases; however, the duration of the phases may change from one cycle to the next.

The nonnegative durations must satisfy

$$\displaystyle\sum _{U\,\in \,\mathcal{U}}d_{U} \leq T - L.$$
(2.12)

A fixed-cycle controller is specified by the cycle T and durations {d U } satisfying (2.12).

We make two assumptions concerning the configuration of queues and service rates. First, vehicles entering input link l in order to make movement (l, m) join a separate queue dedicated to that movement. For example, the standard intersection of Fig. 2.3 has eight queues, one for each phase. A separate queue for each phase requires more space. For performance analysis, this assumption implies that vehicles intending different movements join different queues and do not block each other. Thus in Fig. 2.3, if the same queue was used by both phases \(\phi \,_{7}\) and \(\phi _{4}\), a vehicle intending to make a through movement \(\phi _{4}\) may be blocked by a vehicle in front of it intending to make a left turn \(\phi _{7}\). Such “head of line” blocking is precluded by this assumption. The loss of throughput due to head of line blocking could be evaluated as in the study of “input-buffered switches” (McKeown et al. 1993), but such an evaluation is not carried out here.

Second, it is assumed that whenever phase (l, m) is actuated, vehicles in queue (l, m) leave this queue at a known saturation rate of s(l, m) vehicles per period, whereas if (l, m) is not actuated, no vehicle in this queue can leave. The saturation rate is associated with the phase and not with the stage. Thus in the standard intersection, in both stages \(\{\phi _{1},\phi _{4}\}\) and \(\{\phi _{1},\phi _{6}\}\), the queue associated with \(\phi _{1}\) is served at the same saturation rate.

2.3.1 Analysis of a Single Movement

The following notation is used.

$$\displaystyle\begin{array}{rcl} (l,m)& =& \mbox{ phase with input link $l$ and output link $m$} \\ s(l,m)& =& \mbox{ saturation rate for phase $(l,m)$} \\ g(l,m)(r(l,m))& =& \mbox{ effective green (red) duration for phase $(l,m)$} \\ c(l,m)(t)& =& \mbox{ service that phase $(l,m)$ receives in period $t$} \\ C(l,m)(t)& =& \mbox{ cumulative service for phase $(l,m)$ up to $t$} \\ \end{array}$$

Consider a fixed-cycle controller with cycle T and durations \(\{d_{U}\}\) satisfying (2.12). Let \(u(t),t \geq 0\), be the resulting periodic signal control sequence. The service c(l, m)(t) that phase (l, m) receives depends on when u(t) actuates the phase and its saturation rate:

$$c(l,m)(t) = \left \{\begin{array}{ll} s(l,m),\,\,\,\,\mbox{ if }(l,m) \in u(t)\\ 0,\,\,\,\, \mbox{ if } (l, m)\not\in u(t) \end{array} \right..$$
(2.13)

The resulting cumulative service process is (with C(l, m)(0) = 0)

$$C(l,m)(t) =\displaystyle\sum _{ r\,=\,1}^{t}c(l,m)(r) = s(l,m)\displaystyle\sum _{ r\,=\,1}^{t}\mathbf{1}[(l,m) \in u(r)],\;t \geq 1,$$
(2.14)

in which \(\mathbf{1}[\cdot ]\) is the indicator function. In each cycle phase \((l,m)\) is actuated for a (green) duration g(l, m), and it is not actuated for an effective (red) duration r(l, m):

$$g(l,m) =\displaystyle\sum \{ d_{U}\ \vert \ (l,m) \in U\};\;r(l,m) = T - g(l,m).$$
(2.15)

So the average service rate for the queue at phase (l, m) is

$$\lim \limits_{t\rightarrow \infty }C(l,m)(t)/t = s(l,m)g(l,m)/T.$$

Lemma 2.

The cumulative service process C(l,m)(t) provides service rate s(l,m) g(l,m)∕T with delay r(l,m).

Proof.

Drop the phase index and write C(t) = C(l, m)(t), s = s(l, m), g = g(l, m), r = r(l, m), etc. Let c = sg ∕ T be the average service rate. Assisted by Fig. 2.4a and c one can see that if 0 ≤ t − 1 − s = kT + τ for some k and τ = (t − 1 − s) − kT,

$$C(t-1,s) = C(t-1)-C(s) = ckT+\displaystyle\sum _{i=t-1-\tau }^{t-1}c(i) \geq ckT+s[\tau -r]_{ +} \geq c[t-s-r]_{+},$$
(2.16)

so that C(t) provides (c, r) service.

Fig. 2.4
figure 4

(a) Service rate c(t) for one phase: s is saturation rate, g, r, T are the durations of effective green, effective red, and cycle. (b) The cumulative arrival process A(t) is \((\sigma, \rho )\) upper-bounded. (c) The cumulative service process C(t) provides service rate c = sg ∕ T with delay r. (d) \(C(t,\tau ) \geq s[t - \tau - r]_{+}\) for \(t - \tau \leq T\)

Full size image

Suppose arriving vehicles intending to move during phase (l, m) form the (σ, ρ) upper-bounded process A(t):

$$A(t) - A(s) \leq \sigma + \rho (t - s),\;t \geq s.$$
(2.17)

Suppose

$$\rho \leq c = sg/T.$$
(2.18)

By Corollary 1 the queue size, the delay at the signal, and the busy period for this movement are then bounded by

$$q(t) \leq \sigma + \rho (T - g)$$
(2.19)
$$d(t) \leq (T - g) + \sigma /c$$
(2.20)
$$BP \leq (\sigma + c(T - g))/(c - \rho ).$$
(2.21)

The departure process B(t) is (σ + ρ(T − g), ρ) upper-bounded:

$$B(t) - B(s) \leq \sigma + \rho (T - g) + \rho (t - s).$$
(2.22)

Note that (2.16) and hence (2.19)–(2.22) hold even if the g duration is distributed anywhere within the cycle instead of contiguously as in Fig. 2.4a.

The model is simple. According to (2.17), vehicles arrive at average rate ρ and at most σ vehicles arrive in a “burst” or “platoon.” If the average arrival rate is not more than the average service rate, the queue size is bounded by the maximum number of arrivals during an effective red, namely σ + ρ(T − g); and the longest delay is faced by the last vehicle arriving in a burst of size σ just before red, namely (T − g) + σ ∕ c. Lastly, the burst size of the departure process may exceed the arrival burst size σ by the number of vehicles ρ(T − g) that can accumulate during red.

Suppose we know that the busy period never exceeds the cycle T, i.e., the queue clears in every cycle. In this case we can see from Fig. 2.4d or (2.16) that C(t) provides the larger service s[t − r] + , so in place of (2.21) we have the bound

$$BP \leq \frac{\sigma + sr} {s - \rho }, $$

which is smaller than T if

$$\sigma + \rho T < gs.$$
(2.23)

For arrivals with no bursts, σ = 0, (2.23) reduces to ρ < sg ∕ T = c, as in (Newell 1989, Eq. (2.1.6)). In reality, because of an upstream signal, the burst σ is likely to increase linearly with T. If σ ≈ ηT, (2.23) becomes

$$\eta + \rho < gs/T,$$
(2.24)

which requires a larger proportion of the cycle to be green than (2.18) in order to clear the queue in every cycle.

Remark.

The parameters of the performance bounds (2.19)–(2.21) may be estimated if individual vehicle arrivals a(t) are measured by a detector located sufficiently upstream of the signal so that the queue rarely reaches the location. Then:

  • Cumulative arrivals A(t) = ∑ 1 t a(τ)

  • Average arrival rate ρ ≈ A(t) ∕ t

  • Burst size σ ≈ max s ≤ t {[∑ s t(a(τ)] − ρ(t − s)]}

  • Service parameters g, r, T are known from the signal plan.

Estimating saturation rate s requires measurement of departures from the signal during green [see, e.g., (Kwong et al. 2009, §3.3)]. But note that the max pressure algorithm does not require knowledge of these parameters.

2.3.2 Analysis of All Movements at an Intersection

A stage U is henceforth represented by the binary \(I \times O\) matrix U, with U(l, m) = 1 or 0 accordingly as U actuates phase (l, m) or not. (I (O) is the set of input (output) links at the intersection. See Fig. 2.3 (right).) \(\mathcal{U}\) is the set of all stages or control matrices. Any signal controller is represented by a matrix sequence \(u(t),\;t \geq 0\), with values in \(\mathcal{U}\).

Let \(S =\{ s(l,m),\;l \in I,m \in O\}\) denote the matrix of saturation rates of all phases. If phase (l, m) is not permitted, take s(l, m) = 0. The matrix \(S \circ U\) defined by coordinate-wise multiplication, \((S \circ U)(l,m) = s(l,m)U(l,m)\), gives the service rates of all the phases simultaneously actuated by U.

Consider a fixed-cycle controller \(u(t),\;t \geq 0\), with cycle T. During each cycle u(t) takes the value \(U \in \mathcal{U}\) for duration d U , with

$$\displaystyle\sum _{U}d_{U} \leq T - L.$$

Expressed as proportions of the cycle, the durations

$$\lambda _{U} = d_{U}/T,\;U \in \mathcal{U},$$

satisfy

$$\displaystyle\sum _{U\,\in \,\mathcal{U}}\lambda _{U} \leq 1 - L/T;\;\lambda _{U} \geq 0.$$
(2.25)

We identify a fixed-cycle controller with the array \([\lambda _{U},U \in \mathcal{U};T]\). In each cycle, this controller actuates phase (l, m) for an effective green duration

$$g(l,m) = T\displaystyle\sum _{U\,\in \,\mathcal{U}}\lambda _{U}U(l,m),$$

an effective red duration

$$r(l,m) = T - g(l,m) = T[1 -\displaystyle\sum _{U}\lambda _{U}U(l,m)],$$

and provides average service rate

$$c(l,m) = s(l,m)g(l,m)/T = (S \circ \displaystyle\sum _{U}\lambda _{U}U)(l,m).$$

By Lemma 2 the fixed-cycle controller \([\lambda _{U},U \in \mathcal{U};T]\) serves phase (l, m) at rate c(l, m) with delay r(l, m).

In a discrete-time setting, each duration g(l, m) is an integer number of periods, so the proportions \(\lambda _{U}\) are multiples of 1 ∕ T. If we allow the proportions to be arbitrary real numbers in [0, 1] the service that fixed-cycle controllers can provide is characterized by Theorem 2.

Theorem 2.

There is a fixed-cycle controller that serves each phase (l,m) at rate \(c(l,m)\) with delay r(l,m) if and only if there exist \(\lambda _{U} \geq 0\), \(\sum _{U}\lambda _{U} \leq 1 - L/T\) such that

$$c(l,m) = \left (S \circ \displaystyle\sum _{U}\lambda _{U}U\right )(l,m),\;r(l,m) = T[1 -\left (\displaystyle\sum _{U}\lambda _{U}U\right )(l,m)].$$
(2.26)

If vehicle arrivals for phase (l,m) are \((\sigma (l,m),\rho (l,m))\) upper-bounded and \(\rho (l,m) \leq c(l,m)\) , these vehicles will experience a queue size, delay, and busy period bounded by

$$\displaystyle\begin{array}{rcl} & q(l,m)(t) \leq \sigma (l,m) + \rho (l,m)r(l,m) &\end{array}$$
(2.27)
$$\displaystyle\begin{array}{rcl} & d(l,m) \leq r(l,m) + \sigma (l,m)/c(l,m) & \end{array}$$
(2.28)
$$\displaystyle\begin{array}{rcl} & BP(l,m) \leq [\sigma (l,m) + c(l,m)r(l,m)]/[c(l,m) - \rho (l,m)]&\end{array}$$
(2.29)

The departure process from phase (l,m) is bounded by rate \(\rho (l,m)\) with burst size \(\sigma (l,m) + \rho (l,m)r(l,m)\).

If the burst size \(\sigma (l,m) = \eta (l,m)T\) , the queue size bound is

$$q(l,m)(t) \leq T\left [\eta (l,m) + (1 -\left (\displaystyle\sum _{U}\lambda _{U}U\right )(l,m))\rho (l,m)\right ],$$
(2.30)

and the queue is cleared in each cycle if

$$\eta (l,m) + \rho (l,m) \leq c(l,m) = \left (S \circ \displaystyle\sum _{U}\lambda _{U}U\right )(l,m).$$
(2.31)

Theorem 2 illustrates the use of network calculus. In a deterministic model that ignores bursts, \(\sigma (l,m) = 0\), the stability condition is \(\rho (l,m) \leq c(l,m)\) and so, by (2.31), the queue must clear in every cycle; hence this deterministic model cannot explain why vehicles may wait at the intersection for one or more cycles, except by hypothesizing over-saturated traffic (\(\rho (l,m) > c(l,m)\)). By explicitly modeling bursts (which, in turn, may be due to a variety of conditions upstream of the intersection) (2.27) and (2.29) show how some vehicles may wait for a long time, even with undersaturated traffic (\(\rho (l,m) < c(l,m)\)). One way of explaining long delay with undersaturated traffic is to consider stochastic arrivals, whose variability creates bursts as in (Newell 1965). However, although there is no stochastic analysis of queues for a network of intersections, network calculus can be fruitfully used as will seen in Sect. 2.4.

A larger cycle T increases (1 − L ∕ T), so by (2.26) it increases the set of arrival rates \(\rho (l,m)\) that can be accommodated, i.e., \(\rho (l,m) \leq c(l,m)\). However, a larger T also increases the queue size bound (2.30), because it increases both the burst entering the queue (from upstream) and the red duration during which the queue grows (see (2.30)). Hence it is of interest to minimize T as in Corollary 2 which, for the no-burst case \(\sigma (l,m) = 0\), is due to (Allsop 1972).

Corollary 2.

The shortest cycle needed by a fixed-cycle controller to accommodate all the arrivals bounded by rate \(\rho (l,m)\) with burst size \(\sigma (l,m) = \eta (l,m)T\) and clear all queues in every cycle is

$$T = \frac{L} {1 -\displaystyle\sum \lambda _{U}^{{\ast}}},$$
(2.32)

in which \(\{\lambda _{U}^{{\ast}}\}\) is the solution of the linear program:

$$\begin{array}{rlrlrl} \min &\displaystyle\sum \lambda _{U} & & \\ \text{s.t.}\, &(S \circ \displaystyle\sum \lambda _{U}U)(l,m) \geq \eta (l,m) + \rho (l,m),\;\text{ all }(l,m) & & \\ &\lambda _{U} \geq 0\;\text{ all }U \in \mathcal{U}. &\end{array}$$
(2.33)

If \(\sum \lambda _{U}^{{\ast}} > 1\) , no fixed-cycle controller can clear all queues in every cycle.

Instead of minimizing the cycle, one can formulate a linear programming problem that minimizes (say) a linear combination of queue sizes, delays, or clearance times using (2.27)–(2.29), thereby extending the discussion in (Newell 1989, §2.2).

Remark.

In the special case that each control value or stage U actuates only one phase (l, m), one may identify U with (l, m) and write \(\lambda _{U} = \lambda _{(l,m)}\). The optimal solution to (2.33) is

$$\lambda _{(l,m)}^{{\ast}} = \frac{\rho (l,m) + \eta (l,m)} {s(l,m)}, $$

and the shortest cycle is

$$T = \frac{L} {1 -\displaystyle\sum _{(l,m)}[(\rho (l,m) + \eta (l,m))/s(l,m)]},$$

which may be compared with Webster’s rule.

2.3.3 Work-Conserving Controllers

A fixed-cycle controller \([\lambda _{U},U \in \mathcal{U};T]\) assigns the intersection to stage U for duration \(\lambda _{U}T\) in each cycle. Consequently there will be time instants when stage u(t) = U serves no queue even though there are nonempty queues at phases not served by U. To prevent this waste (which will lead to larger delays than necessary) the signal controller must select the control matrix as a function of the queue sizes, i.e., it must be traffic-responsive or in feedback form. Of special interest are work-conserving controllers, which are never idle when there is a nonempty queue. The controller still has a fixed cycle T, for L periods of which the intersection is not used by vehicles, but it need not be periodic.

We ignore the discrete-time restriction and allow u(t) to take a value U for an arbitrary portion \(\lambda _{U}\) of a period. In effect at each t the controller selects u(t) from the convex set \([\mathcal{U}]\):

$$[\mathcal{U}] = \left\{\displaystyle\sum \lambda _{U}U\ \vert \ \lambda _{U} \geq 0,\;\displaystyle\sum \lambda _{U} \leq 1 - L/T\right\}.$$
(2.34)

Call \([\mathcal{U}]\) the set of relaxed controls. Let \(u(t) =\sum \lambda _{U}(t)U,\;t \geq 0,\) be a relaxed control sequence. Suppose vehicle arrivals A (l, m)(t) for phase (l, m) are \((\sigma (l,m),\rho (l,m))\) upper-bounded. These vehicles join queue (l, m), which therefore evolves as \((q_{(l,m)}(0) = 0)\)

$$q_{(l,m)}(t + 1) = [q_{(l,m)}(t) -\left (S \circ \displaystyle\sum \lambda _{U}(t)U\right )(l,m)]_{+} + a_{(l,m)}(t + 1),\;t \geq 0.$$
(2.35)

Here \(a_{(l,m)}(t) = A_{(l,m)}(t) - A_{(l,m)}(t - 1)\).

Definition 3.

The controller \(u(t) =\sum \lambda _{U}(t)U,\;t \geq 0,\) is work-conserving if

$$\displaystyle\begin{array}{rcl} & & \exists U,\;\forall (l,m)\mbox{ with }U(l,m) = 1 : q_{(l,m)}(t) - (S \circ \displaystyle\sum \lambda _{U}(t)U)(l,m) < 0 \\ & & \Rightarrow \forall (l,m) : q_{(l,m)}(t) - (S \circ \displaystyle\sum \lambda _{U}(t)U)(l,m) \leq 0. \end{array}$$
(2.36)

In words: control U may waste service in every phase that U actuates only if no phase has a nonzero queue.

Definition 4.

The controller \(u(t) =\sum _{U}\lambda _{U}(t)U,\;t \geq 0,\) is stabilizing if all queues are bounded:

$$\max \limits_{(l,m)}\sup _{t\geq 0}q_{(l,m)}(t) < \infty.$$

2.3.3.1 Actuating Single Phase Intersections

This section is devoted to single-phase intersections, in which each stage U actuates only one phase, say (l, m), \(U = \delta _{(l,m)}\) is the \(I \times O\) matrix whose (l, m)th entry is 1 and other entries are 0. A relaxed control matrix has the form \(\sum \lambda _{(l,m)}\delta _{(l,m)}\). Let \(u(t) =\sum \lambda _{(l,m)}(t)\delta _{(l,m)},\;t \geq 0,\) be the control sequence. Then (2.35) simplifies:

$$q_{(l,m)}(t + 1) = [q_{(l,m)}(t) - s(l,m)\lambda _{(l,m)}(t)]_{+} + a_{(l,m)}(t + 1),\;t \geq 0.$$
(2.37)

Here s(l, m) is the saturation rate for phase (l, m). Equation (2.36) also simplifies: \(u(t) =\sum \lambda _{(l,m)}(t)\delta _{(l,m)},t \geq 0,\) is work-conserving if

$$\displaystyle\begin{array}{rcl} & \exists (l,m) :\; q_{(l,m)}(t) - s(l,m)\lambda _{(l,m)}(t) < 0 \\ \Rightarrow &\forall (l,m) :\; q_{(l,m)}(t) - s(l,m)\lambda _{(l,m)}(t) \leq 0.\end{array}$$
(2.38)

Let \(u(t),\;t \geq 0\), be work-conserving and define the weighted total queue size

$$q(t) =\displaystyle\sum _{(l,m)}\frac{q_{(l,m)}(t)} {s(l,m)}.$$

From (2.37)

$$q(t + 1) =\displaystyle\sum \left [\frac{q_{(l,m)}(t)} {s(l,m)} - \lambda _{(l,m)}(t)\right ]_{+} +\displaystyle\sum \frac{a_{(l,m)}(t + 1)} {s(l,m)}.$$
(2.39)

Because of (2.38) terms within the square brackets \([\quad ]\) all have the same sign, and so

$$\displaystyle\begin{array}{rcl} q(t + 1) = \left [\displaystyle\sum \left (\frac{q_{(l,m)}(t)} {s(l,m)} -\lambda _{(l,m)}(t)\right )\right ]_{+}+\displaystyle\sum \frac{a_{(l,m)}(t + 1)} {s(l,m)} = [q(t) - c(t)]_{+}+a(t+1),& & \\ \end{array}$$

in which \(a(t) =\sum [a_{(l,m)}(t)/s(l,m)]\), and

$$c(t) =\displaystyle\sum \lambda _{(l,m)}(t) = 1 - L/T.$$
(2.40)

Theorem 3.

The weighted arrivals \(A(t) =\sum [A_{(l,m)}(t)/s(l,m)]\) are upper-bounded by rate \(\rho =\sum [\rho (l,m)/s(l,m)]\) with burst size \(\sigma =\sum [\sigma (l,m)/s(l,m)]\) . The cumulative service \(C(t) =\sum _{s\leq t}c(s)\) serves at rate 1 − L∕T with delay L. If

$$\rho =\displaystyle\sum [\rho (l,m)/s(l,m)] \leq 1 - L/T,$$
(2.41)

the size, the delay at the signal, and the busy period of the weighted queue are bounded by

$$\displaystyle\begin{array}{rcl} & q(t) \leq \sigma + \rho L, & \end{array}$$
(2.42)
$$\displaystyle\begin{array}{rcl} & d(t) \leq L + \sigma /[1 - L/T], & \end{array}$$
(2.43)
$$\displaystyle\begin{array}{rcl} & BP \leq [\sigma + (1 - L/T)L][1 - L/T - \rho ]&.\end{array}$$
(2.44)

If the bursts \(\sigma (l,m) = \eta (l,m)T\) and

$$\rho + [\displaystyle\sum \eta (l,m)/s(l,m)] \leq 1 - L/T,$$
(2.45)

then every queue will be cleared in every cycle.

Consequently, if any fixed-cycle controller is stabilizing, then every work-conserving controller is also stabilizing.

Proof.

First, for \(s \leq t\),

$$\displaystyle\begin{array}{rcl} A(t)-A(s) =\displaystyle\sum \frac{A_{(l,m)}(t)-A_{(l,m)}(s)} {s(l,m)} \leq \displaystyle\sum [\sigma (l,m)+\rho (l,m)(t-s)]/s(l,m) = \sigma +\rho (t-s).& & \\ \end{array}$$

Next, by (2.40) and Lemma 2, C(t) serves at rate \([1 - L/T]\) with delay L. Then (2.18)–(2.21) translate into (2.41)–(2.44), and (2.24) into (2.45). The last assertion follows from Theorem 2. \(\square \)

Consider the simplest example of an intersection with two phases, only one of which can be actuated at any time. The controller in (Mirchandani and Zou 2007) actuates one phase until its queue is empty, whereupon it switches to the other phase. The controller in (Lin and Lo 2008) switches from phase 1 to phase 2 accordingly as the ratio of the queues \(q_{1}(t)/q_{2}(t)\) drops below or exceeds a desired ratio. In network calculus terms this ratio is analogous to \([(\rho _{1} + \eta _{1})/s_{1}]/[(\rho _{2} + \eta _{2})/s_{2}]\). One may consider a third controller that gives priority to say, phase 1, and actuates that phase whenever q 1(t) > 0; otherwise it actuates phase 2. (Priorities may be used for buses or emergency vehicles.) These three controllers are all work-conserving, and Theorem 2 gives the same bounds on the weighted queue size and delay. Of course, bounds on individual queue lengths will be different for each controller: for example, the queue at phase 1 will have the smallest bound for the third controller that gives priority to phase 1.

In (Mirchandani and Zou 2007) and (Lin and Lo 2008) arrivals are Poisson processes, and evaluating performance measures such as queue size and delay ultimately requires simulation, although (Mirchandani and Zou 2007) also provides an analytical approximation. The complexity of the analysis and simulations grows exponentially with the number of phases. By contrast, network calculus provides simple computable bounds for arbitrarily many phases. Furthermore, when we consider a network of intersections, arrivals are not Poisson and standard stochastic queuing approaches are inapplicable, even though network calculus bounds can be constructed as in Sect. 2.4.

Condition (2.45) to clear all queues is significantly weaker than its counterpart in (2.33) for fixed-cycle controllers, and shows the benefit of work-conserving controllers. In fact the following result proved in Appendix C.

Theorem 4.

Let \({Q}^{w}(t) =\{ q_{(l,m)}^{w}(t)\}\) be the queues for any work-conserving controller and let \(Q(t) =\{ q_{(l,m)}(t)\}\) be the queues for any controller, with \({Q}^{w}(0) = Q(0) = 0\) . Then for all t,

$$\displaystyle\sum _{(l,m)}\frac{q_{(l,m)}^{w}(t)} {s(l,m)} \leq \displaystyle\sum _{(l,m)}\frac{q_{(l,m)}(t)} {s(l,m)}.$$
(2.46)

2.3.3.2 Two Counter-Examples

The first example shows that Theorem 3 does not extend to a network of two intersections in which only one phase is actuated in each stage. In the network of Fig. 2.5 phases \(\phi _{1}\) and \(\phi _{4}\) are fast, with saturation rates \(s_{1} = s_{4} = \infty \); \(\phi _{2}\) and \(\phi _{3}\) are slow, with s 2 = s 3 = 1. 5. The arrival rate is \(\rho = 1\)​, with no bursts. T = 1​, L = 0. Clearly there is a stabilizing fixed-time controller for this network. Now consider work-conserving controllers that give priority to the slow phases, \(\phi _{2},\phi _{3}\), i.e., these phases are served immediately if they have a nonempty queue. Consider the initial condition: \(q_{1}(0) = 1,\;q_{2}(0) = q_{3}(0) = q_{4}(0) = 0\). One can check that

$$q_{1}(4) = 2,\;q_{1}(8) = 4,\cdots \,,q_{1}(4n) = 2n,\;n \geq 1,$$

so that these controllers are unstable. This example is from (Lu and Kumar 1991). There are also examples that do not require infinite service rates, but these are more complex to describe, see, e.g., (Dai 1995). The second example shows that Theorem 3 does not extend to the case of the isolated intersection of Fig. 2.3 in which multiple phases may be actuated simultaneously. The intersection depicted in Fig. 2.6 only includes part of the standard intersection. (The example obviously extends to the standard intersection.)

Fig. 2.5
figure 5

One phase can be actuated at a time in each intersection

Full size image
Fig. 2.6
figure 6

The intersection permits four of eight phases of the standard intersection

Full size image

There are four phases and three stages, each actuating one phase pair (cf (2.11)):

$$\{\phi _{1},\phi _{2}\},\{\phi _{3},\phi _{4}\},\{\phi _{2},\phi _{4}\}.$$

The cumulative arrivals at each phase have the same rate \(\rho \) with burst size \(\sigma \). The saturation rate at all phases is the same, s = 1. Let \(\alpha = [1 - L/T]\). Consider the fixed-cycle controller that actuates phase pairs \(\{\phi _{1},\phi _{2}\}\) and \(\{\phi _{3},\phi _{4}\}\) each for half the time, i.e., for duration \(0.5[T - L] = 0.5\alpha T\) in each cycle. By Theorem 2, this controller serves every phase at rate \(0.5\alpha \) with delay 0. 5[T + L] and if

$$\rho \leq 0.5\alpha, $$
(2.47)

the controller is stabilizing, and the queue in every phase is bounded by

$$q(t) \leq \sigma + \rho \times 0.5[T + L].$$

There will be instants when vehicles simultaneously arrive for phases \(\phi _{2}\) and \(\phi _{4}\). Suppose this occurs at rate \(\delta > 0\). Formally:

$$\displaystyle\sum _{s<i\leq t}\mathbf{1}[a_{2}(i) > 0\mbox{ and }a_{4}(i) > 0] \geq \delta (t - s).$$
(2.48)

Now consider any controller \(u(t),\;t \geq 0\), that selects stage \(\{\phi _{2},\phi _{4}\}\) whenever both \(q_{2}(t) > 0\) and \(q_{4}(t) > 0\), i.e., \(\{\phi _{2},\phi _{4}\}\) gets priority in the event that vehicles are queued up at both phases. Because of the priority and (2.48), \(\{\phi _{2},\phi _{4}\}\) receives service for duration at least \(\delta T\) in each cycle; hence the two remaining pairs \(\{\phi _{1},\phi _{2}\},\{\phi _{3},\phi _{4}\}\) together will receive service for duration at most \(T - L - \delta T\). Consequently one of these two pairs, say \(\{\phi _{1},\phi _{2}\}\), will receive service for duration at most \(0.5(T - L - \delta T)\) in each cycle that is at rate at most \(0.5(1 - L/T - \delta ) = 0.5(\alpha - \delta )\). Comparison with (2.47) shows that if

$$0.5(\alpha - \delta ) < \rho \leq 0.5\alpha, $$
(2.49)

every controller with this priority is unstable and the queue length at phase \(\phi _{1}\) must become unbounded! Note that any controller that always serves a nonempty queue while keeping this priority is work-conserving.

A controller that gives priority to \(\{\phi _{2},\phi _{4}\}\) if either q 2(t) > 0 or q 4(t) > 0 will have worse performance, since the instability condition (2.49) is replaced by the weaker inequality,

$$0.5(\alpha - \rho ) < \rho \leq 0.5\alpha.$$

Such a controller is commonly used to give priority to buses (Chada and Newland 2002).

It is easy to construct a stable work-conserving controller by modifying any stable fixed-cycle controller so that it actuates a phase with a nonempty queue whenever the controller becomes idle. (This recalls the common practice of terminating the green phase on a “cross street” when there is no queue.) However, this controller is not adaptive, since constructing a stable fixed-cycle controller requires knowledge of the demands. This suggests the following problem: Construct a stable, adaptive, work-conserving controller. The problem is solved in the next section for an isolated intersection.

2.3.3.3 The Adaptive Controller Problem

Here is the precise problem. For a relaxed control sequence \(u(t) =\sum \lambda _{U}(t)U\), \(t \geq 0\), the evolution of the intersection’s queues is given by \((q_{(l,m)}(0) = 0)\)

$$q_{(l,m)}(t + 1) = \Big{[}q_{(l,m)}(t) -\Big{(}S \circ \displaystyle\sum \lambda _{U}(t)U\Big{)}(l,m)\Big{]}_{+} + a_{(l,m)}(t + 1),\;\;t \geq 0.$$
(2.50)

Let q denote the array \(\{q_{(l,m)}\}\) of all the queues. The problem is to find a function \(\lambda _{U}^{{\ast}}(q)\) of q such that the feedback control sequence \(u(t) =\sum \lambda _{U}^{{\ast}}(q(t))U\) stabilizes the queues for any set of demands for which a stabilizing fixed-cycle controller exists. We exhibit such a feedback control.

Define the pressure exerted by stageU at q by

$$w(q,U) =\displaystyle\sum _{(l,m)}q_{(l,m)}S \circ U(l,m) =\displaystyle\sum _{(l,m)}q_{(l,m)}s(l,m)U(l,m),$$
(2.51)

i.e., it is the sum of the queue lengths multiplied by the saturation rates of the phases that U actuates. Extend linearly the pressure to any relaxed control \([U] =\sum \lambda _{U}U\),

$$w(q,[U]) =\displaystyle\sum \lambda _{U}w(q,U) =\displaystyle\sum q_{(l,m)}s(l,m)[U](l,m).$$

Define the max-pressure stage by

$${U}^{{\ast}}(q) =\arg \max \{ w(q,U)\ \vert \ U \in \mathcal{U}\}.$$
(2.52)

In (2.52) ties are broken arbitrarily. The name “max-pressure policy” was apparently first introduced in (Dai and Lin 2005), although similar policies were studied earlier; Tassiulas and Ephremides (1992) was the first study to investigate its stability properties in the context of wireless networks.

Definition 5.

The max-pressure controlleru  ∗ (t) selects the max-pressure stage at q(t):

$${u}^{{\ast}}(t) = (1 - L/T){U}^{{\ast}}(q(t)).$$

Lemma 3.

u ∗ (t) maximizes w(q,[U]) over the set \([\mathcal{U}]\) of relaxed controls.

Proof.

w(q, [U]) is linear in [U] and \([\mathcal{U}]\) is the convex hull of its vertices \(\{(1 - L/T)U,\;U \in \mathcal{U}\}\). Hence the maximum of w(q, [U]) is achieved at \((1 - L/T){U}^{{\ast}}(q)\).

Theorem 5.

Let q(t) be the queues resulting from the max-pressure controller:

$$q_{(l,m)}(t+1) = [q_{(l,m)}(t)-(S\circ (1-L/T){U}^{{\ast}}(q(t)))(l,m)]_{ +}+a_{(l,m)}(t+1),\;\;t \geq 0.$$
(2.53)

Suppose that in (2.53) the arrivals A (l,m) are \((\sigma (l,m),\rho (l,m))\) upper-bounded and there exists a (fixed-cycle) relaxed control [U] such that

$$c(l,m) = S \circ [U](l,m) > \rho (l,m),\mbox{ all }(l,m).$$
(2.54)

Then \(\{q(t),\;t \geq 0\}\) is a bounded sequence, i.e., the max-pressure controller is stabilizing.

Proof.

Write \({c}^{{\ast}}(l,m)(t) = (S \circ (1 - L/T){U}^{{\ast}}(q(t)))(l,m)\), so under the max-pressure controller

$$q_{(l,m)}(t + 1) = [q_{(l,m)}(t) - {c}^{{\ast}}(l,m)(t)]_{ +} + a_{(l,m)}(t + 1).$$
(2.55)

For any q let \(\vert q{\vert }^{2} =\sum q_{(l,m)}^{2}\). It is shown in Appendix D that there exist \(k < \infty \), \(\epsilon > 0\), and \(\sigma (t) \geq 0\) with \(\sum _{t}\sigma (t) < \infty \), so that

$$\vert q(t + 1){\vert }^{2} -\vert q(t){\vert }^{2} \leq k - (2\epsilon - \sigma (t))\vert q(t)\vert, $$
(2.56)

Suppose (2.56) holds. With T such that \(\sigma (t) < \epsilon, \;t \geq T\), (2.56) gives

$$\vert q(t + 1){\vert }^{2} -\vert q(t){\vert }^{2} \leq k - \epsilon \vert q(t)\vert, \;t > T,$$

and so

$$\vert q(t + 1){\vert }^{2} -\vert q(t){\vert }^{2} < 0,\;\vert q(t)\vert > k/\epsilon, \;t > T,$$

which implies that \(\vert q(t)\vert, \;t \geq 0,\) is bounded.

The max-pressure controller is adaptive since it requires no knowledge of the parameters \((\sigma (l,m),\rho (l,m))\) of the arrival processes. It is robust in the sense that if any controller can keep queues bounded, so can the max-pressure controller. From the proof of Theorem 5 one gains the intuition that the max-pressure controller attempts at each t to minimize | q(t + 1) | 2 given q(t).

2.4 Performance Bounds for a Network of Intersections

The model of a network of signalized intersections is formulated in Sect. 2.4.1. The performance bounds of Corollary 1 are applied to the network with fixed-cycle controllers in Sect. 2.4.2. The extension of the max-pressure controller to an arbitrary network is carried out in Sect. 2.4.3.

2.4.1 Network Model

This section is based on (Chang 2000, §1.7). The concept of router is needed to extend the discussion of Sect. 2.2 to a network of intersections. A router \(P \in \mathcal{F}\) is a network element with cumulative arrivals \(A \in \mathcal{F}\) and departures \(B \in \mathcal{F}\) given by B(t) = P(A(t)) for all t. The interpretation is that the router selects or samples P(n) among its first n arrivals so that B(t) = P(A(t)) is the cumulative number of selections by time t. Routers are used to model turn movements.

Suppose A is \((\sigma, \rho )\) upper-bounded, and P is \((\delta, \gamma )\) upper-bounded. Since

$$B(t)-B(s) = P(A(t))-P(A(s)) \leq \delta +\gamma (A(t)-A(s)) \leq (\delta +\gamma \sigma )+\gamma \rho (t-s),$$

it follows that B is \((\gamma \sigma + \delta, \gamma \rho )\) upper-bounded.

Figure 2.7 will help explain the notation and the model.

$$\displaystyle\begin{array}{rcl} \mathcal{L} =\{ 1,\cdots \,,L\}& =& \mbox{ set of all links, elements $l,m,k$} \\ \mathcal{N}& =& \mbox{ set of nodes or intersections, elements $n$} \\ I_{n}& \subset & \mathcal{L},\mbox{ set of input links to $n \in \mathcal{N}$} \\ O_{n}& \subset & \mathcal{L},\mbox{ set of output links from $n \in \mathcal{N}$} \\ E_{l},(\alpha _{l},\beta _{l})& =& \mbox{ external arrivals into link $l$, $(\alpha _{l},\beta _{l})$ upper-bounded} \\ B_{(l,m)}& =& \mbox{ departures from $l$ to $m$ } \\ C(l,m)& =& \mbox{ service for phase $(l,m)$ at rate $c(l,m)$ with delay $r(l,m)$} \\ A_{l}& =& E_{l} +\displaystyle\sum _{k}B_{(k,l)}\mbox{ total arrivals into link $l$} \\ P_{(l,m)},(\delta _{(l,m)},\gamma _{(l,m)})& =& \mbox{ router from link $l$ to link $m$, $(\delta _{(l,m)},\gamma _{(l,m)})$ upper-bounded} \\ q_{(l,m)}& =& \mbox{ queue (in link $l$) for phase $(l,m)$} \\ s(l,m)& =& \mbox{ saturation rate of phase $(l,m)$} \\ \end{array}$$

Although \(P_{(l,m)},B_{(l,m)},C(l,m),q_{(l,m)}\), etc. are only defined for permissible phases, it will be convenient to define them for all \((l,m) \in \mathcal{L}\times \mathcal{L}\) by setting their values to 0 for phases that are not permitted.

Fig. 2.7
figure 7

E l are external arrivals into link l, B (k, l) are internal arrivals routed from link k to l, and C (l, m) is the service process for phase (l, m)

Full size image

Suppose A l is \((\sigma _{l},\rho _{l})\) upper-bounded (\(\sigma _{l},\rho _{l}\) are determined below). Then \(P_{(l,m)}(A_{l})\) is \((\delta _{(l,m)} + \gamma _{(l,m)}\sigma _{l},\gamma _{(l,m)}\rho _{l})\) upper-bounded. Suppose C(l, m) provides service (c(l, m), r(l, m)) with \(c(l,m) \geq \gamma _{(l,m)}\rho _{l}\). By Corollary 1

$$\begin{array}{rlrlrl} &q_{(l,m)}(t) \leq \delta _{(l,m)} + \gamma _{(l,m)}\sigma _{l} + \gamma _{(l,m)}\rho _{l}r(l,m), & & \\ &B_{(l,m)}\mbox{ is $(\delta _{(l,m)} + \gamma _{(l,m)}\sigma _{l} + \gamma _{(l,m)}\rho _{l}r(l,m),\gamma _{(l,m)}\rho _{l})$ upper-bounded}, & & \\ &d_{(l,m)}(t) \leq r(l,m) + [\delta _{(l,m)} + \gamma _{(l,m)}\sigma _{l}]/c(l,m), & & \\ &BP_{(l,m)} \leq [\delta _{(l,m)} + \gamma _{(l,m)}\sigma _{l} + c(l,m)r(l,m)]/[c(l,m) - \gamma _{(l,m)}\rho _{l}]. &\end{array}$$
(2.57)

So \(A_{l} = E_{l} +\sum _{k}B_{(k,l)}\) is \((\sigma _{l},\rho _{l})\) upper-bounded with

$$\displaystyle\begin{array}{rcl} & \sigma _{l} = \alpha _{l} +\displaystyle\sum _{k}[\delta _{(k,l)} + \gamma _{(k,l)}\sigma _{k} + \gamma _{(k,l)}\rho _{k}r(k,l)],&\end{array}$$
(2.58)
$$\displaystyle\begin{array}{rcl} & \rho _{l} = \beta _{l} +\displaystyle\sum _{k}\gamma _{(k,l)}\rho _{k}. &\end{array}$$
(2.59)

It is convenient to use vector–matrix notation. All vectors below are row vectors of dimension L and all matrices are of dimensions \(L \times L\).

Let \(\alpha = (\alpha _{1},\cdots \,,\alpha _{L})\), \(\beta = (\beta _{1},\cdots \,,\beta _{L})\), \(\sigma = (\sigma _{1},\cdots \,,\sigma _{L})\), \(\rho = (\rho _{1},\cdots \,,\rho _{L})\). Define matrices \(\Gamma =\{ \gamma _{(l,m)}\}\), \(\Delta =\{ \delta _{(l,m)}\}\), \(R =\{ r(l,m)\}\), \(\Gamma \circ R =\{ \gamma _{(l,m)}r(l,m)\}\). Let \(e = (1,\cdots \,,1)\) be the row vector with all entries 1, and \(\delta = e\Delta \). Write (2.58)–(2.59) as

$$\displaystyle\begin{array}{rcl} \sigma & =& \alpha + \delta + \sigma \Gamma + \rho \Gamma \circ R \\ \rho & =& \beta + \rho \Gamma \\ \end{array}$$

Assume that for all l, \(\sum _{m}\gamma _{(l,m)} \leq 1\), and the spectral radius of \(\Gamma \), which equals its maximum eigenvalue, is strictly less than 1. (This is equivalent to the condition that every vehicle eventually leaves the network.) Then

$$\displaystyle\begin{array}{rcl}{ [I - \Gamma ]}^{-1}& =& I + \Gamma + {\Gamma }^{2} + \cdots \,, \\ \rho & =& \beta + \rho \Gamma = \beta {[I - \Gamma ]}^{-1}, \end{array}$$
(2.60)
$$\displaystyle\begin{array}{rcl} \sigma & =& \alpha + \delta + \rho \Gamma \circ R + \sigma \Gamma = (\alpha + \delta + \rho \Gamma \circ R){[I - \Gamma ]}^{-1}.\end{array}$$
(2.61)

Let \(q =\{ q_{(l,m)}\}\), \(C =\{ c(l,m)\}\), \(B =\{ B_{(l,m)}\}\), and let \([\sigma ],[\rho ]\) denote diagonal matrices with entries \(\sigma _{l},\rho _{l}\).

Lemma 4.

Suppose the external arrivals E l are \((\alpha _{l},\beta _{l})\) upper-bounded, the spectral radius of the routing matrix \(\Gamma \) is strictly less than 1, and C(l,m) provides service \((c(l,m),r(l,m))\) with \(c(l,m) \geq \gamma _{(l,m)}\rho _{l}\) . Then, with \(A = (A_{1},\cdots \,,A_{L})\), \(B =\{ B_{(l,m)}\}\), \(q =\{ q_{(l,m)}\}\) , the following bounds hold:

$$\displaystyle\begin{array}{rcl} & A(t)\mbox{ is $(\sigma, \rho )$ upper-bounded}, & \end{array}$$
(2.62)
$$\displaystyle\begin{array}{rcl} & B(t)\mbox{ is $(\Delta + [\sigma ]\Gamma + [\rho ]\Gamma \circ R,[\rho ]\Gamma )$ upper bounded}, & \end{array}$$
(2.63)
$$\displaystyle\begin{array}{rcl} & q(t) \leq \Delta + [\sigma ]\Gamma + [\rho ]\Gamma \circ R, & \end{array}$$
(2.64)
$$\displaystyle\begin{array}{rcl} & d_{(l,m)}(t) \leq r(l,m) + [\delta _{(l,m)} + \sigma _{l}\gamma _{(l,m)}]/c(l,m), & \end{array}$$
(2.65)
$$\displaystyle\begin{array}{rcl} & BP_{(l,m)} \leq [\delta _{(l,m)} + \gamma _{(l,m)}\sigma _{l} + c(l,m)r(l,m)]/[c(l,m) - \gamma _{(l,m)}\rho _{l}].&\end{array}$$
(2.66)

Above \(\rho \) and \(\sigma \) are given by (2.60) and (2.61).

2.4.2 Performance of Fixed-Cycle Controller

We extend the notation of Sect. 2.3 for a single controller to that for a network, and use Lemma 4 to design fixed-cycle controllers for the network.

A node or intersection \(n \in \mathcal{N}\) is specified by input links \(l \in I_{n}\), output links \(m \in O_{n}\), and a set of \(I_{n} \times O_{n}\) binary control matrices \(U_{n} \in \mathcal{U}_{n}\) representing all permissible stages at n. Let \(S_{n} =\{ s(l,m),\;l \in I_{n},m \in O_{n}\}\) be the matrix of saturation rates of all phases at intersection n, with s(l, m) = 0 if (l, m) is not permitted. If U n is the stage selected at intersection n, the matrix \(S_{n} \circ U_{n}\) is the matrix of service rates at t provided by U n to the phases at n.

We can take the “direct product” of the control matrices U n at each intersection n to obtain a network stage matrix \(U =\prod _{n}U_{n}\) of dimension \(L \times L\) for the entire network,

$$U(l,m) = \left \{\begin{array}{ll} U_{n}(l,m),&\mbox{ if }(l,m) \in I_{n} \times O_{n} \\ 0, &\mbox{ otherwise } \end{array} \right..$$

One may picture U in block-diagonal form as in Fig. 2.8. Analogously, let \(S =\prod _{n}S_{n}\) be the \(L \times L\) matrix of the saturation rates of all phases (l, m). Let \(\mathcal{U} =\prod \mathcal{U}_{n}\) be the set of all network stage matrices. We now proceed as in Sect. 2.3.2. For simplicity, assume that all intersections have the same cycle T and the same lost time L. (Having different cycles at different intersections only complicates the notation.) Let

$$ [\mathcal{U}] = \left \{\displaystyle\sum _{U}\lambda _{U}U\ \vert \ \lambda _{U} \geq 0,\;\displaystyle\sum _{U}\lambda _{U} \leq 1 - L/T\right \}, $$
(2.67)

be the set of all relaxed controls. Theorem 6 is the network counterpart of Theorem 2.

Theorem 6.

There is a fixed-cycle network controller that serves each phase (l,m) at rate c(l,m) with delay r(l,m) if and only if there exist \(\lambda _{U} \geq 0\), \(\sum _{U}\lambda _{U} \leq 1 - L/T\) such that

$$c(l,m) = \left (S \circ \displaystyle\sum _{U}\lambda _{U}U\right )(l,m);\quad r(l,m) = T\left [1 -\left (\displaystyle\sum _{U}\lambda _{U}U\right )(l,m)\right ].$$
(2.68)

Suppose the external arrivals E l are \((\alpha _{l},\beta _{l})\) upper-bounded, and \(c(l,m) \geq \rho _{l}\gamma _{(l,m)}\) for every (l,m), or in matrix notation

$$S \circ \displaystyle\sum _{U}\lambda _{U}U \geq [\rho ]\Gamma = [\beta {[I - \Gamma ]}^{-1}]\Gamma.$$
(2.69)

Then the performance of the controller satisfies the bounds (2.62)–(2.66).

The external arrival rates \(\beta \) are “inflated” by the routing matrix multiplier \({[I - \Gamma ]}^{-1}\) to give the aggregate arrival rates \(\rho = \beta {[I - \Gamma ]}^{-1}\), as is to be expected. More interesting is the impact of routing on transforming the bursts \(\alpha \) in the external arrivals into the bursts \(\sigma \) in (2.61). Both impacts affect the maximum queue size, delay, and clearance times (2.64)–(2.66). Corollary 3 is the network counterpart of Corollary 2.

Corollary 3.

The shortest cycle needed by a stabilizing fixed-cycle controller for all external arrivals A l bounded by rate \(\beta _{l}\) with burst size \(\alpha _{l}\) is

$$T = \frac{L} {1 -\displaystyle\sum \lambda _{U}^{{\ast}}},$$
(2.70)

in which \(\{\lambda _{U}^{{\ast}}\}\) is the solution of the linear program:

$$\displaystyle\begin{array}{rcl} & & \min \displaystyle\sum \lambda _{U} \\ & & \text{s.t.}(S \circ \displaystyle\sum \lambda _{U}U)(l,m) \geq \left [\beta {[I - \Gamma ]}^{-1}\Gamma \right ](l,m),\mbox{ all $(l,m)$} \\ & & \lambda _{U} \geq 0\;\text{ all }U \in \mathcal{U}. \end{array}$$
(2.71)

If \(\sum \lambda _{U}^{{\ast}} > 1\) , there is no stabilizing fixed-cycle controller.

Because U and S are block-diagonal, the linear program decomposes into a set of independent linear programs, one per intersection.

Fig. 2.8
figure 8

A network stage matrix U is a block-diagonal matrix with intersection stage matrices \(U_{n},U_{n^{\prime}}\) along the diagonal

Full size image

One of the \(L \times L\) inequalities in (2.71), corresponding to say (l  ∗ , m  ∗ ), will hold as an equality in the solution. One could call (l  ∗ , m  ∗ ) the critical phase and the intersection n  ∗  for which \({l}^{{\ast}}\in I_{{n}^{{\ast}}},{m}^{{\ast}}\in O_{{n}^{{\ast}}}\) as the critical intersection. Following (Allsop 1972) one may also define the capacity of this intersection.

2.4.3 Max-Pressure Controller

The max-pressure controller of Sect. 2.3.3.3 is extended to a network in this section. Define the pressure exerted by network stageU at \(q =\{ q_{(l,m)}\}\) by

$$w(q,U) =\displaystyle\sum _{(l,m)}\left [q_{(l,m)} -\displaystyle\sum _{p}\gamma _{(m,p)}q_{(m,p)}\right ]S \circ U(l,m),$$
(2.72)

and linearly extend the definition to \([U] =\sum \lambda _{U}U\),

$$w(q,[U]) =\displaystyle\sum \lambda _{U}w(q,U) =\displaystyle\sum _{(l,m)}\left [q_{(l,m)} -\displaystyle\sum _{p}\gamma _{(m,p)}q_{(m,p)}\right ]S \circ [U](l,m).$$

This definition of pressure differs from (2.51) in that for each phase (l, m) we take the product of its queue length \(q_{(l,m)}\) and saturation rate s(l, m) and subtract the corresponding amount from the downstream queue q (m, p) weighted by the average turn ratio \(\gamma _{(m,p)}\). For the isolated intersection considered in Sect. 2.3.3.3 with no downstream queue, (2.72) reduces to (2.51).

Note that to calculate the pressure (2.72) exerted by a network stage one needs to know the turn ratios \(\{\gamma _{(l,m)}\}\) in addition to the queue lengths. (It is of course easy to estimate turn ratios.) However, no knowledge of the parameters \((\alpha _{l},\beta _{l})\) of the external demands E l is needed.

Define the max-pressure stage as

$${U}^{{\ast}}(q) =\arg \max \{ w(q,U)\ \vert \ U \in \mathcal{U}\}.$$
(2.73)

In (2.73) ties are broken arbitrarily. Let \(q(t) =\{ q_{(l,m)}(t)\}\) be the queue length array.

Definition 6.

The max-pressure network controlleru  ∗ (t) selects the max-pressure stage at q(t):

$${u}^{{\ast}}(t) = (1 - L/T){U}^{{\ast}}(q(t)).$$

The pressure (2.72) of a network stage is the sum of the pressures exerted at each intersection stage, so the max-pressure network stage (2.73) is simply the collection of the max-pressure stages at all the intersections. Hence, the max-pressure controller is decentralized. If the network of intersections is expanded, the max-pressure controller for the original network is unchanged, so the max-pressure controller can be introduced incrementally.

The proof of Lemma 5 is identical to that of Lemma 3.

Lemma 5.

u ∗ (t) maximizes w(q,[U]) over the set \([\mathcal{U}]\) of relaxed controls.

Referring to Fig. 2.7, let \(\tilde{A}_{(l,m)}(t) = P_{(l,m)}(A_{l}(t))\) be the cumulative number of vehicles routed from link l to m. Under the max-pressure controller \(\tilde{A}_{(l,m)}\) receives service

$${c}^{{\ast}}(l,m)(t) = S \circ (1 - L/T){U}^{{\ast}}(q(t))(l,m),$$

so the evolution of the array q(t) is governed by these equations:

$$\displaystyle\begin{array}{rcl} & q_{(l,m)}(t + 1) = [q_{(l,m)}(t) - {c}^{{\ast}}(l,m)(t)]_{+} +\tilde{ a}_{(l,m)}(t + 1),& \end{array}$$
(2.74)
$$\displaystyle\begin{array}{rcl} & \tilde{a}_{(l,m)}(t + 1) = \gamma _{(l,m)}a_{l}(t + 1) + \delta _{(l,m)}(t), & \end{array}$$
(2.75)
$$\displaystyle\begin{array}{rcl} & a_{l}(t + 1) = e_{l}(t + 1) +\displaystyle\sum _{k}\ b_{(k,l)}(t), & \end{array}$$
(2.76)
$$\displaystyle\begin{array}{rcl} & b_{(k,l)}(t) =\min \{ q_{(k,l)}(t),{c}^{{\ast}}(k,l)(t)\}. &\end{array}$$
(2.77)

Above as elsewhere, \(\tilde{a}_{(l,m)}(t + 1) =\tilde{ A}_{(l,m)}(t + 1) -\tilde{ A}_{(l,m)}(t)\), \(a_{l}(t + 1) = A_{l}(t + 1) - A_{l}(t + 1)\), etc. Since \(P_{(l,m)}\) is \((\delta _{(l,m)},\gamma _{(l,m)})\) upper-bounded,

$$\displaystyle\sum _{t}\delta _{(l,m)}(t) \leq \delta _{(l,m)},\;\mbox{ where }\delta _{(l,m)}(t) = a_{(l,m)}(t) - \gamma _{(l,m)}a_{l}(t).$$
(2.78)

Substitution into (2.74) gives the evolution of q(t) directly in terms of the external arrivals:

$$\displaystyle\begin{array}{rcl} q_{(l,m)}(t + 1)& =& \left [q_{(l,m)}(t)-{c}^{{\ast}}(l,m)(t)\right ]_{ +}+\gamma _{(l,m)}\left [e_{l}(t+1)+\displaystyle\sum _{k}\min \{q_{(k,l)}(t),{c}^{{\ast}}(k,l)(t)\}\right ] \\ & & +\delta _{(l,m)}(t + 1). \end{array}$$
(2.79)

Theorem 7 extends Theorem 5 to the network case.

Theorem 7.

Let q(t) be the queues resulting from the max-pressure controller. Suppose that the external arrivals E l are \((\alpha _{l},\beta _{l})\) upper-bounded, the routers \(P_{(l,m)}\) are \((\delta _{(l,m)},\gamma _{(l,m)})\) upper-bounded and there exists a (fixed-cycle) relaxed network control matrix [U] such that

$$c(l,m) = S \circ [U](l,m) > \rho _{l}\gamma _{(l,m)},\mbox{ all }(l,m),$$
(2.80)

in which \(\rho = \beta {[I - \Gamma ]}^{-1}\) . Then \(\{q(t),\;t \geq 0\}\) is a bounded sequence and the max-pressure controller is stabilizing.

Proof.

Under the max-pressure controller the queues evolve according to (2.79). Let \(\vert q{\vert }^{2} =\sum q_{(l,m)}^{2}\). It is shown in Appendix E that there exist \(k < \infty \), \(\epsilon > 0\), and \(\sigma (t) \geq 0\) with \(\sum _{t}\sigma (t) < \infty \), so that

$$\vert q(t + 1){\vert }^{2} -\vert q(t){\vert }^{2} \leq k - (2\epsilon - \sigma (t))\vert q(t)\vert, $$
(2.81)

Suppose (2.81) holds. With T such that \(\sigma (t) < \epsilon, \;t \geq T\), (2.81) gives

$$\vert q(t + 1){\vert }^{2} -\vert q(t){\vert }^{2} \leq k - \epsilon \vert q(t)\vert, \;t > T,$$

and so

$$\vert q(t + 1){\vert }^{2} -\vert q(t){\vert }^{2} < 0,\;\vert q(t)\vert > k/\epsilon, \;t > T,$$
(2.82)

which implies that \(\vert q(t)\vert, \;t \geq 0\) is bounded.

2.4.4 Two Extensions of Max-Pressure Controller

The pressure w(q, U) defined in (2.72) treats all queues equally. It may be desirable to treat them differently by giving them weights. Let \(\kappa _{(l,m)} > 0\) be pre-specified weights and define the weighted pressure exerted by stage U as

$$w_{\kappa }(q,U) =\displaystyle\sum _{(l,m)}\left [\kappa _{(l,m)}q_{(l,m)} -\displaystyle\sum _{p}\gamma _{(m,p)}\kappa _{(m,p)}q_{(m,p)}\right ]S \circ U(l,m),$$
(2.83)

simply by replacing q (l, m) in (2.72) by \(\kappa _{(l,m)}q_{(l,m)}\). Define the max-pressure stage as

$$U_{\kappa }^{{\ast}}(q) =\arg \max \{ w_{ \kappa }(q,U)\ \vert \ U \in \mathcal{U}\},$$

and the max-pressure controller at q(t) by

$$u_{\kappa }^{{\ast}}(t) = (1 - L/T)U_{ \kappa }^{{\ast}}(q(t)).$$

Theorem 7 remains true with this definition of the max-pressure controller. The proof of Theorem 7 applies with appropriate changes.

The weighted pressure (2.83) can be used to give preference to the clearance of certain queues. For example, (Aboudolas et al. 2009b, Eq. (11)) suggests using

$$\kappa _{(l,m)} = {[Q_{(l,m)}]}^{-1},$$

where Q (l, m) is the maximum permissible queue length for phase (l, m). Another possibility is to give more weight to phases that are restricted to buses, giving them greater priority.

The second extension might be termed max-pressure-lite. Suppose the intersection controllers already have in place several timing plans, scheduled depending on time of day. In our notation a timing plan is just a relaxed control. Suppose K timing plans are in place, denoted as in (2.67) by

$$[{U}^{i}] =\displaystyle\sum _{ U}\lambda _{U}^{i}U,\;\;\displaystyle\sum \lambda _{ U}^{i} \leq 1 - L/T,\quad i = 1,\cdots \,,K.$$
(2.84)

Depending on the time of day, the controller selects one of the [U i] without regard to traffic conditions. If queue measurements are available, one can select the timing plan that exerts the maximum pressure:

$$[{U}^{{\ast}}](q) =\arg \max \{ w(q,[{U}^{i}])\ \vert \ i = 1,\cdots \,,K\}.$$

The max-pressure-lite controller is given by

$$u_{lite}^{{\ast}}(t) = [{U}^{{\ast}}](q(t)).$$

The following result can be proved in a way similar to Theorem 7.

Theorem 8.

Suppose there exists a convex combination of the fixed timing plans \([U] =\sum _{ i=1}^{K}\mu _{i}[{U}^{i}]\), \(\mu _{i} \geq 0,\;\sum \mu _{i} = 1\) such that

$$S \circ [U](l,m) > \rho _{l}\gamma _{(l,m)},\mbox{ all }(l,m).$$

Then the max-pressure-lite controller is stabilizing.

2.5 Discussion

We present the intuition underlying the max-pressure controller. This is followed by a comparison with other controller designs. Lastly, we discuss model limitations, followed by some open problems.

2.5.1 Intuition

For any relaxed network control sequence [U(t)] let \(c(l,m)(t) = S \circ [U(t)](l,m)\) be the resulting service rates. The evolution of queues in response to the control and the external arrivals is given by (2.79):

$$\displaystyle\begin{array}{rcl} q_{(l,m)}(t+1)& =& \left [q_{(l,m)}(t)-c(l,m)(t)\right ]_{+}+\gamma _{(l,m)}\left [e_{l}(t+1)+\displaystyle\sum _{k}\min \{q_{(k,l)}(t),c(k,l)(t)\}\right ] \\ & & +\delta _{(l,m)}(t + 1).\end{array}$$

If the queues are sufficiently large (saturated case, q (l, m)(t) > c(l, m)(t)) this simplifies to

$$\displaystyle\begin{array}{rcl} q_{(l,m)}(t + 1) - q_{(l,m)}(t)& =& -c(l,m)(t) + \gamma _{(l,m)}\displaystyle\sum _{k}c(k,l)(t) + \gamma _{(l,m)}\left [\beta _{l} + \alpha _{l}(t + 1)\right ] \\ & & +\delta _{(l,m)}(t + 1). \end{array}$$
(2.85)

Regard (2.85) as a discrete-time approximation of the differential equation

$$\frac{\mathrm{d}} {\mathrm{d}t}q_{(l,m)}(t) = -c(l,m)(t) + \gamma _{(l,m)}\displaystyle\sum _{k}c(k,l)(t) + \gamma _{(l,m)}\beta _{l} + \psi _{(l,m)}(t),$$
(2.86)

in which \(\psi _{(l,m)}(t) = \gamma _{(l,m)}\alpha _{l}(t) + \delta _{(l,m)}(t)\) is a “disturbance” input. Then

$$\displaystyle\begin{array}{rcl} \frac{1} {2} \frac{\mathrm{d}} {\mathrm{d}t}\vert q(t){\vert }^{2}& =& \langle q(t),\dot{q}(t)\rangle \\ & =& -\displaystyle\sum q_{(l,m)}(t)\left [c(l,m)(t) - \gamma _{(l,m)}\displaystyle\sum _{k}c(k,l)(t)\right ] +\displaystyle\sum q_{(l,m)}(t)\gamma _{(l,m)}\beta _{l} \\ & & +\displaystyle\sum q_{(l,m)}(t)\psi _{(l,m)}(t) \\ & =& -w(q(t),[U(t)]) +\displaystyle\sum q_{(l,m)}(t)\gamma _{(l,m)}\beta _{l} +\displaystyle\sum q_{(l,m)}(t)\psi _{(l,m)}(t).\qquad \end{array}$$
(2.87)

The third term on the right is evanescent and may be ignored since \(\sum \psi _{(l,m)}(t) < \infty \). The max-pressure controller selects stage \([U(t)] \in [\mathcal{U}]\) that makes the first term as negative as possible. The second constant forcing term is due to the average rate of external arrivals. Theorem 7 says that if there is a stabilizing fixed-cycle controller the first term will dominate the second term. In fact, (2.108) says that

$$-w(q(t),[U(t)]) +\displaystyle\sum q_{(l,m)}(t)\gamma _{(l,m)}\beta _{l} < -\epsilon \vert q(t)\vert, $$

which is why the max-pressure controller is stabilizing. The fact that the inequality above does not require knowledge of the arrival rates \(\{\beta _{l}\}\) explains why the max-pressure controller is adaptive.

2.5.2 Comparison with Other Designs

Previous designs of traffic-responsive controllers (Aboudolas et al. 2009b; Cai et al. 2009; Heydecker 2004; Mirchandani and Head 2001; Robertson and Bretherton 1991) require (or make) an estimate of the arrivals over a finite or infinite horizon and select the control that minimizes queues or delay over that horizon. The presumption is that the longer is the horizon, the better will be the controller performance. By contrast, the max-pressure controller is “myopic” and does not make any estimate of the arrivals. In addition, previous designs require estimates of the queues to be communicated to a central controller. By contrast, the max-pressure controller requires only local communication, since the pressure of a stage at any intersection depends only on the queues adjacent to the intersection. Lastly, none of the cited references proves that their controller design is stabilizing as is the case with the max-pressure controller.

We compare in some detail the max-pressure controller with that of (Aboudolas et al. 2009b), which uses the same model as (2.85), expresses \(c(l,m)(t) = S \circ [\sum _{U}\lambda _{U}(t)](l,m)\), and also takes the proportions \(\{\lambda _{U}(t),\;U \in \mathcal{U}\}\) of the available time (T − L) as the control vector. The control vector is decomposed as

$$\lambda _{U}(t) = \lambda _{U}^{F} + \Delta \lambda _{ U}(t),$$

in which \(\{\lambda _{U}^{F}\}\) is, by assumption, a known stabilizing fixed-cycle controller for the external arrivals \(\{\beta _{l}\}\). With this assumption, (2.85) simplifies to

$$q_{(l,m)}(t+1)-q_{(l,m)}(t) = -S\circ \left [\displaystyle\sum _{U}\Delta \lambda _{U}(t)\right ](l,m)+\gamma _{(l,m)}\displaystyle\sum _{k}S\circ \left [\displaystyle\sum _{U}\Delta \lambda _{U}(t)\right ](k,l)+\psi _{(l,m)}(t).$$
(2.88)

The control deviations \(\{\Delta \lambda _{U}(t),U \in \mathcal{U}\}\) are selected to minimize the quadratic cost

$$\displaystyle\sum _{t}\vert q_{(l,m)}(t){\vert }^{2} + p\displaystyle\sum _{ t}\displaystyle\sum _{U\,\in \,\mathcal{U}}\vert \Delta \lambda _{U}(t){\vert }^{2}.$$

Neglecting the evanescent disturbances \(\{\psi _{(l,m)}(t)\}\), this cost is minimized by easily calculated linear feedback rules:

$$\Delta \lambda _{U}(t) =\displaystyle\sum _{l,m}G_{U}(l,m)q_{(l,m)}(t),\;U \in \mathcal{U}.$$

Since the resulting proportions will not satisfy the constraint

$$\displaystyle\sum _{U}\left [\lambda _{U}^{F} + \Delta \lambda _{ U}(t)\right ] \leq T - L,$$
(2.89)

the “gain” matrices G U are changed to \(\tilde{G}_{U}\) so that the modified deviations \(\{\Delta \lambda _{U}(t)\} =\sum _{l,m}\tilde{G}_{U}(l,m)q_{(l,m)}(t)\) do meet this constraint.

Note that if the true arrivals are different from the assumed arrivals, a steady-state bias in the queue lengths must be present to compensate for the error in the assumed arrivals. Of course, the linear model (2.85) will be quite inaccurate when the queues are small. Two more complex optimization methods are considered in (Aboudolas et al. 2009b) but not discussed here.

2.5.3 Model Limitations

We discuss four limitations. In a “store and forward” (SF) model, there is no limit to how much a queue can grow, so the condition in which a downstream queue blocks upstream vehicles is not modeled. It is straightforward to modify (2.79) to model blocking. The first term on the right of (2.79), namely \([q_{(l,m)}(t) - c(l,m)(t)]_{+}\) indicates that the queue q (l, m)(t) is decremented by the saturation rate s(l, m) whenever the phase (l, m) is actuated, regardless of the congestion in the downstream link m. If link m has a queue capacity of Q(m) and its average queue size is \(q(m)(t) =\sum \gamma _{(m,p)}q_{(m,p)}(t)\), one could replace \([q_{(l,m)}(t) - c(l,m)(t)]_{+}\) by

$$\mathbf{1}[q(m)(t) < Q(m)] \times [q_{(l,m)}(t) - c(l,m)(t)]_{+},$$

so that the movement of vehicles from link l to m is blocked when q(m)(t) exceeds Q(m). Unfortunately, with this model of blocking, it is easy to construct examples that create “gridlock” in such a way that there is no stabilizing controller. On the other hand, (2.82) implies that the max-pressure controller is stabilizing if the Q(m) are large enough.

Second, the model does not take into account that it takes time for vehicles to traverse a link. If this time is constant (so called free flow travel time), it can be modeled by a constant delay network element as in (Chang 2000, Lemma 2.3.9). It is not difficult to see that the max-pressure controller is stabilizing in this case as well.

The third limitation is related to the second. The store and forward model leaves no room for signal offset. A signal offset design can be grafted on to the max-pressure controller in the same manner as in Diakaki et al. (2003).

Fourth, the model assumes turn ratios as opposed to O–D patterns. If O–D patterns are fixed, i.e., each O–D demand is distributed in fixed proportions over a set of routes, the demand can be equivalently described by turn ratios. But if drivers respond to delays by changing their route, the turn ratios will also change, and the max-pressure controller needs to adapt to the changes. The resulting system could be studied in a two-level control framework similarly to Wong and Yang (1997).

2.5.4 Future Work

Several questions seem worth investigation. The first concerns priorities: Which priorities in a single-phase network or in a multiphase isolated intersection permit stabilizing work-conserving controllers?

The second question concerns an evacuation scenario in which there is an initial set of queues q(0) and no external inputs, and one wishes to design a fixed-time controller and a feedback controller that minimize \(\sum _{t}q(t)\). How should one restrict the phases actuated by each stage U to a subset [U′] (i.e., \(U^{\prime}(l,m) = 1\rightarrow U(l,m)=1)\) so as to minimize \(\sum _{t}q(t)\)? The idea here is that whereas U may permit left-turns (say) it may be more efficient to prevent such turns.

The third question concerns over-saturated networks in which the average rates \(\{\beta _{l}\}\) of external arrivals \(\{e_{l}\}\) in (2.79) are such that there is no stabilizing controller. How should one design an adaptive scheme to “meter” these arrivals so that the network can be stabilized? For a macroscopic discussion see (Daganzo 2007).

2.6 Conclusion

The max-pressure controller appears to offer advantages over other adaptive controllers. The controller at each intersection only needs to know the queues on adjoining links and the computation required to select the max-pressure stage is trivial. No knowledge of demand (or even the network topology) is needed, although each intersection controller does need to know local turn ratios. Max-pressure is provably stable whenever there exists any stabilizing controller. Lastly, max-pressure is attractive from an implementation viewpoint: it requires less communication and computational infrastructure than other adaptive controllers; and it can be incrementally deployed since addition of new intersections entails no change in the control of existing intersections.

AcknowledgementsThis research was supported by National Science Foundation Award CMMI-0941326 and the California Department of Transportation. The author is very grateful to François Baccelli for guiding his study of network calculus and for discussions about the proofs, and to Andy Chow, Nik Geroliminis, Gabriel Gomes, Werner Kraus, Pitu Mirchandani, Markos Papageorgiou, and Bart De Schutter for important critical comments concerning signal control.