Powers of Square-Free Monomial Ideals and Combinatorics

Abstract

We survey research relating algebraic properties of powers of squarefree monomial ideals to combinatorial structures. In particular, we describe how to detect important properties of (hyper)graphs by solving ideal membership problems and computing associated primes. This work leads to algebraic characterizations of perfect graphs independent of the Strong Perfect Graph Theorem. In addition, we discuss the equivalence between the Conforti-Cornuéjols conjecture from linear programming and the question of when symbolic and ordinary powers of squarefree monomial ideals coincide.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Powers of ideals are instrumental objects in commutative algebra. In addition, square-free monomial ideals are intimately connected to combinatorics. In this chapter, we survey work on secant, symbolic, and ordinary powers of square-free monomial ideals and their combinatorial consequences in (hyper)graph theory and linear integer programming.

There are two well-studied basic correspondences between square-free monomial ideals and combinatorics. Each arises from the identification of square-free monomials with sets of vertices of either a simplicial complex or a hypergraph. The Stanley–Reisner correspondence associates to the nonfaces of a simplicial complex Δ the generators of a square-free monomial ideal, and vice-versa. This framework leads to many important results relating (mostly homological) ideal-theoretic properties of the ideal to properties of the simplicial complex; see [4, Chap. 5] and [25, Sects. 61–64].

The edge and cover ideal constructions identify the minimal generators of a square-free monomial ideal with the edges (covers) of a simple hypergraph. The edge ideal correspondence is more naïvely obvious but less natural than the Stanley–Reisner correspondence, because the existence of a monomial in this ideal does not translate easily to its presence as an edge of the (hyper)graph. Nevertheless, this correspondence has proven effective at understanding properties of (hyper)graphs via algebra. We focus on powers of square-free monomial ideals when they are viewed as edge (or cover) ideals of hypergraphs. To the best of our knowledge, there has been little systematic study of the powers of square-free ideals from the Stanley–Reisner perspective.

The general theme of this chapter is the relationship between symbolic and ordinary powers of ideals. This topic has been investigated extensively in the literature (cf. [2, 8, 17, 20]). Research along these lines has revealed rich and deep interactions between the two types of powers of ideals, and often their equality leads to interesting algebraic and geometric consequences (cf. [15, 22, 29–31]). We shall see that examining symbolic and ordinary powers of square-free monomial ideals also leads to exciting and important combinatorial applications.

The chapter is organized as follows. In the next section, we collect notation and terminology. In Sect. 3, we survey algebraic techniques for detecting important invariants and properties of (hyper)graphs. We consider three problems:

• 1. Computing the chromatic number of a hypergraph

• 2. Detecting the existence of odd cycles and odd holes in a graph

• 3. Finding algebraic characterizations of bipartite and perfect graphs

We begin by describing two methods for determining the chromatic number of a hypergraph via an ideal-membership problem, one using secant ideals, and the other involving powers of the cover ideal. Additionally, we illustrate how the associated primes of the square of the cover ideal of a graph detect its odd induced cycles.

The results in Sect. 3 lead naturally to the investigation of associated primes of higher powers of the cover ideal. This is the subject of Sect. 4. We explain how to interpret the associated primes of the sth power of the cover ideal of a hypergraph in terms of coloring properties of its sth expansion hypergraph. Specializing to the case of graphs yields two algebraic characterizations of perfect graphs that are independent of the Strong Perfect Graph Theorem.

Section 5 is devoted to the study of when a square-free monomial ideal has the property that its symbolic and ordinary powers are equal. Our focus is the connection between this property and the Conforti–Cornuéjols conjecture in linear integer programming. We state the conjecture in its original form and discuss an algebraic reformulation. This provides an algebraic approach for tackling this long-standing conjecture.

2 Preliminaries

We begin by defining the central combinatorial object of the chapter.

Definition 2.1.

A hypergraph is a pair G = (V, E) where V is a set, called the vertices of G, and E is a subset of 2^V, called the edges of G. A hypergraph is simple if no edge contains another; we allow the edges of a simple hypergraph to contain only one vertex (i.e., isolated loops). Simple hypergraphs have also been studied under other names, including clutters and Sperner systems. All hypergraphs in this chapter will be simple.

A graph is a hypergraph in which every edge has cardinality exactly two. We specialize to graphs to examine special classes, such as cycles and perfect graphs.

If W is a subset of V, the induced subhypergraph of G on W is the pair (W, E _W ) where E _W = E ∩ 2^W is the set of edges of G containing only vertices in W.

Notation 2.2.

Throughout the chapter, let $V =\{ x_{1},\ldots,x_{n}\}$ be a set of vertices. Set $S = K[V ] = K[x_{1},\ldots,x_{n}]$, where K is a field. We will abuse notation by identifying the square-free monomial $x_{i_{1}}\ldots x_{i_{s}}$ with the set $\{x_{i_{1}},\ldots,x_{i_{s}}\}$ of vertices. If the monomial m corresponds to an edge of G in this way, we will denote the edge by m as well.

Definition 2.3.

The edge ideal of a hypergraph G = (V, E) is

$$I(G) = (m : m \in E) \subset S.$$

On the other hand, given a square-free monomial ideal I ⊂ S, we let G(I) = (V, gens(I)) be the hypergraph associated to I, where gens(I) is the unique set of minimal monomial generators of I.

Definition 2.4.

A vertex cover for a hypergraph G is a set of vertices w such that every edge hits some vertex of w, i.e., w ∩ e≠∅ for all edges e of G.

Observe that, if w is a vertex cover, then appending a variable to w results in another vertex cover. In particular, abusing language slightly, the vertex covers form an ideal of S.

Definition 2.5.

The cover ideal of a hypergraph G is

$$J(G) = (w : w\text{ is a vertex cover of }G).$$

In practice, we compute cover ideals by taking advantage of duality.

Definition 2.6.

Given a square-free monomial ideal I ⊂ S, the Alexander dual of I is

$${I}^{\vee } = \bigcap\limits _{m\in \mathrm{gens}(I)}\mathfrak{p}_{m},$$

where $\mathfrak{p}_{m} = (x_{i} : x_{i} \in m)$ is the prime ideal generated by the variables of m.

Observe that if I = I(G) is a square-free monomial ideal, its Alexander dual I ^∨ is also square-free. We shall denote by G ^∗ the hypergraph corresponding to I ^∨, and call G ^∗ the dual hypergraph of G. That is, I ^∨ = I(G ^∗). The edge ideal and cover ideal of a hypergraph are related by the following result.

Proposition 2.7.

The edge ideal and cover ideal of a hypergraph are dual to each other: $J(G) = I{(G)}^{\vee } = I({G}^{{_\ast}})$ (and I(G) = J(G) ^∨ ). Moreover, minimal generators of J(G) correspond to minimal vertex covers of G, covers such that no proper subset is also a cover.

Proof.

Suppose w is a cover. Then for every edge e, w ∩ e≠∅, so $w \in \mathfrak{p}_{e}$. Conversely, suppose w ∈ I(G)^∨. Then, given any edge e, we have $w \in \mathfrak{p}_{e}$, i.e., w ∩ e≠∅. In particular, w is a cover.

We shall also need generalized Alexander duality for arbitrary monomial ideals. We follow Miller and Sturmfels’s book [21], which is a good reference for this topic. Let a and b be vectors in ℕ ⁿ such that b _i ≤ a _i for each i. As in [21, Definition 5.20], we define the vector a \ b to be the vector whose ith entry is given by

$$a_{i}\setminus b_{i} = \left \{\begin{array}{l l} a_{i} + 1 - b_{i}&\text{ if }b_{i} \geq 1 \\ 0 &\text{ if }b_{i} = 0.\\ \end{array} \right.$$

Definition 2.8.

Let a ∈ ℕ ⁿ, and let I be a monomial ideal such that all the minimal generators of I divide x ^a. The Alexander dual of I with respect to a is the ideal

$${I}^{[\mathbf{a}]} = \bigcap\limits _{{\mathbf{x}}^{\mathbf{b}}\in \mathrm{gens}(I)}\,(x_{1}^{a_{1}\setminus b_{1} },\ldots,x_{n}^{a_{n}\setminus b_{n} }).$$

For square-free monomial ideals, one obtains the usual Alexander dual by taking a equal to 1, the vector with all entries 1, in Definition 2.8.

By Definition 2.6, Alexander duality identifies the minimal generators of a square-free ideal with the primes associated to its dual. The analogy for generalized Alexander duality identifies the minimal generators of a monomial ideal with the irreducible components of its dual.

Definition 2.9.

A monomial ideal I is irreducible if it has the form $I = (x_{1}^{e_{1}},\ldots,x_{n}^{e_{n}}\!)$ for $e_{i} \in \mathbb{Z}_{>0} \cup \{\infty \}$. (We use the convention that x _i ^∞ = 0.) Observe that the irreducible ideal I is $\mathfrak{p}$-primary, where $\mathfrak{p} = (x_{i} : e_{i}\neq \infty )$.

Definition 2.10.

Let I be a monomial ideal. An irreducible decomposition of I is an irredundant decomposition

$$I = \bigcap Q_{j}$$

with the Q _j irreducible ideals. We call these Q _j irreducible components of I. By Corollary 2.12 below, there is no choice of decomposition, so the irreducible components are an invariant of the ideal.

Proposition 2.11.

Let I be a monomial ideal, and a be a vector with entries large enough that all the minimal generators of I divide x ^a. Then (I^[a] ) ^[a] = I.

Corollary 2.12.

Every monomial ideal has a unique irreducible decomposition.

A recurring idea in our paper is the difference between the powers and symbolic powers of square-free ideals. We recall the definition of the symbolic power.

For a square-free monomial ideal I, the sth symbolic power of I is

$${I}^{(s)} = \bigcap\limits _{\mathfrak{p}\in \mathrm{Ass}(S/I)}{\mathfrak{p}}^{s}.$$

(This definition works because square-free monomial ideals are the intersection of prime ideals. For general ideals (even general monomial ideals) the definition is more complicated.) In general we have I ^s ⊆ I ^(s), but the precise nature of the relationship between the symbolic and ordinary powers of an ideal is a very active area of research.

In commutative algebra, symbolic and ordinary powers of an ideal are encoded in the symbolic Rees algebra and the ordinary Rees algebra. More specifically, for any ideal $I \subseteq S = K[x_{1},\ldots,x_{n}]$, the Rees algebra and the symbolic Rees algebra of I are

$$\mathcal{R}(I) = \mathop{\oplus}\limits _{q\geq 0}{I}^{q}{t}^{q} \subseteq S[t]\quad \text{ and }\quad \mathcal{R}_{ s}(I) = \mathop{\oplus}\limits _{q\geq 0}{I}^{(q)}{t}^{q} \subseteq S[t].$$

The symbolic Rees algebra is closely related to the Rees algebra, but often is richer and more subtle to understand. For instance, while the Rees algebra of a homogeneous ideal is always Noetherian and finitely generated, the symbolic Rees algebra is not necessarily Noetherian. In fact, non-Noetherian symbolic Rees algebras were used to provide counterexamples to Hilbert’s Fourteenth Problem (cf. [24, 26]).

3 Chromatic Number and Odd Cycles in Graphs

In this section, we examine how to detect simple graph-theoretic properties of a hypergraph G from (powers of) its edge and cover ideals. Since the results in this section involving chromatic number are the same for graphs as for hypergraphs, modulo some essentially content-free extra notation, we encourage novice readers to ignore the hypergraph case and think of G as a graph.

Definition 3.1.

Let k be a positive integer. A k-coloring of G is an assignment of colors $c_{1},\ldots,c_{k}$ to the vertices of G in such a way that every edge of cardinality at least 2 contains vertices with different colors. We say that G is k-colorable if a k-coloring of G exists, and that the chromatic number χ(G) of G is the least k such that G is k-colorable.

Remark 3.2.

Since loops do not contain two vertices, they cannot contain two vertices of different colors. Thus the definition above considers only edges with cardinality at least two. Furthermore, since the presence or absence of loops has no effect on the chromatic number of the graph, we will assume throughout this section that all edges have cardinality at least two.

Remark 3.3.

For hypergraphs, some texts instead define a coloring of G to be an assignment of colors to the vertices such that no edge contains two vertices of the same color. However, this is equivalent to a coloring of the one-skeleton of G, so the definition above allows us to address a broader class of problems.

Running Example 3.4.

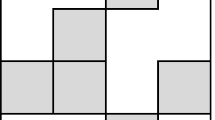
Let G be the graph obtained by gluing a pentagon to a square along one edge, shown in Fig. 1. The edge ideal of G is I(G) = (ab, bc, cd, de, ae, ef, fg, dg). The chromatic number of G is 3: for example, we may color vertices a, c, and g red, vertices b, d, and f yellow, and vertex e blue.

The chromatic number of G can be determined from the solutions to either of two different ideal-membership problems.

Fig. 1

The graph G in the running example

Observe that a graph fails to be k-colorable if and only if every assignment of colors to its vertices yields at least one single-colored edge. Thus, it suffices to test every color-assignment simultaneously. To that end, let $Y _{1},\ldots,Y _{k}$ be distinct copies of the vertices: $Y _{i} =\{ y_{i,1},\ldots,y_{i,n}\}$. We think of Y _i as the ith color and the vertices of Y _i as being colored with this color. Now let I(Y _i ) be the edge ideal I = I(G), but in the variables Y _i instead of V. Now an assignment of colors to G corresponds to a choice, for each vertex x _j , of a colored vertex y _{i, j} ; or, equivalently, a monomial of the form $y_{i_{1},1}y_{i_{2},2}\ldots y_{i_{n},n}$. This monomial is a coloring if and only if it is not contained in the monomial ideal $\widetilde{I} = I(Y _{1}) + \cdots + I(Y _{k})$. In particular, G is k-colorable if and only if the sum of all such monomials is not contained in $\widetilde{I}$.

We need some more notation to make the preceding discussion into a clean statement. Let $\mathbf{m} = x_{1}\ldots x_{n}$, let $T_{k} = K[Y _{1},\ldots,Y _{k}]$, and let ϕ _k : S → T _k be the homomorphism sending x _i to $y_{1,i} + \cdots + y_{k,i}$. Then ϕ _k (m) is the sum of all color-assignments, and we have shown the following:

Lemma 3.5.

With notation as above, G is k-colorable if and only if $\phi _{k}(\mathbf{m})\not\in \widetilde{I}$.

We recall the definition of the kth secant ideal. Secant varieties are common in algebraic geometry, including in many recent papers of Catalisano, Geramita, and Gimigliano (e.g., [5]), and, as Sturmfels and Sullivant note in [28], are playing an important role in algebraic statistics.

Definition 3.6.

Let I ⊂ S be any ideal, and continue to use all the notation above. Put $T = K[V,Y _{1},\ldots,Y _{k}]$ and regard S and T _k as subrings of T. Then the kth secant power of I is

$${I}^{\{k\}} = S \cap \left (\,\widetilde{I} + \left (\{x_{ i} - \phi _{k}(x_{i})\}\right )\right ).$$

Lemma 3.5 becomes the following theorem of Sturmfels and Sullivant [28]:

Theorem 3.7.

G is k-colorable if and only if m∉I(G)^{k}. In particular,

$$\chi (G) =\min \{ k\ \vert \ \mathbf{m}\not\in I{(G)}^{\{k\}}\}.$$

Running Example 3.8.

Let G and I be as in Example 3.4. Then I ^{1} = I and I ^{2} = (abcde) both contain the monomial abcdefg. However, I ^{3} = 0. Thus G is 3-colorable but not 2-colorable.

Alternatively, we can characterize chromatic number by looking directly at the powers of the cover ideal.

Observe that, given a k-coloring of G, the set of vertices which are not colored with any one fixed color forms a vertex cover of G. In particular, a k-coloring yields k different vertex covers, with each vertex missing from exactly one. That is, if we denote these vertex covers $w_{1},\ldots,w_{k}$, we have $w_{1}\ldots w_{k} ={ \mathbf{m}}^{k-1}$. In particular, we have the following result of Francisco, Hà, and Van Tuyl. [11].

Theorem 3.9.

G is k-colorable if and only if m ^k−1 ∈ J(G)^k. In particular,

$$\chi (G) =\min \{ k\ \vert \ {\mathbf{m}}^{k-1} \in J{(G)}^{k}\}.$$

Proof.

Let J = J(G). Given a k-coloring, let w _i be the set of vertices assigned a color other than i. Then ${\mathbf{m}}^{k-1} = w_{1}\ldots w_{k} \in {J}^{k}$. Conversely, if m ^{k − 1} ∈ J ^k, we may write ${\mathbf{m}}^{k-1} = w_{1}\ldots w_{k}$ with each w _i a square-free monomial in J. Assigning the color i to the complement of w _i yields a k-coloring: indeed, we have $\prod \frac{\mathbf{m}} {w_{i}} = \frac{{\mathbf{m}}^{k}} {{\mathbf{m}}^{k-1}} = \mathbf{m}$, so the $\frac{\mathbf{m}} {w_{i}}$ partition V.

Running Example 3.10.

In Example 3.4, let m = abcdefg. The cover ideal J(G) is (abdf,acdf,bdef,aceg,bceg,bdeg). Because J does not contain m ⁰ = 1, G is not 1-colorable. All 21 generators of J ² are divisible by the square of a variable, so G is not 2-colorable. Thus m ∉ J ², so J is not 2-colorable. However, J ³ contains m ², so G is 3-colorable.

Remark 3.11.

One can adapt the proof of Theorem 3.9 to determine the b-fold chromatic number of a graph, the minimum number of colors required when each vertex is assigned b colors, and adjacent vertices must have disjoint color sets. See [11, Theorem 3.6].

Remark 3.12.

The ideal membership problems in Theorems 3.7 and 3.9 are for monomial ideals, and so they are computationally simple. On the other hand, computing the chromatic number is an NP-complete problem. The bottleneck in the algebraic algorithms derived from Theorems 3.7 and 3.9 is the computation of the secant ideal I(G)^{k} or the cover ideal J(G) given G; these problems are both NP-complete.

It is naturally interesting to investigate the following problem.

Problem 3.13.

Find algebraic algorithms to compute the chromatic number χ(G) based on algebraic invariants and properties of the edge ideal I(G).

For the rest of this section, we shall restrict our attention to the case when G is a graph (i.e., not a hypergraph), and consider the problem of identifying odd cycles and odd holes in G. As before, let I = I(G) and J = J(G).

Recall that a bipartite graph is a two-colorable graph, or, equivalently, a graph with no odd circuits. This yields two corollaries to Theorem 3.9:

Corollary 3.14.

G is a bipartite graph if and only if m ∈ J².

Corollary 3.15.

If G is a graph, then G contains an odd circuit if and only if m∉J².

It is natural to ask if we can locate the offending odd circuits. In fact, we can identify the odd induced cycles from the associated primes of J ².

Definition 3.16.

Let $C = (x_{i_{1}},\ldots,x_{i_{s}},x_{i_{1}})$ be a circuit in G. We say that C is an induced cycle if the induced subgraph of G on $W =\{ x_{i_{1}},\ldots,x_{i_{s}}\}$ has no edges except those connecting consecutive vertices of C. Equivalently, C is an induced cycle if it has no chords.

Running Example 3.17.

G has induced cycles abcde and defg. The circuit abcdgfe isn’t an induced cycle, since it has the chord de.

Simis and Ulrich prove that the odd induced cycles are the generators of the second secant ideal of I [27].

Theorem 3.18.

Let G be a graph with edge ideal I. Then a square-free monomial m is a generator of I ^{2} if and only if G _m is an odd induced cycle.

Proof (Sketch of proof).

If G _m is an odd induced cycle, then G _m and hence G are not 2-colorable. On the other hand, if m ∈ I ^{2}, then G _m is not 2-colorable and so has an odd induced cycle.

Now suppose that G is a cycle on (2ℓ − 1) vertices, so without loss of generality $I = (x_{1}x_{2},x_{2}x_{3},\ldots,x_{2\ell-1}x_{1})$. Then the generators of J include the (2ℓ − 1) vertex covers $w_{i} = x_{i}x_{i+2}x_{i+4}\ldots x_{i+2\ell-2}$ obtained by starting anywhere in the cycle and taking every second vertex until we wrap around to an adjacent vertex. (Here we have taken the subscripts mod (2ℓ − 1) for notational sanity.) All other generators have higher degree. In particular, the generators of J all have degree at least ℓ, so the generators of J ² have degree at least 2ℓ. Thus m ∉ J ², since $\deg (\mathbf{m}) = 2\ell - 1$. However, we have $\mathbf{m}x_{i} = w_{i}w_{i+1} \in {J}^{2}$ for all x _i . Thus m is in the socle of S ∕ J ², and in particular this socle is nonempty, so $\mathfrak{p}_{\mathbf{m}} = (x_{1},\ldots,x_{2\ell-1})$ is associated to J ². In fact, it is a moderately difficult computation to find an irredundant primary decomposition:

Proposition 3.19.

Let G be the odd cycle on $x_{1},\ldots,x_{2\ell-1}$ . Then

$${J}^{2} = \left [\bigcap\limits _{i=1}^{2\ell-1}{(x_{ i},x_{i+1})}^{2}\right ] \cap (x_{ 1}^{2},\ldots,x_{ 2\ell-1}^{2}).$$

Remark 3.20.

Proposition 3.19 picks out the difference between J ² and the symbolic square J ⁽²⁾ when G is an odd cycle. The product of the variables m appears in ${\mathfrak{p}}^{2}$ for all $\mathfrak{p} \in \mathrm{ Ass}(S/J)$, but is missing from J ². (Combinatorially, this corresponds to m being a double cover of G that cannot be partitioned into two single covers.) Thus m ∈ J ⁽²⁾\ J ².

Remark 3.21.

We can attempt a similar analysis on an even cycle, but we find only two smallest vertex covers, $w_{\text{ odd}} = x_{1}\ldots x_{2\ell-1}$ and $w_{\text{ even}} = x_{2}\ldots x_{2\ell}$. Then m = w _{{ odd}} w _{{ even}} ∈ J ² is not a socle element. In this case Theorem 3.22 will tell us that J ² has primary decomposition ⋂(x _i , x _{i + 1})², i.e., J ⁽²⁾ = J ².

In fact, Francisco, Hà, and Van Tuyl show that, for an arbitrary graph G, the odd cycles can be read off from the associated primes of J ² [9]. Given a set W ⊂ V, put $\mathfrak{p}_{W}^{\langle 2\rangle } = (x_{i}^{2} : x_{i} \in W)$. Then we have:

Theorem 3.22.

Let G be a graph. Then J ² has irredundant primary decomposition

$${J}^{2} = \left [\bigcap\limits _{e\in E(G)}\mathfrak{p}_{e}^{2}\right ] \cap \left [\bigcap\limits _{G_{ W}\text{ \textit{is an induced odd cycle}}}\mathfrak{p}_{W}^{\langle 2\rangle }\right ].$$

Corollary 3.23.

Let G be a graph. Then we have

$$\mathrm{Ass}(S/{J}^{2}) = \left \{\mathfrak{p}_{ e} : e \in E(G)\right \} \cup \left \{\mathfrak{p}_{W} : G_{W} \text{ \textit{is an induced odd cycle}}\right \}.$$

Corollary 3.23 and Theorem 3.18 are also connected via work of Sturmfels and Sullivant [28], who show that generalized Alexander duality connects the secant powers of an ideal with the powers of its dual.

Running Example 3.24.

We have $\mathrm{Ass}(S/{J}^{2}) = E(G) \cup \{ (a,b,c,d,e)\}$. The prime (a, b, c, d, e) appears here because abcde is an odd induced cycle of G. The even induced cycle defg does not appear in Ass(S ∕ J ²), nor does the odd circuit abcdgfe, which is not induced. Furthermore, per Theorem 3.18, I ^{2} is generated by the odd cycle abcde.

Theorem 3.22 and Corollary 3.23 tell us that the odd cycles of a graph G exactly describe the difference between the symbolic square and ordinary square of its cover ideal J(G). It is natural to ask about hypergraph-theoretic interpretations of the differences between higher symbolic and ordinary powers of J(G), and of the differences between these powers for the edge ideal I(G). The answer to the former question involves critical hypergraphs, discussed in Sect. 4. The latter question is closely related to a problem in combinatorial optimization theory. We describe this relationship in Sect. 5.

The importance of detecting odd induced cycles in a graph is apparent in the Strong Perfect Graph Theorem, proven by Chudnovsky, Robertson, Seymour, and Thomas in [6] after the conjecture had been open for over 40 years. A graph G is perfect if for each induced subgraph H of G, the chromatic number χ(H) equals the clique number ω(H), where ω(H) is the number of vertices in the largest clique (i.e., complete subgraph) appearing in H. Perfect graphs are an especially important class of graphs, and they have a relatively simple characterization. Call any odd cycle of at least five vertices an odd hole, and define an odd antihole to be the complement of an odd hole.

Theorem 3.25 (Strong Perfect Graph Theorem).

A graph is perfect if and only if it contains no odd holes or odd antiholes.

Let G be a graph with complementary graph G ^c (i.e., G ^c has the same vertex set as G but the complementary set of edges). Let J(G) be the cover ideal of G and J(G ^c) be the cover ideal of G ^c. Using the Strong Perfect Graph Theorem along with Corollary 3.23, we conclude that a graph G is perfect if and only if neither S ∕ J(G)² nor S ∕ J(G ^c)² has an associated prime of height larger than three. It is clear from the induced pentagon that the graph from Running Example 3.4 is imperfect; this is apparent algebraically from the fact that (a, b, c, d, e) is associated to R ∕ J(G)².

4 Associated Primes and Perfect Graphs

Theorem 3.22 and Corollary 3.23 exhibit a strong interplay between coloring properties of a graph and associated primes of the square of its cover ideal. In this section, we explore the connection between coloring properties of hypergraphs in general and associated primes of higher powers of their cover ideals. We also specialize back to graphs and give algebraic characterizations of perfect graphs.

Definition 4.1.

A critically d-chromatic hypergraph is a hypergraph G with χ(G) = d whose proper induced subgraphs all have smaller chromatic number; G is also called a critical hypergraph.

The connection between critical hypergraphs and associated primes begins with a theorem of Sturmfels and Sullivant on graphs that generalizes naturally to hypergraphs.

Theorem 4.2.

Let G be a hypergraph with edge ideal I. Then the square-free minimal generators of I ^{s} are the monomials W such that G _W is critically (s + 1)-chromatic.

Higher powers of the cover ideal J = J(G) of a hypergraph have more complicated structure than the square. It is known that the primes associated to S ∕ J ² persist as associated primes of all S ∕ J ^s for s ≥ 2 [11, Corollary 4.7]. As one might expect from the case of J ², if H is a critically (d + 1)-chromatic induced subhypergraph of G, then $\mathfrak{p}_{H} \in \mathrm{ Ass}(S/{J}^{d})$ but $\mathfrak{p}_{H}\notin \mathrm{Ass}(S/{J}^{e})$ for any e < d. However, the following example from [11] illustrates that other associated primes may arise as well.

Example 4.3.

Let G be the graph with vertices $\{x_{1},\ldots,x_{6}\}$ and edges

$$x_{1}x_{2},x_{2}x_{3},x_{3}x_{4},x_{4}x_{5},x_{5}x_{1},x_{3}x_{6},x_{4}x_{6},x_{5}x_{6},$$

where we have abused notation by writing edges as monomials. Thus G is a five-cycle on $\{x_{1},\ldots,x_{5}\}$ with an extra vertex x ₆ joined to x ₃, x ₄, and x ₅. Let J be the cover ideal of G. The maximal ideal $\mathfrak{m} = (x_{1},\ldots,x_{6})$ is associated to S ∕ J ³ but to neither S ∕ J nor S ∕ J ². However, G is not a critically 4-chromatic graph; instead, χ(G) = 3.

Consequently, the critical induced subhypergraphs of a hypergraph G may not detect all associated primes of S ∕ J ^s. Fortunately, there is a related hypergraph whose critical induced subhypergraphs do yield a complete list of associated primes. We define the expansion of a hypergraph, the crucial tool.

Definition 4.4.

Let G be a hypergraph with vertices $V =\{ x_{1},\ldots,x_{n}\}$ and edges E, and let s be a positive integer. We create a new hypergraph G ^s, called the sth expansion of G, as follows. We create vertex sets $V _{1} =\{ x_{1,1},\ldots,x_{n,1}\}$, …, $V _{s} =\{ x_{1,s},\ldots,x_{n,s}\}$. (We think of these vertex sets as having distinct flavors. In the literature, the different flavors x _{i, j} of a vertex x _i are sometimes referred to as its shadows.) The edges of G ^s consist of all edges x _{i, j} x _{i, k} connecting all differently flavored versions of the same vertex, and all edges arising from possible assignments of flavors to the vertices in an edge of G.

We refer to the map sending all flavors x _{i, j} of a vertex x _i back to x _i as depolarization, by analogy with the algebraic process of polarization.

Example 4.5.

Consider a five-cycle G with vertices $x_{1},\ldots,x_{5}$. Then G ² has vertex set $\{x_{1,1},x_{1,2},\ldots,x_{5,1},x_{5,2}\}$. Its edge set consists of edges $x_{1,1}x_{1,2},\ldots,x_{5,1}x_{5,2}$ as well as all edges $x_{i,j}x_{i+1,{j}^{{\prime}}}$, where 1 ≤ j ≤ j ^′ ≤ 2, and the first index is taken modulo 5. Thus, for example, the edge x ₁ x ₂ of G yields the four edges x _{1, 1} x _{2, 1}, x _{1, 1} x _{2, 2}, x _{1, 2} x _{2, 1}, and x _{1, 2} x _{2, 2} in G ² (Fig. 2).

Fig. 2

The second expansion graph of a 5-cycle

Our goal is to understand the minimal monomial generators of the generalized Alexander dual (J(G)^s)^[s], where s is the vector $(s,\ldots,s)$, one entry for each vertex of G. Under generalized Alexander duality, these correspond to the ideals in an irredundant irreducible decomposition of J(G)^s, yielding the associated primes of S ∕ J(G)^s.

By generalized Alexander duality, Theorem 4.2 identifies the square-free minimal monomial generators of (J(G)^s)^[s]. Understanding the remaining monomial generators requires the following theorem [11, Theorem 4.4]. For a set of vertices T, write m _T to denote the product of the corresponding variables.

Theorem 4.6.

Let G be a hypergraph with cover ideal J = J(G), and let s be a positive integer. Then

$${({J}^{s})}^{[\mathbf{s}]} = (\overline{\mathbf{m}_{ T}}\ \big{\vert }\ \chi (G_{T}^{s}) > s)$$

where $\overline{\mathbf{m}_{T}}$ is the depolarization of m _T.

The proof relies on a (hyper)graph-theoretic characterization of the generators of I(G ^s)^{s} from Theorem 4.2. One then needs to prove that (J ^s)^[s] is the depolarization of I(G ^s)^{s}, which requires some effort; see [11].

Using Theorem 4.6, we can identify all associated primes of S ∕ J(G)^s in terms of the expansion graph of G.

Corollary 4.7.

Let G be a hypergraph with cover ideal J = J(G). Then $P = (x_{i_{1}},\ldots,x_{i_{r}}) \in \mathrm{ Ass}(S/{J}^{s})$ if and only if there is a subset T of the vertices of G ^s such that G _T ^s is critically (s + 1)-chromatic, and T contains at least one flavor of each variable in P but no flavors of other variables.

We outline the rough idea of the proof. If P ∈ Ass(S ∕ J ^s), then $(x_{i_{1}}^{e_{i_{1}}},\ldots,x_{i_{ r}}^{e_{i_{r}}})$ is an irreducible component of J ^s, for some $e_{i_{j}} > 0$. This yields a corresponding minimal generator of (J ^s)^[s], which gives a subset W of the vertices of G ^s such that G _W ^s is critically (s + 1)-chromatic, and W depolarizes to $x_{i_{1}}^{e_{i_{1}}}\ldots x_{i_{ r}}^{e_{i_{r}}}$. Conversely, given a critically (s + 1)-chromatic expansion hypergraph G _T ^s, we get a minimal generator of (J ^s)^[s] of the form $x_{i_{1}}^{e_{i_{1}}}\cdots x_{i_{ r}}^{e_{i_{r}}}$, where $1 \leq e_{i_{j}} \leq s$ for all i _j . Duality produces an irreducible component of J ^s with radical P.

Corollary 4.7 explains why $\mathfrak{m} \in \mathrm{ Ass}(S/{J}^{3})$ in Example 4.3. Let T be the set of vertices

$$T =\{ x_{1,1},x_{2,1},x_{2,2},x_{3,1},x_{4,1},x_{5,1},x_{6,1}\},$$

a subset of the vertices of G ³. Then G _T ³ is critically 4-chromatic.

As a consequence of this work, after specializing to graphs, we get two algebraic characterizations of perfect graphs that are independent of the Strong Perfect Graph Theorem. First, we define a property that few ideals satisfy (see, e.g., [18]).

Definition 4.8.

An ideal I ⊂ S has the saturated chain property for associated primes if given any associated prime P of S ∕ I that is not minimal, there exists an associated prime Q⊊P with height(Q) = height(P) − 1.

We can now characterize perfect graphs algebraically in two different ways [11, Theorem 5.9]. The key point is that for perfect graphs, the associated primes of powers of the cover ideal correspond exactly to the cliques in the graph.

Theorem 4.9.

Let G be a simple graph with cover ideal J. Then the following are equivalent:

• (1) G is perfect.

• (2) For all s with 1 ≤ s < χ(G), $P = (x_{i_{1}},\ldots,x_{i_{r}}) \in \mathrm{ Ass}(R/{J}^{s})$ if and only if the induced graph on $\{x_{i_{1}},\ldots,x_{i_{r}}\}$ is a clique of size 1 < r ≤ s + 1 in G.

• (3) For all s ≥ 1, J ^s has the saturated chain property for associated primes.

Proof.

We sketch (1) implies (2) to give an idea of how expansion is used. Suppose G is a perfect graph. A standard result in graph theory shows that G ^s is also perfect. Let P ∈ Ass(S ∕ J ^s), so P corresponds to some subset T of the vertices of G ^s such that G _T ^s is critically (s + 1)-chromatic. Because G ^s is perfect, the clique number of G _T ^s is also s + 1, meaning there exists a subset T ^′ of T such that $G_{{T}^{{\prime}}}^{s}$ is a clique with s + 1 vertices. Thus $G_{{T}^{{\prime}}}^{s}$ is also a critically (s + 1)-chromatic graph contained inside G _T ^s, forcing T = T ^′. Hence G _T ^s is a clique, and the support of the depolarization of $\bar{\mathbf{m}_{T}}$ is a clique with at most s + 1 vertices. Therefore G _P is a clique.

Remark 4.10.

If J is the cover ideal of a perfect graph, its powers satisfy a condition stronger than that of Definition 4.8. If P ∈ Ass(S ∕ J ^s), and Q is any monomial prime of height at least two contained in P, then Q ∈ Ass(S ∕ J ^s). This follows from the fact that P corresponds to a clique in the graph.

Theorem 4.9 provides information about two classical issues surrounding associated primes of powers of ideals. Brodmann proved that for any ideal J, the set of associated primes of S ∕ J ^s stabilizes [3]. However, there are few good bounds in the literature for the power at which this stabilization occurs. When J is the cover ideal of a perfect graph, Theorem 4.9 demonstrates that stabilization occurs at χ(G) − 1. Moreover, though in general associated primes may disappear and reappear as the power on J increases (see, e.g., [1, 14] and also [23, Example 4.18]), when J is the cover ideal of a perfect graph, we have $\mathrm{Ass}(S/{J}^{s}) \subseteq \mathrm{ Ass}(S/{J}^{s+1})$ for all s ≥ 1. In this case, we say that J has the persistence property for associated primes, or simply the persistence property. Morey and Villarreal give an alternate proof of the persistence property for cover ideals of perfect graphs in [23, Example 4.21].

While there are examples of arbitrary monomial ideals for which persistence fails, we know of no such examples of square-free monomial ideals. Francisco, Hà, and Van Tuyl (see [9, 10]) have asked:

Question 4.11.

Suppose J is a square-free monomial ideal. Is $\mathrm{Ass}(S/{J}^{s}) \subseteq \mathrm{ Ass}(S/{J}^{s+1})$ for all s ≥ 1?

While Question 4.11 has a positive answer when J is the cover ideal of a perfect graph, little is known for cover ideals of imperfect graphs. Francisco, Hà, and Van Tuyl answer Question 4.11 affirmatively for odd holes and odd antiholes in [10], but we are not aware of any other imperfect graphs whose cover ideals are known to have this persistence property. One possible approach is to exploit the machinery of expansion again. Let G be a graph, and let x _i be a vertex of G. Form the expansion of G at {x _i } by replacing x _i with two vertices x _{i, 1} and x _{i, 2}, joining them with an edge. For each edge {v, x _i } of G, create edges {v, x _{i, 1}} and {v, x _{i, 2}}. If W is any subset of the vertices of G, form G[W] by expanding all the vertices of W. Francisco, Hà, and Van Tuyl conjecture:

Conjecture 4.12.

Let G be a graph that is critically s-chromatic. Then there exists a subset W of the vertices of G such that G[W] is critically (s + 1)-chromatic.

In [10], Francisco, Hà, and Van Tuyl prove that if Conjecture 4.12 is true for all s ≥ 1, then all cover ideals of graphs have the persistence property. One can also state a hypergraph version of Conjecture 4.12; if true, it would imply persistence of associated primes for all square-free monomial ideals.

Finally, in [23], Morey and Villarreal prove persistence for edge ideals I of any graphs containing a leaf (a vertex of degree 1). Their proof passes to the associated graded ring, and the vital step is identifying a regular element of the associated graded ring in I ∕ I ². Morey and Villarreal remark that attempts to prove persistence results for more general square-free monomial ideals lead naturally to questions related to the Conforti–Cornuéjols conjecture, discussed in the following section.

5 Equality of Symbolic and Ordinary Powers and Linear Programming

We have seen in the last section that comparing symbolic and ordinary powers of the cover ideal of a hypergraph allows us to study structures and coloring properties of the hypergraph. In this section, we address the question of when symbolic and ordinary powers of a square-free monomial ideal are the same and explore an algebraic approach to a long-standing conjecture in linear integer programming, the Conforti–Cornuéjols conjecture. In what follows, we state the Conforti–Cornuéjols conjecture in its original form, describe how to translate the conjecture into algebraic language, and discuss its algebraic reformulation and related problems.

The Conforti–Cornuéjols conjecture states the equivalence between the packing and the max-flow-min-cut (MFMC) properties for clutters which, as noted before, are essentially simple hypergraphs.

As before, G = (V, E) denotes a hypergraph with n vertices $V =\{ x_{1},\ldots,x_{n}\}$ and m edges $E =\{ e_{1},\ldots,e_{m}\}$. Let A be the incidence matrix of G, i.e., the (i, j)-entry of A is 1 if the vertex x _i belongs to the edge e _j and 0 otherwise. For a nonnegative integral vector $\mathbf{c} \in \mathbb{Z}_{\geq 0}^{n}$, consider the following dual linear programming system:

$$\begin{array}{rcl} \max \left \{\langle \mathbf{1},\mathbf{y}\rangle \ \vert \ \mathbf{y} \in \mathbb{R}_{\geq 0}^{m},A\mathbf{y} \leq \mathbf{c}\right \} =\min \left \{\langle \mathbf{c},\mathbf{z}\rangle \ \vert \ \mathbf{z} \in \mathbb{R}_{ \geq 0}^{n},{A}^{\text{ T}}\mathbf{z} \geq \mathbf{1}\right \}.& &\end{array}$$

(1)

Definition 5.1.

Let G be a simple hypergraph.

• (1) The hypergraph G is said to pack if the dual system (1) has integral optimal solutions y and z when c = 1.

• (2) The hypergraph G is said to have the packing property if the dual system (1) has integral optimal solutions y and z for all vectors c with components equal to 0, 1, and + ∞.

• (3) The hypergraph G is said to have the MFMC property or to be Mengerian if the dual system (1) has integral optimal solutions y and z for all nonnegative integral vectors $\mathbf{c} \in \mathbb{Z}_{\geq 0}^{n}$.

Remark 5.2.

In Definition 5.1, setting an entry of c to + ∞ means that this entry is sufficiently large, so the corresponding inequality in the system A y ≤ c can be omitted. It is clear that if G satisfies the MFMC property, then it has the packing property.

The following conjecture was stated in [7, Conjecture 1.6] with a reward prize of $5,000 for the solution.

Conjecture 5.3 (Conforti–Cornuéjols).

A hypergraph has the packing property if and only if it has the MFMC property.

As we have remarked, the main point of Conjecture 5.3 is to show that if a hypergraph has the packing property then it also has the MFMC property.

The packing property can be understood via more familiar concepts in (hyper) graph theory, namely, vertex covers (also referred to as transversals), which we recall from Sect. 1, and matchings.

Definition 5.4.

A matching (or independent set) of a hypergraph G is a set of pairwise disjoint edges.

Let α₀(G) and β₁(G) denote the minimum cardinality of a vertex cover and the maximum cardinality of a matching in G, respectively. We have α₀(G) ≥ β₁(G) since every edge in any matching must hit at least one vertex from every cover.

The hypergraph G is said to be König if α₀(G) = β₁(G). Observe that giving a vertex cover and a matching of equal size for G can be viewed as giving integral solutions to the dual system (1) when c = 1. Thus, G is König if and only if G packs.

There are two operations commonly used on a hypergraph G to produce new, related hypergraphs on smaller vertex sets. Let x ∈ V be a vertex in G. The deletionG ∖ x is formed by removing x from the vertex set and deleting any edge in G that contains x. The contraction G ∕ x is obtained by removing x from the vertex set and removing x from any edge of G that contains x. Any hypergraph obtained from G by a sequence of deletions and contractions is called a minor of G. Observe that the deletion and contraction of a vertex x in G has the same effect as setting the corresponding component in c to + ∞ and 0, respectively, in the dual system (1). Hence,

G satisfies the packing property if and only if G and all of its minors are König.

Example 5.5.

Let G be a 5-cycle. Then G itself is not König (α₀(G) = 3 and β₁(G) = 2). Thus, G is does not satisfy the packing property.

Example 5.6.

Any bipartite graph is König. Therefore, if G is a bipartite graph, then (since all its minors are also bipartite) G satisfies the packing property.

We shall now explore how Conjecture 5.3 can be understood via commutative algebra, and, more specifically, via algebraic properties of edge ideals.

As noted in Sect. 2, symbolic Rees algebras are more complicated than the ordinary Rees algebras, and could be non-Noetherian. Fortunately, in our situation, the symbolic Rees algebra of a square-free monomial ideal is always Noetherian and finitely generated (cf. [15, Theorem 3.2]). Moreover, the symbolic Rees algebra of the edge ideal of a hypergraph G can also be viewed as the vertex cover algebra of the dual hypergraph G ^∗.

Definition 5.7.

Let G = (V, E) be a simple hypergraph over the vertex set $V =\{ x_{1},\ldots,x_{n}\}$.

• (1) We call a nonnegative integral vector $\mathbf{c} = (c_{1},\ldots,c_{n})$ a k-cover of G if $\sum _{x_{i}\in e}c_{i} \geq k$ for any edge e in G.

• (2) The vertex cover algebra of G, denoted by $\mathcal{A}(G)$, is defined to be

  $$\mathcal{A}(G) = \mathop\oplus\limits _{k\geq 0}\mathcal{A}_{k}(G),$$

  where $\mathcal{A}_{k}(G)$ is the k-vector space generated by all monomials $x_{1}^{c_{1}}\ldots x_{n}^{c_{n}}{t}^{k}$ such that $(c_{1},\ldots,c_{n}) \in \mathbb{Z}_{\geq 0}^{n}$ is a k-cover of G.

Lemma 5.8.

Let G be a simple hypergraph with edge ideal I = I(G), and let G ^∗ be its dual hypergraph. Then

$$\mathcal{R}_{s}(I) = \mathcal{A}({G}^{{_\ast}}).$$

We are now ready to give an algebraic interpretation of the MFMC property.

Lemma 5.9.

Let G = (V, E) be a simple hypergraph with n vertices and m edges. Let A be its incidence matrix. For a nonnegative integral vector $\mathbf{c} \in \mathbb{Z}_{\geq 0}^{n}$, define

$$\begin{array}{lll}\sigma (\mathbf{c}) =\max \{\langle \mathbf{1},\mathbf{y}\rangle \ \vert \ \mathbf{y} \in \mathbb{Z}_{\geq 0}^{m},A\mathbf{y} \leq \mathbf{c}\} \ \text{and} \\ \gamma (\mathbf{c}) =\min \{\langle \mathbf{c},\mathbf{z}\rangle \ \vert \ \mathbf{z} \in \mathbb{Z}_{\geq 0}^{n},{A}^{\text{ T}}\mathbf{z} \geq \mathbf{1}\}.\end{array}$$

Then

• (1) c is a k-cover of G ^∗ if and only if k ≤ γ(c).

• (2) c can be written as a sum of k vertex covers of G ^∗ if and only if k ≤ σ(c).

Proof.

By definition, a nonnegative integral vector $\mathbf{c} = (c_{1},\ldots,c_{n}) \in \mathbb{Z}_{\geq 0}^{n}$ is a k-cover of G ^∗ if and only if

$$\begin{array}{rcl} k \leq \min \left \{\sum\limits _{x_{i}\in e}c_{i}\ \vert \ e\text{ is any edge of }{G}^{{_\ast}}\right \}.& &\end{array}$$

(2)

Let z be the (0, 1)-vector representing e. Observe that e is an edge of G ^∗ if and only if e is a minimal vertex cover of G, and this is the case if and only if A ^{{ T}} z ≥ 1. Therefore, the condition in (2) can be translated to

$$\begin{array}{ll} k \leq \min \{\langle \mathbf{c},\mathbf{z}\rangle \ \vert \ \mathbf{z} \in \{ 0,{1\}}^{n},{A}^{\text{ T}}\mathbf{z} \geq \mathbf{1}\} \\ \ \ =\min \{\langle \mathbf{c},\mathbf{z}\rangle \ \vert \ \mathbf{z} \in \mathbb{Z}_{\geq 0}^{n},{A}^{\text{ T}}\mathbf{z} \geq \mathbf{1}\} = \gamma (\mathbf{c}).& \\ \end{array}$$

To prove (2), let $\mathbf{a}_{1},\ldots,\mathbf{a}_{m}$ be representing vectors of the edges in G (i.e., the columns of the incidence matrix A of G). By Proposition 2.7, $\mathbf{a}_{1},\ldots,\mathbf{a}_{m}$ represent the minimal vertex cover of the dual hypergraph G ^∗. One can show that a nonnegative integral vector $\mathbf{c} \in {\mathbb{Z}}^{n}$ can be written as the sum of k vertex covers (not necessarily minimal) of G ^∗ if and only if there exist integers $y_{1},\ldots,y_{m} \geq 0$ such that $k = y_{1} + \cdots + y_{m}$ and $y_{1}\mathbf{a}_{1} + \cdots + y_{m}\mathbf{a}_{m} \leq \mathbf{c}$. Let $\mathbf{y} = (y_{1},\ldots,y_{m})$. Then

$$\langle \mathbf{1},\mathbf{y}\rangle = y_{1} + \cdots + y_{m}\text{ and }A\mathbf{y} = y_{1}\mathbf{a}_{1} + \cdots + y_{m}\mathbf{a}_{m}.$$

Thus,

$$\sigma (\mathbf{c}) =\max \{ k\ \vert \ \mathbf{c}\text{ can be written as a sum of }k\text{ vertex covers of }{G}^{{_\ast}}\}.$$

Theorem 5.10.

Let G be a simple hypergraph with dual hypergraph G ^∗ . Then the dual linear programming system(1) has integral optimal solutions y and z for all nonnegative integral vectors c if and only if $\mathcal{R}_{s}(I(G)) = \mathcal{A}({G}^{{_\ast}})$ is a standard graded algebra or, equivalently, if and only if I(G)^(q) = I(G)^q for all q ≥ 0.

Proof.

Given integral optimal solutions y and z of the dual system (1) for a nonnegative integral vector c, we get

$$\sigma (\mathbf{c}) = \gamma (\mathbf{c}).$$

The conclusion then follows from Lemmas 5.8 and 5.9.

The following result (see [16, Corollary 1.6] and [12, Corollary 3.14]) gives an algebraic approach to Conjecture 5.3.

Theorem 5.11.

Let G be a simple hypergraph with edge ideal I = I(G). The following conditions are equivalent:

• (1) G satisfies the MFMC property.

• (2) I ^(q) = I ^q for all q ≥ 0.

• (3) The associated graded ring $gr _{I} := \oplus _{q\geq 0}{I}^{q}/{I}^{q+1}$ is reduced.

• (4) I is normally torsion-free , i.e., all powers of I have the same associated primes.

Proof.

The equivalence between (1) and (2) is the content of Theorem 5.10. The equivalences of (2), (3), and (4) are well-known results in commutative algebra (cf. [19]).

The Conforti–Cornuéjols conjecture now can be restated as follows.

Conjecture 5.12.

Let G be a simple hypergraph with edge ideal I = I(G). If G has packing property then the associated graded ring gr _I is reduced. Equivalently, if G and all its minors are König, then the associated graded ring gr _I is reduced.

It remains to give an algebraic characterization for the packing property. To achieve this, we shall need to interpret minors and the König property. Observe that the deletion G ∖ x at a vertex $x \in \mathcal{X}$ has the effect of setting x = 0 in I(G) (or equivalently, of passing to the ideal (I(G), x) ∕ (x) in the quotient ring S ∕ (x)), and the contraction G ∕ x has the effect of setting x = 1 in I(G) (or equivalently, of passing to the ideal I(G) _x in the localization S _x ). Thus, we call an ideal I ^′ a minor of a square-free monomial ideal I if I ^′ can be obtained from I by a sequence of taking quotients and localizations at the variables. Observe further that α₀(G) = htI(G), and if we let m-grade I denote the maximum length of a regular sequence of monomials in I then $\beta _{1}(G) = m-grade I(G)$. Hence, a simple hypergraph with edge ideal I is König if $\mathrm{ht}I = m-grade I$. This leads us to a complete algebraic reformulation of the Conforti–Cornuéjols conjecture:

Conjecture 5.13.

Let I be a square-free monomial ideal such that I and all of its minors satisfy the property that their heights are the same as their m-grades. Then gr _I is reduced; or equivalently, I is normally torsion-free.

The algebraic consequence of the conclusion of Conjecture 5.13 (and equivalently, Conjecture 5.3) is the equality I ^(q) = I ^q for all q ≥ 0 or, equivalently, the normally torsion-freeness of I. If one is to consider the equality I ^(q) = I ^q, then it is natural to look for an integer l such that I ^(q) = I ^q for 0 ≤ q ≤ l implies I ^(q) = I ^q for all q ≥ 0, or to examine square-free monomial ideals with the property that I ^(q) = I ^q for all q ≥ q ₀. On the other hand, if one is to investigate the normally torsion-freeness then it is natural to study properties of minimally not normally torsion-free ideals. The following problem is naturally connected to Conjectures 5.3 and 5.13, and part of it has been the subject of work in commutative algebra (cf. [13]).

Problem 5.14.

Let I be a square-free monomial ideal in $S = K[x_{1},\ldots,x_{n}]$.

• (1) Find the least integer l (may depend on I) such that if I ^(q) = I ^q for 0 ≤ q ≤ l then I ^(q) = I ^q for all q ≥ 0.

• (2) Suppose that there exists a positive integer q ₀ such that I ^(q) = I ^q for all q ≥ q ₀. Study algebraic and combinatorial properties of I.

• (3) Suppose I is minimally not normally torsion-free (i.e., I is not normally torsion-free, but all its minors are). Find the least power q such that $\mathrm{Ass}(\!S/{I}^{q}\!)\not =\mathrm{Ass}(S/I)$.