Constructal Design of Vortex Tubes

Abstract

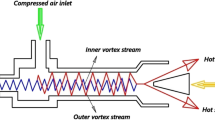
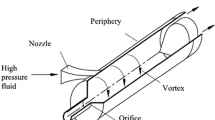
The vortex tube (also known as Ranque-Hilsch vortex tube) is a mechanical device which splits a compressed high-pressure gas stream into cold and hot lower pressure streams without any chemical reactions or external energy supply [1–3]. Such a separation of the flow into regions of low and high total temperature is referred to as the temperature (or energy) separation effect. The device consists of a simple circular tube, one or more tangential nozzles, and a throttle valve. Figure 15.1 depicts schematically two types of vortex tubes: Counter flow (Fig. 15.1a) and parallel flow (Fig. 15.1b). The operational principle of a counter flow vortex tube, which is the scope of the present work, Fig. 15.1a, consists of a high-pressure gas that enters the vortex tube and passes through the nozzle(s). The gas expands through the nozzle and achieves a high angular velocity, causing a vortex-type flow in the tube. There are two exits: the hot exit that is placed near the outer radius of the tube at the end away from the nozzle and the cold exit that is placed at the center of the tube at the same end as the nozzle. By adjusting a throttle valve (cone valve) downstream of the hot exit it is possible to vary the fraction of the incoming flow that leaves through the cold exit, referred as cold fraction. This adjustment affects the amount of cold and hot energy that leaves the vortex tube in the device exits.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

15.1 Introduction

The vortex tube (also known as Ranque-Hilsch vortex tube) is a mechanical device which splits a compressed high-pressure gas stream into cold and hot lower pressure streams without any chemical reactions or external energy supply [1–3]. Such a separation of the flow into regions of low and high total temperature is referred to as the temperature (or energy) separation effect. The device consists of a simple circular tube, one or more tangential nozzles, and a throttle valve. Figure 15.1 depicts schematically two types of vortex tubes: Counter flow (Fig. 15.1a) and parallel flow (Fig. 15.1b). The operational principle of a counter flow vortex tube, which is the scope of the present work, Fig. 15.1a, consists of a high-pressure gas that enters the vortex tube and passes through the nozzle(s). The gas expands through the nozzle and achieves a high angular velocity, causing a vortex-type flow in the tube. There are two exits: the hot exit that is placed near the outer radius of the tube at the end away from the nozzle and the cold exit that is placed at the center of the tube at the same end as the nozzle. By adjusting a throttle valve (cone valve) downstream of the hot exit it is possible to vary the fraction of the incoming flow that leaves through the cold exit, referred as cold fraction. This adjustment affects the amount of cold and hot energy that leaves the vortex tube in the device exits.

Fig. 15.1

Operating principle of two types of vortex tubes: (a) counter flow and (b) parallel flow

The vortex tube has been a subject of studies due to its enormous applications in engineering, such as cooling of machine parts, refrigeration, cool electric or electronic control cabinets, cooling of equipment in laboratories dealing with explosive chemicals, chill environmental chambers, cool foods, liquefaction of natural gas, and cooling suits [3–7]. Moreover, the lack of moving parts, electricity, and other advantages make the device attractive for a number of specialized applications where simplicity, robustness, reliability, and general safety are desired [8].

Another important motivation for the study of vortex tube is the complexity of the energy separation phenomenon in the compressible and turbulent flow. Several studies have been performed to explain the phenomena occurring during the energy separation inside the vortex tube. For example, Harnet and Eckert [9] invoked turbulent eddies. Stephan et al. [10] stated that the drive of fluid motion is related with Goërtler vortices. Ahlborn and Groves [11] presented the theory of secondary circulation to explain energy separation. Lewis and Bejan [8] suggested that angular velocity gradients in the radial direction give rise to frictional coupling between different layers of the rotating flow resulting in a migration of energy via shear work from the inner layers to the outer layers.

Recently, computational fluid dynamics (CFD) modeling has been utilized to improve the comprehension about the energy separation. For instance, Schlenz [12] numerically investigated the energy separation for an axisymmetric compressible flow. The turbulence was treated with a zero-equation turbulence model and the calculations agreed only qualitatively with the experimental data. Cockerill [13] presented a mathematical model for the simulation of a compressible turbulent flow in a vortex tube. He observed that the formation of forced vortex and a strong radial pressure gradient were the two driving forces behind energy separation. Aljuwayhel et al. [14] investigated the energy separation mechanism using the commercial code FLUENT, based on the finite volume method (FVM). They observed that the standard k–ε turbulence model predicted the velocity and temperature separation better than the RNG k–ε turbulence model. Dutta et al. [7] studied the influence of different Reynolds Averaged Navier-Stokes (RANS) turbulence models: standard k–ε, RNG k–ε, standard k–ω, and SST k–ω. A comparison of the temperature separation obtained numerically and experimentally corroborates the previous findings of Aljuwayhel et al. [14]. Farouk and Farouk [15] used large eddy simulation (LES) and compared with previous experimental results of Skye et al. [16] and k–ε predictions. The authors noticed that temperature separation predicted with LES was closer to the experimental results in comparison with those reached with RANS model. It is worthy to mention that the computational effort for LES is, in general, several times higher than that observed for RANS simulations. This fact prevents the use of LES for optimization studies, since several simulations are required.

Concerning the optimization of the vortex tube, according to Eiamsa-ard and Promvonge [3] two important parameters must be taken into account. The first is the geometrical characteristics of the vortex tube (diameter and length of the hot and cold tubes, diameter of the cold orifice, shape of the hot tube, number of inlet nozzles, and others). The second is focused on the thermo-physical parameters such as inlet gas pressure, cold mass fraction, and type of gas (air, oxygen, helium, and methane). Studies in this subject have been presented in the literature. For example, Promvonge and Eiamsa-ard [17] reported the effects of the number of inlet tangential nozzles, the cold orifice diameter and the tube insulations on the temperature reduction and isentropic efficiency of the vortex tube. Aydin and Baki [18] investigated experimentally the energy separation in a counter flow vortex tube having various geometrical and thermo-physical parameters. Pinar et al. [19] investigated the effects of inlet pressure, nozzle number, and fluid type factors on the vortex tube performance by means of Taguchi method. However, as long as we know, it has not been presented in studies concerned with the geometric optimization of the vortex tube by means of constructal design [20, 21].

Constructal theory has been used to explain deterministically the generation of shape in flow structures of nature (river basins, lungs, atmospheric circulation, animal shapes, vascularized tissues, etc) based on an evolutionary principle of flow access in time. That principle is the Constructal law: for a flow system to persist in time (to survive), it must evolve in such way that it provides easier and easier access to the currents that flow through it [21]. This same principle is used to yield new designs for electronics, fuel cells, and tree networks for transport of people, goods, and information [22]. The applicability of this method/law to the physics of engineered flow systems has been widely discussed in recent literature [23–26].

In the present work it is considered as the numerical optimization of a vortex tube device by means of constructal design. It is evaluated in a vortex tube with axisymmetric computational domain. The compressible and turbulent flows are solved with a commercial CFD package code based on the Finite Volume Method, FLUENT [27]. The turbulence is tackled with the standard k–ε model into the Reynolds Averaged Navier-Stokes (RANS) approach. The geometry evaluated here has one global restriction, the total volume of the cylindrical tube, and four degrees of freedom: d/D (the ratio between the diameter of the cold outlet and the diameter of the vortex tube, cold orifice ratio), d ₁/D (the ratio between the nozzle diameter of the entering air and the diameter of the vortex tube), L ₁/L (the ratio between the length of the hot exit annulus and the length of the vortex tube), and D/L (the ratio between the diameter of the vortex tube and its length). However, only the degree of freedom d/D is optimized while the other degrees of freedom are kept fixed. The purpose is to maximize the amount of energy extracted from the cold region (cooling effect) for several geometries. All evaluated geometries are simulated for several ratios between the fixed inlet pressure (p ₁) and the pressure of the hot exit (p ₂), which is adjusted to obtain several cold mass fractions.

15.2 Mathematical Model

The analyzed physical problem consists of a two dimensional axisymmetric cylindrical cavity, as illustrated in Fig. 15.2. The air entering the tube is modeled as an ideal gas with constant specific heat capacity, thermal conductivity, and viscosity. The inlet stagnation conditions are fixed at p ₁ = 300 kPa and T ₁ = 300 K for the verification case and p ₁ = 700 kPa for the optimization cases. The intake air enters with an angle of α = 9° with respect to tangential direction. The static pressure at the cold exit boundary is fixed at atmospheric pressure. For the hot exit boundary, several simulations are performed with various pressures in order to simulate the effect of throttle valve. For each fixed pressure of the hot exit boundary, one specific value of cold mass fraction (y _c = m _c/m) is reached. Once it is considered as a two-dimensional axisymmetric domain, an axis is imposed in the lower surface of the domain, Fig. 15.2. The other surfaces present the no-slip and adiabatic conditions. The vortex tube dimensions are assumed: L = 1.0 × 10⁻¹ m, L ₁ = 1.5 × 10⁻³ m, D = 2 × 10⁻² m, d ₁ = 1.0 × 10⁻³ m, and d = 6.0 × 10⁻³ m for the verification case. The degrees of freedom are also fixed: d ₁/D = 0.05, L ₁/L = 0.015, and D/L = 0.2. The objective of the analysis is to determine the optimal remaining geometry d/D that leads to the maximum cooling heat transfer rate (Q _c).

Fig. 15.2

Domain of the vortex tube

According to constructal design [21], optimization can be subjected to the total volume constraint,

$$ V = \pi {D^{{2}}}L/{4}{.} $$

(15.1)

For all evaluated cases, it solved the time-averaged conservation equations of mass, momentum, and energy for the turbulent flow, which is given respectively by:

$$ \frac{{\partial \bar{\rho }{{\bar{v}}_i}}}{{\partial {x_i}}} = 0\quad \left( {i = 1,2{\text{and}}3} \right){\text{in}}\;t \times \Omega, $$

(15.2)

$${\frac{{\partial \bar{\rho }{{\bar{v}}_i}}}{{\partial t}}+ \frac{{\partial \left( {\bar{\rho }{{\bar{v}}_i}{{\bar{v}}_j}}\right)}}{{\partial {x_j}}} = - \frac{{\partial\bar{p}}}{{\partial{x_j}}}{\delta_{{ij}}} + \frac{\partial }{{\partial {x_j}}}\left\{{\mu \left( {\frac{{\partial {{\bar{v}}_i}}}{{\partial {x_j}}} +\frac{{\partial {{\bar{v}}_j}}}{{\partial {x_i}}}} \right) -{\tau_{{ij}}}} \right\}\quad \left( {i,j = 1,2{\text{ and }}3}\right){\text{ in}}\;t \times \Omega,} $$

(15.3)

$$ \frac{{\partial \bar{\rho }\bar{T}}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {\bar{\rho }{{\bar{v}}_j}\bar{T}} \right) = \frac{\partial }{{\partial {x_j}}}\left\{ {\frac{k}{{{c_p}}}\frac{{\partial \bar{T}}}{{\partial {x_j}}} - {q_j}} \right\}\quad \left( {i,j = 1,2{\text{ and }}3} \right){\text{ in}}\;t \times \Omega, $$

(15.4)

where $\overline {\left( {} \right)}$ represents the time-averaged variables, ρ is the density of the fluid (kg⋅m⁻³), μ is the dynamical viscosity (kg⋅m⁻¹⋅s⁻¹), k is the thermal conductivity of the fluid (W⋅m⁻¹⋅K⁻¹), v _i is the velocity in i-direction, i = 1, 2 and 3 (m⋅s⁻¹), p is the pressure (N⋅m⁻²), T is the temperature (K), δ _ij is the Kronecker delta, Ω is the spatial domain (m), and t is the temporal domain (s).

The turbulent tensor can be written by [28]:

$$ {\tau_{{ij}}} = {\mu_t}\left( {\frac{{\partial {{\bar{v}}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\bar{v}}_j}}}{{\partial {x_i}}}} \right)\quad \left( {i,j = 1,2{\text{ and }}3} \right). $$

(15.5)

The turbulent transport of temperature is obtained through an analogy with the Reynolds tensor [28] and is given by:

$$ {q_j} = \bar{\rho }{\alpha_t}\frac{{\partial \overline T }}{{\partial {x_j}}}\quad \left( {j = 1,2{\text{ and }}3} \right). $$

(15.6)

The time-averaged fields of velocity, pressure, and temperature are obtained by means of standard k–ε model [29, 30]. According to this model it is required that the solution of two additional equations for the turbulent kinetic energy k and its dissipation rate ε, which can be expressed as follows:

$$ \frac{{\partial k}}{{\partial t}} + {\bar{v}_j}\frac{{\partial k}}{{\partial {x_j}}} = {\tau_{{ij}}}\frac{{\partial {{\bar{v}}_i}}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\upsilon + \frac{{{\upsilon_t}}}{{{\sigma_k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] - \varepsilon \quad \left( {i,j = 1,2{\text{ and }}3} \right), $$

(15.7)

$${ \frac{{\partial \varepsilon }}{{\partial t}} +{\bar{v}_j}\frac{{\partial \varepsilon }}{{\partial {x_j}}} =\frac{\partial }{{\partial {x_j}}}\left[ {\left( {\upsilon +\frac{{{\upsilon_t}}}{{{\sigma_{\varepsilon }}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] +{C_{{\varepsilon 1}}}\frac{\varepsilon }{k}{\tau_{{ij}}}\frac{{\partial {{\bar{v}}_i}}}{{\partial {x_j}}} -{C_{{\varepsilon 2}}}\frac{{{\varepsilon^2}}}{k}\quad \left( {i,j =1,2{\text{ and }}3} \right),} $$

(15.8)

where:

$$ {\upsilon_t} = {C_{\mu }}\frac{{{k^2}}}{\varepsilon }, $$

(15.9)

$$ {\alpha_t} = \frac{{{\upsilon_t}}}{{{{\Pr }_t}}}. $$

(15.10)

The model constants appearing in the governing equations, (15.7)–(15.10), are given in Table 15.1.

Table 15.1 Model constants appearing in the governing equations

In order to calculate turbulence quantities accurately in the near-wall region, wall functions for velocity and temperature fields are employed.

15.3 Numerical Model

We simulate the compressible turbulent flows by solving (15.2)–(15.4) using a CFD package based on rectangular finite volume method [27]. The solver is density based and all simulations were performed with the second-order upwind advection scheme. More details about the finite volume method can be found in Patankar [31] and Versteeg and Malalasekera [32].

The spatial discretization is performed with rectangular finite volumes. The grid is more refined for the highest velocity and temperature gradients regions. The grid independence is reached according to the criterion |(T ^j _min − T ^j+1 _min)/T ^j _min| < 5 × 10⁻⁴, where T ^j _min represents the minimal temperature along the domain for the actual grid and T ^j+1 _min corresponds to the minimal temperature for the following grid. The number of volumes is increased approximately two times from one grid to the next. The grid sensibility study is presented for the verification case in Table 15.2. The independent grid was obtained with 11,760 volumes.

Table 15.2 Grid independence study

15.4 Results and Discussion

Firstly, the accuracy of the numerical code is evaluated. A qualitatively evaluation is performed in Fig. 15.3, where the stream function obtained in the present work (Fig. 15.3a) is compared with that numerically predicted in ref. [14] (Fig. 15.3b). It can be observed that there is a similarity between both topologies. For both simulations a steep gradient of velocity near the intake region is noticed. Besides, it is observed that the split of the flux is in three different regions: periphery region (flux that leaves the domain by the hot outlet), central region (fluid that leaves the domain by the cold outlet), and the recirculation region. It is also observed that there are minor differences for the recirculation, such as the lower deformation of the recirculation near the cold exit in the simulation performed in the present study.

Fig. 15.3

Comparison of the stream function obtained numerically: (a) present work, (b) ref. [14]

For the quantitative analysis, the temperature profiles as a function of the vortex tube radius obtained with the present work are compared with those predicted by Aljuwayhel et al. [14] for two different placements of azimuthal coordinates: z = 0.06 m and z = 0.08 m. Figure 15.4 shows for both placements that the temperature profiles have the same tendency. However, the magnitude of the temperature is higher for the simulations of the present work than that predicted in the literature. The highest differences are 2.36% and 1.70% for z = 0.06 m and 0.08 m, respectively. These differences were not expected, since both solutions are obtained with the same numerical code [27]. One possible explanation for the deviations is related with the selection of numerical parameters used in the solution, such as, the advection scheme or the residuals of convergence. In spite of this fact, the results showed a very good agreement.

Fig. 15.4

Comparison of the static temperature profiles as a function of the vortex tube radius for the azimuthal coordinates (z = 0.06 m and 0.08 m) obtained in the present work and predicted in ref. [14]

After the numerical verification, the effect of the cold mass fraction (y _c) on the heat transfer rate that leaves the cold exit (Q _c) is investigated. Figure 15.5 shows the effect of y _c on the heat transfer rate in the cold exit for p ₁ = 700 kPa, d/D = 0.3, d ₁/D = 0.05, L ₁/L = 0.015, and D/L = 0.2. There is one optimal cold mass fraction, y _c,o = 0.56 and the corresponding maximal heat transfer rate obtained for this cold mass fraction is Q _c,m = 221.61 W, which is 39.39% and 9.10% higher than that found for y _c = 0.24 (lower extreme) and y _c = 0.72 (upper extreme), respectively. This is an important result and shows that there is one opportunity for geometric optimization. Note that the cold mass fraction is directly linked with the adjustment of the throttle valve, i.e., with the opening area of the valve. In the present study, the cold mass fraction is varied as a function of the hot outlet pressure, but the same effect would be obtained for a fixed hot exit pressure and varying the degree of freedom L ₁/L.

Fig. 15.5

First maximization of the cold heat transfer rate (Q _c) as function of the cold mass fraction (y _c)

Figure 15.6 shows the effect of the cold mass fraction (y _c) on the temperatures of cold (T _C) and hot (T _H) outlets. The results show that T _C and T _H increase with the augment of the cold mass fraction. The results of Figs. 15.5 and 15.6 also show that the optimal adjustment of the throttle valve, which leads to the maximal cold heat transfer rate Q _c,_m is not obtained for the highest cold air temperature drop (ΔT _C) nor for the highest mass flow rate that leaves the cold boundary (m _c).

Fig. 15.6

The effect of the cold mass fraction (y _c) over the temperatures of cold (T _C) and hot (T _H) outlets

Figure 15.7 illustrates the temperature distribution in the vortex tube for the following cold mass fractions: y _c = 0.24 (Fig. 15.7a), y _c,o = 0.56 (Fig. 15.7b), and y _c = 0.72 (Fig. 15.7c) that represent the lower extreme, the optimal and the upper extreme of the curve shown in Fig. 15.5, respectively. For the lower extreme (Fig. 15.7a) it is observed that the steepest temperature gradients is in the radial direction. With the increase of y _c the heat flux became more intense in the azimuthal direction (Fig. 15.7b and c). It is interesting to notice that the optimal shape (Fig. 15.7b) has the best distribution of temperature between the hottest and coldest regions, i.e., in agreement with the constructal principle of optimal distribution of imperfections.

Fig. 15.7

Temperature distribution when d/D = 0.3 for several cold mass fractions: (a) y _c = 0.24, (b) y _c,o = 0.56, (c) y _c = 0.72

Figure 15.8 shows the effect of the cold mass fraction (y _c) on the cooling heat transfer rate (Q _c) for several ratios of d/D. In general, one optimal intermediate value of y _c,o is observed for each curve d/D and its corresponding Q_c,m, with exception of the curve d/D = 0.6, where the maximum is reached in the higher extreme of y _c. An interesting behavior is noticed for curves of d/D = 0.3 and d/D = 0.6. For the range 0.47 ≤ y _c ≤ 0.56 the geometry with d/D = 0.3 leads to a better performance than that reached for d/D = 0.6, while the opposite effect is obtained for the range 0.56 ≤ y _c ≤ 0.68. In other words, one ratio of d/D does not lead necessarily to the best thermal performance for all ranges of y _c evaluated.

Fig. 15.8

The maximization of the cooling heat transfer rate (Q _c) as function of the of the cold mass fraction (y _c) for several ratios of d/D

The best ratios d/D obtained in Fig. 15.8 are compiled in Fig. 15.9. In this figure it is possible to observe that there is one optimal ratio of (d/D)_o = 0.43, which conducts to the second maximization of Q _c,mm = 270 W and its corresponding y _c,oo = 0.685, where the subscripts mm and oo mean that the cold heat transfer rate and the cold mass fraction are optimized twice. Other important observation is that the twice maximized cooling heat transfer rate Q _c,mm is 87.33% and 14.63% better than the Q _c,m obtained for the ratios d/D = 0.1 and 0.6, respectively. Moreover, the best cold mass fractions curve y _c,o has the same tendency observed for the cooling heat transfer rate curve Q _c,m. Nonetheless, the ratio of d/D that leads to the highest value of y _c is not the same that leads to the optimal Q _c.

Fig. 15.9

Second optimization of the cooling heat transfer rate (Q _c,m) and the optimal cold mass fraction (y _c,o) as function of d/D

Figure 15.10 shows the effect of the ratio d/D on the temperature of cold T _C,o and hot T _H,o outlets. Differently from the effect of y _c on the cold air temperature drop (ΔT _C), Fig. 15.6, there is one minimal cold temperature T _C,_o, for (d/D)_o = 0.43. In other words, the same ratio d/D that once maximizes the cold heat transfer rate (Q _c,m) is the same for determination of the maximum cold air temperature drop ΔT _C,o. Figure 15.11 shows the vortex tube temperature distribution for the following ratios d/D: d/D = 0.1 (Fig. 15.11a), (d/D)_o = 0.43 (Fig. 15.11b) and d/D = 0.6 (Fig. 15.11c). For the lower ratio d/D = 0.1, the temperature gradient is more intense in the radial direction. Similarly to the results observed for the simulations with lower cold mass fractions (Fig. 15.7c). For (d/D) _o  = 0.43, Fig. 15.11b, the heat flux became more intense in the azimuthal direction, as it occurred when the y _c,o is increased (Fig. 15.7b). As the ratio d/D increases, Fig. 15.11c, the temperature gradients are again more intense in the radial direction, reflecting the decrease of y _c,o as a function of d/D observed in the Fig. 15.9. It is important to reinforce that, independent of the parameter used for the improvement of the thermal performance (y _c or d/D), the best vortex tube shape is the one that distributes the imperfections better, i. e., the shape that has the best distribution of temperature between the hot and cold outlets.

Fig. 15.10

The effect of d/D over the optimal temperature of cold T _C,_o and hot T _H,_o outlets

Fig. 15.11

Temperature distribution obtained for several ratios of d/D: (a) d/D = 0.1, (b) (d/D)_o = 0.43, and (c) d/D = 0.6

15.5 Conclusions

In the present work the numerical optimization of a vortex tube device by means of constructal design was considered. A vortex tube with axisymmetric computational domain was evaluated. The compressible and turbulent flows were numerically solved with a commercial CFD package code based on the Finite Volume Method [27]. The turbulence was tackled with the standard k–ε model into the Reynolds Averaged Navier-Stokes (RANS) approach. The cold heat transfer rate Q _c was maximized twice : First, with respect to the cold mass fraction y _c and later with respect to the degree of freedom d/D (the ratio between the diameter of the cold outlet and the diameter of the vortex tube). The other degrees of freedom (d ₁/D, L ₁/L, and D/L) and the total volume of the vortex tube were kept fixed. It was observed that one optimal ratio y _c,o led to the maximum heat transfer rate Q _c,m when the ratio d/D was fixed.

The results showed that the best thermal performance of the vortex tube was obtained as a function of the product of the cold mass (m _c), which increases with the increase of y _c, and the cold air temperature drop (ΔT _C), which decreases with the increase of y _c.

The results also showed one optimal geometry given by the ratio (d/D)_o = 0.43. The twice maximized cold heat transfer rate (Q _c,mm) was approximately 87% and 15% better than the lower and upper studied extremes of d/D and its corresponding cold mass fraction was y _c,oo = 0.685. The same optimal ratio (d/D)_o = 0.43 that maximized the cold heat transfer rate was also obtained for the maximization of the cold air temperature drop ΔT _C,_o. Another important observation was that, independent of the parameter used for the improvement of the thermal performance (y _c or d/D), the best shapes were reached according to the constructal principle of optimal distribution of imperfections.