Synchronization for Uncertain Chaotic Systems with Channel Noise and Chaos-based Secure Communications

Abstract

In order to deal with the problems of chaotic synchronization and chaos-based secure communication for uncertain chaotic systems with channel noise, a robust sliding mode observer is constructed to synchronize the chaotic system which is regarded as the transmitter. By introducing an augmented vector, an augmented system is formed, and the channel noise of chaotic system is estimated by the robust sliding mode observer. Then, a first-order robust differentiator is considered to exactly estimate the derivative of drive signal. Based on the estimated states and the derivative of drive signal, a recovery method which can recover the information signal is proposed. For illustration, a numerical simulation is given to show the effectiveness of the proposed methods. The simulation results show that the receiver which is the combination of the robust sliding mode observer and the first-order differentiator can not only synchronize the transmitter but also recover the information signal. The proposed method can effectively achieve synchronization and information recovery when the chaotic system with channel noise is used as the transmitter.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Chaos synchronization and chaos-based secure communication have been a hot topic in the literatures [1–8]. Some recent work in chaos-based secure communication can be found in [5–8]. For example, an adaptive observer-based synchronization scheme for private communication is proposed in [5]. Based on the singular system observer, an approach for chaotic synchronization and private communication is developed in [6]. Within the drive-response configuration, the synchronization of chaotic systems and chaos-based secure communication are discussed in [7]. The problems of the synchronization and secure communication are explored using techniques based on knowledge of statistics in [8].

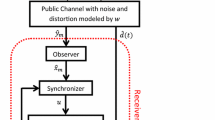
This chapter discusses the topics of synchronization and secure communication, but the chaotic system with channel noise is used as the transmitter, which is a distinction from the above-mentioned papers. The receiver is the combination of robust sliding mode observer and a first robust differentiator, which can not only synchronize the transmitter but also recover the information signal.

2 General Model and Problem Statement

Consider a class of uncertain chaotic system with channel noise which is used as the transmitter in chaos-based secure communication:

$$ \left\{ \begin{array}{ll}\dot{x} =Ax+Bf(x)+Bs+D\eta \hfill \\y =Cx+Ed \end{array} \right. $$

(1)

where $x\in {\mathrm{{R}}^n}$ is the state vector, $y\in {\mathrm{{R}}^p}$ is the drive or transmitted signal, $s\in {\mathrm{{R}}^m}$ is the information signal vector which should be recovered in the receiver end, $f(\cdot ):{\mathrm{{R}}^n}\to {\mathrm{{R}}^m}$ stands for the nonlinear term, $\eta \in {\mathrm{{R}}^q}$ is the disturbance vector, and $d\in {\mathrm{{R}}^l}$ is the channel noise vector which is assumed to be a piecewise continuous vector function. We assume that $\mathrm{rank}{\it B}={\it m}$, $\mathrm{rank}{\it C}={\it p}$, $\mathrm{rank}{\it D}={\it q}$, $\mathrm{rank}{\it E}={\it l}$, $\mathrm{rank}{\it H}={\it m}+{\it q}$, and $n\geq p\geq w$, where $H=\left[ {\begin{array}{llll} B & D \\\end{array}} \right]$ and $w=m+q+l$.

Assumption 1

For System (1), the following condition

$$ \mathrm{rank}\left( {\left[ {\begin{array}{llll} {{\it s_{*}}\it I-A} & \it 0 & \it H \\\it C & \it E & \it 0 \\\end{array}} \right]} \right)=\it n+w $$

(2)

holds for all complex number ${s_{*}}$ with $\operatorname{Re}({s_{*}})\geq 0$.

Assumption 2

$\mathrm{rank}\left[ {\begin{array}{llll} {\it CH} & \it E \\\end{array}} \right]=\it w$.

Assumption 3

The state $x(t)$, nonlinear function $f(x)$, information signal $s(t)$, disturbance vector $\eta (t)$ and their derivatives, are all bounded in norm.

Assumption 4

The nonlinear function $f(x)$ satisfy Lipschitz conditions

$$ \left\| {f(x)-f\left( {\hat{x}} \right)} \right\|\leq {L_f}\left\| {x-\hat{x}} \right\|,\quad \forall x,\hat{x}\in {\mathrm{{R}}^n} $$

(3)

where the Lipschitz constant ${L_f}$ are unknown.

Lemma 1

[ 9 ] For any piecewise continuous vector function $f(t)\in {{{R}}^l}$ , and a stable $l\times l$ matrix ${A_f}$ , there will always exist an input vector $\zeta \in {{{R}}^l}$ such that differential equation $\dot{f}={A_f}f+\zeta$ holds.

Based on Lemma 1, the measurement noise d can be regarded as the output of the following dynamical system

$$ \dot{d}={A_d}d+v $$

(4)

where $\it v\in {{{R}}^l}$ is an additive unknown bounded noise and ${A_d}\in {{{R}}^{{l\times l}}}$ is Hurwitz.

If we set $\bar{x}={\left[ {\begin{array}{llll} {{x^{{T}}}} & {{d^\mathrm{{T}}}} \\\end{array}} \right]}^\mathrm{{T}}$ as an augmented state vector, we obtain

$$ \left\{ \begin{array}{llll} \dot{\bar{x}}=\bar{A}\bar{x}+\bar{B}f\left( {K\bar{x}} \right)+\bar{B}s+\bar{D}\phi \hfill \\y=\bar{C}\bar{x} \end{array}\right. $$

(5)

where

$$ \begin{array}{llll} \bar{A}=\left[ {\begin{array}{llll} A & 0 \\0 & {{A_d}} \\\end{array}} \right],\bar{B}=\left[ \begin{array}{llll} B \hfill \\0 \end{array} \right],\bar{D}=\left[ {\begin{array}{llll} D & 0 \\0 & {{I_l}} \\\end{array}} \right],\bar{C}={\left[ \begin{array}{llll} {C^T} \hfill \\{E^T} \end{array}\right]^T},K=\left[\begin{array}{llll} {{I_n}} & {} \\\end{array}0 \right],\phi =\left[ \begin{array}{llll} \eta \\ \nu \end{array}\right] \end{array}$$

Lemma 2

The System ( 4) is minimum phase, i.e., the invariant zeros of the triple $\left\{ {\bar{A},\bar{C},\bar{H}} \right\}$ are all in the open left-hand complex plane, or

$${ \mathrm{Rank}}\left[ {\begin{array}{llll} {{s_{*}}I-\bar{A}} & {\bar{H}} \\{\bar{C}} & 0 \\\end{array}} \right]=n+w+l $$

(6)

holds for all complex number ${s_{*}}$ with ${\mathop{ Re}\nolimits}({s_{*}})\geq \it0$ if and only if ( 2 ) holds for all complex number ${s_{*}}$ with ${\mathop{ Re}\nolimits}(s)\geq \it 0$ , where $\bar{H}=\left[ {\begin{array}{llll} {\bar{B}} & {\bar{D}} \\\end{array}} \right]$.

Based on ( 2 ), it is easy to prove Lemma 2.

Lemma 3

[ 10 ] Lemma 2 together with the observer matching condition

$$ \mathrm{{rank}}\bar{H}=\mathrm{{rank}}(\bar{C}\bar{H})=w $$

(7)

holds if and only if for symmetric positive definite matrix $\bar{Q}\in {{{R}}^{{(n+l)\times (n+l)}}}$ , there exist matrices $\bar{L}\in {\mathrm{{R}}^{{(n+l)\times p}}}$, $\bar{F}=[\begin{array}{llll} {{{\bar{F}}_1}} & {{{\bar{F}}_2}} \\\end{array}]\in {\mathrm{{R}}^{{(m+q+l)\times p}}}$ and a symmetric positive definite matrix $\bar{P}\in {{{R}}^{{(n+l)\times (n+l)}}}$ such that

$$ \left\{\begin{array}{llll} {{{{(\bar{A}-\bar{L}{}\bar{C})}}^\mathrm{{T}}}\bar{P}+\bar{P}(\bar{A}-\bar{L}{}\bar{C})=-\bar{Q}} \hfill \\{{{\bar{H}}^\mathrm{{T}}}\bar{P}=\bar{F}{}\bar{C}} \hfill \\\end{array}\right. $$

(8)

holds where ${{\bar{F}}_1}\in {{{R}}^{{m\times p}}}$ and ${{\bar{F}}_2}\in {\mathrm{{R}}^{{\left( {q+l} \right)\times p}}}$.

Because of Assumption 2, we have ${{rank}}(\bar{C}\bar{H})={{rank}}\begin{array}{llll} [CH & E \\\end{array}]=w$ and ${{rank}}\bar{H}={{rank}}H+l=w$ . So, the observer matching condition ( 5 ) is satisfied.

3 Synchronization and Channel Noise Estimation Based on Robust Sliding Mode Observers

Consider the following system with the same state and output equations as (4)

$$ \left\{ \begin{array}{ll}\dot{\bar{x}} =\bar{A}\bar{x}+\bar{B}f(K\bar{x})+\bar{H}\varphi \hfill \\y =\bar{C}\bar{x} \end{array}\right. $$

(9)

where $\varphi ={[\begin{array}{llll} {{s^\mathrm{{T}}}} & {{\phi^\mathrm{{T}}}} \\\end{array}]^\mathrm{{T}}}$. There exists a positive constant ${\rho_{\varphi }}$ such that $\left\| \varphi \right\|\leq {\rho_{\varphi }}$.

Theorem 1

Under Assumptions 1–4, an adaptive robust full-order observer ( 10) with (11) and (12) is designed as

$$ \dot{\hat{\bar{x}}}=\bar{A}\hat{\bar{x}}+\bar{B}f(K\hat{\bar{x}})+\frac{1}{2}\hat{k}\bar{B}{}{{\bar{F}}_1}(y-\bar{C}\hat{\bar{x}})+\bar{L}(y-\bar{C}\hat{\bar{x}})+\alpha (y,\hat{\bar{x}},t) $$

(10)

$$ \dot{\hat{k}}={l_k}{{\left\| {{{\bar{F}}_1}(y-\bar{C}\hat{\bar{x}})} \right\|}^2} $$

(11)

$$ \alpha (y,\hat{\bar{x}},t)={\rho_{\varphi }}\frac{{\bar{H}{}\bar{F}(y-\bar{C}\hat{\bar{x}})}}{{\left\| {\bar{F}(y-\bar{C}\hat{\bar{x}})} \right\|}} $$

(12)

and the state estimation $\hat{\bar{x}}$ converges to the actual state $\bar{x}$ asymptotically.

Proof

The error dynamic system between (10) and the first equation of (9) is

$$ \dot{\tilde{\bar{x}}}=(\bar{A}-\bar{L}\bar{C})\tilde{\bar{x}}+\bar{B}\tilde{f}+\bar{H}\varphi -\frac{1}{2}\hat{k}\bar{B}{{\bar{F}}_1}(y-\bar{C}\hat{\bar{x}})-\alpha (y,\hat{\bar{x}},t) $$

(13)

where $\tilde{\bar{x}}=\bar{x}-\hat{\bar{x}}$, $\tilde{f}=f\left( {K\bar{x}} \right)-f\left( {K\hat{\bar{x}}} \right)$. Consider the Lyapunov function $V={{\tilde{\bar{x}}}^T}\bar{P}\tilde{\bar{x}}+\frac{1}{2}l_k^{-1 }{{\tilde{k}}^2}$, where $\tilde{k}=k-\hat{k}$ and k is a constant which will be determined later. The derivative of V along the error dynamic System (13) is

$$ \dot{V}={{\tilde{\bar{x}}}^\mathrm{{T}}}\bar{Q}\tilde{\bar{x}}+2{{\tilde{\bar{x}}}^\mathrm{{T}}}\bar{P}{}\bar{B}\tilde{f}+2{{\tilde{\bar{x}}}^\mathrm{{T}}}\bar{P}{}\bar{H}\varphi -{{\tilde{\bar{x}}}^\mathrm{{T}}}\bar{P}{}\bar{B}{}{{\bar{F}}_1}\hat{k}(y-\bar{C}\hat{\bar{x}})-2{{\tilde{\bar{x}}}^\mathrm{{T}}}\bar{P}\alpha +l_k^{-1}\tilde{k}\dot{\tilde{k}} $$

The second equation of (8) means that ${{\bar{B}}^\mathrm{{T}}}\bar{P}={{\bar{F}}_1}\bar{C}$, we can obtain

$$ 2{{\tilde{\bar{x}}}^\mathrm{{T}}}\bar{P}\bar{H}\varphi \leq 2\left\| \varphi \right\|\left\| {{{\bar{H}}^\mathrm{{T}}}\bar{P}\tilde{\bar{x}}} \right\|\leq 2{\rho_{\varphi }}\left\| {\bar{F}{}\bar{C}\tilde{\bar{x}}} \right\| $$

(14)

$$ {{\tilde{\bar{x}}}^\mathrm{{T}}}\bar{P}{}\bar{B}{}{{\bar{F}}_1}\hat{k}(y-\bar{C}\hat{\bar{x}})=\hat{k}{{\tilde{\bar{x}}}^\mathrm{{T}}}\bar{P}{}\bar{B}{}{{\bar{F}}_1}\bar{C}\tilde{\bar{x}}=\hat{k}{{\left\| {{{\bar{F}}_1}\bar{C}\tilde{\bar{x}}} \right\|}^2} $$

(15)

$$ 2{{\tilde{\bar{x}}}^\mathrm{{T}}}\bar{P}\alpha =2{\rho_{\varphi }}\left\| {\bar{F}{}\bar{C}\tilde{\bar{x}}} \right\| $$

(16)

We can obtain $\left\| {\tilde{f}} \right\|=\left\| {f(K\bar{x})-f(K\hat{\bar{x}})} \right\|\leq {L_f}\left\| K \right\|\left\| {\tilde{\bar{x}}} \right\|={L_f}\left\| {\tilde{\bar{x}}} \right\|$, so

$$ 2{{\tilde{\bar{x}}}^\mathrm{{T}}}\bar{P}{}\bar{B}\tilde{f}\leq 2{L_f}\left\| {{{\bar{F}}_1}\bar{C}\tilde{\bar{x}}} \right\|\left\| {\tilde{\bar{x}}} \right\|\leq \frac{{L_f^2}}{\varepsilon }{{\left\| {{{\bar{F}}_1}\bar{C}\tilde{\bar{x}}} \right\|}^2}+\varepsilon {{\left\| {\tilde{\bar{x}}} \right\|}^2} $$

(17)

where $\varepsilon >0$. Here k is selected as $k=L_f^2/\varepsilon$. Based on (14)–(17), we have

$$ \begin{array}{ll}\dot{V}\leq -{{\tilde{\bar{x}}}^\mathrm{{T}}}(\bar{Q}-\varepsilon I)\tilde{\bar{x}}+((L_f^2/\varepsilon )-\hat{k}){{\left\| {{{\bar{F}}_1}\bar{C}\tilde{\bar{x}}} \right\|}^2}-l_k^{-1}\tilde{k}\dot{\hat{k}}=-{{\tilde{\bar{x}}}^\mathrm{{T}}}(\bar{Q}-\varepsilon I)\tilde{\bar{x}}=-\omega (t)\end{array} $$

(18)

From the above inequality, free parameters ε can be chosen to be small enough such that $\left( {\bar{Q}-\varepsilon I} \right)$ is a positive definite matrix, i.e., $\dot{V}<0$. So based on Lyapunov stability theory, we know that the equilibrium $\tilde{\bar{x}}=0$ is stable. Now integrating (18) from zero to t yields $V(t)+\int\nolimits_0^t {\omega (\tau )} \mathrm{d}\tau \leq \it V(0)$ and the above inequality means that $\int\nolimits_0^t {\omega (\tau )} \mathrm{d}\tau \leq \it V(0)$, since $V\geq 0$. As t approach to infinity, the above integral is less than or equal to V(0), so $\mathop{\lim}\limits_{{t\to \infty }}\int\nolimits_0^t {\omega (\tau )} \mathrm{d}\tau$ exists and is finite. By Barbalat’s Lemma, we have $\mathop{\lim}\limits_{{t\to \infty }}\omega (t)=0$ which implies that $\mathop{\lim}\limits_{{t\to \infty }}\tilde{\bar{x}}(t)=0$.

After we obtain the state estimation $\hat{\bar{x}}$ from adaptive robust sliding mode observer (10)–(12), according to $\bar{x}=\left[ {\begin{array}{llll} {{x^\mathrm{{T}}}} & {{d^\mathrm{{T}}}} \\\end{array}} \right]^\mathrm{{T}}$ we can get the state and channel noise estimations as $\hat{x}=\left[ {\begin{array}{llll} {{I_n}} & {{0_{{n\times l}}}} \\\end{array}} \right]\hat{\bar{x}},\quad \hat{d}=\left[ {\begin{array}{llll} {{0_{{l\times}}}_n} & {{I_l}} \\\end{array}} \right]\hat{\bar{x}}$.

4 Chaos-Based Secure Communication

4.1 The Derivative Estimation of Drive Signal

In this section, a first-order robust exact differentiator is considered to exactly estimate the derivative of drive signal. Then, a method which can recover the information signal is developed.

Denote $y=\bar{C}\bar{x}={{[\begin{array}{llll} {y_1^\mathrm{{T}}} & {y_2^\mathrm{{T}}} & \cdots & {y_p^\mathrm{{T}}} \\\end{array}]}^\mathrm{{T}}}$, ${y_i}={{\bar{C}}_i}\bar{x}$, where ${{\bar{C}}_i}$ is the ith row of matrix $\bar{C}$. Differentiating ${y_i}\;(i=1,2,\ldots,p)$ with respect to time t, we have

$$ {{\dot{y}}_i}={{\bar{C}}_i}\dot{\bar{x}}={{\bar{C}}_i}A\bar{x}+{{\bar{C}}_i}\bar{B}f(K\bar{x})+{{\bar{C}}_i}\bar{H}\varphi $$

(19)

If we introduce a new variable ${y_{is }}={\psi_i}(\bar{x},t)={{\bar{C}}_i}A\bar{x}+{{\bar{C}}_i}\bar{B}f(K\bar{x})+{{\bar{C}}_i}\bar{H}\varphi$, and regard ${y_{io }}={y_i}$ as the output equation, the system (19) can be expanded into

$$ {{\dot{y}}_i}={y_{is }},\;{{\dot{y}}_{is }}={{\dot{\psi}}_i},\;{y_{io }}={y_i} $$

(20)

where ${{\dot{\psi}}_i}$ is unknown but bounded in norm by some known constant or known function of time because of Assumption 3.

In order to exactly estimate ${{\dot{y}}_i}$ in a finite time, the following first-order robust exact differentiator is proposed based on the work in [11].

$$ \left\{ \begin{array}{ll} {{\dot{\xi}}_i} ={\alpha_{i1 }},\;{\alpha_{i1 }}=-{\lambda_{i,1 }}{{\left| {{\xi_i}-{y_i}} \right|}^{1/2 }}\mathrm{sign}({\xi_i}-{\it y_i})+{\xi_{is }} \hfill \\{{\dot{\xi}}_{is }} =-{\lambda_{i,2 }}\mathrm{sign}({\xi_{is }}-{\alpha_{i1 }}) \end{array} \right. $$

(21)

where ${\lambda_{i,j }}>0\;\left( {j=1,2} \right)$ are the observer gains. If we denote ${z_{i,0 }}={\xi_i}-{y_i}$ and ${z_{i,j }}={\lambda_{i,j }}{{\left| {{z_{i,j-1 }}} \right|}^{(2-j)/(3-j) }}\mathrm{sign}({\it z_{i,j-1 }})$, then (21) is equivalent to

$$ {{\dot{\xi}}_i}={\xi_{is }}-{z_{i,1 }},\;{{\dot{\xi}}_{is }}=-{z_{i,2 }} $$

(22)

The error dynamic system between (20) and (22) is ${{\dot{e}}_i}={e_{is }}-{z_{i,1 }},\;{{\dot{e}}_{is }}=-{z_{i,2 }}-{{\dot{\psi}}_i}$, where ${e_i}={\xi_i}-{y_i}$, ${e_{is }}={\xi_{is }}-{y_{is }}$. Now by a similar way to [11], we can show that the sliding mode moving appears on the manifold ${e_i}={e_{is }}=0$ in a finite time by choosing ${\lambda_{i,j }}$ properly. So, the exact estimate of ${{\dot{y}}_i}$ can be obtained as ${\xi_{is }}$. So, ${\xi_s}={[\begin{array}{llll} {{\xi_{1s }}} & \cdots & {{\xi_{ps }}} \\\end{array}]^\mathrm{{T}}}$ is the estimate of $\dot{y}={[\begin{array}{llll} {{{\dot{y}}_1}} & \cdots & {{{\dot{y}}_p}} \\\end{array}]^\mathrm{{T}}}$ in a finite time.

4.2 The Chaos-Based Secure Communication Mechanism

The robust exact differentiator (21) together with the sliding mode observer (10) becomes the receiver. The recovery of S and η can be obtained in receiver end.

Theorem 2

Under Assumption 1–4, we provide information signal recovery and disturbance estimation methods as follows

$$ \hat{\varphi}={{({M^\mathrm{{T}}}M)}^{-1 }}{M^\mathrm{{T}}}[{\xi_s}-\bar{C}{}\bar{A}\hat{\bar{x}}-\bar{C}{}\bar{B}f(K\hat{\bar{x}})] $$

(23)

$$ \hat{s}=\left[ \begin{array}{llll} {{I_m}} & {{0_{{m\times q}}}} & {{0_{{m\times l}}}} \\\end{array} \right]\hat{\varphi},\quad \hat{\eta}=\left[ {\begin{array}{llll} {{0_{{q\times m}}}} & {{I_q}} & {{0_{{q\times l}}}} \\\end{array}} \right]\hat{\varphi} $$

(24)

where $M=\bar{C}\bar{H}$. $\hat{\varphi}$ is the estimate of $\varphi =\left[ {\begin{array}{llll} {{s^\mathrm{{T}}}} & {{\eta^\mathrm{{T}}}} & {{v^\mathrm{{T}}}} \\\end{array}} \right]^\mathrm{{T}}$ , so $\hat{s}$ and $\hat{\eta}$ are the information signal recovery of S and disturbance vector η, respectively.

Proof

According to (7), we have $M\varphi =\dot{y}-\bar{C}{}\bar{A}\bar{x}-\bar{C}{}\bar{B}f(K\bar{x})$. ${M^\mathrm{{T}}}M$ is invertible because M is of full column rank. So

$$ \varphi ={{({M^\mathrm{{T}}}M)}^{-1 }}{M^\mathrm{{T}}}\left[ {\dot{y}-\bar{C}{}\bar{A}\bar{x}-\bar{C}{}\bar{B}f(K\bar{x})} \right] $$

(25)

The error equation between (23) and (25) is $\tilde{\varphi}={{({M^\mathrm{{T}}}M)}^{-1 }}{M^\mathrm{{T}}}\left[ {{{\tilde{\xi}}_s}-\bar{C}{}\bar{A}\tilde{\bar{x}}-\bar{C}{}\bar{B}\tilde{f}} \right],$where $\tilde{\varphi}(t)=\varphi (t)-\hat{\varphi}(t)$, ${{\tilde{\xi}}_s}(t)=\dot{y}(t)-{\xi_s}(t)$, $\tilde{\bar{x}}(t)=\bar{x}(t)-\hat{\bar{x}}(t)$, and $\; \tilde{f}=f(K\bar{x})-f(K\hat{\bar{x}})$. So we have $\mathop{\lim}\limits_{{t\to \infty }}\tilde{\varphi}(t)=0$ since $\mathop{\lim}\limits_{{t\to \infty }}{{\tilde{\xi}}_s}=0$, $\mathop{\lim}\limits_{{t\to \infty }}\tilde{\bar{x}}=0$, and $\mathop{\lim}\limits_{{t\to \infty }}\tilde{f}(t)=0$.

5 Simulation

In order to demonstrate the effectiveness of the proposed scheme, a four-dimension hyperchaos system is given by [12]

$$ \left\{ \begin{array}{ll} {{\dot{x}}_1} =a{x_1}-1.2{x_2} \hfill \\{{\dot{x}}_2} =1.1{x_1}-0.1{x_2}x_3^2 \hfill \\{{\dot{x}}_3} =0.65{x_1}-0.05{x_2}-1.2{x_3}-5{x_4} \hfill \\{{\dot{x}}_4} =0.1{x_1}+0.62{x_3}+0.8{x_4} \end{array}\right. $$

(26)

It is known that the system shows hyperchaos behavior if the parameter is chosen as $a=0.58$. Suppose that the parameters a is affected by disturbance of $\eta =0.02\sin (t+2.5)$, then the system with disturbance and injecting information signal can be written as in the form of (1) with

$$ \begin{array}{llll} A=\left[ {\begin{array}{llll} {0.58} & {-1.2} & 0 & 0 \\1 & 0 & 0 & 0 \\{0.65} & {-0.05} & {-1.2} & {-5} \\{0.1} & 0 & {1.62} & {0.8} \\\end{array}} \right],B=\left[ {\begin{array}{llll} 0 \\1 \\0 \\0 \\\end{array}} \right],D=\left[ {\begin{array}{llll} 1 \\0 \\0 \\0 \\\end{array}} \right],C=\left[ {\begin{array}{llll} 0 & 1 & 0 & 0 \\1 & 0 & 0 & 0 \\0 & 0 & 1 & 0 \\\end{array}} \right],\end{array} $$

$E={\left[ {\begin{array}{llll} 0 & 0 & 1 \\\end{array}} \right]^\mathrm{{T}}}$ and the nonlinear term $f(x)=-0.1{x_2}x_3^2$, where $H=\left[ {\begin{array}{llll} B & D \\\end{array}} \right]$. Let ${A_d}=-2$, according to (4) we can get $\bar{A}$, $\bar{B}$, $\bar{C}$, $\bar{D}$, $K$, and $\bar{H}=\left[ {\begin{array}{llll} {\bar{B}} & {\bar{D}} \\\end{array}} \right]$. By Matlab’s LMI toolbox, we can obtain $\bar{Q}$, $\bar{P}$, $\bar{L}$ and $\bar{F}$ which can satisfy (6).

We set the information signal and additive noise as $s=1.5\cos \left( {2t+8.5} \right)$ and $v=\cos \left( {t+4.5} \right)$, respectively. Figure 1a is the project on the x1, x2, and x3. Figure 1b, c are the projects on x1–x4 and x2–x4, respectively, and Fig. 1d is the project on x3–x4. We known that the chaotic properties are still kept even if the original chaotic system is suffering from some parameter deviation η and the unknown injecting information signal S.

Fig. 1

The phase portraits of (26) with η and d

In the simulation, the initial values are set as $x(0)={[\begin{array}{llll} {0.5} & {0.3} & {0.2} & {0.4} \\\end{array}]}^\mathrm{{T}}$, $\hat{x}(0)=[\begin{array}{llll} {0.2} & {0.5} & {1.2} & {2.1} \\\end{array}]^\mathrm{{T}}$, the state estimations can be obtained from Fig. 2, which shows that the performances of robust full-order observer are satisfactory.

Fig. 2

The chaos synchronization for all states. (a) State estimation for x1 and x2 and (b) state estimation for x3 and x4

The simulation for both information signal and the channel noise reconstruction performances are given in Fig. 3a, b, respectively. Figure 3c shows the estimation performances of disturbance. From Fig. 3, we know that the recovering and estimated effectiveness is good.

Fig. 3

Information recovery and estimates of channel noise and parameter disturbance. (a) Recovery of signal S, (b) the estimated d and (c) the estimated η

6 Conclusion

In this chapter, we discussed the problems of chaotic synchronization and chaos-based secure communication for a class of uncertain chaotic system with channel noise. An augmented system is formed based on an augmented vector. The combination of an adaptive robust sliding mode observer and a first-order robust exact differentiator is regarded as the receiver. A novel information recovering method which can not only recover the information signal but also reconstruct the unknown parameter disturbance and channel noise is developed. The proposed method doesn’t require constant information signal, so we just assume that the method and its derivative is bounded.