Identification and Control of Nonlinear Systems Using a Piecewise-Linear Hammerstein Model

Abstract

This chapter introduces a new method for the identification and control of nonlinear systems, which is based on the derivation of a piecewise-linear Hammerstein model. The approach is motivated by several drawbacks accompanying identification and control via the classical type of Hammerstein models. The most notable drawbacks are the need for specific identification signals; the limited ability to approximate strongly nonlinear and discontinuous processes; high computational load during the operation of certain control algorithms, etc. These problems can be overcome by replacing the polynomial in the original model with a piecewise linear function. As a consequence, the resulting model opens up many new possibilities. In the chapter, first the new form, i.e., the piecewise-linear form of the Hammerstein model, is introduced. Based on this model, two new algorithms are derived and connected into a uniform design approach: first, a recursive identification algorithm, based on the well-known least-squares method, and second, a control algorithm that is a modification of the pole-placement method. Both algorithms are tested in an extensive simulation study and demonstrated on a case study involving control of a ferromagnetic material sintering process. Finally, some problems and limitations regarding the practical application of the proposed method are discussed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

This chapter addresses the problem of identification and control of a special class of nonlinear processes whose dynamics can be approximated by a Hammerstein model. A Hammerstein model consists of a serial connection of a static nonlinear function and a linear dynamic transfer function. These models are very relevant to practice since many industrial processes exhibit this type of nonlinear dynamic behaviour. Both identification and control design for this class of processes has therefore attracted considerable attention from researchers in academia as well as from practitioners in industry.

Identification has been addressed by many authors and a rich set of methods for parameter estimation of the nonlinear and linear part of the model have been proposed. Examples include iterative methods [28, 30] and non-iterative over-parameterisation methods [7, 19, 25]. The least squares method is usually employed to estimate the model parameters [21], although other approaches are also used, e.g. instrumental variables [31] and the maximum likelihood method [8, 15].

The nonlinear static part of the Hammerstein model was originally proposed in the form of a polynomial function. However, models with various other representations were studied as well, e.g. models with two-segment piecewise-linear nonlinearity [24], cubic splines [36], preload nonlinearity [25], two-segment polynomial nonlinearities [33], discontinuous asymmetric nonlinearities [32], hysteresis [20] and Bezier functions [18]. These methods assume that input signals used for the identification ensure persistent excitation, which means that signals are distributed over the entire range of operation. A popular choice for excitation signals is white noise or related random inputs, although simpler waveforms like the random phase multisine signals proposed in [9] and [10] can also be used. The main problem with such signals is that they cannot always be applied to industrial processes, or their use is even prohibited because of strict technological limitations as well as system performance requirements.

All the mentioned methods are parametric methods. Nonparametric methods represent an alternative approach that has also been used to represent and identify the Hammerstein model [6, 14].

The use of a Hammerstein model for control is also widely discussed in the literature. A common approach is to adopt the existing linear controller design, such as [2, 3, 22, 34, 35], where the linear pole placement method was adapted in various ways. A similar approach can be found in [27], where a generalised minimum variance controller is accommodated to the single polynomial-based Hammerstein model. In [17] the utilisation of the Hammerstein model is proposed in a way such that the nonlinearity is approximated by the Bezier function. Several other control laws based on the Hammerstein model are also discussed in the literature, e.g. dead-beat control [29], adaptive dead-beat feedforward compensation of measurable disturbances [5], indirect adaptive control based on linear quadratic control and an approximation of the nonlinear static function using neural networks [23], nonlinear dynamic compensation with passive nonlinear dynamics [16], etc. Another possibility is to use the Hammerstein model within predictive control laws, e.g. [1, 13], which has gained in popularity, not only in research, but also in industrial practice.

The problem with the majority of the methods mentioned above is that constraints and limitations encountered in the commissioning and operation stage are largely ignored in the design stage. A serious issue is the fact that a high level of expertise is needed to put the controllers mentioned above to work, particularly during the commissioning and tuning stage. Additional problems may arise due to the high computational load and limited freedom in selecting the excitation signals. In order to accommodate these issues, we present and demonstrate an approach to identification and control of nonlinear processes of the Hammerstein type, based on piecewise-linear approximation of the static nonlinear function.

This chapter is organised as follows. First, we will review the original form of the Hammerstein model and briefly highlight the shortcomings that limit its practical applicability. Based on this, we will introduce a new form of the Hammerstein model with modified parameterisation, which will eliminate the main practical limitations inherent in the original formulation of the Hammerstein model. Next, we will propose a parameter estimation algorithm, accommodated to the proposed model structure. Finally, we will present a novel pole placement controller, tuned according to the identified model parameters. The usability of the identification and control algorithms will be demonstrated by a simulation example and experimental application on a sintering process.

2 Original Form of the Hammerstein Model and Its Limitations

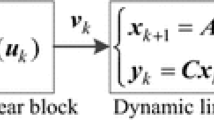
The Hammerstein model belongs to the class of block-oriented nonlinear models, which can be decomposed into nonlinear static blocks and linear dynamic blocks. In the case of a single input, single output Hammerstein model, the nonlinear static function is followed by a linear dynamic system, as follows from Fig. 2.1. If the sequence of blocks is reversed, we get a Wiener model.

Fig. 2.1

Structure of the Hammerstein model

The nonlinear static function is originally proposed in the form of a polynomial function, while the linear dynamic system is assumed to be either a linear discrete time or a continuous time transfer function. The internal signal x, which links the nonlinear static function and the linear dynamic system, is assumed to be non-measurable. Consequently, the parameters of the nonlinear static function and the linear dynamic system cannot be estimated separately.

The original form of the Hammerstein model has several practical limitations:

• 1. Parameter estimation is very sensitive to the type of excitation signal. If the excitation signal is limited within a narrow interval, the model will properly predict the process output only if inputs are from this interval. Elsewhere, model predictions might be quite poor. The original Hammerstein model thus requires excitation signals distributed over the entire range of operation. This is a serious drawback, since the application of such signals may often be prohibitive in real processes due to various technological limitations.

• 2. Polynomial representation of the input nonlinearity of the original Hammerstein model does not enable the approximation of discontinuous processes; however, such processes appear quite frequently in practical applications.

• 3. If the original form of the Hammerstein model is integrated into a control law, the calculation of the control signal usually requires inversion of the polynomial equation, which can in general only be done numerically. This inversion has to be repeated in every control interval, which leads to a high computational load.

To alleviate these drawbacks, we propose a modified model structure, the main idea of which is to use a piecewise-linear function to represent the model nonlinearity.

3 The Piecewise-Linear Hammerstein Model

The model and the essentials of the associated parameter estimation algorithm were presented in [11]. The idea was to use piecewise-linear representation of the nonlinear static function of the model. It should be noted that the idea of using piecewise representations is not new, different kinds of piecewise representations have been used in the Hammerstein model [9, 10, 36]. But this was usually motivated by achieving more accurate approximation of the nonlinear static function compared to that obtained by continuous functions (e.g. single polynomials). Our motivation for using piecewise representation is different, we want to improve the practical applicability of the model. We will show that using the piecewise-linear approximation directly reduces practical limitations presented in the previous section.

First, owing to the piecewise-linear representation of the static nonlinearity, identification does not require rich excitation signals over the entire range of operation, as presented in Fig. 2.2. This kind of signal can cause the process to go out of control or can even cause damage to the process.

Fig. 2.2

An example of rich excitation signal

Identification can be performed in the presence of more realistic, temporarily bounded signals. Here we mean signals which can be expressed as a sum of two components: a slow varying component and a fast varying one. The first component can be slowly increasing or decreasing signal, e.g. a ramp function (Fig. 2.3, left). The second component is bounded on an interval which is significantly narrower than the entire region of the input signal. For example, it can be implemented in terms of sequence of pulses (Fig. 2.3, centre). The sum of both components is shown in Fig. 2.3, right.

Fig. 2.3

Realistic signal with temporarily bounded amplitude

Such kinds of signals are much more likely to be acceptable for applications in industrial processes than classical persistent excitation waveforms. Since the amplitude is temporarily bounded within a narrow range, it means that only a tiny section of the nonlinear static function will be excited at that time. Piecewise-linear representation of the static nonlinearity and the corresponding identification algorithm, which will be presented below, allow for identification of the excited section only, while keeping unexcited sections unchanged.

The second benefit of a piecewise-linear representation of the nonlinear static function is the possibility to account for the discontinuous static functions as well as static functions with a discontinuous first derivative.

And third, the problem of the computational burden of the inversion of the nonlinear static function is completely circumvented since the piecewise-linear function has a very simple analytical inverse, and thus requires only a minimum computational effort during each control interval of the controller.

These advantages become extremely important when practical applications of the control algorithm are considered.

3.1 Piecewise-Linear Functions

A general nonlinear static function can be approximated by a piecewise-linear function [26], which is composed of a number of line segments connected to each other

$$ x ( u ) = \mathbf{l} ( u,\mathbf{u} )^{T} \cdot\mathbf{x} $$

(2.1)

In (2.1) u is input to the nonlinear static function and x is an output. The function is defined by vectors u and x, which determine the positions of the joints of line segments:

$$\begin{aligned} &\mathbf{x} = {[x _{0}\quad x _{1}\quad \dots\quad x _{j}\quad \dots\quad x _{ {m}}]}^{{T}}_{((m+1) \times 1)} \end{aligned}$$

(2.2)

$$\begin{aligned} &\mathbf{u} = {[u _{0}\quad u _{1}\quad \dots \quad u _{{j}} \quad \dots\quad u _{ {m}}]}_{((m+1) \times 1)}^{{T}} \end{aligned}$$

(2.3)

The vector x contains x-coordinates of joints while vector u contains u-coordinates, which are called knots. Knots have to be arranged in a monotonically increasing order

$$ u _{0} < u _{1} <\cdots< u _{j} < u _{j+1} < \dots< u _{m} $$

(2.4)

Furthermore, in (2.1) l(u,u) is a vector of “tent functions”

$$ \mathbf{l}(u,\mathbf{u}) = [l _{0}\quad l _{1}\quad \dots\quad l _{j}\quad \dots\quad l _{m}]^{T}_{((m+1) \times 1)} $$

(2.5)

Hereinafter, instead of l(u,u), the shorter denotation l(u) will be used. The elements of vector l(u) are defined as follows:

$$\begin{aligned} &l_{0} ( u ) = \begin{cases} \frac{u_{1} - u}{u_{1} - u_{0}}&\mbox{if}\ u_{0} \le u < u_{1}\\ 0&\mbox{if}\ u_{1} \le u \le u_{m} \end{cases} \end{aligned}$$

(2.6)

$$\begin{aligned} &l_{j} ( u ) = \begin{cases} 0&\mbox{if}\ u_{0} \le u < u_{j - 1} \\ \frac{u - u_{j - 1}}{u_{j} - u_{j - 1}}&\mbox{if}\ u_{j - 1} \le u < u_{j} \\ \frac{u_{j + 1} - u}{u_{j + 1} - u_{j}}&\mbox{if}\ u_{j} \le u < u_{j + 1} \\ 0&\mbox{if}\ u_{j + 1} \le u \le u_{m} \end{cases} \quad j = 1 \ldots m - 1 \end{aligned}$$

(2.7)

$$\begin{aligned} &l_{m} ( u ) = \begin{cases} 0&\mbox{if}\ u_{0} \le u < u_{m - 1} \\ \frac{u - u_{m - 1}}{u_{m} - u_{m - 1}}&\mbox{if}\ u_{m - 1} \le u \le u_{m} \end{cases} \end{aligned}$$

(2.8)

It can be seen that the vector l(u) contains only two nonzero elements for any value u. Their position and values depend on the amplitude of the input signal u, as follows from Eqs. (2.6)–(2.8) The situation is illustrated in Fig. 2.4.

Fig. 2.4

Parameterisation of the piecewise-linear function (u _j ≤u<u _j+1)

The inversion of a piecewise-linear function results in another piecewise-linear function, where vectors x and u exchange roles

$$ u = \mathbf{l}(x,\mathbf{x})^{T} \cdot\mathbf{u} $$

(2.9)

The piecewise-linear function x(u) is always continuous and contains discontinuities of the first derivative, which are located in knots. Therefore, it is possible to approximate nonlinear functions with the discontinuous first derivative as well as the discontinuous nonlinear functions. In the first case, the position of the discontinuity of the first derivative and the position of the arbitrary knot should match as closely as possible. In the second case, a position of discontinuity u _d of the nonlinear function has to be surrounded by two knots (u _d −Δu ₁) and (u _d +Δu ₂), where Δu ₁ and Δu ₂ represent small distances from the point of discontinuity, as follows from Fig. 2.5.

Fig. 2.5

Approximation of the discontinuous static function

3.2 Parameterisation of the Hammerstein Model with Piecewise-Linear Functions

Now, let us merge the piecewise-linear function and the linear dynamic system of the model. First, let us assume the classical structure of the Hammerstein model (Fig. 2.1), where u is the input and x is output of the nonlinear static function. Simultaneously, x is the input and y is the output of the linear dynamic system. The linear dynamic system is described by the discrete time difference equation

$$\begin{aligned} &y(k) + a_{1} y(k-1) + a_{2} y(k-2) + \cdots+ a_{n} y(k-n) \\&\quad = b_{0} x(k-d) + b_{1} x(k-d-1) + b_{n} x(k-d-n) \end{aligned}$$

(2.10)

where n is the order and d is the delay of the linear dynamic system. Let the output x from the nonlinear static function be expressed using the piecewise-linear function (2.1). The terms b _i x(k−d−i), appearing on the right-hand side of Eq. (2.10), can then be expressed as

$$ b _{i} x(k-d-i) = b _{i} \mathbf{l}\bigl(u(k-d-i) \bigr)^{T} \mathbf{x} = \mathbf{l}\bigl(u(k-d-i)\bigr)^{T} b _{i} \mathbf{x},\quad i=0\dots n $$

(2.11)

If the rightmost term of Eq. (2.11) is put into Eq. (2.10) and if y(k) is expressed explicitly, the following discrete time difference equation is obtained, which represents the piecewise-linear Hammerstein model:

$$\begin{aligned} y(k) =& - a _{1} y(k-1) - a _{2} y(k-2) - \cdots- a _{n} y(k-n) + \mathbf{l}\bigl(u(k-d)\bigr)^{T} b _{0} \mathbf{x} \\\quad& + \mathbf{l}\bigl(u(k-d-1)\bigr)^{T} b _{1} \mathbf{x} + \cdots + \mathbf{l}\bigl(u(k-d-n)\bigr)^{T} b _{n} \mathbf{x} \end{aligned}$$

(2.12)

Equation (2.12) is multilinear in parameters and can be arranged in the following vector form:

$$ y(k) = \boldsymbol{\psi}^{T} (k) \boldsymbol{\theta} $$

(2.13)

In Eq. (2.13) ψ is the data vector and θ is the parameter vector structured as follows:

$$\begin{aligned} \boldsymbol{\boldsymbol{\psi}} =& \bigl[-y(k-1)\quad -y(k-2)\quad \dots\quad -y(k-n) \quad \mathbf{l}(u(k-d))^{T} \\\quad& \mathbf{l}(u(k-d-1))^{T}\quad \mathbf{l}(u(k-d-n))^{T}\bigr]^{T}_{((n+(n+1)(m+1)) \times 1)} \end{aligned}$$

(2.14)

$$\begin{aligned} \boldsymbol{\theta} =& \bigl[a _{1}\quad a _{2}\quad \dots\quad a _{n}\quad b _{0} \mathbf{x} ^{T}\quad b _{1} \mathbf{x} ^{T}\quad \dots\quad b _{n} \mathbf{x} ^{T}\bigr]^{T}_{((n+(n+1)(m+1)) \times 1)} \end{aligned}$$

(2.15)

In the data vector, the terms l(u(k−d−i)), i=0…n, are vectors of the “tent functions” in particular time instances, defined by Eqs. (2.5), (2.6), (2.7) and (2.8). The structure of elements b _i x, i=0…n, of the parameter vector θ is the following:

$$\begin{aligned} b _{i} \mathbf{x} =& b _{i}[x _{0} \quad x _{1}\quad \dots \quad x _{m}]^{T} = [b _{i} x _{0} \quad b _{i} x _{1}\quad \dots\quad b _{i} x _{m}]^{T} \\=& [bx _{i,0}\quad bx _{i,1} \quad \dots\quad bx _{i,m}]^{T}_{((m+1) \times 1)} = \mathbf{bx} _{i} \end{aligned}$$

(2.16)

In Eq. (2.16) the products b _i x _j represent “linear parameters”, denoted as bx _i,j , i=0…n, j=0…m.

$$ bx _{ i, j} = b _{i} x _{j} $$

(2.17)

They are called linear since in the model they appear in linear combination with the data. The linear parameters bx _i,j can be arranged in subvectors bx _i , i=0…n of the data vector θ. Considering this, θ can be rewritten in terms of “linear parameters”

$$\begin{aligned} \boldsymbol{\theta} =& [a _{1}\quad a _{2}\quad \dots\quad a _{n}\ |\ bx _{0,0}\quad bx _{0,1}\quad \dots\quad bx _{0,m}\ |\ bx _{1,0}\quad bx _{1,1}\quad \dots\quad bx _{1,m}\ | \\\quad& \ \,bx _{n,0}\quad bx_{n,1s} \quad \dots\quad bx _{n,m}]^{T} \\=& \bigl[a _{1}\quad a _{2}\quad \dots\quad a _{n}\ |\ \mathbf{bx} _{0} ^{T}\quad \mathbf{bx} _{1} ^{T}\quad \dots\quad \mathbf{bx} _{n} ^{T}\bigr]^{T} \end{aligned}$$

(2.18)

The identification algorithm, which will be presented below, will estimate the “linear parameters”. The set of “linear parameters” should be distinguished from the set of “basic parameters”, which are

$$ a _{1} \quad a _{2}\quad \dots\quad a _{n}\qquad b _{0}\quad b _{1}\quad b _{2}\quad \dots\quad b _{n} \qquad x _{0}\quad x _{1} \quad x _{2} \quad \dots \quad x _{m} $$

(2.19)

If the “basic parameters” are known, then the “linear parameters” can be uniformly calculated. On the other hand, if the “linear parameters” are known, then the “basic parameters” cannot be uniformly calculated. If the nonlinear static function is multiplied by a nonzero real constant c, and if the linear dynamic part is divided by the same constant, the resulting model has the same input-output behaviour. This redundancy of “basic parameters” can be resolved, for example, by fixing the static gain of the linear dynamic part. This means that the following equality must hold for the parameters of the linear dynamic part, if the static gain is fixed to unity:

$$ \sum_{i = 0}^{n} b_{i} = 1 + \sum _{i = 1}^{n} a_{i} $$

(2.20)

By summating Eq. (2.17) for i=0…n, we get

$$ x_{j} = \frac{\sum_{i = 0}^{n} bx_{i,j}}{\sum_{i = 0}^{n} b_{i}},\quad j = 0 \ldots m $$

(2.21)

In Eq. (2.21) parameters b _i are unknown. The sum of parameters b _i , i=0…n, can be expressed as a sum of parameters a _i , i=1…n, using Eq. (2.20), since parameters a _i appear explicitly in the vector of the “linear parameters” θ

$$ x_{j} = \frac{\sum_{i = 0}^{n} bx_{i,j}}{1 + \sum_{i = 1}^{n} a_{i}},\quad j = 0 \ldots m $$

(2.22)

After parameters x _j are estimated, also parameters b _i can be estimated using the equalities derived from Eq. (2.17)

$$ b_{i} = \frac{bx_{i,0}}{x_{0}} =\cdots = \frac{bx_{i,j}}{x_{j}} =\cdots = \frac{bx_{i,m}}{x_{m}},\quad i = 0\ldots n $$

(2.23)

A solution for b _i can be obtained using least squares

$$ b_{i} = \frac{\sum_{j = 0}^{m} ( x_{j} \cdot bx_{i,j} )}{\sum_{j = 0}^{m} x_{j}^{2}},\quad i = 0\ldots n $$

(2.24)

Alternatively, the basic parameters b _i and x _j can be estimated using an algorithm based on the singular value decomposition [4], which gives more general results but also requires more computational effort.

3.3 Redundancy of Linear Parameters

Redundancy of “linear parameters” is a special property of the piecewise-linear Hammerstein model which becomes important during parameter estimation. It should be distinguished from the already mentioned redundancy of the “basic parameters”. Let us assume that a process is described by the model with parameters θ defined in Eq. (2.18). In that case, there exists a model with parameters θ ^∗ which has the same transfer function between u and y as the model with parameters θ

$$\begin{aligned} \boldsymbol{\theta}^* =& \bigl[a _{1}\quad a _{2}\quad \dots \quad a _{n}\ |\ bx _{0,0} ^*\quad bx _{0,1} ^*\quad \dots\quad bx _{0,m} ^*\ | \\\quad&\ \; bx _{1,0} ^*\quad bx _{1,1} ^*\quad \dots\quad bx _{1,m} ^*\ |\ bx _{n,0} ^*\quad bx _{n,1} ^*\quad \dots\quad bx _{n,m}^ *\bigr]^{T} \end{aligned}$$

(2.25)

The subvectors $\mathbf{bx} _{i} ^{*}$ of θ ^∗ differ from the subvectors bx _i of θ. The relation between bx _i and $\mathbf{bx} _{i} ^{*},\ i=0\ldots n$ reads

$$\begin{aligned} \mathbf{bx} _{i} ^* =& \bigl[bx _{i,0} ^*\quad bx _{i,1} ^*\quad \dots\quad bx _{i,m} ^*\bigr]^{T} \\=& [bx _{i,0}\quad bx _{i,1}\quad \ldots\quad bx _{i,m}]^{T} + c _{i} \textbf{1} _{((m+1) \times 1)} \end{aligned}$$

(2.26)

Finally, the model with parameters θ ^∗ and the model with parameters θ have identical transfer functions if

$$ \sum_{i = 0}^{n} c_{i} = 0 $$

(2.27)

To prove this, the difference Δy(k) between the output y ^∗(k) of the model with parameters θ ^∗ and the output y(k) of the nominal model with parameters θ has to be calculated

$$ \Delta y(k) = y^*(k) - y(k) = \boldsymbol{\psi}^{T} (k) \boldsymbol{\theta}^* - \boldsymbol{\psi} ^{T} (k) \boldsymbol{\theta}= \boldsymbol{\psi}^{T} (k) \bigl(\boldsymbol{\theta}^* - \boldsymbol{\theta}\bigr) $$

(2.28)

Furthermore, the difference (θ ^∗−θ) can be expressed as

$$ \boldsymbol{\theta}^* - \boldsymbol{\theta}= \bigl[\Delta\mathbf{a} ^{T} \quad \Delta\mathbf{bx} _{0} ^{T}\quad \Delta\mathbf{bx} _{1} ^{T}\quad \dots\quad \Delta\mathbf{bx} _{n} ^{T}\bigr]^{T} $$

(2.29)

According to the definition of θ ^∗, it follows that

$$ \Delta\mathbf{a} = \textbf{0} _{(n\times 1)} $$

(2.30)

and

$$ \Delta\mathbf{bx} _{i} = \mathbf{bx} _{i} ^* - \mathbf{bx}_i = c _{i} \textbf{1} _{((m+1) \times 1)}, \quad i=0\dots n $$

(2.31)

By accounting for Eqs. (2.30) and (2.31) in Eq. (2.28), Δy(k) can be expressed

$$ \Delta y ( k ) = \boldsymbol{\psi}^{T} ( k ) \cdot\bigl( \boldsymbol{\theta}^{*} - \boldsymbol{\theta}\bigr) = \sum_{i = 1}^{n} 0 \cdot y ( k - i ) + \sum_{i = 0}^{n} \mathbf{l} \bigl( u ( k - d - i ) \bigr)^{T} \cdot c_{i}\mathbf{1}_{ ( ( m + 1 ) \times1 )} $$

(2.32)

According to the definition of the “tent functions” l, in Eqs. (2.5)–(2.8) the rightmost term of Eq. (2.32) can be expressed as

$$\begin{aligned} &\mathbf{l}\bigl(u(k - d - i)\bigr)^{T} \cdot c_{i}\textbf{1}_{ ( ( m + 1 ) \times1 )} \\&\quad = \biggl[ \mathbf{0}_{1 \times j} \biggl( \frac{u_{i + 1} - u(k - d - i)}{u_{i + 1} - u_{i}} \biggr) \biggl( \frac{u(k - d - i) - u_{i}}{u_{i + 1} - u_{i}} \biggr)\mathbf{0}_{1 \times( m - j - 1 )} \biggr] \\&\qquad \cdot c_{i}\mathbf{1}_{ ( ( m + 1 ) \times1 )} = c_{i} \end{aligned}$$

(2.33)

If this is put into Eq. (2.32), the difference Δy(k) can be expressed as

$$ \Delta y ( k ) = \sum_{i = 1}^{n} 0 \cdot y ( k - i ) + \sum_{i = 0}^{n} c_{i} $$

(2.34)

The first sum of the right side of Eq. (2.34) equals zero. Because of the required condition (2.27) also the second sum of the right side of Eq. (2.34) equals zero, which means that Δy(k)=0. This proves that the model with parameters θ ^∗ has an identical transfer function to the model with parameters θ.

3.4 Active and Inactive Parameters

There is another important property of the proposed piecewise-linear Hammerstein model. At any time instance the output y(k) only depends on some of the model parameters. The output always depends on a _i , i=1…n. In addition, it also depends on two parameters from each subvector bx _i , i=0…n, which are multiplied by the two nonzero elements of l(u(k−d−i)). Let the parameters on which the model output depends be referred to as “active parameters”. The rest are called “inactive parameters”. Let p be a position index defined as

$$ u_{j - 1} \le u ( k - d - i ) < u_{j} \quad \Rightarrow\quad p ( k - d - i ) = j $$

(2.35)

The “active parameters” within subvector bx _i can then be expressed as

$$ bx _{i,p(k-d-i)-1}\quad\mbox{and}\quad bx _{i,p(k-d-i)},\quad i=0\dots n $$

(2.36)

4 Identification of Model Parameters

The parameters of the proposed piecewise-linear Hammerstein model can be identified by many standard methods since the model in Eq. (2.13) is linear in parameters. Online methods, simple to implement, are of primary interest. The well known recursive least squares method (RLS) with forgetting factor λ is appropriate and summarised below:

$$\begin{aligned} y _{e} (k) =& \boldsymbol{\psi}^{T} (k) \boldsymbol{\theta}(k -1) \end{aligned}$$

(2.37)

$$\begin{aligned} e(k) =& y(k) - y _{e} (k) \end{aligned}$$

(2.38)

$$\begin{aligned} \boldsymbol{\theta}(k) =& \boldsymbol{\theta}(k - 1) + \Delta\boldsymbol{\theta}(k) \end{aligned}$$

(2.39)

$$\begin{aligned} \Delta\boldsymbol{\theta}(k) = &\mathbf{K}(k) \cdot e(k) \end{aligned}$$

(2.40)

$$\begin{aligned} \mathbf{K}(k) = &\frac{\mathbf{P}(k - 1) \cdot\boldsymbol{\psi}(k)}{\lambda+ \boldsymbol{\psi} ^{T}(k) \cdot\mathbf{P}(k - 1) \cdot\boldsymbol{\psi}^{T}(k)} \end{aligned}$$

(2.41)

$$\begin{aligned} \mathbf{P}(k) =& \biggl[ \mathbf{P}(k - 1) - \frac{\mathbf{P}(k - 1) \cdot\boldsymbol{\psi}(k) \cdot \boldsymbol{\psi}^{T}(k) \cdot\mathbf{P}(k - 1)}{\lambda+ \boldsymbol{\psi}^{T}(k) \cdot \mathbf{P}(k - 1) \cdot\boldsymbol{\psi}(k)} \biggr] \cdot \frac{1}{\lambda} \end{aligned}$$

(2.42)

In principle, this method is convenient for identification of the piecewise-linear Hammerstein model after the following modifications have been implemented:

• management of active and inactive parameters;

• compensation of parameter offset;

• tracking the inactive parameters.

4.1 Management of Active and Inactive Parameters

In Sect. 2.3.4 it was shown that the model output y(k) only depends on “active parameters”. Since the remaining “inactive parameters” have no influence on the model output, there is no information available to update their values. The identification algorithm should therefore be modified in such a way as to stop the updating of “ inactive parameters” and to restart updating parameters in the transition from “inactive” to “active”. If the identified process is assumed to be time variant, there may be a need to rapidly update the parameters immediately after they become “active”.

To stop identification of a particular parameter in vector θ (to “freeze” its value), a corresponding element (gain) in vector K in Eq. (2.41) has to be set to zero. This is achieved by setting the corresponding row and column of matrix P to zero. To restart identification of the particular parameter in θ, the corresponding element (gain) in vector K should be set to some high value. This is achieved by setting the corresponding diagonal element of matrix P to some high value. A way to achieve the required modifications of matrix P is to perform the following transformation:

$$ \mathbf{P} _{m} (k-1) = \mathbf{A} _{m} \cdot \mathbf{P}(k-1) \cdot \mathbf{A} _{m} + \mathbf{B} _{m} $$

(2.43)

and then use P _m (k−1) instead of P(k−1) in Eqs. (2.41) and (2.42). Both matrices A _m and B _m are diagonal:

$$\begin{aligned} \mathbf{A} _{m} =&\operatorname{diag}(\boldsymbol{\alpha}) \end{aligned}$$

(2.44)

$$\begin{aligned} \mathbf{B} _{m} =&\operatorname{diag}(\boldsymbol{\beta}) \end{aligned}$$

(2.45)

The structures of the vectors α and β are

$$\begin{aligned} \boldsymbol{\alpha} =& \bigl[\boldsymbol{\alpha}_{a} ^{T}\quad \boldsymbol{\alpha}_{bx0} ^{T}\quad \boldsymbol{\alpha}_{bx1} ^{T} \quad \dots\quad \boldsymbol{\alpha}_{bxn}^{T}\bigr]^{T} \end{aligned}$$

(2.46)

$$\begin{aligned} \boldsymbol{\beta} =& \bigl[\boldsymbol{\beta}_{a} ^{T}\quad \boldsymbol{\beta}_{bx0} ^{T}\quad \boldsymbol{\beta}_{bx1} ^{T} \quad \dots\quad \boldsymbol{\beta} _{bxn}^{T}\bigr]^{T} \end{aligned}$$

(2.47)

α _a and β _a correspond to the continuously identified parameters a _i , i=1…n. Thus, both vectors are constants:

$$\begin{aligned} &\boldsymbol{\alpha}_{a}= \textbf{1} _{(n\times 1)} \end{aligned}$$

(2.48)

$$\begin{aligned} &\boldsymbol{\beta}_{a} = \textbf{0} _{(n\times 1)} \end{aligned}$$

(2.49)

Other elements correspond to the parameters in vectors bx _i , i=0…n. For each bx _i , two cases are possible depending on the parameter state (active or inactive):

• (a) there is no change of state within bx _i with respect to the previous step p(k−d−i)=p(k−d−i−1)

  $$ \begin{aligned}[c] &\boldsymbol{\alpha}_{bxi} = \bigl[ \mathbf{0}_{ ( 1 \times( p ( k - d - i ) - 1 ) )} \quad [ 1\quad 1 ]\quad \mathbf{0}_{ ( 1 \times( m - p ( k - d - i ) ) )} \bigr]^{T}_{ ( ( m + 1 ) \times1 )}\\&\boldsymbol{\beta}_{bxi} = \mathbf{0}_{ ( ( m + 1 ) \times1 )} \end{aligned} $$

  (2.50)

• (b) there is a change of state within bx _i with respect to the previous step p(k−d−i)≠p(k−d−i−1).

  $$ \begin{aligned}[c] &\boldsymbol{\alpha}_{bxi} = \mathbf{0}_{ ( ( m + 1 ) \times1 )}\\&\boldsymbol{\beta}_{bxi} = \mathit{rval} \cdot\bigl[ \mathbf{0}_{ ( 1 \times( p ( k - d - i ) - 1 ) )}\quad [ 1\quad 1 ]\quad \mathbf{0}_{ ( 1 \times( m - p ( k - d - i ) ) )} \bigr]^{T}_{ ( ( m + 1 ) \times1 )} \end{aligned} $$

  (2.51)

In case a), the combination of α _bxi and β _bxi allows the identification of “active parameters” within bx _i only. In case b), the combination of α _bxi and β _bxi restarts the identification of these parameters within bx _i that become “active”. This is achieved by setting the corresponding elements of β _bxi to a high value rval (for example rval=10⁵).

4.2 Compensation of the Parameter Offset

In Sect. 2.3.3 it was shown that the model with parameters θ ^∗ described by Eq. (2.25) has the same transfer function as the model with parameters θ described by Eq. (2.18) as long as condition (2.27) is fulfilled. This was called redundancy of the “linear parameters”. Consequently, the identification algorithm has no control over offsets c _i , i=0…n. There is no guarantee that the result of identification will be a model with a nominal parameter set θ with c _i =0, i=0…n. On the contrary, a set of parameters θ ^∗ with an arbitrary set of offsets fulfilling condition (2.27) can be the result of the identification.

In order to estimate the nominal parameters θ from the identified parameters θ ^∗a procedure is needed which estimates offsets c _i of $\mathbf{bx} _{i} ^{*},\ i=0\dots n$, and subtracts them from the parameters of $\mathbf{bx} _{i} ^{*}$ of the identified model θ ^∗. It has to be guaranteed that the procedure does not change the transfer function of the model. Before the introduction of the compensation procedure, some properties of the piecewise-linear Hammerstein model have to be discussed.

Assume that the “basic parameters” (2.19) of the piecewise-linear Hammerstein model are known. Then the particular subvectors of vector θ can be expressed according to Eq. (2.16). Assume also that offsets c _i , i=0…n, satisfying condition (2.27), are known. The subvectors of vector θ ^∗ can then be expressed using Eq. (2.26). Now we can calculate the following quantities:

• average values of the parameters of particular subvectors bx _i , i=0…n of vector θ

  $$ \overline{bx_{i}} = \frac{1}{m + 1}\sum _{j = 0}^{m} bx_{i,j} = \frac{1}{m + 1}\sum _{j = 0}^{m} b_{i}x_{j} = b_{i}\frac{1}{m + 1}\sum_{j = 0}^{m} x_{j} = b_{i}\overline{x} $$

  (2.52)

• average values of the parameters of particular subvectors $\mathbf{bx} _{i} ^{*}$ of vector θ

  $$ \begin{aligned}[b] \overline{bx_{i}^*} &= \frac{1}{m + 1}\sum _{j = 0}^{m} bx_{i,j}^* = \frac{1}{m + 1}\sum _{j = 0}^{m} ( b_{i}x_{j} + c_{i} ) \\&= b_{i}\frac{1}{m + 1}\sum_{j = 0}^{m} x_{j} + \frac{1}{m + 1} ( m + 1 )c_{i} = b_{i}\overline{x} + c_{i} \end{aligned} $$

  (2.53)

• standard deviations of the parameters of particular subvectors bx _i of vector θ

  $$\begin{aligned} \sigma_{bx_{i}} &= \Biggl[ \frac{1}{m + 1}\sum _{j = 0}^{m} ( \overline{bx_{i}} - bx_{i,j} )^{2} \Biggr]^{\frac{1}{2}} \\&= \Biggl[ \frac{1}{m + 1}\sum_{j = 0}^{m} ( b_{i}\overline{x} - b_{i}x_{j} )^{2} \Biggr]^{\frac{1}{2}} \\&= \Biggl[ b_{i}^{2}\frac{1}{m + 1}\sum _{j = 0}^{m} ( \overline{x} - x_{j} )^{2} \Biggr]^{\frac{1}{2}} = |b_{i} |\sigma _{x} \end{aligned}$$

  (2.54)

• standard deviations of the parameters of particular subvectors $\mathbf{bx} _{i} ^{*}$ of vector θ ^∗

  $$\begin{aligned} \sigma_{bx_{i}}^* &= \Biggl[ \frac{1}{m + 1}\sum _{j = 0}^{m} ( \overline{bx_{i}^*} - bx_{i,j}^* )^{2} \Biggr]^{\frac{1}{2}} \\&= \Biggl[ \frac{1}{m + 1}\sum_{j = 0}^{m} ( b_{i}\overline{x} + c_{i} - b_{i}x_{j} - c_{i} )^{2} \Biggr]^{\frac{1}{2}} \\&= \Biggl[ b_{i}^{2}\frac{1}{m + 1}\sum _{j = 0}^{m} ( \overline{x} - x_{j} )^{2} \Biggr]^{\frac{1}{2}} = |b_{i} |\sigma _{x} \end{aligned}$$

  (2.55)

• sum of the average values of all bx _i , i=0…n

  $$ \sum_{i = 0}^{n} \overline{bx_{i}} = \sum_{i = 0}^{n} b_{i} \overline{x} = \overline{x}\sum_{i = 0}^{n} b_{i} $$

  (2.56)

• sum of the average values of all $\mathbf{bx} _{i} ^{*}, i=0\dots n$, by taking into account Eq. (2.27)

  $$ \sum_{i = 0}^{n} \overline{bx_{i}^*} = \sum_{i = 0}^{n} (b_{i} \overline{x} + c_{i}) = \sum_{i = 0}^{n} b_{i}\overline{x} + \sum_{i = 0}^{n} c_{i} = \sum_{i = 0}^{n} b_{i}\overline{x} = \overline{x}\sum_{i = 0}^{n} b_{i} $$

  (2.57)

From the calculations above the following facts are evident:

$$\begin{aligned} \overline{bx_{i}^*} &= \overline{bx_{i}} + c_{i} \\\sigma_{bx_{i}}^* & = \sigma_{bx_{i}} \\\sum_{i = 0}^{n} \overline{bx_{i}^*} &= \sum_{i = 0}^{n} \overline{bx_{i}} \end{aligned}$$

Hence, a procedure for the estimation of the unknown nominal model with parameters θ from the identified model with parameters θ ^∗ can be proposed. From Eqs. (2.52) and (2.57) an expression for the estimation of $\overline{bx_{i}}$ of the nominal model θ can be derived

$$ \overline{bx_{i}} = \frac{b_{i}}{\sum_{i = 0}^{n} b_{i}} \cdot\sum _{i = 0}^{n} \overline{bx_{i}^*} $$

(2.58)

The unknown parameters b _i , i=0…n, appearing in Eq. (2.58) can be estimated from the calculated standard deviation of the parameters of the particular subvector $\mathbf{bx} _{i} ^{*}$ in vector θ ^∗. From (2.55) it follows that

$$ |b_{i} |= \frac{\sigma_{bx_{i}}^*}{\sigma_{x}} $$

(2.59)

To estimate b _i , the $\operatorname {sign}(s)$ of b _i has to be determined. First define

$$\begin{aligned} s_{x} &= \operatorname {sign}( x_{m} - x_{0} ) \end{aligned}$$

(2.60)

$$\begin{aligned} s_{bx_{i}}^* & = \operatorname {sign}\bigl( bx_{i,m}^* - bx_{i,0}^* \bigr) \end{aligned}$$

(2.61)

If Eqs. (2.26) and (2.16) are employed in Eq. (2.61), then it follows

$$\begin{aligned} s_{bx_{i}}^* &= \operatorname {sign}\bigl( ( bx_{i,m} + c_{i} ) - ( bx_{i,0} + c_{i} ) \bigr) = \operatorname {sign}( bx_{i,m} - bx_{i,0} ) \\&= \operatorname {sign}\bigl( b_{i} \cdot( x_{m} - x_{0} ) \bigr) = \operatorname {sign}( b_{i} ) \cdot \operatorname {sign}( x_{m} - x_{0} ) = \operatorname {sign}( b_{i} ) \cdot s_{x} \end{aligned}$$

(2.62)

From Eq. (2.62) we get

$$ \operatorname {sign}( b_{i} ) = \frac{s_{bx_{i}}^*}{s_{x}} $$

(2.63)

Now b _i can be completely estimated as follows:

$$ b_{i} = \operatorname {sign}(b_{i}) \cdot|b_{i} |= \frac{s_{bx_{i}}^*}{s_{x}} \cdot\frac{\sigma _{bx_{i}}^*}{\sigma_{x}} $$

(2.64)

Note that in Eq. (2.64) s _x and σ _x are unknown. If Eq. (2.64) is used in Eq. (2.58), then s _x and σ _x are cancelled and an expression for the estimation of the average values of the parameters of the particular subvector bx _i of the nominal model θ is obtained

$$ \overline{bx_{i}} = \frac{s_{bx_{i}}^*\sigma_{bx_{i}}^*}{\sum_{i = 0}^{n} s_{bx_{i}}^*\sigma _{bx_{i}}^*} \cdot\sum _{i = 0}^{n} \overline{bx_{i}^*},\quad i = 0\ldots n $$

(2.65)

The average values $\overline{bx_{i}^{*}}$ and standard deviations $\sigma _{bx_{i}}^{*}$ in Eq. (2.65) are calculated using the leftmost terms of Eqs. (2.53) and (2.55), while signs $s_{bx_{i}}$ are calculated using Eq. (2.61). By subtracting Eq. (2.52) from Eq. (2.53) the expression for the estimation of c _i is obtained

$$ \tilde{c}_{i} = \overline{bx_{i}^*} - \overline{bx_{i}},\quad i = 0\ldots n $$

(2.66)

The estimates of bx _i can be calculated by subtracting estimates of c _i from the estimated $\mathbf{bx} _{i} ^{*}$

$$ bx_{i,j} = bx_{i,j}^* - \tilde{c}_{i},\quad i = 0\ldots n,\ j = 0\ldots m $$

(2.67)

4.3 Tracking the Inactive Parameters

Assume that the excitation signal used for identification is a ramp function (or a similar signal with the amplitude gradually increasing with time) with an additive excitation component with bounded amplitude. Particular parameters of subvectors bx _i , i=0…n are then estimated consecutively as they interfere with the amplitude of the excitation signal. In the initial phase of identification it is therefore beneficial to introduce a mechanism which would use the already estimated parameters of bx _i to improve the initial values of the parameters of bx _i not yet estimated. The idea is as follows. If the nonlinear static function of the process is continuous, then the values of adjacent parameters of bx _i are very likely close to each other. Setting the value of the parameter not yet estimated close to the value of the closest estimated parameter provides a better starting point for identification than the original initial value. A possible way to implement this idea is to introduce a mechanism of “tracking inactive parameters”. First, note that in each step of the proposed recursive identification algorithm subvectors bx _i , i=0…n are updated. Note also that only “active parameters” are changed in every bx _i , while “inactive parameters” remain unchanged

$$\begin{aligned} \Delta\mathbf{bx} _{i} (k) &= \bigl[\textbf{0} _{(1\times (p(k-d-i)-1))}\quad \Delta bx _{i,p(k-d-i)-1} (k) \\&\quad \Delta bx _{i,p(k-d-i)}(k)\quad \textbf{0} _{(1\times (m-p(k-d-i)))}\bigr]^{T} \end{aligned}$$

(2.68)

In this sense, tracking can be interpreted as equalizing the change of the particular “inactive parameter” of Δbx _i (k) to the change of the closest “active parameter” of the same vector. This means that vector (2.68) has to be replaced with the following vector:

$$\begin{aligned} \Delta\mathbf{bx} _{i}(k)' &= \bigl[s _{1} \Delta bx _{i,p(k-d-i)-1}(k)\textbf{1}_{(1\times (p(k-d-i)-1))}\quad \Delta bx _{i,p(k-d-i)-1}(k) \\& \quad \Delta bx _{i,p(k-d-i)} (k) \quad s _{1} \Delta bx _{i,p(k-d-i)}(k)\quad \textbf{1} _{(1\times (m-p(k-d-i)))}\bigr]^{T} \end{aligned}$$

(2.69)

In Eq. (2.69) s ₁ acts as a two-state switch to enable (s ₁=1) or disable (s ₁=0) the tracking mechanism. Note that if s ₁=0, then Eq. (2.68) equals Eq. (2.69). The modified changes of θ considering the tracking mechanism are

$$ \Delta\boldsymbol{\theta}= \bigl[\Delta a _{1}\quad \Delta a _{2}\quad \dots\quad \Delta a _{n}\quad \Delta\mathbf{bx} _{0}^{\prime T}\quad \Delta\mathbf{bx} _{1}^{\prime T} \quad \dots\quad \Delta \mathbf{bx} _{n}^{\prime T}\bigr]^{T} $$

(2.70)

It is obvious that tracking takes effect only on “inactive parameters”. Tracking is not a mandatory procedure but it can speed up convergence of the parameters during the initial phase of identification, especially if the initial values of the parameters are only poor estimates of the true values. The effect of tracking is illustrated in Figs. 2.6 and 2.7, which present the parameters of vector bx _i in the initial stage of identification.

Fig. 2.6

Tracking the inactive parameters not active

Fig. 2.7

Tracking the inactive parameters activated

First, consider the situation without tracking (Fig. 2.6), where it is assumed that parameters bx _i,j , j=0…h+1 have already been estimated, while parameters bx _i,j , j=h+2…m remain at their initial values since they have not yet interfered with the excitation signal. Then, consider the same situation but with tracking enabled (Fig. 2.7). It can be seen that the values of parameters bx _i,j , j=h+2…m are changed in parallel with the closest active parameter (in this particular case bx _i,h+1). Thus, improved initial estimates were obtained, which are obviously closer to the true values than the original initial values. Due to the much better starting point, the convergence of the parameters is accelerated. After estimates of all parameters have been obtained, and if the process is slowly time variant or invariant, the tracking has no considerable effect and can be switched off. If the process has a discontinuous static function at u=u _d where (u _j <u _d <u _j+1), then the tracking procedure has to be rearranged

$$ \Delta\mathbf{bx}_{i}'' ( k ) = \begin{cases} \operatorname {diag}( [ \mathbf{1}_{1 \times ( j + 1 )}\ \mathbf{0}_{1 \times( m - j )} ]^{T} ) \cdot\Delta \mathbf{bx}_{i}' ( k )&\mbox{if:}\ u < u_{j} \\\operatorname {diag}( [ \mathbf{0}_{1 \times( j + 1 )}\ \mathbf{1}_{1 \times( m - j )} ]^{T} ) \cdot\Delta\mathbf{bx}_{i}' ( k )&\mbox{if:}\ u > u_{j + 1} \\\operatorname {diag}( [ \mathbf{0}_{1 \times( j + 1 )}\ \mathbf{0}_{1 \times ( m - j )} ]^{T} ) \cdot\Delta\mathbf{bx}_{i}' ( k )&\mbox{if:}\ u_{j} \le u \le u_{j + 1} \end{cases} $$

(2.71)

and finally

$$ \Delta\boldsymbol{\theta}= \bigl[\Delta a _{1} \quad \Delta a _{2} \quad \dots\quad \Delta a _{n}\quad \Delta \mathbf{bx} _{0}^{\prime\prime T}\quad \Delta\mathbf{bx} _{1}^{\prime\prime T}\quad \dots\quad \Delta \mathbf{bx} _{n}^{\prime\prime T}\bigr]^{T} $$

(2.72)

5 Controller Design

In this section the proposed piecewise-linear Hammerstein model is utilised for control. We will begin with the design of a general linear controller and then modify this approach to be integrated with the piecewise-linear Hammerstein model as presented in [12].

5.1 Linear Controller

First, let us recall the well-known general linear controller with two degrees of freedom, as shown in Fig. 2.8.

Fig. 2.8

General linear controller setup

In Fig. 2.8, the transfer function G _P represents the process and is defined as

$$ G_{P}\bigl(z^{ - 1}\bigr) = \frac{y(z^{ - 1})}{x(z^{ - 1})} = \frac{B(z^{ - 1})}{A(z^{ - 1})} $$

(2.73)

The design goal is that the closed loop transfer function between y _r and y equals the desired closed loop transfer function G _D

$$ G_{D}\bigl(z^{ - 1}\bigr) = \frac{y(z^{ - 1})}{y_{r}(z^{ - 1})} = \frac{B_{D}(z^{ - 1})}{A_{D}(z^{ - 1})} $$

(2.74)

The controller consists of two transfer functions, G _FF and G _FB , which are defined by the polynomials R, S and T:

$$ \begin{aligned}[c] &G_{\mathit{FF}}\bigl(z^{ - 1}\bigr) = \frac{x_{\mathit{ff}}(z^{ - 1})}{y_{r}(z^{ - 1})} = \frac{T(z^{ - 1})}{R(z^{ - 1})},\qquad G_{\mathit{FB}}\bigl(z^{ - 1}\bigr) = \frac{x_{\mathit{fb}}(z^{ - 1})}{y(z^{ - 1})} = \frac{S(z^{ - 1})}{R(z^{ - 1})} \\& x\bigl(z ^{-1} \bigr) = x _{\mathit{ff}}\bigl(z ^{-1} \bigr) - x _{\mathit{fb}}\bigl(z ^{-1}\bigr) \end{aligned} $$

(2.75)

The polynomials R, S and T should be designed in such a way that the closed-loop transfer function G _CL

$$ G_{\mathit{CL}}\bigl(z^{ - 1}\bigr) = \frac{y(z^{ - 1})}{y_{r}(z^{ - 1})} = \frac{B(z^{ - 1})T(z^{ - 1})}{A(z^{ - 1})R(z^{ - 1}) + B(z^{ - 1})S(z^{ - 1})} $$

(2.76)

of the process and the controller equals the desired transfer function G _D (2.74). Polynomials R, S and T are designed by the pole placement method, details can be found in [3]. It is assumed that all zeros of the process G _P are minimum phase and well damped. Consequently, they can be cancelled within the closed-loop transfer function. To achieve cancellation, the controller polynomial R has to fulfil the following condition:

$$ R = R_{1}B $$

(2.77)

The two controller polynomials R ₁ and S are used to match the closed-loop poles of the transfer function (2.76) to the desired closed-loop poles of the transfer function (2.74). To achieve this, the following equality, known as a Diophantine equation, must hold:

$$ AR_{1} + S = A_{0}A_{D} $$

(2.78)

In Eq. (2.78) A ₀ represents an observer polynomial that is a part of the controller but is cancelled within the closed-loop transfer function (2.76). To solve Eq. (2.78), one must first determine the orders of the polynomials R, S, T and A ₀, as well as the orders of the polynomials of the desired closed-loop transfer function (2.74). Following the results in [3], the orders of the polynomials have to fulfil the following conditions:

$$\begin{aligned} &\operatorname{deg}A_{D} - \operatorname{deg}B_{D} \ge \operatorname{deg}A - \operatorname{deg}B \end{aligned}$$

(2.79)

$$\begin{aligned} &\operatorname{deg}A_{0} \ge2\operatorname{deg}A - \operatorname{deg}A_{D} - \operatorname{deg}B - 1 \end{aligned}$$

(2.80)

$$\begin{aligned} &\operatorname{deg}R_{1} = \operatorname{deg}A_{0} + \operatorname{deg}A_{D} - \operatorname{deg}A \end{aligned}$$

(2.81)

$$\begin{aligned} &\operatorname{deg}S < \operatorname{deg}A \end{aligned}$$

(2.82)

Finally, by solving Eq. (2.78), polynomials R ₁ and S are determined. Polynomial R is then determined using Eq. (2.77) and polynomial T using Eq. (2.83)

$$ T = B_{D}A_{0} $$

(2.83)

The controller difference equation can be expressed using polynomials R, S and T

$$ r_{0}x ( k ) = \sum_{i = 0}^{\operatorname{deg}T} t_{i}y_{r} ( k - i ) - \sum_{i = 0}^{\operatorname{deg}S} s_{i}y ( k - i ) - \sum_{i = 1}^{\operatorname{deg}R} r_{i}x ( k - i ) $$

(2.84)

and finally the control signal x(k) can be calculated

$$ x ( k ) = \frac{1}{r_{0}} \Biggl[ \sum_{i = 0}^{\operatorname{deg}T} t_{i}y_{r} ( k - i ) - \sum_{i = 0}^{\operatorname{deg}S} s_{i}y ( k - i ) - \sum_{i = 1}^{\operatorname{deg}R} r_{i}x ( k - i ) \Biggr] $$

(2.85)

In Eqs. (2.84) and (2.85), r _i , s _i and t _i are parameters of polynomials R, S and T, respectively. Note that the polynomial R is the result of polynomial multiplication, as follows from Eq. (2.77). Consequently, the corresponding vector of parameters r of polynomial R can be expressed using the convolution (∗) of the vectors of parameters r ¹ and b of polynomials R ₁ and B, respectively

$$ \mathbf{r}=\mathbf{r} ^{1} *\mathbf{b} $$

(2.86)

The particular element of vector r can be expressed as

$$ r_{i} = \sum_{h = h_{\min}} ^{h_{\max}} r^{1}_{i} \cdot b_{i - h},\quad i = 0\ldots \operatorname{deg}R $$

(2.87)

where

$$\begin{aligned} &h_{\min} = \max( 0,i - \operatorname{deg}B ) \end{aligned}$$

(2.88)

$$\begin{aligned} &h_{\max} = \min( i,\operatorname{deg}R_{1} ) \end{aligned}$$

(2.89)

5.2 Controller Design Based on a Piecewise-Linear Hammerstein Model

Let us now move on to the control design of nonlinear processes described by a piecewise-linear Hammerstein model. Let the linear part of the piecewise-linear Hammerstein model be equal to the linear process model described by Eq. (2.10) or Eq. (2.74) and let the nonlinear static function be expressed using the piecewise-linear function defined by Eq. (2.1). The idea is to design the nonlinear controller in such a way that the closed loop transfer function of the resulting controller and the piecewise-linear Hammerstein model given by Eq. (2.12) become equivalent to the desired closed loop transfer function (2.74). This means that the controller must compensate for the input nonlinearity (2.1) of the process. If the basic parameters (2.19) were known, the input nonlinearity (2.1) could be compensated for simply by inserting its inverse into the input of the piecewise-linear Hammerstein model. In such a case, the linear controller (2.84) could be used with parameters tuned according to the parameters of Eq. (2.10). But the result of the identification algorithm is a set of linear parameters (2.18), while the basic parameters are in general not known. Consequently, the controller in Eq. (2.84) has to be modified to take into account the input nonlinearity, which is integrated in the set of linear parameters. The idea is to express x(k−i) in Eq. (2.84) by u(k−i) using Eq. (2.1). In this way, the terms r _i x(k−i) can be expressed as follows:

$$ r_{i}x ( k - i ) = r_{i} \cdot\mathbf{l} \bigl( u ( k - i ),\mathbf{u} \bigr)^{T} \cdot\mathbf{x} = \mathbf{l} \bigl( u ( k - i ),\mathbf{u} \bigr)^{T} \cdot r_{i} \cdot\mathbf{x} $$

(2.90)

In Eq. (2.90), r _i x represents a vector with elements

$$ r_{i} \cdot\mathbf{x} = [ r_{i}x_{0}\quad r_{i}x_{1}\quad \ldots\quad r_{i}x_{m} ]^{T} $$

(2.91)

Using expression (2.87), a particular element r _i x _j of vector (2.91) can be expressed as

$$ r_{i}x_{j} = x_{j}r_{i} = x_{j}\sum_{h = h_{\min}} ^{h_{\max}} r^{1}_{i} \cdot b_{i - h} = \sum _{h = h_{\min}} ^{h_{\max}} r^{1}_{i} \cdot( b_{i - h}x_{j} ),\quad i = 0\ldots \operatorname{deg}R $$

(2.92)

The terms (b _i−h x _j ) appearing in Eq. (2.92) represent “linear parameters” of the piecewise-linear Hammerstein model. This means that it is not necessary to know the basic parameters (2.19) of the model. The set of linear parameters given by Eq. (2.18) is sufficient to express the controller parameters. This is an important fact, since the set of linear parameters is a direct result of the proposed identification procedure.

If the rightmost term of Eq. (2.90) is used in Eq. (2.84), then the following equation is obtained:

$$ \mathbf{l} \bigl( u ( k ),\mathbf{u} \bigr)^{T} \cdot r_{0} \cdot\mathbf{x} = \sum_{i = 0}^{\operatorname{deg}T} t_{i}y_{r} ( k - i ) - \sum_{i = 0}^{\operatorname{deg}S} s_{i}y ( k - i ) - \sum_{i = 1}^{\operatorname{deg}R} \mathbf{l} \bigl( u ( k - i ),\mathbf{u} \bigr)^{T} \cdot r_{i} \cdot\mathbf{x} $$

(2.93)

The equation can be arranged in a vector form

$$ \mathbf{l} \bigl( u ( k ),\mathbf{u} \bigr)^{T} \cdot r_{0} \cdot\mathbf{x} = \boldsymbol{\psi}_{C}^{T} ( k ) \cdot\boldsymbol{\theta} _{C} $$

(2.94)

where ψ _C is the data vector and θ _C is the parameter vector, as follows:

$$\begin{aligned} \boldsymbol{\psi}_{C} &= \bigl[-\mathbf{l}\bigl(u(k-1),\mathbf{u}\bigr)\quad \ldots\quad -\mathbf{l} \bigl(u(k-\mathrm{deg}\, R),\mathbf{u}\bigr)\ |\ y _{r} (k) \quad y _{r}(k-1)\quad \ldots \\&\quad y _{r}(k-\mathrm{deg}\, T)\ | \quad \dots\quad -y(k) \quad -y(k-1)\quad \ldots \quad -y(k-\mathrm{deg}\ S)\bigr]^{T} \end{aligned}$$

(2.95)

$$\begin{aligned} \boldsymbol{\theta}_{C} = \bigl[r _{1} \mathbf{x} ^{T}\quad \ldots\quad r_{\mathrm{deg}\,R} \mathbf{x} ^{T}\ |\ t _{0}\quad t _{1}\quad \ldots\quad t_{\mathrm{deg}\, T}\ |\ s _{0} \quad s _{1}\quad \ldots\quad s_{\mathrm{deg}\, S}\bigr]^{T} \end{aligned}$$

(2.96)

Note that Eq. (2.94) does not express the control signal u explicitly; instead it expresses the following product, denoted as g(k):

$$ \mathbf{l} \bigl( u ( k ),\mathbf{u} \bigr)^{T} \cdot r_{0} \cdot\mathbf{x} = g ( k ) $$

(2.97)

To express the control signal u(k) explicitly, Eq. (2.97) has to be inverted. As explained above, this is very simple because inversion of a piecewise-linear function is also a piecewise-linear function, while the roles of u and x are reversed, as follows from Eq. (2.9),

$$ u ( k ) = \mathbf{l} \bigl( g ( k ), ( r_{0}\mathbf{x} ) \bigr)^{T} \cdot\mathbf{u} $$

(2.98)

The equation represents the inversion of the nonlinear static function embedded in the model and not explicitly known. Note that due to the simplicity of expression (2.98), calculation of the control signal u(k) is a computationally undemanding task. This is not so in the case of the classic, i.e. single-polynomial-based Hammerstein model. In this case it is necessary to invert the embedded polynomial, of a possibly high degree, in order to calculate the control signal u(k), as shown in, e.g., [2]. The inversion of a polynomial can, in general, only be done numerically, which is a very demanding computational task that needs to be repeated in each sampling interval of the controller. The advantage of a controller based on the piecewise-linear Hammerstein model thus becomes obvious.

6 Simulation Study

The simulation study is divided in two parts: identification and control. First the identification algorithm was tested. The process was simulated by a continuous time system arranged in the form of the Hammerstein model. The static function of the process, shown in Fig. 2.9, was nonlinear and discontinuous

$$ x ( u ) = \begin{cases} 0.1953u + 0.6233u^{\frac{1}{2}} &\mbox{if:}\ 0.0 \le u < 0.6 \\- 6.6229 - 6.4046u + 14.0275u^{\frac{1}{2}} &\mbox{if:}\ 0.6 \le u \le1.0 \end{cases} $$

(2.99)

Fig. 2.9

The nonlinear static function of the process

The linear dynamic system of the process implemented in terms of the following second order continuous time transfer function is

$$ G_{P} ( s ) = \frac{y ( s )}{u ( s )} = \frac{ ( 15s + 1 )}{ ( 35s + 1 ) ( 10s + 1 )} $$

(2.100)

The input signal u was a sum of two components. The first component was a periodic slowly increasing/decreasing ramp (T _period=2000 s, u _min=0.0, u _max=1.0). The second component was a periodic square pulse sequence (T _period=37.7 s, u _min=−0.006, u _max=0.006, duty cycle δ=50 %). The sum of both components was bounded in the range of operation (0≤u≤1). The measurement noise v was added to the process output to achieve a more realistic situation. The time profiles of the resulting signal u, the process output y and the measurement noise v are shown in Fig. 2.10.

Fig. 2.10

Time profiles of the signals during identification

It can be seen that the amplitude of the signal u is temporarily bounded in the range, which is relatively narrow when compared to the range of operation. As mentioned above, the identification of the classical (single polynomial based) Hammerstein model would require an excitation signal with amplitude fairly distributed over the entire range of operation.

The linear dynamic part of the piecewise-linear Hammerstein model was chosen to be of the second order (n=2) and the number of knots of the piecewise linear static function was 11 (m=10). Note that the position of knots u has to be chosen by the user considering possible a priori information on the degree of nonlinearity and positions of possible discontinuities:

• if the nonlinear static function of the process is highly nonlinear, then equidistant positioning of knots may not be optimal, instead the density of knots should be increased in the regions where higher nonlinearity is expected;

• if the nonlinear static function is discontinuous, then each point of discontinuity, u _d , has to be surrounded by two knots at positions u _d ±Δu, where Δu is a small deviation from the point of discontinuity;

• if the input static nonlinearity has a discontinuous first derivative at u _d , then one of the knots should be placed at this point, since the first derivative of the piecewise-linear function is discontinuous at knots u.

Since the nonlinear static function defined in Eq. (2.99) is discontinuous at u=0.6, the position of the knots had to be arranged so as to closely surround the position of the discontinuity by positioning two knots at u=0.6±0.05, i.e. u=0.595 and u=0.605

$$ \mathbf{u}=[0.0\quad 0.12\quad 0.24\quad 0.36\quad 0.48\quad \textbf{0.595} \quad \textbf{0.605}\quad 0.7\quad 0.8 \quad 0.9\quad 1.0] $$

(2.101)

During the experiment all modifications of the identification algorithm (described in Sects. 2.4.1, 2.4.2 and 2.4.3) were activated. Signals were sampled with a sampling interval T _S =3 s. To compare the identified model and the process, the continuous transfer function of the process G _P (s) was transformed into the discrete time transfer function G _P (z ⁻¹) assuming signal sampling using the zero-order hold element

$$ G_{P} \bigl( z^{ - 1} \bigr) = \frac{y ( z^{ - 1} )}{u ( z^{ - 1} )} = \frac{b_{0} + b_{1}z^{ - 1} + b_{2}z^{ - 2}}{1 + a_{1}z^{ - 1} + a_{2}z^{ - 2}} = \frac{0 + 0.1176z^{ - 1} - 0.0963z^{ - 2}}{1 - 1.6587z^{ - 1} + 0.6800z^{ - 2}} $$

(2.102)

The identified model parameters a _i , i=1…n can be directly compared with the corresponding ideal parameters of the process G _P (z ⁻¹), given by Eq. (2.102). The model parameters b _i , i=0…n, and x _j , j=0…m are not expressed explicitly in the set of identified parameters θ, but only implicitly within the identified subvectors bx _i , i=0…n. Therefore, we compared elements of the identified subvectors bx _i with the elements of the ideal subvectors, which were calculated using Eq. (2.16), by taking the ideal parameters b _i and x _j . The ideal parameters b _i were taken from the discrete time transfer function of the linear part of the process in Eq. (2.102). The ideal parameters x _j were calculated by Eq. (2.99) for u=u _j , j=0…m, as given by (2.101). Thus we obtain

$$\begin{aligned} \mathbf{x} &= [0.0 \quad 0.2394\quad 0.3522 \quad 0.4443\quad 0.5256 \quad 0.5970\quad 0.4132\quad 0.6301 \quad 0.80 \\&\quad 0.9206\quad 1.0]^{T} \end{aligned}$$

(2.103)

Based on this, we can write down a complete set of ideal process parameters:

$$ \begin{aligned}[c] &[a _{1}\quad a _{2}]^{T} = [-1.6587\quad 0.6800]^{T}\\& \mathbf{bx} _{0} = [0.0 \quad 0.0\quad 0.0\quad 0.0 \quad 0.0\quad 0.0 \quad 0.0 \quad 0.0 \quad 0.0\quad 0.0\quad 0.0]^{T} \\& \begin{aligned}[t] \mathbf{bx} _{1} &= [0.0000 \quad 0.0281\quad 0.0414\quad 0.0523\quad 0.0618\quad 0.0702 \quad 0.0486\\&\quad 0.0741\quad 0.0941\quad 0.1083\quad 0.1176]^{T} \end{aligned} \\& \begin{aligned}[t] \mathbf{bx} _{2} &= [0.0000 \quad -0.0231 \quad -0.0339\quad -0.0428 \quad -0.0506\quad -0.0575\\& \quad -0.0398\quad -0.0607\quad -0.0770\quad -0.0887\quad -0.0963]^{T} \end{aligned} \end{aligned} $$

(2.104)

The result of identification is the following set of parameters:

$$ \begin{aligned}[c] &[a _{1}\quad a _{2}]^{T} =[-1.6271\quad 0.6520]^{T} \\& \mathbf{bx} _{0} = [0.0001\quad 0.0004\quad 0.0018\quad 0.0013 \quad 0.0013\quad 0.0014 \quad -0.0009\\&\quad \qquad -0.0005\quad -0.0007 \quad -0.0009\quad -0.0012]^{T} \\& \mathbf{bx} _{1} = [0.0006\quad 0.0225 \quad 0.0364\quad 0.0479 \quad 0.0577\quad 0.0660 \quad 0.0526\\&\quad \qquad 0.0783\quad 0.0990\quad 0.1131 \quad 0.1227]^{T} \\&\mathbf{bx} _{2} = [0.0004\quad -0.0194\quad -0.0286\quad -0.0374\quad -0.0452 \quad -0.0521\\&\quad \qquad -0.0417\quad -0.0622\quad -0.0787\quad -0.0897\quad -0.0974]^{T} \end{aligned} $$

(2.105)

We can observe good agreement between the ideal and identified parameters a ₁ and a ₂. Comparison of the ideal and identified subvectors bx _i can most easily be performed graphically, as in Fig. 2.11. Also in this case we observe good agreement. The minor deviation is mainly a consequence of the measurement noise added during the identification.

Fig. 2.11

Comparison between the ideal and the identified subvectors bx ₀, bx ₁, bx ₂

Once the model parameters are known, the control system can be designed. The controller was designed according to the identified set of “linear parameters” given in Eq. (2.105) and the desired closed-loop transfer function, which was chosen to be

$$ G_{D} ( s ) = \frac{y ( s )}{y_{r} ( s )} = \frac{ ( s + 1 )}{ ( 5s + 1 )^{2}} $$

(2.106)

The discrete time equivalent of this function is

$$\begin{aligned} G_{D} \bigl( z^{ - 1} \bigr) &= \frac{y ( z^{ - 1} )}{y_{r} ( z^{ - 1} )} = \frac{b_{d1}z^{ - 1} + b_{d2}z^{ - 2}}{1 + a_{d1}z^{ - 1} + a_{d2}z^{ - 2}} \\& = \frac{0.1878z^{ - 1} + 0.0158z^{ - 2}}{1 - 1.0976z^{ - 1} + 0.3012z^{ - 2}} \end{aligned}$$

(2.107)

Note that the orders of the polynomials in this transfer function have to fulfil the condition in Eq. (2.79). The orders of the other polynomials are as follows: $\operatorname{deg} A _{0} =0$, $\operatorname{deg} R _{1} =0$ and $\operatorname{deg} S=1$. This fulfils conditions (2.80)–(2.82). The controller parameters were expressed in terms of the linear parameters of the piecewise-linear Hammerstein model and the parameters of the desired closed-loop transfer function. First, by solving Eq. (2.78) the parameters of R ₁ and S were expressed. Next, using Eq. (2.83) the parameters of T were obtained. Finally, using Eq. (2.92) the controller parameters rx _i were expressed in terms of the linear parameters bx _i . The result is the following set of controller parameters, which is automatically tuned based on identified model parameters:

$$\begin{aligned} &\bigl[\mathbf{rx} _{0} ^{T}\quad \mathbf{rx} _{1} ^{T}\bigr]^{T} = \bigl[\mathbf{bx} _{1} ^{T}\quad \mathbf{bx} _{2} ^{T}\bigr]^{T} \\&[s _{0} \quad s _{1}]^{T} = \bigl[(a _{d1} -a _{1} )\quad (a _{d2} -a _{2})\bigr]^{T} \\& [t _{0}\quad t _{1}]^{T} = [b _{d1} \quad b _{d2}]^{T} \end{aligned}$$

(2.108)

To test the control performance of the control system, the output y of the controlled process was compared to the output y _d of the desired closed-loop transfer function. During the simulation, both the controlled process and the desired closed-loop transfer function were exposed to the same reference signal y _r as the input. In Fig. 2.12 it can be seen that the output of the controlled process y agrees very well with the output of the desired closed-loop transfer function y _d . The nonlinearity and discontinuity of the process are almost completely compensated for. In fact, the presence of the nonlinearity can only be seen from the control signal u. A minor deviation (e=y _d −y) is only noticeable in case the control signal u is saturated and around the point of discontinuity. This simulation example confirms the usability of the proposed controller. The controller successfully compensates for the process nonlinearity as well as for the discontinuity.

Fig. 2.12

Controller operation (u—control signal, y—process output, y _d —output of the desired closed-loop transfer function, y _r —reference signal, e=y _d −y)

7 Experimental Implementation

Let us now demonstrate the usability of the piecewise-linear Hammerstein model on an industrial case study, i.e. oxygen concentration control in a sintering process of ferromagnetic material.

7.1 Description of the Process and the Experimental Environment

Sintering is a process that produces solid objects from powder by heating the material in sintering furnaces. The sintering process is also widely used in the production of ferromagnetic materials. The properties of a ferromagnetic material strongly depend on the process parameters during sintering (i.e. the time profiles of the temperature and atmosphere composition). During the development of the material production process it is therefore necessary to determine the optimal time profile of the process parameters which lead to the desired properties of the ferromagnetic material. In order to do this, a theoretical background is usually combined with experimental optimisation, which takes place in a laboratory environment using special sintering furnaces and corresponding control equipment providing accurate and repeatable control of the main process parameters, i.e. the temperature and atmosphere composition. In this example we will focus on a specific experimental sintering process where the atmosphere is composed of oxygen and nitrogen. During the process, the oxygen concentration and temperature in the furnace have to follow the prescribed time profiles. We will focus only on the problem of the oxygen concentration, which is controlled by adjusting the flow rates of oxygen and nitrogen. The two gasses continuously mix, enter the furnace, mix with the gas inside the furnace, and finally exit to the atmosphere. The flow rates of the oxygen and nitrogen are controlled by mass flow control valves. Depending on the material produced, the oxygen concentration time profile may be required to vary over a very wide range, e.g. from 100 % vol. down to very low values, such as 0.01 % vol. To achieve such a wide control range of the oxygen concentration, the oxygen flow rate has to be adjusted over a very wide range, too. Since the useful control range of a typical mass flow control valve is limited to, e.g., 2–100 % of the full scale range, several mass flow control valves with different maximum flow rates must be used, and a wide enough range of the oxygen flow rate is achieved by valve switchover. In the installation considered two valves are used, V ₁ with a small range and V ₂ with a big range. V ₃ is the mass flow control valve for nitrogen. The simplified situation is shown in Fig. 2.13.

Fig. 2.13

Setup for oxygen concentration control during the sintering process

The process equipment consists of the following three subsystems (see Fig. 2.14): A—electrically heated sintering furnace, B—oxygen concentration sensor and C—oxygen concentration and temperature control device, containing the mass flow control valves (V ₁, V ₂ and V ₃), the auxiliary on/off valves and the Mitsubishi programmable logic controller (PLC), series A1S. The PLC reads concentration from the oxygen concentration sensor and adjusts the control signals to the mass flow control valves using a PID control algorithm.

Fig. 2.14

Experimental setup: A—sintering furnace, B—oxygen concentration sensor and C—oxygen concentration and temperature control device

For the purpose of experimental assessment of the piecewise-linear Hammerstein control algorithm, a personal computer was connected to the PLC via an RS-232 serial communication. On the personal computer the identification and control environment for the piecewise-linear Hammerstein model was implemented.

Two types of experiments were performed, identification and control. During the identification experiments, the personal computer generated the control signal u, sending it to the PLC and simultaneously sampling the oxygen concentration response. As soon as the experiment was completed, the parameters of the piecewise-linear Hammerstein model were identified and the controller parameters were calculated. The controller parameters were then downloaded from the personal computer to the PLC, where controller Eqs. (2.94)–(2.98) were implemented in addition to the existing default PID algorithm. During the control experiment, the control signal u was generated by the PLC and sampled together with the oxygen concentration by the personal computer for the purpose of documenting and evaluating the results.

7.2 Process Analysis and Controller Design

Application of the piecewise-linear Hammerstein controller was motivated by problems caused by drifts in the control valves V ₁, V ₂ and V ₃. These drifts result in discontinuities during valve switchover which seriously compromise the control performance of the existing PID controller.

In order to better understand the problem of oxygen concentration control, let us analyse the process of gas mixing by mathematical modelling. The resulting mathematical model will also help us to determine the structure of the piecewise-linear Hammerstein model.

The model should describe the dynamic relation between the control input u and the process output, i.e. the oxygen concentration c _O2 inside the furnace. Let us start with modelling of the input flow rate ϕ _s , which is the sum of the volumetric flow rates of oxygen ϕ _O2 and nitrogen ϕ _N2 entering the furnace. Due to technological reasons, ϕ _s must always be constant and in our case is 30 standard litres per hour (sl/h)

$$ \phi_{O2} + \phi_{N2} = \phi_{s} = 30\ \mathrm{sl}/\mathrm{h} $$

(2.109)

The above requirement can be fulfilled by controlling both gas flow rates by means of the common control signal u(0…1) using the following functions:

$$\begin{aligned} &\phi_{O2} ( u ) = 30u \end{aligned}$$

(2.110)

$$\begin{aligned} &\phi_{N2} ( u ) = 30 ( 1 - u ) \end{aligned}$$

(2.111)

As explained above, the system has two mass flow control valves for oxygen (V ₁, V ₂) and one for nitrogen (V ₃). The flow rates of valves are proportional to their voltage command signals (v ₁, v ₂ and v ₃) as follows:

$$ \begin{aligned}[c] &\phi_{O2} ( v_{1} ) = k_{1}\frac{v_{1}}{5} + n_{1},\qquad\phi_{O2} ( v_{2} ) = k_{2}\frac{v_{2}}{5} + n_{2},\\&\phi_{N2} ( v_{3} ) = k_{3}\frac{v_{3}}{5} + n_{3} \end{aligned} $$

(2.112)

whereby the valve gains k ₁, k ₂ and k ₃ represent maximum flow rates. Nominally, they have the following values:k ₁=20 l/h, k ₂=100 l/h and k ₃=30 l/h. Constants n ₁, n ₂ and n ₃ represent offsets of the control valves and are ideally zero. All three command signals (v ₁, v ₂ and v ₃) are in the range 0…5 V, where 0 V means zero flow and 5 V means the maximum flow rate. They are generated by analogue outputs of the programmable logic controller and are functions of the common control signal u:

$$ v_{1} = g_{1}u,\qquad v_{2} = g_{2}u, \qquad v_{3} = g_{3} ( 1 - u ) $$

(2.113)

where g ₁, g ₂ and g ₃ are gains implemented in the programmable logic controller. Let us now express flow rates as functions of the common control signal u(0…1). For the oxygen flow rate we take into account the switchover between the small (V ₁) and big (V ₂) mass flow control valves. The switching point is set at 15 l/h, which corresponds to u=0.5, as follows from Eq. (2.110). Below 15 l/h, valve V ₁ is used and V ₂ is closed, above 15 l/h valve V ₁ is closed and V ₂ is in use:

$$\begin{aligned} &\phi_{O2} ( u ) = \begin{cases} k_{1}\frac{g_{1}u}{5} + n_{1} &\mbox{if}\ 0 \le u \le 0.5 \\ k_{2}\frac{g_{2}u}{5} + n_{2} &\mbox{if}\ 0.5 < u \le1 \end{cases} \end{aligned}$$

(2.114)

$$\begin{aligned} &\phi_{N2} ( u ) = k_{3}\frac{g_{3} ( 1 - u )}{5} + n_{3} \end{aligned}$$

(2.115)

Since relations (2.114) and (2.115) must equal relations (2.110) and (2.111), the gains g ₁, g ₂ and g ₃ must be appropriately determined:

$$ g_{1} = \frac{30 \cdot5}{k_{1}} = 7.5,\qquad g_{2} = \frac{30 \cdot5}{k_{2}} = 1.5,\qquad g_{3} = \frac{30 \cdot5}{k_{3}} = 5 $$

(2.116)

If gains (g ₁, g ₂ and g ₃) equal the values calculated above in Eq. (2.116) and if the valve gains (k ₁, k ₂ and k ₃) and offsets (n ₁, n ₂ and n ₃) equal their nominal values, then Eq. (114) is continuous and linear. But if valve gains and offsets differ from the nominal values, Eq. (114) becomes discontinuous. Since the valve gains and offsets are defined by the analogue electronic circuits of control valves which are subject to drift, the nonlinearity and discontinuity of the relation between the control signal u and the flow rate of oxygen is a common situation during normal operation.

The outputs of mass flow control valves are connected together and gasses then enter the furnace via a common pipeline. Within the pipeline, gases are blended into a uniform gas mixture. Since the cross section of the pipeline is small (4 mm), the nitrogen and oxygen are assumed to blend completely already before entering the furnace. The oxygen concentration in the gas mixture entering the furnace is denoted by c _{O2_IN} and it can be expressed as a ratio between the oxygen flow rate and the total flow rate

$$ c_{\mathit{O}2\_\mathit{IN}} = \frac{\phi_{O2}}{\phi_{s}} $$

(2.117)

Equations (2.114), (2.115) and (2.117) are all static relations and represent the nonlinear static function of the Hammerstein system.

Let us now concentrate on the dynamic part of the process. We are interested in the dynamic relationship between the oxygen concentration c _{O2_IN} in the gas mixture entering the furnace and the oxygen concentration c _O2 in the mixture leaving the furnace. If gas diffusion inside the furnace was instantaneous, the relationship between the input and output concentration could be represented by a linear first order differential equation with static gain equal to one and a time constant proportional to the furnace volume. However, due to the specific shape of the furnace volume (a tube with an internal diameter of approximately 6 cm and length 1.3 m), gas diffusion is not instantaneous and introduces additional dynamics into the system. Theoretical modelling of the mixing and diffusion dynamics would be complex and possibly inaccurate. Instead, we estimated the actual gas mixing process dynamics by observing the response of the output concentration to the step change of the control signal u. We found that the response follows a second order linear system with a dominating time constant around 600 s. In our analysis we did not take into account the following two phenomena:

• the transport delay due to the transport of the gas via pipelines from the mass flow control valves to the furnace and from the furnace to the oxygen concentration sensor;

• the dynamic response of the oxygen concentration sensor mounted at the outlet of the furnace.

However, further evaluation shows that the transport delay in the pipes and the time constant of the oxygen sensor are both within a few seconds, which can obviously be neglected.

The analysis performed up to this point shows that the process under consideration can be described by a Hammerstein model. The relations (2.114), (2.115) and (2.117) represent the nonlinear static function of the model, while the dynamic relation between c _{O2_IN} and c _O2 represents the linear dynamic part. As explained, the linear dynamic part can be described in terms of a second order linear differential equation with static gain equal to one.

In order to implement the piecewise-linear Hammerstein controller, it was first necessary to determine its structure. We have chosen the order of the dynamic linear part to be n=2, which is in accordance with the measured process response. The number of knots was kept at the default value (m=10), although a lower number would probably also be acceptable, since the characteristics of both valves are expected to remain more or less linear. The knots were arranged to surround the point of switchover (u=0.5)

$$ \mathbf{u} = [0.0 \quad 0.1\quad 0.2\quad 0.3\quad 0.4\quad \textbf{0.495} \quad \textbf{0.505}\quad 0.625 \quad 0.750 \quad 0.875 \quad 1.0]^{T} $$

(2.118)

Note that just before experimenting, all three mass flow control valves were calibrated, which means that all three valve gains and offsets (k,n) were close to their ideal values. To demonstrate the effect of non-ideal valve gains and offsets, we simulated a change in the valve gain k ₁ of the oxygen valve V ₁ from a nominal 20 l/h to 24 l/h by multiplying gain g ₁ by a factor of 1.2. As explained above, such a change in the valve characteristic may happen in reality due to drift.

The next step was to determine the time profile of the excitation signal u. For model identification, the excitation signal u should skim across the whole operation region. This was achieved by changing the signal in steps from 0.06 to 0.8 and back to 0.06. The level of each step was 0.02 and the step duration was 500 seconds, which is comparable to the estimated predominant time constant of the process. Figure 2.15 shows the time profile of the excitation signal u and the resulting oxygen concentration response (c _O2 measured) on which the effect of the discontinuous static function is clearly visible. During identification, the sampling interval was chosen to be T _S =30 sec, which is adequate for the estimated time constants of the process. The identification procedure provided the following set of “linear parameters”:

$$ \begin{aligned}[c] &[a _{1} \quad a _{2}]^{T} = [-1.6647\quad 0.6775]^{T}\\& \mathbf{bx} _{0} = [0.0\quad 0.0\quad 0.0 \quad 0.0\quad 0.0\quad 0.0\quad 0.0\quad 0.0\quad 0.0\quad 0.0\quad 0.0]^{T} \\& \mathbf{bx} _{1} = [0.0000\quad 0.0135\quad 0.0269\quad 0.0404\quad 0.0538\quad 0.0666 \quad 0.0680\\&\qquad \quad 0.0841\quad 0.1010\quad 0.1178\quad 0.1346]^{T} \\& \mathbf{bx} _{2} = [0.0000\quad -0.0116\quad -0.0232\quad -0.0347\quad -0.0463\quad -0.0573 \\&\quad \qquad -0.0585\quad -0.0724\quad -0.0868\quad -0.1013\quad -0.1158]^{T} \end{aligned} $$

(2.119)

Fig. 2.15

Identification and model evaluation (u—control signal, c _O2 measured—oxygen concentration response, c _O2 model—simulated concentration)

Figure 2.15 also shows the response of the identified piecewise-linear Hammerstein model (the c _O2 model). It can be seen that the actual concentration and the model response are very similar, which means that the model quality is adequate.

The next step was the determination of the controller parameters. To do this, we first defined the desired closed loop response in terms of the following continuous time transfer function:

$$ G_{D}(s) = \frac{1}{(200s + 1)^{3}} $$

(2.120)

Note that in the preceding simulation study a second order transfer function was used to define the desired closed loop response. But in this case we designed the controller with additional integral action, which required a third order transfer function. The continuous time transfer function was then converted to a discrete time form using a 30 sec sampling interval

$$\begin{aligned} G_{D}\bigl(z^{ - 1}\bigr) & = \frac{b_{d1}z^{ - 1} + b_{d2}z^{ - 2} + b_{d3}z^{ - 3}}{1 + a_{d1}z^{ - 1} + a_{d2}z^{ - 2} + a_{d3}z^{ - 3}} \\&= \frac{0.0005z^{ - 1} + 0.0018z^{ - 2} + 0.0004z^{ - 3}}{1 - 2.5821z^{ - 1} + 2.2225z^{ - 2} - 0.6376z^{ - 3}} \end{aligned}$$

(2.121)

Finally, the controller parameters were determined from the identified linear parameters (2.119) and the parameters of the desired closed loop transfer function (2.121). Note that the presence of the integrator in the controller required an extended set of parameters:

$$\begin{aligned} &\bigl[\mathbf{rx} _{0} ^{T}\quad \mathbf{rx} _{1} ^{T} \quad \mathbf{rx} _{2} ^{T}\bigr]^{T} = \bigl[\mathbf{bx} _{1} ^{T}\quad \bigl(\mathbf{bx} _{2} ^{T} -\mathbf{bx} _{1} ^{T} \bigr)\quad -\mathbf{bx} _{2} ^{T}\bigr]^{T} \\& [s _{0}\quad s _{1} \quad s _{2}]^{T} = \bigl[(a _{d1} -a _{1} +1) \quad (a _{d2} -a _{2} +a _{1} ) \quad (a _{d3} +a _{2})\bigr]^{T} \\& [t _{0}\quad t _{1}\quad t _{2}]^{T} = [b _{d1} \quad b _{d2}\quad b _{d3}]^{T} \end{aligned}$$

(2.122)

The operation of the controller was tested on the real process and the results are shown in Fig. 2.16. It can be seen that the measured oxygen concentration (c _O2) follows the desired closed loop response (c _O2d ) very well, which means that the controller is well tuned to the process dynamics. Note that the parameters of the piecewise-linear controller are derived directly from the identified model parameters and no manual tuning is necessary. In addition, the presence of the process discontinuity can only be observed from the control signal (u) and not from the oxygen concentration, which means that the controller effectively identifies and compensates for the discontinuity.

Fig. 2.16

Piecewise-linear Hammerstein controller operation (u—control signal, c _O2—concentration, c _O2d —output of the desired closed-loop transfer function, c _O2r —reference signal)

In Fig. 2.16 one can notice a time delay between the desired closed loop response (c _O2d ) and the concentration setpoint (c _O2r ). This delay is induced by the closed loop transfer function (2.120). By reducing the time constants of the poles of (2.120) we could reduce the time delay but then we would also increase the risk of system instability. Note that the existence of the time delay is tolerable in all cases where the setpoint (c _O2r ) is prescribed in advance in terms of a time profile. In such cases the time delay is easily compensated for by modifying the time profile of the setpoint (c _O2r ). The considered oxygen concentration control problem belongs to this class of problems, so the time delay does not entail any drawback.

For comparison, the results of control using the built-in PID controller are shown in Fig. 2.17. Here we can see the non-ideal time profile of the concentration at the point of valve switchover since the discontinuity is not compensated for by the controller. The effect is visible in time intervals 6000–7000 and 12,000–13,000 seconds. We can also notice overshoots when the setpoint signal changes from ramp to constant value. The overshoots are a consequence of the imperfect manual tuning of the PID controller parameters. Note that overshoots do not appear in Fig. 2.16 since the piecewise-linear Hammerstein controller is tuned according to the identification results, which means nearly perfect tuning.

Fig. 2.17

PID controller operation (u—control signal, c _O2—concentration, Ref—reference signal)

8 Problems and Limitations in Applying the Theory

As explained above in Sect. 2.2, several problems and limitations may occur while applying the concept of the original form of the Hammerstein model in practice. We identified three major properties of the model which restrict the practical applicability and lead to potential problems. The main goal of this chapter was to overcome the identified drawbacks and to improve the practical applicability by modifying the original form of the model. A theoretical analysis along with the simulation results and experimental implementation demonstrate that the principal goal was achieved and the main drawbacks were eliminated relatively effectively.

However, both the identification procedure and the control algorithm may still face some problems or limitations when applied to particular processes. Below we identify them briefly.

One of the problems is related to the number and arrangement of knots. Both the number and the position of the knots are not determined automatically, but rather are a matter of designer decision. In cases of mild nonlinearity, the identification will most likely provide good results with the default arrangement, i.e. 11 equidistantly distributed knots. But in cases of functions with a higher degree of nonlinearity, discontinuities, or a discontinuous first derivative, the default arrangement is no longer optimal and must be set manually. This can be done either by using prior knowledge about the process or from information gathered during initial identification with default parameters.

The identification algorithm of the piecewise-linear Hammerstein model is based on recursive least squares identification of linear systems. It is well known that this kind of algorithm is sensitive to the presence of measurement noise in the measured process output signal. If noise level is relatively low or moderate (as in the presented simulation study and experimental implementation), the estimated model parameters are expected to be close to true values. However, if the level of noise is high, then the estimated parameters will likely be inaccurate and the model will not describe the process well enough. If such model is employed for control, the control performance is not expected to be good. Therefore special attention has to be devoted to the quality of the signals, and the proper measures must be taken to either prevent the noise or at least minimise it. Sometimes the noise is not a consequence of the measurement method and/or signals, but it originates from the process itself. In such cases the noise cannot easily be reduced and identification will most likely face problems. A possible solution would be the application of an identification algorithm less sensitive to noise, e.g. instrumental variables.

For successful identification, special attention has to be devoted to the selection of the input signal and sampling of the process response. If the input signal is composed of serial step functions (as in the experimental implementation presented in Fig. 2.15), then the duration and amplitude of the step is important. Step duration should be sufficiently long to capture the response of the largest time constant of the process and the sampling interval should be short enough to not miss the response of the shortest time constant. The amplitude of the steps is also important. It should be smaller than the distance between knots, but also big enough so that the amplitude of the process response is well above the measurement noise. In order to determine the right excitation signal, some a priori information about the process dynamic structure is very useful. Alternatively, preliminary identification based on a single step response should be performed in order to obtain the initial information about the process dynamics. Once this is done, the identification signal can be determined and complete identification can be performed.

The control algorithm is based on a linear pole placement controller for linear processes. This method is relatively simple and theoretically sound, but the major problem is that its design parameters are not directly related to the classical performance requirements. More specifically, the design parameters of the pole placement controller are given in terms of poles and zeros of the desired closed loop transfer function (2.74), (2.106). But the typical performance requirements are less specific and they are usually given in terms of rise time, settling time, etc. The problem is related to the fact that a given set of performance requirements can be fulfilled by many different desired closed loop transfer functions, and some of them may lead to a less robust controller, i.e. one that is sensitive to the mismatch between the process and the identified model. In such a case, several different desired transfer functions may need to be tested before a satisfactory result is obtained.

The pole placement controller may also be sensitive to the measurement noise, which can be reflected in the control signal u, which can harm the performance of the closed-loop system and increase wear in the actuators. The problem of measurement noise can be reduced by filtering the process output. However, the presence of the filter generally changes the process dynamics, which may decrease control performance and stability due to mismatch between the process and the model. If filtering is used, it is necessary to treat it as part of the process and identification should be performed according to the filtered process output.

If the mentioned problems and limitations occur, they can be handled in most cases, but they require designer intervention and experience. Unfortunately, this interaction cannot easily be generalised since it is very case-dependent.

9 Conclusion

The research presented in this chapter was a response to the challenge presented by the need to modify the standard form of the Hammerstein model in order to alleviate the drawbacks which hinder its implementation in practice. We proposed a piecewise-linear Hammerstein model with piecewise-linear representation of the nonlinear static function, as opposed to the single polynomial that is used in the original version of the Hammerstein model. Thanks to this, three improvements were obtained which directly increase the practical applicability of the model.

Firstly, the proposed algorithm does not require persistent excitation over the entire range of operation. Instead, an excitation signal with temporarily bounded amplitude is sufficient. This is important when industrial processes are considered, since in this case only signals with a bounded amplitude region are allowed to be applied. Due to the linearity in the model parameters, a classic least squares-based identification algorithm could be used as a basis for the development of the new identification approach. This algorithm was then adapted and enhanced to take into account the specifics of the identification signal and properties of the applied piecewise-linear Hammerstein model.

Secondly, the proposed model is very convenient for describing processes with highly nonlinear and/or discontinuous memoryless static functions. In the case of highly nonlinear static functions, the density of knots can be increased in the region of high nonlinearity, thus increasing the precision. In the case of discontinuous static functions, each point of discontinuity can be surrounded by two close-standing knots, thus enabling approximation of the discontinuity.

Finally, it was shown that the proposed model can very easily be integrated into a self-tuning control algorithm with a simple structure and low computational effort, which enables execution also in programmable logic controllers. This is due to simple analytical inversion of the embedded nonlinear static function of the model, implemented as a piecewise-linear function. In addition, it was shown that the controller parameters can be expressed in terms of “linear model parameters”, which are a direct result of the identification, while the basic parameters of the piecewise-linear Hammerstein model do not have to be expressed explicitly. This enables automatic tuning of the controller parameters.

Although the motivation of the work was to improve the practical applicability of the control method, there are still some remaining issues which may hinder implementation in some cases and reduce control performance. One such problem is the level of measurement noise, which can worsen both identification and control if it is too high. Experience also shows that the proper selection of the time profile of the identification signal and the sampling interval are very important for successful identification. Furthermore, the structure of the model (the order of the linear part and the distribution of knots) has to be determined manually, which may be difficult when the process is not well understood or no information exists. Finally, the control goal is expressed in terms of the desired closed loop transfer function. This is not directly related to traditional engineering design criteria and leads to redundancy, since many different transfer functions may satisfy the particular engineering criteria. The mentioned issues can be handled, but they require manual interaction, based on designer experience.