Keywords

Introduction

The \(\mathcal{H}_{\infty }\)-norm probably first entered the study of robust control with the observations made by Zames (1981) in the considering optimal sensitivity. The so-called \(\mathcal{H}_{\infty }\) methods were subsequently developed and are now routinely available to control engineers. In this entry we consider the \(\mathcal{H}_{\infty }\) methods for control, and for simplicity of exposition, we will restrict our attention to linear, time-invariant, finite dimensional, continuous-time systems. Such systems can be represented by their transfer function matrix, G(s), which will then be a rational function of \(s\). Although the Hardy Space, \(\mathcal{H}_{\infty }\), also includes nonrational functions, a rational G(s) is in \(\mathcal{H}_{\infty }\) if and only if it is proper and all its poles are in the open left half plane, in which case the \(\mathcal{H}_{\infty }\)-norm is defined as:

$$\displaystyle{ \left \|G(s)\right \|_{\infty } =\sup _{\mathrm{Re}s>0}\sigma _{\mathrm{max}}\left (G(s)\right ) =\sup _{-\infty <\omega <\infty }\sigma _{\mathrm{max}}\left ((j\omega )\right ) }$$

(where σmax denotes the largest singular value). Hence for a single input/single output system with transfer function, g(s), its \(\mathcal{H}_{\infty }\)-norm, \(\left \|g(s)\right \|_{\infty }\) gives the maximum value of | g(j ω) | and hence the maximum amplification of sinusoidal signals by a system with this transfer function. In the multi-input/multi-output case a similar result holds regarding the system amplification of a vector of sinusoids. There is now a good collection of graduate level textbooks that cover the area in some detail from a variety of approaches, and these are listed in the Recommended Reading section and the references in this article are generally to these texts rather than to the original journal papers.

Consider a system with transfer function, G(s), input vector, u(t) ∈ ℒ2(0, ∞) and an output vector, y(t), whose Laplace transforms are given by \(\bar{u}(s)\) and \(\bar{y}(s)\). Such a system will have a state space realization,

$$\displaystyle{ \dot{x}(t) = Ax(t) + Bu(t),\ \ \ y(t) = Cx(t) + Du(t) }$$

giving \(G(s) = D + C(sI - A)^{-1}B\), which we also denote

$$\displaystyle{ G(s) = \left [\begin{array}{c|c} A &B\\ \hline C &D \end{array} \right ], }$$

and hence \(\bar{y}(s) = G(s)\bar{u}(s)\) if x(0) = 0.

There are two main reasons for using the \(\mathcal{H}_{\infty }\)-norm. Firstly in representing the system gain for input signals u(t) ∈ ℒ2(0, ∞) or equivalently \(\bar{u}(j\omega ) \in \mathcal{L}_{2}(-\infty,\infty )\), with corresponding norm \(\|u\|_{2}^{2} =\int _{ 0}^{\infty }u(t)^{{\ast}}u(t)\,dt\) (where x∗ denotes the conjugate transpose of the vector x (or a matrix)). With these input and output spaces the induced norm of the system is easily shown to be the \(\mathcal{H}_{\infty }\)-norm of G(s), and in particular,

$$\displaystyle{ \|y\|_{2} \leq \| G(s)\|_{\infty }\|u\|_{2} }$$

Hence in a control context the \(\mathcal{H}_{\infty }\)-norm can give a measure of the gain, for example, from disturbances to the resulting errors. In the interconnection of systems, the property that \(\|P(s)Q(s)\|_{\infty }\leq \| P(s))\|_{\infty }\|Q(s)\|_{\infty }\) is often useful.

The second reason for using the \(\mathcal{H}_{\infty }\)-norm is in representing uncertainty in the plant being controlled, e.g., the nominal plant is P o (s) but the actual plant is \(P(s) = P_{o}(s) + \Delta (s)\) where \(\|\Delta (s)\|_{\infty }\leq \delta\).

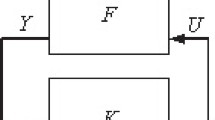
A typical control design problem is given in Fig. 1, i.e.,

$$\begin{array}{ll} \left [\begin{array}{ll} \bar{z} \\ \bar{y} \end{array} \right] & = P\left [\begin{array}{l} \bar{w}\\ \bar{u} \end{array} \right ] = \left [\begin{array}{l} P_{11}\bar{w} + P_{12}\bar{u} \\ P_{21}\bar{w} + P_{22}\bar{u} \bar{u} \end{array}\right] \\ \quad \bar{u} & = K \bar{y} \\ \Rightarrow \bar{ y} & = (I - P_{22}K)^{-1}P_{ 21}\bar{w},\\ \quad \bar{u} & = K(I - P_{22}K)^{-1}P_{ 21}\bar{w} {}\\ \quad \bar{z} & = \left (P_{11} + P_{12}K(I - P_{22}K)^{-1}P_{ 21}\right )\bar{w} \\& =: \mathcal{F}_{l}(P,K)\bar{w} =: T_{z\leftarrow w}\bar{w} \end{array}$$

where \(\mathcal{F}_{l}(P,K)\) denotes the lower Linear Fractional Transformation (LFT) with connection around the lower terminals of P as in Fig. 1.

H-Infinity Control, Fig. 1
figure 81figure 81

Lower linear fractional transformation: feedback system

Full size image

The standard \(\mathcal{H}_{\infty }\)-control synthesis problem is to find a controller with transfer function, K, that

stabilizes the closed-loop system in Fig.1 and minimizes\(\\||\mathcal{F}_{ l}(P,K)\|_{\infty }\)

That is, the controller is designed to minimize the worst-case effect of the disturbance w on the output/error signal z as measured by the \(\mathcal{L}_{2}\) norm of the signals. This article will describe the solution to this problem.

Robust Stability

Before we describe the solution to the synthesis problem, consider the problem of the robust stability of an uncertain plant with a feedback controller. Suppose the plant is given by the upper LFT, \(\mathcal{F}_{u}(P,\Delta )\) with \(\|\Delta \|_{\infty }\leq 1/\gamma\) as illustrated in Fig. 2,

$$\displaystyle\begin{array}{rcl} \bar{y}& =& \mathcal{F}_{u}(P,\Delta )\bar{u}, \\ \mbox{ where}\;\mathcal{F}_{u}(P,K)& :=& P_{22} + P_{21}\Delta \left (I - P_{11}\Delta \right )^{-1}P_{ 12}{}\end{array}$$
(1)
H-Infinity Control, Fig. 2
figure 82figure 82

Upper linear fractional transformation

Full size image

The small gain theorem then states that the feedback system of Fig. 3 will be stable for all such \(\Delta\) if the feedback connection of P22 and K is stable and \(\|\mathcal{F}_{l}(P,K)\|_{\infty } <\gamma\). This robust stability result is valid if P and \(\Delta\) are both stable; more care is required when either or both are unstable but with such care a similar result is true.

H-Infinity Control, Fig. 3
figure 83figure 83

Feedback system with plant uncertainty

Full size image

Let us consider a couple of examples. First suppose that the uncertainty is represented as output multiplicative uncertainty,

$$\displaystyle{ P_{\Delta } = (I+W_{1}\Delta W_{2})P_{o} = \mathcal{F}_{u}\left (\left [\begin{array}{cc} 0 &W_{2}P_{o} \\ W_{1} & P_{o} \end{array} \right ],\Delta \right ) }$$

with robust stability test given by

$$\displaystyle\begin{array}{rcl} & & \|\mathcal{F}_{l}\left (\left [\begin{array}{cc} 0 &W_{2}P_{o} \\ W_{1} & P_{o} \end{array} \right ],K\right )\|_{\infty } {}\\ & &\quad =\| W_{2}P_{o}K(I - P_{o}K)^{-1}W_{ 1}\|_{\infty } <\gamma {}\\ \end{array}$$

As a second example consider the plants \(P_{\Delta } = (\tilde{M} + \Delta _{M})^{-1}(\tilde{N} + \Delta _{N})\), with \(\Delta = \left [\begin{array}{@{}c@{}c@{}} \Delta _{N}&\Delta _{M} \end{array} \right ]\) and \(\|\Delta \|_{\infty }\leq 1/\gamma\). Here \(P_{o} =\tilde{ M}^{-1}\tilde{N}\) is a left coprime factorization of the nominal plant and the plants \(P_{\Delta }\) are represented by perturbations to these coprime factors. In this case \(P_{\Delta } = \mathcal{F}_{u}(P,\Delta )\), where

$$\displaystyle{ P = \left [\begin{array}{cc} \left [\begin{array}{@{}c@{}} 0 \\ -\tilde{ M}^{-1} \end{array} \right ]&\left [\begin{array}{@{}c@{}} I \\ -\tilde{ M}^{-1 } \tilde{N} \end{array} \right ] \\ \tilde{M}^{-1} & \tilde{M}^{-1}\tilde{N} \end{array} \right ] }$$

and the robust stability test will be

$$\displaystyle{ \|\mathcal{F}_{l}(P,K)\|_{\infty } = \left \|\left [\begin{array}{@{}c@{}} K \\ - I \end{array} \right ](I - P_{o}K)^{-1}\tilde{M}^{-1}\right \|_{ \infty } <\gamma }$$

This is related to plant perturbations in the gap metric (see Vinnicombe 2001). It is therefore observed that the robust stability test for these useful representations of uncertain plants is given by an \(\mathcal{H}_{\infty }\)-norm test just as in the controller synthesis problem.

Derivation of the \(\mathcal{H}_{\infty }\) -Control Law

In this section we present a solution to the \(\mathcal{H}_{\infty }\)-control problem and give some interpretations of the solution. The approach presented is as in by Doyle et al. (1989); see also Zhou et al. (1996). We will make some simplifying structural assumptions to make the formulae less complex and will not state the required assumptions on rank, stabilizability, and detectability. Let the system in Fig. 1 be described by the equations:

$$\displaystyle\begin{array}{rcl} \dot{x}(t)& =& Ax(t) + B_{1}w(t) + B_{2}u(t){}\end{array}$$
(2)
$$\displaystyle\begin{array}{rcl} z(t)& =& C_{1}x(t) + D_{12}u(t){}\end{array}$$
(3)
$$\displaystyle\begin{array}{rcl} y(t)& =& C_{2}x(t) + D_{21}w(t){}\end{array}$$
(4)

i.e., in Fig. 1

$$\displaystyle{ P = \left [\begin{array}{c|cc} A & B_{1} & B_{2} \\ \hline C_{1} & 0 &D_{12} \\ C_{2} & D_{21} & 0 \end{array} \right ] }$$

where we also assume, with little loss of generality, that \(D_{12}^{{\ast}}D_{12} = I\), \(D_{21}D_{21}^{{\ast}} = I\), \(D_{12}^{{\ast}}C_{1} = 0\) and \(B_{1}D_{21}^{{\ast}} = 0\). Since we wish to have \(\|T_{z\leftarrow w}\|_{\infty } <\gamma\), we need to find u such that

$$\displaystyle{ \|z\|_{2}^{2} -\gamma ^{2}\|w\|_{ 2}^{2} <0\ \ \mbox{ for all }\ w\neq 0 \in \mathcal{L}_{ 2}(0,\infty ). }$$

We could consider w to be an adversary trying to make this expression positive, while u has to ensure that it always remains negative in spite of the malicious intentions of w, as in a noncooperative game. Suppose that there exists a solution, X ∞ , to the Algebraic Riccati Equation (ARE),

$$\displaystyle\begin{array}{rcl} & & A^{{\ast}}X_{ \infty } + X_{\infty }A + C_{1}^{{\ast}}C_{ 1} \\ & & \quad + X_{\infty }(\gamma ^{-2}B_{ 1}B_{1}^{{\ast}}- B_{ 2}B_{2}^{{\ast}})X_{ \infty } = 0{}\end{array}$$
(5)

with X ∞ ≥ 0 and \(A + (\gamma ^{-2}B_{1}B_{1}^{{\ast}}- B_{2}B_{2}^{{\ast}})X_{\infty }\) a stable “A-matrix.” A simple substitution then gives that

$$\displaystyle\begin{array}{rcl} \frac{d} {dt}(x(t)^{{\ast}}X_{ \infty }x(t))& =& -z^{{\ast}}z +\gamma ^{2}w^{{\ast}}w {}\\ & & +v^{{\ast}}v -\gamma ^{2}r^{{\ast}}r {}\\ \end{array}$$

where

$$\displaystyle{ v := u + B_{2}^{{\ast}}X_{ \infty }x,\ \ \ r := w -\gamma ^{-2}B_{ 1}^{{\ast}}X_{ \infty }x. }$$

Now let x(0) = 0 and assuming stability so that x(∞) = 0, then integrating from 0 to ∞ gives

$$\displaystyle{ \|z\|_{2}^{2} -\gamma ^{2}\|w\|_{ 2}^{2} =\| v\|_{ 2}^{2} -\gamma ^{2}\|r\|_{ 2}^{2} }$$
(6)

If the state is available to u, then the control law \(u = -B_{2}^{{\ast}}X_{\infty }x\) gives v = 0 and \(\|z\|_{2}^{2} -\gamma ^{2}\|w\|_{2}^{2} <0\) for all w ≠ 0. It can be shown that (5) has a solution if there exists a controller such that \(\|\mathcal{F}_{l}(P,K)\|_{\infty } <\gamma\). In addition since transposing a system does not change its \(\mathcal{H}_{\infty }\)-norm, the following dual ARE will also have a solution, Y ∞ ≥ 0,

$$\displaystyle\begin{array}{rcl} & & AY _{\infty } + Y _{\infty }A^{{\ast}} + B_{ 1}B_{1}^{{\ast}} \\ & &\quad + Y _{\infty }(\gamma ^{-2}C_{ 1}^{{\ast}}C_{ 1} - C_{2}^{{\ast}}C_{ 2})Y _{\infty } = 0{}\end{array}$$
(7)

To obtain a solution to the output feedback case, note that (6) implies that \(\|z\|_{2}^{2} <\gamma ^{2}\|w\|_{2}^{2}\) if and only if \(\|v\|_{2}^{2} <\gamma ^{2}\|r\|_{2}^{2}\) and \(\bar{v} = \mathcal{F}_{l}(P_{\mathrm{tmp}},K)\bar{r}\) where

$$\displaystyle{ \left [\begin{array}{@{}c@{}} \bar{v}\\ \bar{y} \end{array} \right ] = P_{\mathrm{tmp}}\left [\begin{array}{@{}c@{}} \bar{r}\\ \bar{u} \end{array} \right ], }$$

and

$$\displaystyle{ P_{\mathrm{tmp}} = \left [\begin{array}{c|cc} A +\gamma ^{-2}B_{1}B_{1}^{{\ast}}X_{\infty }& B_{1} & B_{2} \\ \hline B_{2}^{{\ast}}X_{\infty } & 0 & I \\ C_{2} & D_{21} & 0 \end{array} \right ] }$$

The special structure of this problem enables a solution to be derived in much the same way as the dual of the state feedback problem. The corresponding ARE will have a solution \(Y _{\mathrm{tmp}} = (I -\gamma ^{-2}Y _{\infty }X_{\infty })^{-1}Y _{\infty }\geq 0\) if and only if the spectral radius ρ(Y ∞ X ∞ ) < γ2.

The above outline, supported by significant technical detail and assumptions, will therefore demonstrate that there exists a stabilizing controller, K(s), such that the system described by (2–4) satisfies \(\|T_{z\leftarrow w}\|_{\infty } <\gamma\) if and only if there exist stabilizing solutions to the AREs in (5) and (7) such that

$$\displaystyle{ X_{\infty }\geq 0,\ \ Y _{\infty }\geq 0,\ \ \rho (Y _{\infty }X_{\infty }) <\gamma ^{2} }$$
(8)

The state equations for the resulting controller can be written as

$$\displaystyle\begin{array}{rcl} \dot{\hat{x}}& =& A\hat{x} + B_{1}\hat{w}_{\mathrm{worst}} + B_{2}u + Z_{\infty }L_{\infty }(C_{2}\hat{x} - y) {}\\ u& =& F_{\infty }\hat{x},\ \ \hat{w}_{\mathrm{worst}} =\gamma ^{-2}B_{ 1}^{{\ast}}X_{ \infty }\hat{x} {}\\ F_{\infty }& :=& -B_{2}^{{\ast}}X_{ \infty },\ \ L_{\infty } := -Y _{\infty }C_{2}^{{\ast}}, {}\\ Z_{\infty }& :=& (I -\gamma ^{-2}Y _{ \infty }X_{\infty })^{-1} {}\\ \end{array}$$

giving feedback from a state estimator in the presence of an estimate of the worst-case disturbance.

As \(\gamma \rightarrow \infty\) the standard LQG controller is obtained with state feedback of a state estimate obtained from a Kalman filter. In contrast to the LQG problem, the controller depends on the value of γ, and if this is chosen to be too small, then one of the conditions in (8) will be violated. In order to determine the minimum achievable value of γ, a bisection search over γ can be performed checking (8) for each candidate value of γ.

In the limit as \(\gamma \rightarrow \gamma _{\mathrm{opt}}\) (its minimum value), a variety of situations can arise and the formulae given here may become ill-conditioned. Typically achieving γopt is more of an interesting and sometimes challenging mathematical exercise rather than a control system requirement.

This control problem does not have a unique solution, and all solutions can be characterized by an LFT form such as \(K = \mathcal{F}_{l}(M,Q)\) where \(Q \in \mathcal{H}_{\infty }\) with \(\|Q\|_{\infty } <1\), the present solution is sometimes referred to as the “central solution” obtained with Q = 0.

Relations for Other Solution Methods and Problem Formulations

The \(\mathcal{H}_{\infty }\)-control problem has been shown to be related to an extraordinarily wide variety of mathematical techniques and to other problem areas, and investigations of these connections have been most fruitful. Earlier approaches (see Francis 1988) firstly used the characterization of all stabilizing controllers of Youla et al. (see Vidyasagar 1985) which shows that all stable closed-loop systems can be written as

$$\displaystyle{ \mathcal{F}_{l}(P,K) = T_{1} + T_{2}QT_{3},\ \mbox{ where}\ Q \in \mathcal{H}_{\infty } }$$

and then solved the model matching problem \(\inf _{Q\in \mathcal{H}_{\infty }}\|T_{1} + T_{2}QT_{3}\|_{\infty }\). This model matching problem is related to interpolation theory and resulted in a productive interaction with the operator theory. One solution method reduces this problem to J-spectral factorisation problems \(\left (\text{where}\ J = \left [\begin{array}{cc} I & 0\\ 0 & -I \end{array} \right ]\right )\) and generates state-space solutions to these problems (Kimura 1997).

The derivation above clearly demonstrates relations to noncooperative differential games, and this is fully developed in Başar and Bernhard (1995) and Green and Limebeer (1995).

The model matching problem is clearly a convex optimization problem. The solution of linear matrix inequalities can give effective methods for solving certain convex optimization problems (e.g., calculating the \(\mathcal{H}_{\infty }\) norm using the bounded real lemma) and can be exploited in the \(\mathcal{H}_{\infty }\)-control problem. See Boyd and Barratt (1991) for a variety of results on convex optimization and control and Dullerud and Paganini (2000) for this approach in robust control.

As noted above there is a family of solutions to the \(\mathcal{H}_{\infty }\)-control problem. The central solution in fact minimizes the entropy integral given by

$$\displaystyle\begin{array}{rcl} & & I(T_{z\leftarrow w};\gamma ) := -\frac{\gamma ^{2}} {2\pi }\int _{-\infty }^{\infty }\ln \\ & &\quad \left \vert \det (I -\gamma ^{-2}T_{ z\leftarrow w}(j\omega )^{{\ast}}T_{ z\leftarrow w}(j\omega ))\right \vert \ d\omega {}\end{array}$$
(9)

It can be seen that this criterion will penalize the singular values of \(T_{z\leftarrow w}(j\omega )\) from being close to γ for a large range of frequencies.

One of the more surprising connections is with the risk-sensitive stochastic control problem (Whittle 1990) where w is assumed to be Gaussian white noise and it is desired to minimize

$$\displaystyle\begin{array}{rcl} J_{T}(\gamma )& := \frac{\gamma ^{2}} {T}\ln \mathbf{E}\left \{e^{\frac{1} {2} \gamma ^{-2}V _{ T}}\right \}&{}\end{array}$$
(10)
$$\displaystyle\begin{array}{rcl} \mathrm{where}\ \ V _{T}& :=\int _{ -T}^{T}z(t)^{{\ast}}z(t)\ dt&{}\end{array}$$
(11)

The situation with γ2 > 0 corresponds to the risk averse controller since large values of V T are heavily penalized by the exponential function. It can be shown that if \(\|T_{z\leftarrow w}\|_{\infty } <\gamma\), then

$$\displaystyle{ \lim _{T\rightarrow \infty }J_{T}(\gamma ) = I(T_{z\leftarrow w};\gamma ) }$$

and hence the central controller minimizes both the entropy integral and the risk-sensitive cost function. When γ is chosen to be too small, Whittle refers to the controller having a “neurotic breakdown” because the cost will be infinite for all possible control laws! If in (10) we set \(\gamma ^{2} = -\theta ^{-1}\), then the entropy minimizing controller will have θ < 0 and will be risk-averse. The risk neutral controller is when \(\theta \rightarrow 0\), \(\gamma \rightarrow \infty\) and gives the standard LQG case. If θ > 0, then the controller will be risk-seeking, believing that large variance will be in its favor.

Controller Design with \(\mathcal{H}_{\infty }\) Optimization

The above solutions to the \(\mathcal{H}_{\infty }\) mathematical problem do not give guidance on how to set up a problem to give a “good” control system design. The problem formulation typically involves identifying frequency-dependent weighting matrices to characterize the disturbances, w, and the relative importance of the errors, z (see Skogestad and Postlethwaite 1996). The choice of weights should also incorporate system uncertainty to obtain a robust controller.

One approach that combines both closed-loop system gain and system uncertainty is called \(\mathcal{H}_{\infty }\)loop-shaping where the desired closed-loop behavior is determined by the design of the loop-shape using pre- and post-compensators and the system uncertainty is represented in the gap metric (see Vinnicombe 2001). This makes classical criteria such as low frequency tracking error, bandwidth, and high-frequency roll-off all easily incorporated. In this framework the performance and robustness measures are very well matched to each other. Such an approach has been successfully exploited in a number of practical examples (e.g., Hyde (1995) for flight control taken through to successful flight tests). Standard control design software packages now routinely have \(\mathcal{H}_{\infty }\)-control design modules.

Summary and Future Directions

We have outlined the derivation of \(\mathcal{H}_{\infty }\) controllers with straightforward assumptions that nevertheless exhibit most of the features of linear time-invariant systems without such assumptions and for which routine design software is now available. Connections to a surprisingly large range of other problems are also discussed.

Generalizations to more general cases such as time-varying and nonlinear systems, where the norm is interpreted as the induced norm of the system in \(\mathcal{L}_{2}\), can be derived although the computational aspects are no longer routine. For the problems of robust control, there are necessarily continuing efforts to match the mathematical representation of system uncertainty and system performance to the physical system requirements and to have such representations amenable to analysis and computation.

Cross-References