Keywords

1 Introduction

In modern society, computers are used for many different applications, such as nuclear reactors, aircraft, banking systems, and hospital patient monitoring systems [1, 2]. As the demand of the application quality becomes higher and higher, the research on the computer software reliability becomes more and more essential [3, 4]. The software reliability is defined as the probability that the software will operate without a failure under a given environmental condition during a specified period of time. To date, the software reliability model is one of the most important tools in software reliability assessment [5, 6].

There are still some issues that need more discussions. For example, should all failure data or only recent failure data be used in model training? Due to the common knowledge in software testing, early failure behavior of the testing process may have less impact on later failure process. Many researchers suggested that not all available failure data should be used in model training; rather only the last m recorded data should be used, but to our best knowledge, there were not any experimental results to support this. We study this problem by analyzing the trend of AE serials when m changes on four data sets using the Mann–Kendall test method and Sen’s slope estimator and confirmed that early failure behavior of the testing process may have less impact on later failure process.

2 Methods for Software Reliability Prediction

2.1 Support Vector Machine

SVM has gained an increasing attention from its original application in pattern recognition to the extended application in function approximation and regression estimation [7, 8]. Based on the SRM principle, the learning scheme of SVM is focused on minimizing an upper bound of the generalization error that includes the sum of the empirical training error and a regularized confidence interval, which will eventually result in better generalization performance. Moreover, unlike other gradient descent–based learning scheme with the danger of getting trapped into local minima, the regularized risk function of SVM can be minimized by solving a linearly constrained quadratic programing problem, which can always obtain a unique and global optimal solution. Thus, the possibility of being trapped at local minima can be effectively avoided.

The basic idea of SVM for function approximation is mapping the DATA x into a high-dimensional feature space by a nonlinear mapping and then performing a linear regression in this feature space. The SVM model used for function approximation is given by:

$$ t\, = \,f(T;w)\, = \,\sum\limits_{i = 1}^{M} {w_{i} k(T,T_{i} )} \, + \,w_{0} $$
(107.1)

\( k(x,x_{i} ) \) is defined as the kernel function, which is the inner product of two vectors in feature space φ(x) and φ(x i ). By introducing the kernel function, we can deal with the feature spaces of arbitrary dimensionality without computing the mapping relationship φ(x) explicitly. Some commonly used kernel functions are polynomial kernel function and Gaussian kernel function. In this paper, we made the choice to utilize Gaussian data-center basis functions:

$$ K\,\left( {x_{i} ,x_{j} } \right)\, = \,\exp \;\left\{ { - \frac{{\left\| {x_{i} - x_{j} } \right\|^{2} }}{{r^{2} }}} \right\} $$
(107.2)

where \( r > 0 \) is a constant that defines the kernel width, and the value of r plays a very important role in SVM prediction.

Thus, a nonlinear regression in the low-dimensional input space is transferred to a linear regression in a high-dimensional feature space. The coefficients w and b can be estimated by minimizing the following regularized risk function R

$$ \begin{gathered} R\, = \,\frac{1}{2}\left\| w \right\|^{2} \, + \,R_{\text{emp}} [f] \hfill \\ = \frac{1}{2}\left\| w \right\|^{2} \, + \,C\frac{1}{l}\sum\limits_{i = 1}^{l} {\left| {T_{i} - f\left( {t_{i} } \right)} \right|_{\varepsilon } } \hfill \\ \end{gathered} $$
(107.3)

where

$$ \left| {T_{i} - f\left( {t_{i} } \right)} \right|_{\varepsilon } = \left\{ {\begin{array}{*{20}l} 0 \qquad{if\left| {T_{i} - f\left( {t_{i} } \right)} \right| \le \varepsilon ,} \\ {\left| {T_{i} - f\left( {t_{i} } \right)} \right| - \varepsilon } \quad {\text{otherwise}} \\ \end{array} } \right. $$
(107.4)

\( \left\| w \right\|^{2} \) is the weighting vector norm, which is used to constrain the model structure capacity in order to obtain better generalization performance. The second term is the Vapnik’s linear loss function with \( \varepsilon \)-insensitivity zone as a measure for empirical error. The loss is zero if the difference between the predicted and observed value is less than or equal to \( \varepsilon \). For all other cases, the loss is equal to the magnitude of the difference between the predicted value and the radius \( \varepsilon \) of \( \varepsilon \)-insensitivity zone. C is the regularization constant, representing the trade-off between the approximation error and the model structure. \( \varepsilon \) is equivalent to the approximation accuracy requirement for the training data points. Further, two positive slack variables \( \xi \) and \( \xi^{*} \) are introduced.

Thus, minimizing the risk function R in Eq. (107.2) is equivalent to minimizing the objective function:

$$ \hbox{min} \, J\, = \,\frac{1}{2}\left\| w \right\|^{2} \, + \,C\sum\limits_{i = 1}^{l} {\left( {\xi_{i}^{*} \, + \,\xi_{i} } \right)} $$
(107.5)
$$ {\text{s}} . {\text{t}} .\left\{ {\begin{array}{*{20}c} {\left( {\omega ,\phi (T_{i} ) + b - t_{i} \le \varepsilon + \xi_{i} } \right)} \\ {t_{i} - \left( {\omega ,\phi (T_{i} ) - b \le \varepsilon + \xi_{i}^{*} } \right)} \\ {\xi_{i} ,\xi_{i}^{*} \ge 0} \\ \end{array} } \right. $$
(107.6)

2.2 Experiments

2.2.1 Data Sets

The performance of our proposed approach is tested using the same real-time control application and flight dynamic application data sets as cited in Park et al. and Karunanithi et al. We choose a common baseline to compare our results with related work cited in the literature. All six data sets used in the experiments are summarized as follows in Table 107.1:

Table 107.1 Data sets
Full size table

2.2.2 Measures for Evaluating Predictability

In comparing different models, it is necessary to quantify their prediction accuracy, in terms of some meaningful measures [9, 10]. Three distinct approaches that are very common in software reliability research community [1] are reviewed next. The need to predict the behavior at a distant future of the test phase using present failure history is very important [2]. Using the variable-term-predictability approach, a two-component predictability measure is average relative prediction error (AE) as follows:

$$ AE\, = \,\frac{1}{k - m}\sum\limits_{i = m + 1}^{k} {\left| {\frac{{\mathop {t_{i} }\limits^{ \wedge } - t_{i} }}{{t_{i} }}} \right|} $$
(107.7)

where \( \mathop {t_{i} }\limits^{ \wedge } \) denotes the predicted value of failure time, and \( t_{\text{i}} \) denotes the actual value of failure time. AE is a measurement of how well a model predicts throughout the test phase.

3 Trend Test and Estimation

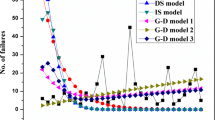
We computed the relative prediction error for DATA 1–4 in the cases m = 5–30, 35, 40, 45, 50, 55, 60 on each models. All the values are computed with \( \sigma^{2} = 1 \) and \( \alpha_{i} \) = 0.5 (i = 1,2,3,…,m), and the value of r is 1, 2.2, 3.5 for DATA-1, 2, 3.7, 5 for DATA-2, 1, 2.2, 4 for DATA-3 and 0.4, 1.2, 3 for DATA-4. We can see from the table that the values of AE change when m varies. For example, the values of AE vary from 0.27 (m = 26) to 1.72 (m = 60) when DATA-1 is used with r = 2.2 and 1.64 (m = 10)–6.32 (m = 60) and when DATA-3 is used with r = 4. Due to the variation as well as the existence of outliers, it is difficult to visually discern any trends from Table 107.1 and the plots of the relative prediction error for each data. Because mere eyeballing does not suffice, we will apply statistical techniques for trend test and trend estimation in this section.

To verify the null hypothesis that a sample \( x_{1} ,\;x_{2} , \ldots x_{n} \) does not exhibit a trend, Mann [3] used a linear function of a test statistic originally developed by Kendall [4] to test whether two sets of rankings are s-independent. The direct application of this test statistic S for our purposes is known as the Mann–Kendall test for trend. In this context, the value of the test statistic is computed by:

$$ S\, = \,\sum\limits_{j = 1}^{n - 1} {\;\sum\limits_{k = j + 1}^{n} {{\text{sgn}}\;\left( {x_{k} - x_{j} } \right)} } \, = \,\sum\limits_{j = 1}^{n - 1} {\;\sum\limits_{k = j + 1}^{n} {\left\{ {\begin{array}{*{20}c} 1 & {x_{k} - x_{j} } & { > 0} \\ 0 & {x_{k} - x_{j} } & { = 0} \\ { - 1} & {x_{k} - x_{j} } & { < 0} \\ \end{array} } \right.} } $$
(107.8)

Of all \( n^{'} \, = \,\left( {\begin{array}{*{20}c} n \\ 2 \\ \end{array} } \right)\, = \,n\left( {n - 1} \right)/2 \) pairs of values \( x_{k} ,\;x_{j} \left( {k < j} \right) \), S counts those pairs for which the earlier observation \( x_{k} \) is smaller than \( x_{j} \) and subtracts the number of pairs for which the latter observation is smaller. When a value of S is close to zero, it suggests that there is no trend in the data, whereas a high absolute value of the test statistic hints at the existence of a trend. For the calculation of S, tied pairs, that is, those pairs for which \( x_{k} = x_{j} \), are not taken into account. However, the existence of such tied pairs does influence the variance of the test statistic. The variance of S is given by:

$$ {\text{Var}}\;(S)\, = \,\frac{1}{18}\left[ {n\;(n - 1)\;(2n + 5)} \right] $$
(107.9)

Under null hypothesis, the distribution of S is always symmetric and the expected value of S is equal to zero. Moreover, for n approaching infinity, the distribution of S converges to the S-normal distribution. Allowing for a continuity correction, the value of the test statistic \( Z_{\text{statistic}} \, = \,\frac{{S - {\text{sgn}}(S)}}{{\sqrt {{\text{Var}}(S)} }} \) can be compared with the quantile of the standard S-normal distribution in order to check whether the null hypothesis of no trend in the data can be rejected.

The values of Z calculated for the series of AE on four data sets are listed in Table 107.1. Both are larger than \( \lambda_{ 0. 9 7 5} = 1.960 \), which is the 97.5 % quantile of the standard S–normal distribution. Consequently, in each case, the null hypothesis shows that the time series with no trend can be rejected at a Type I error level (i.e., a long-term probability of rejecting the null hypothesis when it is true) of 5 %. This means that although we have not been able to visually discover any trends in Table 107.2, trends are present in the data, and these trends are S-significant. Moreover, the positive signs of the Z values show that the four trends are increasing.

Table 107.2 Trend test for data 1–4
Full size table

To determine the estimates for the slopes, we apply a nonparametric procedure developed. This method is not affected by outliers, and it is robust to missing data. Like the calculation of the value of the test statistic S, the approach focuses on all pairs of data points \( x_{l} ,\;x_{k} \;(l\, < \,k) \). For each of these pairs, the slope \( q_{\text{kl}} = (x_{l} - x_{k} )/(l - k) \) is calculated. Sen’s slope estimate is defined as the median of the \( n^{'} = n\;(n - 1)/2 \) slopes obtained.

A two-sided S-confidence interval for the estimated slope can be derived by the procedure described in [4]: After sorting the \( n^{'} \) slopes in increasing order, the lower limit of the S-confidence interval is given by the \( \left( {(n^{'} - c_{\alpha } )/2} \right){\text{th}} \) largest of these slopes, while the upper limit is given by the largest slope, where \( c_{\alpha } = \lambda_{1 - \alpha /2} \sqrt {{\text{Var}}(S)} \).

At last, the slope estimates and their respective 95 % confidence intervals are shown in Table 107.2. As anticipated, after the calculation of the values of the statistic, the estimated slope is positive for both AE series. Moreover, none of the S-confidence intervals contains the value zero, and this corroborates the earlier finding that the trends are S-significant at a Type I error level of 5 %.

With regard to the AE series on all data sets, we would have expected an increasing trend rather than the decreasing one that we detected. A possible explanation for the observed behavior is the fact that recent failure history records the latest characteristics of the testing process; thus, it could contribute to more accurate prediction of near-future failure event.

4 Conclusion

In this paper, we have conducted comparative studies on model performance between SVM-based and ANN-based SRMs. Data collected from real software projects are used in the studies. Then, we have analyzed the trend of AE serials when m changes on four data sets using the Mann–Kendall test method and Sen’s slope estimator and confirmed that early failure behavior of the testing process may have less impact on later failure process.