Steiner Minimal Trees: An Introduction, Parallel Computation, and Future Work

Abstract

Given a set of N cities, construct a connected network which has minimum length. The problem is simple enough, but the catch is that you are allowed to add junctions in your network. Therefore, the problem becomes how many extra junctions should be added and where should they be placed so as to minimize the overall network length. This intriguing optimization problem is known as the Steiner minimal tree (SMT) problem, where the junctions that are added to the network are called Steiner points. This chapter presents a brief overview of the problem, presents an approximation algorithm which performs very well, then reviews the computational algorithms implemented for this problem. The foundation of this chapter is a parallel algorithm for the generation of what Pawel Winter termed T_list and its implementation. This generation of T_list is followed by the extraction of the proper answer. When Winter developed his algorithm, the time for extraction dominated the overall computation time. After Cockayne and Hewgill’s work, the time to generate T_list dominated the overall computation time. The parallel algorithms presented here were implemented in a program called PARSTEINER94, and the results show that the time to generate T_list has now been cut by an order of magnitude. So now the extraction time once again dominates the overall computation time. This chapter then concludes with the characterization of SMTs for certain size grids. Beginning with the known characterization of the SMT for a 2 ×m grid, a grammar with rewrite rules is presented for characterizations of SMTs for 3 ×m, 4 ×m, 5 ×m, 6 ×m, and 7 ×m grids.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Minimizing a network’s length is one of the oldest optimization problems in mathematics, and, consequently, it has been worked on by many of the leading mathematicians in history. In the mid-seventeenth century a simple problem was posed: Find the point P that minimizes the sum of the distances from P to each of three given points in the plane. Solutions to this problem were derived independently by Fermat, Torricelli, and Cavalieri. They all deduced that either P is inside the triangle formed by the given points and that the angles at P formed by the lines joining P to the three points are all 120^∘ or P is one of the three vertices and the angle at P formed by the lines joining P to the other two points is greater than or equal to 120^∘.

In the nineteenth century a mathematician at the University of Berlin, named Jakob Steiner, studied this problem and generalized it to include an arbitrarily large set of points in the plane. This generalization created a star when P was connected to all the given points in the plane and is a geometric approach to the two-dimensional center of mass problem.

In 1934 Jarník and Kössler generalized the network minimization problem even further [41]: Given n points in the plane, find the shortest possible connected network containing these points. This generalized problem, however, did not become popular until the book, What is Mathematics, by Courant and Robbins [16], appeared in 1941. Courant and Robbins linked the name Steiner with this form of the problem proposed by Jarník and Kössler, and it became known as the Steiner minimal tree problem. The general solution to this problem allows multiple points to be added, each of which is called a Steiner point, creating a tree instead of a star.

Much is known about the exact solution to the Steiner minimal tree problem. Those who wish to learn about some of the spin-off problems are invited to read the introductory article by Bern and Graham [5], the excellent survey paper on this problem by Hwang and Richards [37], or the volume in The Annals of Discrete Mathematics devoted completely to Steiner tree problems [38]. Some of the basic pieces of information about the Steiner minimal tree problem that can be gleaned from these articles are (a) the fact that all of the original n points will be of degree 1, 2, or 3, (b) the Steiner points are all of degree 3, (c) any two edges meet at an angle of at least 120^∘ in the Steiner minimal tree, and (d) at most n − 2 Steiner points will be added to the network.

This chapter concentrates on the Steiner minimal tree problem, henceforth referred to as the SMT problem. Several algorithms for calculating Steiner minimal trees are presented, including the first parallel algorithm for doing so. Several implementation issues are discussed, some new results are presented, and several ideas for future work are proposed.

Section 2 reviews the first fundamental algorithm for calculating SMTs. Section 3 presents a proposed heuristic for SMTs. In Section 4 problem decomposition for SMTs is outlined. Section 5 presents Winter’s sequential algorithm which has been the basis for most computerized calculation of SMTs to the present day. Section 6 presents a parallel algorithm for SMTs. Extraction of the correct answer is discussed in Section 7. Computational Results are presented in Section 8 and Future Work and open problems are presented in Section 9.

2 The First Solution

A typical problem-solving approach is to begin with the simple cases and expand to a general solution. As was seen in Section 1, the trivial three point problem had already been solved in the 1600s, so all that remained was the work toward a general solution. As with many interesting problems, this is harder than it appears on the surface.

The method proposed by the mathematicians of the mid-seventeenth century for the three-point problem is illustrated in Fig. 1. This method stated that in order to calculate the Steiner point given points A, B, and C, you first construct an equilateral triangle (ACX) using the longest edge between two of the points (AC) such that the third (B) lies outside the triangle. A circle is circumscribed around the triangle, and a line is constructed from the third point (B) to the far vertex of the triangle (X). The location of the Steiner point (P) is the intersection of this line (BX) with the circle.

Fig. 1

AP + CP = PX

The next logical extension of the problem, going to four points, is attributed to Gauss. His son, who was a railroad engineer, was apparently designing the layout for tracks between four major cities in Germany and was trying to minimize the length of these tracks. It is interesting to note at this point that a general solution to the SMT problem has recently been uncovered in the archives of a school in Germany (Graham, Private Communication).

For the next 30 years after Kössler and Jarník presented the general form of the SMT problem, only heuristics were known to exist. The heuristics were typically based upon the minimum length spanning tree (MST), which is a tree that spans or connects all vertices whose sum of the edge lengths is as small as possible, and tried in various ways to join three vertices with a Steiner point. In 1968 Gilbert and Pollak [26] linked the length of the SMT to the length of an MST. It was already known that the length of an MST is an upper bound for the length of an SMT, but their conjecture stated that the length of an SMT would never be any shorter than $\frac{\sqrt{ 3}} {2}$ times the length of an MST. This conjecture was recently proved [17] and has led to the MST being the starting point for most of the heuristics that have been proposed in the last 20 years including a recent one that achieves some very good results [29].

In 1961 Melzak developed the first known algorithm for calculating an SMT [44]. Melzak’s algorithm was geometric in nature and was based upon some simple extensions to Fig. 1. The insight that Melzak offered was the fact that you can reduce an n point problem to a set of n − 1 point problems. This reduction in size is accomplished by taking every pair of points, A and C in our example; calculating where the two possible points, X ₁ and X ₂, would be that form an equilateral triangle with them; and creating two smaller problems, one where X ₁ replaces A and C and the other where X ₂ replaces A and C. Both Melzak and Cockayne pointed out however that some of these subproblems are invalid. Melzak’s algorithm can then be run on the two smaller problems. This recursion, based upon replacing two points with one point, finally terminates when you reduce the problem from three to two vertices. At this termination the length of the tree will be the length of the line segment connecting the final two points. This is due to the fact that $BP + AP + CP = BP + PX$. This is straightforward to prove using the law of cosines, for when P is on the circle, $\angle APX = \angle CPX = 6{0}^{\circ }$. This allows the calculation of the last Steiner point (P) and allows you to back up the recursive call stack to calculate where each Steiner point in that particular tree is located.

This reduction is important in the calculation of an SMT, but the algorithm still has exponential order, since it requires looking at every possible reduction of a pair of points to a single point. The recurrence relation for an n-point problem is stated quite simply in the following formula:

$$T(n) = 2{\ast}\left (\begin{array}{c} n\\ 2 \end{array} \right ){\ast}T(n-1).$$

This yields what is obviously a non-polynomial time algorithm. In fact Garey, Graham, and Johnson [18] have shown that the Steiner minimal tree problem is NP-Hard (NP-Complete if the distances are rounded up to discrete values).

In 1967, just a few years after Melzak’s paper, Cockayne [11] clarified some of the details from Melzak’s proof. This clarified algorithm proved to be the basis for the first computer program to calculate SMTs. The program was developed by Cockayne and Schiller [15] and could compute an SMT for any placement of up to seven vertices.

3 A Proposed Heuristic

3.1 Background and Motivation

By exploring a structural similarity between stochastic Petri nets (see [45, 49]) and Hopfield neural nets (see [27, 35]), Geist was able to propose and take part in the development of a new computational approach for attacking large, graph-based optimization problems. Successful applications of this mechanism include I/O subsystem performance enhancement through disk cylinder remapping [23, 24], file assignment in a distributed network to reduce disk access conflict [22], and new computer graphics techniques for digital halftoning [21] and color quantization [20]. The mechanism is based on maximum-entropy Gibbs measures, which is described in Reynold’s dissertation [53], and provides a natural equivalence between Hopfield nets and the simulated annealing paradigm. This similarity allows you to select the method that best matches the problem at hand. For the SMT problem, the first author implemented the simulated annealing approach [29].

Simulated annealing [42] is a probabilistic algorithm that has been applied to many optimization problems in which the set of feasible solutions is so large that an exhaustive search for an optimum solution is out of the question. Although simulated annealing does not necessarily provide an optimum solution, it usually provides a good solution in a user-selected amount of time. Hwang and Richards [37] have shown that the optimal placement of s Steiner points to n original vertices yields a feasible solution space of the size

$${2}^{-n}\left (\begin{array}{c} n\\ s + 2 \end{array} \right )\frac{(n - s - 2)!} {s!}$$

provided that none of the original points have degree 3 in the SMT. If the degree restriction is removed, they showed that the number is even larger. The SMT problem is therefore a good candidate for this approach.

3.2 Adding One Junction

Georgakopoulos and Papadimitriou [25] have provided an $\mathcal{O}({n}^{2})$ solution to the 1-Steiner problem, wherein exactly one Steiner point is added to the original set of points. Since at most n − 2 Steiner points are needed in an SMT solution, repeated application of the algorithm offers a “greedy” $\mathcal{O}({n}^{3})$ approach. Using their method, the first Steiner point is selected by partitioning the plane into oriented Dirichlet cells, which they describe in detail. Since these cells do not need to be discarded and recalculated for each addition, subsequent additions can be accomplished in linear time. Deletion of a candidate Steiner point requires regeneration of the MST, which Shamos showed can be accomplished in $\mathcal{O}(n\ \log \ n)$ time if the points are in the plane [50], followed by the cost for a first addition ($\mathcal{O}({n}^{2})$). This approach can be regarded as a natural starting point for simulated annealing by adding and deleting different Steiner points.

3.3 The Heuristic

The Georgakopoulos and Papadimitriou 1-Steiner algorithm and the Shamos MST algorithm are both difficult to implement. As a result, Harris chose to investigate the potential effectiveness of this annealing algorithm using a more direct, but slightly more expensive $\mathcal{O}({n}^{3})$ approach. As previously noted, all Steiner points have degree 3 with edges meeting in angles of 120^∘. He considered all $\left({n}\atop{3}\right)$ triples where the largest angle is less than 120^∘, computed the Steiner point for each (a simple geometric construction), selected that Steiner point giving greatest reduction, or least increase in the length of the modified tree (increases are allowed since the annealing algorithm may go uphill), and updated the MST accordingly. Again, only the first addition requires this (now $\mathcal{O}({n}^{3})$) step. He used the straightforward $\mathcal{O}({n}^{2})$ Prim’s algorithm to generate the MST initially and after each deletion of a Steiner point.

The annealing algorithm can be described as a nondeterministic walk on a surface. The points on the surface correspond to the lengths of all feasible solutions, where two solutions are adjacent if they can be reached through the addition or deletion of one Steiner point. The probability of going uphill on this surface is higher when the temperature is higher but decreases as the temperature cools. The rate of this cooling typically will determine how good your solution will be. The major portion of this algorithm is presented in Fig. 2. This nondeterministic walk, starting with the MST, has led to some very exciting results.

Fig. 2

Simulated annealing algorithm

3.4 Results

Before discussion of large problems, a simple introduction into the results from a simple six-point problem is in order. The annealing algorithm is given the coordinates for six points: (0,0), (0,1), (2,0), (2,1), (4,0), and (4,1). The first step is to calculate the MST, which has a length of 7, as shown in Fig. 3. The output of the annealing algorithm for this simple problem is shown in Fig. 4. In this case the annealing algorithm calculates the exact SMT solution which has a length of 6. 616994.

Fig. 3

Spanning tree for 6-point problem

Fig. 4

6-point solution

Harris proposed as a measure of accuracy the percentage of the difference between the length of the MST and the exact SMT solution that the annealing algorithm achieves. This is a new measure which has not been discussed (or used) because exact solutions have not been calculated for anything but the most simple layouts of points. For the six-point problem discussed above, this percentage is 100. 0 % (the exact solution is obtained).

After communicating with Cockayne, data sets were obtained for exact solutions to randomly generated 100-point problems that were developed for [14]. This allows us to use the measure of accuracy previously described. Results for some of these data sets provided by Cockayne are shown in Table 1.

Table 1 Results from 100-point problems

An interesting aspect of the annealing algorithm that cannot be shown in the table is the comparison of execution times with Cockayne’s program. Whereas Cockayne mentioned that his results had an execution cutoff of 12 h, these results were obtained in less than 1 h. The graphical output for the first line of the table, which reaches over 96 % of the optimal value, appears as follows: The data points and the MST are shown in Fig. 5, the simulated annealing result is in Fig. 6, and the exact SMT solution is in Fig. 7. The solution presented here is obtained in less than $\frac{1} {10}$ of the time with less than 4 % of the possible range not covered. This indicates that one could hope to extend our annealing algorithm to much larger problems, perhaps as large as 1, 000 points. If you were to extend this approach to larger problems, then you would definitely need to implement the Georgakopoulos–Papadimitriou 1-Steiner algorithm and the Shamos MST algorithm.

Fig. 5

Spanning tree

Fig. 6

Simulated annealing solution

Fig. 7

Exact solution

4 Problem Decomposition

After the early work by Melzak [44], many people began to work on the Steiner minimal tree problem. The first major effort was to find some kind of geometric bound for the problem. In 1968 Gilbert and Pollak [26] showed that the SMT for a set of points, $\mathcal{S}$, must lie within the convex hull of $\mathcal{S}$. This bound has since served as the starting point of every bounds enhancement for SMTs.

As a brief review, the convex hull is defined as follows: Given a set of points $\mathcal{S}$ in the plane, the convex hull is the convex polygon of the smallest area containing all the points of $\mathcal{S}$. A polygon is defined to be convex if a line segment connecting any two points inside the polygon lies entirely within the polygon. An example of the convex hull for a set of 100 randomly generated points is shown in Fig. 8.

Fig. 8

The convex hull for a random set of points

Shamos in his PhD thesis [54] proposed a divide and conquer algorithm which has served as the basis for many parallel algorithms calculating the convex hull. One of the first such approaches appeared in the PhD thesis by Chow [8]. This approach was refined and made to run in optimal $\mathcal{O}(\log \ n)$ time by Aggarwal et al. [1], and Attalah and Goodrich [2].

The next major work on the SMT problem was in the area of problem decomposition. As with any non-polynomial algorithm, the most important theorems are those that say “If property $\mathcal{P}$ exists, then the problem may be split into the following sub-problems.” For the Steiner minimal tree problem, property $\mathcal{P}$ will probably be geometric in nature. Unfortunately, decomposition theorems have been few and far between for the SMT problem. In fact, at this writing there have been only three such theorems.

4.1 The Double Wedge Theorem

The first decomposition theorem, known as the Double Wedge Theorem, was proposed by Gilbert and Pollak [26]. This is illustrated in Fig. 9 and can be summarized quite simply as follows: If two lines intersect at point $\mathcal{X}$ and meet at 120^∘, they split the plane into two 120^∘ wedges and two 60^∘ wedges. If R ₁ and R ₂ denote the two 60^∘ wedges and all the points of $\mathcal{S}$ are contained in $R_{1}\bigcup R_{2}$, then the problem can be decomposed. There are two cases to be considered. In case 1 $\mathcal{X}$ is not a point in $\mathcal{S}$; therefore, the Steiner minimal tree for $\mathcal{S}$ consists of the SMT for R ₁, the SMT for R ₂, and the shortest edge connecting the two trees. In case 2 $\mathcal{X}$ is a point in $\mathcal{S}$; therefore, the Steiner minimal tree for $\mathcal{S}$ is the SMT for R ₁ and the SMT for R ₂. Since $\mathcal{X}$ is in both R ₁ and R ₂, the two trees are connected.

Fig. 9

An illustration of the Double Wedge

4.2 The Steiner Hull

The next decomposition theorem is due to Cockayne [12] and is based upon what he termed the Steiner hull. The Steiner hull is defined as follows: Let P ₁ be the convex hull. P _{i + 1} is constructed from P _i by finding an edge (p, r) of P _i that has a vertex (q) near it such that ∠pqr ≥ 120^∘, and there is not a vertex inside the triangle pqr. The final polygon, P _i , that can be created in such a way is called the Steiner hull. The algorithm for this construction is shown in Fig. 10. The Steiner hull for the 100 points shown in Fig. 8 is given in Fig. 11.

Fig. 10

The Steiner hull algorithm

Fig. 11

The Steiner hull for a random set of 100 points

After defining the Steiner hull, Cockayne showed that the SMT for $\mathcal{S}$ must lie within the Steiner hull of $\mathcal{S}$. This presents us with the following decomposition: The Steiner hull can be thought of as an ordered sequence of points, $\{p_{1},p_{2},\ldots,p_{n}\}$, where the hull is defined by the sequence of line segments, $\{p_{1}p_{2},p_{2}p_{3},\ldots,p_{n}p_{1}\}$. If there exists a point p _i that occurs twice in the Steiner hull, then the problem can be decomposed at point p _i . If a Steiner hull contains such a point, then the Steiner hull is referred to as degenerate. This decomposition is accomplished by showing that the Steiner hull splits $\mathcal{S}$ into two contained subsets, R ₁ and R ₂, where R ₁ is the set of points contained in the Steiner hull from the first time p _i appears until the last time p _i appears, and R ₂ is the set of points contained in the Steiner hull from the last time p _i appears until the first time p _i appears. With this decomposition it can be shown that $\mathcal{S} = R_{1}\bigcup R_{2}$, and the SMT for S is the union of the SMT for R ₁ and the SMT for R ₂. This decomposition is illustrated in Fig. 12. Cockayne also proved that the Steiner hull decomposition includes every decomposition possible with the Double Wedge Theorem.

Fig. 12

An illustration of the Steiner hull decomposition

In their work on 100-point problems, Cockayne and Hewgill [14] mention that approximately 15 % of the randomly generated 100-point problems have degenerate Steiner Hull’s. The Steiner hull shown in Fig. 11 is not degenerate, while that in Fig. 12 is.

4.3 The Steiner Hull Extension

The final decomposition belongs to Hwang et al. [39]. They proposed an extension to the Steiner hull as defined by Cockayne. Their extension is as follows:

If there exist four points a, b, c, and d on a Steiner hull such that:

• 1. a, b, c, and d form a convex quadrilateral

• 2. There does not exist a point from $\mathcal{S}$ in the quadrilateral (a, b, c, d)

• 3. ∠a ≥ 120^∘ and ∠b ≥ 120^∘

• 4. The two diagonals (ac) and (bd) meet at O, and $\angle bOa \geq \angle a + \angle b - 15{0}^{\circ }$, then the SMT for $\mathcal{S}$ is the union of the SMTs for R ₁ and R ₂ and the edge ab where R ₁ is the set of points contained in the Steiner hull from c to b with the edge bc and R ₂ is the set of points contained in the Steiner polygon from a to d with the edge ad. This decomposition is illustrated in Fig. 13.

Fig. 13

An illustration of the Steiner hull extension

These three decomposition theorems were combined into a parallel algorithm for decomposition presented in [28].

5 Winter’s Sequential Algorithm

5.1 Overview and Significance

The development of the first working implementation of Melzak’s algorithm sparked a move into the computerized arena for the calculation of SMTs. As we saw in Section 2, Cockayne and Schiller [15] had implemented Melzak’s algorithm and could calculate the SMT for all arrangements of 7 points. This was followed almost immediately by Boyce and Seery’s program which they called STEINER72 [6]. Their work done at Bell Labs could calculate the SMT for all 10-point problems. They continued to work on the problem and in personal communication with Cockayne said they could solve 12-point problems with STEINER73. Yet even with quite a few people working on the problem, the number of points that any program could handle was still very small.

As mentioned toward the end of Section 2, Melzak’s algorithm yields invalid answers and invalid tree structures for quite a few combinations of points. It was not until 1981 that anyone was able to characterize a few of these invalid tree structures. These characterizations were accomplished by Pawel Winter and were based upon several geometric constructions which enable one to eliminate many of the possible combinations previously generated. He implemented these improvements in a program called GeoSteiner [60]. In his work he was able to calculate in under 30 s SMTs for problems having up to 15 vertices and stated that “with further improvements, it is reasonable to assert that point sets of up to 30 V-points could be solved in less than an hour [60].”

5.2 Winter’s Algorithm

Winter’s breakthrough was based upon two things: the use of extended binary trees and what he termed pushing. Winter proposed an extended binary tree as a means of constructing trees only once and easily identifying a full Steiner tree (FST: trees with n vertices and n − 2 Steiner points) on the same set of vertices readily.

Pushing came from the geometric nature of the problem and is illustrated in Fig. 14. It was previously known that the Steiner point for a pair of points, a and b, would lie on the circle that circumscribed that pair and their equilateral third point. Winter set out to limit this region even further. This limitation was accomplished by placing a pair of points, a′ and b′, on the circle at a and b, respectively, and attempting to push them closer and closer together. In his work Winter proposed and proved various geometric properties that would allow you to push a′ toward b and b′ toward a. If the two points ever crossed, then it was impossible for the current branch of the sample space tree to contain a valid answer.

Fig. 14

An illustration of Winter’s pushing

Unfortunately, the description of Winter’s algorithm is not as clear as one would hope, since the presence of goto statements rapidly makes his program difficult to understand and almost impossible to modify. Winter’s goal is to build a list of FSTs which are candidates for inclusion in the final answer. This list, called T_list, is primed with the edges of the MST, thereby guaranteeing that the length of the SMT does not exceed the length of the MST.

The rest of the algorithm sets about to expand what Winter termed as Q_list, which is a list of partial trees that the algorithm attempts to combine until no combinations are possible. Q_list is primed with the original input points. The legality of a combination is determined in the construct procedure, which uses pushing to eliminate cases. While this combination proceeds, the algorithm also attempts to take newly created members of Q_list and create valid FSTs out of them. These FSTs are then placed onto T_list.

This algorithm was a turning point in the calculation of SMTs. It sparked renewed interest into the calculation of SMTs in general. This renewed interest has produced new algorithms such as the negative edge algorithm [57] and the luminary algorithm [36]. Winter’s algorithm has also served as the foundation for most computerized computation for calculating SMTs and is the foundation for the parallel algorithm we present in Section 6.

5.3 Algorithm Enhancements

In 1996, Winter and Zachariasen presented GEOSTEINER96 [61, 62] an enhancement to their exact algorithm that strongly improved the pruning and concatenation techniques of the GEOSTEINER algorithm just presented. This new algorithm modified the pruning tests to exploit the geometry of the problem (wedge property, bottleneck Steiner distances) to yield effective and/or faster pruning of nonoptimal full Steiner trees (FSTs). Furthermore, efficient concatenation of FSTs was achieved by new and strong compatibility tests that utilize pairwise and subset compatibility along with very powerful preprocessing of surviving FSTs. GEOSTEINER96 has been implemented in C++ on an HP9000 workstation and solves randomly generated problem instances with 100 terminals in less than 8 min and up to 140 terminals within an hour. The hardest 100-terminal problem was solved in less than 29 min. Previously unsolved public library instances (OR-Library [3, 4]) have been solved by GEOSTEINER96 within 14 min. The authors point out that the concatenation of FSTs still remains the bottleneck of both GEOSTEINER96 and GEOSTEINER algorithms. However, the authors show that FSTs are generated 25 times faster by GEOSTEINER96 than by EDSTEINER89.

In their follow-up work [58], Winter and Zachariasen presented performance statistics for the exact SMT problem solved using the Euclidean FST generator from Winter and Zachariasen’s algorithm [61, 62] and the FST concatenator of Warme’s algorithm [59]. Optimal solutions have been obtained by this approach for problem instances of up to 2,000 terminals. Extensive computational experiences for randomly generated instances [100–500 terminals], public library instances (OR-Library [100–1,000 terminals] [3, 4], TSPLIB [198–7,397 terminals] [34]), and difficult instances with special structure have been shared in this work. The computational study has been conducted on an HP9000 workstation; the FST generator was implemented in C++ and the FST concatenator was implemented in C using CPLEX. Results indicate that (1) Warme’s FST concatenation solved by branch-and-cut is orders of magnitude faster than backtrack search or dynamic programming based FST concatenation algorithms and (2) the Euclidean FST generator is more effective on uniformly randomly generated problem instances than for structured real-world instances.

6 A Parallel Algorithm

6.1 An Introduction to Parallelism

Parallel computation is allowing us to look at problems that have previously been impossible to calculate, as well as allowing us to calculate faster than ever before problems we have looked at for a long time. It is with this in mind that we begin to look at a parallel algorithm for the Steiner minimal tree problem.

There have been volumes written on parallel computation and parallel algorithms; therefore, we will not rehash the material that has already been so excellently covered by many others more knowledgeable on the topic, but will refer the interested readers to various books currently available. For a thorough description of parallel algorithms, and the PRAM model, the reader is referred to the book by Joseph JáJá [40], and for a more practical approach to implementation on a parallel machine, the reader is referred to the book by Vipin Kumar et al. [43], the book by Michael Quinn [51], or the book by Justin Smith [55].

6.2 Overview and Proper Structure

When attempting to construct a parallel algorithm for a problem, the sequential code for that problem is often the starting point. In examining sequential code, major levels of parallelism may become self-evident. Therefore, for this problem the first thing to do is to look at Winter’s algorithm and convert it into structured code without gotos. The initialization (step 1) does not change, and the translation of steps 2–7 appears in Fig. 15.

Fig. 15

The main loop properly structured

Notice that the code in Fig. 15 lies within a for loop. In a first attempt to parallelize anything, you typically look at loops that can be split across multiple processors. Unfortunately, upon further inspection, the loop continues while p<q and, in the large if statement in the body of the loop, is the statement q++ (line 30). This means that the number of iterations is data dependent and is not fixed at the outset. This loop cannot be easily parallelized.

Since the sequential version of the code does not lend itself to easy parallelization, the next thing to do is to back up and develop an understanding of how the algorithm works. The first thing that is obvious from the code is that you select a left subtree and then try to mate it with possible right subtrees. Upon further examination we come to the conclusion that a left tree will mate with all trees that are shorter than it and all trees of the same height that appear after it on Q_list, but it will never mate with any tree that is taller.

6.3 First Approach

The description of this parallel algorithm is in a master–slave perspective. This perspective was taken due to the structure of most parallel architectures at the time of its development, as well as the fact that all nodes on the Q_list need a sequencing number assigned to them. The master will therefore be responsible for numbering the nodes and maintaining the main Q_list and T_list.

The description from the slave’s perspective is quite simple. A process is spawned off for each member of Q_list that is a proper left subtree (Winter’s algorithm allows members of Q_list that are not proper left subtrees). Each new process is then given all the current nodes on Q_list. With this information the slave then can determine with which nodes its left subtree could mate. This mating creates new nodes that are sent back to the master, assigned a number, and added to the master’s Q_list. The slave also attempts to create an FST out of the new Q_list member, and if it is successful, this FST is sent to the master to be added to the T_list. When a process runs out of Q_list nodes to check, it sends a request for more nodes to the master.

The master also has a simple job description. It has to start a process for each initial member of the Q_list, send them all the current members of the Q_list, and wait for their messages.

This structure worked quite well for smaller problems (up to about 15 points), but for larger problems it reached a grinding halt quite rapidly. This was due to various reasons such as the fact that for each slave started the entire Q_list had to be sent. This excessive message passing quickly bogged down the network. Secondly, in their work on 100-point problems, Cockayne and Hewgill [14] made the comment that T_list has an average length of 220, but made no comment about the size of Q_list, which is the number of slaves that would be started. From our work on 100 point problems this number easily exceeds 1, 000 which means that over 1, 000 processes are starting, each being sent the current Q_list. From these few problems, it is quite easy to see that some major changes needed to be made in order to facilitate the calculation of SMTs for large problems.

6.4 Current Approach

The idea for a modification to this approach came from a paper by Quinn and Deo [52], on parallel algorithms for Branch-and-Bound problems. Their idea was to let the master have a list of work that needs to be done. Each slave is assigned to a processor. Each slave who requests work, is given some, and during its processing creates more work to be done. This new work is placed in the master’s work list, which is sorted in some fashion. When a slave runs out of work to do, it requests more from the master. They noted that this leaves some processors idle at times (particularly when the problem was starting and stopping), but this approach provides the best utilization if all branches are independent.

This description almost perfectly matches the problem at hand. First, we will probably have a fixed number of processors which can be determined at runtime. Second, we have a list of work that needs to be done. The hard part is implementing a sorted work list in order to obtain a better utilization. This was implemented in what we term the Proc_list, which is a list of the processes that either are currently running or have not yet started. This list is primed with the information about the initial members of Q_list, and for every new node put on the Q_list, a node which contains information about the Q_list node is placed on the Proc_list in a sorted order.

The results for this approach are quite exciting, and the timings are discussed in Section 8.

7 Extraction of the Correct Answer

7.1 Introduction and Overview

Once the T_list discussed in Sect. 5 is formed, the next step is to extract the proper answer from it. Winter described this in step 7 of his algorithm. His description stated that unions of FSTs saved in T_list were to be formed subject to constraints described in his paper. The shortest union is the SMT for the original points.

The constraints he described were quite obvious considering the definition of an SMT. First, the answer had to cover all the original points. Second, the union of FSTs could not contain a cycle. Third, the answer is bounded in length by the length of the MST.

This led Winter to implement a simple exhaustive search algorithm over the FSTs in T_list. This approach yields a sample space of size $\mathcal{O}({2}^{m})$ (where m is the number of trees in T_list) that has to be searched. This exponentiality is born out in his work where he stated that for problems with more than 15 points “the computation time needed to form the union of FSTs dominates the computation time needed for the construction of the FSTs [60].” An example of the input the last step of Winter’s algorithm receives (T_list) is given in Fig. 16. The answer it extracts (the SMT) is shown in Fig. 17.

Fig. 16

T_list for a random set of points

Fig. 17

SMT extracted from T_list for a random set of points

7.2 Incompatibility Matrix

Once Cockayne published the clarification of Melzak’s proof in 1967 [11] and Gilbert and Pollak published their paper giving an upper bound the SMT length in 1968 [26], many people were attracted to this problem. From this time until Winter’s work was published in 1985 [60], quite a few papers were published dealing with various aspects of the SMT problem, but the attempt to computerize the solution of the SMT problem bogged down around 12 vertices. It wasn’t until Winter’s algorithm was published that the research community received the spark it needed to work on computerized computation of the SMT problem with renewed vigor. With the insight Winter provided into the problem, an attempt to computerize the solution of the SMT problem began anew.

Enhancement of this algorithm was first attempted by Cockayne and Hewgill at the University of Victoria. For this implementation Cockayne and Hewgill spent most of their work on the back end of the problem, or the extraction from T_list, and used Winter’s algorithm to generate T_list. This work on the extraction focused on what they termed an incompatibility matrix. This matrix had one row and one column for each member of T_list. The entries in this matrix were flags corresponding to one of three possibilities: compatible, incompatible, or don’t know. The rationale behind the construction of this matrix is the fact that it is faster to look up the value in a matrix than it is to check for the creation of cycles and improper angles during the union of FSTs.

The first value calculations for this matrix were straightforward. If two trees do not have any points in common, then we don’t know if they are incompatible or not. If they have two or more points in common, then they form a cycle and are incompatible. If they have only one point in common and the angle at the intersection point is less than 120^∘, then they are also incompatible. In all other cases they are compatible.

This simple enhancement to the extraction process enabled Cockayne and Hewgill to solve all randomly generated problems of size up to 17 vertices in a little over 3 min [13].

7.3 Decomposition

The next focus of Cockayne and Hewgill’s work was in the area of the decomposition of the problem. As was discussed earlier in Sect. 4, the best theorems for any problem, especially non-polynomial problems, are those of the form “If property $\mathcal{P}$ exists then the problem can be decomposed.” Since the formation of unions of FSTs is exponential in nature, any theorem of this type is important.

Cockayne and Hewgill’s theorem states: “Let A ₁ and A ₂ be subsets of A satisfying (a) $A_{1}\bigcup A_{2} = A$ (b) $\vert A_{1}\bigcap A_{2}\vert = 1$ and (c) the leaf set of each FST in T_list is entirely contained in A ₁ or A ₂. Then any SMT on A is the union of separate SMTs on A ₁ and A ₂ [13].” This means that if you break T_list into biconnected components, the SMT will be the union of the SMTs on those components.

Their next decomposition theorem allowed further improvements in the calculation of SMTs. This theorem stated that if you had a component of T_list left from the previous theorem and if the T_list members of that component form a cycle, then it might be possible to break that cycle and apply the previous algorithm again. The cycle could be broken if there existed a vertex v whose removal would change that component from one biconnected component to more than one.

With these two decomposition theorems, Cockayne and Hewgill were able to calculate the SMT for 79 of 100 randomly generated 30-point problems. The remaining 21 would not decompose into blocks of size 17 or smaller and thus would have taken too much computation time [13]. This calculation was implemented in the program they called EDSTEINER86.

7.4 Forest Management

Cockayne and Hewgill’s next work focused on improvements to the incompatibility matrix previously described and was implemented in a program called EDSTEINER89. Their goal was to reduce the number of don’t know’s in the matrix and possibly remove some FSTs from T_list altogether.

They proposed two refinements for calculating the entry into the incompatibility matrix and one Tree Deletion Theorem. The Tree Deletion Theorem stated that if there exists an FST in T_list that is incompatible with all FSTs containing a certain point a, then the original FST can be deleted since at least one FST containing a will be in the SMT.

This simple change allowed Cockayne and Hewgill to calculate the SMT for 77 of 100 randomly generated 100-point problems [14]. The other 23 problems could not be calculated in less than 12 h and were therefore terminated. For those that did complete, the computation time to generate T_list had become the dominate factor in the overall computation time.

So the pendulum had swung back from the extraction of the correct answer from T_list to the generation of T_list dominating the computation time. In Sect. 8 we will look at the results of the parallel algorithm presented in Sect. 9 to see if the pendulum can be pushed back the other way one more time.

8 Computational Results

8.1 Previous Computation Times

Before presenting the results for the parallel algorithm presented in Sect. 6, it is worthwhile to review the computation times that have preceded this algorithm in the literature. The first algorithm for calculating FSTs was discussed in a paper by Cockayne [12] where he mentioned that preliminary results indicated his code could solve any problem up to 30 points that could be decomposed with the Steiner hull into regions of 6 points or less.

As we saw in Sect. 2, the next computational results were presented by Cockayne and Schiller [15]. Their program, called STEINER, was written in FORTRAN on an IBM 360/50 at the University of Victoria. STEINER could calculate the SMT for any 7-point problem in less than 5 min of CPU time. When the problem size was increased to 8, it could solve them if 7 of the vertices were on the Steiner hull. When this condition held it could calculate the SMT in under 10 min, but if this condition did not hold it would take an unreasonable amount of time.

Cockayne called STEINER a prototype for calculating SMTs and allowed Boyce and Serry of Bell Labs to obtain a copy of his code to improve the work. They improved the code, renamed it STEINER72, and were able to calculate the FST for all 9-point problems and most 10-point problems in a reasonable amount of time [6]. Boyce and Serry continued their work and developed another version of the code that they thought could solve problems of size up to 12 points, but no computation times were given.

The breakthrough we saw in Sect. 5 was by Pawel Winter. His program called GEOSTEINER [60] was written in SIMULA 67 on a UNIVAC-1100. GEOSTEINER could calculate SMTs for all randomly generated sets with 15 points in under 30 s. This improvement was put into focus when he mentioned that all previous implementations took more than an hour for nondegenerate problems of size 10 or more. In his work, Winter tried randomly generated 20-point problems but did not give results since some of them did not finish in his CPU time limit of 30 s. The only comment he made for problems bigger than size 15 was that the extraction discussed in Sect. 7 was dominating the overall computation time.

The next major program, EDSTEINER86, was developed in FORTRAN on an IBM 4381 by Cockayne and Hewgill [13]. This implementation was based upon Winter’s results, but had enhancements in the extraction process. EDSTEINER86 was able to calculate the FST for 79 out of 100 randomly generated 32-point problems. For these problems the CPU time for T_list varied from 1 to 5 min, while for the 79 problems that finished the extraction time never exceeded 70 s.

Cockayne and Hewgill subsequently improved their SMT program and renamed it EDSTEINER89 [14]. This improvement was completely focused on the extraction process. EDSTEINER89 was still written in FORTRAN, but was run on a SUN 3/60 workstation. They randomly generated 200 32-point problems to solve and found that the generation of T_list dominated the computation time for problems of this size. The average time for T_list generation was 438 s, while the average time for forest management and extraction averaged only 43 s. They then focused on 100-point problems and set a CPU limit of 12 h. The average CPU time to generate T_list was 209 min for these problems, but only 77 finished the extraction in the CPU time limit. These programs and their results are summarized in Table 2.

Table 2 SMT programs, authors, and results

8.2 The Implementation

8.2.1 The Significance of the Implementation

The parallel algorithm we presented has been implemented in a program called PARSTEINER94 [28, 31]. This implementation is only the second SMT program since Winter’s GEOSTEINER in 1981 and is the first parallel code. The major reason that the number of SMT programs is so small is due to the fact that any implementation is necessarily complex.

PARSTEINER94 currently has over 13,000 lines of C code. While there is a bit of code dealing with the parallel implementation, certain sections of Winter’s algorithm have a great deal of code buried beneath the simplest statements. For example, line 13 of Fig. 15 is the following:

        if(Construct(p_star,r_star,&(E(q)))){.

To implement the function Construct() over 4, 000 lines of code were necessary, and this does not include the geometry library with functions such as equilateral_third_point(), center_of_equilateral_triangle(),line_circle_intersect(), and a host more.

Another important aspect of this implementation is the fact that there can now be comparisons made between the two current SMT programs. This would allow verification checks to be made between EDSTEINER89 and PARSTEINER94. This verification is important since with any complex program it is quite probable that there are a few errors hiding in the code. This implementation would also allow other SMT problems, such as those we will discuss in Sect. 9, to be explored independently, thereby broadening the knowledge base for SMTs even faster.

8.2.2 The Platform

In the design and implementation of parallel algorithms, you are faced with many decisions. One such decision is what will your target architecture be? There are times when this decision is quite easy due to the machines at hand or the size of the problem. In our case we decided not to target a specific machine, but an architectural platform called PVM [19].

PVM, which stands for Parallel Virtual Machine, is a software package available from Oak Ridge National Laboratory. This package allows a collection of parallel or serial machines to appear as a large distributed memory computational machine (MIMD model). This is implemented via two major pieces of software, a library of PVM interface routines, and a PVM demon that runs on every machine that you wish to use.

The library interface comes in two languages, C and ORTRAN. The functions in this library are the same no matter which architectural platform you are running on. This library has functions to spawn off (start) many copies of a particular program on the parallel machine, as well as functions to allow message passing to transfer data from one process to another. Application programs must be linked with this library to use PVM.

The demon process, called pvmd in the user’s guide, can be considered the back end of PVM. As with any back end, such as the back end of a compiler, when it is ported to a new machine, the front end can interface to it without change. The back end of PVM has been ported to a variety of machines, such as a few versions of Crays, various Unix machines such as Sun workstations, HP machines, Data General workstations, and DEC Alpha machines. It has also been ported to a variety of true parallel machines such as the iPSC/2, iPSC/860, CM2, CM5, BBN Butterfly, and the Intel Paragon.

With this information it is easy to see why PVM was picked as the target platform. Once a piece of code is implemented under PVM, it can be recompiled on the goal machine, linked with the PVM interface library on that machine, and run without modification. In our case we designed PARSTEINER94 on a network of SUN workstations, but, as just discussed, moving to a large parallel machine should be trivial.

8.2.3 Errors Encountered

When attempting to implement any large program from another person’s description, you often reach a point where you don’t understand something. At first you always question yourself, but as you gain an understanding of the problem you learn that there are times when the description you were given is wrong. Such was the case with the SMT problem. Therefore, to help some of those that may come along and attempt to implement this problem after us, we recommend that you look at the list of errors we found while implementing Winter’s algorithm  [28].

8.3 Random Problems

8.3.1 Hundred-Point Random Problems

From the literature it is obvious that the current standard for calculating SMTs has been established by Cockayne and Hewgill. Their work on SMTs has pushed the boundary of computation out from the 15-point problems of Winter to being able to calculate SMTs for a large percentage of 100-point problems.

Cockayne and Hewgill, in their investigation of the effectiveness of EDSTEINER89, randomly generated 100 problems with 100 points inside the unit square. They set up a CPU limit of 12 h, and 77 of 100 problems finished within that limit. They described the average execution times as follows: T_list construction averaged 209 min, forest management averaged 27 min, and extraction averaged 10.8 min.

While preparing the code for this project, Cockayne and Hewgill were kind enough to supply us with 40 of the problems generated for [14] along with their execution times. These data sets were given as input to the parallel code PARSTEINER94, and the calculation was timed. The wall clock time necessary to generate T_list for the two programs appears in Table 3. For all 40 cases, the average time to generate T_list was less than 20 min. This is exciting because we have been able to generate T_list properly while cutting an order of magnitude off the time.

Table 3 Comparison of T_list times

These results are quite promising for various reasons. First, the parallel implementation presented in this work is quite scalable and therefore could be run with many more processors, thereby enhancing the speedup provided. Second, with the PVM platform used, we can in the future port this work to a real parallel MIMD machine, which will have much less communication overhead, or to a shared memory machine, where the communication could all but be eliminated, and expect the speedup to improve much more.

It is also worth noting that proper implementation of the cycle breaking which Cockayne and Hewgill presented in [13] is important if extraction of the proper answer is to be accomplished. In their work, Cockayne and Hewgill mentioned that 58 % of the problems they generated were solvable without the cycle breaking being implemented, which is approximately what we have found with the data sets they provided. An example of such a T_list that would need cycles broken (possibly multiple times) is provided in Fig. 18.

Fig. 18

T_list with more than 1 cycle

8.3.2 Larger Random Problems

Once the 100-point problems supplied by Cockayne and Hewgill had been successfully completed, the next step was to try a few larger problems. This was done with the hope of gaining an insight into the changes that would be brought about from the addition of more data points.

For this attempt we generated several random sets of 110 points each. The length of T_list increased by approximately 38 %, from an average of 210 trees to an average of 292 trees. The time to compute T_list also increased drastically, going from an average of 15 min to an average of more than 40 min.

The interesting thing that jumped out the most was the increase in the number of large biconnected components. Since the extraction process must do a complete search of all possibilities, the larger the component, the longer it will take. This is a classic example of an exponential problem, where when the problem size increases by 1, the time doubles. With this increased component size, none of the random problems generated finished inside a 12 h cut off time.

This rapid growth puts into perspective the importance of the work previously done by Cockayne and Hewgill. Continuation of their work with incompatibility matrices as well as decomposition of T_list components appears at this point to be very important for the future of SMT calculations.

8.4 Grids

The problem of determining SMTs for grids was mentioned to the author by Ron Graham. In this context we are thinking of a grid as a regular lattice of unit squares. The literature has little of information regarding SMTs on grids, and most of the information that is given is conjectured and not proven. In Sect. 8.4.1 we will look at what is known about SMTs on grids. In the following subsections, we will introduce new results for grids up through 7 ×m in size. These results presented are computational results from PARSTEINER94 [28, 30, 31] which was discussed previously.

8.4.1 2×m and Square Grids

The first proof for anything besides a 2 ×2 grid came in a paper by Chung and Graham [10] in which they proved the optimality of their characterization of SMTs for 2 ×m grids. The only other major work was presented in a paper by Chung, Gardner, and Graham [9]. They argued the optimality of the SMT on 2 ×2, 3 ×3, and 4 ×4 grids and gave conjectures and constructions for those conjectures for SMTs on all other square lattices.

In their work Chung, Gardner, and Graham specified three building blocks from which all SMTs on square (n ×n) lattices were constructed. The first, labeled $\mathcal{I}$, is just a K ₂ or a path on two vertices. This building block is given in Fig. 19a. The second, labeled $\mathcal{Y}$, is a full Steiner tree (FST) (n vertices and n − 2 Steiner points) on 3 vertices of the unit square. This building block is given in Fig. 19b. The third, labeled $\mathcal{X}$, is an FST on all 4 vertices of the unit square. This building block is given in Fig. 19c. For the generalizations we are going to make here, we need to introduce one more building block, which we will label $\mathcal{S}$. This building block is an FST on a 3 ×2 grid and appears in Fig. 19d.

Fig. 19

Building blocks

SMTs for grids of size 2 ×m have two basic structures. The first is an FST on all the vertices in the 2 ×m grid. An example of this for a 2 ×3 grid is given in Fig. 19d. The other structure is constructed from the building blocks previously described. We hope that these building blocks, when put in conjunction with the generalizations for 3 ×m, 4 ×m, 5 ×m, 6 ×m, and 7 ×m will provide the foundation for a generalization of m ×n grids in the future.

In their work on ladders (2 ×m grids) Chung and Graham established and proved the optimality of their characterization for 2 ×m grids. Before giving their characterization, a brief review of the first few 2 ×m SMTs is in order. The SMT for a 2 ×2 grid is shown in Fig. 19c, the SMT for a 2 ×3 grid is shown in Fig. 19d, and the SMT for a 2 ×4 grid is given in Fig. 20.

Fig. 20

SMT for a 2 ×4 grid

Chung and Graham [10] proved that SMTs for ladders fell into one of two categories. If the length of the ladder was odd, then the SMT was the FST on the vertices of the ladder. The SMT for the 2 ×3 grid in Fig. 19d is an example of this. If the length of the ladder was even, the SMT was made up of a series of $(\frac{m} {2} - 1)$ $\mathcal{X}\mathcal{I}$s followed by one last $\mathcal{X}$. The SMT for the 2 ×4 grid in Fig. 20 is an example of this.

8.4.2 3×m Grids

The SMT for 3 ×m grids has a very easy characterization which can be seen once the initial cases have been presented. The SMT for the 3 ×2 grid is presented in Fig. 19d. The SMT for the 3 ×3 grid is presented in Fig. 21.

Fig. 21

SMT for a 3 ×3 grid

From here we can characterize all 3 ×m grids. Except for the 3 ×2 grid, which is an $\mathcal{S}$ building block, there will be only two basic building blocks present, $\mathcal{X}$s and $\mathcal{I}$s. There will be exactly two $\mathcal{I}$s and $(m - 1)\mathcal{X}$s. The two $\mathcal{I}$s will appear on each end of the grid. The $\mathcal{X}$s will appear in a staggered checkerboard pattern, one on each column of the grid the same way that the two $\mathcal{X}$s are staggered in the 3 ×3 grid. The 3 ×5 grid is a good example of this and is shown in Fig. 22.

Fig. 22

SMT for a 3 ×5 grid

8.4.3 4×m Grids

The foundation for the 4 ×m grids has already been laid. In their most recent work, Cockayne and Hewgill presented some results on square lattice problems [14]. They looked at 4 ×m grids for m = 2 to m = 6. They also looked at the SMTs for these problems when various lattice points in that grid were missing. What they did not do, however, was characterize the structure of the SMTs for all 4 ×m grids.

The 4 ×2 grid is given in Fig. 20. From the work of Chung et al. [9], we know that the SMT for a 4 ×4 grid is a checkerboard pattern of 5 $\mathcal{X}$s. This layout gives us the first two patterns we will need to describe the 4 ×m generalization. The first pattern, which we will call pattern $\mathcal{A}$, is the same as the 3 ×4 grid without the two $\mathcal{I}$s on the ends. This pattern is given in Fig. 23. The second pattern, denoted as pattern $\mathcal{B}$, is the 2 ×4 grid in Fig. 20 without the connecting $\mathcal{I}$. This is shown in Fig. 24.

Fig. 23

4 ×m pattern $\mathcal{A}$

Fig. 24

4 ×m pattern $\mathcal{B}$

Before the final characterization can be made, two more patterns are needed. The first one, called pattern $\mathcal{C}$, is a 4 ×3 grid where the pattern is made up of two non-connected 2 ×3 SMTs, shown in Fig. 25. The next pattern, denoted by pattern $\mathcal{D}$, is quite simply a $\mathcal{Y}$ centered in a 2 ×4 grid. This is shown in Fig. 26. The final pattern, denoted by $\mathcal{E}$, is just an $\mathcal{I}$ on the right side of a 2 ×4 grid. This is shown in Fig. 27.

Fig. 25

4 ×m pattern $\mathcal{C}$

Fig. 26

4 ×m pattern $\mathcal{D}$

Fig. 27

4 ×m pattern $\mathcal{E}$

Now we can begin the characterization. The easiest way to present the characterization is with some simple string rewriting rules. Since the 4 ×2, 4 ×3, and 4 ×4 patterns have already been given, the rules will begin with a 4 ×5 grid. This grid has the string $\mathcal{A}\mathcal{C}$. The first rule is that whenever there is a $\mathcal{C}$ on the right end of your string, replace it with $\mathcal{B}\mathcal{D}\mathcal{B}$. Therefore, a 4 ×6 grid is $\mathcal{A}\mathcal{B}\mathcal{D}\mathcal{B}$. The next rule is that whenever there is a $\mathcal{B}$ on the right end of your string, replace it with a $\mathcal{C}$. The final rule is whenever there is a $\mathcal{D}\mathcal{C}$ on the right end of your string, replace it with an $\mathcal{E}\mathcal{A}\mathcal{B}$. These rules are summarized in Table 4. A listing of the strings for m from 5 to 11 is given in Table 5.

Table 4 Rewrite rules for 4 ×m grids

Table 5 String representations for 4 ×m grids

8.4.4 5 ×m Grids

For the 5 ×m grids, there are 5 building blocks (and their mirror images which are donated with an $'$) that are used to generate any 5 ×m grid. These building blocks appear in Figs. 28–32.

Fig. 28

5 ×m pattern $\mathcal{A}$

Fig. 29

5 ×m pattern $\mathcal{B}$

Fig. 30

5 ×m pattern $\mathcal{C}$

Fig. 31

5 ×m pattern $\mathcal{D}$

Fig. 32

5 ×m pattern $\mathcal{E}$

With the building blocks in place, the characterization of 5 ×m grids is quite easy using grammar rewrite rules. The rules used for rewriting strings representing a 5 ×m grid are given in Table 6. The SMTs for 5 ×2, 5 ×3, and 5 ×4 have already been given. For a 5 ×5 grid the SMT is made up of the following string: $\mathcal{E}\mathcal{A}'\mathcal{B}\mathcal{D}$. As a reminder, the $\mathcal{A}'$ signifies the mirror of building block $\mathcal{A}$. A listing of the strings for m from 5 to 11 is given in Table 7.

Table 6 Rewrite rules for 5 ×m grids

Table 7 String representations for 5 ×m grids

8.4.5 6×m Grids

For the 6 ×m grids, there are five building blocks that are used to generate any 6 ×m grid. These building blocks appear in Figs. 33–37.

Fig. 33

6 ×m pattern $\mathcal{A}$

Fig. 34

6 ×m pattern $\mathcal{B}$

Fig. 35

6 ×m pattern $\mathcal{C}$

Fig. 36

6 ×m pattern $\mathcal{D}$

Fig. 37

6 ×m pattern $\mathcal{E}$

The solution for 6 ×m grids can now be characterized by using grammar rewrite rules. The rules used for rewriting strings representing a 6 ×m grid are given in Table 8. The basis for this rewrite system is the SMT for the 6 ×3 grid which is $\mathcal{A}\mathcal{C}$. It is also nice to see that for the 6 ×m grids, there is a simple regular expression which can characterize what the string will be. That regular expression has the form $\mathcal{A}{(\mathcal{B}\mathcal{E})}^{{\ast}}(\mathcal{C}\vert \mathcal{B}\mathcal{D})$, which means that the $\mathcal{B}\mathcal{E}$ part can be repeated 0 or more times and the end can be either $\mathcal{C}$ or $\mathcal{B}\mathcal{D}$. A listing of the strings for m from 6 to 11 is given in Table 9.

Table 8 Rewrite rules for 6 ×m grids

Table 9 String representations for 6 ×m grids

8.4.6 7×m Grids

For the 7 ×m grids, there are six building blocks that are used to generate any 7 ×m grid. These building blocks appear in Figs. 38–43.

Fig. 38

7 ×m pattern $\mathcal{A}$

Fig. 39

7 ×m pattern $\mathcal{B}$

Fig. 40

7 ×m pattern $\mathcal{C}$

Fig. 41

7 ×m pattern $\mathcal{D}$

Fig. 42

7 ×m pattern $\mathcal{E}$

Fig. 43

7 ×m pattern $\mathcal{F}$

The grammar rewrite rules for strings representing a 7 ×m grid are given in Table 10. The basis for this rewrite system is the SMT for the 7 ×5 grid which is $\mathcal{F}\mathcal{A}'\mathcal{E}'\mathcal{F}'$. A listing of the strings for m from 6 to 11 is given in Table 11.

Table 10 Rewrite rules for 7 ×m grids

Table 11 String representations for 7 ×m grids

9 Future Work

9.1 Grids

In this work we reviewed what is known about SMTs on grids and then presented results from PARSTEINER94 [28, 31] which characterize SMTs for 3 ×m to 7 ×m grids. The next obvious question is the following: What is the characterization for an 8 ×m grid or an n ×m grid? Well, this is where things start getting nasty. Even though PARSTEINER94 cuts the computation time of the previous best program for SMTs by an order of magnitude, the computation time for an NP-Hard problem blows up sooner or later, and 8 ×m is where we run into the computation wall.

We have been able to make small chips into this wall though and have some results for 8 ×m grids. The pattern for this seems to be based upon repeated use of the 8 ×8 grid which is shown in Fig. 44. This grid solution seems to be combined with smaller 8 ×solutions in order to build larger solutions. However, until better computational approaches are developed, further characterizations of SMTs on grids will be very hard and tedious.

Fig. 44

8 ×8

9.2 Further Parallelization

9.2.1 Algorithm Enhancements

There remains a great deal of work that can be done on the Steiner minimal tree problem in the parallel arena. The first thing to consider is whether there are other ways to approach the parallel generation of T_list that would be more efficient. Improvement in this area would push the computation pendulum even further away from T_list generation and toward SMT extraction.

The next thing to consider is the entire extraction process. The initial generation of the incompatibility matrix has the appearance of easy parallelization. The forest management technique introduced by Cockayne and Hewgill could also be put into a parallel framework, thereby speeding up the preparation for extraction quite a bit.

With this initialization out of the way, decomposition could then be considered. The best possible enhancement here might be the addition of thresholds. As with most parallel algorithms, for any problem smaller than a particular size, it is usually faster to solve it sequentially. These thresholds could come into play in determining whether to call a further decomposition, such as the cycle decomposition introduced by Cockayne and Hewgill that was discussed in Sect. 7.

The final option for parallelization is one that may yield the best results and that is in the extraction itself. Extraction is basically a branch-and-bound process, using the incompatibility matrix. This branch and bound is primed with the length of the MST as the initial bound and continues until all possible combinations have been considered. The easiest implementation here would probably be the idea presented in the paper by Quinn and Deo [52] that served as the basis for the parallel algorithm in Sect. 6.

9.2.2 GPU Implementation

With games and visualization driving the evolution of graphics processors, the fixed functionality of the rendering pipeline once offered has been steadily replaced by the introduction of programmable pipeline components called shaders. These shaders not only allow the GPU to be used for more elaborate graphical effects but also allow it to be used for more general purpose computations. By storing general data as texture data, user-programmed vertex and fragment shaders can transform the GPU into a highly data parallel multiprocessor [48].

In 2007, Nvidia released CUDA [46], a programming language which allows for direct GPGPU programming in a C-like environment. Modern GPUs offer 512 processing cores [47], which is far more than any CPU currently provides. Many researchers have taken advantage of the environment provided by CUDA to easily map their parallel algorithms to the GPU.

Of note is the work being done by Joshua Hegie [33]. In his thesis, Hegie has mapped out an implementation of Winter’s work onto the GPU. Preliminary results are very promising, and in the future work, he maps out a methodology for the use of multiple GPUs which will open the door for much larger problems at a reasonable computation time.

9.3 Additional Problems

9.3.1 1-Reliable Steiner Tree Problem

If we would like to be able to sustain a single failure of any vertex, without interrupting communication among remaining vertices, the minimum length network problem takes on a decidedly different structure. For example, in any FST all of the original vertices are of degree 1, and hence, any one can be disconnected from the network by a single failure of the adjacent Steiner point.

We would clearly like a minimum length 2-connected network. The answer can be the minimum length Hamiltonian cycle (consider the vertices of the unit square), but it does not need to be, as shown in the Θ graph given in Fig. 45.

Fig. 45

Theta graph

Here we can add Steiner points near the vertices of degree 3 and reduce the network length without sacrificing 2-connectivity. This is not just a single graph, but is a member of a family of graphs that look like ladders, where the Θ graph has only one internal rung. We hope to extend earlier work providing constructions on 2-connected graphs [32] to allow effective application of an annealing algorithm that could walk through graphs within the 2-connected class.

9.3.2 Augmenting Existing Plane Networks

In practical applications, it frequently happens that new points must be joined to an existing Steiner minimal tree. Although a new and larger SMT can, in principle, be constructed which connects both the new and the existing points, this is typically impractical, e.g., in cases where a fiber optic network has already been constructed. Thus, the only acceptable approach is to add the new points to the network as cheaply as possible. Cockayne has presented this problem which we can state as follows:

Augmented Steiner Network: Given a connected plane graph G = (V, E) (i.e., an embedding of a connected planar graph in E ²) and a set V′ of points in the plane which are not on edges of G, construct a connected plane supergraph G” = (V”, E”), such that V” contains $V \bigcup V '$, E” contains E, and the sum of the Euclidean lengths of the set of edges in E” − E is a minimum. In constructing the plane graph G”, it is permitted to add an edge connecting a point in V′ to an interior point of an edge in G. It is also permitted to add Steiner points. Thus, strictly speaking, G” does not need to be a supergraph of G.

The Augmented Steiner Network Problem clearly has applications in such diverse areas as canal systems, rail systems, housing subdivisions, irrigation networks, and computer networks. For example, given a (plane) fiber optic computer network G = (V, E) and a new set V′ of nodes to be added to the network, the problem is to construct a set F′ of fiber optic links with minimum total length that connects V′ to G. The set F′ of new links is easily seen to form a forest in the plane, because the minimum total length requirement ensures that there cannot be cycles in F′.

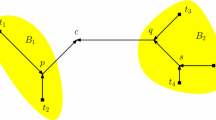
As an example, consider the situation in Fig. 46 where G consists of a single, long edge and V′ = v ₁, …, v ₈. The optimal forest F′ consists of three trees joining G at f ₁, f ₂, and f ₃. It is necessary that extra Steiner points s ₁, s ₂, and s ₃ be added so that F has minimum length.

Fig. 46

An optimal forest

While we are aware of several algorithms for solving special cases of the Augmented Existing Plane Network Problem, such as those by Chen [7] and Trietsch [56] or the special case where the graph G consists of a single vertex, in which case the problem is equivalent to the classical Steiner minimal tree problem, we are not aware of any algorithms or computer programs available for exact solutions to the general form of this problem. Here, “exact” means provably optimal except for roundoff error and machine representation of real numbers. Non-exact (i.e., heuristic) solutions are suboptimal although they may often be found considerably faster.

10 Cross-References

Gradient-Constrained Minimum Interconnection Networks

Steiner Minimum Trees in E ³: Theory, Algorithms, and Applications