Bin Packing Approximation Algorithms: Survey and Classification

Abstract

The survey presents an overview of approximation algorithms for the classical bin packing problem and reviews the more important results on performance guarantees. Both on-line and off-line algorithms are analyzed. The investigation is extended to variants of the problem through an extensive review of dual versions, variations on bin sizes and item packing, as well as those produced by additional constraints. The bin packing papers are classified according to a novel scheme that allows one to create a compact synthesis of the topic, the main results, and the corresponding algorithms.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In the classical version of the bin packing problem, one is given an infinite supply of bins with capacity C and a list L of n items with sizes no larger than C: the problem is to pack the items into a minimum number of bins so that the sum of the sizes in each bin is no greater than C. In simpler terms, a set of numbers is to be partitioned into a minimum number of blocks subject to a sum constraint common to each block. Bin packing rather than partitioning terminology will be used, as it eases considerably the problem of describing and analyzing algorithms.

The mathematical foundations of bin packing were first studied at Bell Laboratories by M.R. Garey and R.L. Graham in the early 1970s. They were soon joined by J.D. Ullman; then at Princeton, these three published the first [103] of many papers to appear in the conferences of the computer science theory community over the next 40 years. The second such paper appeared within months; in that paper, D.S. Johnson [125] extended the results in [103] and studied general classes of approximation algorithms. In collaboration with A. Demers at Princeton, researchers Johnson, Garey, Graham, and Ullman published the first definitive analysis of bin packing approximation algorithms [129]. In parallel with the research producing this landmark paper, Johnson completed his 1973 Ph.D. thesis at MIT which gave a more comprehensive treatment and more detailed versions of the abbreviated proofs in [129].

The pioneering work in [129] opened an extremely rich research area; it soon turned out that this simple model could be used for a wide variety of different practical problems, ranging from a large number of cutting stock applications to packing trucks with a given weight limit, assigning commercials to station breaks in television programming, or allocating memory in computers. The problem is well-known to be $\mathcal{N}\mathcal{P}$-hard (see, e.g., Garey and Johnson [100]); hence, it is unlikely that efficient (i.e., polynomial-time) optimization algorithms can be found for its solution. Researchers have thus turned to the study of approximation algorithms, which do not guarantee an optimal solution for every instance, but attempt to find a near-optimal solution within polynomial time. Together with closely related partitioning problems, bin packing has played an important role in applications of complexity theory and in both the combinatorial and average-case analysis of approximation algorithms (see, e.g., the volume edited by Hochbaum [115]).

Starting with the seminal papers mentioned above, most of the early research focused on combinatorial analysis of algorithms leading to bounds on worst-case behavior, also known as performance guarantees. In particular, letting $A(L)$ be the number of bins used by an algorithm A and letting ${\it \text{OPT}}(L)$ be the minimum number of bins needed to pack the items of L, one tries to find a least upper bound on $A(L)/{\it \text{OPT}}(L)$ over all lists L (for a more formal definition, see Sect. 2). Much of the research can be divided along the boundary between on-line and off-line algorithms. In the case of on-line algorithms, items are packed in the order they are encountered in a scan of L; the bin in which an item is packed is chosen without knowledge of items not yet encountered in L. These algorithms are the only ones that can be used in certain situations. For example, the items to be packed may arrive in a sequence according to some physical process and have to be assigned to a bin as soon as they arrive. Off-line algorithms have complete information about the entire list throughout the packing process.

Since the early 1980s, progressively more attention has been devoted to the probabilistic analysis of packing algorithms. A book by Coffman and Lueker [46] covers the methodology in some detail (see also the book by Hofri [119, Chap. 10]). Nevertheless, combinatorial analysis remains a central research area, and from time to time, numerous new results need to be collected into survey papers. The first comprehensive surveys of bin packing algorithms were by Garey and Johnson [101] in 1981 and by Coffman et al. [50] in 1984. The next such survey was written some 10 years later by Galambos and Woeginger [96] who gave an overview restricted to on-line algorithms. New surveys appeared at the end of the 1990s. Csirik and Woeginger [62] concentrated on on-line algorithms, while Coffman et al. [52] extended the coverage to include off-line algorithms, and Coffman et al. [53] considered both classes of algorithms in an earlier version of the present survey. Worst-case and average-case analysis are surveyed in [62] and [52]. More recently, classical bin packing and its variants were covered in Coffman and Csirik [43] and in Coffman et al. [54, 55].

This survey gives a broad summary of results in the one-dimensional bin packing arena, concentrating on combinatorial analysis, but in contrast to other surveys, greater space is devoted to variants of the classical problem. Important new variants continue to arise in many different settings and help account for the thriving interest in bin packing research. The survey does not attempt to give a self-contained work, for example, it does not present all algorithms in detail nor does it give formal proofs, but it refers to certain proof techniques which have been used frequently to establish the most important results. Also, in the coverage of variants, the restriction to partitioning problems in one dimension is maintained. Packing in higher dimensions, for example, strip packing and two-dimensional bin packing, is itself a big subject, one deserving its own survey. The interested reader is referred to the recent survey by Epstein and van Stee [79].

Another important feature of this survey is that it adopts the novel classification scheme for bin packing papers recently introduced by Coffman and Csirik [44]. This scheme allows one to create a compact synthesis of the topic, the main results, and the corresponding algorithms.

Section 2 covers the main definitions and as well as a full description of the classification scheme. For the classical bin packing problem, on-line (and semi-on-line) algorithms are discussed in Sect. 3 and off-line algorithms in Sect. 4. (Section 4.4 is a slight departure from this organization: it deals with anomalous behavior both for on-line and off-line algorithms.)

The second part of this survey concentrates on special cases and variants of the classical problem. Variations on bin size are considered in Sect. 5, dual versions in Sect. 6, variations on item packing in Sect. 7, and additional conditions in Sect. 8. Finally, Sect. 9 gives a series of examples to familiarize the reader with the classification scheme. The classification of the papers considered in the survey is also given, when appropriate, in the Bibliography.

2 Definitions and Classification

This section introduces more formally all of the relevant notation required to define, analyze, and classify bin packing problems. Starting with the classical problem, the notation is then extended to more general versions, and finally, the new classification scheme is described. Additional definitions needed by specific variants are introduced in the appropriate sections.

2.1 Basic Definitions for Classical Bin Packing

The classical bin packing problem is defined by an infinite supply of bins with capacity C and a list $L = (a_{1},\ldots,a_{n})$ of items (or elements). A value $s_{i} \equiv s(a_{i})$ gives the size of item $a_{i}$ and satisfies $0 < s_{i} \leq C,\ 1 \leq i \leq n.$ The problem is to pack the items into a minimum number of bins under the constraint that the sum of the sizes of the items in each bin is no greater than C.

In the classical problem, the bin capacity C is just a scale factor, so without loss of generality, one can adopt the normalization $C = 1.$ Unless stated otherwise, this convention is in force throughout. One of the exceptions will be in the sections treating variants of the classical problem in which bins $B_{j}$ have varying sizes. In those sections, bin sizes will be denoted by $s(B_{j}).$

In the algorithmic context, nonempty bins will be classified as either open or closed. Open bins are available for packing additional items. Closed bins are unavailable and can never be reopened. It is convenient to regard a completely full bin as open under any given algorithm until it is specifically closed, even though such bins can receive no further items. Denote the bins by $B_{1},B_{2},\ldots.$ When no confusion arises, $B_{j}$ will also denote the set of items packed in the $j$-th bin, and $\vert B_{j}\vert$ will denote the number of such items.

The items are always organized into a list L (or a list $L_{j}$ in some indexed set of lists). The notation for list concatenation is as usual; $L = L_{1}L_{2}\ldots L_{k}$ means that the items of list $L_{i}$ are followed by the items of list $L_{i+1}$ for each $i = 1,2,\ldots,k - 1.$ When the number of items in a list is needed as part of the notation, an index in parentheses is used: $L_{(n)}$ denotes a list of n items.

If $B_{j}$ is nonempty, its current content or level is defined as

$$c(B_{j}) =\displaystyle\sum _{a_{i}\in B_{j}}s_{i}.$$

A bin (necessarily empty) is opened when it receives its first item. Of course, it may be closed immediately thereafter, depending on the algorithm and the item size. It is assumed, without loss of generality, that all algorithms open bins in order of increasing index. Within any collection of nonempty bins, the earliest opened, the leftmost, and the lowest indexed all refer to the same bin.

In general, in the considered lists, the item sizes are taken from the interval $(0,\alpha ]$, with $\alpha \in (0,1].$ It is usually assumed that $\alpha = \frac{1} {r}$, for some integer $r \geq 1$, and many results apply only to $r =\alpha = 1.$

There are two principal measures of the worst-case behavior of an algorithm. Recall that $A(L)$ denotes the number of bins used by algorithm A to pack the elements of L; ${\it \text{OPT}}$ denotes an optimal algorithm, one that uses a minimum number of bins. Define the set $V _{\alpha }$ of all lists L for which the maximum size of the items is bounded from above by $\alpha.$ For every $k \geq 1$, let

$$R_{A}(k,\alpha ) =\sup _{L\in V _{\alpha }}\left \{\frac{A(L)} {k} : \mathit{OPT}(L) = k\right \}.$$

Then the asymptotic worst-case ratio (or asymptotic performance ratio, APR) as a function of $\alpha$ is given by

$$R_{A}^{\infty }(\alpha ) = \overline{\lim }_{ k\rightarrow \infty }R_{A}(k,\alpha ).$$

Clearly, $R_{A}^{\infty }(\alpha ) \geq 1$, and this number measures the quality of the packings produced by algorithm A compared to optimal packings in the worst case. In an equivalent definition, $R_{A}^{\infty }(\alpha )$ is a smallest number such that there exists a constant $K \geq 0$ for which

$$A(L) \leq R_{A}^{\infty }(\alpha )\mathit{OPT}(L) + K.$$

for every list $L \in V _{\alpha }.$ Hereafter, if $\alpha$ is left unspecified, the APR of algorithm A refers to $R_{A}^{\infty }\equiv R_{A}^{\infty }(1).$

The second way to measure the worst-case behavior of an algorithm A is the absolute worst-case ratio (AR)

$$R_{A}(\alpha ) =\sup _{L\in V _{\alpha }}\left \{ \frac{A(L)} {\mathit{OPT}(L)}\right \}.$$

The comparison of algorithms by asymptotic bounds can be strikingly different from that by absolute bounds. Generally speaking, the number of items n must be sufficiently large (how large will depend on the algorithm) for the asymptotic bounds to be the better measure for purposes of comparison. Note that the ratios are bounded below by 1; the better algorithms have the smaller ratios. When algorithm A is an on-line algorithm, the asymptotic ratio is also called the competitive ratio.

There are some further proposals to measure the quality of a packing, like differential approximation measure (see Demange et al. [66], [67]), random-order ratio (see Kenyon [136]), relative worst-order ratio (see Boyar and Favrholdt [27]), and accommodation function (see Boyar et al. [28]).

It is finally worth mentioning a special sequence $t_{i}$ of integers which was investigated by Sylvester [170] in connection with a number theoretic problem and later generalized by Golomb [107]. (In describing the performance of various algorithms in later sections, such sequence will occasionally be considered.) For an integer $r \geq 1$, define

$$\displaystyle\begin{array}{rcl} t_{1}(r)& =& r + 1 \\ t_{2}(r)& =& r + 2 \\ t_{i+1}(r)& =& t_{i}(r)(t_{i}(r) - 1) + 1,\quad \mbox{ for }i \geq 2.\end{array}$$

(The Sylvester sequence was defined for $r = 1$). It was conjectured by Golomb that for $r = 1$, this sequence gives the closest approximation to $1$ from below among the approximations by sums of reciprocals of k integers, the basis of the conjecture being

$$\displaystyle\sum _{i=1}^{k} \frac{1} {t_{i}(1)} + \frac{1} {t_{k+1}(1) - 1} = 1.$$

Furthermore, it is also easily proved that the following expression is valid for the Golomb sequences:

$$\frac{(r - 1)} {t_{1}(r)} +\displaystyle\sum _{ i=2}^{k} \frac{1} {t_{i}(r)} + \frac{1} {t_{k+1}(r) - 1} = 1\quad \quad \mbox{ for any }r \geq 1.$$

On the other hand, the following value appears in several results:

$$h_{\infty }(r) = 1 +\displaystyle\sum _{ i=2}^{\infty } \frac{1} {t_{i}(r) - 1}.$$

The first few values of $h_{\infty }(r)$ are the following: $h_{\infty }(1) \approx 1.69103$, $h_{\infty }(2) \approx 1.42312$, $h_{\infty }(3) \approx 1.30238.$

2.2 General Definitions

This survey covers results on several variants of the one-dimensional bin packing problem. In such variants, the meaning of a number of notations can be different, so more general definitions are necessary. These will be introduced in the present section, together with the basic ideas behind the adopted classification scheme.

The notion of packing items into a sequence of initially empty bins helps visualize algorithms for constructing partitions. It is also helpful in classifying algorithms according to the various constraints under which they must operate in practice. The items are normally given in the form of a sequence or list $L = (a_{1},\ldots,a_{n}),$ although the ordering in many cases will not have any significance. To economize on notation, a harmless abuse is adopted whereby $s_{i}$ denotes the name as well as the size of the $i$-th item. The generic symbol for packing is $\mathsf{P}$, the number of items in $\mathsf{P}$ is denoted by $\vert \mathsf{P}\vert,$ the sum of the sizes of the items in $\mathsf{P}$ is denoted by $c(\mathsf{P})$, and the number of bins in $\mathsf{P}$ is denoted by $\#\mathsf{P}.$ In the classical bin packing optimization problem, the objective is to find a packing $\mathsf{P}$ of all the items in L such that $\#\mathsf{P}$ is minimized over all partitions of L satisfying the sum constraints. Recall that C is only a scale factor in this problem; it is usually convenient to replace the $s_{i}$ by $s_{i}/C$ and take $C = 1.$

Let $\mathsf{P}_{A}(L)$ denote the packing of L produced by algorithm $A.$ In the literature, one finds the notation $A(L)$ representing metrics such as $\#\mathsf{P}$, but since $A(L)$ may denote different metrics for different problems (the same algorithm A may apply to problems with different objective functions), the alternative notation will be necessary on occasion. The minimum of $\#\mathsf{P}$ over all partitions $\mathsf{P}$ of L satisfying the sum constraints will have the notation ${OPT}(L) :=\min _{\pi (L)}\#\mathsf{P}(L)$, where $\pi (L)$ denotes the set of all such partitions. The notation ${\it \text{OPT}}(L)$ suffers from the same ambiguity as before, that is, the objective function to which it applies is determined by context. Moreover, in contrast to other algorithm notation, ${\it \text{OPT}}$ does not denote a unique algorithm.

There are two variants of classical bin packing that arise immediately from the definition. In one, a general bin capacity $C$ and a number m of bins are part of the problem instance, and the problem is to find a maximum cardinality subset of $\{s_{i}\}$ that can be packed into m bins of capacity $C.$ In the other, all $n$ items must be packed into m bins, and the problem is to find a smallest bin capacity C such that there exists a packing of all the items in m bins of capacity $C.$ The first problem suggests yet another in which the total size of the items in a subset $\mathcal{S}$ is the quantity of interest rather than the number $\vert \mathcal{S}\vert$ of items. Problems fixing the number of bins fall within scheduling theory whose origins in fact predate those of bin packing theory. In scheduling theory, which is very large in its own right, makespan scheduling is more likely to be described as scheduling a list of tasks or jobs (items) on m identical processors (bins) so as to minimize the schedule length or makespan (bin capacity). This incursion into scheduling problems will be limited to the most elementary variants and applications of bin packing problems, such as those above.

Bin covering problems are also included in bin packing theory for classification purposes, and these change the sum constraints to $c(B_{j}) \geq 1,$ where again, bin capacity is normalized to 1. The classical covering problem asks for a partition, $\mathsf{C}$, called a cover, which maximizes the number $\#\mathsf{C}$ of bins satisfying the new constraint. Both the packing and covering combinatorial optimization problems are $\mathcal{N}\mathcal{P}$-hard. With problems defined on restricted item sizes or number of items per bin being the major exceptions, this will be the case for nearly all problem variants in the classification scheme. Note that there are immediate variants to bin covering, just as there were for bin packing. For example, one can take the number $m$ of bins to be fixed and ask for a minimum cardinality subset of $\{a_{i}\}$ from which a cover of m bins can be obtained. Or one can consider the problem of finding a largest capacity C such that L can be made to cover m bins of capacity $C.$

Order-of-magnitude estimates of time complexities of fundamental algorithms and their extensions are usually easy to derive. The analysis of parallel algorithms for computing packings is an example where deriving time complexities is not always so easy. However, the research in this area, in which results take the form of complexity measures, has been very limited.

Several results quantify the trade-off between the running time of algorithms and the quality of the packings. They produce polynomial-time (or fully polynomial-time) approximation schemes [100], denoted by PTAS (or FPTAS). In simplified terms, a typical form of such results is illustrated by “Algorithm A produces packings with $O(\epsilon )$ wasted space and has a running time that is polynomial in $1/\epsilon.$”

The most common approach to the analysis of approximation algorithms has been worst-case analysis by which the worst possible performance of an algorithm is compared with the performance of an optimization algorithm. (Detailed definitions will be provided shortly.) The term performance guarantee puts a more positive slant on results of this type. So also does the term competitive analysis, which usually refers to a worst-case analysis comparing an on-line approximation algorithm with an optimal off-line algorithm. Probability models also enjoy wide use and have grown in popularity, as they bring out typical, average-case behavior rather than the normally rare worst-case behavior. In probabilistic analysis, algorithms have random inputs; the items are usually assumed to be independent, identically distributed random variables. For a given algorithm $A$, $A(L_{n})$ is a random variable whose distribution becomes the goal of the analysis. Because of the major differences in probabilistic results and in the analysis that produces them, they are not covered in this survey, which focuses exclusively on combinatorial analysis. For a general treatment of average-case analysis of packing and related partitioning problems, see the text by Coffman and Lueker [46].

2.3 Classification Scheme

The scheme for classifying problems and solutions is aimed at giving the reader a good idea of the results in bin packing theory to be found in any given paper on the subject. Although in many, if not most cases, it is impractical to describe every result contained in a paper, an indication of the main results should be useful to the reader.

The classification uses four fields, presented in the form

problem $\vert$ algorithm class $\vert$ results $\vert$ parameters

For a brief preview, observe that, normally, the problem is to minimize or maximize a metric under sum constraints and refers, for example, to the number of bins of fixed capacity and the capacity of a fixed number of bins. The algorithm class refers to paradigms such as on-line, off-line, or bounded space. The results field specifies performance in terms of absolute or asymptotic worst-case ratios, problem complexity, etc. Lastly, the parameters field describes restrictions on problem parameters, such as a limit on item sizes or on the number of items per bin, and a restriction of all data to finite or countable sets. In many cases, there are no additional parameters to specify, in which case the parameters field will be omitted. The three remaining fields will normally be nonempty.

In the following, a detailed description of the classification scheme is introduced. Section 9 gives a number of annotated examples to familiarize the reader with the proposed classification. The special terms or abbreviations adopted for entries will be given in bold face. In the large majority of cases, the entry will have a mnemonic quality that makes the precise meaning of an entry clear in spite of its compact form.

2.3.1 Problem

The combinatorial optimization problems of interest can easily be expressed in the notation given so far, but for readability, abbreviations of the names by which the problems are commonly known will be used. Most, but not all, of the problems below were discussed earlier. Moreover, some of them are not treated in this survey and are listed for the sake of completeness.

• 1. pack refers to the problem of minimizing $\#\mathsf{P}(L).$ The default sum constraints are $c(B_{j}) \leq 1.$ But they are $c(B_{j}) \leq s(B_{j})$, if variable bin capacities $s(B_{j})$ are considered, and more simply $c(B_{j}) \leq C$ if there is only a common bin capacity $C.$

• 2. maxpack problems invert the problem above, that is, $\#\mathsf{P}$ is to be maximized. Clearly, such problems trivialize unless there is some constraint placed on opening new bins. The tacit assumption will be that packings under approximation algorithms must obey a conservative, any-fit constraint: a new bin cannot be opened for an item $s_{i}$ unless $s_{i}$ cannot fit into any currently open bin. Optimal packings by definition must be such that, for some permutation of the bins, no item in $B_{i}$ fits into $B_{j}$ for any $j < i.$

• 3. mincap refers to the problem of minimizing the common bin capacity needed to pack L into a given number m of bins. Bin-stretching analysis applies if the problem instances are restricted to those for which an optimization rule can pack $L$ into m unit-capacity bins. Under this assumption, in the analysis of algorithm $A$, one asks how large must the bin capacity be (how much must it be stretched) for algorithm A to pack L into the same number of bins.

• 4. maxcard(subset) has the number m of bins and their common capacity C as part of the problem instance. The problem is to find a largest cardinality subset of L that can be packed into m bins of capacity $C.$

• 5. maxsize(subset) has the number m of bins and their common capacity C as part of the problem instance. The problem is to find a subset of L with maximum total item size that can be packed into m bins of capacity $C.$

• 6. cover refers to the problem of finding a partition of L into bins that maximizes $\#\mathsf{P}(L)$ subject to the constraints $c(B_{j}) \geq 1.$ The partition is called a cover.

• 7. capcover refers to the problem of finding, for a given number m of bins, the maximum capacity C such that a covering of m bins of capacity C can be obtained from $L.$

• 8. cardcover(subset) is the related problem of minimizing the cardinality of the subset of L needed to cover a given number $m$ of bins with a given capacity $C.$

2.3.2 Algorithm Class

• 1. on-line algorithms sequentially assign items to bins, in the order encountered in $L$, without knowledge of items not yet packed. Thus, the bin to which $a_{i}$ is assigned is a function only of the sizes $s_{1},\ldots,s_{i}.$

• 2. off-line algorithms have no constraints beyond the intrinsic sum constraints; an off-line algorithm simply maps the entire list L into a packing $\mathsf{P}(L).$ All items are known in advance, so the ordering of L plays no role.

• 3. bounded-space algorithms decide where an item is to be packed based only on the current contents of at most a finite number $k$ of bins, where k is a parameter of the algorithm. A more precise definition and further discussion of these algorithms appear later.

• 4. linear-time algorithms have $O(n)$ running time. More precisely, all such algorithms take constant time to pack each item.

  The three characterizations above are orthogonal. But the literature suggests that the following convention allows to use one term in classifying algorithms most of the time: bounded space implies linear time and linear time implies on-line. Exceptions will be noted explicitly: it will be seen below (under repack) how off-line algorithms can be linear time.

• 5. open-end refers to certain cover approximation algorithms. An open bin $B_{j}$, that is, one for which $c(B_{j})< s(B_{j})$ and further packing is allowed, must be closed just as soon as $c(B_{j}) \geq s(B_{j}).$ (The item causing the “overflow” is left in the bin.)

• 6. conservative algorithms are those required to pack the current item into an open bin with sufficient space, whenever such a bin exists; in particular, it cannot choose to open a new bin. Scheduling algorithms satisfying a similar constraint are sometimes called work conserving.

• 7. repack refers to packing problems which allow the repacking (possibly limited in some way) of items, that is, moving an item, say $s_{i}$, from one bin to another.

• 8. dynamic packing introduces the time dimension; an instance L of this problem consists of a sequence of triples $(s_{i},b_{i},d_{i})$ with $b_{i}$ and $d_{i}$ denoting arrival and departure times, respectively. Under a packing algorithm $A$, $A(L,t)$ denotes the number of bins occupied at time $t$, that is, the number of bins occupied by those items $a_{i}$ for which $b_{i} \leq t < d_{i}.$

2.3.3 Results

Almost all results fall into the broad classes mentioned in Sect. 2.1.

• 1. $\mathbf{R}_{\mathbf{A}}^{\infty }$ is the asymptotic worst-case ratio, with algorithm A specified when appropriate. When only a bound is proved, the word bound is appended.

• 2. $\mathbf{R}_{\mathbf{A}}$ is the absolute worst-case ratio. When only a bound is proved, the word bound is appended.

• 3. Where possible, complexity of the problem will be given in the standard notation of problem complexity. Approximation schemes are classified as complexity results and have entries like PTAS and FPTAS as noted earlier.

• 4. Complexity of the algorithm may also be a result; it refers to running-time complexity and will be signaled by the entry running time.

A paper classified as a worst-case analysis may also have complexity results (but not conversely, unless both types of results figure prominently in the paper, in which case both classifications will be given).

2.3.4 Parameters

These typically correspond to generalizations whereby limitations can be placed on the problem instance, or further properties of the algorithm classification. In some cases, problems may be simplified by certain limitations, such as a specific upper limit of two to the number of items per bin.

• 1. $\{\mathbf{B}_{\mathbf{i}}\}$ means that there can be more than one bin size and an unlimited supply of each size.

• 2. stretch refers to certain asymptotic bounds which compare the number of bins of capacity C needed to pack L by algorithm A to the number of unit-capacity bins needed by an optimal packing.

• 3. mutex stands for mutual exclusion and introduces constraints, where needed, in the form of a sequence of pairs $(s_{i},s_{j}),\ i\neq j,$ meaning that $s_{i}$ and $s_{j}$ cannot be put in the same bin.

• 4. $\mathbf{card(B) \leq k}$ gives a bound on the number of items that can be packed in a bin.

• 5. $\mathbf{s}_{\mathbf{i}} \leq \alpha$ or $\mathbf{s}_{\mathbf{i}} \geq \alpha$ denotes bounds on item sizes, the former being far more common in the literature. In some cases, $\alpha$ is specialized to a discrete parameter $1/k$, k an integer. The problems with item-size restrictions are called parametric cases in the literature.

• 6. restricted $\mathbf{s}_{\mathbf{i}}$ refers to simplified problems where the number of different item sizes is finite.

• 7. discrete calls for discrete sets of item sizes, in particular, item sizes that, for a given integer $r$, are all multiples of $1/r$ with $C = 1.$ Equivalently, the bin size could be taken as r and item sizes restricted to the set $\{1,\ldots,j\}$ for some $j \in \{ 1,\ldots,r\}.$ While this may not be a significant practical constraint, it will affect the difficulty of the analysis and may create significant changes in the results.

• 8. controllable means that one has the possibility not to pack an item as is, but to first take some decision about it, such as rejecting it or splitting it into parts.

3 On-Line Algorithms

Recall that a bin packing algorithm is called on-line if it packs each element as soon as it is inspected, without any knowledge of the elements not yet encountered (either the number of them or their sizes). This review starts with results for some classical algorithms and then generalizes to the Any-Fit and the Almost Any-Fit classes of on-line algorithms. The subclass of bounded-space on-line algorithms will also be considered: an algorithm is bounded space if the number of open bins at any time in the packing process is bounded by a constant. (The practical significance of this condition is clear; e.g., one may have to load trucks at a depot where only a limited number of trucks can be at the loading dock). This section will be concluded by a detailed discussion of lower bounds on the APRs of certain classes of on-line algorithms, but before doing so, relevant variations of old algorithms and the current best-in-class algorithms will be presented. Anomalous behavior occurring in on-line algorithms is discussed in Sect. 4.4.

3.1 Classical Algorithms

In describing an on-line algorithm, it will occasionally be convenient, just before a decision point, to refer to the next item to be packed as the current item; right after A packs $a_{i},\ i < n$, $a_{i+1}$ becomes the current item. A simple approach is to pack the bins one at a time according to

Next-Fit (NF): After packing the first item, NF packs each successive item in the bin containing the last item to be packed, if it fits in that bin; if it does not fit, NF closes that bin and packs the current item in an empty bin.

The time complexity of NF is clearly $O(n).$ Note that only one bin is ever open under NF, so it is bounded space. This advantage is compensated by a relatively poor APR, however.

Theorem 1 (Johnson et al. [129])

One has

$$R_{\mathrm{NF}}^{\infty }(\alpha ) = \left \{\begin{array}{l@{\quad }l@{\quad }l} 2 \quad &\mbox{ if}\quad &{ 1 \over 2} \leq \alpha \leq 1 \\ {(1-\alpha )}^{-1}\quad &\mbox{ if}\quad &0 <\alpha <{ 1 \over 2} \end{array}.\right.$$

Fisher [86] discovered an interesting property that NF does not share with other classical approximation algorithms. He proved that NF packs any list and its reverse into the same number of bins. The conspicuous disadvantage of NF is that it closes bins that could be used for packing later items. An immediate improvement would seem to be never to close bins. But then the next question is: if an item can be put into more than one open bin, which bin should be selected? One possible rule drawn from scheduling theory (where it is known as the greedy or largest processing time rule) is the following

Worst-Fit (WF): If there is no open bin in which the current item fits, then WF packs the item in an empty bin. Otherwise, WF packs the current item into an open bin of smallest content in which it fits; if there is more than one such bin, WF chooses the lowest indexed one.

Although one might expect WF to behave better than NF, it does not.

Theorem 2 (Johnson [127])

For all $\alpha \in (0,1]$

$$R_{\mathrm{WF}}^{\infty }(\alpha ) = R_{\mathrm{ NF}}^{\infty }(\alpha ).$$

To achieve smaller APRs, there are many better rules for choosing from among the open bins. One that quickly comes to mind is

First-Fit (FF): FF packs the current item in the lowest indexed nonempty bin in which it fits, assuming there is such a bin. If no such bin exists, FF packs the current item in an empty bin. FF is neither linear time nor bounded space.

A natural complement to WF packs each item into a bin that minimizes the space leftover.

Best-Fit (BF): If there is no open bin in which the current item fits, then BF packs the item in an empty bin. Otherwise, BF packs the current item into an open bin of largest content in which it fits; if there is more than one, such bin BF chooses the lowest indexed one.

By adopting appropriate data structures for representing packings, it is easy to verify that the time complexity of these algorithms is $O(n\log n).$ The analysis of the worst-case behavior of the packings they produce is far more complicated. The basic idea of the upper bound proofs is the weighting function technique, which has played a fundamental role in bin packing theory. So, before proceeding with other algorithms, it is convenient to describe this technique, which was introduced in [103, 129] and subsequently applied in many other papers (see, e.g., [13, 92, 127, 143]).

3.2 Weighting Functions

To bound the asymptotic worst-case behavior of an algorithm $A$, one can try to find a function $W_{A} : (0,1]\rightarrow IR$ with the properties: (i) There exists a constant $K \geq 0$ such that for any list $L$

$$\displaystyle\sum _{a\in L}W_{A}(a) \geq A(L) - K$$

(1)

and (ii) there exists a constant ${K}^{{\ast}}$ such that for any set B of items summing to no more than 1

$$\displaystyle\sum _{a\in B}W_{A}(a) \leq {K}^{{\ast}}.$$

(2)

The value $W_{A}(a)$ is the weight of item a under $A$’s weighting function $W_{A}.$ Note that (1) requires that, for large packings (large $A(L)$), the average total weight of the items in a bin must satisfy a lower bound close to 1 for all lists $L.$ On the other hand, (2) says that the total weight in any bin of any packing is at most ${K}^{{\ast}}$, so for an optimal packing

$$\displaystyle\sum _{a\in L}W_{A}(a) =\displaystyle\sum _{ j=1}^{\mathit{OPT}(L)}\displaystyle\sum _{ a\in B_{j}}W_{A}(a) \leq {K}^{{\ast}}\mathit{OPT}(L).$$

(3)

Together, (1) and (3) obviously imply the bound $A(L) \leq {K}^{{\ast}}{\it \text{OPT}}(L) + K$, and hence $R_{A}^{\infty }\leq {K}^{{\ast}}.$ Note that the technique above is only representative; it is easy to find weaker conditions on the weighting function which will produce the same upper bound for the APR.

The proof of the NF upper bound is not appreciably simplified by a weighting function argument, but it does offer a simple example of such arguments. Consider the case $\alpha = 1$ and define $W_{\mathrm{NF}}(a) = 2s(a)$ for all $a$, where $s(a)$ denotes the size of item $a.$ An observation is needed about NF when $\mathrm{NF}(L)>1$: Since the first item of $B_{j+1}$ did not fit in $B_{j},\ 1 \leq j < \mathrm{NF}(L)$, the sum of the item sizes in $B_{j} \cup B_{j+1}$ exceeds 1, and hence the sum of the weights of the items in $B_{j} \cup B_{j+1}$ exceeds 2. Then

$$\displaystyle\begin{array}{rcl} \displaystyle\sum _{j=1}^{\mathrm{NF}(L)}\displaystyle\sum _{ a\in B_{j}}W_{\mathrm{NF}}(a)& \geq & \displaystyle\sum _{j=1}^{\lfloor \mathrm{NF}(L)/2\rfloor }\displaystyle\sum _{ a\in B_{2j-1}\cup B_{2j}}W_{\mathrm{NF}}(a) \\ & \geq & 2\lfloor \mathrm{NF}(L)/2\rfloor \geq \mathrm{NF}(L) - 1, \\ \end{array}$$

so (1) holds with $K = 1.$ The inequality (2) with ${K}^{{\ast}} = 2$ is immediate from the definition of $W_{\mathrm{NF}}$, so $R_{\mathrm{NF}}^{\infty }\leq 2$, as desired.

There is no systematic way to find appropriate weighting functions, and the approach can be difficult to work out. For example, consider the proof of the following result.

Theorem 3 (Johnson et al. [129])

$$R_{\mathrm{FF}}^{\infty } = R_{\mathrm{ BF}}^{\infty } = \left \{\begin{array}{l@{\quad }l@{\quad }l} \frac{17} {10} \quad &\mbox{ if}\quad &{ 1 \over 2} <\alpha \leq 1 \\ 1 + {\lfloor \frac{1} {\alpha } \rfloor }^{-1}\quad &\mbox{ if}\quad &0 <\alpha \leq { 1 \over 2} \end{array} \right..$$

The proof of the $\frac{17} {10}$ upper bound consists of verifying that the following weighting function suffices

$$W(x) = \left \{\begin{array}{l@{\quad }l@{\quad }l} \frac{6} {5}x \quad &\mbox{ if}\quad &0 \leq x \leq { 1 \over 6} \\ \frac{9} {5}x - \frac{1} {10}\quad &\mbox{ if}\quad &{ 1 \over 6} < x \leq { 1 \over 3} \\ \frac{6} {5}x + \frac{1} {10}\quad &\mbox{ if}\quad &{ 1 \over 3} < x \leq { 1 \over 2} \\ \frac{6} {5}x + \frac{2} {5} \quad &\mbox{ if}\quad &{ 1 \over 2} < x \leq 1 \end{array} \right.$$

and it requires a substantial effort. (The argument encompasses several pages of case analysis.) Yet, despite a few hints that emerge in this effort, a clear understanding of how this function was obtained in the first place requires still more effort.

Theorem 3 for $\alpha \leq \frac{1} {2}$ can be proved without weighting functions (see [129]), but the reader may find it instructive to prove the $1 + {\lfloor \frac{1} {\alpha } \rfloor }^{-1}$ upper bound with the weighting function

$$W_{\mathrm{FF}}(a) = \frac{r + 1} {r} s(a),\ \alpha = \frac{1} {r},\ r \geq 2.$$

Sequences of specific examples establish lower bounds for $R_{A}^{\infty }.$ In particular, one seeks a sequence of lists $L_{(n_{1})},L_{(n_{2})},\ldots$ satisfying $L_{(n_{k})} \in V _{\alpha }$ $(k = 1,2,\ldots )$, $\lim _{k\rightarrow \infty }\mathit{OPT}(L_{(n_{k})}) = \infty$, and for some constant $K_{{\ast}}$,

$$\lim _{k\rightarrow \infty } \frac{A(L_{(n_{k})})} {\mathit{OPT}(L_{(n_{k})})} = K_{{\ast}}.$$

Then $R_{A}^{\infty }\geq K_{{\ast}}$, and if $K_{{\ast}}$ is equal to ${K}^{{\ast}}$ of the upper bound analysis, one has the APR for the algorithm considered. Finding worst-case examples can be anywhere from quite easy to quite hard. For example, the reader would have little trouble with NF but would probably find FF to be quite challenging.

3.3 Any-Fit and Almost Any-Fit Algorithms

The algorithms described so far belong to a much larger class of on-line heuristics satisfying similar worst-case properties. It is clear that FF, WF, and BF satisfy the following condition:

Any-Fit constraint: If $B_{1},\ldots,B_{j}$ are the current nonempty bins, then the current item will not be packed into $B_{j+1}$ unless it does not fit in any of the bins $B_{1},\ldots,B_{j}.$

The class of on-line heuristics satisfying the Any-Fit constraint will be denoted by $\mathcal{A}\mathcal{F}.$ The following result shows that FF and WF are best and worst algorithms in $\mathcal{A}\mathcal{F}$, in the APR sense.

Theorem 4 (Johnson [127])

For every algorithm $A \in \mathcal{A}\mathcal{F}$ and for every $\alpha \in (0,1]$

$$R_{\mathrm{FF}}^{\infty }(\alpha ) \leq R_{ A}^{\infty }(\alpha ) \leq R_{\mathrm{ WF}}^{\infty }(\alpha ).$$

By a slight tightening of the Any-Fit constraint, one can eliminate the high-APR algorithms like WF and define a class of heuristics all having the same APR.

Almost Any-Fit constraint: If $B_{1},\ldots,B_{j}$ are the current nonempty bins, and $B_{k}\ (k \leq j)$ is the unique bin with the smallest content,then the current item will not be packed into $B_{k}$ unless it does not fit in any of the bins to the left of $B_{k}.$

Clearly, WF does not satisfy this condition, but it is easy to verify that both FF and BF do. The class of on-line algorithms satisfying both constraints above will be denoted by $\mathcal{A}\mathcal{A}\mathcal{F}.$

Theorem 5 (Johnson [127])

$R_{A}^{\infty }(\alpha ) = R_{\mathrm{FF}}^{\infty }(\alpha )$ for every A in $\mathcal{A}\mathcal{A}\mathcal{F}.$

Almost Worst-Fit (AWF) is a modification of WF whereby the current item is always placed in a bin having the second lowest content, if such a bin exists and the current item fits in it; the current item is packed in a bin with smallest content only if it fits nowhere else. Interestingly, though it seems to differ little from WF, AWF has a substantially better APR, since it is in $\mathcal{A}\mathcal{A}\mathcal{F}$ and hence $R_{\mathrm{AWF}}^{\infty }(\alpha ) = R_{\mathrm{FF}}^{\infty }(\alpha ) = \frac{17} {10}.$

3.4 Bounded-Space Algorithms

An on-line bin packing algorithm uses $k$-bounded space if, for each item, the choice of where to pack it is restricted to a set of at most k open bins. One obtains bounded-space counterparts of the algorithms of the previous section by specifying a suitable policy for closing bins.

As previously observed, NF uses only 1-bounded space; the only algorithm to use less is the trivial algorithm that puts each item in a separate bin. To improve on the APR of NF, yet stay with bounded-space algorithms, Johnson [126] proposed an algorithm that packs items according to the First-Fit rule, but considers as candidates only the $k$ most recently opened bins; when a new bin has to be opened and there are already k open bins, then the lowest indexed open bin is closed. It can be expected that the APR of the resulting algorithm, which is known as Next-k-Fit (NF$_{k}$), tends to $\frac{17} {10}$ as $k$ increases. Finding the exact bound was not an easy task, although Johnson did give a narrow range for the APR. Later, Csirik and Imreh [58] constructed the worst-case sequences, and then Mao was able to prove the exact bound:

Theorem 6 (Mao [153])

For any $k \geq 2,\quad R_{\mathrm{NF}_{k}}^{\infty } = \frac{17} {10} + \frac{3} {10(k-1)}.$

In general, a bounded-space algorithm is defined by specifying the packing and closing rules. An interesting class of such rules is based on FF and BF as follows:

• Packing rules: The elements are packed following either the First-Fit rule or the Best-Fit rule.

• Closing rules: The next bin to close is either the lowest indexed one or one of largest content.

The algorithm that uses packing rule X, closing rule Y, and $k$-bounded space is denoted by $\mathrm{A}XY _{k}$, where $X =$ F or B for FF or BF and $Y =$ F or B for the lowest indexed (First) open bin or the largest-content (Best) open bin. With this terminology, NF$_{k}$ can also be classified as AFF$_{k}.$ Note that, independently of the chosen rules, if $k = 1$, then one always gets NF.

Algorithm ABF$_{k}$ was first analyzed by Mao, who called it Best-k-Fit. He proved that for any fixed $k$, this algorithm is slightly better than NF$_{k}.$

Theorem 7 (Mao [152])

For any $k \geq 2,\quad R_{\mathrm{ABF}_{k}}^{\infty } = \frac{17} {10} + \frac{3} {10k}.$

The tight asymptotic bound for AFB$_{k}$ was found by Zhang [184] (see also the paper version [187]).

Theorem 8 (Zhang [187])

For any $k \geq 2,\quad R_{\mathrm{AFB}_{k}}^{\infty } = R_{\mathrm{NF}_{k}}^{\infty }.$

Finally, consider the algorithm ABB$_{k}$ whose asymptotic behavior is, rather surprisingly, independent of $k \geq 2$ and equal to that of FF and BF.

Theorem 9 (Csirik and Johnson [60])

If $k \geq 2$ then $R_{\mathrm{ABB}_{k}}^{\infty } = \frac{17} {10}.$

Since all of the above algorithms fulfill the Any-Fit constraint with respect to the open bins, the overall bound $R_{A}^{\infty }\geq \frac{17} {10}$ is to be expected from Theorem 4. A better on-line algorithm can only be obtained without the Any-Fit constraint. In the remaining part of this section, it is shown how the fruitful idea of reservation techniques (introduced by Yao [180] for unbounded-space algorithms and discussed in the next section) led to on-line algorithms which are neither in class $\mathcal{A}\mathcal{F}$ nor in $\mathcal{A}\mathcal{A}\mathcal{F}.$

Yao’s idea appeared in the work of Lee and Lee [143] who developed the Harmonic-Fit algorithm, which will be denoted by HF$_{k}$ since, for the case $\alpha = 1$, it uses at most k open bins. The algorithm divides the interval $(0,1]$ into subintervals $I_{j} = ( \frac{1} {j+1}, \frac{1} {j}](1 \leq j \leq k - 1)$ and $I_{k} = (0, \frac{1} {k}].$ An element is called an $I_{j}$-element if its size belongs to interval $I_{j}.$ Similarly, there are $k$ different bin types: an $I_{j}$-bin is reserved for $I_{j}$-elements only. An $I_{j}$-element is always packed into an $I_{j}$-bin following the Next-Fit rule, and so at most, k bins are open at the same time. Galambos [92] extended the idea to general $\alpha.$ Observe that, by selecting $\alpha \in \left ( \frac{1} {r+1},{ 1 \over r} \right ]$, the number, say $M$, of bin types exceeds the space bound k by $r - 1$; this is because $I_{j}$-bins for $j < r$ are never opened. Instead of notation HF$_{k}$ with k the space bound, the literature often uses HF$_{M}$ with $M = k + r - 1$ being the number of bin types.

The general APR can be formulated as follows. (See the end of Sect. 2 for the definitions of the quantities $t_{s}(r)$ and $h_{\infty }(r).$)

Theorem 10 (Lee and Lee [143], Galambos [92])

Suppose that $L \in V _{\alpha }$ with $\alpha \in ( \frac{1} {r+1}, \frac{1} {r}]$ for some positive integer r and choose any sequence $k_{s},\ s \geq 1,$ such that $t_{s}(r) < k_{s} + 1 \leq t_{s+1}(r)$. Then

$$\lim _{s\rightarrow \infty }R_{\mathrm{HF}_{k_{s}}}^{\infty }(\alpha ) =\lim _{ s\rightarrow \infty }\left (1 +\displaystyle\sum _{ j=2}^{s} \frac{1} {t_{j}(r) - 1} + \frac{k_{s} + r - 1} {(t_{s+1}(r) - 1)(M - 1)}\right ) = h_{\infty }(r).$$

The results in [92, 143] gave tight bounds only for the cases $k = t_{j}(r) - r + 1$ and $k = t_{j+1}(r) - r$ for integers $j \geq 1.$ Also, considering only the $\alpha = 1$ case, one can see that, to obtain an APR better than $\frac{17} {10}$, at least seven open bins are needed. These observations raised two further questions:

• For the case $\alpha = 1$, is there an on-line, bounded-space algorithm that uses fewer than 7 bins and has an APR better than $\frac{17} {10}$?

• What are tight bounds on HF$_{k}$ for specific $k$?

An affirmative answer to the first question was given by Woeginger [175]. Using a more sophisticated interval structure, one based on the Golomb sequences, the performance of his Simplified Harmonic (SH$_{k}$) algorithm improved on the $\frac{17} {10}$ bound with six open bins; precisely, $R_{\mathrm{SH}_{6}}^{\infty }\approx 1.69444.$ Moreover, Woeginger proved the following deeper, more general result.

Theorem 11 (Woeginger [175])

To achieve the worst-case performance ratio of heuristic HF $_{k}$ with k open bins and $\alpha = 1$, heuristic SH $_{k}$ only needs $O(\log \log k)$ open bins.

The second question was investigated by Csirik and Johnson [60] (see also [59]) and van Vliet [172, 173]. They gave tight bounds for the case $\alpha = 1$ with $k = 4$ and 5. Tight bounds for further k remain open problems.

Similarly, the general case has not been discussed exhaustively, and some questions raised by Woeginger [175] are still open:

• What is the smallest k such that there exists an on-line heuristic using $k$-bounded space and having an APR strictly less than $\frac{17} {10}$?

• What is the best possible APR for any on-line heuristic using 2-bounded space? (ABB$_{2}$ achieves a worst-case ratio of $\frac{17} {10}.$)

• By considering only algorithms that pack the items by the Next-Fit rule according to some fixed partition of $(0,1]$ into $k$ subintervals, which partition gives the best APR ? (It is known that for $k \leq 2$, the best possible APR is $2$ (see Csirik and Imreh [58]), but for $k \geq 3$, no tight bound is known.)

Tables 1 and 2 show the best results known for bounded-space algorithms. Note that the worst-case ratios of all algorithms in Table 1 are never smaller than $h_{\infty }(1) \approx 1.69103.$ As pointed out by Lee and Lee [143] for the $\alpha = 1$ case, bounded-space algorithms cannot do better. The result holds for general $\alpha$ too, as shown by Galambos, that is,

Theorem 12 (Lee and Lee [143], Galambos [92])

Every bounded-space on-line bin packing algorithm $A$ satisfies $R_{A}^{\infty }(\alpha ) \geq h_{\infty }(r)$ for all $\alpha,\ \frac{1} {r+1} <\alpha \leq \frac{1} {r}.$

None of the known bounded-space algorithms achieves the lower bound using a finite number of open bins. It will be later shown (see Sect. 3.7) that the bound can be achieved with three open bins if repacking among the open bins is allowed, but without such a relaxation, the question remains open.

Table 2 APR values for $\mathrm{HF}_{k}({ 1 \over r} ).$ Starred values are tight

Table 1 APR values for bounded-space algorithms, rounded to five decimals. The values in column HF$_{k} \leq$ are upper bounds and are tight if starred. Note that $42 = t_{4}(1) - 1$

3.5 Variations and the Best-in-Class

Chronologically, Yao [180] was the first to break through the $h_{\infty }(1)$ barrier with his Refined First-Fit (RFF) algorithm. RFF classifies items into types 1, 2, 3, or 4 accordingly as their sizes are in the respective intervals $(0, \frac{1} {3}]$, $(\frac{1} {3}, \frac{2} {5}]$, $(\frac{2} {5}, \frac{1} {2}]$, and $(\frac{1} {2},1].$ RFF packs four sequences of bins, one for each type. With one exception, RFF packs type-$i$ items into the sequence of type-$i$ bins using First-Fit. The exception is that every sixth type-2 item (with a size in $(\frac{1} {3}, \frac{2} {5}]$) is thrown in with the type-4 items, that is, packed by First-Fit into the sequence of type-4 bins. It is easily verified that RFF uses unbounded space and has a time complexity $O(n\log n).$ Yao proved that $R_{\mathrm{RFF}}^{\infty } = \frac{5} {3} = 1.666\ldots.$ Yao did not use the usual weighting function technique but based his proof on enumeration of the elements in each class. Also, the APR remains unchanged if the special treatment given every sixth type-2 item is instead given every $m$-th type-2 item, where m is taken to be one of 7, 8, or 9.

It was immediately clear that this reservation technique was a promising approach, a fact supported by the Harmonic-Fit algorithm discussed in the previous section. The main disadvantage of the latter algorithm is that each $I_{1}$-element, even with a size slightly over $\frac{1} {2}$, is packed alone into a bin. An immediate improvement is to try to add other items to these bins. In their algorithm Refined Harmonic-Fit (RHF), Lee and Lee [142, 143] modified HF$_{20}$ by subdividing intervals $I_{1}$ and $I_{2}$ into two subintervals:

$$\begin{array}{l@{\quad }l@{\quad }l} I_{1}\quad & =\quad &I_{1,s} \cup I_{1,b}, \\ I_{2}\quad & =\quad &I_{2,s} \cup I_{2,b} \end{array}$$

with $I_{2,s} = (\frac{1} {3}, \frac{37} {96}]$, $I_{2,b} = (\frac{37} {96}, \frac{1} {2}]$, $I_{1,s} = (\frac{1} {2}, \frac{59} {96}]$, and $I_{1,b} = (\frac{59} {96},1].$ This brought the number of bin types to $M = 22.$ The packing strategy for $I_{j}$-elements ($3 \leq j \leq M - 2 = 20$), $I_{1,b}$-elements, and $I_{2,b}$-elements is the same as in Harmonic-Fit, but the $I_{1,s}$-elements and the $I_{2,s}$-elements are allowed to share the same bins in certain situations. The details are omitted. Note however that the time complexity of RHF is $O(n)$, but the algorithm is no longer bounded space. Its APR is given by

Theorem 13 (Lee and Lee [143])

$R_{\mathrm{RHF}}^{\infty }\leq \frac{373} {228} \approx 1.63596.$

It is not known whether this bound is tight.

In 1989, several improved algorithms were presented by Ramanan et al. [159]. The first one, called Modified Harmonic-Fit (MHF), applies Yao’s idea in a more sophisticated way. Instead of choosing $\frac{59} {96}$ as the point dividing $(\frac{1} {2},1]$, the problem is handled in a more general fashion. Let the number of bin types satisfy $M \geq 5$, and consider the subdivision of $(0,1]$:

$$(0,1] =\displaystyle\bigcup _{ j=1}^{M-2}I_{ j}$$

with $I_{1} = I_{1,s} \cup I_{1,b}$ and $I_{2} = I_{2,s} \cup I_{2,b}$ as earlier, but now

$$\begin{array}{rrlrrl} I_{1,s}& =&(\frac{1} {2},1 - y]\quad &I_{2,s}& =&(\frac{1} {3},y] \\ I_{1,b}& =&(1 - y,1] & I_{2,b}& =&(y, \frac{1} {2}]\\ \end{array}$$

for some y satisfying $\frac{1} {3} < y < \frac{1} {2}.$ Initially, the set of empty bins is divided into M infinite classes, each associated with a subinterval. All $I_{1,b}$-bins, $I_{2,s}$-bins, $I_{2,b}$-bins, and $I_{j}$-bins ($3 \leq j \leq M - 2$) are only used to pack elements from the associated interval (as in Harmonic-Fit). $I_{1,s}$-bins on the other hand can contain $I_{1,s}$-elements and some of the $I_{2,s}$-elements and $I_{j}$-elements ($j \in \{ 3,6,7,\ldots,M - 2\}$). The algorithm also includes more complicated rules for packing and for deciding when items with sizes in different intervals can share the same bin. For this algorithm with $M = 40$, the following bounds hold.

Theorem 14 (Ramanan et al. [159])

$$1.6156146 < \frac{3} {2} + \frac{1} {9} + \frac{1} {222} - \frac{1} {987012} \leq R_{\mathrm{MHF}}^{\infty } < \frac{3} {2} + \frac{1} {9} + \frac{1} {222} = 1.615615\ldots.$$

The above algorithm was further generalized by Ramanan et al. [159] who introduced a sequence of classes of on-line linear-time algorithms, called ${C}^{(h)}$; an algorithm A belongs to ${C}^{(h)}$, for a given $h \geq 1$, if it divides $(0,1]$ into disjoint subintervals including

$$\begin{array}{lrrlrrll} & I_{1,b}& =&(1 - y_{1},1],\quad \quad &I_{2,b}& =&(y_{h}, \frac{1} {2}], & \\ &I_{1,j}& =&(1 - y_{j+1},1 - y_{j}],\quad \quad &I_{2,j}& =&(y_{h-j},y_{h-j+1}],&\quad 1 \leq j \leq h, \\ \mbox{ and} \\ & I_{\lambda,1} & =&(0,\lambda ], & I_{\lambda,2} & =&(\lambda, \frac{1} {3}], &\quad 0 <\lambda \leq \frac{1} {3} \end{array}$$

where $\frac{1} {3} = y_{0} < y_{1} <\ldots < y_{h} < y_{h+1} = \frac{1} {2}$, and $I_{\lambda,2} = \varnothing$ if $\lambda = \frac{1} {3}.$ Elements are classified, as usual, according to the intervals in which their sizes fall.

Note that algorithm MHF belongs to ${C}^{(1)}.$ Ramanan et al. [159] developed an algorithm (Modified Harmonic-2, MH2), which is in ${C}^{(2)}$ and proved that $R_{\mathrm{MH2}}^{\infty }\leq 1.612\ldots.$ The algorithm is quite elaborate and beyond the scope of this survey. The authors discussed further improvements aimed at reducing the APR to $1.59.$ They also proved the lower bound result.

Theorem 15 (Ramanan et al. [159])

There is no on-line algorithm A in ${C}^{(h)}$ such that $R_{A}^{\infty } < \frac{3} {2} + \frac{1} {12} = 1.58333\ldots.$

The HARMONIC+1 algorithm of Richey [160] subdivides intervals $(\frac{1} {2},1]$ and $(\frac{1} {3}, \frac{1} {2}]$ very finely (using 76 classes of subintervals!) in order to allow a precise item pairing in these two intervals. It also allows items of size $(\frac{1} {4}, \frac{1} {3}]$ to be mixed with larger items of various sizes and not just with those of size at least $\frac{1} {2}.$ Seiden [163] showed that such result was flawed and gave a new algorithm, HARMONIC++, whose asymptotic performance ratio is at most 1.58889, which is the current best APR for on-line bin packing.

3.6 APR Lower Bounds

In previous sections, some results concerning lower bounds on the APR were mentioned, but the fundamental problem was not considered yet: what is the best an on-line algorithm can do in the asymptotic worst case? In this section, lower bound results are discussed in chronological order.

Most of the existing lower bounds come from the same idea. To obtain a good packing, it seems advisable to first pack the large elements so that either a bin is “full enough” or its empty space can be reduced by subsequent small elements. Therefore, in order to force bad behavior on a heuristic algorithm $A$, one should challenge it with a list in which small items come first. If A adopts a policy that packs these small items tightly, then it will not be able to find a good packing for the large items which may come later. If, instead, $A$ leaves space for large items while packing the small ones, then the expected large items might not appear in the list. In both cases, the resulting packing will be poor.

To give a more precise description, consider a simple example involving two lists $L_{1}$ and $L_{2}$, each containing n identical items. The size of each element in $L_{1}$ is $\frac{1} {2} - \epsilon$, and the size of each element in $L_{2}$ is $\frac{1} {2} + \epsilon.$ The asymptotic behavior of an arbitrary approximation algorithm A will be investigated on two lists: $L_{1}$ alone and the concatenated list $L_{1}L_{2}.$ It is easy to see that $\mathit{OPT}(L_{1}) = \frac{n} {2}$ and ${\it \text{OPT}}(L_{1}L_{2}) = n.$ Consider the behavior of this algorithm on $L_{1}$: it will pack some elements alone into bins (say x of them), and it will match up the remaining $n - x.$ Hence $A(L_{1}) = \frac{n+x} {2}.$ For the concatenated list $L_{1}L_{2}$, when processing the elements of $L_{2}$, the best that A can do is to add one element of $L_{2}$ to each of x bins containing a single element of $L_{1}$ and to pack alone the remaining $n - x$ elements. Therefore, $A(L_{1}L_{2}) = \frac{3n-x} {2}.$ Since n may be arbitrarily large,

$$R_{A}^{\infty }\geq \max \left \{ \frac{A(L_{1})} {\mathit{OPT}(L_{1})}, \frac{A(L_{1}L_{2})} {\mathit{OPT}(L_{1}L_{2})}\right \} =\max \left \{\frac{n + x} {n},\ \frac{3n - x} {2n} \right \}$$

for which the minimum is attained when $x = \frac{n} {3}$, implying a lower bound of $\frac{4} {3}$ for the APR of any on-line algorithm $A.$

The above idea can be easily generalized by taking a carefully chosen series of lists $L_{1},\ldots,L_{k}$ and evaluating the performance of a heuristic on the concatenated lists $L_{1}\ldots L_{j}$, ($1 \leq j \leq k$). The first step along these lines was made by Yao [180]. He proved a lower bound of $\frac{3} {2}$ based on three lists of equal-size elements, the sizes being $\frac{1} {2} + \epsilon$, $\frac{1} {3} + \epsilon$, and $\frac{1} {6} - 2\epsilon.$ Using Sylvester’s sequences, Brown [32] and Liang [147] independently gave a further improvement to $1.53634577\ldots.$ (The largest sizes in their sequences were as follows: $\frac{1} {2} + \epsilon$, $\frac{1} {3} + \epsilon$, $\frac{1} {7} + \epsilon$, $\frac{1} {43} + \epsilon$, and $\frac{1} {1,807} + \epsilon.$) Galambos [92] used the Golomb sequences to extend the idea to general $\alpha.$ The proof in [92] was considerably simplified by Galambos and Frenk [93]. van Vliet gave an exhaustive analysis of the lower bound constructions with a linear programming technique applied to all $\alpha$ and gave the following lower bound:

Theorem 16 (van Vliet [171])

For any on-line algorithm $A$, $R_{A}^{\infty }\geq 1.54015\ldots$

The current best-in-class, $R_{A}^{\infty }\geq 1.54037$, was given by Balogh et al. [15]. Table 3 gives a comparison for several values of $\alpha = \frac{1} {r}$ between the best lower bounds and the corresponding upper bounds for various algorithms. It is interesting to note that the gap between the lower and upper bounds becomes rather small for $r \geq 2.$

Table 3 Lower bounds and $R_{A}^{\infty }$ for various algorithms

Faigle, Kern, and Turán [83] proved that if there are only two item sizes, then no on-line algorithm can be better that 4/3.

Chandra [38] has examined the effect on lower bounds when randomization is allowed in the construction of on-line algorithms, that is, when coin flips are allowed in determining where to pack items. The performance ratio for randomized algorithm A is now $E[A(L)]/{\it \text{OPT}}(L)$, where $E[A(L)]$ is the expected number of bins needed by A to pack the items in $L.$ Chandra has shown that there are lists such that this ratio exceeds $1.536$ for all randomized on-line algorithms, and so from this limited standpoint, results suggest that randomization is not a valuable tool in the design of on-line algorithms.

3.7 Semi-on-line Algorithms

The APR of on-line algorithms cannot break through the $1.540\ldots$ barrier (see Sect. 3.6). For almost 20 years, only the pure on-line and off-line algorithms were analyzed, and no attention was paid to algorithms lying between these two classes. In a more general setting, one can consider giving the algorithm more information about the list and/or more freedom with respect to the pure on-line case. This section deals with semi-on-line (SOL) algorithms that can

• Repack elements

• Look ahead to later elements before assigning the current one

• Assume some preordering of the elements

First consider the case where repacking is allowed. SOL algorithms allowing only a restricted number of elements to be repacked at each step are called c-repacking SOL algorithms. It was seen in Sect. 3.4 that no known on-line bounded-space algorithm reaches the bound $h_{\infty }(1)$ using finitely many open bins. It will be shown that this is possible with SOL algorithms.

In 1985, Galambos [91] made a first step in this direction. His Buffered Next-Fit (BNF) algorithm uses two open bins, say $B_{1}$ and $B_{2}.$ The arriving elements are initially packed into $B_{1}$, until the first element arrives for which $B_{1}$ does not have enough space. This element and those currently packed in $B_{1}$ are then reordered by decreasing size and repacked in $B_{1}$ and $B_{2}$ following the Next-Fit rule. $B_{1}$ is now closed, $B_{2}$ is renamed $B_{1}$, and a new bin $B_{2}$ is opened. Using a weighting function approach, it was proved that $h_{\infty }(1) \leq R_{\mathrm{BNF}}^{\infty }\leq \frac{18} {10}.$

Galambos and Woeginger [95] generalized the above idea, adopting a better weighting function. Let $w(B)$ be the sum of the weights associated with the items currently packed in bin $B.$ Their Repacking algorithm (REP$_{3}$) uses three open bins. When a new item $a_{i}$ arrives, the following steps are performed: (i) $a_{i}$ is packed into an empty bin; (ii) all the elements in the three open bins, sorted by nonincreasing size, are repacked by the FF strategy, with the result that either one bin becomes empty or at least one bin B has $w(B) \geq 1$; and (iii) all bins B with $w(B) \geq 1$ are closed and replaced by new empty bins. In [95], it was proved that this repacking in fact helps, since $R_{\mathrm{REP}_{3}}^{\infty } = h_{\infty }(1).$ It is not known whether the same result can be obtained with two bins.

Gambosi et al. [99] (see also [97] and [98]) were the first to beat the $1.540$ on-line bound via repacking. They gave two algorithms. Both of them use an unusual step to repack the elements: the small elements are grouped into a “bundle” of $O(n)$ elements, which can be repacked in a single step.

In the first algorithm, A$_{1}$, the interval $(0,1]$ is divided into four subintervals, and the elements are packed into bins in a Harmonic-like way. As each new item is packed, groups of small elements can be repacked – in a bundle – so as to fill up gaps in bins that are not full enough. By using appropriate data structures, this repacking is performed in constant time. The algorithm has linear time and space complexity, and it has an APR, $R_{\mathrm{A}_{1}}^{\infty }\leq \frac{3} {2}.$ In the second algorithm, A$_{2}$, the unit interval is divided into six subintervals, and, as each new item is encountered, the elements are repacked more carefully, in $O(\log n)$ time, by means of a pairing technique analogous to that introduced by Martel (see Sect. 4.2). The time complexity of A$_{2}$ is $O(n\log n)$, and its APR is $R_{\mathrm{A}_{2}}^{\infty }\leq \frac{4} {3}.$

Ivkovic and Lloyd [122] gave a further improvement on SOL algorithms achieving a $\frac{5} {4}$ worst-case ratio. Their algorithm is much more complicated than the previous ones, as it was designed for handling the dynamic packing case. The dynamic bin packing problem will be considered in Sect. 7.1 in detail, but here it is enough to know that in case of dynamic packing, deletions of some elements are allowed in each step and $A(L)$ is considered as the maximum number of occupied bins during the packing. Ivkovic and Lloyd proved a $\frac{4} {3}$ lower bound for the c-repacking SOL algorithms. This result was improved by Balogh et al. [14].

Theorem 17 (Balogh et al. [14])

For any c-repacking SOL algorithm A, the APR satisfies $R_{A}^{\infty }\geq 1.3871\ldots.$

Ivkovic and Lloyd [121] also presented approximation schemes for their dynamic, SOL model, applying the techniques of Fernandez de la Vega and Lueker and those of Karmarkar and Karp cited in Sect. 4.3.

Consider now the case in which the algorithm is allowed to look ahead, in the sense that, when an element arrives, it is not necessary to pack it immediately; one is allowed to collect further elements whose sizes can effect the packing decision. In order to avoid relaxation to off-line algorithms, consider the case of bounded lookahead. Grove [111] proposed a $k$-bounded algorithm which had, in addition, a capacity (or warehouse) constraint $W.$ The algorithm can delay the packing of item $a_{i}$ until it has collected all subsequent elements $a_{i+1},\ldots,a_{j}$ such that $\sum _{r=i}^{j}a_{r} \leq W.$ For any fixed $k$ and $W$, the $h_{\infty }(1)$ lower bound (see Theorem 12) remains valid, but Grove’s Revised Warehouse (RW) algorithm reaches the bound if W is sufficiently large. In his proof, Grove uses a weighting function argument.

Another subclass of the lookahead SOL problems arises if the input list is divided into a number of batches. If an algorithm works on a batched list, then it has to pack each batch as an off-line list (i.e., lookahead is only possible within the current batch). However, while packing elements of the current batch, the items of earlier batches cannot be moved. If the number of batches is bounded by $m$, the problem is called m-batched bin packing (BBP) problem. Gutin et al. [112] were the first to study the BBP problem: they investigated in depth the 2-BBP problem and proved a lower bound of $1.3871\ldots$ for this case.

The rarely considered class of algorithms in which it is assumed that the input list is presorted is finally considered. Because of the lower bound constructions, it is easy to see that, if the list is presorted by increasing item size, the on-line lower bounds remain valid. Moreover, the Johnson result holds: if the list is presorted by decreasing item size, then $\frac{11} {9} \leq R_{A}^{\infty }\leq \frac{5} {4}$ for any algorithm $A \in \mathcal{A}\mathcal{F}$ (see Theorem 21). This begged the broader question of lower bounds: how good can an arbitrary algorithm be? Based on two different lists, a partial answer was given in the early 1980s by Csirik et al. [64]. They proved that if the list is presorted by decreasing item size, then $R_{A}^{\infty }\geq \frac{8} {7}$ for all algorithms A. Although this approach seemed to be very simple (the authors used only two different list types), no progress was made until very recently Balogh et al. [15] gave an improved lower bound:

Theorem 18 (Balogh et al. [15])

If the list is presorted by decreasing item size, then $R_{A}^{\infty }\geq \frac{54} {47}$ for all algorithms A.

4 Off-line Algorithms

An off-line algorithm has all items available for preprocessing, reordering, grouping, etc. before packing. It has been seen that most of the classical on-line algorithms achieve their worst-case ratio when the items are packed in increasing order of size (see, e.g., FF and BF), or if small and large items are merged (see, e.g., NF). Thus, one is led to expect improved behavior by a sorting of the items in decreasing order of size. Note that the $O(n\log n)$ sorting step makes the algorithm no longer linear time.

The review starts with results for approaches that sort the items before executing one of the on-line algorithms. Linear-time heuristics are then considered. The section is concluded by approximation schemes and by a discussion of the anomalous behavior that is exhibited by many bin packing algorithms, including both on-line and off-line algorithms.

4.1 Algorithms with Presorting

When the sorted list is packed according to the Next-Fit rule, one obtains the Next-Fit Decreasing (NFD) algorithm. This heuristic was investigated by Baker and Coffman, who proved by a weighting function argument that its APR is slightly better than that of FF and BF:

Theorem 19 (Baker and Coffman [13])

If $\alpha \in ( \frac{1} {r+1}, \frac{1} {r}]\ (r \geq 1)$, then $R_{\mathrm{NFD}}^{\infty }(\alpha ) = h_{\infty }(r).$

Packing the sorted list according to First-Fit or Best-Fit gives the algorithms First-Fit Decreasing (FFD) and Best-Fit Decreasing (BFD), with much better asymptotic worst-case performance.

Theorem 20 (Johnson et al. [129])

$R_{\mathrm{FFD}}^{\infty } = R_{\mathrm{BFD}}^{\infty } = \frac{11} {9}.$

The original proof was based on the weighting function technique, but subsequent proofs introduced dramatic changes; the giant case analysis made in 1973 by Johnson [126] was considerably shortened by Baker [12] in 1985, and in 1991, Yue [183] presented the shortest proof known so far. In parallel, the additive constant was also improved; Johnson had proved that $\mathrm{FFD}(L) \leq \frac{11} {9} \mathit{OPT}(L) + 4$, but Baker reduced the constant to 3, and Yue reduced it to 1. Then, in 1997, Li and Yue [146] further reduced the constant to $\frac{7} {9}$ and conjectured the tight value to be $\frac{5} {9}.$ However, in 2007, Dósa [68] closed the issue by proving that the tight value is $\frac{6} {9}.$

The behavior of BFD for general $\alpha$ is not known, but that of FFD has been intensively investigated. Johnson et al. [129] analyzed several cases, showing that

$$R_{\mathrm{FFD}}^{\infty }(\alpha ) = \left \{\begin{array}{c@{\quad }l@{\quad }c@{\quad }l@{\quad }c} \frac{11} {9} \quad &\mbox{ if}\quad & \frac{1} {2} \quad & <\alpha \leq \quad &1 \\ \frac{71} {60}\quad &\mbox{ if}\quad & \frac{8} {29}\quad & <\alpha \leq \quad &\frac{1} {2} \\ \frac{7} {6} \quad &\mbox{ if}\quad & \frac{1} {4} \quad & <\alpha \leq \quad &\frac{8} {29} \\ \frac{23} {20}\quad &\mbox{ if}\quad & \frac{1} {5} \quad & <\alpha \leq \quad &\frac{1} {4} \end{array} \right.$$

and conjecturing that, for any integer $m \geq 4$,

$$R_{\mathrm{FFD}}^{\infty }( \frac{1} {m}) = F_{m} := 1 + \frac{1} {m + 2} - \frac{2} {m(m + 1)(m + 2)}.$$

Twenty years later, Csirik [57] proved that the above conjecture is valid only for m even, and that, for m odd,

$$R_{\mathrm{FFD}}^{\infty }( \frac{1} {m}) = G_{m} := 1 + \frac{1} {m + 2} - \frac{1} {m(m + 1)(m + 2)}.$$

In the same year, the complete analysis of FFD for arbitrary values of $\alpha \leq \frac{1} {4}$ was published by Xu [178] (see also [179]), who showed that if m is even, then $F_{m}$ is the correct APR for any $\alpha$ in $( \frac{1} {m+1}, \frac{1} {m}]$, while for m odd, the interval has to be divided into two parts, with

$$R_{\mathrm{FFD}}^{\infty }(\alpha ) = \left \{\begin{array}{l@{\quad }l@{\quad }l} F_{m},\ \ \mbox{ if}\ \ \frac{1} {m+1} <\alpha \leq d_{m}\quad &\quad & \\ G_{m},\ \ \mbox{ if}\ \ d_{m} <\alpha \leq \frac{1} {m} \quad &\quad & \end{array} \right.$$

where $d_{m} := {(m + 1)}^{2}/({m}^{3} + 3{m}^{2} + m + 1).$

Recall that, after a presorting stage, all of the above algorithms belong to the Any-Fit class (see Sect. 3.3). Johnson showed that, after a presort in increasing order, Any-Fit algorithms do not perform well in the worst case; for example, their APRs must be at least $h_{\infty }(1)$ when $\alpha = 1.$ But presorting in decreasing order is much more useful.

Theorem 21 (Johnson [126, 127])

Any algorithm $A \in \mathcal{A}\mathcal{F}$ operating on a list presorted in decreasing-size order must have

$$\begin{array}{rcccl} \frac{11} {9} & \leq &R_{A}^{\infty }(1)& \leq &\frac{5} {4} \\ \frac{1} {m+2} - \frac{2} {m(m+1)(m+2)} & \leq & R_{A}^{\infty }(\alpha ) & \leq & \frac{1} {m+2},\mbox{ where }m = \lfloor \frac{1} {\alpha } \rfloor \mbox{ and }\alpha < \end{array}$$

(1.)

For a long time, the FFD bound was the smallest proved APR. Johnson [126] made an interesting attempt to obtain a better APR. His Most-k-Fit (MF$_{k}$) algorithm takes elements from both ends of the sorted list, packing bins one at a time. At any step, after trying to place the largest unpacked element into the current bin, the algorithm attempts to fill up the remaining space in the bin using the smallest k (or fewer) as yet unpacked items. As soon as the available space becomes smaller than the smallest unpacked element, the algorithm starts packing a new bin. The algorithm has time complexity $O({n}^{k}\log n)$, so it is practical only for small $k.$ Johnson conjectured that $\lim _{k\rightarrow \infty }R_{\mathrm{MF}_{k}}^{\infty } = \frac{10} {9}$, but almost 20 years later, the conjecture was contradicted by Friesen and Langston [90], who gave examples for which $R_{\mathrm{MF}_{k}}^{\infty }\geq \frac{5} {4}$, $k \geq 2.$

Yao [180] devised the first improvement to FFD. He presented a complicated $O({n}^{10}\log n)$ algorithm, called Refined First-Fit Decreasing (RFFD), with worst-case ratio $R_{\mathrm{RFFD}}^{\infty }\leq \frac{11} {9} - 1{0}^{-7}.$ Following this result, further efforts were made to develop better off-line algorithms. Garey and Johnson [102] proposed the Modified First-Fit Decreasing (MFFD) algorithm. The main idea is to supplement FFD with an attempt to improve that part of the packing containing bins with items of sizes larger than $\frac{1} {2}$ by trying to pack in these bins pairs of items (to be called S items) with sizes in $(\frac{1} {6}, \frac{1} {3}].$ The non-FFD decisions of MFFD occur only during the packing of S items. At the time these items come up for packing, the bins currently containing a single item larger than $\frac{1} {2}$ are packed first, where possible, in decreasing-gap order as follows. In packing the next such bin, MFFD first checks whether there are two still unpacked S items that can fit into the bin; if not, MFFD finishes out the remaining packing just like FFD. Otherwise, the smallest available S item is packed first in the bin; the largest remaining available S item that fits with it is packed second. The running time of MFFD is not appreciably larger than that for FFD, but Garey and Johnson proved that

Theorem 22 (Garey and Johnson [102])

$R_{\mathrm{MFFD}}^{\infty } = \frac{71} {60} = 1.18333\ldots.$

Another modification of FFD was presented by Friesen and Langston [90]. Their Best Two-Fit (B2F) algorithm starts by filling one bin at a time, greedily; when no further element fits into the current bin, and the bin contains more than one element, an attempt is made to replace the smallest one by two unpacked elements with sizes at least $\frac{1} {6}.$ When all the unpacked elements have sizes smaller than $\frac{1} {6}$, the standard FFD algorithm is applied. Friesen and Langston proved that $R_{\mathrm{B2F}}^{\infty } = \frac{5} {4}$, which is worse than $\frac{11} {9}.$ However, they further showed that a combined algorithm (CFB), which runs both B2F and FFD and takes the better packing, has an improved APR.

Theorem 23 (Friesen and Langston [90])

$1.16410\ldots = \frac{227} {195} \leq R_{\mathrm{CFB}}^{\infty }\leq \frac{6} {5} = 1.2.$

Concerning the absolute worst-case ratio, Johnson et al. [129] had already conjectured that, if the number of bins in the optimal solution is more than 20, then the absolute worst-case ratio of FF is no more than 1.7. The first results were given by Johnson et al. [129] and Simchi-Levi [169]. They showed that FF and BF have an absolute performance bound not greater than 1.75 and that FFD and BFD have an absolute performance ratio of 1.5. The latter is the best possible for the classical bin packing problem, unless $\mathcal{P} = \mathcal{N}\mathcal{P}.$ Xie and Liu [177] improved the bound for FF to 1.737. Zhang et al. [188] provided a linear-time bounded-space off-line approximation algorithm with an absolute worst-case ratio of 1.5 and a linear-time bounded-space on-line algorithm with an absolute worst-case ratio of 1.75. Berghammer and Reuter [24] gave a different linear-time algorithm with an absolute worst-case ratio of 1.5.

4.2 Linear Time, Randomization, and Other Approaches

The off-line algorithms analyzed so far have time complexity at least $O(n\log n).$ It is also interesting to see what can be accomplished in linear time – in particular, without sorting. The first such heuristic was constructed by Johnson [127]. His Group-X-Fit Grouped (GXFG) algorithm depends on the choice of a set of breakpoints $X$, defined by a sequence of real numbers $0 = x_{0} < x_{1} <\ldots < x_{p} = 1.$ For a given $X$, the algorithm partitions the items, according to their size, into at most $p$ classes, and renumbers them in such a way that items of the same class are consecutive and classes are ordered by decreasing maximum size. The bins are also collected into p groups according to their actual gap, defined as the maximum $x_{j}$ such that the current empty space in the bin is at least $x_{j}.$ The items are packed using the Best-Fit rule with respect to the actual gaps. The algorithm can be implemented so as to require linear time and has the following APR.

Theorem 24 (Johnson [127])

For all $m \geq 1$, if X contains— $\frac{1} {m+2}$, $\frac{1} {m+1}$, and $\frac{1} {m}$, then $R_{\mathrm{GXFG}}^{\infty }(\alpha ) = \frac{m+2} {m+1}$ for all $\alpha \leq 1$ such that $m = \left \lfloor \frac{1} {\alpha } \right \rfloor.$

For $\alpha = 1$, the above theorem gives $R_{\mathrm{GXFG}}^{\infty } = \frac{3} {2}$, a bound subsequently improved by Martel. His algorithm, H$_{4}$, uses a set $X =\{ \frac{1} {4}, \frac{1} {3}, \frac{1} {2}, \frac{2} {3}\}$, but it does not reorder the items. It instead inserts them into heaps and uses a linear search for the median-size item. The packing strategy makes use of an elaborate pairing technique.

Theorem 25 (Martel [154])

$R_{\mathrm{H}_{4}}^{\infty } = \frac{4} {3}.$

Later, Békési et al. [23] applied the Martel idea to a set $X =\{ \frac{1} {5}, \frac{1} {4}, \frac{1} {3}, \frac{3} {8}, \frac{1} {2},$ $\frac{2} {3}, \frac{4} {5}\}$ and improved the bound to $\frac{5} {4}.$ Making experimental comparisons, they further showed that this linear-time algorithm is faster than the less complicated FFD rule even for small problem instances. They also mentioned that, by using more breakpoints, one can further improve the above result, but the resulting algorithms would be linear time with a constant term so large that they would not be useful in practice.

Table 4 summarizes the tightest worst-case ratios of off-line algorithms (H$_{7}$ denotes the algorithm of Békési and Galambos [22]).

Table 4 Worst-case ratios of off-line algorithms. NA means “not analyzed”

As a final note on fast off-line algorithms, the reader is referred to the work of Anderson et al. [4] for the implementation of approximation algorithms on parallel architectures. They show that, with $n/\log n$ processors in the EREW PRAM model, a packing can be obtained in parallel in $O(\log n)$ time which has the same asymptotic $\frac{11} {9}$ bound as FFD.

Caprara and Pferschy [34] proposed a simple (although non-polynomial) algorithm, discussed in Sect. 7.2, for which they proved an upper bound on the worst-case ratio of $4/3 +\ln 4/3 = 1.62102\ldots.$

4.3 Asymptotic Approximation Schemes

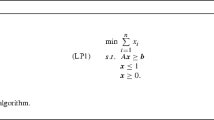
In 1980, Yao [180] raised an interesting question: does there exist an $\epsilon> 0$ such that every $O(n)$-time algorithm $A$ must satisfy the lower bound $R_{A}^{\infty }\geq 1 + \epsilon$? Fernandez de la Vega and Lueker [84] answered the question in the negative by constructing an asymptotic linear approximation scheme for bin packing. In their important paper, LP (linear programming) relaxations were first introduced as a technique for devising bin packing approximation algorithms. (See Sect. 8.1 for an integer programming formulation of the bin packing problem.) In this section, their result is first discussed, and then some improvements proposed by Johnson and by Karmarkar and Karp are introduced. Further discussion can be found in [52, 116].

The main idea in [84] is the following. Given an $\epsilon,\ 0 < \epsilon < 1$, define $\epsilon _{1}$ so that $\frac{\epsilon } {2} < \epsilon _{1} \leq \frac{\epsilon } {\epsilon +1}.$ Instead of packing the given list $L$, the algorithm packs a concatenation of three lists $L_{1}L_{2}L_{3}$ determined as follows:

• $L_{1}$ contains all the elements of L with sizes smaller than $\epsilon _{1}.$

• $L_{2}$ is a list of $(m - 1)h$ dummy elements with “rounded” sizes, corresponding to the $(m - 1)h$ smallest elements of $L \setminus L_{1}$, where $m = \left \lceil \frac{4} {{\epsilon }^{2}} \right \rceil$ and $h = \left \lfloor \frac{\vert L\setminus L_{1}\vert } {m} \right \rfloor.$ The elements of $L_{2}$ have only $m - 1$ different sizes, and, for each size $s$, the list has h elements; the sizes of the corresponding h elements in $L \setminus L_{1}$ are no greater than $s.$

• $L_{3}$ contains the remaining elements of $L \setminus L_{1}$, that is, those not having a corresponding rounded element in $L_{2}$, hence $\vert L_{3}\vert \leq 2h - 1.$

By construction, for each group of h elements of $L_{2}$ having the same size $s$, there exists a distinct group of h elements of $L \setminus L_{1}$ having sizes at least $s.$ It follows that ${\it \text{OPT}}(L_{2}) \leq {\it \text{OPT}}(L \setminus L_{1}).$

It is first proved that for a given $\epsilon$, one can construct, in linear time via an LP relaxation, a packing for the elements of $L_{2}$ that requires no more than $\mathit{OPT}(L \setminus L_{1}) + \frac{4} {\epsilon }$ bins. The next step is to pack each element of $L_{3}$ into a separate bin, so the number of open bins at this point is bounded by

$$\mathit{OPT}(L\setminus L_{1})+\frac{4} {\epsilon }+2h-1 < \mathit{OPT}(L\setminus L_{1})+\frac{4} {\epsilon }+\vert L\setminus L_{1}\vert \frac{{\epsilon }^{2}} {2} \leq \mathit{OPT}(L\setminus L_{1})(1+\epsilon )+\frac{4} {\epsilon }$$

(using the fact that $\mathit{OPT}(L \setminus L_{1}) \geq \frac{\epsilon } {2}\vert L \setminus L_{1}\vert$).

Finally, the items of $L_{1}$ are added to the current packing, one bin at a time, using the Next-Fit rule. If no new bin is opened in this phase, the resulting packing has the desired performance. If at least one new bin is opened, this implies that all the bins, except possibly the last one, are filled to at least $(1 - \epsilon _{1})$, and hence the total number of bins is bounded by

$$\frac{\mathit{OPT}(L)} {1 - \epsilon _{1}} + 1 \leq \mathit{OPT}(L)(1 + \epsilon ) + 1 \leq \mathit{OPT}(L)(1 + \epsilon ) + \frac{4} {\epsilon }.$$

Combining this with an analysis of the time to pack $L_{2}$, Fernandez de la Vega and Lueker proved the following result.

Theorem 26 (Fernandez de la Vega and Lueker [84])

For any $\epsilon> 0$, there exists a bin packing algorithm $A$ with asymptotic worst-case ratio $R_{A}^{\infty }\leq 1 + \epsilon$, requiring time $C_{\epsilon } + Cn\log \frac{1} {\epsilon }$, where $C_{\epsilon }$ depends only on $\epsilon$ and C is an absolute constant.

Although the time complexity of the above approximation scheme is polynomial in the number of elements, it is exponential in $\frac{1} {\epsilon }.$

The first improvement was given by Johnson [128], who observed that, if $\epsilon$ is allowed to grow suitably slowly with ${\it \text{OPT}}(L)$, one can use the above approach to construct a polynomial-time algorithm A such that $A(L) \leq {\it \text{OPT}}(L) + o({\it \text{OPT}}(L))$; incorporating a scheme suggested by Karmarkar and Karp, he achieved $A(L) \leq {\it \text{OPT}}(L) + O({\it \text{OPT}}{(L)}^{1-\delta })$, where $\delta$ is a positive constant. Thus, as a corollary to Theorem 26, there exists a polynomial-time approximation algorithm for bin packing with an APR equal to 1.

Karmarkar and Karp [132] made further improvements and produced an asymptotic fully polynomial-time approximation scheme. They brought several new techniques into play. The ellipsoid method applied to an LP relaxation drove the approach; a feasible packing was determined by an extension of the approach of Fernandez de la Vega and Lueker. A function $T$, estimated below, describes the time complexity of the LP problem in terms of properties of the problem instance. Let $c(L)$ denote the total size of the items in L and recall that k denotes the number, perhaps infinite, of possible item sizes. The main results are several different forms of asymptotic optimality and their associated running-time bounds. Recalling that the absolute error for an algorithm A is simply $A(L) -{\it \text{OPT}}(L)$, one has the following.

Theorem 27 (Karmarkar and Karp [132])

For each row in the table below, there is an approximation algorithm with the given running-time and absolute-error bounds; the approximation parameters in the last two rows satisfy $\alpha \in [0,1]$ and $\epsilon> 0$:

where

$$T_{n}(v) = O({v}^{8}\log {v\log }^{2}n + {v}^{4}n\log v\log n).$$

The bound on $T_{n}(v)$ is not especially attractive, so this approach as it stands is not likely to be very practical, although the authors mention that a mixture of their technique with a column generation method [105, 106] may be very efficient in practice.

Table 5

Taking a complementary approach, Hochbaum and Shmoys [118] (see also [117]) define an $\epsilon$-dual approximation algorithm for bin packing, denoted in the following by M$_{\epsilon }.$ For a given $\epsilon> 0$, M$_{\epsilon }$ finds in polynomial time a packing of L in ${\it \text{OPT}}(L)$ bins, each of capacity $C = 1 + \epsilon.$ A primary objective of M$_{\epsilon }$ is the approximation scheme for the capacity minimization problem discussed in Sect. 6.1, but such algorithms also find use in bin packing settings where precise bin capacities vary or are unknown.

The above dual approach can be likened to a search for near-feasible, optimal solutions rather than feasible, near-optimal solutions. The construction of M$_{\epsilon }$ exploits a reduction of the problem to bin packing with a finite number of item sizes and hence the integer program formulation in Sect. 5.2. A general discussion of the details has been given by Hochbaum [116], who describes a version of M$_{\epsilon }$ that requires only linear running time (with constants depending on $\epsilon$).

4.4 Anomalies

For a given algorithm $A$, one usually expects that if a list is made shorter, or its items made smaller, then the number of bins needed by $A$ to pack the list could not increase, and if the reductions were large enough, then the number of bins required would actually decrease. This is certainly true for optimal algorithms, but as this section shows, it is not the case for many of the better on-line and off-line approximation algorithms. This anomalous behavior can explain the difficulty in analyzing algorithms; with such behavior, inductive arguments cannot normally be expected to work. The following instances illustrate bin packing anomalies. Define

$$\begin{array}{rcllllllllllll} L& =&(0.7,&0.68,&0.5399,&0.3201,&0.15,&0.14,&0.08,&0.08,&0.08,&0.08,&0.08,&0.07)\\ {L}^{{\prime} } & = &(0.7, &0.68, &0.5399, &0.32, &0.15, &0.14, &0.08, &0.08, &0.08, &0.08, &0.08, &0.07) \end{array}$$

and note that the two instances differ only in the fourth element, which is slightly smaller in ${L}^{{\prime}}.$ BF and BFD produce the same packing of $L$:

$$\begin{array}{lll} c(B_{1})& =&0.7 + 0.15 + 0.08 + 0.07 \\ c(B_{2})& =&0.68 + 0.08 + 0.08 + 0.08 + 0.08 \\ c(B_{3})& =&0.5399 + 0.3201 + 0.14\end{array}$$

BF and BFD also produce the same packing of ${L}^{{\prime}}$, which is larger by one bin:

$$\begin{array}{lll} c(B_{1})& =&0.7 + 0.15 + 0.14 \\ c(B_{2})& =&0.68 + 0.32 \\ c(B_{3})& =&0.5399 + 0.08 + 0.08 + 0.08 + 0.08 + 0.08 \\ c(B_{4})& =\,0.07&\end{array}$$

A list $L_{(n)} = (a_{1},a_{2},\ldots,a_{n})$ dominates a list $L_{(m)}^{{\prime}} = (a_{1}^{{\prime}},a_{2}^{{\prime}},\ldots,a_{m}^{{\prime}})$ if $n \geq m$ and the size of each element $a_{i}$ is no less than the size of the corresponding element $a_{i}^{{\prime}}.$ An algorithm A is monotonic if $A(L) \geq A({L}^{{\prime}})$ whenever L dominates ${L}^{{\prime}}.$ An anomalous algorithm is one that is not monotonic.

Graham [110] and Johnson [126] observed that algorithms FF and FFD are anomalous. However, the current insights into the anomalous behavior of bin packing algorithms are due mainly to Murgolo. In the notation of Sect. 3.4 (with W meaning Worst-Fit), he proved

Theorem 28 (Murgolo [156])

Algorithms $NF$ and $NF_{2}$ are monotonic, but each of $BF$,$BFD$,$WF$,$WFD$,$ABF_{2}$,$AWF_{2}$, and $AFF_{k}$ with $k \geq 3$ is anomalous.

Murgolo also obtained upper and lower bounds on the behavior of anomalous algorithms. An algorithm is called conservative if it never opens a new bin unless the current element cannot fit into an open bin. For conservative algorithms, the following bound applies.

Theorem 29 (Murgolo [156])

If ${L}^{{\prime}}$ dominates L and $A$ is conservative, then $A({L}^{{\prime}}) \leq 2A(L)$. In addition, if $A \in \{ FFD,BFD\}$, then $A({L}^{{\prime}}) \leq \frac{11} {9} A(L) + 4.$

He also proved the following complementary results:

Theorem 30 (Murgolo [156])

There exist arbitrarily long lists $L_{i}$ and $L_{i}^{{\prime}}$, with $L_{i}^{{\prime}}$ dominating $L_{i},\ (i = 1,2,3)$, such that

$$\begin{array}{ll} if\ A \in \{\mathrm{BF,BFD}\} & \mathit{then} \; A(L_{1})\geq \frac{43} {42}A(L_{1}^{{\prime}}), \\ if\ A \in \{\mathrm{FF}\} & \mathit{then} \; A(L_{2})\geq \frac{76} {75}A(L_{2}^{{\prime}}), \\ if\ A \in \{\mathrm{WF,WFD}\}&\mathit{then} \; A(L_{3})\geq \frac{16} {15}A(L_{3}^{{\prime}}).\end{array}$$

The following sections discuss problems in which special types of lists, alternative objective functions, or any of various constraints on items or packings are considered. It will be seen that in some cases the problem becomes easier, in the sense of approximability, while in others it becomes harder. Similarly, adaptations of classical heuristics give more or less attractive results depending on the new problem.

5 Variations on Bin Sizes

5.1 Variable-Sized Bins

Consider the case where one is given different bin types, $B_{1},B_{2},\ldots,B_{k}$ with sizes $1 = s(B_{1})> s(B_{2})>\ldots> s(B_{k}).$ For each type, an unlimited number of bins are available, and the aim is to pack a list L of elements $a_{i}$, with $s_{i} \in (0,1]$, into a subset of bins having the smallest total size. Let $s(A,L)$ denote the total size of the bins used by algorithm $A$ to pack the items of $L.$ Then

$$R_{A}^{\infty } =\lim\, \sup _{ k\rightarrow +\infty }\left \{ \frac{s(A,L)} {s(\mathit{OPT},L)} : s(\mathit{OPT},L) \geq k\right \}.$$

The problem has practical importance in many of the classical bin packing applications, for example, cutting stock problems, the assignment of commercials to variable size breaks in television or radio broadcasting, and memory allocation for computer operating systems.

At first glance, one might expect variable-sized bin packing to be harder than the classical problem. However, this need not be true in general. For example, if there are bin types for all sizes between $\frac{1} {2}$ and $1$, then packing large elements with sizes at least $\frac{1} {2}$ can be done without wasted space. Similarly, smaller elements can be packed together without any waste, so long as their sum is at least $\frac{1} {2}.$

For general sets of bin sizes, an on-line algorithm must select the bin size for packing the current element whenever a new bin is opened. Friesen and Langston [89] proposed an on-line algorithm based on the Next-Fit rule, which always selects the largest bin size (Next-Fit, using Largest possible bins, NFL), and proved that its APR is $2.$ Kinnersley and Langston [138] showed that the same APR is obtained by adopting the First-Fit rule, both for an algorithm that uses the largest possible bins and for an algorithm that uses the smallest bins. Burkard and Zhang [33] pointed out that this APR characterizes a large class of algorithms that use one of the above bin-opening rules.

Kinnersley and Langston [138] analyzed other fast on-line algorithms. They proposed a scheme based on a user-specified fill factor, $f \geq \frac{1} {2}$, and proved that this strategy guarantees an APR smaller than $\frac{3} {2} + \frac{f} {2} \leq 1.75.$ Zhang [185] proved that with $f = \frac{1} {2}$, the APR is $\frac{17} {10}.$

Csirik [56] investigated an algorithm based on the Harmonic-Fit strategy (Variable Harmonic-Fit, VH) and showed that its APR is at most $h_{\infty }(1) \approx 1.69103.$ For special collections of bin types, the algorithm may perform better; for example, Csirik proved that if there are only two types of bins, with $s(B_{1}) = 1$ and $s(B_{2}) = \frac{7} {10}$, then $R_{\mathrm{VH}}^{\infty } = \frac{7} {5}.$

This result is very interesting since the bound is smaller than the 1.54 on-line lower bound of Balogh et al. [15] for the classical problem (see Sect. 3.6), and implies that, for certain sets of two or more bin sizes, on-line algorithms can behave better than those restricted to a single bin size.

Csirik’s VH algorithm suffers from the same “illness” as the classical HF$_{k}$ algorithm (see Sect. 3.4); it reaches the $h_{\infty }(1)$ bound only for a very large number of open bins. More precisely, let $M> 1$ be a positive integer, and suppose that the algorithm can use l different bin types. Let $M_{j} = \lceil Ms(B_{j})\rceil$ ($j = 1,\ldots,l$), and denote by VH$_{M}$ the resulting VH algorithm, which is a $k$-bounded-space algorithm with $k =\sum _{ j=1}^{l}M_{j} - l + 1.$ If $M_{l} \leq 5$ then $R_{\mathrm{VH}_{M}}^{\infty }\geq \frac{17} {10}.$

This raised further questions. If there are only two different bin types, which combination of sizes produces the smallest APR? What lower bounds depending on bin sizes can be proved? What can be said about the problem with at least three (or an arbitrary number of) bin sizes?

Some of the above questions were answered by Seiden [162], who revisited the VH algorithm. For the case where there are two bin sizes, he developed an algorithm that provides a lower bound for any fixed $\alpha.$ Specifically, he proved the following result:

$$1.37530 < \frac{78,392,621} {57,000,000} \leq \inf _{\alpha \in (0,1]}R_{OPT}^{\infty }(\alpha ) \leq \frac{395,101,163} {287,280,000} < 1.37532.$$

He additionally proved that the upper bound $h_{\infty }(1) \approx 1.69103$, given in [56], is tight and that algorithm VH is optimal among bounded-space algorithms. To obtain this result, Seiden used the weighting function technique and developed “twin” mathematical programs, which have the same sets of conditions but different objective functions. He used the mathematical programs to get lower and upper bounds for the asymptotic performance ratio of VH. He proved the asymptotic optimality of VH, although the precise value could not be computed.

The third question remained open even in the case of three different sizes.

Burkard and Zhang [33] investigated other bounded-space algorithms for variable-sized bin packing. They distinguished three different components: the opening rule, packing rule, and closing rule. The opening rule was fixed as follows. If the current item has size $s_{i}>\frac{1} {2}$ and there exist bin sizes smaller than 1 that can accommodate $a_{i}$, then the rule opens the smallest such bin; otherwise, it opens a bin of size $1.$ The packing rules analyzed were First-Fit (the F rule) and Best-Fit (the B rule). The closing rule closes a bin of size less than $1$, if one exists; otherwise, it closes either the lowest indexed bin (the first-bin or F rule) or the most nearly full bin (the best-bin or B rule). With this terminology, V$XY _{k}$ denotes the $k$-bounded algorithm that incorporates packing rule X and closing rule $Y.$ Burkard and Zhang showed that, among the four resulting algorithms (VFF$_{k}$, VFB$_{k}$, VBF$_{k}$, and VBB$_{k}$), VBB$_{k}$ is the best and that the following holds.

Theorem 31 (Burkard and Zhang [33])

$R_{\mathrm{VBB}_{k}}^{\infty } = \frac{17} {10}.$ Moreover, $R_{\mathrm{VH}_{M}}^{\infty }\geq R_{\mathrm{VBB}_{k}}^{\infty }$ if and only if $M_{l} < 7$, with $k \geq 6l + 1.$

The authors proved the theorem by a weighting function technique. They also mentioned that, with a small modification in the weighting function, they could prove that $R_{\mathrm{VFB}_{k}}^{\infty } = \frac{17} {10} + \frac{3} {10(k-1)}$ for any $k \geq 2.$ So, one of the more interesting questions remains open: does there exist an on-line algorithm with an APR strictly less than $h_{\infty }(1)$ for all collections of bin sizes?

For the off-line case, few results have been proved. Friesen and Langston [89] presented two algorithms based on the First-Fit Decreasing strategy. The first one, FFD using Largest bins and Repack (FFDLR), begins by packing the presorted elements into the largest bins, then repacks the contents of each open bin into the smallest possible empty bin. The second algorithm, FFD using Largest bins and Shift (FFDLS), improves on the first phase of FFDLR: whenever the bin (say of type $B_{j}$) where the current item has been packed contains an item of size at least $\frac{1} {3}$, the contents of the bin are shifted, if possible, to the smallest empty bin (say of type $B_{h}$) such that $s(B_{h}) \geq \tilde{ c} \geq \frac{3} {4}s(B_{h})$, where $\tilde{c}$ denotes the total item size packed into the current bin. Friesen and Langston proved that $R_{\mathrm{FFDLR}}^{\infty } = \frac{3} {2}$ and $R_{\mathrm{FFDLS}}^{\infty } = \frac{4} {3}.$

Seiden et al. [164] made great strides by improving the upper bound and giving the first – and to this very day the only – general lower bound for the case with two bin sizes. First, they introduced a parameter $\mu \in (\frac{1} {3}, \frac{1} {2}).$ They gave an algorithm $\mathrm{VH1}(\mu )$ for all $\alpha \in (0,1)$, and an algorithm $\mathrm{VH2}(\mu )$, only defined for $\alpha>\max \{ \frac{1} {2(1-\mu )}, \frac{1} {3\mu }\}.$ Both algorithms are combinations of the Harmonic and Refined Harmonic algorithms. The upper bound was achieved by optimizing $\mu$ over each choice of $\alpha$, and the authors chose the best value among $\mathrm{VH1}(\mu )$, $\mathrm{VH2}(\mu )$, and VH. The resulting upper bound is at most $\frac{373} {228} < 1.63597$ for all $\alpha.$ Note that this is the asymptotic performance ratio of the RHF algorithm in the classic bin packing context. The lower bound result is summarized by the following theorem.

Theorem 32 (Seiden et al. [164])

Any on-line algorithm for the variable-sized bin packing problem with two bin sizes has asymptotic performance ratio at least $\frac{495,176,908,800} {370,749,511,199}> 1.33561.$

The result is quite good since the largest gap between the two bounds is 0.18193 for $\alpha = 0.9071,$ and the smallest gap is 0.003371 for $\alpha = 0.6667.$

Murgolo [157] proposed an efficient approximation scheme. He first gave an algorithm with a running time linear in the number of items but exponential in $\frac{1} {\epsilon }$ and the number of bin sizes. Then, following the ideas in Karmarkar and Karp [132], he solved a linear programming formulation of the problem by the ellipsoid method, thus obtaining a fully polynomial-time approximation scheme.

Zhang [186] considered a variant of the on-line version of the problem, in which item-size information is known in advance, but no information on bin sizes is available, except that each bin size is known to be no less than the size of the largest item. Bins arrive one at a time, and one has to decide which items to pack into the current bin. Zhang proved that the analogues of the classical NF, FF, NFD, and FFD algorithms all have an APR equal to 2 and left as an open question whether one can devise an algorithm with an APR better than $2.$

Kang and Park [130] investigated a problem where there are m different bin sizes, and the total cost of a unit of each bin size does not increase with the bin size, that is,

$$\frac{c_{i_{1}}} {s(B_{i_{1}})} \leq \frac{c_{i_{2}}} {s(B_{i_{2}})},\quad \mathrm{if}\quad 1 \leq i_{1} < i_{2} \leq m.$$

They analyzed two algorithms, Iterative First-Fit Decreasing (IFFD) and Iterative Best-Fit Decreasing (IBFD), for three cases. If both the bin and item sizes are divisible, then both algorithms are optimal. If only the bin sizes are divisible, then $R_{\mathrm{IFFD}} = R_{\mathrm{IBFD}} = \frac{11} {9},$ whereas for the general (non-divisible) case, $R_{\mathrm{IFFD}} = R_{\mathrm{IBFD}} = \frac{3} {2}.$ In addition, they proved that an algorithm by Coffman et al. [51] for the variable-sized bin case does not provide the optimal solution.

The case of weak divisibility has not been treated.

5.2 Resource Augmentation

The idea of resource augmentation was introduced by Csirik and Woeginger [63]. The motivation is that the worst-case examples are “pathological,” that is, if for a unit-capacity bin one considers items with size $\frac{1} {2} + \epsilon$ with a sufficiently small $\epsilon,$ then only one item per bin can be packed. If the size of the bins is slightly increased, then two items can be packed in a bin, thus sparing a lot of capacity. (This is also called bin stretching.)

In this problem, an algorithm A has to pack a list L of elements in $(0,1]$ into a minimal number of bins of capacity $C \geq 1.$ Denote by $A_{C}(L)$ the number of bins used by A for packing L into bins of capacity $C.$ Then the APR is defined as follows:

$$R_{C}^{\infty } =\lim _{ OPT_{1}(L)\rightarrow \infty }\sup _{L}A_{C}(L),$$

where $OPT_{1}(L)$ is the optimal (off-line) packing of L into unit-capacity bins. Csirik and Woeginger considered on-line bounded-space algorithms and gave a complete analysis. For each $C$, a sequence $T(C) =\langle t_{1},t_{2},\ldots,\rangle$ of positive integers is defined:

$$t_{1} = \lfloor 1 + C\rfloor \qquad \mathrm{and}\qquad r_{1} = \frac{1} {C} - \frac{1} {t_{1}}$$

and, for $i = 2,3,\ldots$,

$$t_{i} = \left \lfloor 1 + \frac{1} {r_{i-1}}\right \rfloor \qquad \mathrm{and}\qquad r_{i} = r_{i-1} - \frac{1} {t_{i}}.$$

It is clear that this is a simple transformation of the Sylvester sequence, so

$$\frac{1} {C} =\displaystyle\sum _{ i=1}^{\infty }\frac{1} {t_{i}}.$$

They defined a new function

$$\rho (C) =\displaystyle\sum _{ i=1}^{\infty } \frac{1} {t_{i} - 1}$$

for which it is easy to prove that $\rho (C)$ is strictly decreasing on $[1,\infty )$, and $\rho (1) = h_{\infty }(1) \approx 1.69103,$ $\rho (2) \approx 0.69103.$ Furthermore, the following inequalities hold:

$$\frac{1} {m} \leq \rho (m) \leq \frac{1} {m - 1}\mbox{ for integer }m \geq 2.$$

For a given $l \geq 3$, they defined $t_{l}$ intervals: $\mathcal{I}_{j} = \big{(} \frac{C} {j+1}, \frac{C} {j} \big{]}$ for $j = 1,\ldots,t_{l} - 1,$ and $\mathcal{I}_{t_{l}} = \big{(}0, \frac{C} {t_{l}}\big{]}.$ For these intervals, they constructed a Harmonic-Fit type algorithm. There is one active bin for every interval $\mathcal{I}_{j}$, and all items from the interval $\mathcal{I}_{j} \cap \ (0,1]$ are packed into it using a Next-Fit rule. Using a weighting function (which is an adaptation of the one defined for the classical Harmonic-Fit algorithm), they proved the following theorem.

Theorem 33 (Csirik and Woeginger [63])

For every bin size $C \geq 1$, there exist on-line, bounded-space bin packing algorithms with APRs arbitrarily close to $\rho (C).$ For every bin size $C \geq 1$, the bound $\rho (C)$ cannot be beaten by an on-line bounded-space bin packing algorithm.

Azar and Regev [7] presented two on-line algorithms, each guaranteeing a worst-case performance of 5/3 for any number of bins. They also combined the algorithms to obtain an algorithm with a tight worst-case performance of $13/8 = 1.625.$ This turns out to be an interesting result, as the best lower bound for any algorithm is equal to 4/3 for $m \geq 2.$

On-line bounded-space bin packing with limited repacking was considered by Epstein and Kleiman [75], who extended to this case the ideas of Galambos and Woeginger [95]. They defined a semi-on-line algorithm, Resource Augmented $\mathrm{REP}_{3}(C)$ (RAR$_{3}(C)$), which is allowed to repack the elements within three active bins, and proved the following theorem.

Theorem 34 (Epstein and Kleiman [75])

For every bin size $C \geq 1$, and for any on-line bounded-space bin packing algorithm A that allows repacking within k active bins, $R_{\mathrm{A}}^{\infty }(C) \geq \rho (C).$ Algorithm $\mathrm{RAR}_{3}(C)$ has the best possible APR.

Epstein and van Stee [80] extended the study to on-line algorithms, investigating both lower and upper bounds. For the upper bound, they started with an analysis of the harmonic type algorithms. Recall that by introducing two new interval endpoints, $\Delta>1/2$ and $1 - \Delta$, one can combine one small element with an item in the interval $(1/2,\Delta ].$ Also recall that in this case, only a fraction of the bins belonging to interval i can be used to reserve space for a (possibly later arriving) element from the interval $(1/2,\Delta ].$ This fraction is denoted as ${\alpha }^{i}.$ (The values of ${\alpha }^{i}$s obviously depend on the number of intervals, and they are the crucial point of any such algorithm.) On this basis, they developed four algorithms, which are applied to the intervals $[1,6/5)$, $[6/5,4/3)$, $[4/3,12/7)$, and $[12/7,2)$, respectively.

An analytical solution was given only for the Tiny Modified-Fit algorithm, which was applied to interval $[12/7,2).$ To examine the worst-case behavior of the other algorithms, they defined two weighting functions and constructed a linear program $P(f).$ By applying it to the cost function, they could use the method introduced by Seiden [163], thus obtaining upper bounds for the asymptotic behavior of the algorithms. The cost functions were not given explicitly, but program P was solved for many C values, and a diagram was given to show the upper bounds.

Concerning lower bounds, Epstein and van Stee [80] followed the argument laid down by van Vliet [171]. In this case too, an LP was generated for many values of $C$, and appropriate sublists were obtained through specialized greedy algorithms.

Chan et al. [37] further extended the study to dynamic bin packing. They considered the case where the items may depart at any time and where moving items among the open bins is disallowed. They first investigated Any-Fit algorithms, proving the following theorem.

Theorem 35 (Chan et al. [37])

Consider the resource augmentation problem with bin capacity $C,$ and let A be an Any-Fit algorithm. Then A can achieve $1$ -competitiveness if and only if $C = 2.$

They also gave a new lower bound, as a function of $C$, for on-line algorithms. Let m be the largest integer such that $C - \frac{1} {m} < 1$, and define, for any positive integer $1 \leq i \leq m$,

$$\alpha (1) = m!(m - 1)!\qquad \beta (i) =\displaystyle\sum _{ j=1}^{i}\alpha (j)\qquad \alpha (i) = \frac{\beta (i - 1)} {(m - i + 2)(m - i + 1)}.$$

Theorem 36 (Chan et al. [37])

Let A be an on-line algorithm. Then

$$R_{\mathrm{A}}^{\infty }(C) \geq \max \left \{ \frac{\beta (m)} {m!(m - 1)!}, \frac{2} {C}\right \}.$$

They also analyzed certain classical algorithms:

Theorem 37 (Chan et al. [37])

$$\displaystyle\begin{array}{rcl} R_{\mathrm{FF}}^{\infty }(C)& \leq & \min \left \{\frac{2C + 1} {2C - 1}, \frac{5 - C} {2C - 1}, \frac{{C}^{2} + 3} {C(2C - 1)}\right \}, \\ R_{\mathrm{BF}}^{\infty }(C)& =& \frac{1} {C - 1} \\ \end{array}$$

and

$$\min \left \{\frac{2C + 2} {2C}, \frac{{C}^{2} - 8C + 20} {C(4C)} \right \} \leq R_{\mathrm{WF}}^{\infty }(C) \leq \frac{4} {{C}^{2}}\,.$$

(4)

Very recently, Boyar et al. [31] gave a complete APR analysis of algorithms WF and NF for the resource augmentation case. They showed that WF is strictly better than NF in the interval $1 < C < 2$ but has the same APR for all $C \geq 2$:

Theorem 38 (Boyar et al. [31])

Let $t_{C} = \lfloor \frac{1} {C-1}\rfloor.$ Then

$$R_{\mathrm{WF}}^{\infty }(C) = \left \{\begin{array}{lll} \frac{2C} {3C-2},&\mbox{ if}&C \in [1,2] \\ \frac{1} {C-1}, &\mbox{ if}&C \in [2,\infty ) \end{array} \right.$$

and

$$R_{\mathrm{NF}}^{\infty }(C) = \frac{2t_{C}^{2}C - 2t_{ C}^{2} - 4t_{ C} + 2 + 2Ct_{C}} {t_{C}^{2}C + 2Ct_{C} - t_{C}^{2} - 3t_{C} - 2 + 2C}.$$

6 Dual Versions

6.1 Minimizing the Bin Capacity

Suppose that the number of bins is fixed, and let the objective be a smallest C such that a given list L of items can be packed in m bins of capacity $C.$ This dual of bin packing actually predates bin packing and is known as multiprocessor or parallel-machine scheduling. It is a central problem of scheduling theory and is surveyed in depth elsewhere (see, e.g., Lawler et al. [141] and Hall [114]), so only relevant results and research directions will be highlighted. The problem is referred to as $P\vert \vert C_{\max }$ in scheduling notation.

Optimal and heuristic capacities normally differ by at most a maximum item size, so absolute worst-case ratios rather than asymptotic ones are considered. The first analysis of approximation algorithms was presented by Graham [108, 109], who studied the worst-case performance of various algorithms. For the on-line case, he investigated the Worst-Fit algorithm (better known as the List Scheduling, LS algorithm), which initially opens m empty bins and then iteratively packs the current item into the bin having the minimum current content (breaking ties in favor of the lowest bin index). Graham proved that $R_{\mathrm{LS}} = 2 - \frac{1} {m}$, a bound that for many years was thought to be best among on-line algorithms. Galambos and Woeginger were first to prove that the bound could be improved. Let $A(L,m)$ denote the bin capacity needed under A for m bins, and define

$$R_{A}(m) =\sup _{L}\left \{ \frac{A(L,m)} {\mathit{OPT}(L,m)}\right \}\ \ and\ \ R(m) =\inf _{A}R_{A}(m).$$

Theorem 39 (Galambos and Woeginger [94])

There exists a sequence of nonnegative numbers $\epsilon _{1},\epsilon _{2},\ldots$, with $\epsilon _{m}>0,\ m \geq 4$ and $\epsilon _{m} \rightarrow 0$ as $m \rightarrow \infty$, such that $R(m) \leq 2 - \frac{1} {m} - \epsilon _{m}.$

This result encouraged further research; important milestones on the way to the current position on the problem are as follows. Bartal et al. [19] presented an algorithm with a worst-case ratio $2 - \frac{1} {70} = 1.98571\ldots$ for all $m \geq 70.$ Earlier, Faigle et al. [83] proved lower bounds for different values of $m.$ They pointed out that for $m \leq 3$, the LS algorithm is optimal among on-line algorithms, and they proved a $1 + \frac{1} {\sqrt{2}} = 1.70710\ldots$ lower bound for $m \geq 4.$ Then these bounds were improved, as shown below.

Theorem 40 (Chen et al. [41])

For all $m = 80 + 8k$ with k a nonnegative integer, $R(m) \geq 1.83193.$

Theorem 41 (Bartal et al. [20])

For all $m \geq 3,454$,$R(m) \geq 1.8370.$

For some time, the following result gave the best upper bound for $R(m)$ and was a generalization of the methods in [20].

Theorem 42 (Karger et al. [131])

$R(m) \leq 1.945$ for all $m.$

A tighter result was found by Albers [2], who proved the next two bounds.

Theorem 43 (Albers [2])

$R(m) \leq 1.923$ for all $m.$

Just as previous authors, Albers recognized that, during the packing process, a good algorithm must try to avoid packings in which the content of each of the bins is about the same, for in such cases many small items followed by a large item can create a poor worst-case ratio. Albers’ new algorithm attempts to maintain throughout the packing process $\lfloor \frac{m} {2} \rfloor$ bins with small total content and $\lceil \frac{m} {2} \rceil$ bins with large total content. The precise aim is always to have a total content in the small-content bins that is at most $\gamma$ times the total content in the large-content bins. With an optimal choice of $\gamma$, one obtains a worst-case ratio of at most $1.923.$

For her new lower bound, Albers proved

Theorem 44 (Albers [2])

$R(m) \geq 1.852$ for all $m \geq 80.$

Attempts to further reduce the general gap of about $.07$ continue. For the special case $m = 4$, it is proved in Chen et al. [41] that $1.73101 \leq R(4) \leq \frac{52} {30} = 1.7333\ldots$, but the exact value of $R(4)$ remains an open problem. Another enticing open problem is: does $R(m) < R(m + 1)$ hold for any $m$?

The off-line case is now considered. By preordering the elements according to nonincreasing size and applying the LS algorithm, one obtains the so-called Largest Processing Time (LPT) algorithm for $P\vert \vert C_{\max }.$ Graham [109] proved that $R_{\mathrm{LPT}} = \frac{4} {3} - \frac{1} {3m}.$ The Multifit algorithm by Coffman et al. [47] adopts a different strategy, leading to better worst-case behavior. The algorithm determines, by binary search over an interval with crude but easily established lower and upper bounds, the smallest capacity C such that the FFD algorithm can pack all the elements into m bins. Coffman, Garey, and Johnson proved that if k binary search iterations are performed, then the algorithm, denoted by MF$_{k}$, requires $O(n\log n + kn\log m)$ time and has an absolute worst-case ratio satisfying

$$R_{\mathrm{MF}_{k}} \leq 1.22 + {2}^{-k}.$$

Friesen [87] improved the bound uniform in k to $1.2$, but Yue [182] later settled the question by proving that this bound is $\frac{13} {11}.$ Friesen and Langston [89] developed a different version of the Multifit algorithm, proving that its worst-case ratio is bounded by $\frac{72} {61} + {2}^{-k}.$

A different off-line approach was proposed by Graham [109]. His algorithm Z$_{k}$ optimally packs the $\min \{k,n\}$ largest elements and completes the solution by packing the remaining elements, if any, according to the LS algorithm. Graham proved that

$$R_{\mathrm{Z}_{k}} \leq 1 + \frac{1 - \frac{1} {m}} {1 + \left \lfloor \frac{k} {m}\right \rfloor }$$

and that the bound is tight when m divides $k.$ Algorithm Z$_{k}$ implicitly defines an approximation scheme. By selecting $k = k_{\epsilon } = \lceil \frac{m(1-\epsilon )-1} {\epsilon } \rceil$, one obtains $R_{\mathrm{Z}_{k_{\epsilon }}} \leq 1 + \epsilon.$ The running time is $O(n\log n + {m}^{m(1-\epsilon )/\epsilon })$, and so the method is unlikely to be practical. The result was improved by Sahni [161], in the sense that the functional dependence on $m$ and $\epsilon$ was reduced substantially. His algorithm A$_{\epsilon }$ has running time $O(n{(\frac{{n}^{2}} {\epsilon } )}^{m-1})$ and satisfies $R_{\mathrm{A}_{\epsilon }} \leq 1 + \epsilon$; hence it is a fully polynomial-time approximation scheme for any fixed $m.$

For m even moderately large, the approach of Hochbaum and Shmoys [118] offers major improvements. They developed an $\epsilon$-approximate algorithm that removed the running-time dependence on m and reduced the dependence on $n.$ The dependence on $\frac{1} {\epsilon }$ is exponential, which is to be expected, since a polynomial dependence would imply $\mathcal{P} = \mathcal{N}\mathcal{P}.$ Their algorithm is based on the binary search of an interval (like MF$_{k}$), but it uses the $\epsilon$-dual approximation algorithm of Sect. 4.3 at each iteration. Hochbaum and Shmoys show that, after k steps of the binary search, the bin capacity is at most $(1 + \epsilon )(1 + {2}^{-k})$ times optimal. From this fact and the properties of M$_{\epsilon }$ given in Sect. 4.3, one obtains a linear-time approximation scheme for the capacity minimization problem. (See also Hochbaum’s [116] for a more extensive discussion of this interesting technique.) The Hochbaum and Shmoys result was generalized by Alon et al. [3], who gave conditions under which a number of scheduling problems on parallel machines admit a polynomial-time approximation scheme.

6.2 Maximizing the Number of Items Packed

This section considers another variant in which the number of bins is fixed; the objective is now to pack a maximum cardinality subset of a given list $L_{(n)}.$ The problem arises in computing applications, when one wants to maximize the number of records stored in one or more levels of a memory hierarchy or to maximize the number of tasks performed on multiple processors within a given time interval.

The classical bin packing notation is extended in an obvious way by defining

$$\hat{R}_{A}(m,n) =\min \left \{ \frac{A(L_{(n)},m)} {\mathit{OPT}(L_{(n)},m)}\right \}$$

so that the APR is defined by

$$\hat{R}_{A}^{\infty }(m) =\lim _{ n\rightarrow \infty }\inf \hat{R}_{A}(m,n)$$

and has values less than or equal to $1.$

First consider off-line algorithms. The problem was first studied by Coffman et al. [48], who adapted the First-Fit Increasing (FFI) heuristic. The items are preordered according to nondecreasing size, the m bins are opened, and the current item is packed into the lowest indexed bin into which it fits, stopping the process as soon as an item is encountered that does not fit into any bin. It is proved in [48] that $\hat{R}_{\mathrm{FFI}}^{\infty }(m) = \frac{3} {4}$ for all $m.$

The Iterated First-Fit Decreasing (IFFD) algorithm was investigated by Coffman and Leung [45]. The algorithm sorts the items by nonincreasing size and iteratively tries to pack all the items into the m bins following the First-Fit rule. Whenever the current item cannot be packed, the process is stopped, the largest item is removed from the list, and a new FFD iteration is performed on the shortened list. The search terminates as soon as FFD is able to pack all the items of the current list. Coffman and Leung showed that IFFD performs at least as well as FFI on every list and that $\frac{6} {7} \leq \hat{ R}_{\mathrm{IFFD}}^{\infty }(m) \leq \frac{7} {8}.$ The time complexity of IFFD is $O(n\log n + mn\log m)$, but a tight APR is not known.

Lower bounds on the APR are now considered. If an algorithm A packs items $a_{1},\ldots,a_{t}$ from a list $L = (a_{1},\ldots,a_{n})$ so that $s_{i}>1 - s(B_{j})$ for any j and for any $i> t$ (i.e., no unpacked item fits into any bin), then it is said to be a prefix algorithm. Note that both FFI and and IFFD are prefix algorithms.

Theorem 45 (Coffman et al. [48])

Let A be a prefix algorithm and let $k =\min _{1\leq j\leq m}\{\vert B_{j}\vert \}$ be the least number of items packed into any bin. Then

$$\hat{R}_{A}^{\infty }(m) \geq \frac{mk} {mk + m - 1}.$$

Moreover, the bound is achievable for all $m \geq 1$ and $k \geq 1.$

The case of divisible item sizes was investigated by Coffman et al. [51]. They proved that both FFI and IFFD produce optimal packings if $(L,C)$ is strongly divisible. IFFD remains optimal even if $(L,C)$ is weakly divisible, but FFI does not.

The case of variable-sized bins was first analyzed by Langston [140], who proved that if the bins are rearranged by nonincreasing size, then $\hat{R}_{\mathrm{FFI}}^{\infty }(m) = \frac{1} {2}$ and $\frac{2} {3} \leq \hat{ R}_{\mathrm{IFFD}}^{\infty }(m) \leq \frac{8} {11}$ for all $m.$ Friesen and Kuhl [88] gave a new efficient algorithm, which is a hybrid of two algorithms defined earlier: First-Fit Decreasing (FFD) and Best-Two-Fit (B2F). The hybrid is iterative: it attempts to pack smaller and smaller suffixes of its list of items until it succeeds in packing the entire suffix. During each attempt, the hybrid partitions the current list of items and packs one part by B2F and then the other part by FFD. They proved an APR of $\frac{3} {4}$ for this hybrid.

Coming to the on-line case, Azar et al. [9] (see also [8]) studied the behavior of so-called fair and unfair algorithms. When there is a fixed number of bins, an on-line algorithm is fair if it rejects an item only if it does not fit in any bin, while an unfair algorithm is allowed to discard an item even if it fits. They show that an unfair algorithm may get better performance compared with the performance achieved by the fair version. In particular, they show that an unfair variant of First-Fit can pack approximately $2/3$ of the items for sequences for which an optimal off-line algorithm can pack all the items, while the standard (fair) First-Fit algorithm has an asymptotically tight performance arbitrarily close to $5/8.$ Later, Epstein and Favrholdt [74] proved that the APR of any fair, deterministic algorithm is $\frac{1} {2}\leq R_{A}\leq \frac{2} {3}$ and that a class of algorithms including BF has an APR of $\frac{n} {2n-1}.$

6.3 Maximizing the Number of Full Bins

In this variant of the problem, the objective is to pack a list of items into a maximum number of bins subject to the constraint that the content of each bin be no less than a given threshold $T.$ Each such bin is said to be full. Potential practical applications are (i) the packing of canned goods so that each can contains at least its advertised net weight and (ii) the stimulation of economic activity during a recession by allocating tasks to a maximum number of factories, all working at or beyond the minimal feasible level.

This problem is yet another dual of bin packing. A comprehensive treatment can be found in Assmann’s Ph.D. thesis [5]; Assmann’s collaboration with Johnson, Kleitman and Leung (see [6]) established the main results. They first analyzed an on-line algorithm, a dual version of NF (Dual Next-Fit, DNF): pack the elements into the current bin $B_{j}$ until $s(B_{j}) \geq T$, then open a new empty bin $B_{j+1}$ as the current bin. If the current bin is not full when all items have been packed, then merge its contents with those of other full bins. All on-line algorithms are allowed this last repacking step to ensure that all bins are full. It is proved in [6] that $\tilde{R}_{\mathrm{DNF}}^{\infty } = \frac{1} {2}$, where

$$\tilde{R}_{A}^{\infty } =\lim _{ m\rightarrow \infty }\inf \left (\min \left \{ \frac{A(L)} {\mathit{OPT}(L)} : \mathit{OPT}(L) = m\right \}\right ).$$

Assmann et al. [6] also studied a parametrized dual of FF, called Dual First-Fit (DFF[$r$]). Given a parameter $r$ ($1 < r < 2$), the current item $a_{i}$ is packed into the first bin $B_{j}$ for which $c(B_{j}) + s_{i} \leq rT.$ If there are at least two nonempty and unfilled bins (i.e., bins $B_{j}$ with $0 < c(B_{j}) < T$) when all items have been packed, an item is removed from the rightmost such bin and added to the leftmost, thus filling it. Finally, if a single nonempty and unfilled bin remains, then its contents are merged with those of previously packed bins. It was shown that $\tilde{R}_{\mathrm{DFF}[r]}^{\infty } = \frac{1} {2}$, although a better bound might have been expected. But some years later, Csirik and Totik proved that DNF is optimal among the on-line algorithms.

Theorem 46 (Assmann et al. [6] and Csirik and Totik [61])

$\tilde{R}_{\mathrm{DFF}[r]}^{\infty } ={ 1 \over 2}$ and there is no on-line dual bin packing algorithm A for which $\tilde{R}_{A}^{\infty }>\frac{1} {2}.$

Turning now to off-line algorithms, first consider the observation of Assmann et al. [6] that presorting does not help the adaptations of algorithms Next-Fit Decreasing and Next-Fit Increasing, for which $\tilde{R}_{\mathrm{NFD}}^{\infty } =\tilde{ R}_{\mathrm{NFI}}^{\infty } = \frac{1} {2}.$ On the other hand, the off-line version DFFD[$r$] of DFF[$r$], obtained by presorting the items according to nonincreasing size, has better performance.

Theorem 47 (Assmann et al. [6])

$\tilde{R}_{\mathrm{DFFD}[r]}^{\infty } = \frac{2} {3}$ if $\frac{4} {3} < r < \frac{3} {2}$ and $\lim _{r\rightarrow 1}\tilde{R}_{\mathrm{DFFD}[r]}^{\infty } =\lim _{r\rightarrow 2}\tilde{R}_{\mathrm{DFFD}[r]}^{\infty } = \frac{1} {2}.$

The Iterated Lowest-Fit Decreasing (ILFD) algorithm was also investigated in [6]. It is analogous to algorithm IFFD described in Sect. 6.2. The items are preordered by nonincreasing size. At each iteration, a prefixed number m of bins is considered, and a Lowest-Fit packing is obtained by iteratively assigning the current item to the bin with minimum contents. Binary search on m determines the maximum value for which all m bins are filled. Since n is an obvious upper bound on the optimal solution value, it is easily seen that the algorithm has $O({n\log }^{2}n)$ time complexity. Moreover,

Theorem 48 (Assmann et al. [6])

$\tilde{R}_{\mathrm{ILFD}}^{\infty } = \frac{3} {4}.$

It is not difficult to see that DNF does not produce optimal packings even when $(L,C)$ is strongly divisible. However, the following optimality results hold.

Theorem 49 (Coffman et al. [51])

If $(L,C)$ is strongly divisible, then the dual version of NFD (DNFD) produces an optimal packing. For weakly divisible lists, DNFD is no longer optimal, but ILFD is.

Concerning approximation schemes for the dual bin packing problem, first observe that the approach used by Fernandez de la Vega and Lueker [84] and Karmarkar and Karp [132] (see Sect. 4.3), which eliminates the effect of small items on worst-case behavior, does not appear applicable, as in the dual problem, small items can play an important role in filling small gaps. Csirik et al. [65] have given a PTAS for this problem. Later, an FPTAS was presented by Jansen and Solis-Oba [124].

7 Variations on Item Packing

7.1 Dynamic Bin Packing

The idea of Dynamic Bin Packing (DBP) was introduced by Coffman et al. [49]. In the case of dynamic packing, deletion of some elements is allowed at each step, and $A(L)$ is defined as the maximum number of bins used during the packing.

Consider the generalization in which each item $a_{i}$ is characterized by a triple $(s_{i},b_{i},d_{i})$, where $b_{i}$ is the start (arrival) time, $d_{i}$ (with $d_{i}>b_{i}$) is the departure time, and, as usual, $s_{i}$ is the size. Item $a_{i}$ remains in the packing during the time interval $[b_{i},d_{i}).$ Assume that $b_{i} \leq b_{j}$ if $i < j.$ The problem calls for the minimization of the maximum number, $\mathit{OPT}_{D}(L)$, of bins ever required in dynamically packing list L when repacking of the current set of items is allowed each time a new item arrives. More formally, if $A(L,t)$ denotes the number of bins used by algorithm A to pack the current set of items at time $t$, the objective is to minimize

$$A(L) =\max _{0\leq t\leq b_{n}}A(L,t).$$

Note that, in this case, an open bin can later become empty, so the classical open/close terminology is no longer valid. The definition of the APR is straightforward:

$$R_{A}^{\infty } =\lim _{ n\rightarrow \infty }\sup \left \{ \frac{A(L)} {\mathit{OPT}_{D}(L)} : \vert L\vert = n\right \}.$$

The problem models an important aspect of multiprogramming operating systems: the dynamic memory allocation for paged or other virtual memory systems (see, e.g., Coffman [42]), or data storage problems where the bins correspond to storage units (e.g., disk cylinders or tracks), and the items correspond to records which must be stored for certain specified periods of time (see Coffman et al. [49]).

Research on dynamic packing is at the boundary between bin packing and dynamic storage allocation. The most significant difference between the two areas lies in the repacking assumption of dynamic bin packing; repacking is disallowed in dynamic storage allocation, so fragmentation of the occupied space can occur. Coffman et al. [49] studied two versions of the classical FF algorithm. The first is a direct generalization of the classical algorithm. The second is a variant (Modified First-Fit, MFF) in which the elements with $s_{i} \geq \frac{1} {2}$ are handled separately, in an attempt to pair each of them with smaller elements.

Theorem 50 (Coffman et al. [49])

If $\frac{1} {k+1} <\max \{ s_{i}\} \leq \frac{1} {k}$, then

• $\frac{11} {4} \leq R_{\mathrm{FF}}^{\infty }(k) \leq \frac{5} {2} + \frac{3} {2}\ln \frac{\sqrt{13}-1} {2} = 2.89674\ldots$   if $k = 1$;

• $\frac{k+1} {k} + \frac{1} {{k}^{2}} \leq R_{\mathrm{FF}}^{\infty }(k) \leq \frac{k+1} {k} + \frac{1} {k-1}\ln \frac{{k}^{2}} {{k}^{2}-k+1}$   if $k \geq 2$;

• $2.77 \leq R_{\mathrm{MFF}}^{\infty }(1) \leq \frac{5} {2} +\ln \frac{4} {3} = 2.78768\ldots.$

For $k = 2$, one gets $\frac{7} {4} \leq R_{\mathrm{FF}}^{\infty }(2) \leq 1.78768\ldots.$ Although these results are worse than their classical counterparts, relative performance is much better than one might think. This can be seen in the following lower bounds.

Theorem 51 (Coffman et al. [49])

For any on-line dynamic bin packing algorithm $A$,$R_{A}^{\infty }\geq \frac{5} {2}$ and $R_{A}(k) \geq 1 + \frac{k+2} {k(k+1)}$ if $k \geq 2,$ which gives $R_{A}(2) \geq 1.666\ldots.$

By restricting attention to strongly divisible instances (see Sect. 8.1), then matters improve, as expected. The gap between the general lower bound and that for FF disappears. Indeed,

Theorem 52 (Coffman et al. [51])

If $(L,C)$ is strongly divisible and L is such that $s_{1}>s_{2}>\ldots> s_{k}$ $(k \geq 2)$, then the APR of the dynamic version of FF is

$$R_{\mathrm{FF}}^{\infty } =\displaystyle\prod _{ i=1}^{k-1}\left (1 + \frac{s_{i}} {C} -\frac{s_{i+1}} {C} \right ).$$

Moreover, for any on-line algorithm A that operates only on strongly divisible instances, $R_{A}^{\infty }\geq R_{\mathrm{FF}}^{\infty }.$

By a straightforward inductive argument, it can be shown that the continued product has the upper bound

$$\lim _{k\rightarrow +\infty }\left (1 + \frac{1} {{2}^{k-2}}\right )\displaystyle\prod _{i=1}^{k-2}\left (1 + \frac{1} {{2}^{i}}\right ) = 2.384\ldots.$$

Other algorithms were developed, which, in addition to deletion, allow at least one of the following capabilities: repacking, look ahead, and preordering. For those algorithms which may use all of the above operations, Ivkovic and Lloyd [122] (see also [120]) introduced the fully dynamic bin packing (FDBP) term and presented an algorithm, MMP, which is $\frac{5} {4}$-competitive.

7.2 Selfish Bin Packing

Consider the case in which the items are controlled by selfish agents, and the cost of a bin is split among the agents in proportion to the fraction of the occupied bin space their items require. Namely, if an agent packs its item a of size $s(a)$ into bin $B$, then its cost is $\frac{s(a)} {c(B)}$, where $c(B)$ is the content of the bin. In other words, the selfish agents would like their items to be packed in a bin that is as full as possible. Hence, given a feasible solution, the agents are interested in bins ${B}^{{\prime}}$ such that $s(a) + c(B') \leq 1$ and $\frac{s(a)} {s(a)+c(B')} < \frac{s(a)} {c(B)}.$ If such a bin exists, then a unilaterally migrates from B to ${B}^{{\prime}}$, as in this new feasible packing its cost decreases. When no such bin exists for any agent, a stable state has been reached. The social optimum is to minimize the number of bins used, which is the aim of the standard BP problem.

This problem corresponds to a noncooperative game, and the stable state is a pure Nash Equilibrium (NE). There is a Strong Nash Equilibrium (SNE) if there is no subset of agents, which can profit by jointly moving their items to different bins so that all agents in the subset obtain a strictly smaller cost.

More precisely, a noncooperative strategic game is a tuple $G =\langle N,(S_{i})_{i\in N},$ $(c_{i})_{i\in N}\rangle$ where N is a finite set of players. Each player has a finite set $S_{i}$ of strategies and a cost function $c_{i}$, and each player has complete information about the strategy of all players. Players choose their strategies independently of each other. A combination of strategies chosen by the players is denoted by $s = (x_{j})_{j\in N} \in \times _{j\in N}S_{j}$ and is called a strategy profile. The social cost of a game is an objective function $SC(s) : X\rightarrow \mathbb{R},$ that gives the cost of an outcome of the game for a strategy profile $s \in X$, where $X$ denotes the set of all strategy profiles. The social optimum of the game is then $\mathit{OPT}(G) =\min _{s\in X}SC(s).$

The quality of an NE is measured by the Price of Anarchy (PoA) and the Price of Stability (PoS), which are defined as follows:

$$\mathit{PoA} =\sup _{s\in NE(G)} \frac{\mathit{SC(s)}} {\mathit{OPT}(G)}\qquad \mathit{PoS} =\inf _{s\in NE(G)} \frac{\mathit{SC(s)}} {\mathit{OPT}(G)}.$$

By using the SNE, one gets the Strong Price of Anarchy (SPoA) and the Strong Price of Stability (SPoS):

$$SPoA =\sup _{s\in SNE(G)} \frac{SC(s)} {\mathit{OPT}(G)}\qquad SPoS =\inf _{s\in SNE(G)} \frac{SC(s)} {\mathit{OPT}(G)}.$$

For the bin packing problem asymptotic measures are used:

$$PoA(BP) = limsup_{\mathit{OPT}(G)\rightarrow \infty }\sup _{G\in BP}PoA(G)\qquad PoS(BP) = limsup_{\mathit{OPT}(G)\rightarrow \infty }\inf _{G\in BP}PoS(G)$$

and

$$SPoA(BP)=limsup_{\mathit{OPT}(G)\rightarrow \infty }\sup _{G\in BP}SPoA(G)\quad SPoS(BP)=limsup_{\mathit{OPT}(G)\rightarrow \infty }\inf _{G\in BP}SPoS(G).$$

To stress the connection with game theory the problem is called the bin packing game. The first publication which discussed this problem from a game theoretical perspective was presented by Biló (see [25]). He showed that starting from an arbitrary feasible packing, one can always reach an NE using an exponential number of migration steps. This result implies that, for every instance of the bin packing game, there exists an optimal packing which provides a NE, that is, $PoS(BP) = 1.$ He also proved that computing the best NE is $\mathcal{N}\mathcal{P} - hard.$ Yu and Zhang [181] constructed an $O({n}^{4})$-time Recursive First-Fit Decreasing (RFFD) algorithm for finding an NE. They also investigated the $PoA(BP)$ and proved the following theorem:

Theorem 53 (Yu and Zhang [181])

For the bin packing game,

$$1.6416 \approx \displaystyle\sum _{l=1}^{\infty } \frac{1} {{2}^{\frac{l(l-1)} {2} }} \leq PoA(BP) \leq \frac{41 + \sqrt{145}} {32} \approx 1.6575.$$

Epstein and Kleiman [76] improved the upper bound to $1.64286$ and conjectured that the best upper bound is equal to the lower bound.

Bin packing algorithms look for a good global solution; hence, in general, they do not produce a Nash equilibrium. An exception is the Subset Sum (SS) algorithm by Caprara and Pferschy [34], which produces an NE by repeatedly solving a knapsack problem to pack a bin as full as possible. Unfortunately, the knapsack problem is not polynomial unless $\mathcal{P} = \mathcal{N}\mathcal{P}.$ Indeed, Epstein and Kleiman [76] on the one hand proved equality among the $SPoS(BP)$ and the $SPoA(BP)$ and the asymptotic behavior of the Subset Sum algorithm and on the other hand showed that finding an SNE is $\mathcal{N}\mathcal{P}$-hard.

Caprara and Pferschy proved that $1.6062 \leq R_{SS}^{\infty }\leq 1.6210.$ So, by comparing $PoA(BP)$ and $SPoA(BP)$, it appears that they have similar values. Therefore, the efficiency in the bin packing game is only due to selfishness, and coalitions do not help. In addition, $PoS(BP)$ is significantly better than $SPoS(BP)$, which in turn equals $SPoA(BP)$, implying that in the bin packing game the best equilibrium is less efficient if coalition among agents is allowed.

7.3 Bin Packing with Rejection

This variation is motivated by the following problem, arising in file management. Suppose that files are used by a local system. Either a file is downloaded in advance or the system downloads it only when it is actually requested. The first option needs space on a local server, and it has a local transmission cost, while a program uses the file. The second option has a communication cost that one incurs, while the system downloads the file from an external server. An algorithm which manages the local file system has the choice of either packing a file (item) on the local storage device or (according to the costs) downloading it when needed. The problem can be modeled as the following bin packing problem. A pair $(s_{i},r_{i})$ is associated with each item i ($i = 1,\ldots,n)$, where $s_{i}$ is the size and $r_{i}$ is the rejection cost of the item. An algorithm has the choice of either packing an element into the bins or rejecting it. The objective is to minimize the number of bins used, plus the sum of all rejection costs. (If all rejection costs are larger than 1 then every item will be packed, and a standard problem arises.) This model was introduced by Dósa and He [69], who considered both off-line and on-line algorithms, and investigated their absolute and asymptotic behavior.

For off-line algorithms, Dósa and He gave an algorithm with absolute worst-case ratio 2. They also observed that the lower bound for the standard problem remains valid, that is, there is no algorithm with absolute worst-case ratio better than $\frac{3} {2}$, unless $\mathcal{P} = \mathcal{N}\mathcal{P}.$ The lower bound was reached by Epstein [73] (see also [70]). Based on the ratio $r_{i}/s_{i}$, Dósa and He classified the elements into subclasses and used a sophisticated greedy-type algorithm, RFF4, for which they proved that $R_{RFF4}^{\infty }\leq \frac{3} {2}.$

For the on-line case, they investigated an algorithm, called RFF1, and proved that the absolute worst-case ratio of the best on-line algorithm lies in the interval $(2.343,2.618).$ For the asymptotic competitive ratio, they introduced another algorithm, RFF2, and proved the following:

Theorem 54 (Dósa and He [69])

For any positive integer $m \geq 2$,$R_{RFF2}^{\infty }(m) \leq \frac{7m-3} {4m-2}.$ Hence there exists an on-line algorithm with an APR arbitrarily close to $7/4 = 1.75.$

Not surprisingly, this result was beaten by a variant of the HF algorithm proposed by Epstein [73]. Her RejH$_{k}$ algorithm classifies the items as HF. Then thresholds are defined for the rejection choice as follows. Suppose that the next item is $a_{i} \in I_{j},$ where $I_{j} = ( \frac{1} {j+1}, \frac{1} {j}]$ for some $1 \leq j \leq k.$ Item $a_{i}$ will be rejected if either $j = k$ and $r_{i} \leq \frac{k} {k-1}s_{i}$ or $j < k$ and $r_{i} \leq \frac{1} {j}.$ Using the weighting function technique, Epstein proved the following theorem.

Theorem 55 (Epstein [73])

The APR of RejH $_{k}$ tends to $h_{\infty }(1) = 1.6901$ if $k\rightarrow \infty.$ No algorithm with a constant number of open bins can have a smaller APR.

For the unbounded-space case, the latter result was improved by a Rejective Modified Harmonic (MHR) algorithm, which is an adaptation of the Modified Harmonic analyzed by Ramanan et al. [159]:

Theorem 56 (Epstein [73])

The APR of MHR is at most $\frac{538} {333}.$

Starting from the classical results of Fernandez de la Vega and Lueker [84] and Hochbaum and Shmoys [118], Epstein [73] also proposed an APTAS for bin packing with rejection, having time complexity $O({n}^{O({({\epsilon }^{-4})}^{{\epsilon }^{-1}}) }).$ Using some results on the multiple knapsack problem (see Chekuri and Khanna [40] and Kellerer [134]) a faster, $O({n}^{O({\epsilon }^{-2}) })$ time, approximation scheme was constructed by Bein et al. [21].

7.4 Item Fragmentation

Menakerman and Rom [155] investigated a variant of the bin packing problem in which items may be subdivided into pieces of smaller size, called fragments. Fragmenting an item is associated with a cost, which makes the problem $\mathcal{N}\mathcal{P}$-hard. They studied two possible cost functions. In the first variant, called Bin Packing with Size-Increasing Fragmentation (BP-SIF), whenever an item is fragmented, overhead units are added to the size of every fragment. In the second variant, called Bin Packing with Size-Preserving Fragmentation (BP-SPF), each item has a size and a cost, and, whenever it is fragmented, one overhead unit is added to its cost without changing its total size. (Actually, problem BP-SIF was first introduced by Mandal et al. [150] who showed that it is $\mathcal{N}\mathcal{P}$-hard.)

It is supposed that the item sizes are positive integers and the bins are all of size $C.$ It is obvious that a good algorithm should try to perform the minimum number of fragmentations. Menakerman and Rom developed algorithms that do not fragment items unnecessarily. More precisely, an algorithm is said to prevent unnecessarily fragmentation if it follows the next two rules:

• 1. No unnecessary fragmentation: An item (or a fragment of an item) is fragmented only if it must be packed into a bin that cannot contain it. In case of fragmentation, the item (or fragment) is divided into two fragments. The first fragment must fill one of the bins, while the second is packed according to the rules of the algorithm.

• 2. No unnecessary bins: An item is packed into a new bin only if it cannot fit in any of the open bins.

For the BP-SIF problem, it is proved that for any algorithm A that prevents unnecessary fragmentation, $R_{A}^{\infty }\leq { C \over C-2}$ for every $C> 2.$ For the obvious generalization of the Next-Fit algorithm, called Next-Fit with item fragmentation (NF$_{f}$), a ${ C \over C-2}$ bound for all $C \geq 6$ was proved. For a more sophisticated algorithm, which is actually an iterated version of First-Fit Decreasing, they proved that the APR is not greater than ${ C \over C-1}$ when $C \leq 15$, while it is between ${ C \over C-1}$ and ${ C \over C-2}$ when $C \geq 16.$

As to the BP-SPF problem, the performance of an algorithm for a given list $L$, $OH_{A}(L)$ is measured by its overhead, that is, by the difference between the cost of the solution produced by the algorithm and the cost of an optimal solution. The worst-case performance of an algorithm is

$$OH_{A}^{m} =\inf \{ h : OH_{ A}(L) \leq h for all L with \mathit{OPT}(L) = m\}.$$

Menakerman and Rom [155] proved that for any algorithm A that prevents unnecessary fragmentation, $OH_{A}^{m} \leq m - 1$ and that an appropriate modification of Next-Fit reaches this bound. First-Fit Decreasing performs better when the bin size is small.

Naaman and Rom [158] considered two generalizations of the BP-SPF. The first one is quite simple: r overhead units are added to the size of every fragment. This changes the performance of Next-Fit to ${ C \over C-2r}.$ The other generalization is more challenging: a set B of m bins is given, whose (integer) bin sizes may be different. Denote by $\overline{C} ={ 1 \over m} \sum _{j=1}^{m}s(B_{ j})$ the average bin size. In this case, the asymptotic worst-case bound for Next-Fit is ${ \overline{C}\over \overline{C } -2r}$ for every $\overline{C}>4r.$

Shachnai et al. [168] studied slightly modified versions of BP-SIF and BP-SPF. For the BP-SIF, a header of fixed size $\Delta$ is attached to each (whole or fragmented) item, that is, the size required for packing $a_{i}$ is $s_{i} + \Delta.$ When an item is fragmented, each fragment gets the header. For the BP-SPF, the number of possible splits is bounded by a given value. They presented a dual PTAS and an APTAS for each of the problems. The dual PTASs pack all the items in ${\it \text{OPT}}(L)$ bins of size $(1 + \epsilon )$, while the APTASs use at most $(1 + \epsilon ){\it \text{OPT}}(L) + 1$ bins. All of these schemes have running times that are polynomial in n and exponential in $1/\epsilon.$ They also showed that both problems admit a dual AFPTAS, which packs the items in ${\it \text{OPT}}(L) + O(1/{\epsilon }^{2})$ bins of size $1 + \epsilon.$ Shachnai and Yehezkely [167] developed fast AFPTASs for both problems. Their schemes pack the items in $(1 + \epsilon ){\it \text{OPT}}(L) + O({\epsilon }^{-1}\log {\epsilon }^{-1})$ bins in a time that is linear in n and polynomial in $1/\epsilon.$

Epstein and van Stee [81] investigated a version where the items may be split without extra cost, but each bin may contain at most k (parts of) items, for a given constant $k.$ They provided a polynomial-time approximation scheme and a dual approximation scheme for this problem.

7.5 Fragile Objects

Bansal et al. [17] (see also [16]) investigated two interrelated optimization problems: bin packing with fragile objects and frequency allocation in cellular networks (which is a special case of the former problem). In this problem, each item has two attributes: size and fragility. The goal is to pack the items so that the sum of the item sizes in each bin is not greater than the fragility of any item in the bin. They provided a 2-approximation algorithm for the problem of minimizing the number of bins and proved a lower bound of $\frac{3} {2}$ on the asymptotical approximation ratio. They also considered the approximation with respect to fragility and gave a 2-approximation algorithm.

Chan et al. [35] considered the on-line version of the problem and proved that the asymptotic competitive ratio of any on-line algorithm is at least 2. They also considered the case where the ratio between maximum and minimum fragility is bounded by a value $k$, showing that the APR of an Any-Fit algorithm (including First-Fit and Best-Fit) is at least $k.$ For the case where k is bounded by a constant, they developed a class of on-line algorithms which achieves an APR of $\frac{1} {4} + 3\frac{r} {2}$ for any $r> 1.$

7.6 Packing Sets and Graphs

Let the bin capacity C be a positive integer and suppose that the items are sets of elements drawn from some universal set. A collection of items can fit into a bin if and only if their union has at most C elements. As usual, the object is to pack the items in the smallest number of bins. Good approximation algorithms have yet to be analyzed for this problem; adaptations of the classical bin packing approximation algorithms do not have finite APRs. One observes immediately that while classical algorithms prioritize items based on cardinality and position in sequence, a good algorithm for set packing will have to consider the intersections among a given set of items, an orthogonal basis for prioritizing the items. It is thought that approximation algorithms with a finite APR for this problem are unlikely to exist, but a rigorous treatment of this question has yet to appear.

Dror (Dror, Private communication) points out that scheduling setups in a manufacturing process is an application of set packing. As an example, he describes a machine that produces many types of circuit boards, each requiring a given set of components. The machine has a magazine (bin) that holds at most C components. At any time, only the circuit boards with their component sets (items) in the magazine can be in production. The problem is to plan the overall production process so as to minimize the number of setups.

Khanna (Khanna, Private communication) mentions that, in connection with studies of multimedia communications, graph packing is an interesting special case. Items are edges (pairs of vertices) in a given graph $G.$ An edge is packed in a bin if both of the vertices to which it is incident are in the bin, and so the problem is to pack the edges of $G$ into as few bins as possible subject to the constraint that there can be at most C vertices in any bin. The approximability of this problem has yet to be studied.

Katona [133] investigated a special case of graph packing. A graph is called p-polyp if it consists of $p$ simple paths of the same length and sharing a common end vertex. Polyp Packing is the following generalization of bin packing: pack a set of paths of different lengths into a minimum number of edge disjoint polyps. He proved that the problem is $\mathcal{N}\mathcal{P}$-hard and gave bounds on the performance of a modification of First-Fit.

8 Additional Conditions

8.1 Item-Size Restrictions

Perhaps the simplest (and most practical) restriction is simply to have a finite number k of item sizes, say $s_{1},\ldots,s_{k}$, and thus a finite number N of feasible item configurations in a bin. This class of problems arose in studies on approximation schemes (see [84, 132]) and was considered in its own right by Blazewicz and Ecker [26]. Let the $i$-th configuration be denoted by $p_{i} = (p_{i1},\ldots,p_{ik})$ where $p_{ij}$ is the number of items of size $s_{j}$ in $p_{i}.$ By the definition of feasibility, $\sum _{j=1}^{k}p_{ij}s_{j} \leq 1$ for all $i.$ Let $y_{i}$ be the number of bins in a packing of a given list L that contain configuration $p_{i}$, and let $n_{j}$ be the number of items of size $s_{j}$ in $L.$ Then a solution to the bin packing problem for L is a solution to the integer programming formulation:

$$\displaystyle\begin{array}{rcl} \min & \displaystyle\sum _{i=1}^{N}y_{ i} & \\ & \displaystyle\sum _{i=1}^{N}p_{ ij}y_{i}& \geq n_{j}(j = 1,\ldots,k) \\ & y_{i} & \geq 0\mbox{ and integer}(i = 1,\ldots,N).\end{array}$$

Note that, if $\frac{1} {r}$ lower bounds the item sizes, then $N = O({k}^{r-1})$, so the constraint matrix above has $k$ rows and $O({k}^{r-1})$ columns. This problem can be solved in time polynomial in the number of constraints (see Lenstra [144]), which is a constant independent of the number of items. The optimal overall packing can then be constructed in linear time.

If the exact solution is not needed, then one can use the classical approach of Gilmore and Gomory [105, 106]) and compute LP relaxations (see Sect. 4.3); this method gives solutions that are at most k off the optimal in significantly less time.

Gutin et al. [113] investigated an on-line problem in which one only has two different element sizes. They gave a $\frac{4} {3}$ lower bound for this problem and provided an asymptotically optimal algorithm for it. Epstein and Levin [77] focused on the parametric case, where both item sizes are bounded from above by $\frac{1} {k}$ for some natural number $k \geq 1.$

Next consider the classical problem restricted to lists $L$ of items whose sizes form a divisible sequence, that is, the distinct sizes $s_{1}>s_{2}>\ldots$ taken on by the items are such that $s_{i+1}$ divides $s_{i}$ for all $i \geq 1.$ The number of items of each size is arbitrary. Given the bin capacity $C$, the pair $(L,C)$ is weakly divisible if $L$ has divisible item sizes and strongly divisible if in addition the largest item size $s_{1}$ in L divides $C.$

This variant has practical applications in computer memory allocation, where device capacities and memory block sizes are commonly restricted to powers of $2.$ It is important to recognize such applications when they are encountered, because approximation algorithms for many types of $\mathcal{N}\mathcal{P}$-hard bin packing problems generate significantly better packings when items satisfy divisibility constraints. In some cases, the restriction leads to algorithms that are asymptotically optimal. The problem was studied by Coffman, Garey, and Johnson, who proved the following result for classical off-line algorithms.

Theorem 57 (Coffman et al. [51])

If $(L,C)$ is strongly divisible, then NFD and FFD packings are optimal.

Indeed, the residual capacity in a bin is always either zero or at least as large as the last (smallest) item packed in the bin. The last packed item is at least as large as any remaining (unpacked) item, so either the bin is totally full or it has room for the next item. Therefore, the FFD and NFD algorithms have the same behavior: they initialize a new bin only when the previous one is totally full, so the packings they produce are identical and perfect.

The optimality of FFD holds in the less restrictive case of the following theorem as well.

Theorem 58 (Coffman et al. [51])

If $(L,C)$ is weakly divisible, then an FFD packing is always optimal.

For strongly divisible instances, optimal performance can also be obtained without sorting the items.

Theorem 59 (Coffman et al. [51])

If $(L,C)$ is strongly divisible, then an FF packing is always optimal.

In the Unit-Fractions Bin Packing Problem, n items are given, and the size of each item i is $\frac{1} {w_{i}}$, with $w_{i}$ a positive integer ($1 \leq i \leq n$). This problem was initially studied by Bar-Noy et al. [18]. Let $H = \lceil \sum _{i=1}^{n} \frac{1} {w_{i}}\rceil$ be a lower bound on the required number of bins. They presented an off-line algorithm which uses at most $H + 1$ bins. For the on-line version, they analyzed an algorithm which uses $H + O(\sqrt{H})$ bins. It is also proved that any on-line algorithm for the unit-fractions bin packing problem uses at least $H + \Omega (\ln H)$ bins.

Dynamic bin packing problems with unit-fractions items were considered by Chan et al. [36]. They investigated the family of Any-Fit algorithms and proved the following results:

$$R_{\mathrm{BF}}^{\infty } = R_{\mathrm{ WF}}^{\infty } = 3$$

$$2.45 \leq R_{\mathrm{FF}}^{\infty }\leq 2.4985.$$

In addition they proved the following lower bound result:

Theorem 60 (Chan et al. [36])

For a dynamic bin packing problem with unit-fractions items, there is no on-line algorithm A with $R_{A}^{\infty } < 2.428.$

It would be interesting to examine how approximation algorithms behave with other special size sequences (e.g., Fibonacci numbers), as mentioned by Chandra et al. [39] in the context of memory allocation.

8.2 Cardinality Constrained Problems

The present section deals with the generalization in which the maximum number of items packed into a bin is bounded by a positive integer $p.$ The problem has practical applications in multiprocessor scheduling with a single resource constraint, when the number p of processors is fixed, or in multitasking operating systems where the number of tasks is bounded. If the maximum number of items in a bin is bounded by $p$, then the problem is called the $p$ -Cardinality Constrained Bin Packing Problem. Observe which is the difficulty when one tries to construct a good algorithm for this problem. Without the cardinality constraint, a huge number of small elements slightly affect the number of occupied bins: either they can be packed together into few bins, or they can be packed into bins which are “almost full.” In the considered case, having packed many small elements results in almost empty bins, because of the cardinality constraint. Therefore, when a large item arrives, it has to be packed into a new bin even if it would fit into an already open bin.

In the context of the above applications, Krause et al. [139] modified classical algorithms so as to deal with the restricted number of items per bin. Their on-line algorithm, pFF, is FF with an additional check on the number of items in open bins. They proved that if $p \geq 3$, then

$$\frac{27} {10} - \frac{37} {10p} \leq R_{\mathrm{pFF}}^{\infty }\leq \frac{27} {10} - \frac{24} {10p}.$$

As p tends to $\infty$, the bound is much worse than the corresponding APR of the unrestricted problem ($2.7$ versus $1.7$). Whether this upper bound can be improved remains an open question.

On-line algorithms were also studied by Babel et al. [11] (see also [10]), who investigated four algorithms, denoted as $A_{1},\ldots,A_{4}.$

• Algorithm $A_{1}$ operates with the BF strategy while packing the subsequent element. Different classes of blocked bins are defined according to the number of items in a bin. The algorithm tries to pack the element first into all blocked bins that satisfy a threshold condition, then into all formerly blocked and currently unblocked bins, and finally into the remaining bins. It is proved that for every $p \geq 3$,

  $$R(p) = 2 + \frac{p + k_{p}(k_{p} - 3)} {(p - k_{p} + 1)k_{p}},\quad \quad \mathrm{where}\quad \quad k_{p} ={\biggl [ \frac{-p + \sqrt{{p}^{3 } - 2p}} {p - 2} \biggr ]},$$

  so $\lim _{p\rightarrow \infty }A_{1} = 2.$

• In algorithm $A_{2}$, a bin is closed if $c(B) \geq \frac{1} {2}$ and it contains at least $\frac{p} {2}$ items. Furthermore, a pair of bins, $B_{1}$ and $B_{2}$, is also closed if $c(B_{1}) + c(B_{2}) \geq 1$ and $\vert B1\vert + \vert B2\vert \geq k.$ The open bins are subdivided into three classes, and the algorithm tries to pack the current item, in turn, into bins of such classes. If the item does not fit in any of these bins, a new bin is open. It is proved that for every $p \geq 3$, algorithm $A_{2}$ has an APR of $2.$

• Algorithm $A_{3}$ deals with the case $p = 2.$ The basic idea of the algorithm is that, when a small item is packed, a balance should be kept between the number of bins with only one small item and the number of bins which have two such items. It is proved that $R_{A_{3}} = 1 + \frac{1} {\sqrt{5}}.$

• For the $3$-cardinality problem, a Harmonic-type algorithm is defined, with four bin classes. The score intervals are as follows: $I_{1} = (0; \frac{1} {3}],$ $I_{2} = (\frac{1} {3}, \frac{1} {2}],$ $I_{3} = (\frac{1} {2}, \frac{2} {3}],$ and $I_{4} = (\frac{2} {3},1].$ The resulting Algorithm $A_{4}$ is a much more complicated version of the classical HF algorithm and has an asymptotic competitive ratio of $1.8.$

Two lower bounds are also given:

Theorem 61 (Babel et al. [11])

There is no $2$ -cardinality on-line bin packing algorithm A with APR $R_{A} < \sqrt{2}.$

Theorem 62 (Babel et al. [11])

There is no $3$ -cardinality on-line bin packing algorithm A with APR $R_{A} < \frac{3} {2}.$

For unbounded-space algorithms, some further cases were investigated by Epstein [71]. She considered a Harmonic-type algorithm that defines five subintervals and packs the items into bins with a more sophisticated procedure. Her algorithm for the case $p = 3$ improves the APR of [11] to $\frac{7} {4} = 1.75.$ For the cases $p = 4$, $p = 5$ and $p = 6$, she refined the basic algorithm, designing three algorithms with APRs $\frac{71} {38} = 1.86842$, $\frac{771} {398} = 1.93719$, and $\frac{284} {144} = 1.99306.$ She proved that an algorithm with an APR strictly better than 2 cannot be bounded space (unless $p \leq 3$).

For the bounded-space case, Epstein defined the Cardinality Constrained Harmonic-p (CCHp) algorithm. She considered the Sylvester sequence, defined the sum

$$S_{p} =\displaystyle\sum _{ i=1}^{p}\left \{ \frac{1} {t_{i} - 1}, \frac{1} {p}\right \},$$

and proved the following theorems:

Theorem 63 (Epstein [71])

The value of $S_{p}$ is a strictly increasing function of $p \geq 2$ such that $\frac{3} {2} \leq S_{p} < h_{\infty }(1) + 1$ and $lim_{p\rightarrow \infty }S_{p} = h_{\infty }(1) + 1 \approx 2.69103.$

Theorem 64 (Epstein [71])

For every $p \geq 2$, the APR of CCHp is $S_{p}$, and no on-line algorithm which uses bounded space can have a better competitive ratio.

In addition, Epstein extended her results to the variable-sized and the resource-augmentation cases (see Sects. 5.1 and 5.2).

An off-line algorithm (Largest Memory First, LMF), based on an adaptation of FFD, was studied by Krause et al. [139]. They proved that $R_{\mathrm{LMF}}^{\infty } = 2 -\frac{2} {p}$ if $p \geq 2.$ Here the gap between the unrestricted and the restricted case is large ($2$ versus $\frac{11} {9}$). The authors’ search for an algorithm with better worst-case behavior resulted in the Iterated Worst-Fit Decreasing (IWFD) algorithm. IWFD starts by sorting the items according to nonincreasing size, and by opening q empty bins, where $q := \lceil \max (\frac{n} {p},\sum _{i=1}^{n}s_{ i})\rceil$ is an obvious lower bound on ${\it \text{OPT}}(L).$ Then (i) IWFD tries to place the items into these q bins using the Worst-Fit rule (an item is placed into the open bin whose current number of items is less than p and whose current content is minimum, breaking ties by highest bin index); (ii) whenever the current item $a_{i}$ does not fit in any of the q bins, q is increased by $1$, all items are removed from the bins and the processing is restarted from (i). If one implements this approach using a binary search on $q$, the time complexity of IWFD is $O({n\log }^{2}n).$ Krause, Shen, and Schwetman proved that the algorithm behaves very well in certain special cases:

• If $p = 2$, then $\mathrm{IWFD}(L) = {\it \text{OPT}}(L)$ for any list $L.$

• If in the final schedule no capacity constraint is operative, that is, no open bin has residual capacity smaller than the size of the smallest item, then $\mathrm{IWFD}(L) = {\it \text{OPT}}(L).$

• If in the final schedule no cardinality constraint is operative, that is, no open bin containing p items has residual capacity at least equal to the size of the smallest item, then $R_{\mathrm{IWFD}}^{\infty } < \frac{4} {3}.$

For the general case, where the final packing contains both bins for which the capacity constraint is operative and bins for which it is not, the constants are significantly worse but still small: $\frac{4} {3} \leq R_{\mathrm{IWFD}}^{\infty }\leq 2.$ The authors conjecture that $R_{\mathrm{IWFD}}^{\infty } = \frac{4} {3}.$

For a long time, it was an open question whether there exists a heuristic algorithm with an APR better than 2. Kellerer and Pferschy [135] proposed a new algorithm based on a method that proved to be fruitful in scheduling theory, namely, one that performs a binary search on the possible ${\it \text{OPT}}(L)$ values. At each search step, they run a procedure that tries to pack all items into a number of bins equal to $\frac{3} {2}$ times the current search value. The procedure basically tries to solve a multiprocessor scheduling problem using the classical LPT rule with a cardinality constraint. The time complexity of this Binary Search (BS) algorithm is $O({n\log }^{2}n)$, and the improved bound is $\frac{4} {3} \leq R_{\mathrm{BS}}^{\infty }\leq \frac{3} {2}.$ Although the gap has been reduced, the exact bound is still not known.

8.3 Class Constrained Bin Packing

In the Class Constrained Bin Packing Problem (CLCP), each item $a_{i}$ has two parameters: the size $s_{i}$ and the color $c_{i}$, where $s_{i} \in (0,1]$ and a color is represented by a positive integer, that is, $c_{i} \in [1,q].$ A further parameter $Q \in \mathbb{N}$ is associated with the problem as a bound for the number of the different colors within a bin. Different items may have the same color, and the items with the same color are classified into color classes. The objective is to pack the items into the minimum number of bins $\{B_{1},B_{2},\ldots,B_{m}\}$, such that $\sum _{a_{j}\in B_{i}}s_{j} \leq 1$ for $i = 1,\ldots,m$ and each such bin has items from at most Q color classes. Clearly, if $q = n$, then one gets the $p$-cardinality constrained problem (see Sect. 8.2), and if $q \leq Q$, then a classical bin packing problem arises. Shachnai and Tamir [165] proved that the problem is $\mathcal{N}\mathcal{P}$-hard even in the case of identical item sizes.

For the case of on-line bounded-space algorithms, Xavier and Miyazawa [176] presented inapproximability results. More precisely, they proved that if $s_{i} \in [K_{1},K_{2}]$, with $0 < K_{1} < K_{2} \leq 1$, for all $i = 1,\ldots,n$, then any bounded-space on-line algorithm has an APR of $\Omega ( \frac{1} {QK_{1}} ).$

Shachnai and Tamir [166] studied unbounded-space algorithms for the case of identically sized items. Suppose that $s_{i} \in ( \frac{1} {r+1}, \frac{1} {r}]$ for each $a_{i}$: they denoted by $S_{Q,r}(k,h)$ the set of those lists which have $kQ < q \leq (k + 1)Q$ and $hr < n \leq (h + 1)n$, where n is the number of elements in the list. They proved that for any deterministic algorithm $A$,

$$R_{A} \geq 1 + \frac{k + 1 -\lceil \frac{kQ+1} {r} \rceil } {h + 1},$$

and that the lower bound can be reached by the FF algorithm.

Sachnai and Tamir also introduced the notion of Color-Set algorithm (CS). This algorithm partitions the colors into $\lceil q/Q\rceil$ color sets and packs the items of each color set in a greedy way. Note that only one bin is open for each color-set at a time. They proved that $R_{CS} < 2.$ The set of Any-Fit algorithms was also investigated, and it was shown that $R_{A} \leq \min (r/Q,Q + 1)$ for any such algorithm. They further proved that the absolute worst-case ratio of the Next-Fit algorithm is $R_{\mathrm{NF}} = r/Q.$

The idea of CS was used to develop new algorithms. Color classes are divided on-line into sets of Q colors each, in order of appearance. Each open bin is assigned one color set. As a new item arrives, the algorithm tries to pack it into a bin having the color of the item. If the FF rule is used, then one gets the Color-Set First-Fit (CSFF) algorithm, while the NF rule gives the Color-Set Next-Fit (CSNF) algorithm. For the case of identical item sizes considered in [165], the authors proved that the competitive ratio of both CSFF and CSNF is at most $2.$

The case $Q = 2$ was exhaustively studied by Epstein et al. [82], who proved that the upper bound for identical items is tight for algorithms FF and CSFF. Furthermore, they showed that, for arbitrary item sizes, the competitive ratio is at least $9/4.$ A $1.5652$ lower bound was also given for any on-line algorithm with arbitrary item sizes, thus showing that, even if $Q = 2$, the on-line algorithms for CLCP behave worse than those for the classical bin packing. For what concerns upper bounds, they proved that for arbitrary values of $Q$, $R_{CSFF}\infty \leq 3 - \frac{1} {Q}.$

Xavier and Miyazawa [176] investigated the FF algorithm and proved that $R_{\mathrm{FF}}^{\infty }\in [2.7,3].$ They defined algorithm $\mathcal{A}_{Q}$, which subdivides the items, in a harmonic way, into three classes, and packs the next item, according to its size, into the class it belongs to. The algorithm also considers the color constraint $Q.$ It was proved that $R_{\mathcal{A}_{Q}}^{\infty }\in (2.666,2.75].$ Epstein et al. [82] developed an algorithm which has a competitive ratio of $2.65492,$ valid for every $Q.$

For fixed values of $q$, there are approximability results for CLCP. Note that, if q is fixed, then Q is also constant since $Q \leq q.$ For equal item sizes, Shachnai and Tamir [165] constructed a dual PTAS whose time complexity is polynomial in $n.$ The scheme uses the optimal number of bins, but the bin capacity is $1 + \epsilon.$ Xavier and Miyazawa [176] developed an APTAS. They also gave an AFPTAS with time complexity $O( \frac{n} {{\epsilon }^{2}} ).$ Epstein et al. [82] proved that if $q$ is considered as a parameter, then there is no APTAS for CLCP for any value of $Q.$ They also gave an AFPTAS for the case of constant $q$, with time complexity $O( \frac{n} {{\epsilon }^{2}} ).$

8.4 LIB Constraints

In certain applications, the positions of the items within a bin are restricted: a larger item cannot be put on top of a smaller one. This leads to the variant with the LIB (Larger Item on the Bottom) constraint. The problem was first discussed by Finlay and Manyem [85] and Manyem et al. [151]. They studied the Next-Fit algorithm and proved that it cannot achieve a finite APR. For the First-Fit algorithm, they showed that $2 \leq R_{\mathrm{FF}}^{\infty }\leq 3.$ They also analyzed a variant of Harmonic-Fit (HARM) which partitions the items into classes following the classical rule and packs them by applying to each class of bins the FF rule (instead of NF, which performs very badly). They showed that $2 \leq R_{\mathrm{HARM}}^{\infty }.$ The parametric case of HARM was considered in Epstein [72], who proved the following result:

Theorem 65 (Epstein [72])

Let $r> 0$ be a positive integer, and suppose that $\frac{1} {r+1} <\max \{ s_{i}\} \leq \frac{1} {r}$. Let k denote the number of bin classes. Then $R_{\mathrm{HARM}}(r) = \Theta (k - r + 1)$ for any fixed value of $k< \infty.$

This result has an interesting consequence: contrary to the standard problem, for which the performance of the Harmonic-Fit algorithm improves when the number of bin classes is increased, in this case, the competitive ratio worsens, and algorithm HARM has an unbounded ratio as $k \rightarrow \infty.$ Unfortunately, neither BF nor WF nor AWF behave better than HARM, that is, their APRs are also unbounded. In the same paper, Epstein analyzed the FF algorithm, proving that $R_{\mathrm{FF}}(1) = 2.5$ and $R_{\mathrm{FF}}(r) = 2 + \frac{1} {r}$ if $r \geq 2.$ Very recently, her result was improved by Dósa, Tuza, and Ye (Dósa et al., 2010, Private communication), who proved that $R_{\mathrm{FF}}(1) = 2 + \frac{1} {6}$ and $R_{\mathrm{FF}}(r) = 2 + \frac{1} {r(r+2)}$ if $r \geq 2.$

As to lower bounds, very little is known. Clearly, the FFD algorithm automatically fulfills the LIB constraint, so $\frac{11} {9}$ is a lower bound for any semi-on-line algorithm which packs preordered elements. The only nontrivial lower bound was obtained by Epstein [72]:

Theorem 66 (Epstein [72])

The competitive ratio of any on-line algorithm for bin packing with LIB constraints is at least $2$. The result is valid for the parametric case as well, for any value of $r \geq 1.$

8.5 Bin Packing with Conflicts

In this problem, a set of items $L = a_{1},a_{2},\ldots,a_{n}$ with sizes $s_{1},s_{2},\ldots,s_{n}$ and a conflict graph $G(L,E)$ are given. The objective is to find the minimum number of independent sets such that the sum of the sizes within each set is at most one. The problem is a generalization of both the classical bin packing problem (when $E = \varnothing$) and the graph coloring problem (when $s_{i} = 0$ for all $i$). In the on-line version of the problem, when a new item arrives, one gets its size and the edges of the conflict graph which connect it to previous items. Instead of examining the APR, most investigations focused on the absolute worst-case ratio AR, since the conflict graph that proves the worst case is valid both for small and large instances. Therefore, the APR may not be better than the AR.

It is known that graph coloring is hard to approximate for general graphs (see, e.g., Lovász et al. [149]); the problem at hand has been studied for specific graphs. The early studies on the bin packing with conflicts (BPC) dealt with perfect graphs, since the coloring problem is polynomially solvable for them. Jansen and Öhring [123] gave an algorithm with an APR of $2.7.$ Epstein and Levin [78] improved this result with an algorithm having the performance guarantee $h_{\infty }(1) + 1 = 2.690103.$

Jansen and Öhring also proposed an algorithm that uses the so-called Precoloring Extension Problem (PEP) as a preprocessing stage to get a partition of the conflict graph. In the PEP, one is given an undirected graph $G = (V,E)$ and k distinct vertices $v_{1},v_{2},\ldots,v_{k}.$ The aim is to find a minimum coloring f of G such that $f(v_{i}) = i$ for $i = 1,2,\ldots,k.$ The minimum number of colors is denoted by $\chi _{I}(G).$ The PEP is polynomially solvable for a number of graph classes (interval graphs, forests, K-trees, etc.), whereas it is $\mathcal{N}\mathcal{P}$-hard for bipartite graphs. Let $\mathcal{C}$ be the class of those graphs for which the PEP is polynomially solvable for any induced subgraph of $G.$

Let $G \in \mathcal{C}$ be a conflict graph and let $BIG =\{ a_{j} \in L : s_{j}>\frac{1} {2}\}.$ The algorithm by Jansen and Öhring uses BIG as the set of pre-colored vertices and then determines a feasible coloring of G using $\chi _{I}(G)$ colors: in this coloring, each pair of items in BIG has different colors. Finally, it uses a bin packing heuristic for each color class. Denote this algorithm by $\mathcal{A}(H)$, where H is the bin packing heuristic. They proved the following theorem:

Theorem 67 (Jansen and Öhring [123])

For the BPC problem, the $\mathcal{A}(FFD)$ has a performance ratio $2.4231 = h_{\infty }(2) + 1 \leq R_{\mathcal{A}(FFD)} \leq 2.5.$

Later, Epstein and Levin [78] revisited the algorithm, proving that the lower bound of $R_{\mathcal{A}(FFD)}$ is tight. Instead of using the PEP for preprocessing, they used a matching-based preprocessing (MP) algorithm, for which they proved that $R_{MP} = 2.5$, and that the result remains valid for all classes of graphs for which there exists a polynomial-time algorithm to find a coloring with a minimum number of colors. They also suggested a greedy algorithm which tries to pack two or three independent items into a single bin and then applies FFD to each color class. They proved that the approximation ratio of this algorithm is $\frac{7} {3}.$

As already mentioned, the PEP is $\mathcal{N}\mathcal{P}$-hard for bipartite graphs. However, Jansen and Öhring [123] proved that by defining a simple algorithm which finds a coloring of the conflict graph with two colors, and packs each color class with NF, one gets an AR of $2.$ They also pointed out that the AR does not change if NF is replaced by FFD. Using a more complicated pairing technique, Epstein and Levin [78] presented an algorithm with approximation ratio exactly equal to $\frac{7} {4}.$

For the on-line version, the BPC is hard to approximate for many classes of graphs. Success depends on the on-line coloring phase. For interval graphs, Kierstead and Trotter [137] presented an on-line coloring algorithm, which uses $3\omega - 2$ colors in the worst case, where $\omega$ is the maximum clique size of the graph. Epstein and Levin [78] pointed out that, using NF for each color class, one obtains a $5$-competitive algorithm. They also proved a combination of FFD with the algorithm in [137] produces an algorithm with competitive ratio $4.7.$ For interval graphs, there exists a lower bound for any on-line algorithm:

Theorem 68 (Epstein and Levin [78])

The competitive ratio of any on-line algorithm for BPC on interval graphs is at least $\frac{155} {36} \approx 4.30556.$

The theorem is a direct consequence of two interesting lemmas:

Lemma 1 (Epstein and Levin [78])

Let c be a lower bound on the APR of any on-line algorithm for classical bin packing, which knows the value $\mathrm{{\it \text{OPT}}}$ in advance. Then the AR of any on-line algorithm for BPC on interval graphs is at least $3 + c.$

Lemma 2 (Epstein and Levin [78])

Any on-line algorithm for classical bin packing, which knows the value $\mathrm{{\it \text{OPT}}}$ in advance, has an AR of at least $\frac{47} {36} \approx 1.30556.$

The on-line problem for other graph classes is still open.

8.6 Partial Orders

In this generalization, precedence constraints among the elements are given, where precedence refers to the relative ordering of bins. Let $\prec$ denote the partial order giving the precedence constraints. Then $a_{i} \prec a_{j}$ means that, if $a_{i}$ and $a_{j}$ are packed in $B_{r}$ and $B_{s}$, respectively, then $r \leq s.$ Call the model strict if $r < s$ replaces $r \leq s$ in this definition.

Two practical applications have been considered in the literature. The first one is the assembly line balancing problem, in which the assembly line consists of identical workstations (the bins) where the products stop for a period of time equal to the bin capacity. The item sizes are the durations of tasks to be performed, and a partial order is imposed: $a_{i} \prec a_{j}$ means that the workstation to which $a_{i}$ is assigned cannot be downstream of the one to which $a_{j}$ is assigned. The second application arises in multiprocessing scheduling; here each item corresponds to a unit-duration process having a memory (or other resource) requirement equal to the item size. The bin capacity measures the total memory availability. In the given partial order, $a_{i} \prec a_{j}$ imposes the requirement that $a_{i}$ must be executed before $a_{j}$ finishes. The objective is then to find a feasible schedule that finishes the set of processes in minimum time (number of bins).

The first problem was studied by Wee and Magazine [174] and the second one by Garey et al. [104]. In both cases, the Ordered First-Fit Decreasing (OFFD) algorithm was applied. An item is called available if all its immediate predecessors have already been packed. At each stage, the set of currently available items is sorted according to nonincreasing size, and each item is packed into the lowest indexed bin where it fits and no precedence constraint is violated. Note that, if no partial order is given, this algorithm produces the same packing as FFD. In general, however, its worst-case behavior is considerably worse. The APR is $R_{\mathrm{OFFD}}^{\infty } = 2,$ except in the strict model, where $R_{\mathrm{OFFD}}^{\infty } = \frac{27} {10}.$

Liu and Sidney [148] considered the case in which there is an ordinal assumption: initially, the actual sizes of the items are unknown, but their ordering is known, that is, $s_{1} \geq s_{2} \geq \ldots \geq s_{n} \geq 0.$ Now assume that perfect knowledge of some of the sizes can be “purchased” by specifying the ordinal position of the desired sizes. It is shown that a worst-case performance ratio of $\rho$ (where $\rho \geq 2$ is an integer) can be achieved if knowledge of $\lfloor \ln (n(\rho -1) + 1)/\ln \rho \rfloor$ weights can be purchased.

8.7 Clustered Items

In this generalization, a function $f(a_{i},a_{j})$ is given, measuring the “distance” between items $a_{i}$ and $a_{j}.$ A distance constraint D is also given; two items $a_{i}$ and $a_{j}$ may be packed into the same bin only if $f(a_{i},a_{j}) \leq D.$ The problem has several obvious practical applications in contexts where geographical location constraints are present. Chandra et al. [39] studied different cases, their main result being for the case where the items in a bin must all reside within the same unit square. They proposed a geometric algorithm A and proved that $3.75 \leq R_{\mathrm{A}}^{\infty }\leq 3.8.$

8.8 Item Types

In studying the packing of advertisements on Web pages, Adler et al. [1] encountered a variant of bin packing in which items are classified into types; the set of types is given, and there are no constraints on the number of items of any type. The problem is to pack the items into as few bins as possible subject to the constraint that no bin can have two items of the same type. They design optimal algorithms for restricted cases and then bound the performance of these algorithms viewed as approximations to the general problem.

9 Examples of Classification

In this section, the classification scheme proposed in Sect. 2.3 is resumed. The following examples should help familiarize the reader with it:

• 1. The classification of [157] shows a bin-size extension of pack.

  $$pack\vert \mathit{off - line}\vert FPTAS\vert \{B_{i}\}$$

  Results: An approximation algorithm for variable-sized bin packing is presented which for any given positive $\epsilon$ produces a scheme with approximation ratio $1 + \epsilon.$ This algorithm has time complexity polynomial in the number of items, the number of bins, and $1/\epsilon.$

• 2. The classification of [145] gives another such example:

  $$pack\vert \mathit{on - line},\mathit{off - line},\mathit{open - end}\vert R_{A}^{\infty }\mathit{bound};FPTAS$$

  Results: For this hybrid of pack and cover, it is shown that any open-end version of on-line algorithms must have an asymptotic worst-case ratio of at least 2. Next-Fit achieves this ratio. There is a fully polynomial-time approximation scheme for this problem.

• 3. The classification of [7] illustrates a capacity minimization problem with bin-stretching analysis:

  $$mincap\vert \mathit{on - line}\vert R_{A}\mathit{bound}\vert stretching$$

  Results: A combined algorithm achieves a worst-case bound of 1.625. The best lower bound for any on-line algorithm is 4/3.

• 4. Reference [48] studies a subset-cardinality objective function:

  $$maxcard(subset)\vert \mathit{off - line}\vert R_{A}$$

  Results: $R_{\mathrm{WFI}} ={ 1 \over 2},R_{\mathrm{FFI}} ={ 3 \over 4}.$

• 5. Reference [61] is classified as a covering problem.

  $$cover\vert \mathit{on - line}\vert R_{A}^{\infty }\mathit{bound}$$

  Results: Asymptotic bound: $R_{A}^{\infty }\leq 1/2$ for any on-line algorithm $A.$ There exists an asymptotically optimal on-line algorithm.

• 6. The classification of [90] is

  $$pack\vert \mathit{off - line}\vert R_{A}^{\infty }\mathit{bound}$$

  Algorithm: Combined Best-Fit (CBF) which takes the better of the First-Fit Decreasing solution and Best Two-Fit (B2F) solution, where the latter algorithm is a grouping version of Best-Fit limiting the number of items per bin.

  Results: $R_{\mathrm{B2F}}^{\infty } = 5/4,\,\ \ { 227 \over 195} \leq R_{CBF}^{\infty }\leq \frac{6} {5}$

  Note that the word “variant” may be simplistic in that it occasionally hides details of relatively complicated algorithms.

• 7. Reference [95] shows an example for the combination of two algorithm classes:

  $$pack\vert \mathit{bounded - space},repack\vert R_{A}^{\infty }\mathit{bound}$$

  Algorithm: REP$_{3}$, an adaptation of FFD using at most three open bins.

  Result: $R_{\mathrm{REP}_{3}}^{\infty }\approx 1.69\ldots.$

• 8. The classification of [139] illustrates a case where one is allowed to constrain the number of items per bin.

  $pack\vert \mathit{on - line},\mathit{off - line}\vert R_{A}^{\infty }\mathit{bound}\vert card(B) \leq k$

  Result:

  $$\left ({ 27 \over 10} -\left \lceil { 37 \over 10k} \right \rceil \right ) \leq R_{\mathrm{FF}_{k}}^{\infty }\leq \left ({ 27 \over 10} -{ 24 \over 10k} \right ),$$

  where FF$_{k}$ is the obvious adaptation of FF.

• 9. For [175], the classification mentions yet another constraint:

  $pack\vert \mathit{bounded - space},\mathit{on - line}\vert R_{A}^{\infty }$

  Result: $R_{SH_{k}}^{\infty }(k) = R_{H_{k}}^{\infty },$ where SH$_{k}$ is a simplified version of H$_{k}$ that uses only $O(\log k)$ open bins at any time.

• 10. Classification of [6] aggregates several results:

  $cover\vert \mathit{on - line},\mathit{off - line},\mathit{open - end}\vert R_{A}^{\infty }$

  Algorithms: Open-end variant of Next-Fit called DNF, of First-Fit Decreasing with a parameter $r$ (FFD$_{r}$), and of an iterated version of Worst-Fit (IWFD). Results:

  $$R_{\mathrm{DNF}}^{\infty } = \frac{1} {2},FFD_{r}^{\infty } ={ 2 \over 3} \mbox{ for all }r,{ 4 \over 3} \leq r \leq { 3 \over 2},\mbox{ and }R_{\mathrm{IWFD}}^{\infty } ={ 3 \over 4}.$$

• 11. A more recent such publication is [29, 30]:

  $maxpack\vert \mathit{on - line},\mathit{off - line}\vert R_{A}^{\infty }\vert s_{i} \leq 1/k$

  Results:

  • a. No off-line approximation algorithm can have an asymptotic bound larger than 17/10, a bound achieved by FFD.

  • b. For the off-line case, $R_{\mathrm{FFI}}^{\infty } = 6/5$, $R_{\mathrm{FFI}}^{\infty }(1/k) = 1 + 1/k,\ k \geq 2$

  • c. For the on on-line case, $R_{\mathrm{FF}}^{\infty }(1/k) = R_{\mathrm{BF}}^{\infty }(1/k) = 1 + 1/(k - 1),\ k \geq 3.$

  • d. No deterministic algorithm A has a finite asymptotic bound $R_{A}^{\infty }$ for either the card(subset)_min or$c(\mbox{ subset})$_min problems, except for the latter problem in the parametric case with $k> 1$, in which case the bound is again $1 + 1/(k - 1).$

• 12. An analysis with similarities to bin stretching is used in [31] to compare WF and NF.

  $$pack\vert \mathit{on - line}\vert R_{A}^{\infty }\vert stretching$$

  Results: A derivation of the asymptotic ratios for WF and NF under the assumption that they use bins of capacity C while OPT uses unit-capacity bins shows that WF and NF have the same asymptotic bound for all $C \geq 1,$ except when $1 < C < 2$, in which case WF has the smaller bound.

10 Cross-References

Advances in Scheduling Problems

Complexity Issues on PTAS

Online and Semi-online Scheduling