Keywords:

1 Introduction

The microarray technology enables large-scale genomic research by allowing the measurement of the expression levels of thousands of genes in parallel. Expression levels of genes in various samples are collected and stored in a gene expression matrix. Mining these gene expression matrices can provide insights into gene functions and aids in the development and treatment of complex diseases. The discovery of related genes is a challenging task and has been the focus of many research studies [1–4] that search for more sophisticated analysis methods. Most of the time, however, researchers focus on a specific gene or a gene set rather than exploring the whole dataset. Query-based search algorithms [5–10] are proven to be very useful when the objective is to rank the genes according to how strongly they are correlated with the queried gene(s). For example, several genes in S. cerevisiae database are categorized and annotated by Hibbs et al. [6]. Similarly, top-ranked genes co-regulated with breast cancer associated tumor suppressors, BRCA1 and BRCA2, are found to be regulating the mitotic spindle and cytokinesis by Bozdağ et al. [9]. In analyzing this torrent of new data, unsupervised learning methods such as clustering are important as the first step. In particular, a class of clustering algorithms known as biclustering is useful for analyzing gene expression data, or any data whose items are related in only a subset of their samples. Biclustering methods cluster both the items and their features simultaneously. In gene expression context, this means that genes need not be related in all samples to be clustered together. Because many genes only interact under specific circumstances, biclustering may recover relationships that traditional clustering algorithms can miss.

In this chapter, first, we briefly survey the literature on biclustering and proposed algorithms. Then we introduce a novel biclustering algorithm, Correlated Patterns Biclustering (CPB), which attempts to find genes that are related on a subset of their features with a query gene. As mentioned above, identifying the genes co-regulated with a gene of important function is crucial to understand biochemical and genetic pathways in which the gene participates. To quantify gene relationships, CPB uses the Pearson correlation coefficient (PCC), an effective and widely used metric in this type of analysis to quantify co-regulation between pairs of genes [2, 4]. CPB’s novel approach avoids costly pairwise correlation calculations in a manner that also increases its accuracy. It also allows assigning genes to multiple biclusters, because many genes participate in multiple biological pathways. We further introduce a unique method for combining results from multiple datasets, which is important for uncovering uncommon genetic relationships. Initial testing on artificial data shows that CPB outperforms other biclustering methods in finding multiple types of biclusters. CPB’s performance for querying the microarray data is similarly promising: it was able to find many genes that have high correlation with BRCA1, BRCA2, and p53. Of those genes, half are already known to be involved in cancer processes, and the others are promising new candidates for further investigation. The source code of the framework, documentation, and sample datasets is available at http://bmi.osu.edu/hpc/software/cpb/.

The methods in this chapter extend the framework proposed by Bozdağ et al. [9] to increase the efficiency of the algorithms as well as the consistency and relevancy of the results. The novelty of the proposed algorithm can be summarized as follows:

  • A grid-based method is used for generating initial biclusters, which covers the whole dataset.

  • Results are investigated and the statistically insignificant biclusters are filtered out with a non-parametric scheme.

  • The biclustering method is tested on various models, noise levels, and overlap ratios; compared with other techniques.

  • Correlation scores of the genes are computed and combined more efficiently.

The key advantages of the proposed query-based search framework are:

  • It finds co-regulated genes with a given reference gene on a number of diverse microarray datasets having the same genes. This is the case for data obtained from a single microarray.

  • PCC-based biclustering technique is able to discover constant-row, shift, scale, and shift-scale models with positive and negative correlations.

  • CPB is extremely efficient compared to other PCC-based methods because of a novel correlation calculation.

  • Filtering step increases the relevance of the results while eliminating insignificant and overlapping biclusters.

The rest of the chapter is organized as follows: In Section 2, biclustering algorithms from the literature are briefly surveyed. Section 3 describes the CPB algorithm. The results of the proposed algorithm and framework’s experimental evaluation are given in Section 4. Section 5 concludes the chapter.

2 Biclustering of the Microarray Data

Biclustering refers to a class of methods that perform simultaneous clustering of both rows and columns of a data matrix. It was first introduced to gene expression data analysis by Cheng and Church [11]. This initial algorithm was followed by numerous biclustering algorithms to identify additive, multiplicative [12, 13], or more complex relationships [14–22] between the rows and columns of a data matrix that correspond to genes and samples, respectively.

A straightforward two-phase approach to identify the biclusters is applying standard clustering algorithms to the genes and samples separately in the first step, and combine the results in the second one [23]. However, the research on biclustering is focused to a more integrated approach in which the genes and samples are analyzed simultaneously. Several randomized or deterministic algorithms based on both novel and existing techniques from various domains, such as independent component analysis, singular value decomposition, simulated annealing, and local search, have been proposed, i.e., [24–33], and evaluated on the gene expression data for many diseases including the complex ones such as cancer. Some algorithms in this set use greedy techniques, i.e., [11, 34], and some employ evolutionary techniques [35–40]. In addition, graphs, modeling pairwise gene–gene interactions, have also been employed to design novel biclustering methods. For example, a local, correlated structure in the graph obtained by the gene expression data is shown to be promising to be used as a bicluster [41].

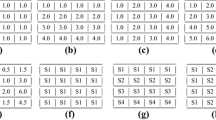
In the literature, bicluster models that a biclustering algorithm seeks for can be divided into two categories. Global biclusters are defined by comparing a metric within the bicluster to the outside of the bicluster. Up-regulated biclusters with higher expression values compared to background, and down-regulated biclusters with lower expression values than the background are examples of global biclusters. Many algorithms have been proposed to capture the global biclusters such as SAMBA [42], ISA [43], Spectral [44], BiMax [45], QUBIC [46], COALESCE [47], BBK [48]. On the other hand, local biclusters can be defined by the relationships within the bicluster columns and rows such as constant, additive, and multiplicative biclusters. Additive models are useful for capturing shifting patterns (see Fig. 1b), whereas multiplicative models are useful for capturing scaling patterns (see Fig. 1c) in the data. However, neither can simultaneously identify the shifting and scaling patterns. In this chapter, we will seek biclusters fitting the shift-scale model (see Fig. 1d) which covers both additive and multiplicative patterns as special cases.

Fig. 1
figure 1

Sample biclusters with various models: (a) constant-row, (b) shift, (c) scale, and (d) shift-scale. In pattern expressions, a ij represents expression level of gene i in sample j, π j a base value, α i scaling, and β i shifting patterns. The parameters are selected as \( {\alpha}_i={\left[1,2,3,-1\right]}^T,{\beta}_i={\left[2,3,4,1\right]}^T,{\pi}_j=\left[-1,2,1,4\right] \). Shift-scale is the most general model, as it has shift and scale models as special cases and can represent both positive and negative correlation

Full size image

How to evaluate the quality of the biclusters is also an important problem: for example, the classical mean squared residue (MSR) has been shown to be successful at finding constant, and additive biclusters, while it is not suitable for multiplicative biclusters. In addition, it is claimed to be biased toward flat biclusters with low row variance, and hence, different scoring schemas have been proposed Bryan and Cunningham [49]. Cheng and Cherch propose a deterministic greedy algorithm that seeks to find the biclusters with low variance, as defined by the MSR [11]. Similarly, the xMOTIFs algorithm has been proposed to capture conserved gene expression motifs that are the biclusters with conserved rows in discretized dataset [50]. A more complex relationship among the genes has been later studied in order-preserving submatrix problem (OPSM) [1, 51]. The authors propose a deterministic greedy algorithm that seeks biclusters for which the columns can be sorted in increasing order for all rows in the bicluster. Although additive and multiplicative biclusters can be captured by OPSM algorithm, it fails to capture constant biclusters. Surveys on biclustering of gene expression data, the proposed algorithms, and their evaluation via bicluster validation from a biological point of view can be found in [3, 45, 52–56].

2.1 PCC-Based Biclustering

PCC is a measure that evaluates positive and negative linear relationships between vectors. It is commonly used in clustering gene expression data [2, 4] due to its power in capturing both shifting and scaling patterns. For a PCC-based biclustering on gene expression dataset, the correlation of two genes is calculated on some specified columns since those genes may or may not be correlated on every experiment. Therefore, our PCC-based similarity measure between rows r and s on selected columns Y is calculated with:

$$ pcc\left(r,s,Y\right)=\frac{\left|{\displaystyle \sum_{i\in Y}}\left({r}_i-\overline{r}\right)\left({s}_i-\overline{s}\right)\right|}{\sqrt{{\displaystyle \sum_{i\in Y}}{\left({r}_i-\overline{r}\right)}^2{\displaystyle \sum_{i\in Y}}{\left({s}_i-\overline{s}\right)}^2}}, $$
(1)

where the equation runs on select columns, and the absolute value of the expression gives a result in [0, 1] interval.

PCC-based biclustering was recently proposed in [9, 57]. In [57], the authors present the bi-correlation clustering algorithm (BCCA), which tries to find biclusters using Pearson correlation. They also discuss the complexity of computing pairwise PCCs, and the inefficiency of the method. Bozdağ et al. [9] discuss potential complexity issues of an exhaustive search using PCC, and propose that, instead of computing all pairwise PCC values, a center-like vector (tendency vector) is sufficient and more efficient at finding correlated rows.

3 Correlated Pattern Biclusters

Given a query gene and a set of microarray datasets, we compute a ranked list of co-regulated genes in three steps. Here we give the details of these steps: In the first step, the CPB algorithm recovers a set of biclusters (Section 3.1). In the next step, we filter out statistically insignificant biclusters (Section 3.2). Finally, the correlation scores gathered from different datasets (Section 3.3). The overview of the framework is given in Fig. 2.

Fig. 2
figure 2

Overview of the proposed framework

Full size image

3.1 The CPB Algorithm

Let R and C denote the set of rows and columns of a data matrix A, respectively. Each element a rc  ∈ A represents the relation between row r and column c. A bicluster B = (X, Y) is a subset of rows X = { x 1, …, x n } and a subset of columns Y = { y 1, …, y m }, where n ≤ N, and m ≤ M.

Definition 1 (Correlated Pattern Biclusters Algorithm).

Given a data matrix A, reference row r r , PCC threshold ρ, and minimum number of columns γ, CPB finds a bicluster B = (X, Y) such that r r  ∈ X, m ≥ γ, \( {\forall}_{x_i,{x}_j\in X}\kern2.77695pt pcc\left({x}_i,{x}_j,Y\right)\ge \rho \).

CPB starts with an initial bicluster B = (X, Y) and improves it by iteratively moving rows and columns in and out of the bicluster using a search technique similar to local search methods. Algorithm 1 outlines the proposed biclustering algorithm. Important steps, i.e., generation of the initial biclusters, computing tendency vector T and normalization parameters, updating rows and columns are described in detail in the following subsections.

Algorithm 1 Correlated Pattern Biclusters

3.1.1 Generating Initial Biclusters

Selecting the rows and columns of the initial bicluster is important since the algorithm converges to a more stable one by adding and removing rows and columns to this bicluster. In [9], initial biclusters were chosen randomly, and the algorithm runs efficiently when discovering small number of biclusters embedded in synthetic datasets. However, we observe that when there are multiple biclusters this approach does not provide a consistent mechanism to return multiple biclusters with good coverage of the whole dataset.

In CPB, we generate initial biclusters with a grid-based approach. We first shuffle the row and column numbers of the dataset, and then partition the dataset into a coarse-grain grid of 10 × 2 initial biclusters. The query gene r r is inserted into each bicluster, if necessary. At the end, all genes and conditions in the dataset are assigned to at least one initial bicluster. Repeating the process gives us enough initial biclusters to find co-regulated genes and corresponding conditions. In addition, different runs obtain more than 75 % of the top-ranked co-regulated genes with the grid-based initialization, even though the generation of the initial biclusters is randomized.

3.1.2 Computing Normalization Parameters and Tendency Vector

In order to avoid making pairwise comparisons of all rows, we compute a tendency vector that represents an average of the rows of the bicluster. We compute a normalized data value

$$ {\hat{a}}_{x_i{y}_k}=\frac{a_{x_i{y}_k}-{\alpha}_{x_i}}{\beta_{x_i}} $$

for each x i  ∈ X and y k  ∈ Y, where \( {\alpha}_{x_i} \) and \( {\beta}_{x_i} \) are shifting and scaling parameters associated with row x i , respectively. Then, each element t k of tendency vector T is computed as the arithmetic mean of \( {\hat{a}}_{x_i{y}_k} \) on all rows x i  ∈ X.

To ensure that the reference row r r has a larger impact on decision mechanisms of the algorithm, we assign a larger weight, ω, to the reference row when computing the vector T. Total contribution from rows except r r is multiplied by (1 −ω) and contribution from r r is multiplied by ω, where ω is an input parameter. Large values for ω allow discovering patterns that resemble r r more closely, whereas small values reduce sensitivity, hence offer a higher tolerance to noise. Therefore, if a reference row and ω specified, the elements are calculated with

$$ {t}_k=\frac{\omega \times {\hat{a}}_{x_i{y}_{r_r}}+\left(1-\omega \right)\times {\displaystyle \sum_{k\in X-\left\{{r}_r\right\}}}{\hat{a}}_{x_i{y}_k}}{\left|X\right|}. $$
(2)

We compute T, \( {\alpha}_{x_i} \) and \( {\beta}_{x_i} \) using an iterative process. Initially we set \( {\alpha}_{x_i}=0 \) and \( {\beta}_{x_i}=1 \), and compute T. Then, we apply least squares fitting on pairs \( \left\{\left({t}_1,{a}_{x_i{y}_1}\right),\dots, \left({t}_m,{a}_{x_i{y}_m}\right)\right\} \) to obtain the best shifting and scaling parameters that maximize alignment of each row x i with the tendency vector T. We assign intercept and slope obtained in least squares fitting to \( {\alpha}_{x_i} \) and \( {\beta}_{x_i} \), respectively. T is updated using these parameters, and the process iterates until convergence.

3.1.3 Updating the Rows of a Bicluster

For a row r to be included in X, we require pcc(r, x i , Y ) > ρ for all x i  ∈ X. To avoid testing this condition against all x i  ∈ X, we utilize the tendency vector T, and only test whether pcc(r, T, Y) is greater than another threshold ρ′ instead. ρ′ is selected such that pcc(r, T, Y) > ρ′ must ensure pcc(r, x i , Y) > ρ for all x i  ∈ X. However, PCC lacks transitivity property [58] and has a complex formula that strongly depends on the values and the length of the vectors. Although it is analytically difficult to compute a lower bound for ρ′, it was empirically shown that there exists a lower bound proportional to ρ [9].

In Algorithm 1, we start with a relaxed threshold and slowly tighten it at Line 18. While tightening ρ′, we relax the constraint on minimum number of columns. This allows sweeping the search space between two extreme combinations of these parameters. The algorithm uses five tightening steps and initial values of \( {\rho}_c^{\prime }=2/3{\rho}^{\prime } \) and γ c  =  ∣Y ∣ (Line 3).

3.1.4 Updating the Columns of a Bicluster

Using PCC to measure the coherence between the columns is too restrictive. For example, although the rows in Fig. 1d are perfectly correlated, Pearson correlation between columns is less than 1. Therefore, we use root mean square error to assess the coherence of the columns. It is computed as:

$$ ERROR\left({y}_k\right)=\sqrt{\frac{1}{n}{\displaystyle \sum_{i=1}^n}{\left({\hat{a}}_{x_i{y}_k}-{t}_k\right)}^2}, $$
(3)

where y k  ∈ Y and n =  ∣Y ∣. For a column c ∉Y, we compute ERROR(c) in a similar way, by using a value t c analogous to t k that quantifies tendency of rows x i  ∈ X in column c.

In CPB, only the columns having ERROR below a threshold ε are included in the bicluster. In order to have comparable ERROR threshold for the column selection with respect to row addition, we select ε in relation to ρ′. To establish this relation, first we note that ERROR can also be computed for rows, and it is a comparable metric for rows and columns. For a row x i  ∈ X, ERROR(x i ) is computed as \( \sqrt{\frac{1}{m}{\displaystyle \sum_{k=1}^m}{\left({\hat{a}}_{x_i{y}_k}-{t}_k\right)}^2} \). Then, it is observed that ERROR(r) generally implies a high pcc(r, T, Y) [9]. Therefore, by setting ε to the ERROR of row r that has the smallest pcc(r, T, Y) above threshold ρ′ c (Line 13), we prevent the algorithm from returning imbalanced biclusters (i.e., very small or very high number of columns).

3.2 Filtering Biclusters Found by Random Chance

Any dataset contains small biclusters with a high Pearson correlation value by random chance. Although we specify a lower bound for PCC ρ′ and minimum number of columns γ, especially when γ is small, in addition to larger biclusters, CPB recovers such small biclusters. To eliminate randomly found biclusters in a non-parametric fashion, we developed following method. Suppose \( \mathbb{B}=\left\{{B}_1,{B}_2,\dots, {B}_z\right\} \) be the set of biclusters found by different runs of CPB on a data matrix A. We first generate A′ by shuffling the elements of A. Then, we find the bicluster B max with the highest number of rows in A′, and use its dimension n′ as a threshold to filter biclusters in \( \mathbb{B} \). Algorithm 2 summarizes the filtering process. Note that the parameter n′ is unique for each dataset, but this method empirically finds a lower bound for n′. The more biclusters generated from the shuffled dataset, the better the estimate of n′.

Algorithm 2 Filter Random Biclusters.

In addition to filtering out the statistically insignificant biclusters, we also remove those that have substantial overlaps. For any bicluster pair that has an overlap of 75 % or more, we remove the smaller bicluster.

3.3 Combining Correlation Information

CPB often produces different resulting biclusters due to the random selection of initial biclusters. Information from these biclusters, each including the reference row r r , is merged to score each row’s relationship with r r .

In [9], bicluster uniqueness (BU) measure was proposed to calculate the correlation score of the genes. Although BU is able to capture the information redundancy caused by overlapping biclusters, we present a similar but more efficient scoring function to be used instead.

Let \( \mathbb{B}=\left\{{B}_1,{B}_2,\dots, {B}_z\right\} \) be the set of biclusters found by different runs of CPB on a data matrix A, and with reference row r r . Suppose IR(r) and IC(c) denote the maximal subset of \( \mathbb{B} \) that contain the given row and column, respectively.

Definition 2 (Correlation Score (CS)).

A score is assigned to a row r based on the number of experiments in which r is co-regulated with r r by:

$$ CS(r)={\displaystyle \sum_{c\in C}}\mid IR(r)\cup IC(c)\mid . $$
(4)

To increase significance and consistency of our findings, we apply our method on different datasets separately and combine correlation scores. To achieve this in a meaningful way, we require datasets to have the same row labels. In gene expression data analysis, this requirement can be met by merging results only from datasets obtained using the same microarray chip.

Definition 3 (Gene Correlation Score (GCS)).

Let \( \mathbb{A}=\left\{{\mathbf{A}}_1,{\mathbf{A}}_2,\dots, {\mathbf{A}}_p\right\} \) be the set of (microarray) datasets with the same row labels (genes). Given a reference row r r and datasets \( \mathbb{A} \), gene correlation score G C S of a row r is calculated with

$$ GCS\left(r,{r}_r\right)={\displaystyle \sum_{{\mathbf{A}}_v\in \mathbb{A}}}\frac{CS(r)}{CS\left({r}_r\right)}. $$
(5)

4 Experimental Results

We test CPB on the probes of three tumor suppressor genes (i.e., BRCA1, BRCA2, and p53) as queries to reveal co-regulated genes involved in the complex process of tumor formation. Experiments on 40 large datasets, each with 22,283 probe sets, show that the results are remarkably enriched for genes that have a role in cancer progression, tumor growth and metastasis regulation, and DNA degradation and repair. We also compare our results with another query-based framework to see how successfully each method finds known and unexplored genes co-regulated with tumor suppressors. While the ratios of known cancer-related genes are similar, the proposed framework finds more unexplored genes that are likely to be missed by earlier clustering-based methods. CPB’s performance for querying the microarray data is promising: it was able to capture many genes that are highly correlated with BRCA1, BRCA2, and p53. We observed that of those genes, half are already known to be involved in cancer processes, and the others are promising new candidates for further investigation.

We first define some evaluation metrics and test CPB on synthetic datasets generated with biclusters with (1) different models, (2) increasing noise levels, and (3) increasing overlaps between embedded biclusters. We selected four other biclustering algorithms; δ-biclusters [11], OPSM [1], BBC [17], and BCCA [57], for comparison, due to their success at capturing shift-scale biclusters.

We test CPB on a number of human microarray datasets using four probes of breast cancer associated BRCA1 and BRCA2 genes, and two probes of p53 tumor suppressor gene as queries. The correlation scores of the genes are combined, and the top-ranked genes are further studied. We also compare our results with MEM framework [8] in terms of the algorithms’ effectiveness of retrieving undiscovered cancer-related genes.

4.1 Experiments on Synthetic Datasets

We first define recovery and relevance metrics to evaluate the results of biclustering algorithms. For each experiment, a synthetic dataset is generated with 1000 rows and 200 samples. Then two 60 × 60 biclusters with the given model are embedded into the dataset. The average score of 100 replication of the same experiment is reported.

4.1.1 Evaluation Metrics

Similar to recall and precision metrics, recovery and relevance scores are proposed to evaluate the biclustering results. These measures can be defined to compare a single found bicluster against an expected one, as well as a set of found biclusters against a set of expected ones.

Let e and f be expected and found biclusters, respectively. The recovery score of a found bicluster against an expected one is calculated by dividing the intersection area by the area of the expected bicluster:

$$ rec\left(e,f\right)=\frac{\mid e\cap f\mid }{\mid e\mid }, $$
(6)

where the recovery score reaches to 1 if and only if \( e\subseteq f \).

Similarly, relevance score is calculated by dividing the intersection area by the area of the found bicluster:

$$ rel\left(e,f\right)=\frac{\mid e\cap f\mid }{\mid f\mid }, $$
(7)

where the relevance score reaches to 1 if and only if \( f\subseteq e \). Examples of how these scores are computed are given in Fig. 3.

Fig. 3
figure 3

Example expected/found biclusters with their recovery and relevance scores

Full size image

Using these rec and rel measures, we define recovery and relevance scores to compare two sets. Let E and F be a set of expected and found biclusters, respectively. The set-based recovery score is calculated by taking the mean of the maximum recovery score for each expected bicluster. An equivalent approach is used for relevance.

$$ REC\left(E,F\right)=\frac{1}{\mid E\mid }{\displaystyle \sum_{e\in E}}\ {\displaystyle \underset{f\in F}{ \max }}\ rec\left(e,f\right) $$
(8)
$$ REL\left(E,F\right)=\frac{1}{\mid F\mid }{\displaystyle \sum_{f\in F}}\ {\displaystyle \underset{e\in E}{ \max }}\ rel\left(e,f\right) $$
(9)

4.1.2 Effects of the Bicluster Model

Biclustering methods often focus on detecting specific types of biclusters, as mentioned in Background section. In this experiment, we compare the success rate of CPB with other algorithms on detecting biclusters generated with various models. Constant-row, shift, scale, and shift-scale models were chosen for this experiment. Examples of these models are given in Fig. 1.

The resulting recovery and relevance scores (see Fig. 4a–d) show that CPB is the only algorithm that can fully recover biclusters generated with all four models with a high relevance score. BBC was able to find shifted and constant-row biclusters with a slightly lower relevance score. BCCA was expected to display similar results to CPB since they both use Pearson correlation; however, it was only able to fully recover shift biclusters. OPSM could not identify shift, scale, or shift-scale biclusters although they are all valid order-preserving submatrices. Our experiments show that when a base row is scaled with a value between −1 and 1, the expression rankings of the columns of a bicluster row lie in a narrow range along the row; therefore, OPSM fails to discover it. Despite this limitation, OPSM was able to identify one of the shifted biclusters, since it reports a single bicluster for each size of column. The δ-biclusters algorithm performed poorly on all the datasets, among which it can partially recover only constant-row biclusters. The other models are not captured by the metric, which was previously discussed in [53].

Fig. 4
figure 4

Experiments on synthetic datasets: (a–d) with different bicluster models, (e) under noise, and (g) with overlapping biclusters

Full size image

For the noise and overlap experiments, CPB and other methods were compared on shift biclusters since the shift model is successfully recovered by most of the algorithms (see Fig. 4b).

4.1.3 Effects of the Noise

Microarrays results are perturbed by many sources of noise. In order to measure the sensitivity of CPB to noise, an error value ε was added to each element of the synthetic datasets. The experiments were run with various noise levels: each error value was drawn from a normal distribution with zero mean and variance equal to the chosen noise level.

Figure 4e shows the recovery and relevance scores of the algorithms on datasets with varying noise levels. OPSM is dramatically affected by noise since it may violate the order-preserving structure. Since BCCA checks for pairwise correlation score for each row, this method is more likely to be affected by the increasing noise. Although BBC seems to be insensitive to noise in recovery plot, its relevance score drops slightly with noise addition (see Fig. 4e). CPB is the second best algorithm that is resistant to noise even though it has a linear metric. Moreover, the noise resistance of CPB can be improved by adjusting a better PCC threshold. We fixed ρ = 0. 9 in order to be consistent with the rest of the experiments.

We also experimented with relative noise, in which the noise is added to each element with respect to its expression value, i.e., element x becomes x + x ε. We observed results similar to the previous experiment.

4.1.4 Effects of the Overlap

A gene may take roles in several functions in a cell, each of which may be occurring simultaneously in a given sample; therefore, there might be overlaps between biclusters. In this experiment we test how CPB and other algorithms perform with increasing overlaps of biclusters. The datasets are generated with two overlapping biclusters. The overlapping regions of these biclusters are increased by 10 rows and 10 columns at each step. The expression values in the these regions are not assumed to be additive; instead, shift values for rows and base vector are chosen in a way to allow both of the biclusters to have the same expression value at overlapping regions.

Figure 4f shows the results of the overlap test. We observe that CPB and BCCA are both insensitive to increasing overlap, while BCCA fails to recover a very small portion of the biclusters. BBC is affected more than BCCA in terms of recovery; also, its relevance score drops with increasing overlap. Although OPSM recovers only one of the biclusters, it increases its recovery score by including more of the overlapping region with increasing overlap.

4.2 Identifying Genes Co-regulated with BRCA1, BRCA2, p53

In this experiment, we employ CPB to identify the most correlated genes with BRCA1, BRCA2, and p53, which are highly penetrant cancer specific tumor suppressors. CPB was run on 40 different datasets obtained from the GPL96 series (GDS{1064, 1284, 1615, 2113, 2362, 2649, 2954, 3116, 3312, 3716, 1067, 1329, 1815, 2190, 2373, 2736, 3057, 3128, 3471, 534, 1209, 1375, 1956, 2255, 2519, 2767, 3096, 3233, 3514, 596, 1220, 1479, 1975, 2297, 2643, 2771, 3097, 3257, 3517, 987}), all of which have the same set of probes. The results of each dataset are then combined with Gene Correlation Score function.

Table 1 gives the top-ranked genes for the probes of BRCA1, BRCA2, and p53. We observe that more than 50 % of the genes found by our framework are already investigated in cancer research, suggesting that CPB is indeed finding genes involved with cancer.

Table 1 Associated top-ranked genes for 6 probes of BRCA1, BRCA2, and p53
Full size table

Among those, for example, MBD2 is shown to have a role in cancer progression and can be therapeutically targeted in aggressive breast cancers [59]. KLK10 provides important prognostic information in early breast cancer patients [60]. CHRNA4 polymorphisms are found to activate factors that participate in DNA degradation and repair, specifically the level of p53 participating in DNA repair [61].

Some genes, highly correlated with p53 in the list, are also investigated in other cancer types. For instance, 4 messenger RNA biomarkers, including ACRV1, may differentiate pancreatic cancer patients from noncancer subjects [62]. GFRA4 is predominantly expressed in normal and malignant thyroid medullary cells [63]. Of those, which are also correlated with BRCA1 and BRCA2 genes, can be further studied to see if they are up- or down-regulated in cancer patients.

The genes that have not already appeared in the literature may play an as-yet unknown role in cancer-related processes. These genes are open for further research.

4.3 Comparison with Other Query-Based Frameworks

There are a limited number of studies on query-based discovery of co-regulated genes in the literature. Gene recommender [5] analyzed Rb protein complex to find new co-regulated genes in worms (specifically C. elegans) using a technique similar to biclustering. SPELL [6], a PCC-based clustering framework was tested on S.cerevisiae datasets, where several genes were categorized and annotated. A probabilistic biclustering framework, QDB [7], was tested on some synthetic and yeast microarray datasets. Adler et al. [8] propose a query engine (MEM) to search for correlated genes across many datasets. Zhao et al. proposed ProBic [10], a probabilistic biclustering algorithm, and tested on E. coli to detect high quality biclusters in the presence of noise.

Among those query-driven search methods, we could compare our framework on cancer-related genes with only MEM [8], because the other studies are either specialized in non-human organisms, or resource is not accessible. Using MEM framework, we retrieved the genes correlated with the selected probes of BRCA1, BRCA2, and p53 genes with Pearson correlation. Top-ranked genes are then investigated to find whether the gene is claimed to be cancer-related in a research study in medical literature.

In Table 2 we compare our results with MEM’s based on how successful each method is on finding known and unexplored genes. Since all samples (columns) of a microarray dataset were included in similarity calculations before biclustering, the top-ranked genes discovered by MEM are expected to be investigated before. While the ratios of known cancer-related genes are similar, we argue that our framework finds more unexplored genes that are likely to be missed by earlier clustering-based methods.

Table 2 Ratio of known and unexplored genes found within top-25 results of MEM (with Pearson and absolute Pearson correlation) and our framework
Full size table

Although PCC is the default similarity measure, we also run MEM with absolute Pearson correlation, which is expected to capture negative correlations as in our pcc function (see Eq. (1)). However, the results on six probes between two runs of MEM framework are 87 % overlapping. Absolute PCC could only introduce 20 new genes, where 60 % of them are already found to be cancer-related. We conclude that altering the similarity measure (in this case, taking the absolute value to capture negative correlations) is not as effective for finding undiscovered correlated genes as applying biclustering.

5 Conclusion

In this chapter, we briefly survey the biclustering algorithms in the literature and introduce a method for querying co-regulated genes using a novel biclustering method, the CPB. Initial testing on artificial data confirms that CPB is capable of finding such biclusters and that it outperforms other biclustering methods in finding multiple types of biclusters. CPB’s performance for querying the microarray data is promising: it finds many genes that have high correlations with BRCA1, BRCA2, and p53. Of those genes, half are already known to be involved in cancer processes, and the others are promising new candidates for further investigation.

There are many possible extensions to CPB that may yet be explored. For instance, PCC is only one of the well-known metrics for evaluating similarity. CPB approach may be extended to use other metrics and benefit from their unique properties. CPB’s iterative optimization process may likewise be improved by choosing initial biclusters differently or using a mathematical optimization method to avoid the local maximas.

6 Acknowledgments

This work was supported in parts by National Institutes of Health/National Cancer Institute (grant number R01CA141090); by the Department of Energy (grant number DE-FC02-06ER2775); and by the National Science Foundation (grants numbers CNS-0643969, OCI-0904809, OCI-0904802).