Quantum Computation with Molecular Nanomagnets: Achievements, Challenges, and New Trends

Abstract

Molecular nanomagnets exhibit quanto-mechanical properties that can be nicely tailored at synthetic level: superposition and entanglement of quantum states can be created with molecular spins whose manipulation can be done in a timescale shorter than their decoherence time, if the molecular environment is controlled in a proper way. The challenge of quantum computation is to exploit the similarities between the coherent manipulation of molecular spins and algorithms used to process data and solve problems. In this chapter we shall firstly introduce basic concepts, stressing analogies between the physics and the chemistry of molecular nanomagnets and the science of computing. Then we shall review main achievements obtained in the first decade of this field and present challenges for the next future. In particular we shall focus on two emerging topics: quantum simulators and hybrid systems made by resonant cavities and molecular nanomagnets.

1 Introduction

Quantum computation exploits tight similarities between the time evolution of a quantum system and some algorithms. This parallelism is essentially given by the mathematical description that accounts – at the same time – for the dynamics of the quantum system and for the calculation rules on which the algorithm relies. Experimentally, performing quantum computation implies to control the dynamics of the quantum system under the action of an external stimulus. Thus, defining the input of the calculation means to prepare our system in a given quantum state, processing data means to let our system evolve under the action of a given stimulus and reading the output stands for measuring the final quantum state of our system. It is clear that basic requirements for a system to be used as quantum computer are the description of its states and the full control of its dynamics in terms of both modeling and experimental procedures. On the other hand, quantum computation exploits specific characteristics of quanto-mechanics, like superposition and entanglement of quantum states; thus, it results to be more efficient than classical computers in solving a number of computationally complex problems. Starting from the suggestive intuition (the aforementioned parallelism) of Richard Feynman in the 1980s, several quantum systems, such as isolated atoms or ions, photons, electrons in quantum dots or superconducting circuits, have been successfully used to encode quantum bits (qubit). Spins are also excellent quantum systems for which both mathematical description and experimental tools for their manipulation have been largely developed.

The spin of molecular clusters may also work well for qubit encoding if we are able to manipulate them as quantum objects. As a matter of fact, the first proposal to use molecular nanomagnets for quantum computation appeared in 2001 when the field of molecular magnetism achieved its maturity with the Agilent Technology Europhysics Prize awarded to Sessoli, Gatteschi, Wernsdorfer, Barbara, and Friedman for their discovery of Quantum Phenomena in molecular nanomagnets (2002). At that time quantum phenomena were primarily studied by magnetization measurements in different conditions. Pulsed ESR experiments at very low temperatures are required to manipulate electron spins in molecules and this introduced new experimental challenges. On the other hand, theoreticians immediately realized the huge potentialities of arranging spins in well-defined architectures like those provided by molecular assemblies and new challenges have been proposed to synthetic chemists since then. After one decade from its start, several important results have been obtained: the decoherence time has been measured on several molecular nanomagnets and different molecules have been designed and synthesized with inspiration to computing schemes.

In this chapter, we firstly introduce some fundamentals and then we review achievements obtained so far. No ambition to be exhaustive since this new field is strongly interdisciplinary and in rapid evolution. We shall rather focus on these questions: how a given molecular spin cluster fits a specific quantum scheme? Which are the advantages in using molecular spins with respect to other quantum systems to encode qubits? How far can a molecule be engineered in order to preserve the spin dynamics from the environmental noise? How should we assemble molecular spins in order to fabricate complex quantum devices?

The chapter is organized as follows: in Sect. 2 we summarize some basic concepts while we refer the reader to textbooks for a systematic presentation of quantum computation [1, 2] and for a detailed description of the spin dynamics [2, 3]. In Sect. 3 we discuss the problem of understanding and controlling the mechanisms of decoherence which limit the spin dynamics in molecular nanomagnets; in Sect. 4 we introduce concept of entanglement and we discuss superposition of quantum states in molecular spin clusters. In Sect. 5 we review results and specific proposals involving molecular spin clusters. The last two paragraphs are devoted to two emerging areas (trends): in Sect. 6 we introduce the idea of quantum simulators, i.e. small quantum computers dedicated to efficiently solve specific problems; finally in Sect. 7 we overview the possibility to link molecular spin clusters with other quantum systems in order to realize hybrid quantum devices. Finally, in the last paragraph we summarize the results and try to highlight open questions.

2 Spin Qubits

While for classical bits only two states 0 or 1 are possible, a qubit can exist as a superposition states: |Ψ〉 = α|0〉 + β|1〉, being |0〉 and |1〉 two eigenvalues representing a basis of the two-level system. In this representation, any unitary transformation that acts on the wavefunction |Ψ〉 can work as a quantum gate. A spin 1/2 is a prototypical case. The spin components along three perpendicular directions follow the commutation rules given for angular momentum. The Pauli operator $\widehat{\sigma}$ with components:

$$ {\sigma}_x=\left(\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill 0\hfill \end{array}\right),\kern1em {\sigma}_y=\left(\begin{array}{cc}\hfill 0\hfill & \hfill -i\hfill \\ {}\hfill i\hfill & \hfill 0\hfill \end{array}\right),\kern1em {\sigma}_z=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill -1\hfill \end{array}\right), $$

satisfy such conditions and are the proper tools to describe the spin operator $\widehat{\mathbf{S}}=\hslash \widehat{\sigma}/2$. We can fix the z-direction by an applied magnetic field B ₀. Two eigenstates of the σ _z operator are the | ↑ 〉 and | ↓ 〉 states, i.e. the spin lying along or opposite to the magnetic field direction. In this context, qubits are well represented by spinors, i.e. any superposition: |Ψ〉 = α| ↑ 〉 + β| ↓ 〉 with |α|² + |β|² = 1. It is also convenient to visualize spinors by points on a Bloch sphere profiting from the correspondence with vectors sin(θ/2)| ↑ 〉 + cos(θ/2)e ^iϕ| ↓ 〉 (Fig. 1).

Fig. 1

Representation of the Hilbert space of a two-level system on the Bloch sphere. The eigenstates | ↑ 〉 and | ↓ 〉 of the Pauli matrix σ _z correspond to the basis states |0〉 and |1〉. A point on the Bloch sphere with polar coordinates θ and ϕ corresponds to a superposition of |0〉 and |1〉

Quantum gates operating on single-spin qubit are elementary rotations along particular directions as we shall see in Sects. 5 and 7 in more detail. We can now realize that spin impurities in solids and nuclear spins in solution can be considered as natural candidates for qubits encoding and the required tools – algebra and experiments – to control their dynamics have been largely developed. Nuclear spins are generally well isolated from the environment and can maintain free rotation for seconds even at room temperature, but it is hard to detect their small magnetic moment. Electron spins can be detected more easily but they are linked to the environment more closely and several damping mechanisms limit their free rotations.

We mentioned S = 1/2 but one may wonder whether higher spins can also be used to encode quantum bit. Certainly yes, if we identify two sub-levels, for instance two m-states of the ground multiplet and the allowed transition related to these sub-levels. There are also (quantum) algorithms that require multi-level registers, thus one can also try to exploit more sub-levels in a high-spin multiplet. Generally speaking, the use of high spin may facilitate the manipulation and the measurement of the final state but high spins are more sensible to the environment, thus a tradeoff needs to be found taking into account also the specific computational scheme.

A quantum computer can be designed to solve different types of problems. Similarly to classical computers, two possible strategies can be adopted: the first one is to build a “universal” computing machine versatile enough to solve – in principle – any type of problem. Alternatively, one can identify specific classes of problems and design specialized quantum machines that result in being more efficient than any classical analogue for that task. In both cases, quantum computers are designed to perform sophisticated quantum algorithms. Like for the classical ones, it is convenient to decompose complex algorithms in sequences of elementary (quantum) gates. Thus the first problem is to identify a set of gates which can be combined to perform more complex algorithms and therefore to constitute the basis for a universal quantum computer. Keeping this scheme in mind, we can now describe quantum operations with spins.

Basic operations on single qubit are given by rotations of the spin about arbitrary directions in the space. Elementary rotations of an angle θ around the x-axis can be described by using the Pauli matrices:

$$ {R}_x\left(\theta \right)={e}^{-i\theta {\sigma}_x/2}; $$

(1)

or – equivalently – by the matrix:

$$ {R}_x\left(\theta \right)=\left[\begin{array}{c}\hfill \cos \left(\theta /2\right)\hfill \\ {}\hfill -i \sin \left(\theta /2\right)\hfill \end{array}\begin{array}{c}\hfill -i \sin \left(\theta /2\right)\hfill \\ {}\hfill \cos \left(\theta /2\right)\hfill \end{array}\right]. $$

(2)

Again, the Bloch sphere helps us to visualize these rotations (Fig. 2) and this is a useful tool to understand how a simple quantum gate actually works on a spin qubit. In practice, a spin flip is obtained by electromagnetic pulses with the magnetic field component along the suited axis (see Sect. 7 for further discussion).

Fig. 2

Representation of spin rotation using the Bloch sphere. This rotation can be generated by the action of a magnetic pulse B ₁. In this case, for θ = π, the rotation represents a NOT-gate inducing a spin flip

In analogy with the classical ones, a convenient way to represent gates is to provide the so-called truth table which gives the final state for each possible combination of initial states.

Next we need to perform gates involving two or more qubits. One qubit is chosen as control while the other(s) are considered as target(s) in such a way that the final state of target is determined also as a function of the initial state of the control. For instance, a basic two-qubit gate is the control-NOT (CNOT) that operates as described by the truth table (see Table 1). Qubit–qubit coupling is an essential resource to build multi-bit quantum gates. That is why it is important to control inter-molecular interaction and spin entanglement in molecular assemblies as described in the Sect. 4. Moreover since the implementation of both single- and multi-qubit gates requires a dynamical control of such interactions, fast molecular switches or protocols to switch the coupling between spin clusters are also of great interest for the realization of multi-bit gates.

Table 1 Truth table of the Controlled-NOT gate. The first qubit acts as control while the second is the target: the target qubit is flipped if and only if the control is set to 1

The key point here is that it is demonstrated that any unitary operation on n-qubits can be implemented by a sequence of single-qubit and CNOT gates. Equivalent universality can be proved with other sets of elementary operations of one- and two-qubit gates [1]. This is an important result that suggests to focus effort in proving the feasibility of elementary quantum gates with new qubit candidates like molecular nanomagnets.

In principle, there are many other quantum algorithms of interest. Yet, not for many of them it has been proved that they are more efficient than classical analogues. That’s why the interest is generally focused on few of them which become popular for their proven efficiency.

A first one is the Shor’s algorithm that is based on the quantum Fourier transform of a given set of N states. The algorithm increases exponentially its efficiency with respect to a classical computer by exploiting both the superposition and the entanglement of quantum states. The Fourier transform allows to solve a large class of problems including the factoring in prime numbers. Worth to be mentioned here is a very nice experiment that proved the ability to factorize the number 15 has been realized by NMR with nuclear spins [4]. Factorization of larger numbers (143) has been recently demonstrated by implementing an adiabatic approach [5].

A second class of problems that quantum computers have been proved to solve more efficiently than classical ones is the search of items in an unsorted database of N entries. Schematically the problem can be simplified as follows: suppose we have to find a number in a phonebook. A classical computer splits the database into two and finds the part where the number is and it will proceed like this until the requested number is found. In 1996, Lev Grover proposed an algorithm exploiting the superposition and interference of quantum states (but not the entanglement!). In this way, the quantum computer operates in parallel by exploring different possibilities at the same time. This requires $\sqrt{N}$ steps instead of N needed by a classical computer.

3 Decoherence Mechanisms in Molecular Nanomagnets

Communication and processing of quantum information is based on the coherent evolution of the system state vector: |Ψ(t)〉 = e ^{− iHt/ℏ}|Ψ(0)〉. In real systems, however, the coupling to the environment (ℰ) tends to spoil the coherent character of the system ($\mathcal{S}$) dynamics. This process is known as decoherence [6, 7], and its characteristic timescale is the (de)coherence time τ _d. The environment can induce transitions between different eigenstates of the system Hamiltonian, as in the relaxation and incoherent excitation. These processes can be made relatively inefficient by introducing a large energy mismatch between the system and the environment excitation energies. The most harmful form of decoherence is typically represented by dephasing, resulting from elastic interactions between $\mathcal{S}$ and ℰ. Dephasing consists in the loss of phase coherence between the components of a linear superposition and implies the evolution of a pure state into a statistical mixture: |Ψ〉 = ∑  _i c _i |ϕ _i 〉 → ρ = ∑  _i |c _i |²|ϕ _i 〉〈ϕ _i |. If relaxation and dephasing display exponential dependences on time, they can be characterized by the so-called longitudinal (T ₁) and transverse (T ₂) relaxation time constants. Decoherence is an ubiquitous phenomenon; yet, its features and timescales depend strongly on the system, the experimental conditions, and the specific linear superpositions under consideration.

In molecular nanomagnets, decoherence of the electron spin mainly arises from the coupling to phonons and nuclear spins [8, 9]. In addition, being most experiments performed on ensembles of nanomagnets, dipolar interactions between different replicas of the system can result in decoherence [10, 11]. While dipolar interactions and coupling to phonons depend on the arrangement of the nanomagnets within the sample, and can be possibly reduced by modifying such arrangement, the coupling between electron and nuclear spins of each molecule represents an intrinsic source of decoherence. Hyperfine interactions might therefore represent the fundamental limitation of the electron-spin coherence.

Let’s consider the case of a nanomagnet with an S = 1/2 ground state doublet, that is initialized into a linear superposition: $\left|\varPsi \right\rangle =\left(\left|{\varPsi}_1\right\rangle +\left|{\varPsi}_2\right\rangle \right)/\sqrt{2}$, where |Ψ ₁〉 = | ⇑ 〉 and |Ψ ₂〉 = | ⇓ 〉 are the lowest eigenstates of the molecule spin Hamiltonian H. In the presence of a static magnetic field B ₀ along z, the molecule spin tends to precess in the xy plane. The (contact and dipole–dipole) coupling between the electron (s _i ) and the nuclear spins (I _k ) modifies such idealized picture in different respects. Firstly, the nuclear bath generates a magnetic field (the so-called Overhauser field B _N ); this adds to B ₀ a contribution that renormalizes the Larmor frequency of the nanomagnet spin S and depends on the state of the nuclei. The state of the nuclear bath is generally undefined and is thus represented by a statistical mixture of different states |ℐ _α 〉, each with probability p _α and each inducing a different renormalization δ _α of the Larmor frequency. As a consequence of such dispersion in the Larmor frequency, the state of the nanomagnet evolves from |Ψ〉 into a mixture ρ = ∑  _α p _α |Ψ _α (t)〉〈Ψ _α (t)|, with $\left|{\varPsi}_{\alpha }(t)\right\rangle =\left[\left|\Uparrow \right\rangle +{e}^{i{\left({\omega}_L+{\delta}_{\alpha}\right)}^t}\left|\Downarrow \right\rangle \right]/\sqrt{2}$. On timescales where the dynamics of the nuclear bath is frozen, the phase coherence can be ideally recovered by refocusing techniques. On timescales where the nuclear bath dynamics can’t be neglected, the electron-spin decoherence tends to be irreversible. In fact, even if the nuclei cannot efficiently induce transitions between electron-spin states (due to the large mismatch between the electron and the nuclear Zeeman energies), these can in turn affect the nuclear dynamics. In first order in the hyperfine coupling, such dependence results from the chemical and Knight shifts, i.e. from the magnetic field generated by the spins s _i on the I _k . Higher-order processes can also contribute, such as those where a (real) transition between nuclear states involves a virtual transition of the electron state. The evolution of the nuclear-bath state, resulting from the interplay between such hyperfine interactions and the (dipole–dipole) ones between the nuclei, nuclei is different if the electron spin of the nanomagnet points in one direction or in the opposite one. As a consequence, electron-nuclear correlations arise, and an initial state which is factorizable into the product of an electron and a nuclear state (e.g., (| ⇑ 〉 + | ⇓ 〉) ⊗ |ℐ〉, evolves into an entangled state | ⇑ 〉 ⊗ |ℐ_⇑〉 + | ⇓ 〉 ⊗ |ℐ_⇓〉, where |ℐ _{χ = ⇑,⇓}〉 are the states of the nuclei conditioned upon the electron spins being in either of the two eigenstates). The state of the electron spins alone is defined by the reduced density matrix, which is obtained by tracing away the nuclear degrees of freedom, i.e. by averaging over the nuclear spins state. One can show that the stronger the dependence of the nuclear state on the electron state, the smaller |〈ℐ_⇑| ℐ_⇓〉|, the smaller the modulus of the electron-spin coherence.

The control of decoherence represents indeed one of the key challenges for the implementation of quantum-information processing. In order to maximize the decoherence time, a detailed understanding of the process is required [9]. This represents the prerequisite for engineering the system by chemical synthesis; besides, it allows one to identify the degrees of freedom that are more robust with respect to decoherence and that are thus more suitable for encoding quantum information. The simulation of the nuclear dynamics in Cr₇Ni rings, for example, has allowed one to highlight the dominant role played by the H nuclei that represent the majority of the nuclear spins in the molecule [12].

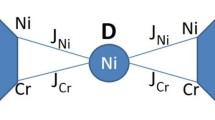
Quantum-information processing heavily relies on linear superpositions of multi-qubit states. The decoherence of such states is therefore also relevant and in general cannot be simply reduced to that of the single qubit. Let’s consider the case of two exchange-coupled Cr₇Ni rings. A linear superposition of two eigenstates of the dimer such as $\left(\left|\Uparrow \Uparrow \right\rangle +\left|\Downarrow \Downarrow \right\rangle \right)/\sqrt{2}$, which is also an entangled state, decoheres under the effect of hyperfine interactions with the same characteristic timescales of linear superpositions in the single ring. Two (effective) 1/2 spins can also be used to encode a single qubit. In the singlet–triplet qubit, for example, the logical states 0 and 1 are identified with the singlet and triplet (with M = 0 states). In the dimer of Cr₇Ni rings, a linear superposition between these two states is much more robust than that between the polarized states (M = ±1) [13]. In fact, for both the M = 0 states, the expectation values of the electron spins vanish. As a consequence, neither state induces a shift of the nuclear energies. The main contribution to the electron-nuclear entanglement is thus represented by processes that are second order in the hyperfine couplings, which are orders of magnitude smaller. These processes consist of flip-flop transitions between pairs of nuclei, mediated by virtual transitions of the electron-spin state. The comparison between these two linear superpositions in the ring dimer shows how decoherence can depend not only quantitatively but also qualitatively on the state in question.

A similar argument applies to the eigenstates of the chirality qubit, where the logical states coincide with eigenstates of opposite spin chirality ${C}_z=\left(4/\sqrt{3}\right){\mathbf{s}}_1\cdot {\mathbf{s}}_2\times {\mathbf{s}}_3$. If C _z is used for the qubit encoding, the states |0〉 and |1〉 also correspond to identical expectation values of the spin projections, both of the total and of the individual spins. As a consequence, the timescale related to nuclear-induced decoherence is enhanced by at least two orders of magnitude with respect to the value of S _z [14]. Such a robustness with respect to decoherence represents a potential advantage of the chirality qubit, along with the possibility of performing the manipulation through electric – rather than magnetic – fields.

Experimentally a first estimation of decoherence effects can be obtained by measuring the line-width of continuous-wave EPR spectra. However this includes several effects and more detailed information can be obtained by pulsed ESR experiments, as also explained in another chapter of this book. Specific pulse-sequences are adopted in order to minimize some contingent effects – like inhomogeneity – and evidence intrinsic dephasing effects. These techniques are normally used to evaluate T ₂. Experimental values measured on specific molecular nanomagnets are reported in Sect. 5.

4 Linear Superpositions and Entanglement of Quantum States in Molecular Nanomagnets

In order to outperform classical devices, quantum computers need to exploit quantum interference and entanglement. A preliminary condition for implementing quantum-information processing is thus represented by the capability of understanding and controlling such quantum-mechanical effects in the systems of interest. In this perspective, we introduce hereafter criteria for quantitatively investigating linear superpositions and entanglement in molecular nanomagnets.

4.1 How Large Is a Linear Superposition?

Quantum mechanics allows superpositions of quantum states in systems of – in principle – arbitrary dimensions. This leads to admit the paradoxical possibility that a macroscopic system be suspended between two classically incompatible states. In the last decades, the controlled generation of linear superpositions in systems of increasing sizes has also gained a practical relevance, especially in the fields of quantum-information processing and quantum metrology. However, the question on whether or not a linear superposition is truly macroscopic, or, more generally, on how large a linear superposition actually is, doesn’t admit a simple and general answer.

This issue was first addressed by Leggett [15], who introduced the so-called disconnectivity as a possible measure of the size of a quantum state. The disconnectivity essentially corresponds to the number of particles within the system that are quantum correlated with each other. Other measures have been proposed in the last years, with reference to a more specific class of linear superpositions, namely that between two semiclassical states: $\left|\varPsi \right\rangle =\left(\left|{\varPsi}_1\right\rangle +\left|{\varPsi}_2\right\rangle \right)/\sqrt{2}$. One possible starting point for quantifying the size of |Ψ〉 is represented by the observation that linear superpositions of this kind tend to be extremely fragile with respect to decoherence. In fact, the rate at which the phase coherence between the components decays is expected to increase exponentially with the number of particles that form the system (Quantum mechanics would thus explain why linear superpositions in the macroscopic world, though possible in principle, are generally not observable). Therefore, the decoherence rate itself can be used to quantify the size of the linear superposition [16]. Another possible criterion is based on the use of macroscopic linear superpositions to increase the sensitivity of interferometric experiments. Here, the typical experimental setting includes a quantum system that evolves in time under the effect of a single-particle Hamiltonian αH, where α is the parameter to be estimated. One can show that the sensitivity of the interferometric estimation of α depends on the time that the quantum system takes to evolve into a state orthogonal to the initial state and is maximized by linear superpositions of semiclassical states [17]. The measures that have been introduced according to this criterion are closely related to the ones that are discussed in the second part of the present paragraph.

Hereafter, we consider pure quantum states of the form $\left|\varPsi \right\rangle =\left(\left|{\varPsi}_1\right\rangle +\left|{\varPsi}_2\right\rangle \right)/\sqrt{2}$, where |Ψ ₁〉 and |Ψ ₂〉 are two ground states of the nanomagnet of interest, and, more specifically, of its spin Hamiltonian. In particular, we shall assume that these ground states have well-defined values of the total spin (S) and of its projection along z (M ₁ and M ₂, respectively). Linear superpositions of this kind can be dynamically generated by pulsed magnetic fields, or statically induced by resonant tunneling.

There are at least two simple and intuitive ways to quantify the size of such a linear superposition. The first one would be to identify the size of the linear superposition with the number of spins that form the cluster (N). The second way would be to quantify the size of |Ψ〉 in terms of the spin length S, or of the difference between the total-spin projections corresponding to the two components (|M ₁ − M ₂|). The shortcomings of such approaches are, however, quite apparent. The first criterion only depends on the structure of the nanomagnet and therefore doesn’t discriminate between any two linear superpositions generated within a given system. On the opposite side, the second criterion leaves completely out of consideration the number of constituent spins involved in the linear superposition, as well as the features of |Ψ ₁〉 and |Ψ ₂〉 that depend on any quantum number but S and M. In the following, we discuss two ways to measure the size of linear superpositions, which can be regarded as two refined versions of the above ones.

In the first measure we consider the size of the linear superposition corresponds to the number N′ of units (or subsystems) into which the spin cluster can be partitioned, such that one can discriminate between the states |Ψ ₁〉 and |Ψ ₂〉 with a probability P larger than some fixed threshold 1 − ε, by performing arbitrary measurements within each subsystem [18]. The definition of such units, and the value of N′, is thus state-dependent. According to such a criterion, the fact that a linear superposition |Ψ〉 is large requires not only large values of N, but also that the which-component information is available within each few microscopic units. In the limiting case where the single-spin states corresponding to |Ψ ₁〉 and |Ψ ₂〉 are orthogonal, the corresponding size attains its theoretical maximum N = N′. This would be the case, for example, with a linear superposition between fully polarized states (|Ψ ₁〉 = | ↑ ↑ ↑ … 〉 and |Ψ ₂〉 = | ↓ ↓ ↓ … 〉), or between two states with maximum values of the staggered magnetization (|Ψ ₁〉 = | ↑ ↓ ↑ … 〉 and |Ψ ₂〉 = | ↓ ↑ ↓ … 〉).

The second measure we consider can be traced back to the intuitive idea that a large linear superposition |Ψ〉, and more specifically a Schrödinger-cat state, is characterized by a high degree of quantumness, while its components |Ψ ₁〉 and |Ψ ₂〉 are classical-like states. A classical-like state of a spin cluster is possibly one where each of the spins is in a defined state, and more specifically one that minimizes the overall fluctuations in the spin-component operator. Conversely, a nonclassical (pure) state is identified by the fact that the state of each spin is undefined, being the spin entangled with the rest of the system. As a result, the fluctuations of any single-spin operator tend to be large. The size of the linear superposition can thus be quantified by the variance of an operator that can be written as the sum of single-spin operators: $\mathcal{V}\left(X,\varPsi \right)=\left\langle \varPsi \right|{X}^2\left|\varPsi \right\rangle -\left\langle \varPsi \right|X{\left|\varPsi \right\rangle}^2$, where $X={\sum}_{i=1}^N{\widehat{\mathbf{n}}}_i\cdot {\mathbf{s}}_i$ [19]. If Ψ _k = 1,2 is given by the product of single-spin coherent states, one can always find a set of versors ${\widehat{\mathbf{n}}}_i$ such that $\mathcal{V}\left(X,{\varPsi}_k\right)$ vanishes. In general, the versors ${\widehat{\mathbf{n}}}_i$ are chosen so as to maximize the fluctuations of X for each given linear superposition. In the simplest case, ${\widehat{\mathbf{n}}}_i=\widehat{\mathbf{z}}$, the operator X reduces to S _z and its variance coincides with (M ₁ − M ₂)²/4. In other cases of interest, ${\widehat{\mathbf{n}}}_i=\pm \widehat{\mathbf{z}}$, and X coincides with the staggered magnetization S ^* _z  = S ^A _z  − S ^B _z , being A and B two sublattices into which the spin cluster is partitioned. In any case, in order to single out the degree of quantumness which specifically comes from the linear superposition of |Ψ ₁〉 and |Ψ ₂〉, rather than from the components themselves, the fluctuations of X in |Ψ〉 can be normalized to those in the states $\left|{\varPsi}_{k=1,2}\right\rangle :{\mathcal{V}}_n\left(X,\varPsi \right)=2\mathcal{V}\left(X,\varPsi \right)/\left[\mathcal{V}\left(X,{\varPsi}_1\right)+\mathcal{V}\left(X,{\varPsi}_2\right)\right]$.

The two criteria outlined above have been used to quantify the size of linear superpositions that have been – or might be – generated in a number of noticeable molecular nanomagnets [20]. Here, a major distinction is that between high-spin molecules, such as Mn₁₂ and Fe₈ ground state, and low-spin systems, such as Cr₇Ni or V₁₅ (S = 1/2). The former ones are characterized by more classical-like ground states (in particular, those with M = ±S) In the latter ones, the ground states are highly nonclassical, and a large amount of quantum fluctuations of the single-spin operators results from the competing exchange interactions. These general features are clearly reflected by the values of N′ and $\mathcal{V}\left(X,\varPsi \right)$ obtained for the different nanomagnets.

The largest linear superpositions can be generated in high-spin molecules, by linearly combining states of maximum spin projection (M = ±S). Here, the size based on the distinguishability of |Ψ ₁〉 and |Ψ ₂〉 by local measurements corresponds to N′ = 8 and N′ = 5 for Mn₁₂ and Fe₈, respectively (Fig. 3). In the case of Mn₁₂, the spins at the center of the sides (even-numbered, blue circles) are highly polarized – and in opposite directions – in the M = ±10 ground states. Therefore, one can discriminate between the two ground states with high probability through local measurements performed on each of these spins. In the remaining spins, the dependence of the state on M is less pronounced. The minimum subsystem that carries the required amount of which-component information is represented by spin pairs (green areas in the Fig. 3). In the case of Fe₈, the only spins that are highly polarized in the M = ±10 ground states are the four external ones: these can thus form a subsystem each. The state of the spins that form the central core is instead less defined and weakly dependent on M. Therefore, one needs to measure the state of the whole central core in order for the measurement to provide the required which-component information, and this should be regarded as a single subsystem. In both cases, the size N′ of the linear superposition remains below the theoretical maximum N. One can show that, without changing the geometry and the pattern of exchange couplings within these clusters, nor the partition in sublattices of (approximately) antiparallel spins, one could increase the value of N′ by modifying the values of the Js [20].

Fig. 3

Schematic view of the Fe₈ (left) and Mn₁₂ (right) molecular nanomagnets. The magnetic core of Fe₈ is formed by N = 8 spins s = 5/2, while that of Mn₁₂ consists of eight external s = 2 spins and four internal s = 3/2 spins. The shaded areas define the subsystems into which each spin cluster can be partitioned, such that the local measurement within each of them allows the discrimination between |Ψ ₁〉(M ₁ = − 10) and |Ψ ₂〉(M ₂ = + 10) with a probability higher than 0.99

The values obtained for the measure N′ in Cr₇Ni and V₁₅ are much smaller, and non-proportionate to the number of spins that compose the two nanomagnets. In both cases, the considered linear superpositions are those between ground states with M = ±1/2. The size of |Ψ〉 in Cr₇Ni (which is formed by seven spins s = 3/2 and one spin s = 1) is N′ = 2. This is essentially due to the fact that each spin is highly entangled with its nearest neighbors, such that its state is highly mixed. As a consequence, the spin states corresponding to the two components are hardly distinguishable, and the smallest subsystem that contains enough which-component information is formed by (any) four spins. The case of V₁₅ is in some sense even more instructive. Here, 12 of the 15 s = 1/2 spins (those belonging to the two hexagons) are practically frozen in a singlet state in the low-energy sector of the system. They thus have (approximately) identical states in the two ground states |Ψ ₁〉 and |Ψ ₂〉 and carry no which-component information. This is distributed amongst the remaining three spins, such that the system cannot be partitioned at all, and N′ = 1. This measure thus gives the same value that would be obtained in a single s = 1/2 spin, in spite of the large number of spins that form the V₁₅ cluster.

The characterization of the above linear superpositions in terms of quantum fluctuations of single-spin operators leads to qualitatively similar results. For the high-spin molecules Mn₁₂ and Fe₈, the values of ${\mathcal{V}}_n$ are 45.4 and 48.7, respectively, denoting that the linear superposition |Ψ〉 of the ground states with M = ±10 has a highly nonclassical character, with respect to the components. This is not the case with Cr₇Ni and V₁₅, where the size ${\mathcal{V}}_n$ of the linear superpositions between the ground states M = ±1/2 is given by 2.7 and 1.1, respectively. In these systems, linear combinations of the ground states are not significantly more quantum than the ground states themselves.

4.2 Which and How Much Entanglement?

Entanglement has been recognized as one of the most peculiar features of quantum mechanics already in its early days. In the last decades, both the theoretical understanding of entanglement and the capability of generating and detecting it in diverse physical system have known a rapid development [21, 22]. This interest has been partly fueled by the identification of entanglement as a fundamental resource in quantum-information processing.

Hereafter, we recall some basic notions on entanglement. Given a two-spin system in some pure state |Ψ ₁₂〉, the spins are entangled if it is impossible to write the overall state as a product of single-spin states (i.e., in a factorized form |Ψ ₁₂〉 = |ψ ₁〉 ⊗ |ψ ₂〉). Here, the presence of entanglement can be inferred from the mixed character of the single-spin reduced density matrices ρ ₁ and ρ ₂. In fact, entanglement measures such as the von Neumann entropy quantify entanglement between s ₁ and s ₂ in terms of the degree of disorder of their states: S = − tr(ρ _k  log  ρ _k ) (k = 1, 2). If the overall state is not pure, then the spins are entangled if the overall density matrix ρ ₁₂ can’t be written as a mixture of factorized states. If, instead, ρ ₁₂ = ∑  _l p _l |ψ ¹ _l 〉〈ψ ¹ _l | ⊗ |ψ ² _l 〉〈ψ ² _l |, then the two spins are said to be in a separable state. Deciding whether or not a mixed state ρ ₁₂ is entangled is in general a nontrivial problem. This is because any given density matrix can in general be obtained by mixing different set of states: the decomposition of the density matrix is not unique. As a consequence, it is not easy to exclude that, e.g., a mixture ρ of entangled states cannot be obtained also by combining factorizable states, in the which case ρ would be separable. Measures such as those used for pure overall states can still be applied, through the so-called convex-roof construction. This corresponds to taking averaging the measure over the states |Ψ _l 〉 that define a given decomposition of ρ ₁₂, and minimizing over all possible decompositions. Such a procedure can be computationally very demanding and the relevant quantities are in general not directly accessible by experimental means. We note that one often deals with mixed two-spin states. This can result from the finite temperature of the system or, if the two spins in question are part of a larger system, by the partial trace performed on the state of the remaining spins in order to obtain ρ ₁₂.

The above considerations apply to other forms of bipartite entanglement, such as that between two generic subsystems A and B. In this case, each of the two parties is itself a composite system, rather than an individual spin. The so-called multipartite entanglement, instead, is substantially different. The state |Ψ ₁₂₃〉 of three spins, for example, is multipartite entangled if it can’t be written in a fully factorized form (|ψ ₁〉 ⊗ |ψ ₂〉 ⊗ |ψ ₂〉), nor in any biseparable form (such as |ψ ₁₂〉 ⊗ |ψ ₃〉, or |ψ ₁〉 ⊗ |ψ ₂₃〉). Prototypical examples of three-spin multipartite entangled states are the so-called GHZ and W states, defined for qubit systems: $\left|\mathrm{G}\mathrm{H}\mathrm{Z}\right\rangle =\left(\left|\uparrow \uparrow \uparrow \right\rangle +\left|\downarrow \downarrow \downarrow \right\rangle \right)/\sqrt{2}$ and $\left|\mathrm{W}\right\rangle =\left(\left|\uparrow \uparrow \downarrow \right\rangle +\left|\uparrow \downarrow \uparrow \right\rangle +\left|\downarrow \uparrow \uparrow \right\rangle \right)/\sqrt{3}$. The above definition can be generalized to the case of a mixed state ρ ₁₂₃ along the same lines of the bipartite case. In particular, three spins are considered multipartite entangled if ρ ₁₂₃ cannot be written as a mixture of factorized and biseparable states. A three-spin cluster is thus the smallest system where one can discuss multipartite entanglement. In a cluster formed by N > 3 spins, one can investigate a hierarchy of multipartite entanglement states, involving k spins at a time, with 2 < k ≤ N. A particularly useful notion in this respect is represented by the so-called k-producibility. A state ρ of the N-spin system is k-producible if it can be written as the mixture of states |Ψ〉, corresponding to a product of n states, |ϕ ^l₁ 〉 ⊗ … ⊗ |ϕ ^l _n 〉, each involving no more than k spins. A state ρ of the N-spin clusters contains k-spin entanglement if it is not (k − 1)-producible.

Molecular spin clusters with dominant antiferromagnetic interactions can be regarded as prototypical examples of strongly correlated systems [23]. The ground state of such system generally exhibits highly nonclassical features and different forms of entanglement (Fig. 4). In the following, we briefly review these forms, as well as the experimental and theoretical tools that can be used to detect and quantify them.

Fig. 4

Different forms of entanglement that can be investigated within a molecular spin cluster: (a) entanglement between two individual spins (circles with squared and linear patterning), tracing out the remaining N − 2 spins (empty circles); (b) entanglement between complementary subsystems A (squared) and B (linear), formed by more than one spin each; (c) k-partite entanglement, involving more than k > 2 spins at a time (and all of them, in the case k = N); (d) entanglement between one spin and the rest of the system

4.2.1 Entanglement Between Individual Spins

Possibly the simplest form of entanglement is that between individual spins. An antiferromagnetic interaction between two spins s _i and s _j (J s _i  · s _j ), with J > 0, tends to entangle them. In particular, if s _i  = s _j , the exchange energy is minimized if the two spins are in a singlet state. If s _i and s _j are part of a wider spin cluster, then the exchange interaction between the two will generally compete with that between s _i (s _j ) and other spins s _k  ≠ s _j  (s _k  ≠ s _i ), and none of these contributions to the overall exchange energy will be minimized in the system ground state. Correspondingly, at low temperatures (T < J), spin-pair entanglement tends to be present, though not maximum, in pairs of exchange-coupled spins.

Given the reduced two-spin density matrix ρ _ij , the entanglement between s _i and s _j can be quantified by functions such as negativity ($\mathcal{N}$), which measures the violation of the positive partial transpose separability criterion [21]. Unfortunately, the only way to derive $\mathcal{N}$ by experimental means is to perform the full tomography of ρ _ij , which is generally unfeasible with the experimental techniques available in molecular magnetism. There are, however, experimentally accessible quantities that allow the detection of spin-pair entanglement, the so-called entanglement witnesses. One such observables is represented by the exchange operator s _i  ⋅ s _j itself, which is now accessible in four-dimensional inelastic neutron scattering [24]. In fact, one can easily show that the expectation value of the above operator corresponding to (mixtures of) factorizable states |ψ _i 〉 ⊗ |ψ _j 〉 of the two spins cannot be lower than a given threshold: 〈s _i  ⋅ s _j 〉 ≥ − s _i s _j . From the violation of such inequality, one can thus infer the presence of entanglement between the two spins.

With these simple tools, one can investigate the presence of spin-pair entanglement in molecular nanomagnets and its dependence on the tunable physical parameters. For example, one can show that in an antiferromagnetic wheel such as Cr₈ entanglement is only present between nearest neighbors and at temperatures T < 1.5 J (this should be contrasted with the classical correlations that are instead present in such a system between any two spins and at any finite temperature). Besides, the controlled introduction of a chemical substitutions allows one to investigate the effect of magnetic defects on the distribution of entanglement. In particular, the replacement of a spin s within a ring with an s ′ ≠ s reduces the amount of frustration (in terms of both energy and entanglement) and tends to induce an oscillating dependence of entanglement as a function of the distance from the defect [25]. These features can be clearly observed in the molecules of the Cr₇M series (with M = Zn, Cu, Ni, Cr, Fe, Mn), together with the dependence of the sign and amplitude in such oscillations on the length of the spin s _M (with respect to s _Cr = 3/2). An analogous effect can be produced by a different kind of magnetic defect, namely the introduction of an exchange coupling J ′ ≠ J. In the presence of two (or more) substitutions, one can observe a constructive or a destructive interference between the oscillations induced by each defect separately, depending on the distance between the two. This can be observed in the molecules of the series Cr_2n Cu₂ [26]. Finally, a suitable engineering of the exchange couplings (in particular, of the ratio between the Cr–Cu coupling J′ and the Cr–Cr coupling J) also allows one to induce entanglement between distant and uncoupled spins, which is generally absent in homometallic rings with nearest-neighbor interactions.

4.2.2 Multipartite Entanglement

There are forms of entanglement that cannot be traced back to entanglement between spin pairs, for they involve more than two spins at a time. As a limiting case, the state |Ψ〉 of an N-spin cluster is said to be N-partite entangled if it can’t be factorized into the any product |Ψ _A 〉 ⊗ |Ψ _B 〉 of states of N _A and N _B  = N − N _A spins. Rather counterintuitively, such a form of entanglement can be detected through the expectation value of the exchange Hamiltonian, even though this only includes spin-pair operators. In fact, one can show that the ground state of a ring or chain of N spins is N-partite entangled, and that its energy is separated from that of the lowest biseparable state by a finite gap [27]. More generally, for any given system, one can calculate a number of lower bounds E _k for 〈H〉, such that the condition 〈H〉 < E _k implies the presence of k-spin entanglement in the systems state, where larger values of k correspond to lower thresholds E _k . Therefore, as the system temperature decreases, the expectation value of the exchange energy progressively violates all lower bounds E _k , thus demonstrating the presence – in the equilibrium state – of higher and higher orders of multipartite entanglement. The approach developed for calculating the lower bounds E _k of a given system applies to arbitrary spins and to spin clusters that include spins of different lengths (such as heterometallic rings) [28].

4.2.3 Entanglement Between Subsystems

Another form of entanglement that is not conceptually reducible to that between spin pairs is that between two subsystems A and B into which the spin cluster can be partitioned. Some molecular systems, such as the dimer of Cr₇Ni nanomagnets, can be naturally thought in terms of two weakly coupled subsystems: in this case, A and B would in fact coincide with the two rings [29]. However, physically motivated bipartitions can be identified in a variety of spin clusters, such as those with ferrimagnetic ordering, where spins belonging to different sublattices point in opposite directions. Entanglement between all these subsystems can be quantified by means of the negativity or, if the overall state is pure, by entropic measures, such as the von Neumann entropy. As already mentioned, the practical disadvantage presented by these quantities is that they cannot be expressed as simple combinations of observable quantities and are therefore difficult to estimate experimentally. A possible solution to this problem is represented by the generalization to the case of composite spins of criteria – based on the use of entanglement witnesses – that allow the detection of entanglement between individual spins. For the sake of simplicity, we refer specifically to the already mentioned inequality, namely 〈S _A  ⋅ S _B 〉 ≥ − S _A S _B , whose violation implies entanglement between the two spins, and consider the case where S _A and S _B are not individual spins, but partial spin sums (${\mathbf{S}}_{\chi }={\sum}_{i=1}^{N_{\chi }}{\mathbf{s}}_i^{\chi },\mathrm{where}\kern0.5em \chi =A,B$), corresponding to subsystems of the spin cluster, which are formed by N _A and N _B spins, respectively. The fact that the spin lengths S _A and S _B are state-dependent quantities, and no longer intrinsic properties of the system, makes the application of the above inequality less straightforward. However, one can show that the criterion can be generalized to the case of composite spins, exploiting the fact that the witness S _A  ⋅ S _B commutes with the partial spin sums S ² _χ = A,B [30]. The generalized inequality reads: $\left\langle {\mathbf{S}}_A\cdot {\mathbf{S}}_B\right\rangle \ge -{\sum}_{S_A,{S}_B}p\left({S}_A{S}_B\right){S}_A{S}_B$, where p(S _A ∙S _B ) is the probability corresponding to each pair of values of the partial spin sums. As a further step, one can show that such probabilities can be expressed in terms of experimentally accessible quantities, and specifically of spin-pair correlation functions. This can be done for a finite but limited amount of fluctuations of S ² _A and S ² _B in the (equilibrium) state of interest. Such condition turns out to be satisfied in a number of system and bipartitions, well beyond the limit where A and B are weakly coupled subsystems (i.e., the couplings between the spins of A, or B, are much larger than those between the spins of A and B, as is the case in typical dimer-like structures).

A particular case of bipartition into complementary subsystems is that where one of the two consists of a single spin. In this case, along the lines of the discussed above, one can derive the minima of exchange energy corresponding to states where the single-spin s _i isn’t entangled with all the others. In the case where the spin clusters are formed by inequivalent spins (as for rings with a magnetic defect, or for spin segments), different minima e _i correspond to different spins. One can thus extract a local, spin-selective information by the measurement of a nonlocal quantity, such as the expectation value of the exchange Hamiltonian H. In fact, the violation of the inequality 〈H〉 ≥ e _i allows one to infer that the spin s _i is entangled with the rest of the system.

5 Molecular Nanomagnets for Quantum Computation

Molecular spin systems have attracted much interest for the almost-unlimited number of possibilities they offer to engineer functionalities at molecular level as extensively presented also in the other chapters of this book. They also constitute an ideal playground for observing quantum phenomena [31]. They possess both electron and nuclear spins. Clusters of transition metals (or lanthanides) are bound together by superexchange interactions in such a way that is possible to define, on the one hand, the pattern of the low-lying molecular states and their relative energy splittings and, on the other hand, the environment in proximity of the magnetic core, an essential ingredient to control decoherence mechanisms as discussed in the previous paragraph. If sufficiently isolated from excited states, the ground S multiplet of one molecule can be used as register for the encoding of quantum information. Chemistry also allows one to control the external part of the molecule by introducing functional organic groups. These allow one to stick two or more molecules together with some control on the magnetic coupling. For instance, the use of organic conjugated groups can induce a permanent super-exchange interaction at supramolecular level [32]. Alternatively, the use of molecular switches between two-spin qubits allows one to create – at the synthetic level! – simple molecular architectures suitable for the implementation of quantum gates.

The independent control on the external ligands also allows the use of functional groups that can stick onto different surface (for a review, see [33] and other chapters of this book). For instance, the use of thiol groups exploits the affinity of the terminal sulfur to bind to gold surface, while the use of cyclic organic terminations, like pyridine or benzene, favors the sticking of the molecule to carbon-based surface (graphite, nanotubes, fullerenes, graphene). Alternatively, the use of polar terminations may allow the exact positioning of molecules on a surface prepared with the corresponding counter-ion. Further examples can be found in another chapter of this book dedicated to the deposition and characterization of molecular spin clusters on surface. All these points indicate clear advantages in using molecular spins, instead of spin impurities, for the design and the realization of architectures for computation. In the following, we review some recent achievements and list real examples of molecular spin systems of interest for data processing. As discussed in the previous paragraphs, it is worth to point out, however, that a systematic investigation is required to consider a system suitable for the encoding of qubits, as clearly spelled out by the DiVincenzo criteria [34] listed here below:

• Individuation of well-defined quantum states for the qubit encoding and scalability of the system.

• Definition of a protocol to initialize the system.

• Ability to perform a set of quantum gates.

• Robustness of the system with respect to decoherence mechanisms and long coherence time as compared to the gating time.

• Definition of read-out of the final state.

5.1 Radicals

Simple molecules provide already the possibility to encode qubits. Radicals with one delocalized electron have a S = 1/2 net spin per molecule. They are well known to spectroscopists to provide very sharp line-width in EPR even at room temperature. For instance, the diphenyl-1-picrylhydrazyl (DPPH) that is commercially available normally shows S = 1/2, g = 2.0037 and about 2.4 gauss line-width in X-band EPR spectroscopy. Among a large variety of radicals the attention is focused on those that are stable in ambient conditions and can be dispersed in solution or safely deposited on surface. The group of Prof. Gatteschi in Florence works on nitronyl nitroxides and measured T ₂ = 0.9 μs at 300 K (5 μs at 80 K) by pulsed ESR [35] (Fig. 5a). The group of Prof. T. Takui at Osaka City University is working on malonyl [36] or TEMPO [37] radicals reporting μs lifetimes at room temperature. Finally, the application of optimal dynamical decoupling was shown to allow an enhancement of the decoherence time of three orders of magnitude, achieving the value of 30 μs at 50 K [38].

Fig. 5

Some examples of molecular spin qubits: (a) S-4-(nitronyl nitroxide) benzyl ethanethioate (NitSAc) radical. (b) Mononuclear Tb bis-phthalocyanine. (c) Mononuclear LnW₁₀ polyoxometallate. (d) High spin (S = 10) Fe₈ [(tacn)₆Fe₈O₂(OH)₁₂]. (e) Supramolecular dimer of low-spin Cr₇Ni rings

5.2 Single-Ion Molecules

Next step is the use of single-ion magnets comprising one single lanthanide per molecule.

After the publication of Ishikawa et al. [40], single-ion magnets comprising one lanthanide sandwiched in a bis-phthalocyanine complex (Fig. 5b) have attracted much attention for the huge energy barrier due to magnetic anisotropy they offer and the versatility and robustness they show when deposited on surfaces. Quantum tunneling of the magnetization has been observed in TbPc₂ [41] which presents well-defined split of the ground J = 6 electronic state due to the hyperfine interaction with I = 3/2 nuclear spin. These features make it an ideal molecule for the realization of molecular quantum spintronic devices as presented in another chapter of this book. Very interestingly, lifetimes exceeding 10 s for nuclear spin states have been measured on a single TbPc₂ molecule in a spin transistor setup [42].

The group of Prof. Coronado at University of Valencia isolated mononuclear Gd polyoxometallates (POM), namely GdW₁₀ and GdW₃₀ (Fig. 5c) for which two states of the ground S = 7/2 multiplet have been identified for the qubit encoding and a transverse relaxation time T ₂ = 410 ns has been measured [39]. POMs offer wide possibilities to control the crystal field acting on the lanthanide magnetic center and to drastically reduce the number of nuclear spins in its environment.

5.3 Molecular Spin Clusters

The possibility to choose among an almost-endless catalog of molecules with core made by several transition metals (or lanthanides) tightly bound each other by ferro- or antiferromagnetic superexchange interactions allows to find molecules with quite different ground state, i.e. with magnetic moment ranging from 0 to values much higher than what is possible to find with a single magnetic ion.

In 2001, Leuenberger and Loss noticed that the M-states of the ground S = 10 multiplet of Mn₁₂ and Fe₈. Single Molecule Magnet are not regularly spaced in energy and they can be addressed separately by microwave radiation. Based on this consideration they proposed to perform the Grover’s algorithm with these molecules [43]. Up to now, the experimental implementation of this proposal has not been realized probably due to the tough experimental requirements. That was, however, the first proposal for using molecular spins for quantum computation in which specific quantum algorithm fits the features of a given molecule, and it drove the attention and curiosity for exploiting molecular spin clusters for quantum computation as promptly realized by Tejada and co-workers [44].

5.4 Low-Spin Molecular Clusters

Few years later, Loss and co-workers proposed to consider antiferromagnetic spin arrangements in order to isolate molecular S = 1/2 qubits [45]. Low-spin (S = 1/2) molecular clusters certainly represent nice examples of two-level systems. Following this line of reasoning, in 2005 we proposed to consider heterometallic rings as suitable candidates for a specific qubit encoding [46]. Heterometallic Cr₇Ni rings with a well-isolated doublet as ground state have been synthesized by Dr. G. Timco in the group of Prof. R.E.P. Winpenny at Manchester University [47]. Coherent spin oscillations within the ground doublet have been shown to persist for timescales as long as 10 μs at 2 K by the group of Dr. A. Ardavan in Oxford [48, 49] (Fig. 6). In these antiferromagnetic rings, the main mechanism for decoherence at low temperature is related to the hyperfine coupling between electron and nuclear spins. The motion of the nuclei can provide an additional decoherence channel, whose presence can, however, be controlled by changing the external organic groups [49]. This molecule can be successfully grafted on different substrates, including gold and graphite, showing to be robust enough to suffer only minor changes in the pattern of its low-lying levels when single units are anchored on surface [50]. Due to the flat ring shape, Cr₇Ni self-assemble when gently sublimed on gold surface [51]. More recently, two or more Cr₇Ni rings have been linked together (see Fig. 6e) and the chemistry behind this seems to provide great flexibility in the choice of the linker (including switchable ones) and therefore in the tunability of the magnetic coupling [52]. Spin entanglement at supramolecular level has been proven and discussed in different cases [23]. Thus, it seems that all the prerequisites for the implementation of universal set of one- and two-qubit gates are present for this family of molecules.

Fig. 6

Hahn-echo pulsed-ESR technique was used in these experiments to evaluate the spin relaxation times as a function of temperature for Cr₇Ni (open circles), Cr₇Mn (open squares), and perdeuterated Cr₇Ni (filled circles). (a) Spin–phonon relaxation T ₁ (expressed in ns). (b) Spin–spin relaxation T ₂ (in ns). Reprinted with permission from Ardavan et al. [48]. Copyright 2007 by American Physical Society

Another prototypical example of low-spin molecule is V₁₅ whose ground state is given by the coupling of 15 V⁴⁺ in spherical arrangement. The lowest lying states are two S = 1/2 doublets, split by only 80 mK and separated by 3.8 K from the first S = 3/2 excited state. Rabi oscillations within these low-lying multiplets have been observed on V₁₅ with a coherence time estimated to be few hundreds of ns at 2.4 K [53] (Fig. 7). More recently, Rabi oscillations have been measured on low-spin Cu₃ antiferromagnetic trimers [54] dispersed in nanoporous Si: the spin coherence time was found to be T ₂ = 1.066 μs at 1.5 K in this case.

Fig. 7

Time dependence of the average 〈S _z 〉 component after a spin-echo sequence. The lower curve shows the Rabi oscillations of the S = 1/2 ground state, while the upper one displays the Rabi oscillations of the S = 3/2 first excited state. Measurements were performed by spin-echo spectroscopy on V₁₅ single crystals at 2.4 K. The inset shows the T ₂ decay measured with Hahn-echo sequence. Reprinted with permission from Yang et al. [53]. Copyright 2012 by American Physical Society

5.5 High-Spin Molecular Clusters, SMM

Coherent oscillations have also been measured in high-spin molecules considering transitions between two M-states of the ground multiplet. For Fe₈ (Fig. 5d) a decoherence time T ₂ of 712 ns at 1.3 K was reported [55]. Similar experimental values have been reported for Fe₄ SMM for which direct experimental evidence for long-lasting, T ₂ = 640 ns, quantum coherence and quantum oscillations between two M-states has been reported by using pulsed W-band ESR spectroscopy [56].

All these results show that the search of molecular spin qubits is at present a very effervescent field. Since the time to manipulate an electronic (molecular) spin range between 1 and 10 ns in real experimental conditions, the above mentioned experimental results demonstrate that the typical figure of merit for molecular spin qubit, i.e. the ratio between the coherence time and the manipulation time Q = T ₂/τ ranges between 10² and 10³. This figure of merit is comparable to what found in other solid state qubits and it is a good starting point to consider the molecular spins suitable for the implementation of one-qubit gate.

5.6 Molecules for the Implementation of Multiple-Qubit Gates

Considerable effort has also been recently devoted to identify and synthesize supramolecular structures comprising two or more molecular qubits (or, more simply, bi- or poly-nuclear clusters). A prototypical example is the (Mn₄)₂ dimer comprising two Mn₄ moieties weakly coupled one to another [57, 58]. The family of Cr₇ Ni rings offers a great deal of possibilities to realize supramolecular architectures, including molecular spin qubits linked by organometallic switches [47]. In 2007, the groups of Coronado and Loss proposed to exploit the properties of [PMo₁₂O₄₀(VO)₂]^q − POM comprising two S = 1/2 spins to perform the $\sqrt{\mathrm{SWAP}}$ gate. Other proposals for the implementation of two-qubit gates with bi-nuclear molecules have been reported for the Tb₂ [59] and manolyn bi-radical [37]. Finally, it is worth mentioning the activity of the group of Dr. G. Aromi who is using β-diketonates ligands to synthesize linked SMMs designed for the implementation of different (multi-)gate schemes [60, 61]. These achievements indicate that the bottom-up – synthetic – approach allows one to assemble complex molecular architectures reflecting the scheme of quantum computers, and many conditions to perform multi-qubit gates appear to be met by different molecular systems. Yet, at the time of writing, no experiments have been successfully completed to prove the functioning of a molecular multi-bit gate. The use of – at least – two frequencies in the pulse sequence (e.g., for separately addressing the qubits, or switching their interaction) requires noncommercial setups, and this is certainly one of the main experimental limitations at the moment. Further difficulties in combining different experimental conditions (low temperature, high power pulse, finite relaxation time) and fitting the properties (frequency) of a specific molecular system need to be overcome in future in order to achieve this fundamental goal and bring this field to maturity.

6 Quantum Simulators

Generally speaking, a simulator is a device able to reproduce the dynamics of a different system. Similarly, a quantum simulator is a device designed to efficiently reproduce the time evolution induced by a given target Hamiltonian, describing the behavior of a specific quantum system (for an extensive review, see [62, 63]). This is a very difficult task for a classical computer. For instance, to simulate a system with few quantum objects it requires an incredibly large amount of power, time and registers to a classical computer and, as soon as the size of the quantum system increases, the problem becomes intractable. In 1982, Richard Feynman firstly pointed out that a specifically designed set of quantum registers and processors may – instead – well do this job [64]. Since then, the idea of using quantum computers to solve problems in quantum physics and chemistry has been identified as one of the most intriguing problems in the field of quantum computation. More recently, simulation of simple quantum systems has become an achievable goal with current technology and a race in this direction has started with interesting proposals and results.

Typical problems that are treated by quantum simulators are those related to basic models in quantum magnetism and phase transitions of frustrated systems, or models for electron pairing in high temperature superconductors. Simulation of many-body fermionic systems is one of the most difficult tasks for a classical computer, also due to the change of sign of the wavefunction when two particles are swapped. Problems such as those related to the Hubbard Hamiltonian could instead be addressed by quantum simulators. Another typical many-body problem is the pairing mechanism at the basis of the BCS theory of superconductivity. In quantum chemistry, quantum simulators have been proposed for the design of new molecules as complex as those used for drugs.

Quantum simulators are nothing but quantum computers designed to solve specific problems. As such, they may not be able to perform a universal set of operations; yet, they can be extremely efficient in performing their specific task. Efficiency is indeed one crucial aspect. In 1996 Lloyd clearly presented cases for which a quantum simulator requires resources (registers and processors) increasing in polynomial way with the size of the simulated system, whilst a classical computer would require a number of resources increasing exponentially [65].

As mentioned above, the typical problem addressed by quantum simulators is the time evolution of a quantum system described by a wavefunction |Ψ(t)〉 under the action of the Hamiltonian $\widehat{H}\left(\hslash \equiv 1\right)$:

$$ \left|\varPsi (t)\right\rangle ={e}^{-i\widehat{H}t}\left|\varPsi (0)\right\rangle . $$

(3)

Different ways to simulate the time evolution of the quantum system have been proposed, but an efficient strategy, if $\widehat{H}\Sigma {\widehat{H}}_i$ only includes local terms ${\widehat{H}}_i$, is that to split the overall time evolution into a discrete sequence of simple steps [65], where the total simulation time T is then divided into N intervals τ = T/N and the overall time evolution is approximated by the so-called Trotter–Suzuki formula:

$$ {e}^{-i\widehat{H}t}\simeq {\left({e}^{-i{\widehat{H}}_1\tau}\dots {e}^{-i{\widehat{H}}_N\tau}\right)}^N, $$

(4)

where terms of higher order can be neglected for sufficiently large N. Thus, the general time-evolution operator is decomposed in a set of gates ${e}^{-i{\widehat{H}}_1\tau },\dots, {e}^{-i{\widehat{H}}_N\tau }$, each operating on a few qubits, and whose number scales favorably with both the time T and the number of qubits. Since elementary gates are known to form basis for a universal computation, each ${e}^{-i{\widehat{H}}_i\tau }$ can be in turn expressed as a sequence of logical gates. We just notice that the type of the interaction between qubits that are exploited in the elementary gates ${e}^{-i{\widehat{H}}_i\tau }$ as well as the architecture of the quantum simulator, need not reflect those of the system to be simulated.

Like in any other (quantum) computer, for quantum simulators we need to define both the preparation of the initial state and the measurement of the final state. The simplest way to initialize a quantum simulator is to let it cool down into its ground state. Another possibility is to measure and project it into a specific state. Besides these simple methods, one might need to define specific sequences of gates to prepare the simulator into the desired state. Measuring the output is also not a trivial task.

From the experimental point of view, the main problem is to engineer the interactions between qubits and at the same time to build up the scalable architectures required to simulate the target system. In the last years, simple quantum simulators have been realized and successfully tested with the most advanced quantum technologies. We can find examples of quantum simulators made of only few qubits, as well as extended architectures.

Nuclear spins benefit from their long coherence time and implementation of elementary and complex algorithms has been extensively carried out in the last two decades [66]. Effective nearest-neighbor Heisenberg interactions are naturally set between nuclear spins, and numerous groups have already attempted to simulate the three- and four-body problem as well as the behavior of spin chains [62]. Simulation of both fermionic and bosonic systems has been successfully performed by NMR [67–69].

The technology to realize arrays of cold atoms with optical lattices, as well as that to trap ions in architectures suitable for quantum simulators, is certainly one of the most advanced in the field. For trapped ions the mutual interaction can also be controlled, and simulation of spin systems has been designed and successfully performed by this technology [70, 71]. Nitrogen vacancies in diamond are one of the most promising ways for the implementation of quantum computation, due to their long coherence time – even at room temperature – and to the advanced optical techniques for the read-out. Recently, important progresses have been made in controlling the position of such vacancies and this opens the way for the fabrication of scalable architectures. Also, a quantum simulator using nuclear spins in diamond has been realized, where nitrogen vacancies have been implanted in a controlled manner [72]. Phase transitions of a frustrated magnetic system have been simulated and successfully tested [72].

Solid state qubits have also been used to realize quantum simulators. For instance, the basic problem of the hydrogen molecule has been simulated by using three quantum dots [73, 74]. Yet, for quantum dots, as well as for superconducting circuits, the main problem for the realization of large simulators remains the fabrication of identical qubits by lithographic methods and bottom-up approaches. The synthesis of molecular qubits looks very appealing in this respect.

In this context, proposals for the realization of quantum simulators with molecular spins have recently appeared [75]. Santini and co-workers considered an infinite chain of alternating A–B molecules, both with spin 1/2 but addressable separately and effectively coupled with each other through antiferromagnetic dimers that may switch on and off such coupling. They demonstrated that the dynamics of such a spin system may actually map different Hamiltonians, including those of fermionic systems or that describing the quantum tunneling of a spin 1. One peculiarity of this simulator is that there is no need to use local fields, thus operations can be run in parallel by microwave pulses [75]. This work has immediately inspired the synthesis of polymeric structures comprising the Cr₇Ni molecular qubits like those reported in [76], and efforts are currently on the way in order to synthesize metallo-organic frameworks fulfilling all the conditions to realize a quantum simulator with molecular qubits.

A different approach has been proposed by the Osaka group who focus the attention to air-stable radicals (hexa-methoxyphenalenyl) with an extremely well-resolved ESR hyperfine splittings a very small line-width in solution. Although the Hamiltonian description still needs to be defined, this molecule provides a specific cluster of both electron and nuclear spins interacting with each other. This suggests that ENDOR technique can also be used in order to exploit the long coherence time of nuclear spins and combine it with the easy read-out of electrons to realize a quantum simulator within only one molecule [77]. Indeed, hyperfine interactions represent one of the major obstacles in many electron-spin-based approaches to quantum computation. However, alternative schemes have been developed where the coupling between electron and nuclear spins represents a key ingredient for the quantum-gate implementation [78, 79].

7 Hybrid Quantum Systems and Devices

So far, the physical implementation of quantum-information processing has been pursued by using different quantum systems and techniques. Hybrid devices, in which different elements are assembled to exploit the best characteristic of each of them, are today considered promising in this perspective. Engineering the interaction of single photons with isolated quantum objects (atoms, ions, spins, etc.) is a fundamental goal in quantum mechanics, as testified by the 2012 Nobel Prize in Physics to Haroche and Wineland. The physics and technology associated with cavity quantum electrodynamics (cavity-QED) [80] has largely contributed to the development of quantum information.

In 2004 the Schoelkopf’s group at the Yale University demonstrated that it is possible to implement cavity-QED on a chip by means of superconducting resonators and qubits [81]. In this approach, planar resonators substitute the 3D mirror cavities, thus opening the way to efficiently couple photons with any two-level systems lying on the same substrate. Hybrid circuits that incorporate superconducting hardware and spin systems were soon proposed to exploit the fast manipulation of superconducting qubits and the long decoherence times of electronic spins [82]. Moreover, superconducting lines can act as a quantum bus, linking different subsystems on the same chip by means of the coherent exchange of microwave radiation.

In this context, molecular nanomagnets can provide alternative elements of hardware. This is an emerging field for which theoretical proposals and experiments started to appear very recently. Besides the coherent coupling between molecular spins and photons in cavities, planar resonators are of interest for magnetic resonance experiments, since they allow measurements on thin films or nanostructured molecular nanomagnets. The purpose of the next paragraphs is to give an overview of these topics and to figure out possible scenarios in which molecular nanomagnets can play a role.

7.1 Coupling a Single Spin to Electromagnetic Radiation

We consider here a prototypical experiment where photons in a cavity interact with a two-level quantum system. An electromagnetic cavity is a physical constriction with mirrors that forces photons to multiple reflections, allowing the electromagnetic (e.m.) field to resonate as a stationary wave. Under appropriate experimental conditions the field has a single harmonic mode at frequency ω. Although the problem can be treated in general terms (the two-level quantum system can be either a cold atom (ion) or a superconducting qubit, a quantum dot, etc.), we consider more specifically the case of an isolated spin 1/2 placed in a static magnetic field B ₀ oriented, let’s say, along the z-axis. When the temperature is sufficiently low, the Boltzmann population of the two levels is different. The spin precesses at the Larmor frequency ω ₀ = − γB ₀ about B ₀ and the degeneracy of the two eigenstates | ↑ 〉 = |0〉 and | ↓ 〉 = |1〉 is lift by the corresponding energy splitting ℏω ₀ = gμ _B B ₀.

The application of an oscillating magnetic field B ₁ induces a change of the magnetic moment μ = γℏ S associated with the spin S, which is given by

$$ \frac{d\mu }{dt}=\gamma \mu \wedge {\mathbf{B}}_1. $$

(5)

When B ₁ is oriented in the x–y plane and oscillates with angular frequency ω ≃ ω ₀, it can induce dipole transitions between the | ↑ 〉 and | ↓ 〉 states and change the relative populations (Fig. 8). This problem was first treated by Rabi and it is still a milestone for the spin resonance techniques [83]. The semiclassical model that describes the motion of a spin 1/2 under the action of a classical e.m. radiation field at the resonant frequency can be easily found in textbooks [2]. The probability P(t) to find the spin in its eigenstates oscillates as:

Fig. 8

Graphical representation of the Rabi nutation of |Ψ〉 in the laboratory frame. The spin, initially in the |0〉 state, evolves under the effect of the static field B ₀ and the oscillating field B ₁

$$ P(t)=\frac{\varOmega_{\mathrm{R}}^2}{\varDelta_c^2+{\varOmega}_{\mathrm{R}}^2}{ \sin}^2\left[\sqrt{\varDelta_c^2+{\varOmega}_{\mathrm{R}}^2}\frac{t}{2}\right], $$

(6)

where Δ _c  = ω − ω ₀ is the detuning of the e. m. field frequency (ω) from ω ₀ and Ω _R = − γB ₁ is the Rabi frequency.

When the intensity of the e.m. radiation is progressively decreased, only few photons (n) statistically interact with the two-level system and the quantum mechanical features of the field come into play. These can be described by the Jaynes–Cummings model in which the e.m. field is quantized. These conditions are typically encountered in cavity-assisted experiments, where few photons are confined in a limited space by multiple reflections at the cavity walls. This topic is described more in detail in Appendix 1 and here we simply summarize the main results. The spin–photon states tend to cross each other as the ω and/or B ₀ change. As ω approach ω ₀(Δ _c  = 0) they strongly interact giving rise to a level repulsion (anticrossing) centered at resonance (Fig. 9a). The energy gap at resonance, known as Rabi splitting, quantifies this interaction. Photon and spin states become tightly correlated and for n = 1 and Δ _c  = 0, the eigenstates of the whole system correspond to the entangled states

Fig. 9

(a) Vacuum Rabi splitting. The repulsion between the dressed states |χ ₊(n)〉 and |χ ₋(n)〉 determines an anticrossing for Δ _c  = 0 (see Appendix 1 for definitions). The energy splitting on resonance is related to the Rabi frequency ℏΩ _n . (b) Reflection spectrum of lithium phthalocyanine (N = 2.2 × 10¹²) measured for varying frequency and applied field by means of a three-dimensional cavity. The anticrossing behavior is well visible and theoretical fitting gives g _c /2π = 0.71 MHz and κ _c  = 2π = 5.4 MHz. Right panel shows the cross sections measured for 3,469.2 G (black, on resonance) and 3,468.5 G (gray). Reprinted with permission from Abe et al. [84]. Copyright 2011 by American Institute of Physics

$$ \left|{\chi}_{+}\right\rangle =\frac{1}{\sqrt{2}}\left[\left|-1/2,1\right\rangle +\left|+1/2,0\right\rangle \right] $$

(7)

$$ \left|{\chi}_{-}\right\rangle =\frac{1}{\sqrt{2}}\left[\left|-1/2,1\right\rangle -\left|+1/2,0\right\rangle \right]. $$

(8)

In realistic physical situations, the effect of the environment on the quantum states of both cavity and spin system is relevant and finite lifetimes must be considered. Photons are either absorbed by the environment or they escape from the feedlines. The decay rate κ is related to the quality factor Q of the resonator $\kappa =\frac{1}{\tau_p}=\frac{\omega }{Q}$. When Q is sufficiently high, the photon can be absorbed and emitted many times before escaping from the cavity and the corresponding lifetime τ _p is long. Similarly, the effects of the environment to the spin dynamics can be taken into account by considering the decoherence mechanism characterized by the rate γ _s  = 1/T ₂ at sufficiently low temperature (see Sect. 3). To observe the coherent dynamics of the coupled spin–photons system, the Rabi frequency must be faster than γ _s and κ, more specifically the coupling strength g _c between spin and photons must be g _c ≫ γ _s , κ. When this condition is met, the system is in the so-called strong-coupling regime. A dimensionless measure of the coupling strength is the cooperativity, defined as $\mathcal{C}=\frac{g^2}{\gamma_s\kappa }$ such that the strong-coupling regime corresponds to $\mathcal{C}\gg 1$.

The strong-coupling regime has been observed in several experiments on Rydberg atoms, cold atoms, Coulomb crystals, or semiconductors by exploiting the electric coupling with the electromagnetic radiation. Coupling strengths in the 100 MHz range have been reported, thanks to either the strong electric dipole or the strong electric component of the cavity field. Conversely the strong coupling of a single spin to electromagnetic radiation is more difficult to observe, as the magnetic dipole gives only fairly weak g _c  ~ 1 Hz. However, this value can be enhanced by using high-spin states, although higher magnetic moments would also result in stronger dipolar coupling to the environment and faster decoherence. Alternatively, the spin photon coupling can be enhanced by using spin ensembles as described in the following.

7.2 Spin Ensembles in a Cavity

Following Dicke [85] who considered the spin ensemble as a single quantum-mechanical system, Tavis and Cummings [86] generalized the problem to an ensemble of N independent two-level (spins) systems (Fig. 10). When the number of photons in the cavity is n ≪ N, the excitations of the spin ensemble can be described in terms of non-interacting spin waves. Due to the constructive interference between single-spin transitions, the effective coupling of the spin ensemble with the field is enhanced to ${g}_{\mathrm{ens}}={g}_{\mathrm{c}}\sqrt{N}$. The strong coupling between spin ensemble and e.m. field can be achieved for N sufficiently high [84, 87].

Fig. 10

Pictorial representation of a N-spin system coupled to the e.m. field of a three-dimensional cavity. The level structure within the spin ensemble has a harmonic character, where the excitation energy is determined by the Zeeman splitting due to the static field B ₀. The coupling strength g _c between the oscillating field (B ₁) and the collective spin system is enhanced by a factor $\sqrt{N}$

For an increasing number of photons that populate the cavity, a transition from pure quantum to classical dynamics is predicted [87]. For n = 1, the ensemble oscillates between two available spin–photon states with energy separation given by the vacuum Rabi splitting $\hslash \sqrt{\varDelta_c^2+{\varOmega}_n^2}$ (Fig. 9a). Each progressive addiction of a photon to the cavity creates a transition whose Rabi splitting depends on n.

Experimentally, the occurrence of the vacuum Rabi splitting in experiments involving spin ensembles is detected by microwave spectroscopy by looking at both dispersive and absorptive signals. The former (usually neglected in conventional EPR spectrometers by locking the source to the central frequency of the resonator) is associated with the frequency shift with respect to the resonance frequency of the unperturbed cavity (ω).

$$ {\omega}_c=\omega -\frac{g^2{\varDelta}_B}{\varDelta_B^2+{\gamma}_s^2}, $$

(9)

where Δ _B  = m ₀(B − B ₀)/ℏ is the field detuning. The absorption signal is associated with an increase of the Q-factor

$$ {\kappa}^{\prime }=\kappa +\frac{g^2{\gamma}_s}{\varDelta_B^2+{\gamma}_s^2}. $$

(10)

The full frequency and magnetic field spectrum shows by the appearance of two branches in the spectrum.

$$ {\omega}_{\pm }={\omega}_c+\frac{\varDelta_B}{2}\pm \frac{\sqrt{\varOmega_n^2+{\varDelta}_B^2}}{2} $$

(11)

This behavior is well visible in Fig. 9b, which shows the EPR signal measured for a lithium phthalocyanine with very narrow line-width (0.0083 G). The anticrossing is seen at about 3,469 G where the absorption line of the cavity meets that of the spin doublets.

The main complication of using ensembles is probably represented by the need of replacing single spin with collection of spins in the physical implementation of each qubit, in order to achieve the strong-coupling regime with the cavity modes. The source of the complication is twofold. On the one hand, spin ensembles behave (in the low-excitation regime) as harmonic systems: the qubit, whose logical states correspond to the presence in the ensemble of 0 or 1 excitations, is not naturally protected from population leakage to states with a higher number of excitations, as is the case for single S = 1/2 spin systems. On the other hand, small differences between the nominally identical systems within the ensemble, as well as inhomogeneities in the applied fields, can result in additional sources of qubit dephasing, with respect to single-spin (cluster) qubits.

7.3 Superconducting Hardware and Spin Ensembles

Hybrid circuits composed by superconducting and spin qubits are intensively studied in order to exploit the best of both worlds. The strong coupling constant of superconducting qubits to external fields makes them easy and fast to manipulate, while the long coherence times of electronic spins, as long as 2 s at room temperature for isolated impurities in crystals [88], make them ideal as quantum memories. Hybrid circuit-QED devices have been proposed in different schemes [89–92], with spin ensembles as quantum memories [93] to complete an architecture formed by the coplanar quantum bus and the superconducting qubits.

The experimental demonstration of the strong coupling with the cavity field is the first, necessary, step for spin ensemble to enter in the realm of circuit-QED. Exploiting the magnetic dipolar interactions, crystals of – typically 10¹² – non-interacting magnetic entities can be placed on the planar resonator directly above the region where the magnetic field antinode is localized (Fig. 11). Different systems have been investigated, namely N–V centers [94–96], ruby [94], Er: Y₂SiO₅ [97] with coupling strengths g _ens ranging between 10 and 65 MHz. Recently, strong-coupling regime has been reported for ferrimagnetic Ga-doped Y₃Fe₅O₁₂(g _ens = 4,540 MHz) [98].

Fig. 11

Schematic representation of a coplanar waveguide microwave resonator realized by conducting strips on a dielectric substrate. For a quasi-TEM e.m. wave, the magnetic field component (B ₁) is maximized at the center of the resonator and the flux lines are perpendicular to the central strip conductor. The physical dimension of the capacitance gaps determines the coupling degree of the resonator to the feedlines

In the strong-coupling regime, the resonator can be implemented to work as a “quantum bus” that coherently transfers the qubit state. Seminal experiments, performed in non-resonant strong dispersive regime, have, for instance, demonstrated the possibility to couple two qubits placed few millimeters apart by means of virtual photons [99]. The controlled phase interaction among the qubits has allowed the production of Bell states with concurrence up to 94%, reporting 1 μs of coherence time of the two-qubit device [100]. The exploitation of these quantum protocols also relies on the generation of a single or few microwave photons [101, 102] and controlled photon states [103], as well as on the possibility to detect the entanglement by means of a two-state tomography [104]. The successful execution of the Grover and Deutsch–Jozsa quantum algorithms has been carried out in proof-of-concept experiments [100].

The storage and retrieval of a quantum state from photons to a spin ensemble has been achieved by means of suitable sequences of magnetic pulses in pulsed EPR experiments by Wu et al. [105]. In a planar device, the direct transfer of a single photon between a superconducting qubit and an ensemble of NV centers has been assessed by the observation of vacuum Rabi oscillations when the qubit is brought to resonance with the spin ensemble [106]. A variable frequency superconducting resonator has been employed by Kubo et al. as quantum bus to perform a SWAP operation. An arbitrary qubit state α|g〉 + β|e〉 has been transferred into a corresponding photonic state α|0〉 + β|1〉 of the bus. The adiabatic SWAPgate has been performed by sweeping the resonance frequency of the bus across the qubit frequency. The resonance frequency of the bus is then tuned to resonance with the spin ensemble for a certain interaction time; hence, it is tuned back to the qubit frequency and the quantum tomography is performed. The fidelity was of about 10% only, limited by hyperfine effects and by the inhomogeneous broadening at resonance. Julsgaard et al. [107] have recently proposed a restoring protocol, based on magnetic resonance refocusing methods, reporting an improved fidelity of 80% for a storage time of 10 μs.

7.4 Molecular Spins in Hybrid Quantum Circuits

The idea to combine molecular spins with resonant cavities has naturally risen in this context. Organic radicals provide narrow EPR lines and long spin–spin decoherence times; thus, they can be used as first testbed. Chiorescu and co-workers studied the spin–photon coupling in a cylindrical cavity exploiting the doublet transition of DPPH radicals, showing the occurrence of a Rabi splitting of 10.9 MHz [87]. The Oxford team (Ardavan, Morton, and others) obtained the strong-coupling regime by using DPPH and lithium phthalocyanine in an X-band cylindrical dielectric ring resonator and they showed the $\sqrt{N}$ dependence of the coupling g-factor to the number of spins N [84]. In Stuttgart, superconducting striplines have been used to demonstrate frequency-swept EPR on organic radicals of the nitronyl-nitroxide family, as well as on Cr³⁺ atoms in ruby [108].

7.4.1 High-Spin Molecular Clusters

High-spin molecular clusters have been theoretically considered by Jenkins et al. [109] for use in hybrid quantum circuits. High spin can actually favor the establishment of strong coupling with modes in a resonating cavity. Thus, allowed transitions in high-spin clusters of Fe₈, GdW₁₀, GdW₃₀, TbW₃₀ have been theoretically investigated in order to find optimal conditions for coupling with superconducting coplanar resonators. Hybrid circuits made of high-spin clusters and flux qubits have also been considered. The authors concluded that high-spin ensembles tend to couple more strongly to flux qubits than to resonators and they demonstrated that coupling strength of 10% of the qubit natural frequency could be obtained under realistic experimental conditions [109].

The case of Mn₁₂ in a resonant superconducting cavity has been theoretically considered by Tsang et al. (private communication) in order to find conditions for strong coupling and then study the Quantum Tunneling of magnetization in this regime. From this study, it turns out that the molecule-cavity system exhibits a three-well potential with tunable inter-well interactions making conditions accessible for novel process of photon-assisted tunneling. Interestingly, this hybrid molecule-cavity system can be further exploited for simulating similar quantum systems.

7.4.2 Low-Spin Molecular Clusters

In the schemes based on the use of molecular nanomagnets, the interaction between the qubits is induced by superexchange bridges (see Sect. 4). It thus has a permanent and short-range character. Therefore, a suitable engineering of the intermolecular bridges is required in order to allow the switching of the effective qubit–qubit coupling or, alternatively, global-field approaches might be needed in order to bypass the requirement of an individual addressing of the nanomagnets [110]. In both these instances, the use of planar cavities offers the possibility of different solutions and suggests the development of different schemes. In particular, cavity photons can be used as bus qubits that possibly induce an effective coupling between distant qubits within the array. Also, neighboring qubits can be separated by larger distances, so as to facilitate their selective addressing.

In schemes based on the use of planar cavities, spins are generally used as quantum memories. The quantum processors are instead represented by systems that can be manipulated on shorter timescales, such as (different kinds of) superconducting qubits. Within such an approach, the role of the cavity is that of coupling the quantum memory and the quantum processor, i.e. the spin and the superconducting qubits. Starting from a similar hybrid device, a different approach to the implementation of quantum-information processing has been theoretically proposed [111]. This is based on a hybrid dual-rail encoding, where each qubit is physically implemented by a spin ensemble and a mode of the stripline resonator, and the logical states 0 and 1 correspond to the localization of an excitation, respectively, in the spin ensemble and in the cavity mode. Therefore, spins and photons don’t have distinct roles, but rather enter on the same footing. The possible advantage resulting from such an encoding is represented by the fact that all the manipulation is performed by the same means, namely the dynamical tuning of the resonator frequency. In particular, the single-qubit rotations of the form ${e}^{i\phi {\sigma}_x/2}$ can be implemented by putting in resonance the cavity mode with the lowest excitation mode of the spin ensemble for a defined time interval, thus allowing an excitation transfer between the two. Rotations around the z axis result instead from the modulation of the cavity frequency alone. The harmonic character of the spin-ensemble qubit represents a potential limitation in the implementation of conditional dynamics, and thus of the two-qubit gates. In order to introduce the required nonlinearity, a Cooper-pair box is added to the hardware, with three relevant energy levels. A suitable sequence of pulses (i.e., variations of the cavity frequencies) transfers the excitations of the two neighboring cavities to such three-level system and back to the qubits, thus adding a phase factor to the two qubits, only if these were initially in the logical state 11. This operation, combined with single-qubit gates, implements the CNOT gate.

In most of the developed schemes, the spin degree of freedom that is considered is the projection along z of the molecule spin. This choice implies the use of the magnetic component of the confined field for the spin manipulation. An alternative possibility is provided by spin chirality, which represents a good quantum number in odd-numbered spin rings with antisymmetric exchange. It has been predicted that such degree of freedom can be manipulated by means of pulsed electric fields [112, 113]. The actual value of the spin-electric coupling has been theoretically estimated in the case of some specific nanomagnets [114]. In suitably chosen molecules, such coupling might exceed that of the magnetic component, thus allowing the achievement of the strong-coupling regime with the cavity mode with smaller ensembles. As another possible advantage, spin chirality is expected to couple weakly to the nuclear-spin environment, and thus to present much longer decoherence times [14].

8 Conclusions and Perspectives

In Sect. 1 we rose some questions at which we can now try to answer.

8.1 Molecules Fitting Quantum Schemes

Many good examples of S = 1/2 molecules are available: while simple radicals provide sharper EPR lines, metallo-organic molecules look more appealing for their extraordinary ability to be functionalized and assembled in complex architectures. While experiments have assessed the feasibility of single-qubit gates, the next goal is the implementation of two-qubit gates with molecular nanomagnets. Noncommercial setups are required for this and dedicated effort should be devoted in order to open the way to more complex algorithms. Alternatively the use of high-spin molecules may allow the implementation of nontrivial qubits but these also require dedicated experiments.

8.2 Advantages in Using Molecular Qubits

One advantage of molecular nanomagnets is related to their functionalization, which opens to the control in positioning and linking them each other or to the surface. From this point of view, molecular nanomagnets are clearly superior with respect to spin impurities. This aspect may really open the way for the design and the synthesis of complex quantum devices being them either purely molecular or hybrid if molecules are further attached to solid state nano-objects. This looks like a real peculiarity of molecular nanomagnets which may give a plus to these systems to solve the problem of scalability.

8.3 Control of Decoherence at Molecular Level

The possibility to have a huge number of identical replicas makes molecular qubits robust with respect to inhomogeneities. However, in order to avoid pairwise dipolar interaction, diluted crystals need to be grown. Coherent dynamics of electron spins is quite sensitive to any excitation from the environment. To avoid incoherent relaxation processes, molecular spins work well only at very low temperature, like most of solid state quantum devices. Dephasing by interaction with nuclear spins remains the main source of noise at low temperature. Here the synthesis of derivatives with suitable ligands of nuclear-free isotopes has proved to be a viable route to improve the coherence time. As a matter of fact, the best T ₂ values measured on molecular spins now range between 1 and 10 μs at 2 K giving up to 10³ as figure of merit for electron-spin manipulation. This is a good starting point that should be used as benchmark for new molecular candidates to quantum computation. Since nuclear spins have much longer coherent lifetime (range of seconds even at room temperature), an interesting route – not yet fully explored – is to use them as qubits instead of trying to avoid them.

In this chapter we have also presented two emerging trends in the field: quantum simulators and spin in QED cavities as example of hybrid devices. Quantum technologies are now pushing in many other interesting directions, for instance, quantum communication and quantum cryptography for which application of molecular nanomagnets has been not explored yet. Very impressive are, at the time of writing, pioneering experiments on single-spin transistors and molecular spin valves: if quantum properties and spin dynamics can be controlled at single molecule level, this can overcome several problems encountered with spin ensembles and open an alternative way to quantum computation with molecular nanomagnets as discussed in another chapter of this book (Molecular Spintronics).

Appendices

Appendix 1: Quantum Description of the Spin Dynamics in a Resonant Cavity

In this section we provide further formalism to describe the interaction of single spin with a quantized electromagnetic field following the quantum approach [80, 87, 115]. We consider a cavity in which the field has a single harmonic mode of frequency ω. The intensity of the electromagnetic field determines the number n of photons in the cavity and we consider the situation for which few photons are present in the resonator. Let’s assume that the quality factor of the cavity Q is very high so that the photons lifetime is very long. Such a quantized electromagnetic field can be described as ${\mathrm{\mathcal{H}}}_c=\hslash \omega\;\left({a}^{\dagger }a+{\scriptscriptstyle \frac{1}{2}}\right)$, where a and a ^† are the creation and annihilation operators for photons, in analogy with a quantum one-dimensional oscillator [116]. The dipolar spin–photon interaction ℋ _cs  = − μ ⋅ B can be written as:

$$ {\mathcal{H}}_{cs}=\hslash {g}_c\left[\left(\mathbf{e}\cdot \mathbf{S}\right)a+\left({\mathbf{e}}^{*}\cdot \mathbf{S}\right){a}^{\dagger}\right]. $$

(12)

For this expression we make use of the Rotating Wave Approximation (RWA) that consists in neglecting fast-oscillating, non-energy-conserving terms which play a minor role in the dynamics of the system. The prefactor g _c is the coupling strength of the magnetic moment with the oscillating magnetic component of the electromagnetic field B ₁(t) The unitary vector e describes the polarization of B ₁(t), which can be conveniently chosen to obtain the circular polarization σ ₊ or σ ₋ with respect to the static field B ₀ along the z-axis. Being S _± = S _x  ± iS _y , we have thus

$$ {\mathrm{\mathcal{H}}}_{\sigma +}=\hslash {g}_c\left(a{S}_{+}+{a}^{\dagger }{S}_{-}\right), $$

(13)

for photons with helicity +ћ along z, and

$$ {\mathrm{\mathcal{H}}}_{\sigma -}=\hslash {g}_c\left(a{S}_{-}+{a}^{\dagger }{S}_{+}\right), $$

(14)

for photons with helicity −ћ along z. The Jaynes–Cummings model [117] considers the full Hamiltonian ℋ = ℋ _c  + ℋ _s  + ℋ _cs , i.e.:

$$ \mathrm{\mathcal{H}}=\hslash \omega \left({a}^{\dagger }a+\frac{1}{2}\right)+\hslash {\omega}_0{S}_z+\hslash {g}_c\left(a{S}_{\pm }+{a}^{\dagger }{S}_{\mp}\right). $$

(15)

being ℋ _s  = μ _B B ₀ S _z  = ℏω ₀ S _z the term describing the spin precession about B ₀. The interaction term ℋ _cs imposes the conservation of the z component of the total angular momentum since it has nonzero matrix element only between eigenstates of ℋ _c  + ℋ _s that are characterized by the same value of m _s  + n. This reproduces the selection rules Δm _s  = 1 for σ ₊ and Δm _s  = − 1 for σ ₋ expected for conventional perpendicular-mode EPR [118]. Since ${m}_s=\pm {\scriptscriptstyle \frac{1}{2}}$, we have only two possible values − 1/2 + n + 1 and + 1/2 + n, so the diagonalization of Eq. (15) can be carried out separately in each of the two-dimensional subspaces. It is convenient to make use of the dressed atom approach to describe the evolution of an isolated system composed by n photons and one spin [115]. Each subspace is represented by the photon plus spin states:

$$ \left|{\varphi}_a\right\rangle =\left|-\frac{1}{2},n+1\right\rangle \kern1em \left|{\varphi}_b\right\rangle =\left|+\frac{1}{2},n\right\rangle $$

(16)

related to the two allowed conditions, ground −1/2 spin state plus n + 1 photons and exited +1/2 spin state plus n photons. The correspondent eigenvalues

$$ {E}_a=\left(n+1\right)\hslash \omega -\left(\hslash {\omega}_0/2\right) $$

(17)

$$ {E}_b= n\mathit{\hslash \omega }+\left(\mathit{\hslash}{\omega}_0/2\right) $$

(18)

are separated by the detuning frequency ${\varDelta}_c={\scriptscriptstyle \frac{1}{\hslash }}\left({E}_a-{E}_b\right)=\omega -{\omega}_0$. At resonance (Δ _c  = 0), the unperturbed levels would be degenerate. The matrix elements of the interaction potential ${\mathrm{\mathcal{H}}}_{\sigma_{+}}$ result

$$ \left\langle {\varphi}_a\left|{\mathrm{\mathcal{H}}}_{\sigma_{+}}\right|{\varphi}_a\right\rangle =\left\langle {\varphi}_b\left|{\mathrm{\mathcal{H}}}_{\sigma_{+}}\right|{\varphi}_b\right\rangle =0 $$

(19)

$$ \left\langle {\varphi}_b\left|{\mathrm{\mathcal{H}}}_{\sigma_{+}}\right|{\varphi}_a\right\rangle =\hslash {g}_c\sqrt{n+1}. $$

(20)

showing that for a system with n photons, the coupling strength scales nonlinearly as $\sqrt{n+1}$. By defining the n-photon Rabi frequency as ${\varOmega}_n=2{g}_c\sqrt{n+1}$, the eigenvalues of Eq. (15) read

$$ {E}_{+}(n)=\hslash \left(n+\frac{1}{2}\right)\omega +\frac{\hslash }{2}\sqrt{\varDelta_c^2+{\varOmega}_n^2} $$

(21)

$$ {E}_{-}(n)=\hslash \left(n+\frac{1}{2}\right)\omega -\frac{\hslash }{2}\sqrt{\varDelta_c^2+{\varOmega}_n^2}. $$

(22)

They form two branches of hyperbola with the unperturbed energies as asymptotes (see Fig. 9a). With respect to the unperturbed states, the interaction potential determines the formation of an anticrossing centered on resonance. The minimum gap between E ₁ and E ₂ is ℏΩ _n for Δ _c  = 0. The corresponding eigenstates, expressed as function of the unperturbed basis, result

$$ \left|{\chi}_{+}(n)\right\rangle = \sin \kern0.5em \theta \left|-\frac{1}{2},n+1\right\rangle + \cos \kern0.5em \theta \left|+\frac{1}{2},n\right\rangle $$

(23)

$$ \left|{\chi}_{-}(n)\right\rangle = \cos \theta \left|-\frac{1}{2},n+1\right\rangle + \sin \theta \left|+\frac{1}{2},n\right\rangle $$

(24)

with mixing angle

$$ \tan \left(2{\theta}_n\right)=-\frac{\varOmega_n}{\varDelta_c}\kern1em 0\le 2{\theta}_n<\pi . $$

(25)

Each added photon creates a two-dimensional subspace, the complete manifold is a ladder of the two-level states shifted in energy by ћω.

Let’s now focus on the resonant case. For Δ _c  = 0 the mixing angle is θ _n  = π/4 and the perturbed states result

$$ \left|{\chi}_{+}(n)\right\rangle =\frac{1}{\sqrt{2}}\left[\left|-\frac{1}{2},n+1\right\rangle +\left|+\frac{1}{2},n\right\rangle \right] $$

(26)

$$ \left|{\chi}_{-}(n)\right\rangle =\frac{1}{\sqrt{2}}\left[\left|-\frac{1}{2},n+1\right\rangle -\left|+\frac{1}{2},n\right\rangle \right]. $$

(27)

The time evolution can be calculated by applying the unitary evolution operator to the perturbed dressed states and by recasting in the | − 1/2〉 or | + 1/2〉 unperturbed basis. The time evolution of the ground |Ψ ₋〉 state is

$$ \left|{\varPsi}_{-}(t)\right\rangle = \cos \left(\frac{\varOmega_nt}{2}\right)\left|-\frac{1}{2},n+1\right\rangle -i \sin \left(\frac{\varOmega_nt}{2}\right)\left|+\frac{1}{2},n\right\rangle $$

(28)

while the excited state evolves as

$$ \left|{\varPsi}_{+}(t)\right\rangle = \cos \left(\frac{\varOmega_nt}{2}\right)\left|-\frac{1}{2},n+1\right\rangle +i \sin \left(\frac{\varOmega_nt}{2}\right)\left|+\frac{1}{2},n\right\rangle $$

(29)

These expressions describe the dynamics of entangled spin and photon states which have a time evolution that recalls the beat signal of two coupled degenerate quantum oscillators. The eigenmodes are a symmetric and antisymmetric combination of the independent modes of the free oscillators. The cavity and the spin coherently exchange a photon, which is absorbed and then emitted following the spin flip.

The population of the | − 1/2, n + 1〉 and | + 1/2, n〉 states oscillates and for n ≫ 1 the transition probability can be written as

$$ {P}_{ba}(t)=\frac{\varOmega_n^2}{\varDelta_c^2+{\varOmega}_n^2}{ \sin}^2\left[\sqrt{\varDelta_c^2+{\varOmega}_n^2}\frac{t}{2}\right]. $$

(30)

This formula reproduces the classical result of Eq. (6) with Ω _n  = Ω _R.

Appendix 2: Planar Resonators

2.1 Fabrication of Microstrip and Coplanar Resonators

Planar transmission lines are commonly used in microwave technology as they provide a simple way to transmit electromagnetic waves on a printed board circuit realized by standard lithographic methods. Among many different geometries, microstrip and coplanar waveguides are the most frequent choices. Microstrip lines are constituted by a dielectric substrate having a metal strip on the top and a ground plane on the bottom side. Coplanar waveguides differ from microstrips for the presence of two ground planes placed beside the central strip on the top side. The ground conductor in the backside can also be removed. With these geometries, it is possible to match the impedance of the feeding coaxial lines (usually 50 Ω) with relative physical dimensions that spans from millimeter to micron size. By design, the transmission of quasi-transverse electromagnetic modes (TEM) can be achieved, while higher-order non-TEM modes can be appropriately suppressed [119].

Coplanar waveguides are the best choice for minimizing the irradiation of the microwave field outside the surface and to arrange ground electrodes close to the central signal line. A coplanar resonator of length l is realized when the central strip is interrupted in correspondence to two selected positions. These dielectric gaps are capacitors that electrically couple resonator and transmission line, acting like mirrors do in an optical cavity. Resonant conditions are met when input and reflected wave signals give constructive interference into the cavity. The value of the resonant frequency ω _c is determined by the length l of the resonator and by the speed of propagation of the electromagnetic wave in the coplanar waveguide. The latter is related to the effective dielectric constant ε _eff of the insulator. For a cavity resonating at half wavelength λ/2 [120], the resonance frequency is:

$$ {\omega}_c=\frac{2\pi c}{\sqrt{\varepsilon_{\mathrm{eff}}}}\frac{1}{2l} $$

(31)

As mentioned in the previous sections, the quality factor of the resonator must be maximized to reduce the decay rate of the cavity κ and to increase the photon lifetime. The Q-factor is defined as the ratio between the energy stored in the cavity and the power dissipated in a time interval 1/ω or, alternatively as the width of the resonance Δω _c since Q = ω _c /Δω _c . For a resonator coupled to the feedlines, the loaded quality factor must be considered

$$ \frac{1}{Q}=\frac{1}{Q_{\mathrm{ext}}}+\frac{1}{Q_{\mathrm{int}}}, $$

(32)

which is calculated by including the external quality factor (Q _ext) related to the coupling capacitances and the intrinsic Q _int, due to the internal losses of the resonators.

The capacitance of the input and output gaps controls the coupling with the transmission line and consequently the power flow κ _in and κ _out along the waveguide. The maximum transfer of microwave energy is obtained when the impedance of the resonator is matched to the feedline. This corresponds to the condition Q _ext = Q _int and the resonator is said to be critically coupled. For Q _ext < Q _int the resonator is undercoupled. This configuration corresponds to reduced transmission, thus lower signal-to-noise ratio, but maximum Q. In the experiments it is often reported because the low output signals can be restored by a low noise microwave amplifier inserted along the output line. Conversely, in the overcoupling regime (Q _ext > Q _int) high κ _in and κ _out are obtained, thus lower Q. This configuration has been used to get fast measurement rates of the cavity photon states [81].

Intrinsic losses often determine the loaded quality factor of the resonator. They are related to different dissipation mechanisms that finally determine the performances of the coplanar resonator. Losses depend on the geometry, material choice, temperature, frequency range, and applied magnetic field. Resonators are rather susceptible to their environment, so they are usually enclosed in metal boxes. Without applied magnetic field, three are the main dissipation mechanisms: resistive, dielectric, and radiative losses [121].

Resistive losses are due to energy dissipated by an electromagnetic wave traveling along a waveguide with finite conductance. Just considering resistive losses, the Q factor passes from ~10¹ to 10², typically obtained for resistive cavities, up to Q ~ 10⁷ for superconducting resonators [122]. Niobium is commonly employed for its relatively high critical temperature (T _c  ≃ 9.2 K) and critical field. Superconducting films of TiN, Al, Ta, Re, or YBCO are also reported. Spin systems usually require the application of static magnetic fields to split the degeneracy of the energy levels. For instance, X-band resonance of a spin 1/2 paramagnet requires about 340 mT. Trapping of magnetic flux can be minimized by aligning the field parallel to the resonator surface and experiments report limited degradation of Q up to 350 mT [123]. For higher field or other orientations the penetration of magnetic flux determines a decrease of the quality factor down to 10³ or lower values. Strategies for the reduction of the magnetic losses have been applied, for instance, by pinning the vortex motion by patterning of slots or microdots [124–126]. Magnetic hysteresis effects are also present and determine the dependence of the Q-factor on the magnetic history of the sample [127].

Dielectric losses are due to absorption of the electromagnetic power by the dielectric substrate. For a lossy material the complex dielectric constant ε = ε _r  + iε _i has a finite imaginary part ε _i and loss tangent (tan δ). The quality factor associated with the dielectric losses is Q _diel = 1/tan δ, thus it is desirable to choose insulating substrates with low loss tangent. Sapphire has very low losses with tan δ ~ 10^− 8 in high-purity crystals [128]. High resistivity silicon and thermally grown SiO₂ provide a valid alternative [129]. Fabrication strategies, like suspended resonators with grooves etched in the regions of high electric field, have been proposed for reducing the dielectric losses [130].

Radiative losses are an additional contribution due to the emission of electromagnetic radiation in the free space. The associated quality factor is Q _rad ~ (l/b)², where l and b are, respectively, the length and the distance between the ground electrodes in the top plane [131]. For a typical coplanar waveguide resonator Q _rad ~ 10⁶.

The temperature dependence of the Q-factor shows a sudden increase below T _c reaching a maximum value for T ≃ T _c /10 (T ≃ 1 K for Nb). At lower temperature, Q progressively decreases due to a further loss mechanism inducted by the two-level (spin) transitions. These losses, which dominate in the millikelvin range, are ubiquitously reported in lithographed resonators and they are independent by the materials used. They have been assigned to oxides or impurities located close to the active region of the resonator [132–135]

The fundamental resonance frequency of planar resonators is usually located in the 2–15 GHz range by appropriate choice of l. Higher-order harmonics provides further resonances, although the quality factor progressively deteriorates by increasing the mode number [136]. Tunable superconducting resonators have been realized by means of Josephson junctions demonstrating large tunable range and high quality factor [137–139], and the possibility to tune ω _c faster than photon lifetime [140].

2.2 Planar Resonators for Magnetic Resonance Experiments

Modern conventional three-dimensional EPR spectrometers report a spin sensitivity up to ~10⁹ spins Hz^−1/2 thanks to the high quality factor of cavity. The minimum detectable number of spins of an EPR cavity depends also on a set of different parameters, such as cavity volume and strength of the microwave field [118]. For small samples, such as thin films or nanostructures, an efficient way to improve the sensitivity of the EPR measurement is to increase the filling factor

$$ \eta =\frac{\int_{V_s}{\left|{B}_1\right|}^2dV}{\int_{V_c}{\left|{B}_1\right|}^2dV} $$

(33)

being V _c and V _s respectively, the e.m. mode and sample volume [141], by fabricating resonators that match the sample size and that can concentrate the microwave field in the sample space.

Planar resonating circuits show microwave fields confined in a small V _c , limited to about 100 μm above the surface, where the intensity of B ₁ can reach the 0.1 mT range with a limited input power (~100 μW). These devices have been proposed as EPR cavities [142, 143], also because they are suitable for low temperature experiments where microwave heating must be avoided. With the purpose to maximize the power to field conversation efficiency on the sample volume, several designs have been studied, including microstrips [144], planar microcoils [145, 146], and surface loop-gap microresonators [147]. These devices, investigated by means of both continuous-wave and pulsed EPR experiments, report an increase of the sensitivity up to ~10⁶ spins Hz^−1/2 [147]. Similar resonators were also used for ferromagnetic resonance measurements [148–150]. In addition, cross-shaped resonators were proposed for controlling the polarization of the microwave mode [151].

Continuous-wave EPR of different spin ensembles has been exploited for strong-coupling experiments with coplanar waveguide resonators [94–97, 152]. Superconducting resonators have also been studied for pulsed EPR [123, 153] or non-resonating frequency-sweeping EPR [108]. Optimized resonators made with parallel arrays of superconducting microstrip have been also developed for improving the homogeneity of B ₁ over a large region [123].