Abstract
Recent advances in reduced density matrix functional theory (RDMFT) and linear response time-dependent reduced density matrix functional theory (TD-RDMFT) are reviewed. In particular, we present various approaches to develop approximate density matrix functionals which have been employed in RDMFT. We discuss the properties and performance of most available density matrix functionals. Progress in the development of functionals has been paralleled by formulation of novel RDMFT-based methods for predicting properties of molecular systems and solids. We give an overview of these methods. The time-dependent extension, TD-RDMFT, is a relatively new theory still awaiting practical and generally useful functionals which would work within the adiabatic approximation. In this chapter we concentrate on the formulation of TD-RDMFT response equations and various adiabatic approximations. None of the adiabatic approximations is fully satisfactory, so we also discuss a phase-dependent extension to TD-RDMFT employing the concept of phase-including-natural-spinorbitals (PINOs). We focus on applications of the linear response formulations to two-electron systems, for which the (almost) exact functional is known.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Density matrix functional
- Reduced density matrix
- Density matrix functional theory
- Time-dependent density matrix functional
- Electron correlation
1 Introduction
The most widely used methods in quantum chemistry are either wavefunction-based or they exploit density functional theory (DFT). The former class of methods offers high accuracy, but unfavorable scaling of the computational cost with system size limits their scope of applicability to relatively small systems. Density functional approximations are known to offer a good balance between computational efficiency and accuracy. Nevertheless, most approximations to DFT are plagued by generic problems related to the fact that DFT employs a simple local object – the electron density. Accurate description of the electronic structure of multireference systems or predicting multiple electronic excitations are examples of problems that still await satisfactory solutions in DFT. There has recently been growing interest in approaches embracing simplicity (in the sense that a wavefunction is not involved), computational efficiency, and versatility of DFT, while lacking the drawbacks. Functionals of one-electron reduced density matrix (1-RDM) γ, defined for an N-electron wavefunction Ψ as
where x = (r, s) is a combined spatial and spin coordinate, should, in principle, lead to formulating methods superior to existing density functional approximations, especially when static electron correlation effects cannot be neglected. An immediate advantage of using 1-RDM as a main variable instead of the electron density, ρ, is that the kinetic energy is an explicit functional of γ but not of ρ. Thus, in reduced (one-electron) density matrix functional theory (RDMFT) there is no need to introduce a fictitious noninteracting system. Moreover, orbitals present in RDMFT are fractionally occupied so functionals of γ seem to be better suited than their density counterparts to account for static correlation and, for example, describe correctly a covalent bond-breaking process. As discussed in this chapter, this presumption has been confirmed by a good performance of the most successful density matrix functionals.
Although the theoretical foundations of RDMFT were set a long time ago [1–11], functionals of practical usefulness which can compete with density functionals in accuracy have only recently been proposed. In this section we present the main ingredients of RDMFT (theorems, definitions, and conditions) and first approximate density matrix functionals proposed for electronic systems. In the following sections more recent and successful developments in RDMFT are shown.
Self-adjointness of γ defined in (1) allows for its spectral representation, namely [12]
Eigenvalues of 1-RDM, {n p }, are called natural occupation numbers, whereas its eigenfunctions, {φ p }, are known as natural spinorbitals. Throughout the chapter we assume a convention that the indices p, q, r, s pertain to natural spinorbitals and a, b, c, d to arbitrary one-electron functions. Self-adjointness of γ implies orthonormality of the natural spinorbitals. Additionally, because γ is assumed to be normalized to a number of electrons N, cf. definition given in (1), the natural occupancies sum up to N. Taking into account that each n p is nonnegative and not greater than 1 [2, 3], the overall properties of the natural spinorbitals and occupation numbers read
Coleman [2] has proved that if a given Hermitian 1-RDM satisfies the conditions (3)–(5) there exists an ensemble of N-electron antisymmetric wavefunctions that yield γ. The conditions are called N-representability conditions. It should be noted that similar sufficient and necessary conditions that would ensure pure-state N-representability are not known, though some significant progress has been reported by Klyachko [A.A. Klyachko, J. Phys. Conf. Ser. 36, 72–86 (2006), doi: 10.1088/1742-6596/36/1/014].
A one-to-one mapping between pure-state v-representable 1-RDMs and non-degenerate ground state wavefunctions has been demonstrated by Gilbert who extended the Hohenberg–Kohn theorem to nonlocal potentials [1, 13]. This establishes existence of a 1-RDM functional [1, 11]
where ĥ stands for a one-electron Hamiltonian comprising kinetic energy and external potential operators,
\( {\widehat{V}}_{\mathrm{ee}}={\displaystyle {\sum}_{i>j}^N\frac{1}{r_{ij}}} \) is an electron interaction operator (note that atomic units are employed throughout the chapter), and Ψ[γ] denotes a ground state wavefunction pertinent to a v-representable γ. A variational principle for the functional defined in (6) exists and reads
where “v-rep” denotes a set of pure-state v-representable 1-RDMs. The equality is achieved for a ground state density matrix. Levy extended the domain of a density matrix functional to all pure-state N-representable 1-RDMs by defining the electron repulsion functional as [4, 5]
The minimization is carried out in a set of all physically admissible wavefunctions Ψ that yield a given 1-RDM γ. Levy’s constrained search definition has been further extended to ensemble N-representable 1-RDMs (belonging to a set “N-rep”) by Valone [7, 8] and the exact functional reads
where the minimization is carried out with respect to N-electron density matrices Γ(N) that yield γ. Because of the linearity of the map Γ(N) → γ and the fact that the set of N-representable γ is convex, a functional E ee[γ] is also convex [6]. For a given external potential \( {\widehat{v}}_{\mathrm{ext}} \), minima of the Hohenberg–Kohn functional given in (6), the Levy functional \( \mathrm{T}\mathrm{r}\left[\widehat{h}\widehat{\gamma}\right]+{E}_{\mathrm{ee}}^{\mathrm{L}}\left[\gamma \right] \) (9), and the functional \( \mathrm{T}\mathrm{r}\left[\widehat{h}\widehat{\gamma}\right]+{E}_{\mathrm{ee}}\left[\gamma \right] \) (10), defined, respectively, for v-rep, pure-state N-representable, and ensemble N-representable (N-rep) 1-RDMs, coincide [7, 9]. Therefore, taking into account a variational principle given in (8), one concludes that a functional defined for N-rep 1-RDMs yields a ground state energy at minimum, i.e.,
A great advantage of working with functionals defined for (ensemble) N-representable γs is that sufficient and necessary conditions for N-representability are known. Equation (11) together with (3)–(5) are a foundation for RDMFT.
The definition of the exact functional (10) is of little practical use in developing approximate functionals. However, in two cases exact forms of E ee[γ] are known, providing some guidelines for developing generally applicable approximate functionals. The first case corresponds to N-electron noninteracting systems. The 1-RDM corresponding to a single determinantal wavefunction is idempotent which implies integer (0 or 1) values of the natural occupation numbers, i.e.,
A two-electron reduced density matrix Γ (2-RDM), defined for a general wavefunction Ψ as
is explicitly expressible in terms of 1-RDM if the wavefunction takes the form of a Slater determinant, namely
The electron interaction functional corresponding to such a noninteracting 2-RDM reads
We refer to it as Hartree–Fock functional (thus the superscript HF) because optimization of the functional which is a sum of the one-electron part and E HFee with respect to N-representable γ leads to an idempotent density matrix coinciding with the solution to the Hartree–Fock equations [14]. The HF functional (15) comprises two components. The Hartree functional, E H, describes the classical part of electron interaction, namely
whereas the exchange functional, E x, reads
Another paradigm case for which an exact density matrix functional is known, is a two-electron closed-shell system. We discuss this case extensively in Sect. 2.1.
The two cases, namely a noninteracting N-electron system and an interacting two-electron species, cover two extreme regimes of electron correlation for an electron pair: the former pertains to an uncorrelated pair, whereas the latter, applied to electrons separated in space (e.g., H2 molecule in a dissociation limit), describes strongly correlated electrons. In other words, exact density matrix functionals for an uncorrelated and a strongly correlated electron pair are known. Ideally, a valid approximate functional should reduce to exact functionals for both cases.
In developing approximate functionals it is convenient to separate out the Hartree functional given in (16) from the electron repulsion E ee functional defined in (10) and to search for approximations to the exchange-correlation complement E xc defined as
The exchange-correlation functional can be further decomposed into an exchange part given in (17) and the remainder called the correlation functional E c
A number of conditions satisfied by the exact E ee functional or its correlation component E c have been revealed, cf. [5, 15–17], and some of them are invoked in this chapter.
The first realization of the approximate density matrix functional has been given by Müller [18] and it was later independently derived from more physical arguments by Buijse and Baerends [19, 20]. The exchange-correlation part of the functional called either Müller functional or BB (we adhere to the latter name) reads
where the natural occupation numbers {n p } and the spinorbitals {φ p } are eigenvalues and eigenfunctions of γ and the exchange integrals {〈pq|qp〉} are written in the representation of the natural spinorbitals. The following notation is adopted in this chapter for two-electron integrals
The BB functional is convex [21] and reduces to the exchange functional (17) for an idempotent γ. It is not exact for two-electron systems, though. It has been shown that this functional severely overestimates correlation energy of atoms and molecules [22–27]. However, the BB functional has been successfully used as a base for developing more sophisticated functionals, as discussed in Sect. 2.1.
Goedecker and Umrigar (GU) have modified the BB functional by removing diagonal (p = q) terms, called electron self-interaction, from the Hartree and the exchange-correlation BB functionals [28, 29], and thus the xc part of the GU functional reads
GU offers an improvement to the BB functional for atoms and molecules around their equilibrium geometries [28, 30] but it is in large error in the bond dissociation region of diatomic molecules [22, 25, 27]. Another simple xc functional – corrected Hartree–Fock (CHF) – has been proposed by Csanyi and Arias [31]
Even though the correlation part of the CHF functional satisfies the particle-hole symmetry condition, cf. (30), which is also satisfied by the exact functional [15], it provides little or no improvement over the HF method for molecules around the equilibrium distances, and it breaks down in the dissociation limit [22, 32].
Although the aforementioned first generation of density matrix functionals has not turned out to be overall competitive with DFT approximations, understanding the origins of their failures has provided insight to developing more advanced and successful functionals described in the next section.
2 Construction of Density Matrix Functionals
Because of the two-particle nature of the electron interaction, given a system described by a ground state wavefunction |0〉, the electronic repulsion energy E ee results from contraction of the two-electron reduced density matrix elements Γ abcd with two-electron integrals 〈ab|cd〉, namely
where, for a given basis set {χ a } and the pertinent sets of the creation and annihilation operators {â †}, {â}, the elements of the 2-RDM are defined as
Formally, the 2-RDM is a functional of the 1-RDM. Most approaches to approximating the electron–electron interaction functional (10) exploit the formula given in (24) and assume that the elements of Γ are functions of the natural occupation numbers {n p }. Consequently, if natural spinorbitals {φ p } are used as a basis set, the whole dependence of the E ee functional on the natural spinorbitals is included in two-electron integrals, which gives rise to the form
This assumption is borrowed from the Hartree–Fock approximation, cf. (14), in which elements of the 2-RDM in the representation of the natural spinorbitals are given solely in terms of the occupation numbers, i.e.,
The functional E ee[γ] in most approximations proposed so far is an explicit function of the occupation numbers and the natural spinorbitals.
Developing an approximate correlation functional, cf. (19), begins with assuming a cumulant expansion of 2-RDM [33] which consists of writing Γ as the antisymmetrized product of γ and the cumulant part, λ being a functional of γ,
A cumulant expansion gives rise to the following expression for E c
It has been shown that the exact correlation 1-RDM functional possesses a particle-hole symmetry [15]
(this symmetry should be understood as invariance of E c to the following replacement ∀ p n p → (1 − n p )) and scales linearly under homogeneous scaling of coordinates in γ(x, x′) [5]
where coordinates in γ η are scaled with a real number η and the normalization is preserved, i.e.,
Some density matrix functionals rely on the reconstruction scheme given in (28). In other cases, the exchange-correlation functional (18) is not partitioned any further and is modeled as a whole. Different approaches to approximating electron–electron density matrix functionals proposed in recent years are discussed in the remaining part of this section.
2.1 Functionals Based on a Paradigm Two-Electron Case
Homogeneous electron gas (HEG) is a paradigm system for density functionals. This is because the exact form of the exchange density functional for this system is known and a highly accurate correlation energy functional is available. Consequently, electron gas has been a reference system for most approximate density functionals and their forms are such that exact energy for a homogeneous electron density is recovered. The situation is different in RDMFT because the exchange-correlation density matrix functional for HEG is not known. However, the exact density matrix functional is available for a two-electron system [29, 34], so it is now considered to be a paradigm in RDMFT. A two-electron molecule seems to be even a more adequate reference than the homogeneous electron gas if one aims at developing a functional accurately describing electronic structure of molecules.
A form of the two-electron density matrix functional can be immediately formulated based on the work of Löwdin and Shull (LS) [35] who showed that in a basis of the natural spinorbitals {φ p } a Slater-determinant-expansion of a singlet wavefunction (assumed to be real-valued) is entirely given by “diagonal” determinants composed of spinorbitals sharing spatial parts, i.e.,
where p and \( \overline{p} \) are spinorbitals of the opposite spin and \( \left|{\varphi}_p{\varphi}_{\overline{p}}\right| \) denotes a normalized Slater determinant. The normalization of the wavefunction imposes the following condition of the expansion coefficients {c p }
Employing the LS wavefunction given in (33) in (1) defining 1-RDM, one immediately obtains γ in its spectral representation, which indicates that squares of the expansion coefficients are simply the natural occupation numbers, i.e.,
Taking the expectation value of the Hamiltonian with the LS wavefunction (33) leads to a simple expression for the energy
where the indices p, q correspond to indices of the natural spinorbitals. It should be noted that (36) is valid for a closed-shell system so it is assumed that the coefficients corresponding to spinorbitals of opposite spins and same spatial parts are equal. The exact ground state energy for a two-electron system follows by minimizing the energy with respect to the expansion coefficients {c p } and the natural spinorbitals {φ p } under the orthonormality condition for the orbitals and a normalization condition given in (34). An exact electron interaction density matrix functional can be immediately written as
where it has been taken into account that the orbitals are real so the integrals 〈pp|qq〉 are equal to the exchange integrals 〈pq|qp〉, and the relation (35) between expansion coefficients in the LS wavefunction and the occupation numbers have been exploited. It is known that for two-electron atoms and molecules at equilibrium geometry the sign of the factor f 1 corresponding to the highest occupation n 1 is predominantly opposite to signs {f p } of all other factors corresponding to weakly occupied \( \left({n}_p<{\scriptscriptstyle \frac{1}{2}}\right) \) orbitals [29]. It should be noted that cases when this rule is violated are known and they include, for example, a hydrogen molecule far from equilibrium bond distance [36–38] or a strongly correlated Hooke’s atom [39]. In such cases, natural orbitals that violate the phase rule, i.e., those orbitals whose phase factor coincides with f 1, are very weakly occupied and their contribution to the energy is small. Consequently, a two-electron functional explicitly depending on the occupation numbers defined as
is not always fully equivalent to the exact LS functional (37) but it provides a very good approximation to it. Inspecting the structure of the functional (39), it is evident that terms corresponding to two weakly occupied orbitals (p, q > 1) are treated differently (enter the functional with a different signs) from products of strongly-weakly occupied orbitals (p = 1, q > 1 or p > 1, q = 1).
Evidently the form of the BB functional given in (20) does not reflect the orbital structure of the functional for two electrons given in (39). Restoring this structure and correcting for the overcorrelation by the BB functional have been motivations behind proposing a number of corrections to it [27]. This has resulted in the development of BB-corrected (BBC) functionals consisting of the Hartree part (16) and the exchange-correlation functional comprising products of exchange integrals and occupation number depending factors G BBC pq , namely
In definitions of the BBC functionals, spinorbitals of the occupancies smaller than 1/2 are called weakly occupied, although those with occupation numbers exceeding 1/2 belong to a set of strongly occupied orbitals (it should be noted that only in the limit of strong correlation are some natural occupation numbers exactly equal to 1/2). Note also that the BB functional is recovered from (41) upon setting \( {G}_{pq}^{\mathrm{BBC}}=-\sqrt{n_p{n}_q} \). A comparison of the orbital structure of the BB functional with that of the accurate two-electron functional (39) has led to proposing a correction restoring positive signs of cross products between weakly occupied natural spinorbitals. Such a corrected BB functional, named BBC1, conforms to a general form of (41) after assuming
where p, q ∈ weak denotes that both spinorbitals are weakly occupied. Self-consistent calculations revealed that, similar to BB, BBC1 overbinds diatomic molecules, which indicates a need for further repulsive corrections [27]. The BBC2 functional emerged after correcting interaction between two different strongly occupied orbitals and replacing square roots of products of the pertinent occupancies with products n p n q . The third functional, BBC3, is a result of adding another two corrections to the BBC2 functional. In the BBC3 functional a pair of bonding and antibonding (both called frontier) spinorbitals which form a breaking bond is distinguished. It is assumed that a bonding orbital belongs only to a set of frontier orbitals, and that, at the same time, antibonding orbitals belong to sets of frontier and weakly occupied orbitals. The first BBC3 correction, added on top of the BBC1 and BBC2 corrections, replaces square roots of products of occupation numbers with pertinent products if one occupancy corresponds to an antibonding orbital and the other to a strongly occupied one. The replacement does not affect pairs of antibonding-bonding orbitals. The second correction removes self-interaction from all orbitals except the frontier (i.e., bonding and antibonding) orbitals. The form of the G pq elements in the BBC3 functional therefore read
where the frontier (weak) spinorbitals are those that belong to a set of frontier orbitals and their occupancy number is smaller than 1/2 (antibonding orbitals). BBC3 functional possesses a correct orbital structure of the two-electron functional (39) if applied to hydrogen molecule in the dissociating limit and it is able to reproduce very accurately the whole dissociation curve [27]. Moreover, based on examples of small atoms and diatomic molecules at equilibrium geometries and in their dissociation limits, it has been shown that BBC3 accounts for both dynamic and static correlation yielding correct potential energy and recovering most of the correlation energy.
A difficulty with practical usage of the BBC3 functional is a need to select bonding and antibonding orbitals. In a computer implementation a strongly occupied orbital of the lowest occupancy is taken as bonding although a weakly occupied orbital of the highest occupancy is taken as an antibonding with a straightforward extension for this selection rule for molecules with more than one bond. This, however, leads to numerical problems because in the optimization procedure occupation numbers are varied and the antibonding character of orbitals may change, which may cause problems with convergence or may result in obtaining discontinuities in potential energy curves. To avoid the previously described problems with selecting frontier orbitals and to improve the overall accuracy of the BBC3 functional, it has been proposed to replace the elements G pq present in the BBC functional, cf. (41), with a function G(n p ,n q ). The function mimics the behavior of the G BBC3 pq elements but does it automatically, based on the values of its arguments. The optimal function has been found by introducing two parameters and fitting the resulting AC3 functional to accurate energies of two molecules at equilibrium and stretched-bond geometries [40]. The AC3 functional yields decent quality potential energy curves for ten-electron molecules, although for some molecules a small hump in the curve is visible.
A two-electron wavefunction (33) is a special case of the more general closed-shell N-electron ansatz (N assumed to be even) involving, apart from a reference determinant Φ0, all determinants arising from diagonal double, diagonal quadruple, etc., excitations; cf. (67). Taking the expectation value of the Hamiltonian with such a wavefunction yields an energy expression involving only Coulomb, exchange, and integrals of the 〈pp|qq〉 type [41]. In [42] the previously mentioned ansatz for the wavefunction has been used in development of the extended Löwdin–Shull (ELS) functional. The functional is applicable to systems for which a set of the natural spinorbitals can be partitioned into “inner” orbitals localized on atoms and the occupancies close to 1 and “outer” orbitals including a bonding orbital and all weakly occupied orbitals, i.e., orbitals localized on a single bond. For N-electron (N being even) systems (N/2 − 1) strongly occupied orbitals (in a spin-restricted formulation each orbital gives rise to two spinorbitals with opposite spins) would be considered “inner” and the remaining strongly occupied orbital of the lowest occupancy would belong to the “outer” orbital set. By analyzing a structure of the energy expression resulting from the assumed ansatz, the following form of the ELS functional has been proposed
where the phase factors {f p } for the outer orbitals are set according to the rule valid for two-electron systems, namely
Note that even though the exchange integrals 〈pq|qp〉 are identical to 〈pp|qq〉 if the spinorbitals are real, the two types of integrals make different contributions to time-dependent linear response equations so they are kept separately in the ELS functional. It is evident that for a two-electron system the set of inner spinorbitals is empty and, unlike the BBC3 or AC3 functionals, the ELS reduces to the accurate functional given in (39). A few models have been tried for the function F L, which is responsible for correlating inner and outer orbitals. The most successful ones include one or two empirical parameters fitted to reproduce potential energy curves of LiH, Li2, and BH+ molecules. Very accurate potential energy curves have been obtained for these molecules [42]. Unfortunately, applications to other systems have not been presented, because the functional has been designed to treat only molecules with one single bond and no lone electron pairs. Nevertheless, ELS is a promising step towards extending the Löwdin–Shull functional to more than two electrons, aiming at providing a balanced description of the dynamic and static correlation.
2.2 Functionals Based on Reconstruction of 2-RDM in Terms of 1-RDM
One of the possible strategies towards development of novel one-electron density matrix functionals consists of assuming the cumulant expansion for the 2-RDM (28) and finding approximations for the cumulant part, γ, by imposing known conditions which the exact cumulant satisfies. The first naive proposition one might try is neglecting γ completely. This would result in the electron interaction functional being just a sum of the Hartree (16) and exchange (17) functionals, with no correlation part. One might then hope that some portion of correlation could still be recovered by allowing nonidempotent γ in the optimization, in other words by allowing fractional occupancies of the natural orbitals. However, it has been shown by Lieb, that for electronic systems the minimum of the functional involving only Hartree and exchange contributions to the electronic repulsion, cf. (15), is achieved at an idempotent 1-RDM [14]. Thus, the minimum of the functional free of the correlation part simply coincides with the Hartree–Fock energy. To go beyond the Hartree–Fock approximation requires not only admitting nonidempotent γ but also including nonzero cumulant part in the reconstructed 2-RDM. Recently, Piris and collaborators proposed a series of natural orbital functionals known as PNOFi (i = 1–6) [43–48] by finding approximations to the cumulant matrix γ in terms of the natural occupation numbers [49, 50]. In reconstructing RDM defined in (25) in terms of 1-RDM the equality conditions satisfied by the N-representable 2-RDM are such that Hermiticity
antisymmetry
and a sum rule
have been imposed. To narrow down the possible form of the 2-RDM as a function of the occupation numbers, it has been required that the final correlation energy functional includes only Coulomb integrals 〈pq|pq〉, exchange integrals 〈pq|qp〉, and integrals of the type 〈pp|qq〉. It should be noted that the last two sets are identical if the orbitals are real, which is the case in practical calculations, but they enter the time-dependent density matrix functional equations in different terms as discussed in Sect. 5. Piris and Ugalde [49, 50] proposed the following structure of the spin-blocks of the cumulant matrix in a spin-restricted formalism
where σ = α, β, the Δ matrices are symmetric, and the Π matrix is Hermitian. Such an ansatz for the cumulant results in the 2-RDM given in (28) satisfying the symmetry and antisymmetry conditions; cf. (46) and (47). For Systems in a singlet state, for which \( {n}_{p_{\alpha }}={n}_{p_{\beta }}={n}_p \), and \( {\lambda}_{pqrs}^{\alpha \alpha }={\lambda}_{pqrs}^{\beta \beta } \), PNOF functionals, resulting from employing a reconstruction of Γ given in (28) with the ansatz (49) and (50), are of the following spin-summed form:
where the indices p, q pertain to spatial parts of the natural spinorbitals. Diagonal elements of the Δαβ and Π matrices have been fixed by imposing conservation of spin [51] which for high-spin states amounts to requiring that the expectation value of the Ŝ 2 operator computed with the assumed form of the 2-RDM is equal to M s (M s + 1), with M s = (N α − N β)/2, N α ≥ N β . The pertinent diagonal elements read [50]
The final forms of the off-diagonal elements of the Δ and Π matrices have been proposed by further imposing a sum rule given in (48) and exploiting the so-called D, G, Q-conditions that state that 2-RDM, the electron–hole density matrix G, and two-hole density matrix Q must be positive [50]. The first PNO functional, PNOF1 [43], has been proposed for singlets after setting Δαα = Δαβ, assuming dependence of the cumulant matrix on two occupation numbers with relevant indices, i.e.,
and defining symmetric functions Π pq (n p ,n q ) = Π pq (n q ,n p ). Three possible cases have been considered for pairs of indices p, q: (1) p and q pertain to strongly occupied spinorbitals of occupancies greater than 1/2, (2) p and q pertain to weakly occupied spinorbitals of occupancies smaller than 1/2, and (3) one orbital is strongly occupied while the other is weakly occupied. Each of the cases is treated with a different function Π pq with the form deduced from the structure of the 2-RDM for two-electron systems. It is worth mentioning that the PNOF1 functional has also been extended to high-spin multiplet states [51]. Despite the fact that PNOF1 has been designed to resemble an exact functional for two-electron systems in singlet state, its performance for potential energy curves is poor [40]. However, it has to be admitted that despite its simple form PNOF1 has turned out to be reliable in reproducing equilibrium bond distances, harmonic vibrational frequency, ionization potentials, and polarizabilities of small molecules [52].
A more involved form of the cumulant than that shown in (54) has been employed in the PNOF3 functional [45]. The same-spin block of the Δ matrix (49) was set to 0 and only the opposite-spin block, cf. (50), has been considered for singlet and high-spin multiplet states. Analogously to the PNOF1 functional different forms of the λ pq and Δ αβ pq functions of {n p } have been proposed depending on the values of occupation numbers of the pertinent spinorbitals p and q. The elements Δ αβ pq for the strongly-weakly occupied pair of orbitals p, q are functions not only of the corresponding occupancies n p and n q but also of the sum of occupation numbers of all weakly occupied spinorbitals. PNOF3 has been applied to computing high/low-spin energy splitting of atoms and atomization energies of molecules showing a remarkable agreement with the accurate coupled cluster accurate data [45]. PNOF3 has also correctly reproduced potential energy surfaces of challenging isomerization reactions [53]. Despite the proved usefulness of PNOF3 for systems dominated by dynamic electron correlation it fails in describing near-degenerate systems which has been illustrated by the breakdown of the functional in reproducing the energy of the Li2 molecule with the stretched bond [46]. This failure has been attributed to violation of the positivity condition of the electron–hole density matrix G corresponding to the reconstruction scheme assumed in PNOF3. This problem has been addressed in [46] and a new form of the Π pq ({n r }) function has been proposed which resulted in a PNOF4 functional. PNOF4 accurately reproduces potential energy surfaces of diatomic molecules. Unfortunately, it has been reported recently that the products of homolytic dissociated molecules may have a non-integer number of electrons [50].
The PNOF5 functional formulated for closed-shell systems [47] can be seen as a simplification to PNOF4, because both the elements Δ pq and Π pq are functions of only the occupation numbers n p and n q (and not of the whole vector n), yet the proposed ansatz for the two-electron reduced density matrix laying the foundation for PNOF5 satisfies the symmetry conditions and the sum rule (46)–(48), as well as the positivity conditions. This has been achieved by assuming that for an N-electron system (N being even) only for N natural orbitals (2N natural spinorbitals) the occupation numbers are different from zero, the rest of orbitals being unoccupied. Additionally, the set of occupied orbitals has been partitioned into N/2 pairs. Each orbital belongs to only one pair and for the p, q orbitals coupled in a pair P the pertinent occupation numbers sum up to 1, i.e.,
It should be noted that imposing the condition (55) immediately implies that the normalization condition for 1-RDM, namely
is satisfied. In (56) the first summation runs over pairs of electrons and the condition (55) has been employed. Analogously to other PNOF functionals, the diagonal elements of the Δ and Π matrices employed in PNOF5 are given by (52) and (53), whereas the off-diagonal elements for the coupled indices p and q have been proposed to take the form
The resulting spin-summed expression of the PNOF5 functional reads [47, 49]
where P and Q stand for indices of pairs of coupled orbitals. PNOF5 has outperformed all its PNOF predecessors in describing multireference systems. In particular it has been shown that it describes qualitatively correctly dissociation curves yielding accurate dissociation energies [54–56] and products of dissociation are of integer numbers of electrons [47, 56]. Dissociating of molecules with multiple bonds, e.g., N2 or CO, leads to products of a correct high-spin symmetry [56]. The ability of the PNOF5 functional to treat homolytic bond cleavage has been exploited in its application to radical formation reactions [54]. Unfortunately, good performance of PNOF5 in recovering static correlation in nearly degenerate systems is paralleled by its insufficient inclusion of the dynamic correlation [49, 57, 58]. Application of the PNOF5 functional for such challenging systems as Cr2, Mo2, and W2 dimers revealed that, although it yields energies of an accuracy between that of the CASSCF and CASPT2 methods, the lack of an important portion of dynamic correlation energy spoils the results [55]. In order to add the missing interpair dynamic correlation to PNOF5 Piris has considered a second-order multiconfiguration perturbation theory [59] and has adopted it for a wavefunction which leads to the PNOF5 energy expression [57]. The method has been named PNOF5-SC2-MCPT. Quite unexpectedly, its application to description of the helium dimer has led to a curve with multiple minima. Moreover, homolytic dissociation of diatomic molecules with the perturbation method resulted in breakdown of the dissociation curves because of singularities in the second-order energy appearing for quasi-degenerate systems. The former problem has been avoided by excluding from the perturbative expansion determinants corresponding to double excitations from spinorbitals of the same spatial parts, whereas singularities have been eliminated by removing second-order terms corresponding to quasi-degenerate orbitals [57]. Such a modified perturbation method has been called PNOF5-PT2. Application of PNOF5-SC2-MCPT and PNOF5-PT2 to the G2/97 test set of molecules has shown that, on average, the methods recover, respectively, around 80% and 70% of the correlation energy (with respect to Hartree–Fock energies) [58].
Good performance of the uncorrected PNOF5 for chemical reactions is a consequence of the observation that the functional can also be derived within the antisymmetrized product of strongly orthogonal geminals (APSG) theory [60]. APSG has not only proven to be successful in describing dissociation curves of singly-bonded molecules [61] but it is also very accurate in predicting equilibrium geometries, vibrational frequencies, and dipole moments of diatomic molecules from G2/97 test set [62, 63]. In the APSG theory a wavefunction for an N-electron system in a singlet state is given by the antisymmetrized product of geminals {ψ P (x 2P−1,x 2P )}
which are strongly orthogonal, i.e., \( {\forall}_{P\ne Q}{\displaystyle \int {\psi}_P}\left({\mathbf{x}}_1,{\mathbf{x}}_2\right){\psi}_Q\left({\mathbf{x}}_1^{\mathbf{\prime}},{\mathbf{x}}_2\right)\mathrm{d}{\mathbf{x}}_2=0 \) [64, 65]. It can be shown that if geminals are expanded in the natural orbitals {φ p (r)} corresponding to the 1-RDM obtained from the ansatz (59), then the expansion for each geminal P is diagonal, i.e.,
the coefficients {c p } are simply square roots of the corresponding occupation numbers taken with “+” or “−” sign
and the strong orthogonality of geminals implies that the sets of orbitals belonging to individual geminals are disjointed, i.e., each natural orbital belongs to only one geminal [66]. It should be noted that for a closed-shell two-electron system the APSG wavefunction is exact and identical with the Löwdin and Shull function given in (33). The expectation value of the Hamiltonian with the APSG wavefunction yields the following spin-summed electron–electron repulsion energy expression
where {f p } are phase factors of the value +1 or −1. The APSG ground state energy follows from optimization of the total energy with respect to phase factors, occupation numbers, and the orbitals. Actually, it turns out that typically each geminal is composed of one strongly occupied orbital of the occupation number greater than 1/2 and a pertinent phase factor f 1 = +1, and all other orbitals, which are weakly occupied (n p < 1/2), of the corresponding phase factors f p = −1 [61, 67]. As already mentioned in Sect. 2.1 for two-electron singlet systems (described within the APSG theory by one geminal), exceptions to this rule have been observed [36, 39], but they occur for very weakly occupied orbitals. Practically, fixing the phases in the APSG functional given in (62) according to the aforementioned rule, instead of finding them variationally, has only a small effect on the APSG energy. The APSG functional with the phase factors fixed can be seen as a density matrix functional. Comparison of the PNOF5 functional defined by (58) and (55) with (62) immediately reveals that they are identical if the dimension of the expansion space for each geminal in the APSG approach is limited to 2 and the phase factors of the two orbitals which form a given geminal are opposite, i.e., f 1 = −f 2 [60]. Because PNOF5 is equivalent to such constrained APSG approximation, it inherits its features from the latter, which explains the good performance of the PNOF5 functional for predicting dissociation energy curves of molecules [47] and the localized character of its optimal orbitals [68].
Lifting the restriction on the dimensionality of expansion spaces for the geminals in PNOF5 functional should allow one to recover a part of the correlation energy missing in this functional. This procedure has been proposed in [69] but clearly such extended PNOF5 functional (PNOF5e) is identical to the APSG functional (62) with fixed phases. For PNOF5 and PNOF5e functionals a systematic reconstruction of the 2-RDM in terms of the 1-RDM has merged with a theory based on the ansatz for the wavefunction [49]. On one hand this may seem to be a desirable result – the functionals are N-representable and bound by the exact ground state energy, but the drawback is that the functionals suffer from the same deficiencies as the APSG approximation.
An interesting idea that leads to incorporating the dynamic correlation that PNOF5 lacks has been proposed in [48]. The intrapair correlation is included in PNOF5 by proposing the elements Δ pq (57a) and Π pq (57b) corresponding to uncoupled orbitals p and q (belonging to different pairs) to be nonzero and expressing them as functions of the occupation numbers. The new functional, PNOF6, employs, similarly to PNOF5, a paired-orbitals picture. Compared to PNOF5, the PNOF6 functional underestimates the dissociation energies to a lesser degree. Unlike its predecessor, PNOF6 yields delocalized orbitals and it avoids spatial symmetry breaking of the benzene equilibrium geometry [48].
An ongoing development of natural orbital functionals, PNOF, originating from reconstruction of 2-RDM in terms of 1-RDM, has already resulted in functionals competing in accuracy with MP2 method for single-reference systems. Unlike the MP2 method, the PNOF4, PNOF5, and PNOF6 functionals are useful in describing potential energy surface also when bonds are stretched and dissociation potential energy curves are often of the quality of the much more expensive CASSCF approach.
2.3 Going Beyond Explicit Density Matrix Functionals
Approximate density matrix functionals discussed so far are explicitly expressed in terms of natural spinorbitals and natural occupation numbers. Ground state energy results from minimization of a functional with respect to orbitals and occupancies under N-representability conditions given in (3)–(5). To afford greater versatility, over the years efforts have been made to develop functionals the forms of which involve other quantities than only spectral components of 1-RDM. The quantities (typically being parameters) are found for a given γ by solving some auxiliary equations. The overall dependence of such functionals on γ is only implicit.
One of the first functionals of this kind has been proposed by Yasuda [15] who, by considering a contracted Schrödinger equation, derived a set of equations yielding, for given sets {n p } and {φ p }, values of partially contracted products of cumulant elements λ (28) and two-electron integrals {〈pq|rs〉}, i.e.,
The resulting Yasuda correlation functional, cf. Eq.(29), E c[γ] = ∑ p ε p [γ] is therefore implicitly dependent on spectral components of γ. Parameters {ε p } are found from a set of auxiliary equations. Despite the fact that the Yasuda correlation functional possesses a number of desirable features, i.e., it satisfies the exact conditions given in (30) and (31), it gives rise to dispersion interaction [70] and recovers a logarithmic divergence of the correlation energy of the homogeneous electron gas in high-density limit [71], its usefulness in practical electronic structure calculations has been undermined by showing that it does not seem to be bound from below even for two-electron systems [72].
Quite a different approach has been assumed in [41, 73–76] where explicit density matrix functionals have been derived by assuming a configuration interaction (CI) ansatz for a wavefunction and parameterizing CI coefficient. In all cases the CI wavefunctions were such that the resulting expression for the energy involved only Coulomb and exchange two-electron integrals. Because the former integrals are often denoted with the letter J and the latter with K, the functionals involving only these two types of integrals are sometimes called “JK-only” functionals. The idea of constructing functionals by parameterizing the CI ansatz is evidently directly related to the Levy constrained search functional (9) which for the CI wavefunction
where {Φ I } is a set of Slater determinants, turns into
C stands for a vector of all CI coefficients and the minimization in the functional (65) is carried out with respect to all vectors C corresponding to the assumed ansatz for a wavefunction (64) which yield a given density matrix γ. Were the expansion in (64) complete, the functional (65) would be exact, i.e., it would be equivalent to the Levy functional (9). Otherwise, for truncated CI expansion, the functional is only approximate. The strategy adopted in [41, 73–76] was to use a CI ansatz leading to a “JK-only” approximation and to replace the whole set of the CI parameters by auxiliary variational matrices, say A and B, such that the functional (65) turns into
where the two-electron integrals are computed with the natural spinorbitals {φ p }. The minimization is done with respect to the matrices A, B constrained to yield a given vector of occupation numbers n and to satisfy some conditions, for example conditions imposing size-consistency on the functional. If the conditions are such that there is a mapping from A and B to the CI coefficients C, the functional given in (66) is variational, i.e., it constitutes an upper bound to the functional (65) and the exact Levy functional (9). If, however, the matrices A, B are constructed to ensure that the underlying 2-RDM only satisfies some of the necessary N-representability conditions, the functional (66) is not necessarily variational. The main advantage of replacing functionals (65) with approximations (66) is to obtain a more efficient method than CI, because the complex objects (CI coefficients) are replaced by matrices of much smaller dimensionalities. Moreover, if the starting CI ansatz (64) is not size-consistent, the proposed reparameterization in terms of A, B could restore this property (but then variationality is lost).
In [74] Kollmar and Hess considered a CI wavefunction being a combination of a closed-shell reference Slater determinant Φ0 and determinants arising from Φ0 by doubly exciting electrons from spinorbitals of the same spatial parts to virtual orbitals also sharing spatial functions, i.e., \( {\Phi}_{i_{\alpha }{i}_{\beta}}^{a_{\alpha }{a}_{\beta }} \), where i and a stand for, respectively, occupied and unoccupied orbitals in the reference state. Such an ansatz leads to an energy expression involving only Coulomb and exchange integrals but it lacks size-consistency. To recover this property a normalization condition has been replaced by a new condition on the CI coefficients. The resulting functional of the form of (66) has been applied to the description of symmetric dissociation of water molecule which has led to a potential energy curve of a reasonable shape. At the same time, it became evident that the functional misses dynamic correlation.
In [41] the most general form of the closed-shell CI wavefunction which leads only to Coulomb and exchange integrals in the energy expression has been considered. The wavefunction can be called pair-excited CI because it includes all possible Slater determinants, each built of N/2 spatial orbitals entering a determinant with the α and β spin component, i.e.,
where Q N/2 = q 1,…,q N/2 is a string of indices, and \( \left|{\phi}_{q1}{\phi}_{\overline{q}1}\cdots {\phi}_{qN/2}{\phi}_{\overline{q}N/2}\right| \) is a Slater determinant built of N/2 elements from the set of one-electron spatial functions {ϕ p }. The coefficients \( \left\{{A}_{Q_{N/2}}\right\} \) are symmetric with respect to exchanging two indices in a string Q N/2 and they satisfy a normalization condition. The wavefunction (67) is size-consistent and it yields a diagonal 1-RDM, i.e.,
Therefore one immediately recognizes that the orbitals {ϕ p } are simply the natural orbitals, i.e., \( {\varphi}_p\left(\mathbf{r}\right)\equiv {\phi}_p\left(\mathbf{r}\right) \). As already mentioned, another property of the ansatz (67) is that the spin-summed electron interaction part of the corresponding energy reading
where
takes a simple “JK-only” form. A reparameterization of the energy expression (69) proposed in [41] consists of replacing the coefficients {A QN/2} by a new variational object: an idempotent matrix ω having occupation numbers on its diagonal and additional phase factors \( \left\{{f}_{Q_{N/2}}\right\} \) (of values 1 or −1). The parameterization preserves the variationality of the energy so the resulting functional
is a strict upper bound to the exact energy functional. A large number of possible phase factors makes minimization of the functional practically impossible. Introducing some fixed pattern for signs of those factors could destroy variationality of the functional. This has been called a “phase dilemma” in [41] and identified as a serious bottleneck in constructing density matrix functionals. A functional free of the phase factors has been obtained by Kollmar and Hess by reconstructing 2-RDM in terms of 1-RDM by imposing N-representability condition (a strategy similar to the one adopted in construction of PNOF functionals presented in Sect. 2.2 [75]). The Kollmar–Hess functional is identical to (72) if a simple approximation for phase factor products is assumed [41]. The functional is therefore not variational in general (except for two-electron systems for which the functional is exact). Numerical applications showed that it is very accurate for four-electron systems [75]. The results for water molecule undergoing symmetric dissociation are much less satisfactory. They are very close, however, to those corresponding to the closed-shell MC-SCF approach with the CI ansatz given in (67). One can therefore conclude that the phase dilemma is not such a serious limitation if a proper model is assumed for the phase factors. Another confirmation of this conclusion comes from considering the exact functional for a two-electron closed-shell system which is a special case of the functional given in (72) for N = 2. As has already been mentioned, fixing the signs of the phase factors corresponding to the weakly occupied orbitals to be opposite to the sign of the phase factor associated with the strongly occupied orbitals leads to only a small change in the energy.
In [76] it has been shown that a computationally hard MC-SCF problem can be replaced by the optimization of a simple 1-RDM functional which parallels the MC-SCF method in accuracy. However, it has also been pointed out that the ansatz (67), i.e., the best possible wavefunction leading to a “JK-only” expression for the energy (67), recovers only a small fraction of the correlation energy for systems as small as a ten-electron molecule. Any variational (or based on an N-representable 2-RDM) “JK-only” functional suffers from the same deficiency. The density matrix functionals tested in [76] developed by imposing basic necessary N-representability conditions on the underlying 2-RDM do not recover more correlation than the wavefunction-based approach, even though they are not variational. In other words, results of parallel accuracy are obtained by minimizing the CI energy given by (69)–(71) with respect to the CI coefficients and the orbitals {ϕ p } and by optimizing “JK-only” functionals proposed as approximations to (69) [76]. This poses a question as to whether the pair-excited CI ansatz (67) is a good starting point for developing functionals. This question is addressed in Sect. 6.
Apart from the implicit density matrix functionals discussed earlier which involve some auxiliary parameters, cf. (66), a promising class of functionals depending on γ and electron density ρ has been proposed by combining density-functional and density matrix functional theory [77, 78]. The method is based on the range-separation of electron–electron interaction operator, \( {\widehat{V}}_{\mathrm{ee}} \), into short- and long-range parts, \( {\widehat{V}}_{\mathrm{ee}}^{\mathrm{sr}} \) and \( {\widehat{V}}_{\mathrm{ee}}^{\mathrm{lr}} \), respectively [79, 80]. Dynamic correlation energy should mostly be described by the short-range density functional, and static correlation energy by the long-range density matrix functional. A formal definition of the exact range-separated functional is possible by exploiting Levy constrained-search construction [4] and it reads [77]
where the long-range functional is defined analogously to the full-range functional in (9), namely
ρ γ is a diagonal part of the density matrix γ and the definition of the short-range universal density functional F sr also employs Levy constrained search construction. Partitioning the long- and short-range functionals into Hartree and exchange-correlation parts results in obtaining the following srDFT-lrRDMFT energy functional
Ground state energy follows from minimizing the range-separated functional with respect to N-representable γ. A short-range PBE exchange-correlation functional [81] has been used for E srxc [ρ]. This is a short-range version of the PBE functional derived for the error function employed in range-separation of electronic interaction. The long-range density matrix functional, E lrxc , has been approximated by the long-range BB functional E lrBBxc obtained by simply replacing two-electron integrals in the full-range BB functional, cf. (20), by their long-range counterparts, namely the spin-summed expression which reads
where r 12 = |r 1 − r 2| and erf stands for the error function. Both short- (sr) and long-range (lr) functionals involve a range-separation parameter μ, the value of which has been empirically chosen to be 0.4 bohr−1. Such an obtained srPBE-lrBB functional has been applied to a few diatomic molecules and, in contrast to full-range BB or PBE functional, the range-separated density matrix functional turned out to be capable of reproducing correct dissociation energy curves [78]. Another direct advantage of range-separated functionals over full-range density matrix functionals is that the former, unlike the latter, are weakly basis set dependent which adds to their favorable computational efficiency.
2.4 Empirical Density Matrix Functionals
Approximate density matrix functionals cannot be rigorously derived. Rather, the form of the functional is proposed by taking into account properties of the exact functional. The applicability of density matrix functionals is not limited to finite systems (atoms and molecules); in principle, most of them could also be applied to solids. However, functionals such as BBC, AC3, or the recent PNOF approximations account for a sophisticated interplay between orbitals which is necessary to predict bond stretching and breaking. It is therefore not so surprising that performance of BBC1 and BBC2 functionals for a model extended system, namely the homogeneous electron gas (HEG), is quite poor. The accuracy of predicted correlation energy and the quality of momentum distribution for the HEG described with these functionals are unsatisfactory even for metallic densities. Admittedly, they still perform better than the other simple density matrix functionals defined in (20) and (23) such as BB or CHF [82, 83]. It should be noted that an exact exchange-correlation density matrix functional working for the HEG is not known even for a high-density limit, which is the reason why this system does not serve as a starting point for developing new density matrix functionals. In order to develop functionals for extended systems one could try introducing some empirical parameters into known approximate functionals and fitting them to experimental data.
Such an approach has been tried in [82, 84–86]. Adopting plane-waves as natural orbitals of the homogeneous electron gas turns a spectral representation of 1-RDM into
where k = |k|, n(k) is called momentum distribution, and V is the volume of the system (V → ∞). BBC functionals, cf. (41)–(43), developed for molecules involve in their definition partitioning natural orbitals into strongly and weakly occupied, which is based on the value of the pertaining occupation number. A straightforward generalization of the BBC functionals to extended systems would assume establishing a type of the natural orbital (a plane wave) on the basis of the k-number i.e., whether it is smaller or greater than some reference value k c [82]. The most obvious choice would be k c = k F, where k F is the Fermi wave vector. As mentioned before, this choice implemented in the BBC1 or BBC2 functionals does not lead to accurate correlation energy of HEG. Lathiotakis et al. proposed two variants of the BBC1 modifications [82]. In the first, k c was treated as a parameter, whereas the second variant assumes keeping k c = k F, multiplying the exchange-correlation terms of the BBC1 functional corresponding to two weakly occupied orbitals by a parameter s (s-functional). In both cases, values of parameters were chosen to reproduce the exact correlation energy of HEG. Unfortunately, momentum distributions resulting from such proposed functionals obtained for metallic densities, even though they show discontinuity, quantitatively still deviate strongly from the accurate references. Adaptation of the s-functional developed for the electron gas to finite systems has led to surprisingly accurate values of energy for molecules at their equilibrium geometry but it has been also revealed that the functional is not size-consistent and it fails in the description of potential energy curves [85].
Motivated by the fact that the exchange-correlation functional (18) in many density matrix functionals is approximated by an expression involving only exchange integrals multiplied by factors depending on two pertinent occupation numbers, i.e.,
Marques and Lathiotakis (ML) proposed to find the function G fully empirically by using a Padé approximant depending on a variable x = n p n q [87]. Coefficients in the Padé approximant were found by minimizing the error of the correlation energies of selected test-molecules. Computing the correlation energies of molecules in a G2 test with different methods has revealed that the empirical ML functional is on average the most accurate of all functionals tested, competing with or being superior to the MP2 method [87]. However, because the exchange-correlation part depends only on products of two occupation numbers, it inevitably lacks the structure needed to describe the breaking of a two-electron bond. The ML functional is not appropriate for describing molecules at geometries far from their equilibrium.
In the quest to develop a computationally efficient 1-RDM functional which is useful for solids, a very simple idea has been proposed and leads to remarkable results. The first and simplest approximate density matrix functional proposed is the BB functional (also known as the Müller functional) [18, 19], cf. (20). Müller has arrived at the particular form for the exchange-correlation functional given in (18) by considering a generalization of the Hartree–Fock exchange functional (17), which assumes replacing |γ(x, x′)|2 present in the HF two-particle density matrix and, consequently, in the functional (17), by a product γ 1−α(x, x′)γ α(x, x′)*. The power α was constrained to belong to the interval 〈0, 1〉, to assure convexity of the functional and integrating of the corresponding exchange-correlation hole to −1 [18]. The BB functional results from choosing α = 1/2. Sharma et al. proposed to consider an approximate exchange-correlation functional of the form [84]
that for α = 1 is just an exchange Hartree–Fock functional (17) whereas for α = 1/2 it turns into a BB form (20). It should be mentioned that a 2-RDM
giving rise (via (26)) to the exchange-correlation power functional (80) satisfies the sum rule (48) only for α = 1/2. Application of the power functional to the homogeneous electron gas revealed that momentum distribution resulting from the functional optimization not only lacks a step structure but is very different from the exact distributions in general [83, 88]. Even though the power functional does not recover the exact high-density limit of the correlation energy of the HEG [83, 89], it has been shown that with a carefully chosen value of α it is possible to obtain rather accurate values of the correlation energy for this system in the broad range of densities [86]. Moreover, the power functional performs remarkably well in predicting accurate band gaps of semiconductors and insulators [84]. The test set included materials of covalent or ionic character with band gaps ranging from 1 to 14.2 eV. It is striking that all these systems are incorrectly predicted to be metallic if described with the α = 1/2 power functional, whereas choosing α = 0.65 or α = 0.7 results in obtaining nonzero gaps deviating on average from experimental values by less than 10%. Reducing α below the value 0.65 leads to zero energy gap for some materials, so it seems the range of admissible values of α is quite narrow.
Performance of the simple power functional (80) with α ∈ (0.65, 0.7) when applied to transition metal oxides (TMO) is even more impressive. TMOs can be regarded as prototypes of strongly correlated Mott insulators, the nonzero band gap of which is a result of strong Mott–Hubbard correlations. Most approximate density functionals incorrectly predict TMO to be metallic. The power density matrix functional, however, yields finite values for band gaps of nonmagnetic TMOs, although deviations of the computed gaps from their experimental counterparts are larger than in the case of conventional insulators [84]. Sharma et al. also showed that apart from band gaps the power functional is capable of accurately predicting other properties of solids such as equilibrium lattice constants. Another successful application of the power functional includes predicting the photoelectron spectra of strongly correlated Mott insulators within a density matrix functional method proposed in [90]. Despite its very simplistic form, the power functional has been shown to be a useful tool for studying solids, including those for which most density functionals provide unreliable results.
3 Predicting Properties of Electronic Systems with Density Matrix Functionals
Reduced density matrix functionals give immediate access to total energies of systems under investigation and, because the 1-RDM is known, to expectation values of local or nonlocal one-electron operators. However, in recent years a number of methods have been formulated within RDMFT allowing one to obtain properties of systems which are not mere traces of products of 1-RDM with one-electron operators. The properties accessible within static RDMFT include second- and higher-order static response properties, photoelectron spectra, or fundamental gaps.
3.1 Response Properties
Response properties follow from RDMFT by considering a one-electron perturbation of the strength λ
where λ = 0 corresponds to the lack of perturbation [91]. Because 1-RDM is obtained variationally, the Hellman–Feynman theorem is satisfied and the first-order response properties result from taking a trace of 1-RDM with the first-order perturbation, i.e.,
where the occupancies {n p } and the natural spinorbitals {φ p } correspond to unperturbed γ. Second-order properties are given by the expression (valid for real orbitals)
where {n (1) p } and U (1) are components of the first-order response of γ, namely
They can be found by solving a set of linear coupled-perturbed equations [91]. If the perturbation is particle-number-conserving then a condition must be imposed that a sum of perturbations {n (1) p } vanishes. Applying the response equations to compute the static polarizabilities has revealed that even functionals which perform well in predicting energies of atoms and diatomic molecules, e.g., BBC3, do not provide satisfactory results for the second-order response properties [91]. The values for polarizabilities are of comparable or even worse quality than those obtained within the coupled-perturbed Hartree–Fock method [91]. Much more encouraging results have been obtained for hyperpolarizabilities of the H2 molecule using the PNOF5 functional within a finite field approach [92]. Good accuracy could have been expected though, because the PNOF5 functional, cf. (58), is equivalent to the two-electron functional (39) if the number of orbitals with nonzero occupancy is restricted to two [60]. Despite this constraint, the PNOF5 functional captures the right physics of two-electron systems.
3.2 Ionization Potentials
A number of methods for predicting vertical ionization potentials (IPs) have been proposed within RDMFT. The most straightforward approach involves performing calculations of energies for a neutral and ionized species [93–95]. Apart from the fact that such multiple calculations are time consuming, it has been pointed out in [95] that inaccuracy may arise because of different treatment of closed- and open-shell systems in RDMFT.
Another way of computing IPs is provided by the Extended Koopmans’ Theorem (EKT) which connects 1- and 2-RDM of a Coulombic system with its ionization potentials [96–98]. It has been shown in [99] that the Lagrangian matrix λ related to imposing orthonormality of the natural orbitals in optimizing a density matrix functional, reading
is equivalent to the generalized Fock matrix of the EKT equations. This implies that diagonalization of a Hermitian matrix Λ defined as
yields IPs as eigenvalues. For small molecules the BBC and GU functionals employed in the EKT formalism yield ionization energies with errors with respect to experimental references of the order of 4–6%. Similar accuracy has been obtained with the PNOF functionals [93, 100]. On average the accuracy is higher than that of the standard Koopmans’ theorem.
The EKT method is not practical for solids as it would require diagonalization of a very large matrix. Sharma et al. proposed an alternative method [90]. This consists of assigning to each natural spinorbital an orbital energy ε p obtained as a derivative of the total energy with respect to the pertinent occupation n p . The derivative is taken at n p = 1/2 with the rest of occupation numbers set equal to their ground state optimal values, i.e.,
Employing orbital energies obtained in this way for predicting densities of states of transition metal oxides has led to excellent agreement with experimental data. The orbital energies defined in (88) have also been used as approximations to ionization energies and electron affinities of molecules. Performance of density matrix functionals within such an approach is satisfactory and for IPs the errors are of the same order as those obtained from the much more theoretically grounded EKT method [95].
A central feature of one-electron approximations such as Hartree–Fock or Kohn–Sham DFT methods is existence of an effective Hamiltonian, the spectrum of which provides approximate ionization potentials. In HF this approximation is justified by Koopmans’ theorem. In the KS-DFT formulation, although only the negative of the HOMO orbital energy yields the exact first IP if the exact potential is employed, it has been shown and theoretically justified that other orbital energies of occupied orbitals also approximate well ionization potentials, on condition that an accurate potential with a correct asymptotics is employed in KS equations [101, 102]. In RDMFT the effective Hamiltonian whose eigenfunctions correspond to natural spinorbitals also exists but its spectrum is infinitely degenerate [1, 103]. Recently, however, a local reduced density matrix functional method has been proposed which, for a given functional, searches for an optimal local potential, such that eigenfunctions of the corresponding effective Hamiltonian minimize a functional (for a fixed set of the occupation numbers) [104]. Although formulation of the local variant of RDMFT is not theoretically grounded, it offers at least two advantages over the standard optimization of the density matrix functional via a nonlocal potential. The first is better computational efficiency of the optimization of the energy functional (see Sect. 4). The other advantage is that local RDMFT formulation yields approximations to IPs as eigenvalues of the effective Hamiltonian with a local potential. Namely, it has been shown that photoelectron spectra of molecular systems obtained from the local-RDMFT with the BB [19], BBC3 [27], power [84], and empirical functional of Marques and Lathiotakis [87] compare well with experiment and are superior to spectra obtained from the Hartree–Fock Koopmans’ method [105].
3.3 Fundamental Gap
Another quantity of key importance for solids accessible in RDMFT is the band gap or more generally the fundamental gap, which is defined as the difference between the ionization potential I and the electron affinity A as
Helbig et al. proved that within exact formulation of RDMFT a Lagrange multiplier μ, used to impose the normalization condition (5) on the occupation numbers in variational equations, possesses a discontinuity at integer particle numbers. This discontinuity amounts to the fundamental gap [106, 107], i.e.,
A system with a fractional number of electrons N + η should be understood as an ensemble of N- and (N + 1)-electron states mixed with the corresponding weights 1 − η and η so that the 1-RDM of the ensemble reads
where 0 ≤ η ≤ 1, and γ N and γ N+1 are one-electron reduced density matrices corresponding to N- and (N + 1)-electron states. γ N+η is normalized to N + η. Necessary and sufficient N-representability conditions for γ N+η, i.e., conditions under which there is a link between a density matrix γ N+η with a fractional number of electrons and an ensemble of N- and (N + 1)-states, have been a proved [108]. They are of the same form as N-representability conditions for an integer-particle system, namely ∑ p n p = N + η and ∀ p 0 ≤ n p ≤ 1.
To find a chemical potential (a Lagrange multiplier) μ(N + η) one just carries out minimization of the density matrix functional under standard N-representability conditions, imposing the normalization of {n p } to N + η. Applying approximate functionals to estimation of the fundamental gap of finite systems shows that μ does not possess a discontinuity. However, for functionals with self-interaction removed, e.g., the GU functional, μ plotted as a function of η displays a steep increase close to η = 0. This increase usually begins with a kink of the function μ (η) which occurs for η larger than 0 [106–108]. Its origin is related to the fact that by adding excess charge η the “HOMO” natural orbital (the orbital whose occupation number is the smallest among all strongly occupied orbitals) is filling up till its occupancy reaches 1. Increasing η further, the “LUMO” natural orbital (the orbital whose occupation number is the largest among all weakly occupied orbitals) begins increasing its occupancy which shows up on a μ(η) plot as a kink from which a steep increase of μ begins. Taking into account the origin of the step-like structure of μ for approximate functionals, it is rather surprising that a crude extrapolation of μ from large η (close to 1) to small η (close to 0) provides very reasonable estimations for the gaps [106, 107]. Formulation of the method for computing Δ within the open-shell RDMFT leads to obtaining a more pronounced step-like structure of the chemical potential μ, which makes the process of estimating Δ by extrapolating less ambiguous [107].
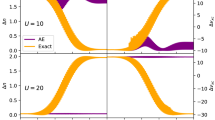
As mentioned in Sect. 2.4, satisfactory band gaps have been obtained for semiconductors, insulators, and even Mott insulators by employing the aforementioned method of finding approximate discontinuity of μ, cf. the formula (90), together with the power functional (80) [84]. Clearly, for periodic solids, the energy and the number of electrons are infinite and adding a charge η to each unit cell would result in an infinitely charged unstable system. It has therefore been proposed in [84] to find band gaps by adding excess charge η per unit cell and, at the same time, adding a constant charge background to keep the total system charge neutral. A band gap corresponds to a difference \( \tilde{\mu}\left(\eta \to {0}^{+}\right)-\tilde{\mu}\left(\eta \to {0}^{-}\right) \), where \( \tilde{\mu}=\partial {\tilde{E}}_{V+\delta v}\left(\eta \right)/\partial \eta \) and \( {\tilde{E}}_{V+\delta v} \) is the energy per volume unit computed self-consistently at the external potential V with the charge neutralizing potential δv added. A chemical potential obtained with the power functional lacks the discontinuity but its curvature changes the sign around η = 0 for nonmetallic systems. It allows the estimation of band gaps by constructing two tangent lines [84].
4 Optimization of Density Matrix Functionals
As mentioned in the introduction, the RDMFT approximations, apart from being accurate, are expected to be competitive with one-electron methods in terms of computational efficiency. RDMFT is based on the variational principle given in (11) according to which a ground state energy of a given system can be obtained by minimizing the energy functional on the set of N-representable density matrices. Thus, the optimization is of the constrained-type, because it must take into account N-representability conditions provided in (3)–(5). Because the conditions are given in the forms of equalities and inequalities involving eigenvalues and eigenvectors of 1-RDM, it implies that imposing N-representability conditions would require carrying out diagonalization of γ even for explicit functionals of γ.
An efficient algorithm offering optimization of the functional directly with respect to the whole density matrix or its square root has been proposed [109]. The N-representability of γ is imposed in each iteration step by projecting γ resulting from unconstrained directional optimization onto the space of N-representable 1-RDMs. An advantage of the proposed projected gradient algorithm is that, because the gradient is taken with respect to the elements of γ, changes in natural orbitals are coupled with variations of the occupancies which should lead to faster convergence. The proposed projection algorithm has been shown to work efficiently for Hartree–Fock (15) or BB (20) functionals. For other functionals, which are given in terms of orbitals and occupation numbers and are not proper functionals of γ (e.g., GU or BBC functionals), it is still possible to compute the gradient with respect to γ but the projected gradient algorithm converges disappointingly slowly [109].
The most robust and universal optimization approach consists of minimizing a functional with respect to the natural orbitals and the natural occupation numbers successively in separate steps. Natural orbitals are typically parameterized using, for a given orthonormal basis set {χ a }, the exponential function of a skew-symmetric matrix X, i.e.,
which assures orthonormality of the orbitals φ, cf. (3), [26, 27]. To satisfy the N-representability condition given in (4) the natural occupation numbers may be parameterized by cosine functions, namely ∀ p n p = cos2(x p ) where parameters {x p } are unconstrained. The normalization condition (5) is taken into account by means of a Lagrange multiplier. A bottleneck of a two-step procedure is optimization of the orbitals. It takes many iterations to meet tight convergence criteria, because energy is almost completely insensitive to variations of very weakly occupied orbitals.
Because of unsatisfactory efficiency of the gradient orbital optimization algorithms, efforts have been made to turn the optimization problem for orbitals into an eigenproblem for an effective Hamiltonian [1, 103, 110–113]. For a given functional and a fixed set of the natural occupation numbers, a one-electron Hamiltonian can be constructed in a self-consistent way such that its eigenfunctions minimize the functional (for fixed occupancies) [103, 110, 112]. The problem is that the self-consistent procedure of calculating orbitals from diagonalization of the effective Hamiltonian is highly divergent [103]. Moreover, the spectrum of this Hamiltonian is infinitely degenerate if it is constructed from optimal natural orbitals and occupation numbers. However, by proper combination of level-shifting and scaling off-diagonal elements of the Hamiltonian matrix, optimal orbitals can be obtained from iterative diagonalization [103, 111]. Such an approach does not, however, seem to surpass gradient methods significantly in terms of speed of convergence.
It has recently been proposed to employ an optimal effective potential (OEP) method formulated originally for optimization of orbital-dependent density functionals [114, 115] in RDMFT [104]. For a given density matrix functional, a local potential is sought such that its orbitals minimize the functional for fixed occupation numbers. The main difference from the above-mentioned scheme which employs a nonlocal Hamiltonian is that in local-RDMFT the potential is constrained to be local and to possess proper asymptotic behavior. Replacing a nonlocal potential with a local one and employing the OEP approach formulated originally for DFT (cf. [116]) leads to an efficient optimization method which enlarges scopes of applicability of the density matrix functionals to larger molecules and provides good estimations for the ionization potentials [105]. These advantages notwithstanding, it should also be noted that there is no theoretical justification for local-RDMFT. Moreover, by definition, the method does not provide a solution to the original variational problem given in (11) and for a given functional the optimal energy resulting from the local method is higher (although not much) than that obtained by solving the “nonlocal” RDMFT optimization problem [104].
5 Time-Dependent RDMFT
The extension of ground state RDMFT to the time domain was recently considered [117–121]. The main motivation to develop time-dependent RDMFT (TD-RDMFT) is the poor performance of time-dependent DFT (TDDFT) in the adiabatic approximation in combination with the approximate ground state density functionals. The best known failure is the inability of approximate TDDFT to capture charge transfer excitations [122, 123], though this deficiency has been remedied with some success using range-separated hybrid functionals [123, 124] and by an explicit reconstruction of the spatial divergence in the kernel [125, 126]. Other failures of adiabatic TDDFT are bond-breaking excitations which are predicted to be too low in energy upon dissociation (they can even go to zero) [127, 128] and a lack of double excitations [128–130]. All these failures are connected to the inability of approximate adiabatic density functionals to deal with static correlation effects. Because approximate 1-RDM functionals have been quite successful in dealing with static correlation effects on the ground state level, we also expect an improvement for the calculation of excitations when using the full 1-RDM in our formalism instead of only the density. It turns out, however, that the formulation of a satisfactory adiabatic approximation in TD-RDMFT is not as straightforward as in TDDFT. Most of the research has therefore been done on formulating an adequate adiabatic approximation, so the formulation of an adiabatic approximation forms the major content of this TD-RDMFT section.
5.1 Equation of Motion of the 1-RDM
The time-dependent 1-RDM is obtained by using the time-dependent wavefunction in the definition of the 1-RDM (1)
The equation of motion for the 1-RDM is readily obtained from the time-dependent Schrödinger equation
where ∂ t denotes a time derivative and the time-dependent 2-RDM is defined as
So we find that we need the 2-RDM to determine the evolution of the 1-RDM. It turns out that the evolution of the 2-RDM is coupled to the 3-RDM and so on, till we hit the full N-RDM. This chain of p-RDMs coupled to each other is known as the Bogoliubov–Born–Green–Kirkwood–Yvon (BBGKY) hierarchy [131–137]. To be of any practical use, the BBGKY hierarchy needs to be truncated at some level. In TD-RDMFT the hierarchy is truncated already at the level of the 1-RDM and it is assumed that the time-dependent 2-RDM is a functional of the 1-RDM, Γ[γ]. For Hamiltonians with only local potentials, we know from the Runge–Gross theorem [138] and its extension [139, 140] that this is indeed true, because all observables are already functionals of the density, so they are also functionals of the 1-RDM. The use of density for the formal foundations of TD-RDMFT is not satisfactory, however, because we would have to limit ourselves to local-potential representable 1-RDMs. The formulation of a solid foundation for TD-RDMFT which allows for non-local potentials is still an open challenge.
The time-dependent 1-RDM can be diagonalized at each time t, allowing one to consider the time-dependent natural spinorbitals, φ p (x t), and time-dependent occupation numbers, n p (t). The equation of motion for the 1-RDM (94) can be transformed to the time-dependent natural spinorbital basis, which gives the equations of motion for the natural spinorbitals and occupation numbers separately [118, 119]
where the dot indicates a time-derivative and we introduced a short-hand notation for the partial contraction of the 2-RDM with the two-electron integrals
It should be noted that the two-electron integrals are also time-dependent here, because they are evaluated with the time-dependent natural spinorbitals.
5.2 Time-Dependent Response Equations
The time-dependent response equations can be derived from the equation of motion of the 1-RDM (96) by considering a small time-dependent perturbation to a stationary system, with the stationary 1-RDM γ 0. The first-order perturbation in the 1-RDM is directly related to perturbation in the natural spinorbitals and occupation numbers as [compare with (85)]
where the indices refer to the natural spinorbital basis at t = 0 and δU pq (t) = 〈φ p |δφ q (t)〉. Collecting the perturbations in all the quantities up to first order, we obtain the first-order time-dependent response equation for the 1-RDM
The response matrix K[γ 0](τ) is the coupling matrix defined as [117, 119, 121, 141, 142]
and plays the same role as the Hartree-exchange-correlation kernel, f Hxc (r, r′, t − t′), in TDDFT [138, 143]. To obtain the frequency-dependent response equations, we simply need to take the Fourier transform of the time-dependent response equations. Because the time-integral over the coupling matrix K(t − t′) and the perturbation in the 1-RDM has the form of a convolution, the Fourier transform turns this integral into a simple product. If we further assume that the natural spinorbitals of the unperturbed 1-RDM can be chosen to be real (no magnetic fields), the frequency-dependent response equations can be cast into a particular simple matrix form
where N pq,rs = (n q − n p )δ pr δ qs and 1 M denotes an M × M unit matrix. The sub-matrices \( \delta {\gamma}^R\left(\omega \right)=\mathrm{\mathcal{F}}\left[Re\gamma \right]\left(\omega \right) \) and \( \delta {\mathbf{U}}^R\left(\omega \right)=\mathrm{\mathcal{F}}\left[Im\mathbf{U}\right]\left(\omega \right) \) denote the Fourier transforms of the real and imaginary parts of the unique off-diagonal parts of δγ(t) and δ U(t), respectively, and likewise, \( \delta {\mathbf{v}}^R\left(\omega \right)=\mathrm{\mathcal{F}}\left[Re\mathbf{v}\right]\left(\omega \right) \) denotes the Fourier transform of the real part of the unique off-diagonal parts of the perturbing potential δ v(t). The matrix on the left is therefore an (M, M, m) × (M, M, m) matrix, where m denotes the number of basis functions and M = m(m − 1)/2 the number of unique off-diagonal elements. The submatrix A + has labels MM and mM to indicate which parts of this matrix need to be used. The response matrices A(ω) and C(ω) combine the one-body and two-body effects to the response of the 1-RDM and are defined as
Positive and negative combinations of the response matrix A(ω) enter the frequency-dependent RDMFT response equations (101) as
5.3 Standard Adiabatic Approximation
To turn the frequency-dependent RDMFT linear response equations (101) into a practical scheme, we need to be able to evaluate the coupling matrix K in some manner. In the standard adiabatic approximation (the one also used in TDDFT), one assumes that the history dependence for slow processes is not very important, so a good approximation would be
If the initial state of the system was the ground state, a ground state functional would probably provide a reasonable approximation and the full standard adiabatic approximation becomes
An additional advantage of the adiabatic approximation for the frequency-dependent response RDMFT equations (101) is that all the response matrices A ± and C become frequency independent, which greatly simplifies the calculation of response properties (excitation energies), because we only need to solve a linear system of equations (eigenvalue equation), instead of a complicated set of coupled nonlinear equations.
The standard adiabatic approximation, however, implies that the natural occupation numbers do not change in time. This is a particularly disappointing result, because the time-evolution of the natural occupation numbers is expected to be important to handle strongly correlated systems such as stretched chemical bonds. For “JK-only” approximate functionals the stationarity of the occupation numbers is easily demonstrated [118, 120, 121]. The “JK-only” 2-RDM is of the general form
Using this approximate 2-RDM in the definition for W(t) (97), and inserting the result into the equation of motion of the natural occupation numbers (96b), we find that they are time-independent, \( \mathrm{i}{\dot{n}}_p(t)=0 \).
More work is needed to demonstrate that the use of a ground state functional for the 2-RDM always leads to stationary occupation numbers in the standard adiabatic approximation [117, 144, 145]. First we note that, because the natural orbitals are the eigenfunctions of the self-adjoint kernel, γ(x,x′;t), their phases are undetermined by the 1-RDM. Therefore, a 1-RDM functional formulated in terms of the natural orbitals and occupation numbers is not allowed to depend on the phase of the natural orbitals. Making the phase of the natural orbital explicit \( {\varphi}_p\left(\mathbf{x}t\right)={\mathrm{e}}^{\mathrm{i}{\alpha}_p(t)}{\phi}_p\left(\mathbf{x}t\right) \), we have the following condition on the derivative of any 1-RDM functional, F
To connect these derivatives with the contractions W(t) (97) in the adiabatic approximation, we express the exact ground state functional as [99]
where the set of variables {ξ i } indicates the additional degrees of freedom over which we can vary the 2-RDM, keeping the 2-RDM ensemble N-representable and such that it yields the prescribed 1-RDM (48). This expression assumes that only the occupation numbers are part of the N-representability conditions for the 2-RDM and not the natural orbitals. This is reasonable, because N-representability should not depend on the particular orthonormal basis we are working in. An advantage of expressing the exact interaction-energy function in this manner is that the functional W is even defined for non-orthogonal natural spinorbitals. Although the value of the functional W does not make any physical sense for non-orthonormal orbitals, it allows us to define derivatives with respect to ϕ p (x) and ϕ * q (x) separately in an unambiguous manner and impose the orthonormality conditions afterwards with the help of Lagrange multipliers or in other ways, e.g., (92).
The optimal 2-RDM parameters which attain the minimum are functionals of the natural orbitals and occupation numbers, and we write these optimal value for the parameters as \( {\overline{\xi}}_i\left[\left\{{\varphi}_p\right\},\left\{{\varphi}_p^{\ast}\right\},\left\{{n}_p\right\}\right] \). Using \( \left\{{\overline{\xi}}_i\right\} \) the exact interaction-energy functional can also be written as
where we suppressed the explicit dependence of the optimal 2-RDM parameters on the natural spinorbitals and occupation numbers. Assuming that the gradient of Γ[{ξ i }, {n p }] with respect to the parameters ξ i exists, we can work out the functional derivative of W with respect to the natural orbitals as
Because we minimize over the parameters ξ i in the functional W, the derivatives with respect to ξ i vanish at the minimum \( \left\{{\overline{\xi}}_i\right\} \), so the first term on the right-hand side does not give any contribution. Projecting the functional derivative against natural spinorbitals, we have
Using this result together with the phase invariance condition (107) in the equation of motion for the occupation numbers (96b) in the standard adiabatic approximation, we find the claimed result
A shorter, though more handwaving argument has been given in [146].
Because the occupation numbers are not perturbed in the standard adiabatic approximation, they drop out of the response equations and the standard adiabatic response equations reduce to
Because no δ n(ω) term is present, we find that even in the static limit ω → 0 the occupation numbers are not perturbed, in contrast to the time-independent response equations presented in Sect. 3.1 [120, 121, 142]. This discrepancy has been demonstrated to be sizable by calculating the polarizability of HeH+ [117, 120, 144, 145]. The Löwdin–Shull functional has been exclusively used for these calculations. There are two possible variants of this functional: one with the exchange integrals (39) and one where we restore the original integrals 〈pp|qq〉 of the singlet two-electron system (36) and replace products c p c q with G LS pq given in (40). For real natural spinorbitals there is no difference, but in the time-dependent case the natural orbitals are complex and hence the two different integrals give rise to different coupling matrices. The advantage of using exchange integrals is that the functional is phase invariant, which is a requirement for a proper 1-RDM functional. Therefore, this variant is called the density matrix LS (DMLS). The variant with the original 〈pp|qq〉 integrals is not phase invariant, so not a proper 1-RDM functional. Because of its phase dependence it is called the phase including LS (PILS). Though the PILS is not a proper 1-RDM functional, its use is appealing, because the breaking of phase invariance implies that the natural occupation numbers do change.
One would expect that the DMLS functional should give superior results. This is indeed the case for the polarizability of HeH+ if only a limited number of transitions between the natural orbitals are taken into account [117, 144, 147], typically only the transitions from the two highest occupied NOs to all the others. If all transitions between the natural orbitals are taken into account, the DMLS functional has spurious divergences in the polarizability at low frequencies [117, 145, 147], severely deteriorating the DMLS result. Though the polarizability from the PILS functional does not follow the exact polarizability as closely as the DMLS, it has the main advantage that no spurious divergences emerge, even when all natural orbital transitions are taken into account in the response calculation [117, 121, 147].
Another disadvantage of the standard adiabatic approximation is that we effectively lose excitation energies. Because the original frequency-dependent response matrix has M + M + m = m 2 entries, the standard adiabatic approximation yields m 2 excitation energies, because the response matrices A and C are frequency independent. However, we only obtain 2M = m(m − 1) sensible excitation energies and m roots ω = 0, which are physically meaningless, so, effectively, these m excitation energies are lost in the standard adiabatic approximation [142].
Test calculations on the excitation spectrum of the hydrogen molecule as a function of the bond length have been carried out to test the performance of both LS functionals. Because divergences in the polarizability correspond to excitations, the spurious divergences of the DMLS functional already indicate that the performance of the DMLS functional for the calculation of excitation energies is not very good. Indeed, the test calculations on H2 have shown that the DMLS functional predicts many spurious low lying excitations which completely clutter the excitation spectrum when all natural orbital transitions are taken into account [117, 145, 148]. Reducing the number of transitions to only transitions from the two heaviest occupied natural orbitals is very effective in cleaning up the DMLS excitation spectrum [117]. Such an approach would not be desirable in practice, because it is orthogonal to the idea that expanding a basis brings one closer to the desired result.
Because the PILS functional is dependent on the phase of the natural orbitals, the occupation numbers are not necessarily stationary any more in the standard adiabatic approximation. However, it can be demonstrated that there are still only 2M = m(m − 1) non-trivial roots of the response equations (113) and m zero excitations [117]. Nevertheless, the PILS functional gives a huge improvement over the DMLS functional for excitation energies. Most notably, no spurious low lying excitations appear when we exhaust the response basis by including more natural orbital transitions. Furthermore, one can show that the \( {}^1{\varSigma}_u^{+}, \) 1Π g and 1Π u excitations become equal to the full CI result when all natural orbital transitions are taken into account [117, 141, 142]. This is caused by the fact that these excitations do not need any perturbation in the natural occupation numbers to be described exactly, which is related to symmetry. This also holds for excitations in other irreducible representations (irreps) that do not couple to the completely symmetric irreducible part of the response matrix, such as the xy component of the Δ g excitations. The x 2 − y 2 component does couple to the occupation numbers, however, so the Δ g excitations of the H2 molecule is symmetry broken when using the PILS functional: the xy components are equal to the full CI result and the x 2 − y 2 components are not [117]. Symmetry breaking does not occur for the DMLS functional, because the occupation numbers are never involved in the standard adiabatic response.
5.4 Alternative Adiabatic Approximation
Because the standard adiabatic approximation used in TD-RDMFT has the undesirable features of stationary occupation numbers and a mismatch with the static response equations (Sect. 3.1) in the ω → 0 limit, an alternative adiabatic approximation has been proposed. The idea is to replace the dynamic equation for the occupation numbers (96b) by its static counterpart and to make the perturbed quantities frequency-dependent, which leads to the following equation
where we use
Though the occupation numbers are not determined by an equation of motion, but follow instantaneously from δγ R(ω) and the diagonal elements of the potential δ v D(ω), there is at least a response of the occupation numbers. The fact that this alternative adiabatic approximation is an instantaneous relaxation of the natural occupation numbers at each time t has been stressed in [149] where the more descriptive name “instantaneous occupation number relaxation” was introduced. The frequency-dependent response equations in this alternative adiabatic approximation become
The correction for the ω → 0 limit to the standard adiabatic approximation proves to be quite effective and improves the description of the polarizability for small frequencies [117, 120, 121]. Additionally, because the frequency-dependent response equations now reduce correctly to the static response equations in the ω → 0 limit, both the DMLS and PILS functionals coincide at ω = 0. The general trend from the standard adiabatic approximation remains: the DMLS is closer to the exact polarizability, though has some spurious divergences which are absent in the PILS calculations [117].
Because ω is only present in the upper two M × M blocks, the determinant of the response matrix is only a 2M = m(m − 1) order polynomial in ω. We therefore find that the alternative adiabatic approximation does not restore the lost roots in the standard adiabatic approximation. Calculations on the H2 and HeH+ have demonstrated that the excitation spectrum does not change much compared to the standard adiabatic approximation for both the DMLS and PILS functionals [117]. The lowest excitation energies decrease somewhat when correcting the incorrect ω → 0 limit in the adiabatic approximation and it depends on the particular system whether this is an improvement. For H2 the results are slightly worse in the alternative adiabatic approximation, whereas for HeH+ they are slightly better [117, 142].
Although the alternative adiabatic approximation is successful in correcting the ω → 0 limit of the standard adiabatic approximation, this adiabatic approximation is still not very satisfactory, because the occupation numbers are still not truly dynamic variables and we still lose m excitations. These m excitations correspond to excitations which require a significant response of the occupation numbers. Because the response of the occupation numbers corresponds to the response of the diagonal of the 1-RDM (98), so they are referred to as the diagonal double excitations. Other double excitations related to perturbations in the off-diagonal parts of the 1-RDM are well accounted for, as the excitation energies in the \( {}^1{\varSigma}_u^{+} \) and 1Π u are perfectly accounted for [117, 142]. It turns out that these diagonal double excitations are important for the correct description of the lowest \( {}^1{\varSigma}_g^{+} \) excitation energy in stretched H2 [141, 142], so including the diagonal double excitations is important.
5.5 Phase Including Natural Orbitals
It is unlikely that the missing m diagonal double excitations can be restored with any decent adiabatic approximation to the TD-RDMFT equations. The problem is that the excitation energies should come out of the response equations in pairs +ω and −ω. This pairing of the frequencies is dictated by an important symmetry of the response function \( \chi \left(\omega \right)=\chi *\left(-\omega \right) \), which follows directly from the Lehmann [150] (sum-over-states) representation. We therefore need to increase the number of roots by m in some manner, because m is not necessarily even. Increasing the number of roots to 2(M + m) results in an even number of roots, which in turn ensures that all excitations are present in both the positive and negative parts of the spectrum.
This partially explains why we had m zero excitations in the standard adiabatic approximation, because ω = 0 is the only number which is its own negative, so it does not destroy the \( \chi \left(\omega \right)=\chi *\left(-\omega \right) \) symmetry even if an odd number of these roots is present. This does not explain why we could not have ⌊m/2⌋ excitation energies occurring both at +ω and −ω in an adiabatic approximation. To explain this, we observe that for a proper quantum evolution a quantity needs to be able to have a complex phase. All the off-diagonal elements of the 1-RDM are able to obtain a complex phase-factor, but because the diagonal is necessarily real, the occupation numbers do not have a quantum phase [117]. This lack of a corresponding quantum phase for the natural occupation numbers is not limited to the 1-RDM, but exists for the diagonal of any p-RDM if the BBGKY hierarchy is truncated at the pth order [151].
The way to solve all these problems together is to include an additional set of m complex phase factors which can act as the conjugate variables for the natural occupation numbers to facilitate a true quantum evolution. It is obvious that the ideal candidate would be the phase factors of the natural orbitals, which is corroborated by the reconstruction of the exact frequency-dependent coupling matrices of the K(ω) for singlet two-electron systems [117, 142]. To distinguish these special natural orbitals with a specific phase from those defined as eigenfunctions of the 1-RDM, we call them phase-including natural orbitals (PINOs) and give them their own symbols,  . Using PINOs, the functionals are also allowed to depend explicitly on the phase of the orbitals, so the PILS functional becomes a legal functional.
. Using PINOs, the functionals are also allowed to depend explicitly on the phase of the orbitals, so the PILS functional becomes a legal functional.
To derive equations of motion for the PINOs and their occupation numbers, we start from the following quantum mechanical action [152]

where we assume that the action can be considered as a functional of the PINOs and occupation numbers. The equations of motion for the PINOs and their occupation numbers follow by making the action stationary with respect to all variations. However, we have to keep in mind that the action is now only a functional of the PINOs and occupation numbers and not of the full many-body wavefunction. Therefore, we cannot set the variation at the end-point t = T to zero and need to take this term into account explicitly [153], so the variational principle becomes
Neglect of the variations in the boundary term at t = T leads to violation of causality as was shown by Vignale in [153], where he showed that explicit treatment of the boundary term solves the causality paradox which has haunted TDDFT for so many years [154].
To obtain more practical and explicit equations, we follow the same approach as in TDDFT [138] and partition the action of the fully interaction system into a non-interacting part, A 0 and a remainder A Hxc

Because the occupation numbers of non-interacting pure-states are stationary by construction, we need to use the action for an ensemble for the non-interacting system to allow for occupation numbers that vary in time

where 0 ≤ d P (t) ≤ 1 are time-dependent weights, \( {\varSigma}_P{d}_P(t)=1 \), and Ĥ0(t) is the one-body part of the fully interacting Hamiltonian, Ĥ(t), so corresponding to a noninteracting system. The states Φ P (t) are time-dependent Slater determinants constructed out of the PINOs. Because the states Φ P (t) are constructed out of PINOs, the expectation values can be worked out as

where p ∊ P means that the sum runs over all PINOs present in the determinant Φ
P
. Because the 1-RDM of the ensemble should have the prescribed occupation numbers, all the weights of the states which contain a particular  need to sum to the corresponding occupation number, n
p
(t). The non-interacting action therefore simplifies even further to
need to sum to the corresponding occupation number, n
p
(t). The non-interacting action therefore simplifies even further to

and the variational principle becomes

Considering variations in δA
0 separately, we find the expected result that the PINOs are solutions of one-electron Schrödinger equations  and that the occupation numbers (weights) are time-independent. We are not interested in the solutions of the non-interacting system, however, but we want the solutions of the interacting system. Therefore, we should add a “bath” term which takes into account that the electrons do not behave independently but move in the “bath” of other electrons. Hence, we subtract the following term
and that the occupation numbers (weights) are time-independent. We are not interested in the solutions of the non-interacting system, however, but we want the solutions of the interacting system. Therefore, we should add a “bath” term which takes into account that the electrons do not behave independently but move in the “bath” of other electrons. Hence, we subtract the following term

from the left-hand side, to make the variational principle equal to the interacting one (118)

Enforcing the orthonormality of the PINOs with the standard Lagrange multiplier technique, we can work out the variations in the action produced by perturbations in the PINOs [117, 145], which recovers the equation of motion for the 1-RDM in the natural orbital basis (96)

where the effects of the electron–electron interaction are now expressed as variations \( \delta \mathcal{W} \) produced by perturbations in the PINOs

An equation of motion for the phase factors of the PINOs is obtained by considering variations produced by perturbations in the occupation numbers, which give [117, 144, 145]

One can combine the equation of motion for the PINO phase factors with the off-diagonal terms of the equation of motion for the 1-RDM (126) to write a Schrödinger equation for the PINOs with an effective potential,  , [117, 144, 145]
, [117, 144, 145]

where is an effective potential which takes the two-body effects into account and is defined via its matrix elements which can be read off from (126) and (128)

It is interesting to consider the effective time-dependent Schrödinger equation for the PINOs (129) in the case of a stationary (ground) state. In that case, the time-dependence of the PINOs factors out as a simple exponential,  , and the exponential factors, ε
p
, are related to the time-independent Schrödinger for the PINOs
, and the exponential factors, ε
p
, are related to the time-independent Schrödinger for the PINOs

The degeneracy of the natural spinorbitals [103] mentioned in Sect. 4 can therefore also be regarded as the complete in-phase time evolution of the PINOs. This makes complete sense, especially for the two-electron system, because the phase factors of the PINOs can be used to reconstruct completely the two-electron wavefunction as [117, 155]

so the PINOs are coupled in pairs in the two-electron wavefunction. This expression is valid for an arbitrary spin state. In the case of a singlet state, the spin-up and spin-down components of the same spatial part form the PINO pairs and, in the case of triplet states, two PINO which are spatially different are coupled together [117]. It is clear from this expression that for all n p ≠ 0, all the PINOs need to have the same time-dependent phase factor in order for the full two-electron wavefunction to be a stationary state, \( \Psi \left({\mathbf{x}}_1,{\mathbf{x}}_2;t\right)={\mathrm{e}}^{-\mathrm{i}Et}\Psi \left({\mathbf{x}}_1,{\mathbf{x}}_2\right) \).
The equations of motion can be used again to formulate time-dependent response equations. Because the zeroth-order time-dependent PINOs already have a (time-dependent) phase factor, we expand the perturbation in the PINO in the order of the perturbation as

The first order of the perturbation in the PINOs, is expanded in the time-independent PINO basis as

The advantage of expressing the first-order perturbation in this manner is that the connection between and δ γ(t) used in the TD-RDMFT response equations at (98) is still valid. Following the same procedure as before, collecting all perturbations up to first order and taking the Fourier transform, the frequency-dependent PINO response equations in the standard adiabatic approximation, \( \mathcal{W}\approx W \) can be cast in the following form [117, 144, 145, 156]
These PINO response equations in the adiabatic approximation have all the desired properties:
-
The ω → 0 exactly coincides with the linear response equations of static RDMFT (see Sect. 3.1)
-
The diagonal double excitations are properly accounted for without destroying the important symmetry of the response function, \( \chi \left(\omega \right)=\chi *\left(-\omega \right) \)
-
The PILS functional is a proper PINO functional, so the exact PINO functional is known for the two-electron system
The dimensionality of the response equations can be reduced by half by eliminating the imaginary components from the response equations, giving
which immediately demonstrates that indeed all the roots occur both at +ω and −ω. The dimensionality of the TD-PINO response equations (m(m + 1)/2) is significantly larger than in TDDFT, where only the transitions between the occupied and unoccupied KS orbitals need to be taken into account (so the dimension would be only m − 1 for two electrons). Though the results from the adiabatic TD-PINO equations are far superior to those from adiabatic TDDFT, the computational cost is equivalent to a full CI calculation. However, one would expect that the transitions between all the low occupied PINOs are not important for the description of low lying excited states. Test calculations have been performed where only transitions from the k highest occupied PINOs to all other PINOs are taken into account. No reduction was made in δ n(ω), because its full treatment turned out to be important for particle number conservation.
Indeed, calculations with low values of k demonstrated that the polarizabilities [147], excitations [156], and oscillator strengths [157] are in excellent agreement with the exact results. Taking transitions from only the highest occupied PINO into account (k = 1) gives reasonable results for the low lying excitations of the hydrogen molecule at its equilibrium. To take properly into account the static correlation effects on the excitation spectrum, one also needs transition from the 1σ u PINO, because that PINO also obtains a significant occupation when the bond is stretched. The truncation to k = 2 already gives results very close to the exact ones along the complete bond-breaking coordinate. Going to k = 3 only provides a small additional improvement over k = 2.
The same idea has also been tested in the time-domain [155, 158]. The same effect as in the frequency-domain has been observed: only a small number of the highest occupied PINOs need explicitly to be taken into account to give a reliable description of the physical processes. This is particularly interesting for the calculation of the double ionization yield of He in strong laser fields, which needs an accurate description of non-sequential double ionization, a highly correlated process [159, 160]. An accurate account of the non-sequential double ionization process has only been given in one dimension by solving the full many-body Schrödinger equation for a one-dimensional He model [161]. A full three-dimensional treatment is still out of reach, because the grid (number of basis functions) needs to be very large to describe the electrons moving very far away from the nucleus and coming back. In a one-dimensional pilot study it has been demonstrated that only ten PINOs are sufficient to give a quantitative prediction of the double ionization yield [162], so an accurate three-dimensional calculation should now come within reach.
The main challenge is to make the PINO approach applicable to systems with more than two electrons. For the two-electron system it is clear how to define the PINO phase factors which gives a very simple expression for the two-body effects, W, and is even exact. For systems with more electrons, it is not so clear what a suitable and convenient definition for the PINO phase would be and which preferably reduces to the exact functional for two electrons. For multi-electron systems which only have one electron pair constituting a chemical bond (Li2 and LiH for example), one can try to use a Hartree–Fock (HF) functional for the core electrons and the PILS functional for the “HONO” which is the highest strongly occupied natural orbital and some encouraging results have already been obtained for diatomic molecules with a single chemical bond [163].
A different route is also explored by combining features from the PINO response equations to the extended RPA equations [164, 165] obtained from Rowe’s equation of motion framework [166]. The advantage is that the response matrices are now formulated as partial contractions of the 1-RDM and 2-RDM instead of functional derivatives with respect to PINOs and occupation numbers. This makes it easier to use other sources for approximate 2-RDMs such as the APSG wavefunction or other correlated methods. However, the APSG wavefunction can also be used to construct a PINO functional (62). The adiabatic PINO response equations with the APSG functional are actually identical to those obtained by applying time-dependent response theory to the APSG wavefunction directly [165]. Calculations on small molecular systems have demonstrated that the lowest excitation energies for the APSG functional (62) are in very good agreement with more sophisticated approaches. Higher excitation energies seem to be less reliable. Experiments using a range-separated version of the APSG functional indicate a shortcoming of the APSG functional rather than an inherent limitation of the adiabatic TD-PINO linear response equations [165]. However, more evidence needs to be gathered before we can make any conclusive statement.
6 Summary and Outlook
Reduced density matrix functional theory is a promising approach to the problem of electron correlation based on the existence of a functional of the one-electron reduced density matrix (1-RDM). One-electron components of the total energy, i.e. the kinetic part and the external potential interaction, are explicitly given in terms of 1-RDM. The electron–electron interaction functional, the two-electron part of the energy, is well defined, cf. (10), but its practical exact realization remains unknown. A formalism that would lead to systematically more accurate and efficient approximations to E ee[γ] is not available. By “efficient” we mean approximations that would avoid searching for minimizing wavefunctions or ensembles proposed in constructions given in (9) or (10), and would be competing in computational efficiency with one-electron methods. Over the years different approaches to construct approximate functionals have been explored, some of them leading to successful functionals. The first generation of functionals such as BB (20), GU (22), or CHF (23) has turned out to be insufficiently accurate for molecules and extended systems. Their failure in predicting potential energy curves of diatomic molecules has led to realizing the importance of incorporating orbital structure of the exact two-electron functional into approximate N-electron functionals. A series of BBC (41)–(43) functionals and the recent ELS (44) functional have emerged as a result of a careful analysis of the orbital structure of the energy expression obtained from a size-consistent CI ansatz. The orbital structure of the most accurate BBC functional – BBC3 – leads to accurate potential energy curves of simple molecules. Because of numerical problems with selecting bonding and antibonding orbitals, assumed in a definition of BBC3 [see (43)], an “automated” version has been proposed – the AC3 functional [40]. The orbital structures of the BBC3, AC3, and ELS functionals account for that of the exact two-electron functional necessary to provide a correct description of electron-pair dissociation.
Almost all approximate electron–electron interaction functionals proposed so far are the so-called “JK-only” functionals, i.e., they include only two-electron integrals of the Coulomb and exchange type. In [76] Kollmar addressed the question of accuracy of the most general “JK-only” variational energy expression. Based on his findings, one is driven to a conclusion of fundamental importance for functional development. Namely, the limits of accuracy of the variational “JK-only” functionals are set by a pair-excited CI ansatz (67) that leads to the best “JK-only” energy expression [41]. This ansatz is known to be insufficiently accurate for chemical problems. It has been shown in [76] that variational (bounded from below by an exact ground state energy) “JK-only” functionals unavoidably miss a significant portion of the dynamic electron correlation. Therefore, successful variational functionals should include other than Coulomb and exchange integrals or one should not try to impose variationality in developing accurate and versatile “JK-only” functionals.
Another class of functionals – Piris natural orbital functionals (PNOF’s) [cf. (51)] – are also of “JK-only” type. They have been proposed by employing a cumulant expansion given in (28) and approximating two-electron reduced density matrix elements in terms of the natural occupation numbers. Reconstruction of 2-RDM in terms of 1-RDM is guided by N-representability conditions for 2-RDM. PNOFs, especially one of the latest ones, PNOF5, have been extensively tested for predicting energy and different properties of molecules of diversified electronic structure. PNOF5 is particularly successful in describing systems for which static electron correlation is nonnegligible. At the same time, it has become apparent that this functional misses an important part of dynamic correlation, which seriously plagues its performance for some systems. These findings are perfectly understandable because, as a variational “JK-only” functional, PNOF5 inherits the aforementioned limitations of the best “JK-only” functional. Thinking about the possible ways of developing functionals based on reconstructing 2-RDM in terms of 1-RDM, it is evident that retaining solely Coulomb and exchange integrals in the functional and reconstructing N-representable 2-RDM would lead to a variational functional deficient in accounting for dynamic electron correlation. However, N-representability conditions for 2-RDM employed in developing novel functionals are of necessary but insufficient character. Consequently, functionals resulting from employing a reconstructional approach are not necessarily variational. As a result, they can yield lower energy than the best “JK-only” functional if the limited “JK-only” form is properly compensated by the lack of N-representability of the underlying 2-RDM.
BBC, ELS, or PNOF functionals are orbital-dependent and, by incorporating a subtle orbital structure of the exact two-electron functional, they are more appropriate for molecular systems than for solids. A functional proposed to work mainly for extended systems is the power functional (80) with the value of the power α found empirically. Because of a simple form of the power functional its optimization is highly efficient. Taking into account that its form has been proposed rather ad hoc without imposing any exact conditions, it is remarkable how well it works for solids. The most spectacular application of the power functional is for Mott insulators which are properly predicted to be nonmetallic [84]. In general, power functional cannot compete with the BBC3 or the recent PNOF functionals in describing the electronic structure of molecular systems.
It should be mentioned that most of the functionals have been proposed in spin-restricted formulation but extensions to open-shell systems are also available [167]. So far, RDMFT for high-spin systems has been tested for only a limited set of systems.
Size-consistency is another property that a useful functional should possess. Apart from the BB or power functionals, most of the other available approximations are, in principle, not size-consistent. However, in [168] it has been shown that violation of size-consistency is negligible for BBC, AC3, and ML functionals.
Undoubtedly there has been significant progress in the last 10 years in the development of methods in RDMFT. More accurate and versatile functionals have been proposed. Surprisingly, the “JK-only” form has not yet been fully exploited and the most recent functionals, ELS [42] and PNOF6 [48], still stay within this form. As has been discussed, future functionals can either include other integrals than Coulomb and exchange or stay within the “JK-only” form at the price of abandoning variationality from the start. Unfortunately, development of RDMFT-based methods is hindered by slow advances in improving computational efficiency of optimization algorithms for density matrix functionals. The lack of sufficiently fast methods has not allowed for application of the existing functionals to systems consisting of more than a few tens of electrons. Only the very recently proposed local-RDMFT approach [104] holds any promise of extending limits of the size of systems that can be treated with RDMFT by at least one order of magnitude.
The practical use of a time-dependent version of RDMFT has recently been explored to calculate excitation energies and other frequency-dependent response properties. A rigorous mathematical foundation for TD-RDMFT is still lacking, because the Runge–Gross proof [138] cannot straightforwardly be extended to 1-RDMs and non-local potentials. Not only is the mathematical foundation of TD-RDMFT more challenging than in TDDFT, but also the formulation of a satisfactory adiabatic approximation has turned out to be rather involved. The standard adiabatic approximation (same as in TDDFT) leads to a mismatch between the static response equations and the frequency-dependent response equations in their ω → 0 limit. This problem can be mitigated by assuming an instantaneous response of the natural occupation numbers. Nevertheless, important diagonal double excitations are still missing and a justification for the use of the PILS functional, which is not a proper 1-RDM functional, is still lacking. All these problems are solved by augmenting the time-dependent 1-RDM with explicit phase-factors for the natural spinorbitals. The TD-PINO equations have all the desired properties of a decent adiabatic approximation. In contrast to TDDFT, even in the adiabatic approximation, the TD-PINO response equations are able to describe excitations of double and bond-breaking character and charge transfer excitations are also recovered without difficulty. A confirmation of this statement has been delivered by the results for the H2 and HeH+ molecules, obtained within the adiabatic TD-PINO formalism with the PILS functional and the extended RPA results with the APSG density matrices. The latter approach has been shown to be equivalent to the adiabatic TD-PINO if the APSG functional is employed [165] and has been tested on several small molecules. Even though it recovers certain double excitations, its overall accuracy is not satisfactory. The main challenges in the time-dependent direction are to formulate a general definition for the PINO phase factors to develop functionals for N-electron systems and to establish a proper mathematical foundation.
References
Gilbert TL (1975) Hohenberg–Kohn theorem for nonlocal external potentials. Phys Rev B 12(6):2111–2120. doi:10.1103/PhysRevB.12.2111
Coleman AJ (1963) Structure of fermion density matrices. Rev Mod Phys 35(3):668–687. doi:10.1103/RevModPhys.35.668
Smith DW (1966) N-representability problem for fermion density matrices. II. The first-order density matrix with N even. Phys Rev 147(4):896–898. doi:10.1103/PhysRev.147.896
Levy M (1979) Universal variational functionals of electron-densities, first-order density-matrices, and natural spin-orbitals and solution of the v-representability problem. Proc Natl Acad Sci U S A 76(12):6062–6065. doi:10.1073/pnas.76.12.6062
Levy M (1987) Correlation energy functionals of one-matrices and Hartree–Fock densities. In: Erdahl R, Smith VHJ (eds) Density matrices and density functionals. Reidel, Dordrecht, pp 479–498
Zumbach G, Maschke K (1985) Density-matrix functional theory for the N-particle ground-state. J Chem Phys 82(12):5604–5607. doi:10.1063/1.448595
Valone SM (1980) Consequences of extending 1 matrix energy functionals from pure-state representable to all ensemble representable 1 matrices. J Chem Phys 73(3):1344–1349. doi:10.1063/1.440249
Valone SM (1980) A one-to-one mapping between one-particle densities and some normal-particle ensembles. J Chem Phys 73(9):4653–4655. doi:10.1063/1.440656
Nguyen-Dang TT, Ludeña EV, Tal Y (1985) Variation of the energy functional of the reduced first-order density operator. J Mol Struct (THEOCHEM) 120:247–264. doi:10.1016/0166-1280(85)85114-9
Donnelly RA (1979) Fundamental difference between energy functionals based on 1st-order and on 2nd-order density matrices. J Chem Phys 71(7):2874–2879. doi:10.1063/1.438678
Donnelly RA, Parr RG (1978) Elementary properties of an energy functional of first-order reduced density matrix. J Chem Phys 69(10):4431–4439. doi:10.1063/1.436433
Löwdin PO (1955) Quantum theory of many-particle systems. I. Physical interpretations by means of density matrices, natural spin-orbitals, and convergence problems in the method of configurational interaction. Phys Rev 97(6):1474–1489. doi:10.1103/PhysRev.97.1474
Hohenberg P, Kohn W (1964) Inhomogeneous electron gas. Phys Rev B 136(3B):B864–B871. doi:10.1103/PhysRev.136.B864
Lieb EH (1981) Variational principle for many-fermion systems. Phys Rev Lett 46(7):457–459. doi:10.1103/PhysRevLett.46.457
Yasuda K (2001) Correlation energy functional in the density-matrix functional theory. Phys Rev A 63:032517. doi:10.1103/PhysRevA.63.032517
Cioslowski J (2005) New constraints upon the electron–electron repulsion energy functional of the one-electron reduced density matrix. J Chem Phys 123:164106
Cioslowski J, Pernal K, Ziesche P (2002) Systematic construction of approximate one-matrix functionals for the electron–electron repulsion energy. J Chem Phys 117(21):9560–9566. doi:10.1063/1.1516804
Müller AMK (1984) Explicit approximate relation between reduced two-particle and one-particle density-matrices. Phys Lett A 105(9):446–452. doi:10.1016/0375-9601(84)91034-X
Buijse MA, Baerends EJ (2002) An approximate exchange-correlation hole density as a functional of the natural orbitals. Mol Phys 100(4):401–421. doi:10.1080/00268970110070243
Buijse MA (1991) Ph.D. thesis, Electron correlation. Fermi and Coulomb holes, dynamical and nondynamical correlation. Vrije Universiteit, Amsterdam
Frank RL, Lieb EH, Seiringer R, Siedentop H (2007) Muller’s exchange-correlation energy in density-matrix-functional theory. Phys Rev A 76(5):052517. doi:10.1103/PhysRevA.76.052517
Staroverov VN, Scuseria GE (2002) Assessment of simple exchange-correlation energy functionals of the one-particle density matrix. J Chem Phys 117(6):2489–2495. doi:10.1063/1.1491395
Herbert JM, Harriman JE (2003) Self-interaction in natural orbital functional theory. Chem Phys Lett 382(1–2):142–149. doi:10.1016/j.cplett.2003.10.057
Herbert JM, Harriman JE (2003) N-representability and variational stability in natural orbital functional theory. J Chem Phys 118(24):10835–10846. doi:10.1063/1.1574787
Cohen AJ, Baerends EJ (2002) Variational density matrix functional calculations for the corrected Hartree and corrected Hartree–Fock functionals. Chem Phys Lett 364(3–4):409–419. doi:10.1016/S0009-2614(02)01345-3
Cioslowski J, Pernal K (2001) Response properties and stability conditions in density matrix functional theory. J Chem Phys 115(13):5784–5790. doi:10.1063/1.1383292
Gritsenko O, Pernal K, Baerends E (2005) An improved density matrix functional by physically motivated repulsive corrections. J Chem Phys 122(20):204102. doi:10.1063/1.1906203
Goedecker S, Umrigar CJ (1998) Natural orbital functional for the many-electron problem. Phys Rev Lett 81(4):866–869. doi:10.1103/PhysRevLett.81.866
Goedecker S, Umrigar CJ (2000) Natural orbital functional theory. In: Cioslowski J (ed) Many-electron densities and reduced density matrices. Kluwer, New York, p 165
Lathiotakis NN, Marques MAL (2008) Benchmark calculations for reduced density-matrix functional theory. J Chem Phys 128(18):184103. doi:10.1063/1.2899328
Csanyi G, Arias TA (2000) Tensor product expansions for correlation in quantum many-body systems. Phys Rev B 61(11):7348–7352. doi:10.1103/PhysRevB.61.7348
Staroverov VN, Scuseria GE (2002) Optimization of density matrix functionals by the Hartree-Fock-Bogoliubov method. J Chem Phys 117(24):11107–11112. doi:10.1063/1.1523060
Kutzelnigg W, Mukherjee D (1999) Cumulant expansion of the reduced density matrices. J Chem Phys 110(6):2800–2809. doi:10.1063/1.478189
Kutzelnigg W (1963) Die losung des quantenmechanischen zwei-elektronenproblems durch unmittelbare bestimmung der naturlichen einelektronenfunktionen. I. Theorie. Theor Chim Acta 1(4):327–342. doi:10.1007/BF00528764
Shull H, Löwdin PO (1956) Correlation splitting in helium-like ions. J Chem Phys 25(5):1035–1040. doi:10.1063/1.1743093
Cioslowski J, Pernal K (2006) Unoccupied natural orbitals in two-electron Coulombic systems. Chem Phys Lett 430(1–3):188–190. doi:10.1016/j.cplett.2006.08.011
Sheng XW, Mentel LM, Gritsenko OV, Baerends EJ (2013) A natural orbital analysis of the long range behavior of chemical bonding and van der Waals interaction in singlet H2: the issue of zero natural orbital occupation numbers. J Chem Phys 138(16):164105. doi:10.1063/1.4801431
Giesbertz KJH, van Leeuwen R (2013) Long-range interactions and the sign of natural amplitudes in two-electron systems. J Chem Phys 139(10):104110. doi:10.1063/1.4820418
Cioslowski J, Pernal K (2000) The ground state of harmonium. J Chem Phys 113(19):8434–8443. doi:10.1063/1.1318767
Rohr DR, Pernal K, Gritsenko OV, Baerends EJ (2008) A density matrix functional with occupation number driven treatment of dynamical and nondynamical correlation. J Chem Phys 129(16):164105. doi:10.1063/1.2998201
Pernal K, Cioslowski J (2004) Phase dilemma in density matrix functional theory. J Chem Phys 120(13):5987–5992. doi:10.1063/1.1651059
Mentel LM, van Meer R, Gritsenko OV, Baerends EJ (2014) The density matrix functional approach to electron correlation: dynamic and nondynamic correlation along the full dissociation coordinate. J Chem Phys 140(21):214105. doi:10.1063/1.4879776
Piris M (2006) A new approach for the two-electron cumulant in natural orbital functional theory. Int J Quant Chem 106(5):1093–1104. doi:10.1002/qua.20858
Piris M, Lopez X, Ugalde JM (2007) Dispersion interactions within the Piris natural orbital functional theory: the helium dimer. J Chem Phys 126(21):214103. doi:10.1063/1.2743019
Piris M, Matxain JM, Lopez X, Ugalde JM (2010) Communications: accurate description of atoms and molecules by natural orbital functional theory. J Chem Phys 132(3):031103. doi:10.1063/1.3298694
Piris M, Matxain JM, Lopez X, Ugalde JM (2010) Communication: the role of the positivity N-representability conditions in natural orbital functional theory. J Chem Phys 133(11):111101. doi:10.1063/1.3481578
Piris M, Lopez X, Ruiperez F, Matxain JM, Ugalde JM (2011) A natural orbital functional for multiconfigurational states. J Chem Phys 134(16):164102. doi:10.1063/1.3582792
Piris M (2014) Interacting pairs in natural orbital functional theory. J Chem Phys 141:044107. doi:10.1063/1.4890653
Piris M, Ugalde JM (2014) Perspective on natural orbital functional theory. Int J Quant Chem 114(18, SI):1169–1175. doi:10.1002/qua.24663
Piris M (2013) A natural orbital functional based on an explicit approach of the two-electron cumulant. Int J Quant Chem 113(5, SI):620–630. doi:10.1002/qua.24020
Piris M, Matxain JM, Lopez X, Ugalde JM (2009) Spin conserving natural orbital functional theory. J Chem Phys 131(2):021102. doi:10.1063/1.3180958
Leiva P, Piris M (2006) Calculation of vertical ionization potentials with the Piris natural orbital functional. J Mol Struct (THEOCHEM) 770(1–3):45–49. doi:10.1016/j.theochem.2006.05.001
Lopez X, Piris M, Matxain JM, Ugalde JM (2010) Performance of PNOF3 for reactivity studies: X[BO] and X[CN] isomerization reactions (X = H, Li) as a case study. Phys Chem Chem Phys 12(40):12931–12934. doi:10.1039/c003379k
Lopez X, Ruiperez F, Piris M, Matxain JM, Matito E, Ugalde JM (2012) Performance of PNOF5 natural orbital functional for radical formation reactions: hydrogen atom abstraction and C-C and O-O homolytic bond cleavage in selected molecules. J Chem Theory Comput 8(8):2646–2652. doi:10.1021/ct300414t
Ruiperez F, Piris M, Ugalde JM, Matxain JM (2013) The natural orbital functional theory of the bonding in Cr2, Mo2 and W2. Phys Chem Chem Phys 15(6):2055–2062. doi:10.1039/c2cp43559d
Matxain JM, Piris M, Ruiperez F, Lopez X, Ugalde JM (2011) Homolytic molecular dissociation in natural orbital functional theory. Phys Chem Chem Phys 13(45):20129–20135. doi:10.1039/c1cp21696a
Piris M (2013) Interpair electron correlation by second-order perturbative corrections to PNOF5. J Chem Phys 139(6):064111. doi:10.1063/1.4817946
Piris M, Ruiperez F, Matxain JM (2014) Assessment of the second-order perturbative corrections to PNOF5. Mol Phys 112(5–6, SI):1–8. doi:10.1080/00268976.2013.854933
Szabados Á, Rolik Z, Tóth G, Surján PR (2005) Multiconfiguration perturbation theory: size consistency at second order. J Chem Phys 122(11):114104. doi:10.1063/1.1862235
Pernal K (2013) The equivalence of the Piris Natural Orbital Functional 5 (PNOF5) and the antisymmetrized product of strongly orthogonal geminal theory. Comput Theor Chem 1003(SI):127–129. doi:10.1016/j.comptc.2012.08.022
Surján PR (1999) An introduction to the theory of geminals. In: Surján PR (ed) Correlation and localization, vol 203, Topics in current chemistry. Springer, Berlin/Heidelberg, pp 63–88
Rassolov V (2002) A geminal model chemistry. J Chem Phys 117(13):5978–5987. doi:10.1063/1.1503773
Rassolov VA, Xu F (2007) Geminal model chemistry. IV. Variational and size consistent pure spin states. J Chem Phys 127(4):044104. doi:10.1063/1.2755738
Hurley AC, Lennard-Jones J, Pople JA (1953) The molecular orbital theory of chemical valency. A theory of paired-electrons in polyatomic molecules. Proc R Soc Lond A Math Phys Sci 220(1143):446–455. doi:10.1098/rspa.1953.0198
Kutzelnigg W (1964) Direct determination of natural orbitals and natural expansion coefficients of many-electron wavefunctions. I. Natural orbitals in geminal product approximation. J Chem Phys 40(12):3640–3647. doi:10.1063/1.1725065
Arai T (1960) Theorem on separability of electron pairs. J Chem Phys 33(1):95–98. doi:10.1063/1.1731142
Mehler EL, Reudenberg K, Silver DM (1970) Electron correlation and separated pair approximation in diatomic molecules. II. Lithium hydride and boron hydride. J Chem Phys 52(3):1181–1205. doi:10.1063/1.1673115
Matxain JM, Piris M, Uranga J, Lopez X, Merino G, Ugalde JM (2012) The nature of chemical bonds from PNOF5 calculations. Chemphyschem 13(9):2297–2303. doi:10.1002/cphc.201200205
Piris M, Matxain JM, Lopez X (2013) The intrapair electron correlation in natural orbital functional theory. J Chem Phys 139(23):234109. doi:10.1063/1.4844075
Cioslowski J, Pernal K (2002) Density matrix functional theory of weak intermolecular interactions. J Chem Phys 116(12):4802–4807. doi:10.1063/1.1446028
Cioslowski J, Ziesche P, Pernal K (2001) Description of a high-density homogeneous electron gas with the Yasuda density matrix functional. J Chem Phys 115(19):8725–8730. doi:10.1063/1.1412604
Cioslowski J, Pernal K (2002) Variational density matrix functional theory calculations with the lowest-order Yasuda functional. J Chem Phys 117(1):67–71. doi:10.1063/1.1481384
Cioslowski J, Buchowiecki M, Ziesche P (2003) Density matrix functional theory of four-electron systems. J Chem Phys 119(22):11570–11573. doi:10.1063/1.1623741
Kollmar C, Hess BA (2003) A new approach to density matrix functional theory. J Chem Phys 119(9):4655–4661. doi:10.1063/1.1590635
Kollmar C, Hess BA (2004) The structure of the second-order reduced density matrix in density matrix functional theory and its construction from formal criteria. J Chem Phys 120(7):3158–3171. doi:10.1063/1.1634554
Kollmar C (2004) The “JK-only” approximation in density matrix functional and wave function theory. J Chem Phys 121(23):11581–11586. doi:10.1063/1.1819319
Pernal K (2010) Long-range density-matrix-functional theory: application to a modified homogeneous electron gas. Phys Rev A 81(5):052511. doi:10.1103/PhysRevA.81.052511
Rohr DR, Toulouse J, Pernal K (2010) Combining density-functional theory and density-matrix-functional theory. Phys Rev A 82(5):052502. doi:10.1103/PhysRevA.82.052502
Stoll H, Savin A (1985) Density functionals for correlation energies of atoms and molecules. In: Dreizler R, da Providencia J (eds) Density functional methods in physics. Plenum, New York, pp 177–207
Toulouse J, Colonna F, Savin A (2004) Long-range-short-range separation of the electron–electron interaction in density-functional theory. Phys Rev A 70(6):062505. doi:10.1103/PhysRevA.70.062505
Goll E, Werner HJ, Stoll H (2005) A short-range gradient-corrected density functional in long-range coupled-cluster calculations for rare gas dimers. Phys Chem Chem Phys 7(23):3917–3923. doi:10.1039/b509242f
Lathiotakis NN, Helbig N, Gross EKU (2007) Performance of one-body reduced density-matrix functionals for the homogeneous electron gas. Phys Rev B 75(19):195120. doi:10.1103/PhysRevB.75.195120
Cioslowski J, Pernal K (2000) Description of a homogeneous electron gas with simple functionals of the one-particle density matrix. Phys Rev A 61(3):034503
Sharma S, Dewhurst JK, Lathiotakis NN, Gross EKU (2008) Reduced density matrix functional for many-electron systems. Phys Rev B 78(20):201103. doi:10.1103/PhysRevB.78.201103
Lathiotakis NN, Helbig N, Zacarias A, Gross EKU (2009) A functional of the one-body-reduced density matrix derived from the homogeneous electron gas: performance for finite systems. J Chem Phys 130(6):064109. doi:10.1063/1.3073053
Lathiotakis NN, Sharma S, Dewhurst JK, Eich FG, Marques MAL, Gross EKU (2009) Density-matrix-power functional: performance for finite systems and the homogeneous electron gas. Phys Rev A 79(4):040501. doi:10.1103/PhysRevA.79.040501
Marques MAL, Lathiotakis NN (2008) Empirical functionals for reduced-density-matrix-functional theory. Phys Rev A 77(3):032509. doi:10.1103/PhysRevA.77.032509
Cioslowski J, Ziesche P, Pernal K (2001) On the exactness of simple natural spin-orbital functionals for a high-density homogeneous electron gas. Phys Rev B 63(20):205105
Cioslowski J, Pernal K (1999) Constraints upon natural spin orbital functionals imposed by properties of a homogeneous electron gas. J Chem Phys 111(8):3396–3400. doi:10.1063/1.479623
Sharma S, Dewhurst JK, Shallcross S, Gross EKU (2013) Spectral density and metal-insulator phase transition in Mott insulators within reduced density matrix functional theory. Phys Rev Lett 110(11):116403. doi:10.1103/PhysRevLett.110.116403
Pernal K, Baerends EJ (2006) Coupled-perturbed density-matrix functional theory equations. Application to static polarizabilities. J Chem Phys 124(1):14102. doi:10.1063/1.2137325
Lopez X, Piris M, Nakano M, Champagne B (2014) Natural orbital functional calculations of molecular polarizabilities and second hyperpolarizabilities. The hydrogen molecule as a test case. J Phys B At Mol Opt Phys 47(1):015101. doi:10.1088/0953-4075/47/1/015101
Leiva P, Piris M (2005) Assessment of a new approach for the two-electron cumulant in natural-orbital-functional theory. J Chem Phys 123(21):214102. doi:10.1063/1.2135289
Leiva P, Piris M (2005) Natural orbital functional theory: ionization potentials, equilibrium geometries and vibrational frequencies. J Mol Struct (THEOCHEM) 719(1–3):63–67. doi:10.1016/j.theochem.2005.01.023
Zarkadoula EN, Sharma S, Dewhurst JK, Gross EKU, Lathiotakis NN (2012) Ionization potentials and electron affinities from reduced-density-matrix functional theory. Phys Rev A 85(3):032504. doi:10.1103/PhysRevA.85.032504
Smith DW, Day OW (1975) Extension of Koopmans theorem. I. Derivation. J Chem Phys 62(1):113–114. doi:10.1063/1.430253
Day OW, Smith DW, Morrison RC (1975) Extension of Koopmans theorem. II. Accurate ionization energies from correlated wavefunctions for closed-shell atoms. J Chem Phys 62(1):115–119. doi:10.1063/1.430254
Morrell MM, Parr RG, Levy M (1975) Calculation of ionization-potentials from density matrices and natural functions, and long-range behavior of natural orbitals and electron-density. J Chem Phys 62(2):549–554. doi:10.1063/1.430509
Pernal K, Cioslowski J (2005) Ionization potentials from the extended Koopmans’ theorem applied to density matrix functional theory. Chem Phys Lett 412(1–3):71–75. doi:10.1016/j.cplett.2005.06.103
Piris M, Matxain JM, Lopez X, Ugalde JM (2012) The extended Koopmans’ theorem: vertical ionization potentials from natural orbital functional theory. J Chem Phys 136(17):174116. doi:10.1063/1.4709769
Gritsenko OV, Braida B, Baerends EJ (2003) Physical interpretation and evaluation of the Kohn-Sham and Dyson components of the ε-I relations between the Kohn-Sham orbital energies and the ionization potentials. J Chem Phys 119(4):1937–1950. doi:10.1063/1.1582839
Chong DP, Gritsenko OV, Baerends EJ (2002) Interpretation of the Kohn-Sham orbital energies as approximate vertical ionization potentials. J Chem Phys 116(5):1760–1772. doi:10.1063/1.1430255
Pernal K (2005) Effective potential for natural spin orbitals. Phys Rev Lett 94(23):233002. doi:10.1103/PhysRevLett.94.233002
Lathiotakis NN, Helbig N, Rubio A, Gidopoulos NI (2014) Local reduced-density-matrix-functional theory: incorporating static correlation effects in Kohn-Sham equations. Phys Rev A 90(3):032511. doi:10.1103/PhysRevA.90.032511
Lathiotakis NN, Helbig N, Rubio A, Gidopoulos NI (2014) Quasi-particle energy spectra in local reduced density matrix functional theory. J Chem Phys 141(16):164120
Helbig N, Lathiotakis NN, Albrecht M, Gross EKU (2007) Discontinuity of the chemical potential in reduced-density-matrix-functional theory. EPL 77(6):67003. doi:10.1209/0295-5075/77/67003
Helbig N, Lathiotakis NN, Gross EKU (2009) Discontinuity of the chemical potential in reduced-density-matrix-functional theory for open-shell systems. Phys Rev A 79(2):022504. doi:10.1103/PhysRevA.79.022504
Lathiotakis NN, Sharma S, Helbig N, Dewhurst JK, Marques MAL, Eich F, Baldsiefen T, Zacarias A, Gross EKU (2010) Discontinuities of the chemical potential in reduced density matrix functional theory. Z Phys Chem 224(3–4, SI):467–480. doi:10.1524/zpch.2010.6118
Cancès E, Pernal K (2008) Projected gradient algorithms for Hartree-Fock and density matrix functional theory calculations. J Chem Phys 128(13):134108. doi:10.1063/1.2888550
Giesbertz KJH, Baerends EJ (2010) Aufbau derived from a unified treatment of occupation numbers in Hartree-Fock, Kohn-Sham, and natural orbital theories with the Karush-Kuhn-Tucker conditions for the inequality constraints n i ≤ 1 and n i ≥ 0. J Comput Chem 132(19):194108. doi:10.1063/1.3426319
Piris M, Ugalde JM (2009) Iterative diagonalization for orbital optimization in natural orbital functional theory. J Comput Chem 30(13):2078–2086. doi:10.1002/jcc.21225
Requist R, Pankratov O (2008) Generalized Kohn-Sham system in one-matrix functional theory. Phys Rev B 77(23):235121. doi:10.1103/PhysRevB.77.235121
Baldsiefen T, Gross EKU (2013) Minimization procedure in reduced density matrix functional theory by means of an effective noninteracting system. Comput Theor Chem 1003(SI):114–122. doi:10.1016/j.comptc.2012.09.001
Talman JD, Shadwick WF (1976) Optimized effective atomic central potential. Phys Rev A 14(1):36–40. doi:10.1103/PhysRevA.14.36
Kümmel S, Kronik L (2008) Orbital-dependent density functionals: theory and applications. Rev Mod Phys 80(1):3–60. doi:10.1103/RevModPhys.80.3
Gidopoulos NI, Lathiotakis NN (2012) Nonanalyticity of the optimized effective potential with finite basis sets. Phys Rev A 85(5):046502. doi:10.1103/PhysRevA.85.052508
Giesbertz KJH (2010) Time-dependent one-body reduced density matrix functional theory; adiabatic approximations and beyond. Ph.D. thesis, Vrije Universiteit, Amsterdam
Appel H (2007) Time-dependent quantum many-body systems: linear response, electronic transport and reduced density matrices. Ph.D. thesis, Freie Universität, Berlin
Pernal K, Gritsenko O, Baerends EJ (2007) Time-dependent density-matrix-functional theory. Phys Rev A 75(1):012506. doi:10.1103/PhysRevA.75.012506
Pernal K, Cioslowski J (2007) Frequency-dependent response properties and excitation energies from one-electron density matrix functionals. Phys Chem Chem Phys 9(45):5956. doi:10.1039/b704797e
Pernal K, Giesbertz K, Gritsenko O, Baerends EJ (2007) Adiabatic approximation of time-dependent density matrix functional response theory. J Chem Phys 127:214101. doi:10.1063/1.2800016
Tozer DJ, Amos RD, Handy NC, Roor BO, Serrano-Andrés L (1999) Does density functional theory contribute to the understanding of excited states of unsaturated organic compounds? Mol Phys 97(7):859–868
Dreuw A, Weisman JL, Head-Gordon M (2003) Long-range charge-transfer excited states in time-dependent density functional theory require non-local exchange. J Chem Phys 119(6):2943. doi:10.1063/1.1590951
Yanai T, Tew DP, Handy NC (2004) A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem Phys Lett 393(1–3):51
Gritsenko O, Baerends EJ (2004) Asymptotic correction of the exchange-correlation kernel of time-dependent density functional theory for long-range charge-transfer excitations. J Chem Phys 121(2):655
Neugebauer J, Gritsenko O, Baerends EJ (2006) Assessment of a simple correction for the long-range charge-transfer problem in time-dependent density-functional theory. J Chem Phys 124(21):214102
Gritsenko O, van Gisbergen SJA, Görling A, Baerends EJ (2000) Excitation energies of dissociating H2: a problematic case for the adiabatic approximation of time-dependent density functional theory. J Chem Phys 113(19):8478
Giesbertz KJH, Baerends EJ (2008) Failure of time-dependent density functional theory for excited state surfaces in case of homolytic bond dissociation. Chem Phys Lett 461:338. doi:10.1016/j.cplett.2008.07.018
Maitra NT, Zhang F, Cave RJ, Burke K (2004) Double excitations within time-dependent density functional theory linear response. J Chem Phys 120(13):5932
Neugebauer J, Baerends E (2004) Vibronic coupling and double excitations in linear response time-dependent density functional calculations: dipole allowed states of N2. J Chem Phys 121(13):6155. doi:10.1063/1.1785775
Yvon J (1935) Theorie statistique des fluides et l’equation et l’equation d’etat (French). In: Actes Sientifique et Industrie, vol. 203. Hermann, Paris
Bogoliubov NN (1946) Kinetic equations. J Phys USSR 10(3):265 (in English)
Bogoliubov NN (1946) Kinetic equations. J Exp Theor Phys 16(8):691 (in Russian)
Kirkwood JG (1946) The statistical mechanical theory of transport processes I. General theory. J Chem Phys 14(3):180
Born M, Green HS (1946) A general kinetic theory of liquids. I. The molecular distribution functions. Proc R Soc Med 188(1012):10–18
Kirkwood JG (1947) The statistical mechanical theory of transport processes II. Transport in gases. J Chem Phys 15(1):72
Bogoliubov NN, Gurov KP (1947) Kinetic equations in quantum mechanics (rus.). J Exp Theor Phys 17(7):614
Runge E, Gross EKU (1984) Density-functional theory for time-dependent systems. Phys Rev Lett 52(12):997. doi:10.1103/PhysRevLett.52.997
Ruggenthaler M, van Leeuwen R (2011) Global fixed-point proof of time-dependent density-functional theory. Europhys Lett 95(1):13001. doi:10.1209/0295-5075/95/13001
Ruggenthaler M, Giesbertz KJH, Penz M, van Leeuwen R (2012) Density-potential mappings in quantum dynamics. Phys Rev A 85(5):052504. doi:10.1103/PhysRevA.85.052504
Giesbertz KJH, Baerends EJ, Gritsenko OV (2008) Charge transfer, double and bond-breaking excitations with time-dependent density matrix functional theory. Phys Rev Lett 101:033004. doi:10.1103/PhysRevLett.101.033004
Giesbertz KJH, Pernal K, Gritsenko OV, Baerends EJ (2009) Excitation energies with time-dependent density matrix functional theory: singlet two-electron systems. J Chem Phys 130(11):114104. doi:10.1063/1.3079821
Peuckert V (1978) A new approximation method for electron systems. J Phys C 11(24):4945
Giesbertz KJH, Gritsenko OV, Baerends EJ (2010) Response calculations with an independent particle system with an exact one-particle density matrix. Phys Rev Lett 105(1):013002. doi:10.1103/PhysRevLett.105.013002
Giesbertz KJH, Gritsenko OV, Baerends EJ (2010) The adiabatic approximation in time-dependent density matrix functional theory: response properties from dynamics of phase-including natural orbitals. J Chem Phys 133(17):174119. doi:10.1063/1.3499601
Requist R, Pankratov O (2011) Time-dependent occupation numbers in reduced-density-matrix-functional theory: application to an interacting Landau–Zener model. Phys Rev A 83(5):052510. doi:10.1103/PhysRevA.83.052510
Giesbertz KJH, Gritsenko OV, Baerends EJ (2014) Response calculations based on an independent particle system with the exact one-particle density matrix: polarizabilities. J Chem Phys 140(18):18A517. doi:10.1063/1.4867000
Giesbertz KJH, Gritsenko OV, Baerends EJ (2012) Time-dependent reduced density matrix functional theory. In: Marques MAL, Maitra N, Nogueira F, Gross EKU, Rubio A (eds) Fundamentals of time-dependent density functional theory, vol 837, Lecture notes in physics. Springer, Berlin, pp 485–498. doi:10.1007/978-3-642-23518-4
Requist R, Pankratov O (2010) Adiabatic approximation in time-dependent reduced-density-matrix functional theory. Phys Rev A 81(4):042519. doi:10.1103/PhysRevA.81.042519
Lehmann H (1954) Über Eigenschaften von Ausbreitungsfunktionen und Renormierungskonstanten quantisierter Felder. Nuovo Cimento 11(4):342
Requist R (2012) Hamiltonian formulation of nonequilibrium quantum dynamics: geometric structure of the Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy. Phys Rev A 86(2):022117. doi:10.1103/PhysRevA.86.02211
Kramer P, Saraceno M (1980) Geometry of the time-dependent variational principle in quantum mechanics. In: Group theoretical methods in physics. Lecture notes in physics, vol 135. Springer, Berlin, pp 112–121
Vignale G (2008) Real-time resolution of the causality paradox of time-dependent density-functional theory. Phys Rev A 77:062511. doi:10.1103/PhysRevA.77.062511
Gross EKU, Dobson JF, Petersilka M (1996) Density functional theory of time-dependent phenomena. In: Nalewajsk RF (ed) Density functional theory II, vol 181, Topics in current chemistry. Springer, Berlin, pp 81–172. doi:10.1007/BFb0016643
Rapp J, Brics M, Bauer D (2014) Equations of motion for natural orbitals of strongly driven two-electron systems. Phys Rev A 90(1):012518. doi:10.1103/PhysRevA.90.012518
Giesbertz KJH, Gritsenko OV, Baerends EJ (2012) Response calculations based on an independent particle system with the exact one-particle density matrix: excitation energies. J Chem Phys 136:094104. doi:10.1063/1.3687344
van Meer R, Gritsenko OV, Giesbertz KJH, Baerends EJ (2013) Oscillator strengths of electronic excitations with response theory using phase including natural orbital functionals. J Chem Phys 138(9):094114. doi:10.1063/1.4793740
Brics M, Bauer D (2013) Time-dependent renormalized natural orbital theory applied to the two-electron spin-singlet case: ground state, linear response, and autoionization. Phys Rev A 88(5):052514. doi:10.1103/PhysRevA.88.052514
de Morisson Faria CF, Liu X (2011) Electron–electron correlation in strong laser fields. J Opt Phys 58(13):1076. doi:10.1080/09500340.2010.543958
Becker W, Liu X, Ho PJ, Eberly JH (2012) Theories of photoelectron correlation in laser-driven multiple atomic ionization. Rev Mod Phys 84(3):1011. doi:10.1103/RevModPhys.84.1011
Lappas DG, van Leeuwen R (1998) Electron correlation effects in the double ionization of He. J Phys B 31(6):L249. doi:10.1088/0953-4075/31/6/001
Brics M, Rapp J, Bauer D (2014) Nonsequential double ionization with time-dependent renormalized-natural-orbital theory. Phys Rev A 90(5):053418. doi:10.1103/PhysRevA.90.053418
van Meer R, Gritsenko OV, Baerends EJ (2014) Excitation energies with linear response density matrix functional theory along the dissociation coordinate of an electron-pair bond in N-electron systems. J Chem Phys 140(2):024101. doi:10.1063/1.4852195
Chatterjee K, Pernal K (2012) Excitation energies from extended random phase approximation employed with approximate one- and two-electron reduced density matrices. J Chem Phys 137(20):204109. doi:10.1063/1.4766934
Pernal K, Chatterjee K, Kowalski PH (2014) How accurate is the strongly orthogonal geminal theory in predicting excitation energies? Comparison of the extended random phase approximation and the linear response theory approaches. J Chem Phys 140(1):014101. doi:10.1063/1.4855275
Rowe DJ (1968) Equations-of-motion method and the extended shell model. Rev Mod Phys 40(1):153–166. doi:10.1103/RevModPhys.40.153
Lathiotakis NN, Helbig N, Gross EKU (2005) Open shells in reduced-density-matrix-functional theory. Phys Rev A 72(3):030501. doi:10.1103/PhysRevA.72.030501
Lathiotakis NN, Gidopoulos NI, Helbig N (2010) Size consistency of explicit functionals of the natural orbitals in reduced density matrix functional theory. J Chem Phys 132(8):084105. doi:10.1063/1.3324699
Acknowledgements
The authors wish to acknowledge Dr. Ewa Pastorczak for critically reading the manuscript. KJHG gratefully acknowledges a VENI grant by the Netherlands Foundation for Research NWO (722.012.013). KP acknowledges support by the National Science Centre of Poland under grant DEC-2012/07/E/ST4/03023.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Pernal, K., Giesbertz, K.J.H. (2015). Reduced Density Matrix Functional Theory (RDMFT) and Linear Response Time-Dependent RDMFT (TD-RDMFT). In: Ferré, N., Filatov, M., Huix-Rotllant, M. (eds) Density-Functional Methods for Excited States. Topics in Current Chemistry, vol 368. Springer, Cham. https://doi.org/10.1007/128_2015_624
Download citation
DOI: https://doi.org/10.1007/128_2015_624
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22080-2
Online ISBN: 978-3-319-22081-9
eBook Packages: Chemistry and Materials ScienceChemistry and Material Science (R0)