Sparse Orthogonal Factor Analysis

Abstract

We propose a sparse orthogonal factor analysis (SOFA) procedure in which the optimal loadings and unique variances are estimated subject to additional constraint which directly requires some factor loadings to be exact zeros. More precisely, the constraint specifies the required number of zero factor loadings without any restriction on their locations. Such loadings are called sparse which gives the name of the method. SOFA solutions are obtained by minimizing a FA loss function under the sparseness constraint making use of an alternate least squares algorithm. We further present a sparseness selection procedure in which SOFA is performed repeatedly by setting the sparseness at each of a set of feasible integers. Then, the SOFA solution with the optimal sparseness can be chosen using an index for model selection. This procedure allows us to find the optimal orthogonal confirmatory factor analysis model among all possible models. SOFA and the sparseness selection procedure are assessed by simulation and illustrated with well known data sets.

1 Introduction

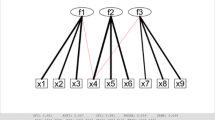
Factor analysis (FA) is a model that aims to explain the interrelationships among observed variables by a small number of latent variables called common factors. The relationships of the factors to observed variables are described by a factor loading matrix. FA is classified as exploratory (EFA) or confirmatory (CFA). In EFA, the loading matrix is unconstrained and has rotational freedom which is exploited to rotate the matrix so that some of its elements approximate zero. In CFA, some loadings are constrained to be zero and the loading matrix has no rotational freedom [9].

One refers to a loading matrix with a number of exactly zero elements as being sparse, which is an indispensable property for loadings to be interpretable. In EFA, a loading matrix is rotated toward a sparse matrix, but the literal sparseness is not attained, since rotated loadings cannot exactly be equal to zero. Thus, the user must decide which of them can be viewed as approximately zeros. On the other hand, some loadings are fixed exactly to zero in CFA. However, the problem in CFA is that the number of zero loadings and their locations must be chosen by users. That is, the users’ subjective decision is needed in both EFA and CFA.

In order to overcome these difficulties, we propose a new FA procedure, which is neither EFA nor CFA. The optimal orthogonal factor solution is estimated such that it has a sparse loading matrix with a suitable number of zero elements. Note that, their locations are also estimated in an optimal way. The procedure to be proposed consists of the following two stages:

• (a) The optimal solution is obtained for a specified number of zero loadings.

• (b) The optimal number of zero loadings is selected among possible numbers.

Stages (a) and (b) would be described in Sects. 2–4, respectively.

In the area of principal component analysis (PCA), many procedures, called sparse PCA, have been proposed in the last decade (e.g. [8, 13, 16]). As in our FA procedure, they obtain sparse loadings. However, besides the difference between PCA and FA, our approach does not rely on penalty functions, which is the standard way to induce sparseness in the existing sparse PCA.

2 Sparse Factor Problem

The main goal of FA is to estimate the p-variables × m-factors matrix $\boldsymbol{\Lambda }$ containing loadings and the p × p diagonal matrix $\boldsymbol{\Psi }^{2}$ including unique variances from the n-observation × p-variables (n > p) column-centered data matrix X. For this goal, FA can be formulated by a number of different objective functions, among which we choose the least squares function

$$\displaystyle{ f =\vert \vert \mathbf{X} -\mathbf{F}\boldsymbol{\Lambda }^{{\prime}}-\mathbf{U}\boldsymbol{\Psi }\vert \vert ^{2} }$$

(1)

recently utilized in several works [1, 4, 14, 15]. Here, F is the n × m matrix containing common factor scores and U is the n × p matrix of unique factor scores. The factor score matrices are constrained to satisfy

$$\displaystyle{ n^{-1}\mathbf{F}^{{\prime}}\mathbf{F} = \mathbf{I}_{ m},n^{-1}\mathbf{U}^{{\prime}}\mathbf{U} = \mathbf{I}_{ p},\,\mathrm{and}\,\mathbf{F}^{{\prime}}\mathbf{U} = _{ m}\mathbf{O}_{p} }$$

(2)

with I _m the m × m identity matrix and $_{m}\mathbf{O}_{p}$ the m × p matrix of zeros.

We propose to minimize (1) over $\mathbf{F},\mathbf{U},\boldsymbol{\Lambda }$, and $\Psi$ subject to (2) and

$$\displaystyle{ \mathit{SP}(\boldsymbol{\Lambda }) = q, }$$

(3)

where $\mathit{SP}(\boldsymbol{\Lambda })$ expresses the sparseness of $\boldsymbol{\Lambda }$, i.e., the number of its elements being zero, and q is a specified integer.

The reason for our choosing loss function (1) is that we can define

$$\displaystyle{ \mathbf{A} = n^{-1}\mathbf{X}^{{\prime}}\mathbf{F} }$$

(4)

to decompose (1) as

$$\displaystyle{ f =\vert \vert \mathbf{X} -\mathbf{FA}^{{\prime}}-\mathbf{U}\boldsymbol{\Psi } - (\mathbf{F}\boldsymbol{\Lambda }^{{\prime}}-\mathbf{FA}^{{\prime}})\vert \vert ^{2} =\vert \vert \mathbf{X} -\mathbf{FA}^{{\prime}}-\mathbf{U}\Psi \vert \vert ^{2} + n\vert \vert \boldsymbol{\Lambda } -\mathbf{A}\vert \vert ^{2}. }$$

(1')

This equality is derived from the fact that $(\mathbf{X} -\mathbf{FA}^{{\prime}}-\mathbf{U}\Psi )^{{\prime}}(\mathbf{F}\boldsymbol{\Lambda }^{{\prime}}-\mathbf{FA}^{{\prime}}) = n\mathbf{A}\boldsymbol{\Lambda }^{{\prime}}- n\mathbf{AA}^{{\prime}}- n\mathbf{A}\boldsymbol{\Lambda }^{{\prime}} + n\mathbf{AA}^{{\prime}} = _{p}\mathbf{O}_{p}$ is given using (2) and (4). In (1′) only a simple function $\vert \vert \boldsymbol{\Lambda } -\mathbf{A}\vert \vert ^{2}$ is relevant to $\boldsymbol{\Lambda }$ and thus can be easily minimized over $\boldsymbol{\Lambda }$ subject to (3) as seen in the next section. It is difficult for other objective functions of FA to be rewritten into simple forms as (1′). For example, the likelihood function for FA includes the determinant of a function of $\boldsymbol{\Lambda }$ which is difficult to handle.

3 Algorithm

For minimizing (1) subject to (2) and (3), we consider alternately iterating the update of each parameter matrix.

First, let us consider updating $\boldsymbol{\Lambda }$ so that (1) or (1′) is minimized subject to (3) while $\mathbf{F},\mathbf{U}$, and $\Psi$ are kept fixed. This amounts to minimizing $g(\boldsymbol{\Lambda }) =\vert \vert \boldsymbol{ \Lambda } -\mathbf{A}\vert \vert ^{2}$ under (3), since of (1′). Using $\boldsymbol{\Lambda } = (\lambda _{\mathit{ij}})$ and A = (a _ij ), we can rewrite $g(\boldsymbol{\Lambda })$ as

$$\displaystyle{ g(\boldsymbol{\Lambda }) =\sum \limits _{(i,j)\in \mathbf{N}}a_{\mathit{ij}}^{2} +\sum \limits _{ (i,j)\in \mathbf{N}^{\perp }}(\lambda _{\mathit{ij}} - a_{\mathit{ij}})^{2} \geq \sum \limits _{ (i,j)\in \mathbf{N}}a_{\mathit{ij}}^{2}, }$$

(5)

where N denotes the set of the q pairs of (i,  j) for the loadings λ _ij to be zero and N ^⊥ is the complement to N. The inequality in (5) shows that $g(\boldsymbol{\Lambda })$ attains its lower limit $\Sigma _{(i,j)\in N}a_{\mathit{ij}}^{2}$ when the loading λ _ij with ($i,j) \in \mathbf{N}^{\perp }$ is set equal to a _ij . Further, the limit $\Sigma _{(i,j)\in N}a_{\mathit{ij}}^{2}$ is minimal when N contains the (i, j) for the q smallest $a_{\mathit{ij}}^{2}$ among all squared elements of A. The optimal $\boldsymbol{\Lambda } = (\lambda _{\mathit{ij}})$ is thus given by

$$\displaystyle{ \lambda _{\mathit{ij}} = \left \{\begin{array}{cc} 0 &\mathrm{iff}\,a_{\mathit{ij}}^{2} \leq a_{[q]}^{2} \\ a_{\mathit{ij}} & \mathrm{otherwise}\\ \end{array} \right. }$$

(6)

with $a_{[q]}^{2}$ the $q$-th smallest value among all $a_{\mathit{ij}}^{2}$.

Next, let us consider the update of the diagonal matrix $\Psi$. Substituting (2) in (1) simplifies the objective function to

$$\displaystyle{ f = n\mathrm{tr}\mathbf{S} + n\mathrm{tr}\boldsymbol{\Lambda }\boldsymbol{\Lambda }^{{\prime}} + n\mathrm{tr}\boldsymbol{\Psi }^{2} - 2n\mathrm{tr}\mathbf{X}^{{\prime}}\mathbf{F}\boldsymbol{\Lambda }^{{\prime}}- 2\mathrm{tr}\mathbf{X}^{{\prime}}\mathbf{U}\boldsymbol{\Psi } }$$

(1'')

with $\mathbf{S} = n^{-1/2}\mathbf{X}^{{\prime}}\mathbf{X}$ the sample covariance matrix. Since (1″) can further be rewritten as $\vert \vert n^{1/2}\boldsymbol{\Psi } - n^{-1/2}\mathrm{diag}(\mathbf{X}^{{\prime}}\mathbf{U})\vert \vert ^{2} + c$ with c a constant irrelevant to $\boldsymbol{\Psi }$, the minimizer is found to be given by

$$\displaystyle{ \boldsymbol{\Psi } = \mathrm{diag}(n^{-1}\mathbf{X}^{{\prime}}\mathbf{U}), }$$

(7)

when F, U, and $\boldsymbol{\Lambda }$ are considered fixed.

Finally, let us consider minimizing (1) over n × (m + p) block matrix [F, U] subject to (2) with $\boldsymbol{\Psi }$ and $\boldsymbol{\Lambda }$ kept fixed. We note that (1″) is rewritten as $f = c^{{\ast}}- 2n\mathrm{tr}\mathbf{B}^{{\prime}}\mathbf{X}^{{\prime}}[\mathbf{F},\mathbf{U}]$ with $\mathbf{B} = [\boldsymbol{\Lambda },\mathbf{U}]$ an p × (m + p) matrix and c ^∗ a constant irrelevant to [F, U]. As proved in Appendix 1, f is minimized for

$$\displaystyle{ n^{-1}\mathbf{X}^{{\prime}}[\mathbf{F},\mathbf{U}] = \mathbf{B}^{{\prime}+}\mathbf{Q}\boldsymbol{\Delta }\mathbf{Q}^{{\prime}}, }$$

(8)

where B ^′+ is the Moore-Penrose inverse of B ^′ and $\mathbf{Q}\boldsymbol{\Delta }\mathbf{Q}^{{\prime}}$ is obtained through the eigenvalue decomposition (EVD) of B ^′ SB:

$$\displaystyle{ \mathbf{B}^{{\prime}}\mathbf{SB} = \mathbf{Q}\boldsymbol{\Delta }^{2}\mathbf{Q}^{{\prime}}, }$$

(9)

with $\mathbf{Q}^{{\prime}}\mathbf{Q} = \mathbf{I}_{p}$ and $\Delta ^{2}$ the positive definite diagonal matrix. Rewriting (8) as $[n^{-1}\mathbf{X}^{{\prime}}\mathbf{F},\,n^{-1}\mathbf{X}^{{\prime}}\mathbf{U}] = \mathbf{B}^{{\prime}+}\mathbf{Q}\boldsymbol{\Delta }Q^{{\prime}}$ and comparing it with (4) and (7), one finds:

$$\displaystyle{ \qquad \mathbf{A} = \mathbf{B}^{{\prime}+}\mathbf{Q}\boldsymbol{\Delta }\mathbf{Q}^{{\prime}}\mathbf{H}_{ m} }$$

(4')

$$\displaystyle{ \boldsymbol{\Psi } = \mathrm{diag}(\mathbf{B}^{{\prime}+}\mathbf{Q}\boldsymbol{\Delta }\mathbf{Q}^{{\prime}}\mathbf{H}^{p}) }$$

(7')

where $\mathbf{H}_{m} = [\mathbf{I}_{m},\,_{m}\mathbf{O}_{p}]^{{\prime}}$ and $\mathbf{H}^{p} = [_{p}\mathbf{O}_{m},\,\mathbf{I}_{p}]^{{\prime}}$.

The above equations show that $\boldsymbol{\Lambda }$ and $\boldsymbol{\Psi }$ can be updated if only the sample covariance matrix $\mathbf{S}(= n^{-1}\mathbf{X}^{{\prime}}\mathbf{X})$ is available. In other words, the updating of [F, U] can be avoided when the original data matrix X is not given, That is, the decomposition (9) gives the matrices Q and $\boldsymbol{\Delta }$ needed in (4′) and (7′), with (4′) being used for (6). Further, the resulting loss function value can be computed without the use of X:  (6) implies $\boldsymbol{\Lambda }^{{\prime}}\mathbf{A} =\boldsymbol{ \Lambda }^{{\prime}}\boldsymbol{\Lambda }$, and substituting this, (4), and $\mathbf{B} = [\boldsymbol{\Lambda },\mathbf{U}]$ into (1″) leads to $f = n\mathrm{tr}\mathbf{S} + n\mathrm{tr}\boldsymbol{\Lambda }\boldsymbol{\Lambda }^{{\prime}}- 2n\mathrm{tr}\boldsymbol{\Lambda }^{{\prime}}\mathbf{A}-n\mathrm{tr}\boldsymbol{\Psi }^{2} = n\{\mathrm{tr}\mathbf{S}-\mathrm{tr}(\boldsymbol{\Lambda \Lambda }^{{\prime}} +\boldsymbol{ \Psi }^{2})\} = n(\mathrm{tr}\mathbf{S}-\mathrm{tr}\mathbf{BB}^{{\prime}})$. Then, the standardized loss function value

$$\displaystyle{ f_{S}(\mathbf{B}) = 1 -\mathrm{tr}\mathbf{BB}^{{\prime}}/\mathrm{tr}\mathbf{S}, }$$

(10)

which takes a value within [0,1], can be used for convenience instead of f.

The optimal $\mathbf{B} = [\boldsymbol{\Lambda },\,\boldsymbol{\Psi }]$ is thus given by the following algorithm:

Step 1.:

Initialize $\boldsymbol{\Lambda }$ and $\boldsymbol{\Psi }$.

Step 2.:

Set $\mathbf{B} = [\boldsymbol{\Lambda },\,\boldsymbol{\Psi }]$ to perform EVD (9).

Step 3.:

Obtain A by (4′) to update $\boldsymbol{\Lambda }$ with (6).

Step 4.:

Update $\boldsymbol{\Psi }$ with (7′).

Step 5.:

Finish if convergence is reached; otherwise, go back to Step 2.

The convergence of the updated parameters in Step 5 is defined as the decrease of (10) being less than 0.1⁷. To avoid missing the global minimum, we run the algorithm multiple times with random start in Step 1. The procedure for selection of the optimal solution is described in Appendix 2. We denote the resulting solution of B as $\hat{\mathbf{B}}_{q} = [\boldsymbol{\hat{\Lambda }}_{q},\,\boldsymbol{\hat{\Psi }}_{q}]$, where the subscript q indicates the particular number of zeros used in (3).

4 Sparseness Selection

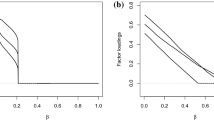
Sparseness can be restated as parsimony: the greater $\mathit{SP}(\boldsymbol{\Lambda })$ implies that fewer parameters are to be estimated and the resulting loss function value is greater. Thus, the sparseness selection means to choose a FA model with the optimal combination of the attained loss function value and parsimony. For such model selection, we can use the information criteria [10] which are defined using maximum likelihood (ML) estimates. Although ML method is not used in our algorithm, we assume that $\hat{\mathbf{B}}_{q} = [\boldsymbol{\hat{\Lambda }}_{q}$, $\boldsymbol{\hat{\Psi }}_{q}$] is equivalent to the ML-CFA solution which maximizes log likelihood $L(\boldsymbol{\Lambda },\boldsymbol{\Psi }) = -0.5n\{\log \vert \boldsymbol{\Lambda \Lambda }^{{\prime}} +\boldsymbol{ \Psi }^{2}\vert + \mathrm{tr}\mathbf{S}(\boldsymbol{\Lambda \Lambda }^{{\prime}} +\boldsymbol{ \Psi }^{2})^{-1}\}$ with the locations of the zero loadings constrained to be those of $\boldsymbol{\hat{\Lambda }}_{q}$. This assumption would be validated empirically in the next section. Under this assumption, we propose to use an information criterion BIC [10] for choosing the optimal q. BIC can be expressed as

$$\displaystyle{ \mathit{BIC}(q) = -2L(\boldsymbol{\hat{\Lambda }}_{q},\boldsymbol{\hat{\Psi }}_{q}) - q\log n + c^{\#} }$$

(11)

for $\hat{\mathbf{B}}_{q}$ with c ^# a constant irrelevant to q. The optimal sparseness is thus defined as

$$\displaystyle{ \hat{q} =\mathop{ \arg \min }\limits _{q_{\min }\leq q\leq q_{\max }}\mathit{BIC}(q) }$$

(12)

and $\hat{\mathbf{B}}_{\hat{q}}$ is chosen as the final solution $\hat{\mathbf{B}}$. Here, we set $q_{\min } = m(m-$ 1)/2, since it prevents $\boldsymbol{\Lambda }$ from rotational indeterminacy if q goes below it. On the other hand, we set $q_{\max } = p(m-$ 1), since it prevents $\boldsymbol{\Lambda }$ from having an empty column if q were greater than the limit.

5 Simulation Study

We performed a simulation study to assess the proposed procedure with respect to (1) identifying the true sparseness and the locations of zero loadings; (2) goodness of the recovery of parameter values; (3) sensitivity to local minima; (4) whether SOFA solutions are equivalent to the solutions of the ML-CFA procedure with the locations of the zero elements in $\boldsymbol{\Lambda }$ set to those obtained by SOFA.

We used the five types of the true $\boldsymbol{\Lambda }$ shown in Table 1, which are desired to be possessed by FA solutions. The first three types have simple structure, while the remaining two have bi-factor simple structure as defined by [6]. For each type, we generated 40 sets of $\{\boldsymbol{\Lambda },\,\boldsymbol{\Psi },\,\mathbf{S}\}$ by the following steps: (1) each diagonal element of $\boldsymbol{\Psi }$ was set to $u(0.1^{1/2},\,0.7^{1/2})$, where u(α, β) denotes a value drawn from the uniform distribution of the range [α, β]. (2) A nonzero value in $\boldsymbol{\Lambda }$ was set to u(0.4, 1), while an element denoted by “r” in Table 1 was randomly set to zero or u(0.4, 1). (3) $\boldsymbol{\Lambda }$ was normalized so as to satisfy diag($\boldsymbol{\Lambda }\boldsymbol{\Lambda }^{{\prime}} +\boldsymbol{ \Psi }^{2}) = \mathbf{I}_{p}$. (4) Setting n = 200p, we sampled each row of X from the centered p-variate normal distribution with its covariance matrix $\boldsymbol{\Lambda \Lambda }^{{\prime}} +\boldsymbol{ \Psi }^{2}$. (5) Inter-variable correlation matrix S was obtained from X. For the resulting data sets, we carried out SOFA: its algorithm was run multiple times for each of $q = q_{\min },\ldots,q_{\max }$ until the two equivalently optimal solutions are found by the procedure in Appendix 2. As done there, we use $L_{q}$ for the number of runs necessitated.

Table 1 Three loading matrices of simple structure (left) and two ones of bi-factor structure (right), with nonzero and zero elements denoted by # and blank cells, respectively

To asses the sensitivity of SOFA to local minima, we counted L _q and averaged it over q for each data set. The sensitivity is indicated by L _q as described in Appendix 2. The quartiles of the averaged L _q values over 200 data sets were 89, 120, and 155: the second quartile 120 implies that the $120 - 2 = 118$ solutions (except two equivalently optimal solutions) are local minimizers among 120 solutions for a half of data sets. This demonstrates high sensitivity to local minima. Nevertheless, good performances of the proposed procedure are shown next.

For each of 200 data sets, we obtained some index values to assess the correctness of the $\hat{q}$ selected by BIC and the corresponding optimal solution $\hat{\mathbf{B}}_{\hat{q}} = [\boldsymbol{\hat{\Lambda }}_{\hat{q}}$, $\boldsymbol{\hat{\Psi }}_{\hat{q}}$]. The percentiles of the index values over the 200 cases are shown in Panels (A), (B), and (C) of Table 2. The first index is $\mathrm{BES} = (\hat{q} - q)/q$ which assesses the relative bias of the estimated sparseness from the true q. The percentiles in Panel (A) show that sparseness was satisfactorily estimated, though it tended to be underestimated. The indices R ₀₀ and R _{# #} in Panel (B) are the rates of the zero and non-zero elements in the true $\boldsymbol{\Lambda }$ correctly identified by $\boldsymbol{\hat{\Lambda }}$. Panel (B) shows that non-zero elements have been exactly identified. The indices in Panel (C) are mean absolute differences $\vert \vert \boldsymbol{\hat{\Lambda }}_{\hat{q}} -\boldsymbol{\Lambda }\vert \vert _{1}/(\mathit{pm})$ and $\vert \vert \boldsymbol{\hat{\Psi }}_{\hat{q}}^{2} -\boldsymbol{ \Psi }^{2}\vert \vert _{1}/p$, where $\vert \vert \cdot \vert \vert _{1}$ denotes the sum of the absolute values of the elements of the argument. The percentiles of the differences show that the parameter values were recovered very well.

Table 2 Percentiles of index values for assessing the SOFA solutions

For each data set, ML-CFA was also performed with the locations of the zero loadings fixed at those in $\hat{\Lambda }_{\hat{q}}$. For ML-CFA, we used the EM algorithm with [2] formulas. Let $\boldsymbol{\Lambda }_{\mathrm{ML}}$ and $\boldsymbol{\Psi }_{\mathrm{ML}}$ denote the resulting $\boldsymbol{\Lambda }$ and $\boldsymbol{\Psi }$. Panel (D) in Table 2 shows the percentiles of $\vert \vert \boldsymbol{\hat{\Lambda }}_{\hat{q}} -\boldsymbol{\Lambda }_{\mathrm{ML}}\vert \vert _{1}/(\mathit{pm})$ and $\vert \vert \boldsymbol{\hat{\Psi }}_{\hat{q}}^{2} -\boldsymbol{ \Psi }_{\mathrm{ML}}^{2}\vert \vert _{1}/p$. There, we find that the differences were small enough to be ignored, which validate the use of ML-based BIC in SOFA.

6 Examples

We illustrate SOFA with two famous examples. The first one is a real data set known as [6] twenty four psychological test data, which contain the scores of n = 145 students for p = 24 problems. The correlation matrix is available in [5], p. 124. From the EFA solution for the matrix, [7] found bi-factor structure using their proposed bi-factor rotation with m = 4. We analyzed the correlation matrix by SOFA with the same number of factors. The optimal $\mathit{SP}(\boldsymbol{\Lambda }) = 48$ was found by BIC. The solution is shown in Table 3. Its first column shows the abilities made up by [5], p. 125, which are considered necessary for solving the corresponding groups of problems. This grouping can be used to give clear interpretation of $\boldsymbol{\hat{\Lambda }}$: the first, second, third, and fourth factors stand in turn for the general ability related to all problems, the skill of verbal processing, the speed of performances, and the accuracy of memory, respectively. It matches the bi-factor structure found by [7]. However, our result allows us to interpret the factors simply by observing the nonzero loadings, while [7] obtain reasonable interpretation only after considering the loadings greater than or equal to 0.3 in magnitude. This choice is subjective and likely to lead to suboptimal and misleading solutions.

Table 3 Solution for 24 psychological test data with empty cells standing for zero

The second example considers [12] box problem which gives simulated data traditionally used as a benchmark for testing FA procedures. As described in Appendix 3, we followed [12] to generate 20 variables using functions of 3 × 1 common factor vector [x, y, z]^′, with the functions defined as in the first column of Table 4. Those procedures gave the correlation matrix (Table 5) to be analyzed. The ideal solution for this problem is the one such that variables load the factor(s) used for defining the variables: for example, the fourth variable should ideally load x and y. The SOFA solution with $\mathit{SP}(\boldsymbol{\Lambda }) = 27$ selected by BIC is shown in Table 4, where we find that the ideal loadings were obtained.

Table 4 Solution for the box problem with empty cells standing for zero

Table 5 Correlation coefficients multiplied by 100 for the box problem

7 Discussions

In this paper, we proposed a new FA procedure named SOFA (sparse orthogonal factor analysis), which is neither EFA nor CFA. In SOFA, FA loss function (1) is minimized over loadings and unique variances subject to the direct sparseness constraint on loadings. This minimization algorithm alternately estimates the locations of the zero loadings and the values of the nonzero ones. Further, the best sparseness is selected using BIC. The simulation study demonstrated that the true sparseness and parameter values are recovered well by SOFA, and the examples illustrated that SOFA produces reasonable sparse solutions.

As stated already, a weakness of the rotation methods in EFA is that the user must decide which rotated loadings can be viewed as potential zeros. Another weakness of the rotation methods is that they do not involve the original data, because the rotation criteria are functions of the loading matrix only [3]. Thus, the rotated loadings may possess structure which is not relevant to the true loadings of the underlying data. In contrast, SOFA minimizes (1) so that the FA model is optimally fitted to the data set under the sparseness constraint, and thus can find the loadings underlying the data set with a suitable sparseness.

Our proposed procedure of SOFA with the sparseness selection by BIC allows us to find an optimal orthogonal solution with the best sparseness. If one tries to find that optimal solution by CFA without any prior knowledge about the solution, CFA must be performed over all possible models, i.e., over all possible locations of q zero loadings with changing q from q _min to q _max. That is, the number of the models to be tested is so enormous that it is unfeasible. An optimal model can, however, be found by our procedure. It is thus regarded as an automatic finder of an optimal orthogonal CFA model.

A drawback of SOFA is that its solutions are restricted to the orthogonal ones without inter-factor correlations. It thus remains for future studies to develop a sparse oblique FA procedure with the correlations included in parameters.

Appendices

Appendix 1: Update of $\mathit{n}^{-1}X^{{\prime}}$ [F,U]

We prove that $c^{{\ast}}-\mathrm{tr}\mathbf{B}^{{\prime}}\mathbf{X}^{{\prime}}[\mathbf{F},\mathbf{U}]$ is minimized, or equivalently, $\mathrm{tr}\mathbf{B}^{{\prime}}\mathbf{X}^{{\prime}}[\mathbf{F},\mathbf{U}]$ is maximized, for (8) subject to (2), supposing that the rank of XB is p. First, let us consider maximizing $\mathrm{tr}\mathbf{B}^{{\prime}}\mathbf{X}^{{\prime}}[\mathbf{F},\mathbf{U}]$ under the constrains in (2) summarized in $n^{-1}[\mathbf{F},\mathbf{U}]^{{\prime}}[\mathbf{F},\mathbf{U}] = \mathbf{I}_{m+p}$. The maximizer is given by

$$\displaystyle{ [\mathbf{F},\mathbf{U}] = n^{1/2}\mathbf{PQ}^{{\prime}} + n^{1/2}\mathbf{P}_{ \perp }\mathbf{Q}_{\perp }^{{\prime}} }$$

(13)

through the singular value decomposition of n × (m + p) matrix $n^{-1/2}\mathbf{XB}$;

$$\displaystyle{ n^{-1/2}\mathbf{XB} = [\mathbf{P},\mathbf{P}_{ \perp }]\left [\begin{array}{ll} \boldsymbol{\Delta }&\\ &_{m}\mathbf{O}_{m}\\ \end{array} \right ]\left [\begin{array}{c} \mathbf{Q}' \\ \mathbf{Q}'_{\perp }\\ \end{array} \right ] = \mathbf{P}\boldsymbol{\Delta }\mathbf{Q}^{{\prime}}. }$$

(14)

Here, [$\mathbf{P},\mathbf{P}_{\perp }$] and [$\mathbf{Q},\mathbf{Q}_{\perp }$] are n × (p + m) and p × (p + m) orthonormal matrices, respectively, whose blocks P and Q consist of p columns, and $\boldsymbol{\Delta }$ is a p × p diagonal matrix [11]. Next, let us note that the rank of XB being p implies B being of full-row rank, which leads to $\mathbf{BB}^{+} = \mathbf{I}_{p}$. Using this fact in (14) we have $n^{-1}\mathbf{X} = n^{-1/2}\mathbf{P}\boldsymbol{\Delta }\mathbf{Q}^{{\prime}}\mathbf{B}^{+}$, which is transposed and post-multiplied by (13) to give (8), since of $\mathbf{P}^{{\prime}}\mathbf{P}_{\perp } = _{p}\mathbf{O}_{p-m}$. Further, (8) is obtained with (9) followed from (14).

Appendix 2: Multiple Runs Procedure

The initial $\boldsymbol{\Lambda }$ and $\boldsymbol{\Psi }$ in the SOFA algorithm (Sect. 3) are chosen randomly. Each diagonal element of $\boldsymbol{\Psi }$ is initialized at u(0. 1^1∕2, 0. 7^1∕2) with u(α, β) a value drawn from the uniform distribution of the range $[\alpha,\,\beta ]$. Each loading of $\boldsymbol{\Lambda } = (\lambda _{\mathit{ij}})$ is set to u(0. 3, 1), and the value $\lambda _{[q]}^{2}$ is obtained that is the q-th smallest among all $\lambda _{\mathit{ij}}^{2}$, which is followed by transforming the loadings with $\lambda _{\mathit{ij}}^{2} \leq \lambda _{[q]}^{2}$ into zeros. Further, the initial $\boldsymbol{\Lambda }$ is normalized so as to satisfy diag($\boldsymbol{\Lambda }\boldsymbol{\Lambda }^{{\prime}} +\boldsymbol{ \Psi }^{2}) = \mathbf{I}_{p}$.

Let $\mathbf{B}_{\mathit{ql}} = [\boldsymbol{\Lambda }_{\mathit{ql}},\,\boldsymbol{\Psi }_{\mathit{ql}}$] denote the solution of B resulting from the l-th run of the SOFA algorithm for $\mathit{SP}(\boldsymbol{\Lambda })$ set at a specified q, with l = 1, …, L _q . We regard $\mathbf{B}_{\mathit{ql}{\ast}} = [\boldsymbol{\Lambda }_{\mathit{ql}{\ast}},\,\boldsymbol{\Psi }_{\mathit{ql}{\ast}}]$ with $l^{{\ast}} =\arg \min _{1\leq l\leq L_{q}}f_{S}(\mathbf{B}_{\mathit{ql}})$ as the optimal solution $\hat{\mathbf{B}}_{q}$, and define B _ql being a local minimizer as $\Delta (\mathbf{B}_{\mathit{ql}},\,\mathbf{B}_{\mathit{ql}{\ast}}) = 0.5(\vert \vert \boldsymbol{\Lambda }_{\mathit{ql}} -\boldsymbol{\Lambda }_{\mathit{ql}{\ast}}\vert \vert _{1}/mp +\vert \vert \boldsymbol{ \Psi }_{\mathit{ql}} -\boldsymbol{ \Psi }_{\mathit{ql}{\ast}}\vert \vert _{1}/p) > 0.1^{3}$, with $\vert \vert \cdot \vert \vert _{1}$ denoting the sum of the absolute values of the elements of the argument. Here, the suitable L _q (number of runs) is unknown beforehand. We thus employ a strategy in which L _q is initialized at an integer and increased until $\{\mathbf{B}_{\mathit{ql}};\,l = 1,\ldots,L_{q}\}$ include the two equivalently optimal solutions B _ql∗ and $\mathbf{B}_{\mathit{ql}^{\# }}$ satisfying $\Delta (\mathbf{B}_{\mathit{ql}{\ast}},\,\mathbf{B}_{\mathit{ql}^{\#}}) \leq 0.1^{3}$ and $l^{{\ast}} = \mathrm{argmin}_{1\leq l\leq L}f(\boldsymbol{\Theta }_{l})$ with $l^{\#}\neq l^{{\ast}}$. This procedure is formally stated as follows:

• 1. Set L _q  = 50 and obtain $l^{{\ast}} =\arg \min _{1\leq l\leq L_{q}}f_{S}(\mathbf{B}_{\mathit{ql}})$

• 2. Go to 6, if $\Delta (\mathbf{B}_{\mathit{ql}{\ast}}$, $\mathbf{B}_{\mathit{ql}^{\#}}) \leq 0.1^{3}$ is satisfied for $l^{{\ast}}\neq l^{\#}$; otherwise, go to 3.

• 3. Set $L_{q}:= L_{q} + 1$, and let $\mathbf{B}_{\mathit{ql}^{\#}}$ be the output from another run.

• 4. Exchange $\mathbf{B}_{\mathit{ql}{\ast}}$ for $\mathbf{B}_{\mathit{ql}^{\#}}$ if $f_{S}(\mathbf{B}_{\mathit{ql}^{\#}}) < f_{S}(\mathbf{B}_{\mathit{ql}{\ast}})$.

• 5. Go to 6 if $\Delta (\mathbf{B}_{\mathit{ql}{\ast}}$, $\mathbf{B}_{\mathit{ql}^{\#}}) \leq 0.1^{3}$ or L _q  = 200; otherwise, go back to 3.

• 6. Finish with $\hat{\mathbf{B}}_{q}$ set at B _ql∗.

In this procedure, except B _ql∗ and $\mathbf{B}_{\mathit{ql}^{\#}}$, the rest L _q − 2 solutions are local minimizers, thus the L _q value clearly indicates the sensitivity to local minima.

Appendix 3: Box Problem Data

In the box problem, the 3 × 1 common factor score vector $\mathbf{f} = [x,\ y,\ z]^{{\prime}}$ is supposed to yield 20 × 1 observation vector x with $\mathbf{x} =\boldsymbol{\phi } (x,\ y,\ z) +\boldsymbol{ \Psi }\mathbf{u}$, where $\boldsymbol{\phi }(x,y,z)$ is the vector function with its 20 elements defined as in the first column of Table 4. The original [12] box data matrix is 20 × 20, whose rows are 20 realizations of $\mathbf{x}^{{\prime}} =\boldsymbol{\phi } ^{{\prime}}(x,y,z)$ without unique factor $\boldsymbol{\Psi }\mathbf{u}$. Here, x, y, z was set to the lengths, widths, and heights of boxes, from which the name of the problem originates. However, the 20 × 20 data matrix does not suit the cases of n > p considered in this paper. We thus simulated the 400 × 20 X based on $\mathbf{x} =\boldsymbol{\phi } (x,y,z) +\boldsymbol{ \Psi }\mathbf{u}$ with the following steps: First, we set x, y, and z at u(1, 10) to have $400 \times 20\boldsymbol{\Phi }$ whose rows are the realizations of $\boldsymbol{\phi }^{{\prime}}(x,y,z)$. Second, we sampled each element of u from the standard normal distribution to have 400 × 20 U with its rows u ^′ and set the diagonal elements of $\boldsymbol{\Psi }$ to 0. 1^1∕2. Third, we standardized the columns of $\boldsymbol{\Phi }$ so that their average and variance were zero and one, and had $\mathbf{X} =\boldsymbol{ \Phi } + \mathbf{U}\boldsymbol{\Psi }$ whose inter-column correlations are shown in Table 5.